
TOWARDS AVERAGE-CASE ALGORITHMS FOR ABSTRACT
ARGUMENTATION
Samer Nofal, Paul Dunne and Katie Atkinson
Computer Science Department, University of Liverpool, Ashton Street, Liverpool, U.K.
Keywords:
Argumentation, Reasoning, Algorithms.
Abstract:
Algorithms for abstract argumentation are created without extensive consideration of average-case analysis.
Likewise, thorough empirical studies have been rarely implemented to analyze these algorithms. This paper
presents average-case methods in the context of value-based argumentation frameworks. These methods solve
decision problems related to arguments’ acceptability. Experiments have shown indications of an improved
average-case behavior in comparison to the naive ones.
1 INTRODUCTION
Argumentation frameworks (AFs) proposed in (Dung,
1995) have proven to be a useful abstract model for
non monotonic reasoning. Since then, the interest
in this model has been increasing for its promis-
ing applications (Bench-Capon and Dunne, 2007).
However, AFs do not take into account the variable
strength of arguments. To handle that issue, several
developments have been proposed such as preference-
based argumentation (Amgoud and Cayrol, 2002)
and value-based argumentation frameworks (VAFs)
(Bench-Capon, 2003). VAFs acknowledge social val-
ues promoted by arguments that play a role in persua-
sive practical reasoning where argument’s weight is
related to the significance of its value. VAFs seem to
be applicable in various scenarios such as facilitating
deliberation in democracies (Atkinson et al., 2006).
Nevertheless, the main decision problems on accept-
ability in VAFs, as it is the case in AFs, are likely to
be intractable (Dunne, 2010).
Average-case algorithms are well-established ap-
proaches in many other problems (e.g. quicksort).
Being neglected in the context of abstract argumen-
tation, we developed and experimented such methods
that decide the acceptability of arguments in VAFs.
As we show, these methods are characterized by in-
exhaustible search at the average case. The paper
is structured as follows: section 2 reviews basics of
VAFs, in section 3 we introduce the new algorithm,
experimental results are reported in section 4 and we
conclude the paper in section 5.
2 PRELIMINARIES
1
A value-based argumentation framework is composed
of: a finite set of arguments Args, an irreflexive binary
relation R ⊂ Args × Args, a non-empty set of values
V and a function val : Args → V where cycles of at-
tacks involve arguments mapped to at least two val-
ues. In VAFs, attacks are successful (or defeats) if the
attacked-argument’s value is not preferred to the value
of the attacker argument according to some value or-
der; a value order is called an audience in VAF’s
terminology. Therefore, the acceptance semantics in
VAFs are amended accordingly based on the notion of
defeat, unlike that of attack in AFs. Let A ∈ Args at-
tacks B ∈ Args but val(B) is preferred to val(A) then,
in VAFs, A does not defeat B. Recall that a preferred
extension in AFs is intuitively defined as any maximal
S ⊆ Args where S is conflict free and defends itself.
Hence, in AFs if A ∈ Args attacks B ∈ Args then {A}
is the only preferred extension. In VAFs, if A ∈ Args
attacks B ∈ Args then we have two value orderings
(or audiences). For the audience who prefers val(B)
to val(A), {A,B} is the preferred extension. As to the
audience who prefers val(A) to val(B), {A} is the pre-
ferred extension. In VAFs there are two types of argu-
ment acceptance: Objective Acceptance (OBA) and
Subjective Acceptance (SBA). An argument A ∈ Args
is objectively acceptable if and only if for all value or-
ders A is in every preferred extension (i.e. acceptable
1
We do not provide a detailed treatment of AFs and
VAFs semantics due to space limitation, see (Dung, 1995)
and (Bench-Capon, 2003) instead.
225
Nofal S., Dunne P. and Atkinson K..
TOWARDS AVERAGE-CASE ALGORITHMS FOR ABSTRACT ARGUMENTATION.
DOI: 10.5220/0003714602250230
In Proceedings of the 4th International Conference on Agents and Artificial Intelligence (ICAART-2012), pages 225-230
ISBN: 978-989-8425-95-9
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

always, irrespective of the audience). On the other
hand, an argument A ∈ Args is subjectively acceptable
if and only if for some value order A is in some pre-
ferred extension (i.e. accepted for some audience). In
the case of A ∈ Args attacks B ∈ Args, A is OBA while
B is SBA.
3 AVERAGE-CASE METHODS
As in any intractable problem, there are classes of
VAFs that could be solved in linear time. The follow-
ing proposition identifies VAFs which allow for lin-
ear time reasoning, in particular, proposition 1 states
that problem instances with unrestricted number of ar-
guments sharing the same value are solvable trivially
with only one property: none of the attacks involves
arguments sharing the same value.
Proposition 1. Let (Args, R, V, val) be a VAF. Then
unattacked arguments are OBA while the attacked
ones are SBA if ∀(A,B) ∈ R(val(A) 6= val(B)).
Proof. For those unattacked arguments the status of
OBA is obvious. By contradiction we can prove that
the remaining attacked arguments are SBA. Assume
that not all of the attacked arguments are SBA, then
one or more are either indefensible or OBA. OBA ar-
guments are attacked by indefensible arguments, and
the indefensible arguments are attacked by similar
value arguments. Contradiction! n
The naive approach needs to check all value or-
ders (i.e. permutations of values in V ) to determine
the acceptability of an argument. Thus, the status of
an argument will be computed in time proportional to
|V |! even if it works on a VAF with linear reasoning.
This motivates us to look for a different approach that
checks the minimum required value orders to find the
acceptance status which results in algorithms with an
improved average-case run-time complexity.
The idea of our algorithm is based on the notion
that an argument’s status is decided according to its
attackers’ statuses, this notion has been used in other
aspects of AFs (see (Modgil and Caminada, 2009) for
an overview). In deed, our algorithm searches the tree
induced by the argument in question s.t. the argument
is the root and its children are its attacker arguments
and the children of these are their attackers and so
on, provided that values are not repeated in a single
branch unless the repetition happens in a row. We call
such tree the dispute tree.
Definition 1. Let (Args, R, V, val) be a VAF. Then
T
A
is the dispute tree induced by A ∈ Args iff A is the
root and ∀B,C ∈ Args : B is a child of C iff ((B,C) ∈
R∧(val(B) does not appear on the directed path from
C to A ∨val(B) = val(C))).
Example 1. Consider the VAF in fig. 1 (a) (through-
out the paper we use the argument-value syntax for
nodes’ labels). The dispute tree T
B
is depicted in fig.
1 (b). Note that we do not consider attacks with re-
peated values unless they are in a row, for instance,
in T
B
the attack from A against C is dropped since A
has the same value of B. The dropped attack is cer-
tainly unsuccessful if V 2 is preferred to V 1, and it is
unreachable if V 1 is preferred to V 2.
The new approach works on the dispute tree of
arguments, it decides the status of an argument col-
lectively based on its statuses under the superiority of
each value in the dispute tree. Before presenting the
strict methods it might be helpful to discuss an exam-
ple just to capture the general idea.
Example 2. Consider the VAF in fig. 1 (a). To decide
the status of B, our algorithm decides its status as SBA
since it is survived if V 1 is most preferred (see fig. 1
(c)) and defeated when V 2 is most preferred (see fig.
1 (d)). In other words, B is accepted for all audiences
who prefer V 1 but rejected by audiences who prefer
V 2. In total, its status is SBA.
Every time a value is considered as most preferred
the dispute tree changes accordingly, we refer to the
new resulted tree as the pruned dispute tree under the
superiority of some value.
Definition 2. Let (Args, R, V, val) be a VAF, A ∈
Args, v ∈ V and T ⊆ T
A
. Then the pruned dispute
tree T
v
is defined as {(B,C) ∈ T | val(B) = val(C) ∨
val(C) 6= v}
Example 3. Let T be the tree T
B
in fig. 1 (b) and
v = V 2. Then T
v
= {(C,B),(D,B), (E, D),(C,E)}.
One more helpful term we have to define is related
to the recursive nature of the new approach. The new
method decides an argument’s status on the basis of
its attackers’ statuses, and therefore, the status of an
attacker is computed in the space of the dispute sub-
tree that is branched from that attacker.
Definition 3. Let (Args, R, V, val) be a VAF and
T ⊆ T
A
. Then the subtree T (B) is defined as {(C, D) ∈
T | D = B ∨ there is a directed path in T from D to B}.
Example 4. Let T be the tree T
v
from example 3. Then
T (D) = {(E,D),(C,E)}.
The methods that decide the acceptability status
for arguments in a VAF are presented in algorithms
1 and 2. Algorithm 1 decides the status of A ∈ Args
while algorithm 2 decides the status of A under the su-
periority of some value. With reference to algorithms
1 and 2, status
A
and status
0
A
stand for the current pro-
visional status of A and the status of A under the su-
periority of some value respectively.
ICAART 2012 - International Conference on Agents and Artificial Intelligence
226

Figure 1: Referenced by examples 1, 2, 3, and 4.
Algorithm 1: DecideStatus(A ∈ Args,T ⊆ T
A
).
1: for all v ∈V : ∃(B,C) ∈ T s.t. (val(B) = v∨val(C) = v)
do
2: status
0
A
← StatusAtValue(A,T,v)
3: if (status
A
is 2 or null) ∧ status
0
A
= 2 then
4: status
A
← 2
5: else
6: if (status
A
is 0 or null) ∧ status
0
A
= 0 then
7: status
A
← 0
8: else
9: if status
0
A
= 1 ∧ T is not chain then
10: status
0
A
← DecideStatus(A,T
v
)
11: if (status
A
is 2 or null) ∧ status
0
A
= 2 then
12: status
A
← 2
13: else
14: if (status
A
is 0 or null) ∧ status
0
A
= 0 then
15: status
A
← 0
16: else
17: return 1
18: else
19: return 1
20: return status
A
Algorithm 2: StatusAtValue(A ∈ Args,T ⊆ T
A
,v ∈ V ).
1: status
0
A
← 2
2: for all B ∈ Args s.t. (B,A) ∈ T do
3: if val(A) 6= v ∨ val(B) = val(A) then
4: status
0
B
= StatusAtValue(B,T (B),v)
5: if status
0
B
= 2∧(val(A) = val(B)∨val(B) = v) then
6: return 0
7: else
8: if status
0
B
6= 0 then
9: status
0
A
= 1
10: return status
0
A
Example 5. Consider the VAF in fig. 2 (a) , to find the
acceptability status of F the values {V1,V 2,V 3,V 4}
are to be investigated. An important note: trees in
fig. 2 are constructed from left to right while statuses
are decided from bottom to top. Now, if V 1 is most
preferred then the status of F is defeated as depicted
in fig. 2 (b). In the same way, F is defeated if V 2
and V 3 are most preferred respectively (see fig. 2 (c)
and fig. 2 (d)). However, if V4 is most preferred then
F is undecided (fig. 2 (e)). At this stage, two more
value orders are to be explored, namely, V 1 is pre-
ferred to V 3 and V 3 is preferred to V 1. In fact, F is
also defeated in the latter two cases (fig. 2 (f) and fig.
2 (g)), and therefore, the status of F is indefensible.
The naive method needs to check 24 value orders (i.e.
|V |!) to decide F’s status, but our algorithms find the
status after checking only 6 value orders.
In the remainder of this section, the correctness
proof of algorithms 1 and 2 is outlined. These algo-
rithms are recursive and so the proof is naturally in-
ductive. These proofs identify the base and inductive
cases that are directly provable from the definition of
SBA/OBA and the definitions presented in this paper.
In fact, algorithm 2 is a depth first search procedure
that visits attacker arguments until it stops and returns
0 for defeated status (i.e. not in any preferred exten-
sion), 1 for undecided status or 2 for survived status
(i.e. member in a preferred extension).
Proposition 2. Let (Args, R, V, val) be a VAF, A ∈
Args and v ∈ V is the most preferred value. Then al-
gorithm 2 decides the acceptability of A w.r.t preferred
semantics as 0, 1 or 2 where 0 ≡ (A /∈ any preferred
extension), 1 ≡ undecided and 2 ≡ (A ∈ some pre-
ferred extension).
Proof (outline). In the base case the algorithm stops
and returns 2 for one of three reasons. Firstly, if there
is no attacker at all (line 2). Secondly, if the value of
the attacked argument is most preferred then attacks
from arguments promoting a different value are not
successful (line 3). Thirdly, if all attackers promote a
repeated value that breaks the current value order (see
def. 1 for dispute trees). The inductive case: given an
attacker with a defined status, if the status of the at-
tacker argument is 2 and either its value is v (the most
preferred value) or its value is equal to the attacked
argument’s value then the status of the attacked argu-
ment is 0 (line 6), otherwise, if the attacker’s status
is not equal to 0 then the attacked argument’s status is
TOWARDS AVERAGE-CASE ALGORITHMS FOR ABSTRACT ARGUMENTATION
227
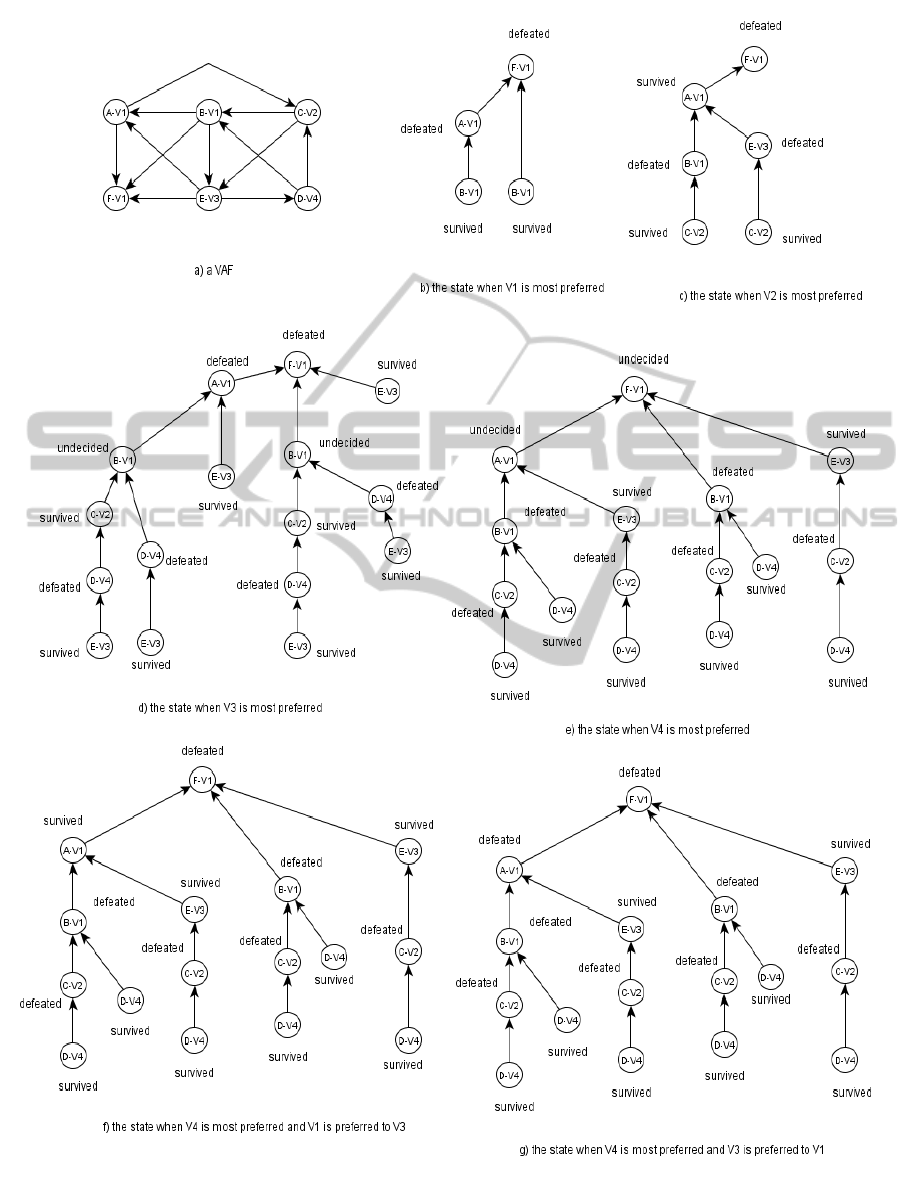
Figure 2: Progress of algorithms in example 5.
undecided (line 9) unless there is another attacker that
defeats it. n
Algorithm 1 is also a recursive procedure that re-
turns: 0 for indefensible status, 1 for SBA status or 2
ICAART 2012 - International Conference on Agents and Artificial Intelligence
228

for OBA status.
Proposition 3. Let (Args, R, V, val) be a VAF and
A ∈ Args. Then algorithm 1 decides the acceptability
status of A w.r.t preferred semantics as 0, 1 or 2 where
0 ≡ indefensible, 1 ≡ SBA and 2 ≡ OBA.
Proof (outline). In the base case the algorithm stops
for one of two reasons. Firstly, if there are no val-
ues left for investigation then the algorithm returns
whatever status (0 or 2) it ends with (line 1). Sec-
ondly, the algorithm stops and returns 1 when the sta-
tus at the superiority of some value (status
0
A
) is not
equal to the provisional status (status
A
) provided that
either status
0
A
6= 1 or the current tree T is a chain (line
19). Inductive case: if the current provisional sta-
tus (status
A
) is 0 or 2 then it is unchanged as long as
the computed status at the superiority of some value
(status
0
A
) is 0 or 2 respectively (lines 12 and 15). Oth-
erwise, the provisional status (status
A
) is 1 (line 17).n
The worst-case scenario of these algorithms is not
better than the naive one. But as we are concerned
with the average-case scenario, experiments have sug-
gested a better average-case run-time; in the subse-
quent section we report these results.
4 EXPERIMENTS
We implemented the algorithms presented in section
3 using Java language on a Linux-based cluster of 4
CPUs and 16GB of system memory. We built VAFs
randomly for these experiments; the random genera-
tor made all decisions randomly with approximately
equal probability. These decisions include choosing
the number of arguments, number of values and num-
ber of attacks, which arguments attack which others
and finally which argument is mapped to which value.
As to the correctness, we tested the algorithm with
200,000 VAFs where |V | ranges from 2 to 7 and |Args|
ranges from 2 to 15.
Concerning the analysis, we ran three experi-
ments. The first experiment was to show how our al-
gorithm compares to the naive approach. For this pur-
pose, we randomly generated 9844 VAFs grouped by
|V |. Table 1 details each group while table 2 presents
the measures of value orders averages and CPU time
averages (in milliseconds) for each group under naive
and new approaches. The second experiment was to
show how our algorithm’s behavior is affected by the
increase of |V |. Figures 3 and 4 show the behavior
in terms of averages of value orders and averages of
CPU time respectively. The charts in figures 3 and 4
are obtained from 9753 VAFs where the number of
attacks against any argument is limited up to 4, |Args|
is 30 and |V | ranges from 2 to 20. The last experiment
was to evaluate, in the context of the new algorithm,
the correlation between the number of attacks against
any single argument and the performance measured
by the average of CPU time and the average of value
orders. The results of last experiment are presented
in figures 5 and 6 where the charts plot 9500 VAFs
with |Args| as 20, |V | as 4 and the number of at-
tacks against any argument ranges from 2 to 20. As
an illustration on how to read these figures, the point
(15,83.22) in figure 3 means that for a group of VAFs
(actually 724 cases) with |V | = 15 the algorithm needs
to check on average 83.22 value orders until it decides
the acceptability status.
Table 1: Random VAFs.
group |V| |VAFs| range(|Args|) range(|R|)
1 2 1284 2-12 0-45
2 3 1400 3-15 0-58
3 4 1505 4-17 1-87
4 5 1422 5-18 3-927
5 6 1405 7-20 8-109
6 7 1404 8-20 10-135
7 8 996 8-20 13-140
8 9 428 9-20 20-138
Table 2: Comparisons.
group
new algorithm naive algorithm
value orders CPU time value orders CPU time
1 1.66 0.04 0.03 2.00
2 2.37 0.11 0.15 6.00
3 3.10 0.33 1.06 24.00
4 3.83 0.91 7.17 120.00
5 4.53 3.46 31.20 720.00
6 5.12 11.00 221.36 5,040.00
7 5.60 32.91 2,438.76 40,320.00
8 5.92 103.40 45,676.53 362,880.00
Figure 3: The effect of increase in |V |.
To sum up, the outcome of the experiments shows
that the new algorithm has a better average case be-
havior than the naive methods as stated by table 2.
Negatively, figures 3 and 4 point that the average case
complexity of the new algorithm might be exponen-
tial, which is not surprising since the problem has
been proven to be hard. Finally, figures 5 and 6 show
that the increase in the number of attacks against any
TOWARDS AVERAGE-CASE ALGORITHMS FOR ABSTRACT ARGUMENTATION
229
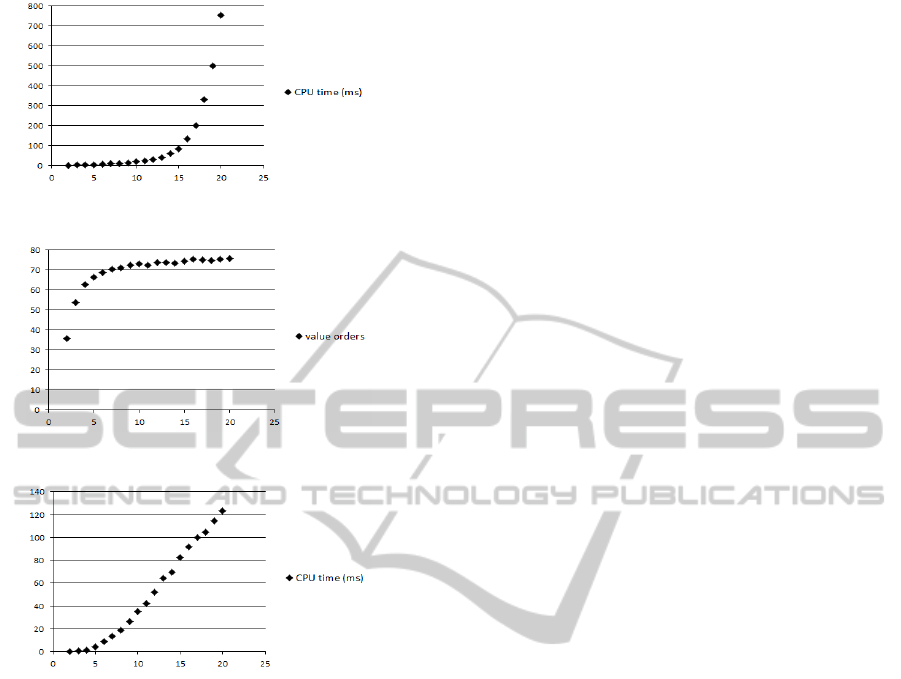
Figure 4: The effect of increase in |V |.
Figure 5: The effect of increase in attacks per argument.
Figure 6: The effect of increase in attacks per argument.
single argument has no extreme impact on the behav-
ior of the new algorithm.
5 CONCLUSIONS
In this paper we argued that hard computations of ab-
stract argumentation developments is not the end of
the story. In light of experiments conducted, average-
case algorithms seem to be candidate methods to-
wards practical implementation of argument systems.
This work developed average-case algorithms for an
instance of AFs developments: value-based argumen-
tation frameworks. From an experimental algorithmic
point of view, the results of this work illustrate the rel-
ative performance of the new approaches compared to
the naive methods.
As future work, we plan to investigate average-
case approaches for classical problems in AF and
the decision problems that have arisen in the context
of AF developments such as extended AFs (Modgil,
2009). Another direction for future work is to ex-
plore the role of heuristics, which might lead to bet-
ter average-case algorithms. For instance, in our ap-
proach attackers are traversed in an arbitrary order
while presumably it could be more efficient if the at-
tackers are visited in an ascending order according to
the number of their attackers. However, the influence
of heuristics on the overall performance would be un-
clear. To be cost-effective, heuristics computations
must not exceed the wasted computations imposed by
the arbitrary order.
ACKNOWLEDGEMENTS
We would like to thank the anynomous reviewers for
their comments that help improve the paper.
REFERENCES
Amgoud, L. and Cayrol, C. (2002). A reasoning model
based on the production of acceptable arguments.
Annals of Mathematics and Artificial Intelligence,
34:197–215.
Atkinson, K., Bench-Capon, T., and McBurney, P. (2006).
Parmenides: facilitating deliberation in democracies.
Artificial Intelligence and Law, 14(4):261–275.
Bench-Capon, T. (2003). Persuasion in practical argument
using value-based argumentation frameworks. Logic
and Computation, 13(3):429–448.
Bench-Capon, T. and Dunne, P. (2007). Argumentation in
artificial intelligence. Artificial Intelligence, 171:619–
641.
Dung, P. (1995). On the acceptability of arguments and its
fundamental role in non monotonic reasoning, logic
programming and n-person games. Artificial Intelli-
gence, 77(2):321–357.
Dunne, P. (2010). Tractability in value-based argumenta-
tion. In proceedings of Computational models of ar-
guments, pages 195–206.
Modgil, S. (2009). Reasoning about preferences in
argumentation frameworks. Artificial Intelligence,
173:901–934.
Modgil, S. and Caminada, M. (2009). Proof theories and
algorithms for abstract argumentation frameworks. In
Rahwan, I. and Simari, G. R., editors, Argumentation
in AI, pages 105–129. Springer-Verlag.
ICAART 2012 - International Conference on Agents and Artificial Intelligence
230
