AN EFFICIENT PARALLEL GPU EVALUATION OF SMALL ANGLE

X-RAY SCATTERING PROFILES

Lubomir D. Antonov

1,∗

, Christian Andreetta

1,∗

and Thomas Hamelryck

The Bioinformatics Section, Department of Biology, University of Copenhagen, Copenhagen, Denmark

∗

These authors contributed equally to this work

Keywords:

SAXS, GPGPU, Protein Structure Determination.

Abstract:

The inference of protein structure from experimental data is of crucial interest in science, medicine and

biotechnology. Unfortunately, high-resolution experimental methods can not yet provide a detailed analy-

sis of the ensemble of conformations adopted under physiological conditions. Low resolution techniques are

often better suited for this task. Small angle X-ray scattering (SAXS) plays a major role in investigating im-

portant biological questions regarding the structure of multidomain proteins connected by ﬂexible linkers or

the aggregation processes that underlie several major diseases in humans.

In silico simulations can bridge the gap between low resolution information and models derived from high-

resolution techniques. For that, it is necessary to be able to calculate the low resolution information from a

given detailed model using a so-called forward model. These calculations need to be performed many times

during a conformational search, and therefore need to be computationally efﬁcient.

We present an efﬁcient implementation of the forward model for SAXS experiments with full hardware utiliza-

tion of General Purpose Graphical Processor Units (GPGPUs). The proposed algorithm is orders of magnitude

faster than an efﬁcient CPU implementation, and implements a caching procedure ready to be employed in the

partial SAXS evaluations required by in silico simulations.

1 INTRODUCTION

Proteins play a crucial role in science, medicine and

biotechnology: without them, cellular activities such

as catalysis, signaling and regulation would be impos-

sible. Protein function is determined by protein struc-

ture, which is in term determined by the amino acid

sequence (Anﬁnsen, 1973).

Despite encouraging improvements, determining

the ensemble of possible conformations in solution

is far from an accomplished goal. High resolution

experimental methods, notably X-ray crystallography

and Nuclear Magnetic Resonance (NMR), can only

partially provide information on such ensembles, and

encounter several limitations in fully describing the

ﬂexibility of large systems in physiological condi-

tions (Zheng and Doniach, 2005).

Low resolution methods, on the other hand, can

more easily provide information on such ensembles.

In particular, Small Angle X-ray Scattering (SAXS)

provides information on the excess electron density of

the sample versus the surrounding environment. Re-

cently, with the advent of automated high-throughput

SAXS analysis of biomolecules (Toft et al., 2008;

Hura et al., 2009), high-throughput data acquisition

is within reach. Since SAXS data only describes the

spherical averaging of the electron density of the av-

erage conformation of the ensemble, additional infor-

mation is needed to assist structural interpretation.

Usual in silico methods propose plausible struc-

tural conformations, and calculate their associated

scattering proﬁle by means of a forward model. Then,

the proposed and the experimental proﬁles are com-

pared using an error model of the experiment. For

this procedure to be successful, an efﬁcient procedure

for both sampling protein structures and calculating

the SAXS proﬁle is required. We focus on the latter

problem.

Early approaches for the evaluation comprise ab

initio shape determinations using spherical harmon-

ics expansions (Svergun and Stuhrmann, 1991). Here,

computational feasibility is attained at the cost of

limiting the possible shapes of the sample, for in-

stance excluding internal cavities (Koch et al., 2003).

Other modeling approaches compute and ﬁt the scat-

tering curve from a condensation of a gas of “dummy

beads” to an experimental SAXS curve. This has been

done using conformational searches by a genetic al-

102

D. Antonov L., Andreetta C. and Hamelryck T..

AN EFFICIENT PARALLEL GPU EVALUATION OF SMALL ANGLE X-RAY SCATTERING PROFILES.

DOI: 10.5220/0003781501020108

In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2012), pages 102-108

ISBN: 978-989-8425-90-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

gorithm in DALAI GA (Chacon et al., 1998) or sim-

ulated annealing in DAMMIN (Svergun, 1999) and

DAMMIF (Franke and Svergun, 2009).

Higher resolution models impose further con-

straints to the proposals. In the GASBOR program

(Svergun et al., 2001), a SAXS proﬁle is calculated

for a packed assembly of spheres placed accord-

ing to a pseudo-C

chain. The scattering intensity

is calculated using the Debye formula, while simu-

lated annealing is used for searching the conforma-

tional space. Other recent structure prediction meth-

ods, such as the ORNL (Tjioe and Heller, 2007) and

IMP (F

orster et al., 2008) programs, utilize the SAXS

curve as an energy term in combination with other en-

ergy contributions from physical force ﬁelds. Since

these descriptors are non-probabilistic in nature, the

weights used for scaling the SAXS energy to other

conformational constraints must be chosen heuristi-

cally (Habeck et al., 2006).

In recent publications, our group developed prob-

abilistic models for the proposal of protein-like con-

formations, in full atomic detail, for both backbone

and side chains (Boomsma et al., 2008; Harder et al.,

2010). We also developed a forward model of the

scattering proﬁle evaluation, that includes the ex-

perimental error associated with SAXS data (Stov-

gaard et al., 2010). The forward model consists of a

coarse-grained computation based on the Debye for-

mula (Debye, 1915). Our main aim is the study of

proteins consisting of multiple domains connected by

ﬂexible linkers. Such proteins play a major role in

the regulation of gene expression, cell growth, cell

cycle, metabolic pathways, signal transduction, pro-

tein folding and transport (Levitt, 2009; Madl et al.,

2010). With this aim, a computationally efﬁcient for-

ward model for the calculation of SAXS curves is

paramount.

We ported our original implementation of the De-

bye formula to General Purpose Graphics Process-

ing Units (GPGPUs), parallel computing engines that

can offer great advantages in terms of cost-efﬁciency

and low power consumption (G

oddeke and Strzodka,

2011). One of the emerging standards of choice for

their programming is the Open Computing Language

(OpenCL), an open standard that provides an abstrac-

tion layer over hardware implementations of highly

parallel computational engines (Stone et al., 2010).

2 METHODS

2.1 Forward SAXS Computation

The observed data in a SAXS experiment is a one-

dimensional intensity curve, I(q), measured at dis-

cretized scattering momenta q = 4πsin(θ)/λ, with λ

the wavelength of the incoming radiation and 2θ the

scattering angle between the principal and the prob-

ing beam rays. The calculation of a theoretical SAXS

proﬁle from a given atomic structure is based on the

well-known Debye formula (Debye, 1915):

I (q) =

∑

i=1

∑

j=1

(q)F

(q)

sin(q · r

i j

)

q · r

i j

(1)

where F

and F

are the scattering form factors of the

individual particles i and j, and r

i j

is the Euclidean

distance between them. The summations run over all

the M scattering particles.

2.2 Coarse-grained Protein Models

If some scatterers are ﬁxed relative to each other, they

can be approximated by a single large scattering body

(dummy body). This approximation, more precise at

low q, fades with the progression of the scattering an-

gle up to a resolution equal to the scattering diameter

of the dummy body. We found that the amino acids

constituent to the protein chain can be approximated

by one or two large bodies (dummy atoms), and that

this approximation holds up to scattering angles nor-

mally not measured in the current experimental stan-

dards (Stovgaard et al., 2010).

In the two body model, the amino acids are indi-

vidually represented by two dummy atoms; one rep-

resenting the backbone, and the other representing

the side chain. Glycine and alanine, lacking a side

chain, are represented by one dummy atom only. The

dummy atoms are placed at the respective centers of

mass (see Figure 1). A total of 21 form factors need to

be estimated for the two body model: one for alanine,

one for glycine, one for the generic backbone and 18

for the remaining side chains.

For the one body model, the single dummy atom

is placed at the center of mass of the amino acid.

Hence, 20 form factors need to be estimated; one

for each amino acid type. For a given protein, the

one body model allows to represent the molecule in

roughly half the number of scattering bodies as com-

pared to the two body model. If the experimental data

is recorded at low resolutions only, the former is thus

clearly preferable for reasons of computational efﬁ-

ciency.

2.3 Form Factor Descriptors

Due to the lack of publicly available high-quality

experimental data needed for the estimation of the

AN EFFICIENT PARALLEL GPU EVALUATION OF SMALL ANGLE X-RAY SCATTERING PROFILES

103

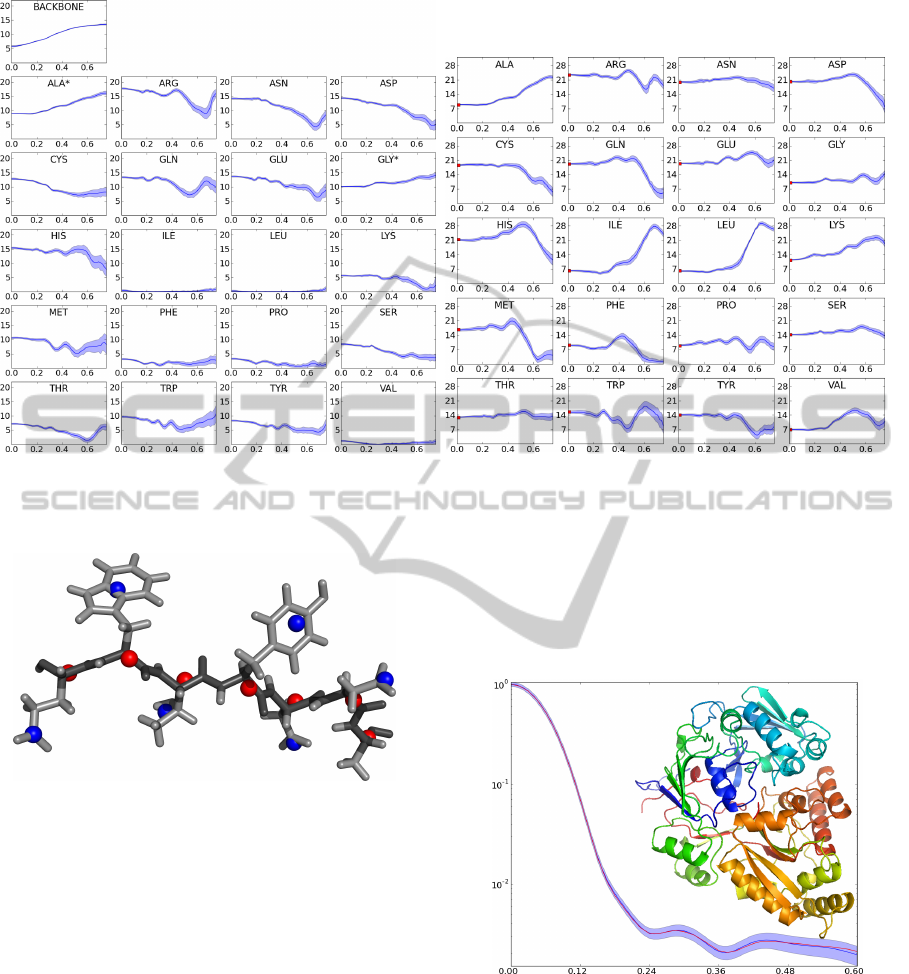
Figure 2: Form factors. Mean (dark blue curve) and standard deviations (blue areas) for the form factors (Y -axis) as a

function of q (X-axis). Left: backbone and side-chains. An asterisk indicates that this form factor describes both the backbone

and side chain atoms of the residue. Right: the single body form factors. Figure adapted from (Stovgaard et al., 2010).

Figure 1: Coarse-grained models of protein structure.

Example of a protein backbone stretch (dark gray) with side

chain atoms (light gray). The placement of the dummy

bodies for the center of mass of the backbone atoms (red

spheres) and for the side chains (blue spheres) are indicated.

Figure prepared with PyMOL (Schr

odinger, 2010), adapted

from (Stovgaard et al., 2010).

form factors, artiﬁcial data curves were generated

for known high-resolution protein structures using

the state-of-the-art program CRYSOL (Svergun et al.,

1995). This program computes the theoretical scat-

tering curve from a given full-atom structure using

spherical harmonics expansions, therefore limiting its

applications at studying compact quasi-globular pro-

teins. We can however use this input to feed a learning

protocol, and make use of the Debye formula in eq. 1

to overcome structural assumptions.

Therefore, a large scale Monte Carlo simulation

has been conducted to estimate the values of the form

factors of the dummy atoms (Stovgaard et al., 2010).

The resulting proﬁles for these descriptors are shown

in Figure 2.

In Figure 3 we show a SAXS curve generated with

our method, and the theoretical scattering computed

by CRYSOL as a reference.

Figure 3: SAXS proﬁle reconstruction example. Compar-

ison of the reference proﬁles I(q) computed by CRYSOL

from the all atom structure (blue) and by the two body

model (red). Error shade indicates the simulated “exper-

imental” error. PDB code 1JET (520 residues). Cartoon

made with PyMOL (Schr

odinger, 2010).

2.4 OpenCL Programming Model

An OpenCL program contains a host program that ex-

ecutes on the CPU, and kernels that execute on the

abstracted parallel hardware. The hardware is deﬁned

BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms

104

as one or more compute units, which are composed of

one or more processing elements and, in some cases,

local memory.

The host program coordinates the execution of the

kernels, and can be written in any programming lan-

guage. Kernels are written in a variant of the latest

released C language standard (C99) and are compiled

at run time to device-speciﬁc instructions. A ker-

nel describes the operations of a single work-item, or

thread, and is run simultaneously by a set of work-

items called a work-group.

The local memory of a compute unit, if present,

is shared by all work-items in a work-group and

provides an efﬁcient communication channel among

them. It has very low latency and is usually imple-

mented with a full crossbar interface, but is limited in

size and does not retain its state between kernel exe-

cutions.

Therefore, kernels execute most efﬁciently when

the size of the work-group matches the size of the

compute unit on the OpenCL device and when all

work-items in a work-group follow the same execu-

tion path.

2.5 Efﬁcient GPU Implementation

2.5.1 Parallel Page-tile SAXS Algorithm

The computation of a SAXS proﬁle is experimentally

discretized in a set of q points, and thus naturally pro-

vides the ﬁrst level of parallelization, into pages. Each

page represents the computation of the intensity curve

I(q) for a single value of q. A page can be visual-

ized as a square problem matrix of side equal to the

number of scattering particles M, with each cell repre-

senting the contribution of a single term of the Debye

formula for particular i and j.

For performance considerations and direct map-

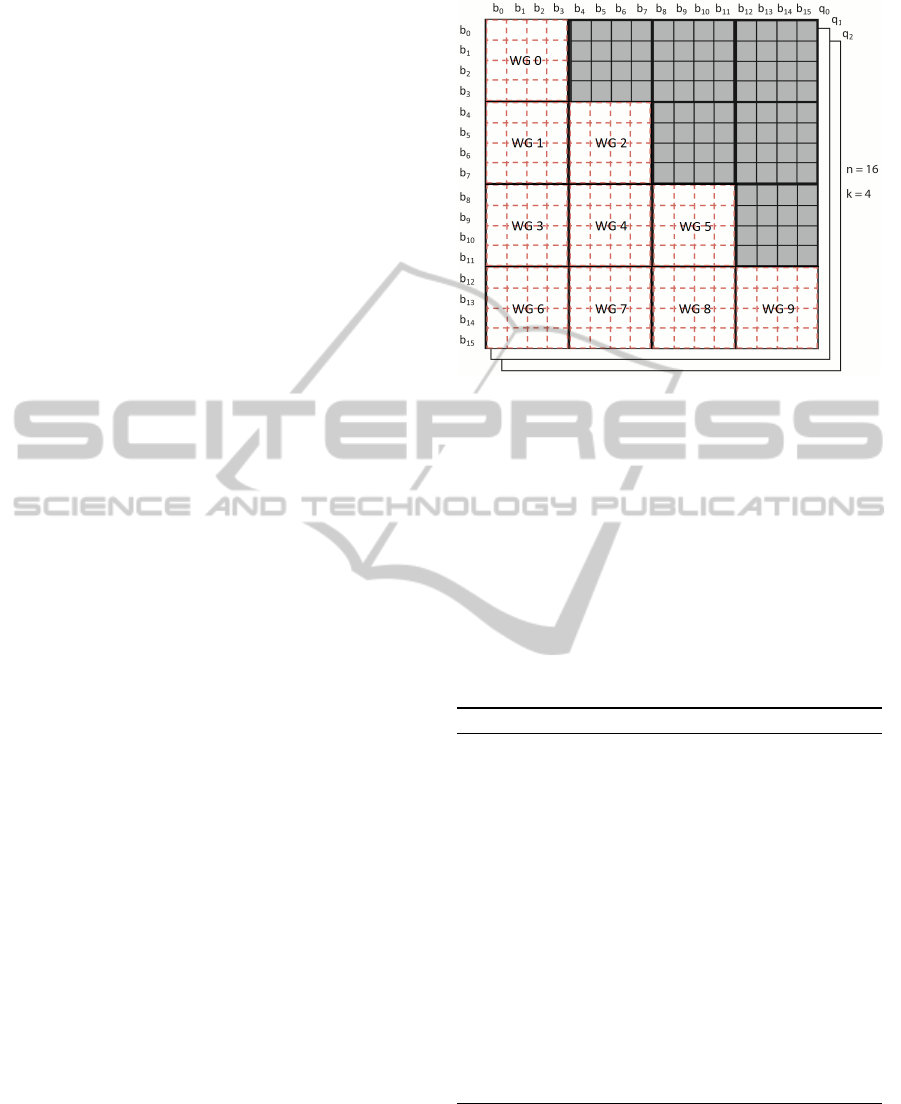
ping to the hardware, pages are partitioned into square

tiles of side k, where k is set to the speciﬁc compute

unit size of the OpenCL device. Since each problem

matrix is symmetrical, only the tiles encompassing

the lower-left triangle and the diagonal are computed

and their value is simply duplicated for the mirror tiles

in the upper-right triangle of the matrix. The domain

decomposition is illustrated in Figure 4 for an exam-

ple of 16 scattering particles and work-group size of

GPUs suffer performance penalties when they

have to work with data that is not aligned to their na-

tive architecture, therefore the algorithm pads the data

and aligns it to the speciﬁed work-group size. The re-

sultant dummy particles participate in the Debye cal-

culations, but they are assigned a form factor of 0, so

Figure 4: Domain decomposition for the Page-Tile algo-

rithm. Work-groups operate on square tiles from the ma-

trix. Only tiles in the lower-left part and the diagonal are

evaluated.

their contribution to the intensity I(q) is null.

Algorithm 1 presents the pseudocode for the Page-

Tile SAXS algorithm. The form factors table, sup-

plied as input, is packed and organized by scattering

momentum and particle type. The scattering particles,

in addition to their position in three dimensions, have

a type in the form of an index into the form factor ta-

ble. The initial intensity curve calculation comprises

four kernels.

Algorithm 1: Page-Tile SAXS algorithm.

Input: scattering momenta, form factors table, scat-

tering particles

Output: intensity curves for the scattering momenta

/*Host program*/

Initialize the parallel algorithm

Transfer input data to GPU global memory and queue

the kernels for initial proﬁle calculation

/*Kernels executed on the GPU*/

Map form factors to scattering particles (Kernel 1)

Compute the Debye sum term for each tile (Kernel 2)

Perform vertical tile sum reduction for each page

(Kernel 3)

Perform horizontal margin sum reduction for each

page to get the intensity curve (Kernel 4)

/*Host program*/

Retrieve the results from GPU global memory

In Kernel 1 the form factor table is mapped into

a form suited for hardware-efﬁcient parallel access.

The form factors are organized by scattering particle,

which enables the work-groups with streaming mem-

ory access for both center coordinates and form fac-

tors.

AN EFFICIENT PARALLEL GPU EVALUATION OF SMALL ANGLE X-RAY SCATTERING PROFILES

105

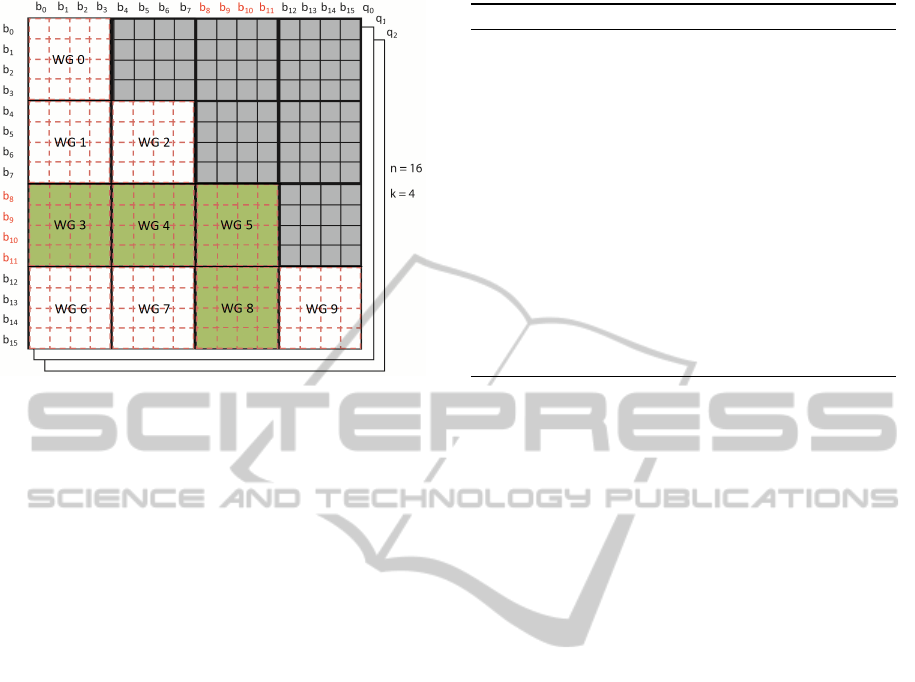
Figure 5: Problem matrix after a move. Particles b8, b9,

b10 and b11 have changed positions. Blocks WG3, WG4,

WG5 and WG8 will be recalculated.

The majority of execution time is spent in Ker-

nel 2, where the Debye sum terms for the individual

tiles are computed. The Debye formula is used for

each term, but i and j are limited to the ranges deﬁned

by the boundaries of the tile within the global index

space. The kernel uses local memory to improve per-

formance, by pre-loading the particles and their form

factors, and by performing an in-place parallel reduc-

tion to produce the partial sum for the tile. During

the Debye calculation, 4x loop unrolling utilizes local

registers to further optimize this stage.

Kernel 3 reduces the tile partial sums, which are

stored in a global cache, to bottom margin sums that

are further reduced by Kernel 4 to yield the ﬁnal in-

tensity curve.

2.5.2 Tile Recalculation

Monte Carlo Markov Chain simulations explore the

conformational space of the protein structures by ap-

plying partial modiﬁcations over an accepted pro-

posal. The average SAXS computation is therefore

a partial re-evaluation of a previously computed pro-

ﬁle, where only a subset of the bodies changed their

position.

It is therefore possible to identify the subset of

tiles that needs to be updated. Since the Page-Tile al-

gorithm caches the partial contribution of each tile to

the global summation, we can impose a partial recal-

culation of only the affected tiles (see Figure 5). This

leads to a substantial reduction in the time necessary

to derive an intensity curve after a move.

Algorithm 2 illustrates the pseudocode for tile re-

calculation. The form factor table from the initial cal-

Algorithm 2: Tile recalculation.

Input: moved scattering particles

Output: updated intensity curve for the scattering

momenta

/*Host program*/

Transfer input data to the GPU global memory and

queue the kernels involved in the proﬁle recalculation

/*Kernels executed on the GPU*/

Compute the Debye sum term for the changed tiles

(Kernel 5)

Perform the vertical tile sum reduction for each page

(Kernel 3)

Perform horizontal margin sum reduction for each

page to get the intensity curve (Kernel 4)

/*Host program*/

Retrieve the results from the GPU global memory

culation is reused, so execution starts directly with

Kernel 5, which identiﬁes the affected tiles and in-

vokes Kernel 2 for them. Kernel 3 and Kernel 4 per-

form the reductions as in the initial calculation.

2.5.3 Floating Point Precision

Floating point numbers can be stored and manipu-

lated with single precision (SP) or double precision

(DP). Mathematical operations on ﬂoating point num-

bers introduce errors, due to the ﬁnite precision avail-

able. Those errors tend to accumulate when a large

number of operations is performed, as is the case

with the double sum of the Debye formula. However,

the Page-Tile algorithm signiﬁcantly reduces this er-

ror growth, because its successive partitioning of the

problem space results in an execution pattern resem-

bling pairwise summation (Higham, 1993). The algo-

rithm can be executed with SP or DP, paying a perfor-

mance penalty of a factor of 2 to 4 with DP.

We measured the divergence between the SP and

DP executions, and no signiﬁcant differences arise be-

tween the results. Therefore, the SP implementation

is used by default.

3 RESULTS AND DISCUSSION

3.1 Computational Efﬁciency of the

SAXS Modeling

The Debye formula (Equation 1) leads to a com-

putational complexity of O(M

), with M the num-

ber of scatterers in the structure under examina-

tion. Our coarse-grained approach reduces M by rep-

resenting several atoms by one scattering body (a

BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms

106

dummy atom), thereby lowering the complexity to



(

/k)



, with k the number of scatterers (atoms)

described by a dummy body.

The precise value of k is dependent on the primary

sequence of the protein. On large datasets, the two

dummy model leads to an average k of 4.24 (with a

performance increase of k

' 18). The single body

model leads to k ' 7.8, allowing for a k

' 60 times

quicker execution.

3.2 GPGPU Implementation

The performance of the Page-Tile algorithm was mea-

sured on a system with a Core i7-920 CPU, 12GB

of DDR3 RAM and a NVIDIA GeForce GTX 560

Ti GPU with 1GB of GDDR5 RAM. The GTX

560 Ti has 8 compute units with 32 processing el-

ements each, comprising 384 processing elements,

with 32KB 32-bit registers and 48KB of local mem-

ory for each compute unit.

Performance was measured against a test protein

of over a thousand amino acids, modeled with 1888

scattering bodies in the dual dummy atom represen-

tation, and a discretization of the q space in 51 scat-

tering momenta. Protein moves were modeled by a

random mutation of 40% of the particles, to approxi-

mate the asymptotic move rate in a Monte Carlo sim-

ulation. The execution times for the model test case

are presented in Table 1.

Table 1: Execution times for SAXS curve calculation for

a protein with 1888 bodies, 51 scattering momenta and 21

form factors per momentum. Execution times from the top

are for a single processor CPU implementation, a parallel

GPU full computation, and GPU partial computation, re-

spectively. Partial computations mimic the costs in a Monte

Carlo simulation, where at each step around 40% of the pro-

posal structure is updated.

Algorithm Time (ms)

CPU SP Time 2408

GPU full calculation 9

GPU recalculation 6.484

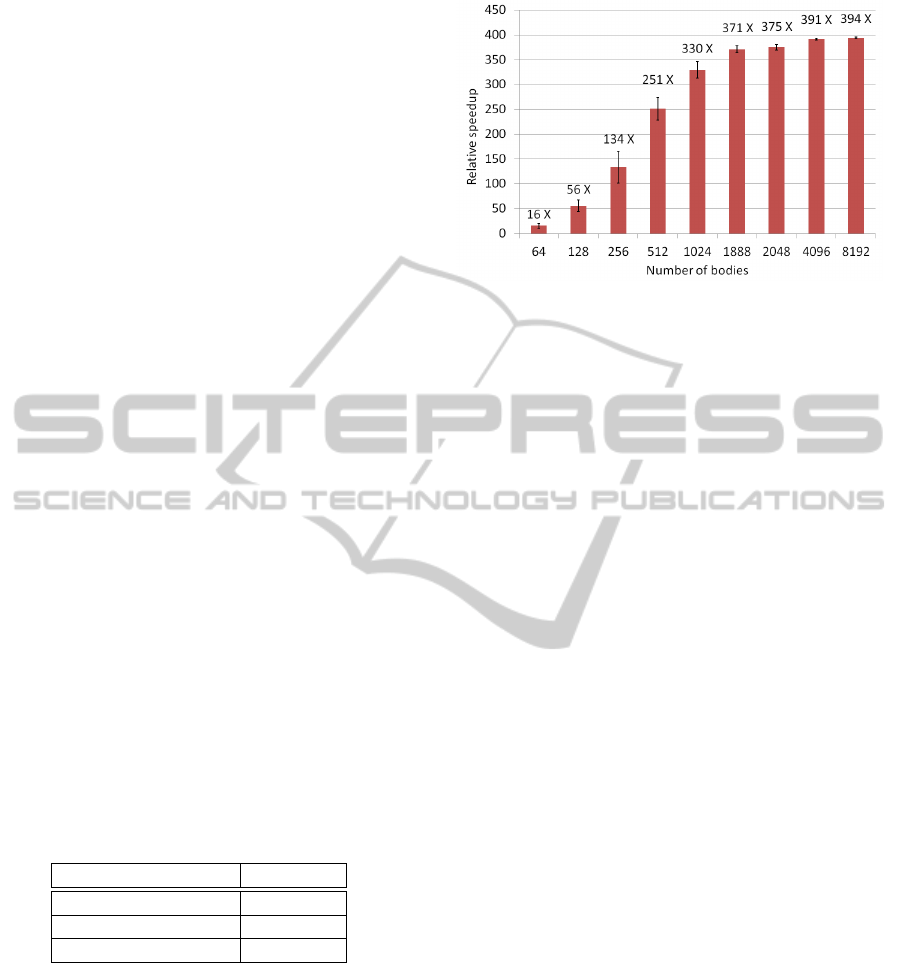
The performance of the algorithm was also mea-

sured for protein sizes ranging from 64 to 8192 scat-

tering particles. Each protein was moved 1000 times,

in order to obtain an average of the recalculation

steps. Figure 6 shows the speed increase, relative to

the CPU single precision implementation, calculated

as t

cpu

gpu

Figure 6 also illustrates the hardware utilization

of the parallel Page-Tile algorithm. The plot shows

an asymptotic behavior around problem sizes of 2000

scattering bodies. The GTX 560 Ti GPU employed in

the tests is composed of 8 compute units operating on

Figure 6: Algorithm performance for problem sizes rang-

ing from 64 to 8192 scattering bodies, including the model

test case of 1888, with error bars showing standard devia-

tion. All SAXS computations involve the summations over

51 scattering momenta. The asymptotic behavior indicates

hardware saturation at around 2000 bodies, which is the the-

oretical maximum for the GPU model used in the tests.

8 cascading work-groups, allowing for a theoretical

peak of 64 active work-groups. The work-group size

is 32, therefore the card would reach theoretical peak

processing power at 2048 bodies. Our tests show sat-

uration at the same level, thus indicating optimal use

of the hardware.

OpenCL is thread-safe and allows access to the

same device from multiple processes and threads, so

by creating multiple instances of the Page-Tile algo-

rithm, more than one calculation can be run at the

same time. This is especially relevant in the case of

problem sizes that would not lead to a full GPU sat-

uration, therefore allowing for multi-threaded Monte

Carlo simulations.

As a proof of concept, two instances of the algo-

rithm were run in parallel on the test system with the

model test problem of size 1888. The recorded time to

complete a move recalculation was 11.962ms, or 93%

of the time to complete two moves sequentially, indi-

cating that the excess processing capacity was indeed

utilized.

4 CONCLUSIONS

We have presented an efﬁcient implementation of the

forward model for the computation of Small Angle

X-ray Scattering proﬁles. The application is multi-

thread safe, and benchmarks show that the General

Purpose Graphic Processor Units deliver the full the-

oretical output allowable by the hardware.

Parallelization is achieved on multiple levels by

taking advantage of the structure of the Debye prob-

lem. The ﬁrst level divides the SAXS evaluation in

AN EFFICIENT PARALLEL GPU EVALUATION OF SMALL ANGLE X-RAY SCATTERING PROFILES

107

multiple independent computations according to the

binning of the scattering momentum. A nested level

then makes full use of the work-groups in the hard-

ware by splitting the inner summation of the Debye

formula in separate partial sums. The resulting pro-

gram runs orders of magnitude faster than an opti-

mized single core CPU implementation.

A caching algorithm on the inner contributions

allows for the efﬁcient re-evaluation of SAXS pro-

ﬁles from partially updated structures, delivering even

greater beneﬁts to applications like Markov Chain

Monte Carlo simulations of important biological and

clinical targets. An open source implementation will

be released shortly.

ACKNOWLEDGEMENTS

This research was funded by the Danish Council for

Independent Research (FTP, 274-09-0184).

SOURCE CODE AVAILABILITY

The source code of our implementation can be

found online at: http://www.phaistos.org and http://

sourceforge.net/projects/phaistos/ﬁles.

REFERENCES

Anﬁnsen, C. B. (1973). Principles that govern the folding

of protein chains. Science, 181(96):223–230.

Boomsma, W., Mardia, K., Taylor, C., Ferkinghoff-Borg, J.,

Krogh, A., and Hamelryck, T. (2008). A generative,

probabilistic model of local protein structure. Proc

Natl Acad Sci U S A, 105(26):8932–8937.

Chacon, P., Moran, F., Diaz, J., Pantos, E., and Andreu, J.

(1998). Low-resolution structures of proteins in so-

lution retrieved from x-ray scattering with a genetic

algorithm. Biophys J, 74:2760–2775.

Debye, P. (1915). Zerstreuung von rontgenstrahlen. Ann

Phys, 351(6):809–823.

orster, F., Webb, B., Krukenberg, K., and Tsuruta, H.

(2008). Integration of small-angle x-ray scattering

data into structural modeling of proteins and their as-

semblies. J Mol Biol, 382:1089–1106.

Franke, D. and Svergun, D. I. (2009). Dammif, a program

for rapid ab-initio shape determination in small-angle

scattering. J Appl Crystallogr, 42(2):342–346.

oddeke, D. and Strzodka, R. a. (2011). Cyclic reduc-

tion tridiagonal solvers on GPUs applied to mixed

precision multigrid. IEEE Transactions on Par-

allel and Distributed Systems, 22(1):22–32. doi:

10.1109/TPDS.2010.61.

Habeck, M., Rieping, W., and Nilges, M. (2006). Weighting

of experimental evidence in macromolecular struc-

ture determination. Proc Natl Acad Sci U S A,

103(6):1756–1761.

Harder, T., Boomsma, W., Paluszewski, M., Frellsen, J., Jo-

hansson, K. E., and Hamelryck, T. (2010). Beyond

rotamers: a generative, probabilistic model of side

chains in proteins. BMC Bioinformatics, 11:306.

Higham, N. J. (1993). The accuracy of ﬂoating point sum-

mation. SIAM J. Sci. Comput, 14:783–799.

Hura, G. L., Menon, A. L., Hammel, M., Rambo, R. P.,

Poole, F. L., Tsutakawa, S. E., Jenney, F. E., Classen,

S., Frankel, K. A., Hopkins, R. C., jae Yang, S., Scott,

J. W., Dillard, B. D., Adams, M. W. W., and Tainer,

J. A. (2009). Robust, high-throughput solution struc-

tural analyses by small angle x-ray scattering (saxs).

Nat Methods, 6(8):606–614.

Koch, M., Vachette, P., and Svergun, D. (2003). Small-

angle scattering: a view on the properties, structures

and structural changes of biological macromolecules

in solution. Q Rev Biophys, 36(2):147–227.

Levitt, M. (2009). Nature of the protein universe. Proc Natl

Acad Sci U S A, 106(27):11079–11084.

Madl, T., Gabel, F., and Sattler, M. (2010). NMR and small-

angle scattering-based structural analysis of protein

complexes in solution. J Struct Biol, pages 1–11.

Schr

odinger, L. (2010). The PyMOL molecular graphics

system, version 1.3r1.

Stone, J. E., Gohara, D., and Shi, G. (2010). Opencl: A par-

allel programming standard for heterogeneous com-

puting systems. Computing in Science and Engineer-

ing, 12:66–73.

Stovgaard, K., Andreetta, C., Ferkinghoff-Borg, J., and

Hamelryck, T. (2010). Calculation of accurate small

angle X-ray scattering curves from coarse-grained

protein models. BMC Bioinformatics, 11:429.

Svergun, D. (1999). Restoring low resolution structure

of biological macromolecules from solution scattering

using simulated annealing. Biophys J, 76:2879–2886.

Svergun, D., Barberato, C., and Koch, M. (1995). Crysol -

a program to evaluate x-ray solution scattering of bi-

ological macromolecules from atomic coordinates. J

Appl Crystallogr, 28:768–773.

Svergun, D., Petoukhov, M., and Koch, M. (2001). Deter-

mination of domain structure of proteins from x-ray

solution scattering. Biophys J, 80(6):2946–2953.

Svergun, D. I. and Stuhrmann, H. B. (1991). New develop-

ments in direct shape determination from small-angle

scattering. 1. theory and model calculations. Acta

Crystallogr A, 47(6):736–744.

Tjioe, E. and Heller, W. (2007). Ornl sas: software for cal-

culation of small-angle scattering intensities of pro-

teins and protein complexes. J Appl Crystallogr,

40:782–785.

Toft, K., Vestergaard, B., Nielsen, S., and Snakenborg, D.

(2008). High-throughput small angle x-ray scattering

from proteins in solution using a microﬂuidic front-

end. Anal Chem, 80(10):3648–3654.

Zheng, W. and Doniach, S. (2005). Fold recognition aided

by constraints from small angle x-ray scattering data.

Protein Eng Des Sel, 18(5):209–219.

BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms

108