
Similarity of Membership Functions
A Shaped based Approach
Ana Tapia-Rosero
1,2
, Antoon Bronselaer
2
and Guy De Tr
´
e
2
1
FIEC, Escuela Superior Polit
´
ecnica del Litoral, Campus Gustavo Galindo V, Guayaquil, Ecuador
2
Department of Telecommunications and Information Processing, Ghent University, Ghent, Belgium
Keywords:
Membership Function, Similarity, Cluster, Fusion, Decision-making.
Abstract:
In this paper, we propose a method to group similar membership functions, each of them representing the
opinion of an expert, to obtain a resulting membership function that represents alike opinions among a group.
The similarity is based on the shape characteristics of membership functions used to represent the expert
opinions on a specific criterion. There are several applications for the proposed method which include group
decision making, suitability analysis and consensual processes. In each of these applications diverse points of
view are present. The goals of the method are to detect similar membership functions, to establish a manner
that allows the selection of representative opinions and to obtain a result membership function that represents
a specific trend or a suitable concept for a group of similar membership functions. Our approach is based on
soft computing techniques, considering expert preferences as a matter of degree, including a novel method to
process similar opinions with more ease.
1 INTRODUCTION
A decision-making problem could be solved involv-
ing several experts, each of them, with a different
perspective of the problem (technical, economic, ad-
ministrative, etc.). When there are several people in-
volved it is desired to build a consensus; but some-
times if most of the experts follow a different trend
on the criteria (optimistic, risky, etc.), this is a hard
task to pursue. However, it is possible to suggest a
solution based on the fusion of similar opinions that
follow for a specific trend or which represent a suit-
able concept.
Nowadays, using soft computing techniques, a
person could express his/her expertise or preferences
through membership functions setting his/her level of
agreement over a specific criterion. It is not neces-
sary that all of the experts have preknowledge on soft
computing techniques to represent their preferences
P(x) as a matter of degree (i.e., 0 ≤ P(x) ≤ 1, where 0
denotes a complete disagreement on the criteria and 1
denotes the highest level of agreement) as long as they
provide some values (Dujmovi
´
c and De Tr
´
e, 2011)
that will be used for defining the attribute criterion in
a membership function.
For example, consider that a company has to de-
cide if a product will stay in the market or not based
on its “acceptable level of sales” (criterion). One
strategy to solve this decision-making problem is that
each expert uses a membership function to express
what he or she understands to be an acceptable sales
level. Nevertheless, we will have a number of mem-
bership functions that equals the number of experts
involved. If there is a large number of experts the de-
cision maker could be overwhelmed with all of their
opinions, and taking a final decision will become a
complex task. But, if there are some experts with sim-
ilar opinions (each opinion represented by a member-
ship function) in the group, it is possible to build clus-
ters considering the similarity of membership func-
tions in order to allow the decision maker to decide
among a reduced amount of opinions (Figure 1).
Among different experts, using membership
functions to represent the level of agreement over a
specific criterion, three scenarios might be possible:
1) all the experts have a similar opinion and hence
give a similar representation; 2) they all give a dis-
similar representation; or 3) there are several groups
of experts with similar representations. Considering
that all the experts contribute to some extent to the
final decision, all these scenarios deserve to be ana-
lyzed. However, this paper will focus only on the third
scenario reflecting the preferences of expert groups
with similar membership functions. Notice that the
402
Tapia-Rosero A., Bronselaer A. and De Tré G..
Similarity of Membership Functions - A Shaped based Approach.
DOI: 10.5220/0004148204020409
In Proceedings of the 4th International Joint Conference on Computational Intelligence (FCTA-2012), pages 402-409
ISBN: 978-989-8565-33-4
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)
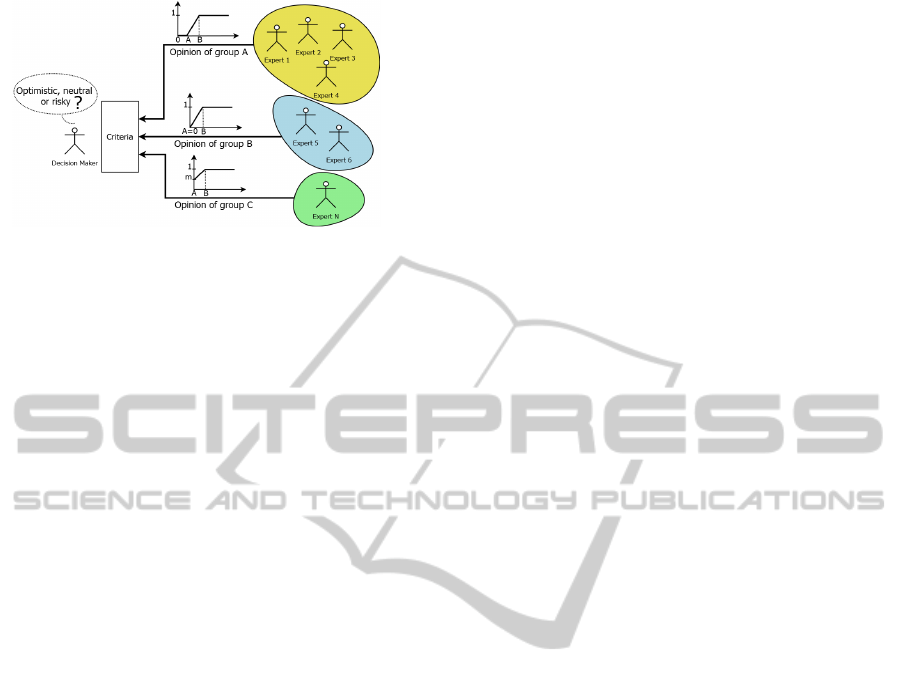
Figure 1: Representation of the opinions of multiple experts
grouped by similar membership functions.
remaining scenarios correspond to special cases of the
selected one.
A relevant question within the selected scenario
is: What happens if there exists a minority group
with a similar opinion (evaluation of the criteria) and
these experts are the most reliable among the others?
Should their opinions be considered or not? It is pos-
sible that this minority has relevant information that
should be considered related to the criteria or maybe
this minority is correct about some facts that may af-
fect the preference level.
There are several approaches to solve similar
decision-making problems. Some of them are focused
on the optimistic and the pessimistic points of view
(Rodr
´
ıguez et al., 2012) while others quantify the
number of experts that follow a trend (e.g., majority)
(Kacprzyk et al., 1992). Aditionally, there are various
similarity measures to compare fuzzy sets character-
ized by membership functions. This paper aims to
propose a method to group similar membership func-
tions using a shape based approach. This method al-
lows the decision-maker to select the group of opin-
ions that best suits the trend or concept of his/her
choice in order to obtain a resulting membership func-
tion that represent alike opinions among a group.
The proposed method uses a sequence of charac-
ters selected from a finite set of symbols {0, +, 1,
−, L, I, H} to annotate each membership function
considering slopes and different levels of agreement.
Within this paper, the term cluster will be used to rep-
resent a group of membership functions that have a
common shape characterized by the same character
string. As a result of the method a reduced amount
of opinions, each of them represented by a mem-
bership function, will be obtained. Several strate-
gies to fuse the membership functions, in a selected
group, could be considered; but, for illustrative pur-
poses only two basic operations are detailed within
this paper. Within the scope of this paper we will as-
sume that the decision-maker must select the cluster
of his/her preference to be analyzed taking into ac-
count that some sets of opinions could be, in some
extent, more representative than others.
The goals of the proposed method are: 1) to detect
similar membership functions, 2) to establish a man-
ner that allows the selection of representative opin-
ions and 3) to obtain a resulting membership function
that represents a specific trend or a suitable concept
of a group. This proposal is based on soft computing
techniques including the novelty of using a sequence
of characters to annotate and process similar opinions
represented by membership functions with ease.
The remainder of this paper is structured as fol-
lows. The second section includes some preliminary
concepts and related work. Section 3 provides details
on the main approach of this paper. Section 4 explains
the developed experiment. Section 5 concludes the
paper and proposes topics for further investigation.
2 PRELIMINARIES
A fuzzy set is a concept, fruitfully extended, from the
basic mathematical concept of a set (Zadeh, 1965).
According to Zadeh, a fuzzy set A on a universe X is
characterized by a membership function f
A
which as-
sociates each point x in X with a real number f
A
(x) in
the unit interval [0, 1 ] to represent its grade of mem-
bership in A. Values that are closer to the unit de-
note higher degrees of membership. Using a graph-
ical representation of the membership functions we
could identify different shape functions including the
trapezoidal membership function.
Trapezoidal membership functions, widely known
and frequently used for representing linguistic terms
(Klir and Yuan, 1995), have been selected in this pa-
per to represent the level of agreement of each expert
on the criteria. This selection has two main advan-
tages: 1) they could be built with only a few input val-
ues and 2) the definition of trapezoidal shaped func-
tions includes five intervals establishing a fixed form
to represent different kinds of trapeziums.
The values used to build trapezoidal membership
functions are represented by letters (a, b, c, d) and the
relation among these values is that a≤b≤c≤d. Cases
like triangular membership functions are treated as a
special case of trapezium where b=c.
2.1 Fuzzy Similarity
This paper establishes, as a starting point, that two
membership functions are considered to be similar if
they have a similar shape. In order to detect similar
membership functions with ease, we use a sequence
of characters to represent the shape of a membership
SimilarityofMembershipFunctions-AShapedbasedApproach
403

function. One remark within this respect is that the
symbolic annotation must be done in such a way that
membership functions symbolized with the same se-
quence of characters must represent the same trend or
concept as expressed by the expert.
There are several ways to compare fuzzy sets and,
nowadays, various similarity measures have been dis-
cussed (Zwick and Carlstein, 1987; Le Capitaine,
2012). It is well known that most of the similarity
measures are either based on similarity relations, dis-
tance among fuzzy sets or set-theoretic operations.
2.1.1 Similarity Relations
The similarity relation definition was introduced by
(Zadeh, 1971) as an extension of the equivalence re-
lation concept for crisp sets. The definition states that
a similarity relation S on a universe X is a fuzzy rela-
tion that holds the following properties for all x, y, z
∈ X:
S(x,x) = 1 Reflexivity
S(x,y) = S(y,x) Symmetry
S(x,y) ∧ S(y, z) ≤ S(x, z) Transitivity
These properties have been considered in several
studies and we will recall the fuzzy similarity measure
for fuzzy sets defined by Le Capitaine (2012):
A mapping S: F(X) x F(X) → [0, 1 ], with F(X)
denoting the powerset of all fuzzy sets that can be de-
fined on X, is called a similarity measure if it satisfies:
P1. S(A,B) = S(B,A)
P2. S(A,A) = 1
P3. S(A,A
C
) = 0, A
C
denotes the complement of A
P4. A ⊆ B ⊆ C ⇒ S(A,C) ≤ S(A, B) ∧ S(B,C)
2.1.2 Distance among Fuzzy Sets
We found extensive literature (Xuecheng, 1992; Lee-
Kwang et al., 1994; Johany
´
ak and Kov
´
acs, 2005)
defining different measures for the distance d(x, y)
between objects x and y based on known metrics
(e.g., Hausdorff, Hamming and Euclidean distances).
The notion of a distance between fuzzy sets has been
used as a measure of similarity, although some of
these similarity measures are considered theoretical
approaches because they suppose the existence of an
“ideal” fuzzy set (Merig
´
o and Casanovas, 2010). On
the other hand, most of the decision-making problems
do not have a given “ideal” solution considering that
we are looking for a resulting fuzzy set that better rep-
resents a trend or a concept in a given context.
To the best of our knowledge none of the dis-
tance based proposals make a distinction related to
the shape of the membership functions.
2.1.3 Set-theoretic Operations
This paper recalls the basic definitions of the
union and intersection operations proposed by Zadeh
(1965), considering two fuzzy sets A, B with respec-
tive membership functions f
A
and f
B
defined on the
same universe X:
f
A∪B
(x) = max[f
A
(x), f
B
(x)], ∀x ∈ X (1)
f
A∩B
(x) = min[f
A
(x), f
B
(x)], ∀x ∈ X (2)
We must regard that other definitions based on tri-
angular norms and triangular conorms can be used
(e.g., the product and the probabilistic sum, the
Lukasiewicz t-norm and t-conorm, among others) to
combine the membership functions among a group.
There are several similarity measures based on
set-theoretic operations including Tversky (1977),
Dice (1945) and Jaccard indexes (1908). Within the
scope of this proposal, the main disadvantage on these
set-theoretic operations is that loss of information is
possible. Besides, it is feasible to consider that the
resulting membership functions could also include a
degree of confidence to represent to what extent the
decision maker agrees on the resulting membership
function.
3 SIMILAR MEMBERSHIP
FUNCTIONS
This proposal is based on detecting similar member-
ship functions by comparing character strings. The
aforementioned string is easily built and it corre-
sponds to a sequence of characters that represents
the shape of a normalized membership function. Af-
ter the membership functions are clustered based on
their similarity this method incorporates two addi-
tional steps: 1) to choose a group of membership
functions that best suits the trend or concept accord-
ing to the selection of the decision-maker, and 2) to
select a strategy for fusion of the membership func-
tions that belong to the selected group.
3.1 String Representation for
Membership Functions
Bearing in mind that trapezoidal membership func-
tions have been selected, we could identify, graphi-
cally, the presence of segments in a trapezium shape.
These segments are based on the intervals of the trape-
zoidal membership function definition and all of them
belong to one of the following categories: positive
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
404

slope, negative slope, fully disagreement level, fully
agreement level, or point.
Each segment of the trapezium will use a symbol
among a sign {+, −} to represent the slope, a value
{0, 1} to represent the level of agreement (on seg-
ments without a slope) and a letter {L, I, H} to de-
note a point. The string representation of the mem-
bership function is built concatenating the character
that represents each segment considering the order in
the x-axis. Each character must correspond to a sin-
gle category. Figure 2, illustrates a trapezium and its
corresponding categories.
Figure 2: Segments of a trapezium and its categories.
The string representation of the presented trapez-
ium is “0+1−0” where each character of the string
corresponds to each segment of its function definition.
A feature that is noticeable graphically in some
trapezoidal membership functions is the absence of
segments on their shape. This case could be annotated
likewise resulting in shorter strings (Figure 3).
Figure 3: Examples of short string representations for mem-
bership functions.
The point category has a special use to depict a
specific value (on the x-axis) of non continuous func-
tions. In this case, we must represent this special
point with a letter corresponding to its level of agree-
ment. For simplicity, the letter is selected according
to the (high, intermediate or low) value of member-
ship at the mentioned point. Notice that the member-
ship functions of Figure 4, without the point category,
would be represented by the same string.
Figure 4: Examples of the string representations using the
point category in non continuous functions.
A triangular membership function is a special case
where b=c that is also annotated using a point cate-
gory. In this case we must represent the b=c point
at the highest (H) level of agreement for normalized
membership functions. In addition, the point cat-
egory allows representing different kinds of mem-
bership functions including those that have segments
with extreme values (start or end of the segment) at
intermediate levels of agreement. These membership
functions require representing the intermediate point
with the corresponding letter (Figure 5).
Figure 5: Examples of the string representation using the
point category at high and intermediate level of agreement.
The proposed string could represent different
kinds of membership functions using characters as de-
scribed before. Nevertheless, this method might be
extended in order to include other characteristics of
shapes (e.g., small core or long support based on a
threshold). Other adjustments could allow represent-
ing periodical functions and other special cases not
considered within the scope of this paper.
3.2 Similarity Measure
Within the scope of this paper, the similarity of mem-
bership functions is based on their shape characteris-
tics disregarding aspects as linear shifting. The shape
characteristics include the presence of slopes and lev-
els of agreement, components that are present in the
string representation detailed in Section 3.1.
To detect if two membership functions are similar
we need to accomplish the properties mentioned in
Section 2.1.1. This paper will use a straightforward
similarity measure based on the string representation
of the membership functions as follows:
S(A, B) =
0 , StrA 6= StrB
1 , StrA = StrB
(3)
where StrA and StrB are the string representations of
the corresponding membership functions.
The selected similarity measure will give us a
value, where 0 denotes no similarity and 1 denotes full
similarity among two fuzzy sets based on the shape of
their membership functions. Notice that the proposed
similarity measure allowed us to achieve the reflexiv-
ity, symmetry and transitivity properties.
3.3 Grouping Similar Membership
Functions
This proposal aims to build groups of membership
functions that represent a trend or concept in a
SimilarityofMembershipFunctions-AShapedbasedApproach
405

decision-making environment. Considering that sev-
eral experts might be involved and each expert could
suggest a membership function that represents his/her
level of agreement over a specific criterion, we should
group those membership functions that are consid-
ered similar. According to the similarity measure in
(3), two membership functions are considered simi-
lar if they have the same string representation. Within
this paper, the term cluster will be used to represent
a group of membership functions that have a com-
mon shape characterized by the same string; and it
is possible to obtain a cluster that contains a single
membership function. An important remark is that
membership functions that belong to the same cluster
or group accomplished the commutative, distributive
and associative properties to be considered similar.
3.4 Cluster Profile
Considering that all experts contribute to some ex-
tent to the final decision then all clusters deserve to
be analyzed; Furthermore, if we compare the number
of membership functions, that belongs to each clus-
ter, we could evaluate if a specific cluster represents
a majority, a minority or the same number of opin-
ions expressed by the membership functions present
in other clusters. It is achievable that some problems
could have a solution based on this number, but if we
return to the introductory questions it is possible that
other characteristics of the cluster must be taken into
account (e.g., the reliability of experts). It is possi-
ble that trying to represent the expert reliability might
become a subjective task. However, it is also possi-
ble that this reliability could be built based on some
characteristics that reflect the expert experience (e.g.,
number of hits on historic representations within the
same context).
3.5 Fusion of Similar Membership
Functions
When several membership functions are present to
represent a single trend or concept it is necessary to
select a strategy to obtain, as a result, the most repre-
sentative membership function. If we consider apply-
ing the set-theoretic operations to the following alter-
natives: a)the complete set of available membership
functions; b)a reduced set of membership functions
grouped by shape-similarity; then remarkable differ-
ences in the results are expected. For illustrative pur-
poses, this paper includes the results of applying the
union and intersection functions to both alternatives.
4 DEVELOPED EXPERIMENT
Considering that membership functions could be built
with some values to define the attribute criterion (Du-
jmovi
´
c and De Tr
´
e, 2011) and that several member-
ship functions were required to pursue the goals of
this paper an experiment was developed. A small
form was sent to different groups of people to col-
lect the values that will represent the agreement (of
each person) on a specific criterion. The groups were
not uniform considering different levels of knowledge
(students and profesionals), areas of expertise (engi-
neering, medicine and journalism) and personal pro-
files (single, married, parents, etc.). All the partici-
pants were adults (age≥18) with knowledge of ver-
balized terms that represent people’s age. The form
asked the participants, to suggest the range of ages
that they considered representative for different terms
like “baby”, “child” and “toddler”.
Two main cases were distinguished: 1) Some par-
ticipants expressed their preference among small val-
ues trying to represent that the term “baby” is suitable
since a boy or a girl was born until a certain age, and
2) other participants expressed their preference using
a range of values for fully agreement and fully dis-
agreement to represent the term “baby” (i.e., they use
the term “new born” for a small period).
4.1 Building the Membership Functions
A total of 74 membership functions were built using
the (a, b, c, d) values. Among participants who pre-
ferred small values, as shown in Figure 6, we distin-
guished cases where c6=d and others where c=d. The
last case depicts a non continuous function where c
represents fully agreement and values greater than d
represent fully disagreement.
Figure 6: Membership functions for preferred small values.
Among participants who preferred ranges of val-
ues we found cases where c<d and cases where c=d.
The last case represents a non continuous membership
function (Figure 7).
Figure 7: Membership functions for preferred range of val-
ues.
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
406
4.2 Detection of Similarity
The similarity is based on the shape characteristics
(slope, levels of agreement and continuity) of the
available membership functions represented by a se-
quence of characters. When the string representation
of each membership function is obtained, the similar-
ity detection based on the similarity measure stated in
(3) is performed. Equation 3 is the basis of a string
comparison where the same string represents a sim-
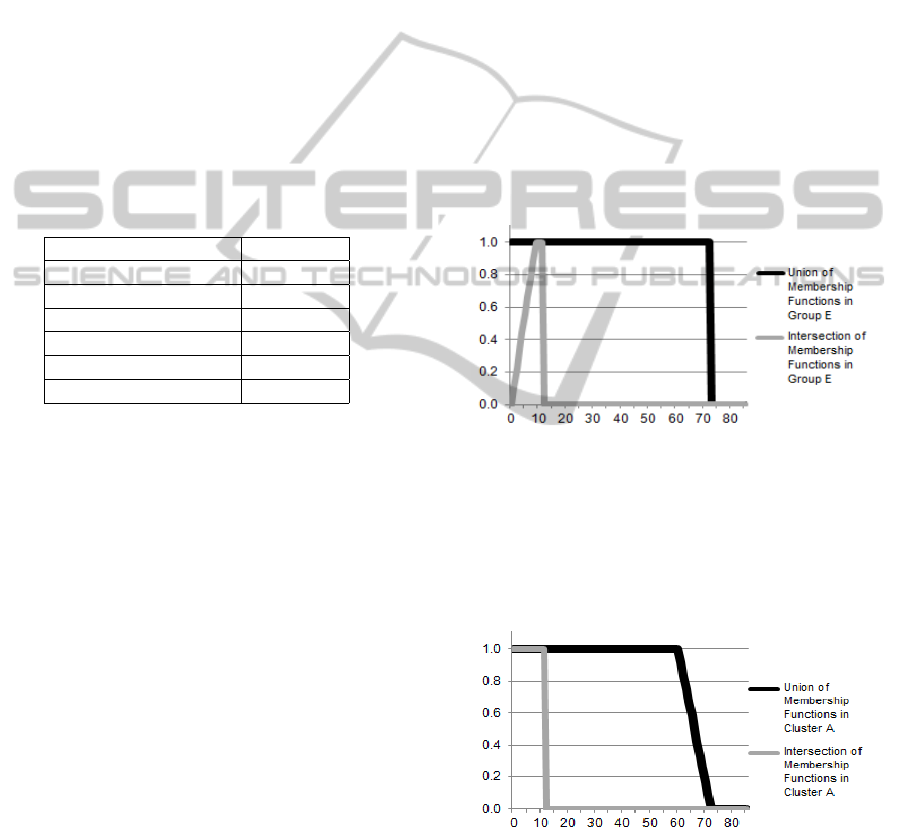
ilar shape. Table 1, shows the number of member-
ship functions on each group (represented by a string).
Note that two of these groups have a high number of
membership functions, which is consistent, because
“graphs of membership functions (elicited from dif-
ferent subjects) tend to have the same shape” (Klir
and Yuan, 1995).
Table 1: String representations and their corresponding fre-
quency.
String Representation Frequency
+1−0 1
+1H0 1
1−0 34
1H0 33
L1−0 1
L1H0 4
4.2.1 Selection of a Representative Opinion
To establish a manner that allows the selection of rep-
resentative opinions we prefer taking into account the
characteristics mentioned in Section 3.4. However,
within the scope of this paper we will assume that the
decision-maker will select the cluster of opinions that
best suits the trend or concept of his/her choice to be
analyzed.
In our case, we selected a cluster that represents
our preference expressed by a trapezoidal member-
ship function using small values. This selection tries
to represent that the term “baby” is suitable to rep-
resent the period starting when a boy or a girl was
born until a certain age. Our selection during the per-
formed experiment is the group represented by the
string “1−0” and we will refer to it as cluster A. Clus-
ter A corresponds to a majority, containing 34 trape-
zoidal membership functions. We will consider that
cluster A has a high reliability taking into account that
our participants have knowledge of verbalized terms
that represent ages including the term “baby”.
4.3 Fusion of Membership Functions
The union and intersection operations on fuzzy sets
were selected as basic operations to illustrate the
shape-similarity of membership functions. These set-
theoretic operations were executed over cluster A and
the entire group of membership functions. From now
on, we will refer to the entire group of membership
functions as group E.
The union and intersection operations use equa-
tions (1) and (2) respectively ∀x ∈ [0, n] where n is
greater than all the values d given by the participants.
The purpose of applying these operations is to ob-
tain as a result a reduced amount of opinions rep-
resented by a fuzzy set. For example, the group E
that contains 74 membership functions could be rep-
resented by the result of the union or the intersection
operation shown in Figure 8.
Figure 8: Result membership functions of Group E.
In an analogous form, the cluster A that con-
tains 34 similar-shaped membership functions could
be represented by the union operation or the intersec-
tion of its membership functions. Figure 9 shows the
result membership functions of these operations.
Figure 9: Result membership functions of Cluster A.
As expected, we obtain some differences between
the union and intersection operations over the com-
plete set of membership functions (Group E) and a re-
duced set of membership functions grouped by shape-
similarity (Cluster A). Graphically we could observe
that using the fusion of the membership functions of
SimilarityofMembershipFunctions-AShapedbasedApproach
407

a selected cluster will give us better results than se-
lecting the fusion of the entire group of membership
functions. This is confirmed by calculating the mem-
bership function over the set-theoretic operations on
group E and cluster A. It is seen that the membership
grades in group E for small values (x≤10) are lower
than the membership grades in cluster A for the same
values.
For validation purposes, other clusters were ana-
lyzed and we obtained similar results but they are not
shown here due to space limits. Based on set-theoretic
operations, several membership functions were fu-
sioned to obtain a result membership function that
represents a trend or a suitable concept among several
opinions. Although, we have presented our results us-
ing the basic operations proposed by Zadeh, we have
evaluated our proposal with: 1) the Lukasiewicz t-
norm and t-conorm; and 2) the product and the proba-
bilistic sum. However, we obtained slightly different
results only for the t-norm over group E. More ad-
vanced fusion techniques are possible and subject to
further study. Here the use of union and intersection
operations are used to demonstrate the shape-based
similarity of membership functions.
5 CONCLUSIONS AND FURTHER
WORK
This paper proposed a novel method to annotate mem-
bership functions and build a string representation for
them. This string is used to detect similar-shaped
membership functions by string comparisons.
Similar membership functions were clustered con-
sidering that they represent a trend or a suitable con-
cept in a decision-making context. We proposed some
cluster characteristics to be taken into account for fur-
ther analysis. Additionally, for any selected cluster,
positive differences are obtained when comparing the
complete set of membership functions and a reduced
set grouped by shape-similarity.
The cluster selected for fusion is further processed
using set-theoretic operations. Other strategies are ex-
posed for further consideration.
The proposed similarity measure could be ex-
tended in order to take into account other shape char-
acteristics like the core length (e.g., a triangular mem-
bership function and a trapezoidal membership func-
tion with a tiny core).
This proposal settles some opportunities for future
work on different areas where diverse points of view
are present like group decision-making and suitability
analysis. Some application areas like fuzzy control,
based on this proposal (e.g., to find similarities on rule
engines) among other applications could be explored.
ACKNOWLEDGEMENTS
This research is supported by Escuela Superior
Polit
´
ecnica del Litoral (ESPOL) and it is financed by
Secretar
´
ıa de Educaci
´
on Superior en Ciencia y Tec-
nolog
´
ıa (SENESCYT) under Ph.D. studies 2012.
REFERENCES
Bouchon-Meunier, B. and Rifqi, M. (1996). Towards gen-
eral measures of comparison of objects. Fuzzy Sets
and Systems, 84:143–153.
Dice, L. R. (1945). Measures of the Amount of Ecologic
Association Between Species. Ecology, 26(3):297–
302.
Dubois, D. and Prade, H. (1980). Fuzzy Sets and Systems:
Theory and Applications. Academic Press, Inc.
Dujmovi
´
c, J. and De Tr
´
e, G. (2011). Multicriteria meth-
ods and logic aggregation in suitability maps. Inter-
national Journal of Intelligent Systems, 26(10):971–
1001.
Jaccard, P. (1908). Nouvelles recherches sur la distribution
florale. Bulletin de la Soci
`
ete Vaudense des Sciences
Naturelles, 44:223–270.
Johany
´
ak, Z. and Kov
´
acs, S. (2005). Distance based sim-
ilarity measures of fuzzy sets. Proceedings of SAMI,
1.
Kacprzyk, J., Fedrizzi, M., and Nurmi, H. (1992). Group
decision making and consensus under fuzzy prefer-
ences and fuzzy majority. Fuzzy Sets and Systems,
49(1):21–31.
Klir, G. J. and Yuan, B. (1995). Fuzzy Sets and Fuzzy Logic:
Theory and Applications. Prentice Hall.
Le Capitaine, H. (2012). A relevance-based learning model
of fuzzy similarity measures. IEEE Transactions on
Fuzzy Systems, 20(1):57–68.
Lee-Kwang, H., Song, Y.-S., and Lee, K.-M. (1994). Sim-
ilarity measure between fuzzy sets and between ele-
ments. Fuzzy Sets and Systems, 62(3):291–293.
Merig
´
o, J. and Casanovas, M. (2010). Decision mak-
ing with distance measures and linguistic aggregation
operators. International Journal of Fuzzy Systems,
12(3):190–198.
Rodr
´
ıguez, R. M., Mart
´
ınez, L., and Herrera, F. (2012).
Hesistant Fuzzy Linguistic Term Sets for Decision
Making. IEEE Transactions on Fuzzy Systems,
20(1):109–119.
Tversky, D. (1977). Features of similarities. Psychological
Review, 84:327–352.
Xuecheng, L. (1992). Entropy, distance measure and simi-
larity measure of fuzzy sets and their relations. Fuzzy
Sets and Systems, 52(3):305–318.
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
408

Zadeh, L. (1965). Fuzzy sets. Information and control,
8(3):338–353.
Zadeh, L. (1971). Similarity relations and fuzzy orderings+.
Information sciences, 3(2):177–200.
Zwick, R. and Carlstein, E. (1987). Measures of similarity
among fuzzy concepts: A comparative analysis. In-
ternational Journal of Approximate, pages 221–242.
SimilarityofMembershipFunctions-AShapedbasedApproach
409
