Towards Multi-agent Reinforcement Learning using

Quantum Boltzmann Machines

Tobias M

uller, Christoph Roch, Kyrill Schmid and Philipp Altmann

Mobile and Distributed Systems Group, LMU Munich, Germany

Keywords:

Multi-agent, Reinforcement Learning, D-Wave, Boltzmann Machines, Quantum Annealing, Quantum

Artiﬁcial Intelligence.

Abstract:

Reinforcement learning has driven impressive advances in machine learning. Simultaneously, quantum-

enhanced machine learning algorithms using quantum annealing underlie heavy developments. Recently, a

multi-agent reinforcement learning (MARL) architecture combining both paradigms has been proposed. This

novel algorithm, which utilizes Quantum Boltzmann Machines (QBMs) for Q-value approximation has out-

performed regular deep reinforcement learning in terms of time-steps needed to converge. However, this

algorithm was restricted to single-agent and small 2x2 multi-agent grid domains. In this work, we propose

an extension to the original concept in order to solve more challenging problems. Similar to classic DQNs,

we add an experience replay buffer and use different networks for approximating the target and policy values.

The experimental results show that learning becomes more stable and enables agents to ﬁnd optimal policies

in grid-domains with higher complexity. Additionally, we assess how parameter sharing inﬂuences the agents’

behavior in multi-agent domains. Quantum sampling proves to be a promising method for reinforcement

learning tasks, but is currently limited by the Quantum Processing Unit (QPU) size and therefore by the size

of the input and Boltzmann machine.

1 INTRODUCTION

Recently, adiabatic quantum computing has proven

to be a useful extension to machine learning tasks

(Benedetti et al., 2018; Biamonte et al., 2017; Li et al.,

2018; Neukart et al., 2017a). Especially hard com-

putational tasks with high data volume and dimen-

sionality have beneﬁtted from the possibility of using

quantum devices with manufactured spins to speed-

up computational bottlenecks (Neven et al., 2008;

Rebentrost et al., 2014; Wiebe et al., 2012).

One speciﬁc type of machine learning is Rein-

forcement Learning (RL), where an interacting entity,

called agent, aims to learn an optimal state-action pol-

icy through trial and error (Sutton and Barto, 2018).

Reinforcement Learning has gained the public atten-

tion by defeating the 9-dan Go grandmaster Lee Sedol

(Silver et al., 2016), which has been thought to be

impossible for a machine. In the latest years, re-

inforcement learning has seen many improvements,

gained a large variety of application ﬁelds like eco-

nomics (Charpentier et al., 2020), autonomous driv-

ing (Kiran et al., 2020), biology (Mahmud et al.,

2018) and even achieved superhuman performance

in chip design (Mirhoseini et al., 2020). Reinforce-

ment Learning has only seen quantum speed-ups for

specials models (Levit et al., 2017; Neukart et al.,

2017a; Neukart et al., 2017b; Paparo et al., 2014).

Especially multi-agent domains have rarely been re-

searched (Neumann et al., 2020).

Real-world reinforcement learning frameworks

predominantly use deep neural networks (DNNs) as

function approximators. Since DNNs are powerful -

see the latest prominent example AlphaFold2 (Jumper

et al., 2020) - and can be run efﬁciently for large

datasets on classical computers, deep reinforcement

learning is able to tackle complex problems in large

data spaces. Hence, there was little need for improve-

ments.

However, since recent work has proved speed-

ups for classical RL by leveraging quantum comput-

ing (Levit et al., 2017; Neumann et al., 2020) and

the application ﬁeld gets more and more complex,

it could be beneﬁcial to explore quantum RL algo-

rithms. These inspiring studies considered Boltzmann

machines (Ackley et al., 1985) as function approxi-

mator - instead of traditionally used DNNs. Boltz-

mann machines are stochastic neural networks, which

Müller, T., Roch, C., Schmid, K. and Altmann, P.

Towards Multi-agent Reinforcement Learning using Quantum Boltzmann Machines.

DOI: 10.5220/0010762100003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 1, pages 121-130

ISBN: 978-989-758-547-0; ISSN: 2184-433X

121

are mainly avoided due to the fact, that their training

times are exponential to the input size. Since ﬁnd-

ing the energy minimum of Boltzmann machines can

be formulated as a ”Quadratic Unconstrained Binary

Optimization” (QUBO) problem, simulated anneal-

ing respectively quantum annealing is well suited to

accelerate training time.

Nevertheless, the combination of RL and Boltz-

mann machines using (simulated) quantum annealing

only worked properly for small single-agent environ-

ments and reached its limit at a simple 3 × 3 multi-

agent domain. This work proposes an architecture in-

spired by DQNs (Mnih et al., 2015) to enable more

complex domains and stabilize learning by using ex-

perience replay buffer and separating policy and tar-

get networks. We thoroughly evaluate the effects of

these augmentations on learning.

Lately, an inspiring novel method to speed-up

quantum reinforcement learning for large state and

action spaces by proposing a combination of reg-

ular NNs and DBMs/QBMs, namely Deep Energy

Based Networks (DEBNs) was proposed (Jerbi et al.,

2020). More speciﬁcally, these architectures are con-

structed with an input layer consisting of action and

state units, which are connected with the ﬁrst hidden

layer through directed weights. This is followed by

a single undirected stochastic layer. The remaining

layers are linked with directed deterministic connec-

tions. Lastly, a ﬁnal output layer returns the negative

free energy −F(s, a).

In contrast to QBMs, DEBNs therefore only com-

prise one stochastic layer, return an output similar to

traditional deep neural networks and can be trained

through backpropagation. DEBNs also use an expe-

rience replay buffer and separate the policy and tar-

get network. Additionally, they allow to trade off

learning performance for efﬁciency of computation.

Jerbi et al. brieﬂy stated, that QBMs are applica-

ble. Unfortunately, no numerical results were given

for purely stochastic, energy-based QBM agents or

domains with multiple agents. We aim to build on

this.

Summarized, our contribution is three-fold:

• We provide a Quantum Reinforcement Learn-

ing (Q-RL) framework, which stabilizes learning

leading to more optimal policies

• Based on single- and multi-agent domains, we

provide a thorough evaluation on the effects of an

Experience Replay Buffer and an additional Tar-

get Network compared to traditional QBM agents

• Additionally, we demonstrate and discuss limita-

tions to the concept

We ﬁrst describe the preliminaries about rein-

forcement learning and quantum Boltzmann ma-

chines underlying the proposed architectures. After-

wards, the state-of-the-art algorithm and extensions

made to it will be explained. We test and evaluate the

approach and ﬁnally discuss restrictions and potential

grounds for future work.

2 PRELIMINARIES

This chapter describes the basics needed to under-

stand our proposed architecture. First, reinforcement

learning and the underlying Markov Decision Process

will be explained followed by Boltzmann Machines

and the process of quantum annealing.

2.1 Reinforcement Learning

We ﬁrst describe Markov Decision Processes as the

underlying problem formulation which is followed by

an introduction to reinforcement learning in general.

The subsequent sections specify independent and co-

operative multi-agent reinforcement learning.

Markov Decision Processes. The problem formu-

lation is based on the notion of Markov Decision Pro-

cesses (MDP) (Puterman, 1994). MDPs are a class

of sequential decision processes and described via the

tuple M = hS, A, P, Ri, where

• S is a ﬁnite set of states and s

∈ S the state of the

MDP at time step t.

• A is the set of actions and a

∈ A the action the

MDP takes at time step t.

• P(s

t+1

, a

) is the probability transition function.

It describes the transition that occurs when action

is executed in state s

. The resulting state s

t+1

is chosen according to P.

• R(s

, a

) is the reward, when the MDP takes action

in state s

. We assume R(s

, a

) ∈ R

Consequently, the cost and transition function

only depend on the current state and action of the

system. Eventually, the MDP should ﬁnd a policy

π : S → A in the space of all possible policies Π, which

maximizes the return G

at state s

over an inﬁnite

horizon via:

∞

∑

k=0

· R(s

t+k

, a

t+k

), (1)

with γ ∈ [0, 1] as the discount factor. This policy is

called the optimal policy π.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

122

Reinforcement Learning. Model-free reinforce-

ment learning (Strehl et al., 2006) is considered to

search the policy space Π in order to ﬁnd the opti-

mal policy π

∗

. The interacting reinforcement learn-

ing agent executes an action a

for every time step

t ∈ [1, ..] in the MDP environment. In model-free al-

gorithms, the agent acts without any knowledge of the

environment and the algorithm only keeps informa-

tion of the value-function. Therefore, the agent knows

its current state s

and the action space A, but neither

the reward nor the next state s

t+1

of any action a

any state s

Consequently, the agent needs to learn from delayed

rewards without having a model of the environment.

A popular value-based approach to solve this problem

is Q-learning (Peng and Williams, 1994). In this ap-

proach, the action-value function Q

: SxA → R, π ∈ Π

describes the accumulated reward Q

, a

) for an ac-

tion a

in state s

. The optimal Q-learning function Q

∗

is approximated by starting from an initial guess for

Q and updating the function via:

Q(s

, a

) ← Q(s

, a

) + α[r

+ γ max

Q(s

t+1

, a) − Q(s

, a

)]

(2)

The learned Q-function will eventually converge

to Q

∗

, which then implies an optimal policy. In the

traditional experiments a deep neural network is used

as a parameterized function approximator to calculate

the optimal action for a given state.

Independent Multi-agent Learning. When mul-

tiple agents interact with the environment, A fully

cooperative multi-agent task can be described as a

stochastic game G, deﬁned as in (Foerster et al., 2017)

via the tuple G = hS, A, P, R, Z, O, n, γi, where:

• S is a ﬁnite set of states. At each time step t, the

environment has a true state s

∈ S.

• A is the set of actions. At each time step t each

agent ag simultaneously chooses an action a

∈

A, forming a joint action a ∈ A ≡ A

• P(s

t+1

, a

) is the probability transition function

as previously deﬁned.

• R(s

, a

) is the reward as previously deﬁned. All

agents share the same reward function.

• Z is a set of observations of a partially or fully

observable environment.

• O(s, ag) is the observation function. Each agent

draws observations z ∈ Z according to O(s, ag).

• n is the number of agents identiﬁed by ag ∈ AG ≡

{1, ..., n}.

• γ ∈ [0, 1) is the discount factor.

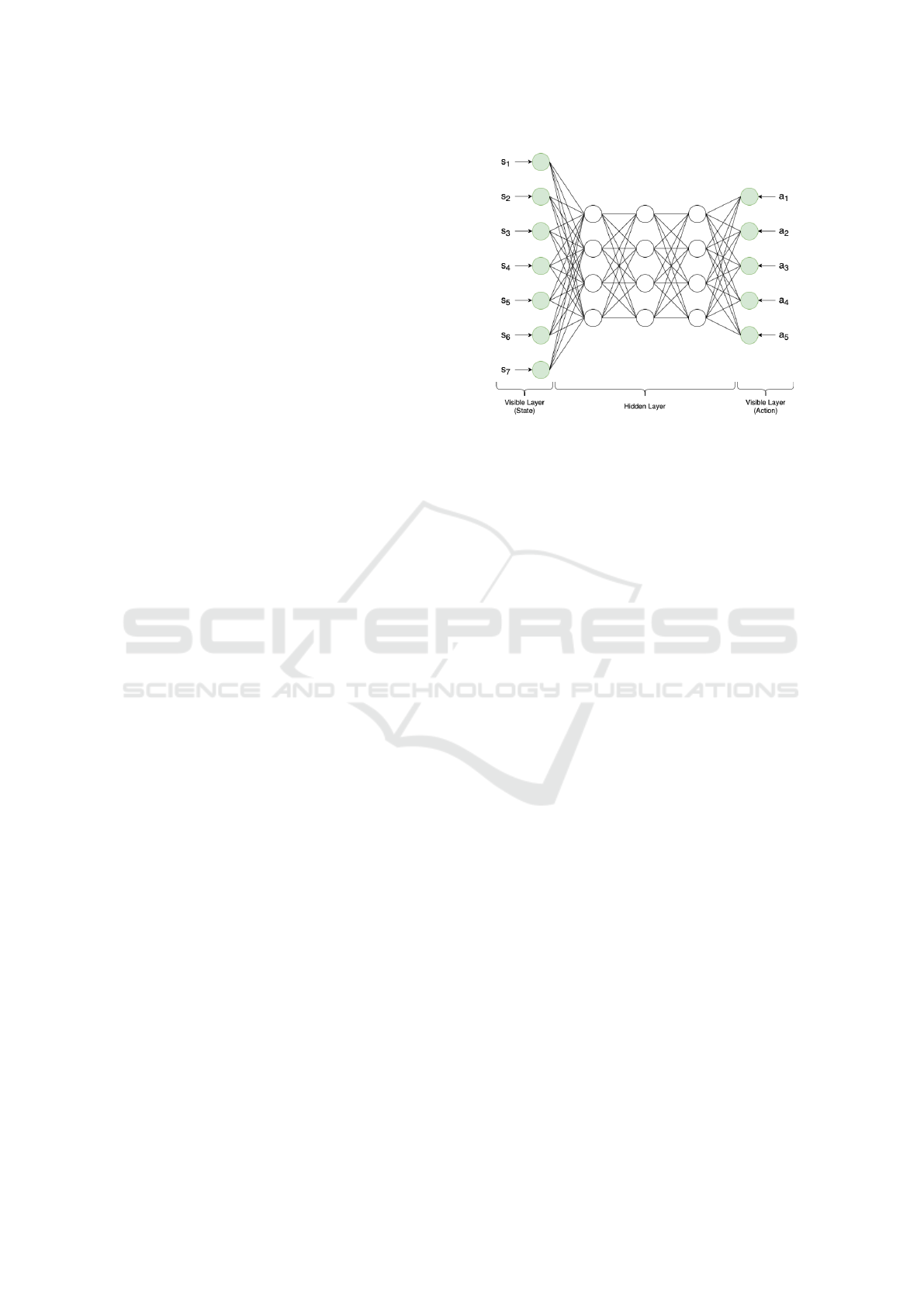
Figure 1: A Deep Quantum Boltzmann Machine with seven

input state neurons and ﬁve input action neurons. The QBM

additionally consists of three hidden layers with four neu-

rons each. The state and action are given as ﬁxed input

and the conﬁguration of the hidden neurons are sampled via

(simulated) quantum annealing. The weights between two

neurons are updated in the Q-learning step as described in

section 3.

In independent multi-agent learning algorithms, each

agent learns from its own action-observation history

and is trained independently. This means, every agent

simultaneously learns its own Q-function (Tan, 1993).

2.2 Boltzmann Machines

The structure of a Boltzmann machine (BM) (Ack-

ley et al., 1985) is similar to Hopﬁeld networks and

can be described as a stochastic energy-based neural

network. A traditional BM consists of a set of visi-

ble nodes V and a set of hidden nodes H, where ev-

ery node represents a binary random variable. The

binary nodes are connected through real-valued, bidi-

rected, weighted edges of the underlying undirected

graph. The global energy conﬁguration is generally

given by the energy level of Hopﬁeld networks. Since

clamped BMs ﬁx the assignment of the visible binary

variables, these nodes are removed from the under-

lying graph and contribute as constant coefﬁcients to

the associated energy. Therefore the formula, which

we aim to minimize, is given as the energy level of

Hopﬁeld networks with constant visible nodes:

E(h) = −

∑

−

∑

j j

−

∑

i j

, (3)

with v

as the visible nodes, h

as the hidden nodes

and weights w.

For this work, we implemented a Deep Boltzmann

Machine (DBM) as trainable state-action approxima-

tor, which is constructed with multiple hidden layers,

Towards Multi-agent Reinforcement Learning using Quantum Boltzmann Machines

123

one visible input layer for the state and one visible ac-

tion input layer. Finally, we modiﬁed the DBM to get

a Quantum Boltzmann Machine (QBM), where qubits

are associated to each node of the network instead of

random binary variables (Crawford et al., 2019; Neu-

mann et al., 2020; Levit et al., 2017). A visualization

of a QBM for seven state neurons and ﬁve input action

neurons can be seen in ﬁgure 1. For any QBM with

v ∈ V and h ∈ H, the energy function is described by

the quantum Hamiltonian H

= −

∑

v,h

vσ

−

∑

v,v

−

∑

h,h

− Γ

∑

(4)

Furthermore, Γ is the annealing parameter, while

and σx

are spin-values of node i in the z− and

x− direction. Because measuring the state of one

direction destroys the state of the other, we follow

the architecture of Neumann et al. (2020) (Neumann

et al., 2020) and replace all σ

by σ

by using replica

stacking based on the Suzuki-Trotter expansion of the

Hamiltonian H

. The BM is replicated r times in to-

tal and connections between corresponding nodes in

adjacent replicas are added. By this, we obtain a new

effective Hamiltonian H

e f f

v=(s,a)

in its clamped version

given by:

e f f

v=(s,a)

= −

∑

h∈H

h−s ad j

∑

k=1

h,k

−

∑

h∈H

h−a ad j

∑

k=1

h,k

−

∑

(h,h

)⊆H

∑

k=1

h,k

− Γ

∑

h∈H

∑

k=0

h,k

h,k+1

(5)

For each evaluation of the Hamiltonian, we get a

spin conﬁguration

h. After n

reads

reads for a ﬁxed

combination of s and a, we get a multi-set

s,a

{

, ...,

reads

}. We average over this multi-set to gain

a single spin conﬁguration C

s,a

, which will be used

for updating the network. If a node is +1 or −1 de-

pends on the global energy conﬁguration:

node i=1

1 + exp(−

∆E

)

, (6)

with T as the current temperature.

Since the structure of Boltzmann Machines are

inherent to Ising models, we sample spin values

from the Boltzmann distribution by using simulated

quantum annealing, which simulates the effect of

transverse-ﬁeld Ising model by slowly reducing the

temperature or strength of the transverse ﬁeld at ﬁnite

temperature to the desired target value (Levit et al.,

2017). As proven in (Morita and Nishimori, 2008),

spin system deﬁned by simulated quantum annealing

converges to quantum Hamiltonian. Therefore it is

straightforward to use simulated quantum annealing

(SQA) to ﬁnd a spin conﬁguration for h ∈ H - given

s ∈ S - which minimizes the free energy.

3 QUANTUM REINFORCEMENT

LEARNING

Recently, quantum reinforcement learning algorithms

(QRL) using boltzmann machines and quantum an-

nealing of single agent (Crawford et al., 2019) and

multi-agent domains (Neumann et al., 2020) for learn-

ing grid-traversal policies have been proposed. Al-

though, these architectures were able to learn opti-

mal policies in less time steps compared to classic

deep reinforcement learners (DRL), they could only

be applied to single-agent or small multi-agent do-

mains. Unfortunately, already 3 × 3 domains with 2

agents could not be solved optimally (Neumann et al.,

2020). QRL seems to be unstable for more complex

domains. We intuitively assume that BMs underlie

similar instability problems as traditional neural net-

works. Hence, by correlations present in the sequence

of observations and how small updates to the Q-values

change the policy, data distribution and therefore the

correlations between free energy F(s

, a

) and target

energy F(s

n+1

, a

n+1

). Inspired by Deep Q-Networks

(Mnih et al., 2015), we propose to enhance the state-

of-the-art architecture as described in section 3.1 by

adding an experience replay buffer (see section 3.2)

to randomize over transitions and by separating the

network calculating the policy and the network ap-

proximating the target value (see section 3.3) in order

to reduce correlations with the target.

3.1 State of the Art

Traditionally, single-agent reinforcement learning us-

ing quantum annealing and QBMs is an adaption

of Sallans and Hintons (2004) (Sallans and Hinton,

2004) RBM RL algorithm and structured as follows:

Initialization. The weights of the QBM are initial-

ized by setting the weights using Gaussian zero-mean

values with a standard deviation of 1.00. The topol-

ogy of the hidden layers is set beforehand.

Policy. At the beginning of each episode, every

agent is set randomly onto the grid and receives its

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

124

corresponding observation. At each time step t, ev-

ery agent i independently chooses an action a

accord-

ing to its policy π

. To enable exploration, we imple-

mented an ε-greedy policy, where the agent acts ran-

dom with probability ε, which decreases by ε

decay

0.0008 with each training step until ε

min

= 0.01 is

reached. When the agent follows its learned policy,

we sweep across all possible actions and choose the

action which maximizes the Q-value for state s

. The

Q-function of state s and action a is deﬁned as the

corresponding negative free-energy −F:

Q(s, a) ≈ −F(s, a) = −F(s, a;w), (7)

with w as the vector of weights of a QBM and F(s, a)

as:

F(s, a) = hH

e f f

v=(s,a)

i −

P(s

t+1

, a

)logP(s

t+1

, a

)

(8)

Summarized, the agent acts via:

π =



random, i f p ≥ ε

argmax Q(s, a), i f p < ε

(9)

for a ∈ A and random variable p.

Weight Update. The environment returns a reward

t+1

and second state s

t+1

← a

) for each agent i.

Based on this transition, the QBM is trained. The

used update rules are an adaption of the state-action-

reward-state-action (SARSA) rule by Rummery et al.

(1994) (Rummery and Niranjan, 1994) with negative

free energy instead of Q-values (Levit et al., 2017)

deﬁned as:

∆w

= µ(r

, a

) − γF(s

n+1

, a

n+1

)

+F(s

, a

))vhσ

(10)

∆w

= µ(r

, a

) − γF(s

n+1

, a

n+1

)

+F(s

, a

))vhσ

(11)

with γ as the discount factor and µ as the learning

rate. The free energy and conﬁgurations of the hid-

den neurons are gained by applying simulated quan-

tum annealing respectively quantum annealing to the

formulation of the effective Hamiltonian H

e f f

v=(s,a)

described in the previous section. At each episode,

this process is repeated for a deﬁned number of steps

or until the episode ends.

3.2 Experience Replay Buffer

The ﬁrst extension is a biologically inspired mech-

anism named experience replay (Mcclelland et al.,

1995; O’Neill et al., 2010). O’Neill et al. (2010)

found, that the human brain stabilizes memory traces

from short- to long-term memory by replaying mem-

ories during sleep and rest. The reactivation of brain-

wide memory traces could underlie memory consoli-

dation. Similar to the human brain, experience replay

buffers used in deep Q-networks (DQN) store experi-

enced transitions and provides randomized data dur-

ing updating neural connections. Hence, correlations

of observation sequences are removed and changes in

the data distribution are smoothed. Furthermore, due

to the random choice of training samples, one transi-

tion can be used multiple times to consolidate experi-

ences.

To enable experience replay, at each time step t we

store the each agents’ experience e

= (s

, a

, r

, s

t+1

)

in a data set D

= (e

, ..., e

). For every training

step, we randomly sample mini-batches from D

from

which to Q-learning updates are performed.

This means, instead of updating the weights on

state-action pairs as they occur, we store discovered

data and perform training on random mini-batches

from a pool of random transitions.

3.3 Policy and Target Network

In order to perform a training step, it is necessary to

calculate the policy value F(s

, a

) and target value

F(s

n+1

, a

n+1

). Currently, policies and target val-

ues are approximated by the same network. Conse-

quently, Q-values and target values are highly corre-

lated. Small updates to Q-values may signiﬁcantly

change the policy, data distribution and target.

To counteract, we separate policy network calcu-

lating F(s

, a

) from the target network approximat-

ing F(s

n+1

, a

n+1

). Both networks are initialized simi-

larly. The policy network is updated with every train-

ing step, whereas the target network is only periodi-

cally updated. Every m steps, the weights of the pol-

icy network are simply adopted by the target network.

3.4 Multi-agent Quantum

Reinforcement Learning

In this work, we explore independent quantum learn-

ing in cooperative and non-cooperative settings. The

explicit requirement for cooperation is communica-

tion (Binmore, 2007). We enable communication

via parameter sharing as proposed by Foerster et al.

(2016) (Foerster et al., 2016). In this case, every

agents’ transition is stored in a centralized experi-

ence replay buffer and only one BM is trained. Each

agent receives its own observation and the centralised

network approximates the agents’ Q-value indepen-

dently. Whereas in non-cooperative settings, every

Towards Multi-agent Reinforcement Learning using Quantum Boltzmann Machines

125

agent keeps and updates its own BM solely with its

own experiences without any information exchange.

The policy and weight updates are performed as de-

scribed in the previous section.

4 EVALUATION

4.1 Domain

To evaluate our approach, we implemented a discrete

n × m multi-agent grid-world domain with i deter-

ministic rewards and i agents. At every time step t

each agent independently chooses an action from ac-

tion space A = {up, down, le f t, right, stand still}

depending on the policy π. More speciﬁcally, the

goal of every agent is to collect corresponding balls

while avoiding obstacles (e.g. walls and borders) and

penalty states (e.g. pits and others’ balls). The envi-

ronment size, number of agents, balls and obstacles

can be easily modiﬁed. Reaching a target location is

rewarded by a value of 220, whereas penalty states are

penalized by -220 and an extra penalty of -10 is given

for every needed step. An agent is done, when all

its corresponding balls were collected. Consequently,

we consider the domain as solved, when every agent

is done. The main goal lies in efﬁciently navigating

through the grid. Two example domains can be seen

in ﬁgure 2.

The starting position of all agents are chosen ran-

domly at the beginning of each episode whereas the

locations of their goals are ﬁxed. The observation is

one-hot-encoded and divided into two layers. One

layer describes the agents’ position and its goal and

the other layer details the position of all other agents

and their goals. This observation is issued as input for

the algorithm. Therefore, the input shape is n×m×2.

To asses the learned policies, we use the accumulated

episode rewards as quality measure.

(a) 3x3 grid (b) 5x3 grid

Figure 2: Example ﬁgures of two single-agent domains.

Picture a) shows a 3 × 3 grid domain with one reward,

whereas b) illustrates a bigger 5 × 3 grid domain with an

additional penalty state.

4.2 Single-agent Results

First, we evaluate how adding an experience replay

buffer (ERB) and separating policy and target net-

work inﬂuences the learning process and performance

of a single agent. We started by running the tradi-

tional Q-RL algorithm as proposed by Neumann et

al. (2020) (Neumann et al., 2020) including their pa-

rameter setting. Then, we only added an experience

replay buffer (ERB) respectively solely the target net-

work. Finally, we extended the original algorithm

with a combination of both, an ERB and target net-

work. The resulting rewards on running all four ar-

chitecture on the 3 × 3 domain (see ﬁgure 2) can be

seen in ﬁgure 3 a) and the corresponding learned pol-

icy in ﬁgure 3 b). All graphs have been averaged

over ten runs. The traditional Q-RL agent without

any extensions (blue line) learns unstable with occa-

sional high swings down to -1700 and -1000 reward

points. Extended versions seem to be show less out-

liers. This observation gets more evident, when con-

ducting the same experiment on a bigger 5 × 3 en-

vironment. As seen in ﬁgure 3 c) - d) the achieved

rewards of non-extended agents (blue) collapses fre-

quently. The ERB (black) respectively target network

(green) alone stabilize learning, but the combination

of both (red) yields smoothest training curve. Hence,

these enhancements are getting more important with

bigger state space and more complex environments.

After training, we evaluate the resulting policies

for 100 episodes without further training. The av-

erage rewards of ten test-runs on the 3 × 3 domain

can be seen in ﬁgure 3 b). As already described, an

agent is rewarded +220 points for reaching its goal

and -10 for each taken step. So, when considering

an optimal policy, the agent would be awarded +190

for the 3 × 3 domain (respectively +170 for 5 × 3) if

the agent is spawned furthest from its goal and +220

for the best starting position. Assuming the starting

positions over all episodes are distributed evenly, the

optimal median reward would be at +205 for the 3×3

domain and +195 for the 5 × 3 environment.

The traditional QBM agent shows multiple out-

liers and a higher spread of rewards throughout the

evaluation episodes compared to the other architec-

tures. As it can be seen, adding only one of the ex-

tensions leads to a better median reward and a seem-

ingly optimal policy is gained through a combination

of both. Again, this observation gets more distinct

with bigger domains, see ﬁgure 3 d). Even though

ERB or target network alone signiﬁcantly enhance

the median reward, the plots still show outliers. The

combined architecture is free of outliers with less in-

terquartile range and lower overall span indicating re-

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

126

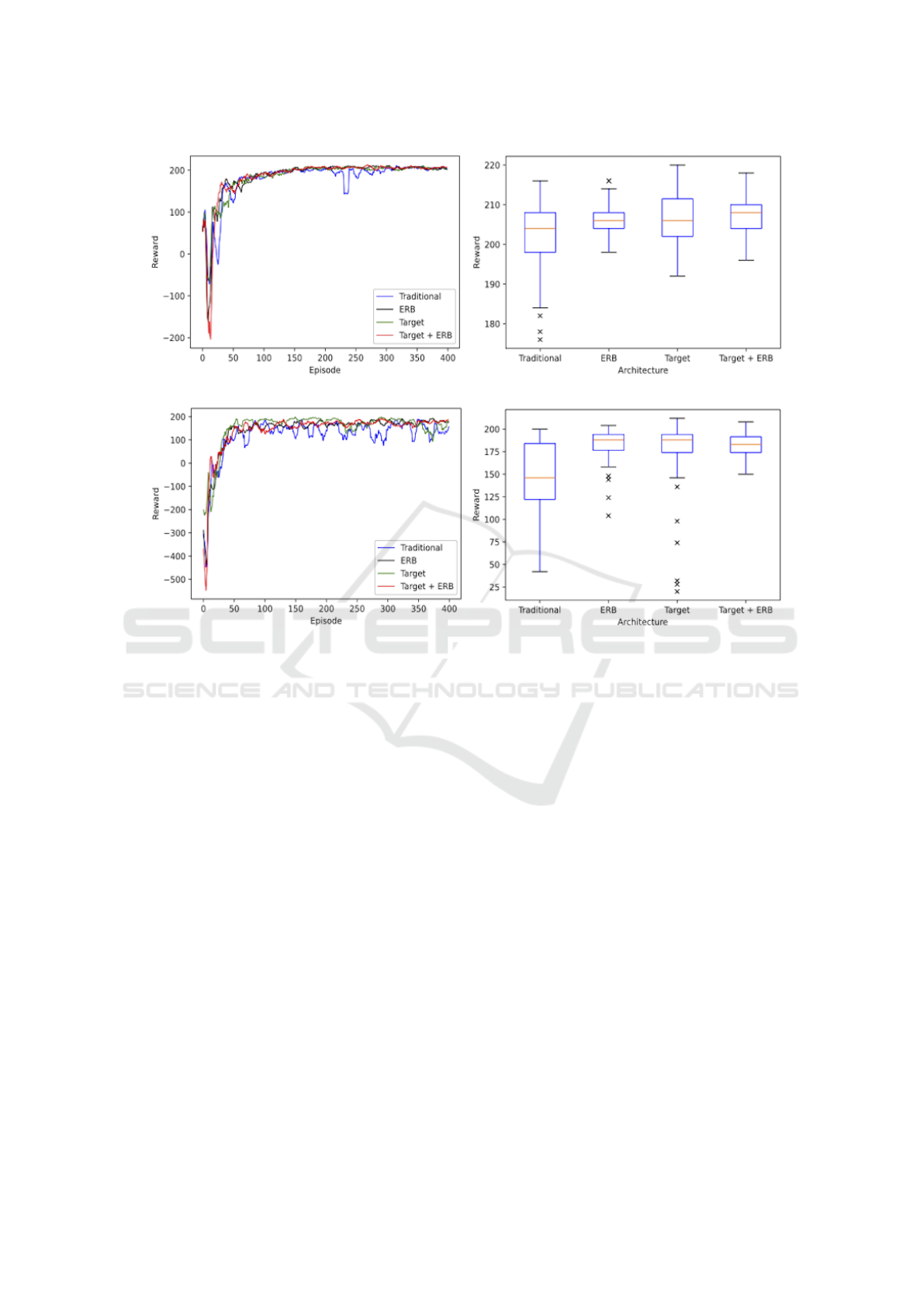
(a) Training: Reward per Episode (3x3) (b) Evaluation: Boxplot of Rewards (3x3)

Figure 3: Performance of a single agent with different architectures. a) Shows the gained reward per episode on a 3 × 3

domain of different architectures, whereas b) displays the corresponding achieved rewards of the learned policy on 400 test

episodes. c) illustrates the reward of the same experiment on a 5 × 3 domain and d) the corresponding learned policy of test

episodes.

duced variance of training performance and nearly

optimal policy. In summary, alleviating data correla-

tion and the problems non-stationary distributions by

randomly sampling previous transitions and separat-

ing target and policy network increases stable learning

leading to robust and more optimal policies. Compar-

ing the results for 3 × 3 with the 3 × 5 gridworld, a

correlation of impact through the extensions and in-

put size can be suspected.

4.3 Multi-agent Results

Traditional Q-RL was limited so 2 ×2 multi-agent do-

mains and bigger domains could not be solved ratio-

nally (Neumann et al., 2020). This section explores,

if the proposed architecture enables multi-agent rein-

forcement learning. We modify the known environ-

ments by adding one agent and one corresponding

goal. If an agents picks up the others goal, it is pe-

nalized with -220. The averaged results over 10 runs

can be seen in ﬁgure 4.

The graphs suggest, that 3 × 3 domain (blue) can

be solved in contrast to the bigger environment (red).

Looking at ﬁgure 4 b), the median reward of the

learned policy on the smaller domain is around +350,

which is near optimum. Unfortunately, the bigger do-

main could not be solved with a median reward of

-450. Additionally, the 5 × 3 learning curve does not

seem to converge. Therefore, we can conclude, that

it is possible to solve bigger domains with the pro-

posed architecture, but Q-RL with ERB and extra tar-

get network still fails in somewhat larger multi-agent

domains.

Lastly, we explore if the cooperation method of

parameter sharing enhances quantum multi-agent re-

inforcement learning. With parameter sharing no

explicit communication is necessary since only one

centralized entity is trained and shared between the

agents. More speciﬁcally, the experience of every

agent is stored in a centralized ERB. At each train-

ing step, one QBM is trained with a randomized sam-

ple from the ERB similar to the single-agent case.

Towards Multi-agent Reinforcement Learning using Quantum Boltzmann Machines

127

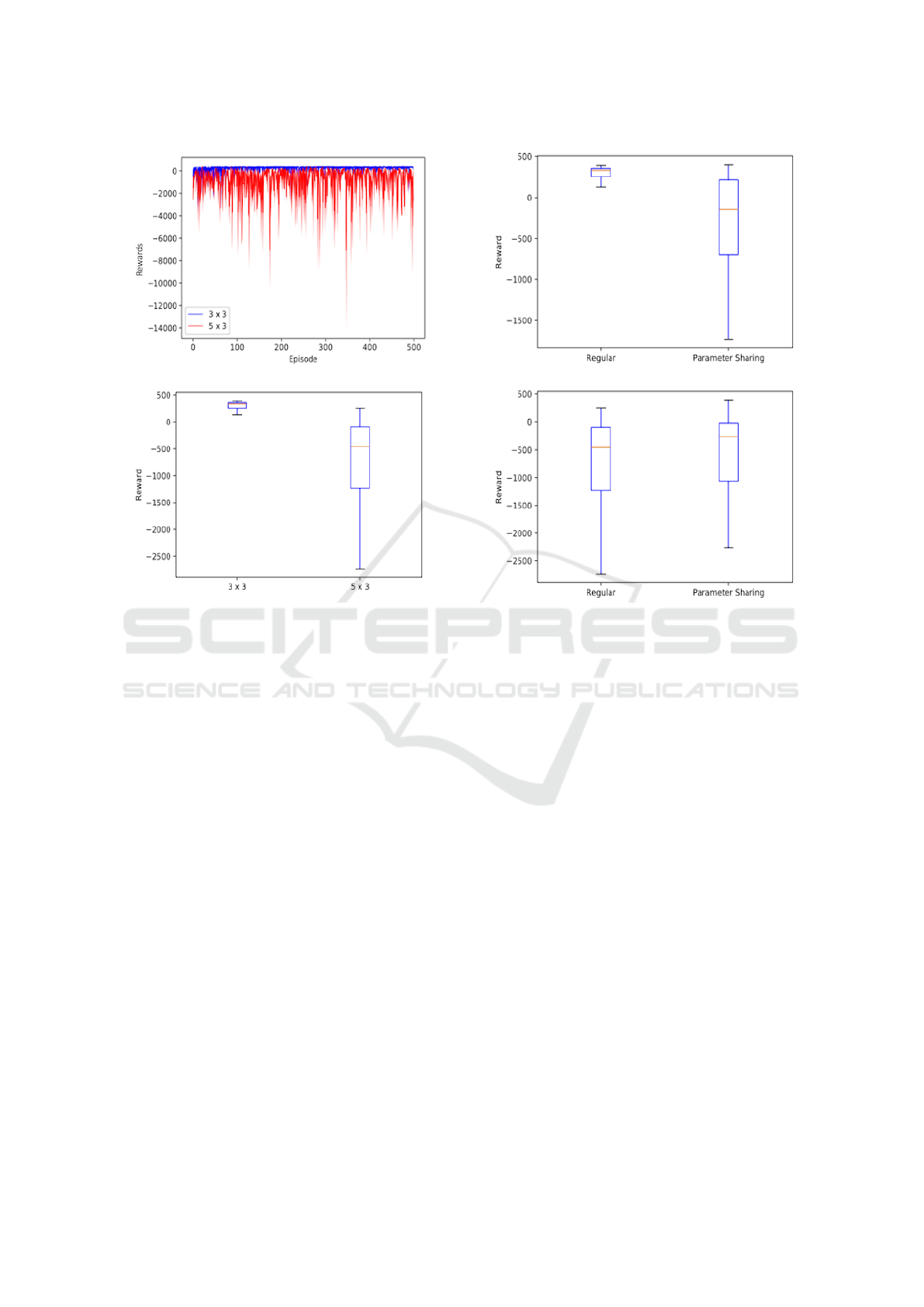
a) Learning Process on Both Domains

b) Learned Policy on Both Domains

Figure 4: Performance of two agents on the 3 × 3 (blue) re-

spectively 3 × 5 (red) domain. Figure a) shows the learning

process over 500 episodes, whereas ﬁgure b) displays the

learned policy over 100 testing episodes.

Both agents use this network to independently calcu-

late their Q-values based their observation. By this,

we additionally smooth the data distribution hoping

to achieve a more general policy and not two speciﬁc

policies adjusted to particular observations.

The results with and without parameter sharing

are illustrated in ﬁgure 5. Unfortunately, parameter

sharing seems to have a negative effect on the small

3 × 3 domain. In this case, the agents seem to have

learned a worse policy with this adaption. Rewards

on the bigger environments have increased. However,

the 5 × 3 domain can still not be considered solved.

Hence, parameter sharing is sub-optimal for the eval-

uated use case.

The complexity of the task and size of the in-

put did not increase, so this observation is counter-

intuitive. Since the centralized entity is simultane-

ously learning two independent behaviors, it might be

possible that in this case two independently optimal

action-state probability distributions (as learned with-

out parameter sharing) cancel out each other when

learned together. To proof this assumption, more ex-

periments must be conducted.

a) Learned Policy (3x3)

b) Learned Policy (5x3)

Figure 5: Performance of a two agents with and without pa-

rameter sharing. a) Shows the gained reward of the learned

policy of 100 testing episodes on a 3 × 3 domain, whereas

b) displays the same experiment on the bigger environment.

5 DISCUSSION

In summary, adding an ERB and additional target

network alleviates data correlation and the problem

of non-stationary distribution resulting in stabilized

learning and a more optimal policies. With the pro-

posed architecture, we were able to solve bigger

environments compared to traditional MARL using

QBMs. However, this architecture is still limited to

relatively small domains.

Even though it is possible to coordinate a single

agent in the 5 × 3 domain and multiple agents in a

smaller domain. The question remains why the 5 × 3

multi-agent domain fails. The QBM-agent receives

an input of 15 neurons on 5 × 3 single-agent domain

since only one input layer is needed. When adding

more agents to the environment, there is another in-

put layer necessary in order to distinguish between

the acting agent and other opposing agents. Hence,

the 3 × 3 multi-agent domain returns an observation

size of 18 and bigger multi-agent domain of size 30.

The input are considered in the QUBO formulation,

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

128

which therefore increases. Hence, simulated quan-

tum annealing is applied to a bigger formulation. A

bigger formulation demands more qubits, which may

limit the accuracy, variation and stability of the quan-

tum annealing algorithm. This is only an assumption

and needs to be examined more closely. Neumann et

al. (2020) also already stated, that Q-RL is limited

by the current Quantum Processing Unit (QPU) size.

However, with the extension of an Experience Replay

Buffer and Target Network, we are able to stabilize

learning and therefore may reduce the needed QPU

size compare to previous approaches.

Quantum sampling has been proven to be a

promising method to enhance reinforcement learn-

ing tasks to speed-up learning in relation to needed

time steps (Neumann et al., 2020). Further work con-

cerning the relation between QPU size and domain

complexity (respectively state input) would needed to

strictly determine current limitations.

ACKNOWLEDGEMENTS

This work was funded by the BMWi project PlanQK

(01MK20005I).

REFERENCES

Ackley, D. H., Hinton, G. E., and Sejnowski, T. J. (1985). A

learning algorithm for boltzmann machines. Cognitive

Science, 9(1):147 – 169.

Benedetti, M., Realpe-G

omez, J., and Perdomo-Ortiz, A.

(2018). Quantum-assisted helmholtz machines: A

quantum–classical deep learning framework for in-

dustrial datasets in near-term devices. Quantum Sci-

ence and Technology, 3(3):034007.

Biamonte, J., Wittek, P., Pancotti, N., Rebentrost, P., Wiebe,

N., and Lloyd, S. (2017). Quantum machine learning.

Nature, 549(7671):195–202.

Binmore, K. (2007). Game Theory: A Very Short Introduc-

tion. Oxford University Press.

Charpentier, A., Elie, R., and Remlinger, C. (2020). Rein-

forcement learning in economics and ﬁnance.

Crawford, D., Levit, A., Ghadermarzy, N., Oberoi, J. S.,

and Ronagh, P. (2019). Reinforcement learning using

quantum boltzmann machines.

Foerster, J. N., Assael, Y. M., de Freitas, N., and Whiteson,

S. (2016). Learning to communicate with deep multi-

agent reinforcement learning.

Foerster, J. N., Farquhar, G., Afouras, T., Nardelli, N., and

Whiteson, S. (2017). Counterfactual multi-agent pol-

icy gradients. In AAAI.

Jerbi, S., Trenkwalder, L. M., Nautrup, H. P., Briegel, H. J.,

and Dunjko, V. (2020). Quantum enhancements for

deep reinforcement learning in large spaces.

Jumper, J., Evans, R., Pritzel, A., Green, T., Figurnov,

M., Tunyasuvunakool, K., Ronneberger, O., Bates,

R.,

ıdek, A., Bridgland, A., Meyer, C., Kohl, S.

A. A., Potapenko, A., Ballard, A. J., Cowie, A.,

Romera-Paredes, B., Nikolov, S., Jain, R., Adler,

J., Back, T., Petersen, S., Reiman, D., Steinegger,

M., Pacholska, M., Silver, D., Vinyals, O., Senior,

A. W., Kavukcuoglu, K., Kohli, P., and Hassabis, D.

(2020). High accuracy protein structure prediction us-

ing deep learning. In Fourteenth Critical Assessment

of Techniques for Protein Structure Prediction (Ab-

stract Book), 14.

Kiran, B. R., Sobh, I., Talpaert, V., Mannion, P., Sallab, A.

A. A., Yogamani, S., and P

erez, P. (2020). Deep rein-

forcement learning for autonomous driving: A survey.

Levit, A., Crawford, D., Ghadermarzy, N., Oberoi, J. S.,

Zahedinejad, E., and Ronagh, P. (2017). Free energy-

based reinforcement learning using a quantum proces-

sor.

Li, R. Y., Di Felice, R., Rohs, R., and Lidar, D. A. (2018).

Quantum annealing versus classical machine learning

applied to a simpliﬁed computational biology prob-

lem. npj Quantum Information, 4(1).

Mahmud, M., Kaiser, M. S., Hussain, A., and Vassanelli,

S. (2018). Applications of deep learning and rein-

forcement learning to biological data. IEEE Trans-

actions on Neural Networks and Learning Systems,

29(6):2063–2079.

Mcclelland, J., Mcnaughton, B., and O’Reilly, R. (1995).

Why there are complementary learning systems in the

hippocampus and neocortex: Insights from the suc-

cesses and failures of connectionist models of learning

and memory. Psychological review, 102:419–57.

Mirhoseini, A., Goldie, A., Yazgan, M., Jiang, J., Songhori,

E., Wang, S., Lee, Y.-J., Johnson, E., Pathak, O., Bae,

S., Nazi, A., Pak, J., Tong, A., Srinivasa, K., Hang, W.,

Tuncer, E., Babu, A., Le, Q. V., Laudon, J., Ho, R.,

Carpenter, R., and Dean, J. (2020). Chip placement

with deep reinforcement learning.

Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A., Veness, J.,

Bellemare, M., Graves, A., Riedmiller, M., Fidjeland,

A., Ostrovski, G., Petersen, S., Beattie, C., Sadik,

A., Antonoglou, I., King, H., Kumaran, D., Wierstra,

D., Legg, S., and Hassabis, D. (2015). Human-level

control through deep reinforcement learning. Nature,

518:529–33.

Morita, S. and Nishimori, H. (2008). Mathematical founda-

tion of quantum annealing. Journal of Mathematical

Physics, 49(12):125210.

Neukart, F., Compostella, G., Seidel, C., von Dollen, D.,

Yarkoni, S., and Parney, B. (2017a). Trafﬁc ﬂow opti-

mization using a quantum annealer.

Neukart, F., Dollen, D. V., Seidel, C., and Compostella, G.

(2017b). Quantum-enhanced reinforcement learning

for ﬁnite-episode games with discrete state spaces.

Neumann, N., Heer, P., Chiscop, I., and Phillipson, F.

(2020). Multi-agent reinforcement learning using sim-

ulated quantum annealing.

Neven, H., Denchev, V. S., Rose, G., and Macready, W. G.

(2008). Training a binary classiﬁer with the quantum

adiabatic algorithm.

Towards Multi-agent Reinforcement Learning using Quantum Boltzmann Machines

129

O’Neill, J., Pleydell-Bouverie, B., Dupret, D., and

Csicsvari, J. (2010). Play it again: Reactivation of

waking experience and memory. Trends in neuro-

sciences, 33:220–9.

Paparo, G. D., Dunjko, V., Makmal, A., Martin-Delgado,

M. A., and Briegel, H. J. (2014). Quantum speedup

for active learning agents. Physical Review X, 4(3).

Peng, J. and Williams, R. J. (1994). Incremental multi-

step q-learning. In Cohen, W. W. and Hirsh, H., edi-

tors, Machine Learning Proceedings 1994, pages 226

– 232, San Francisco (CA). Morgan Kaufmann.

Puterman, M. L. (1994). Markov Decision Processes: Dis-

crete Stochastic Dynamic Programming. John Wiley

& Sons, Inc., New York, NY, USA, 1st edition.

Rebentrost, P., Mohseni, M., and Lloyd, S. (2014). Quan-

tum support vector machine for big data classiﬁcation.

Physical Review Letters, 113(13).

Rummery, G. and Niranjan, M. (1994). On-line q-

learning using connectionist systems. Technical Re-

port CUED/F-INFENG/TR 166.

Sallans, B. and Hinton, G. E. (2004). Reinforcement learn-

ing with factored states and actions. J. Mach. Learn.

Res., 5:1063–1088.

Silver, D., Huang, A., Maddison, C., Guez, A., Sifre, L.,

Driessche, G., Schrittwieser, J., Antonoglou, I., Pan-

neershelvam, V., Lanctot, M., Dieleman, S., Grewe,

D., Nham, J., Kalchbrenner, N., Sutskever, I., Lill-

icrap, T., Leach, M., Kavukcuoglu, K., Graepel, T.,

and Hassabis, D. (2016). Mastering the game of go

with deep neural networks and tree search. Nature,

529:484–489.

Strehl, A. L., Li, L., Wiewiora, E., Langford, J., and

Littman, M. L. (2006). Pac model-free reinforcement

learning. In Proceedings of the 23rd International

Conference on Machine Learning, ICML ’06, pages

881–888, New York, NY, USA. ACM.

Sutton, R. S. and Barto, A. G. (2018). Reinforcement Learn-

ing: An Introduction. A Bradford Book, Cambridge,

MA, USA.

Tan, M. (1993). Multi-agent reinforcement learning: In-

dependent vs. cooperative agents. In In Proceedings

of the Tenth International Conference on Machine

Learning, pages 330–337. Morgan Kaufmann.

Wiebe, N., Braun, D., and Lloyd, S. (2012). Quantum algo-

rithm for data ﬁtting. Physical Review Letters, 109.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

130