An Integrated Recurrent Neural Network and Regression Model with

Spatial and Climatic Couplings for Vector-borne Disease Dynamics

Zhijian Li

, Jack Xin

and Guofa Zhou

Department of Mathematics, UC Irvine, Irvine, CA 92617, U.S.A.

Program in Public Health, School of Medicine, UC Irvine, Irvine, CA 92617, U.S.A.

Keywords:

Geospatial and Climatic Data, Integrated Spatio-temporal Network Model, Vector-borne Disease Forecasting.

Abstract:

We developed an integrated recurrent neural network and nonlinear regression spatio-temporal model for

vector-borne disease evolution. We take into account climate data and seasonality as external factors that

correlate with disease transmitting insects (e.g. ﬂies), also spill-over infections from neighboring regions sur-

rounding a region of interest. The climate data is encoded to the model through a quadratic embedding scheme

motivated by recommendation systems. The neighboring regions’ inﬂuence is modeled by a long short-term

memory neural network. The integrated model is trained by stochastic gradient descent and tested on leish-

maniasis data in Sri Lanka from 2013-2018 where infection outbreaks occurred. Our model out-performed

ARIMA models across a number of regions with high infections, and an associated ablation study renders

support to our modeling hypothesis and ideas.

1 INTRODUCTION

Leishmaniases are tropical diseases caused by leish-

mania parasites and transmitted through the bites of

vector sand ﬂies. The cutaneous leishmaniasis (CL)

is the most common threat and health risk in devel-

oping countries in the tropical regions. In this pa-

per, we study data from Sri Lanka that has reported a

substantial surge in clinical leishmaniasis cases in the

past 20 years (Fig.1, a)). Previous studies Siriwardana

et al. (2010); Karunaweera et al. (2018) found that (1)

leishmaniasis epidemics in Sri Lanka had two trans-

mission hot spots, one on the south coast and another

in the north central region of the country (Fig.1,b)),

with a biannual seasonal variation; (2) outdoor activ-

ities, including occupational exposure and living near

a vector breeding area, are some of the key risk fac-

tors of infection. An important scientiﬁc task for pub-

lic health is to model the spatio-temporal dynamics

in leishmaniasis transmission and the driving forces

behind it, thereby help predict future infections and

outbreaks.

In this paper, we aim to generalize and advance

existing geo-statistical and ecological models Kyri-

akidis and Journel (1999); Elith and Leathwick (2009)

by incorporating spatio-temporal transmission factors

such as climate effects and local carryover of infec-

tions from neighboring regions. Our main contribu-

tions are:

(1) modeling leishmaniasis spread between neighbor-

ing areas by a recurrent neural network with input

data from up to three most infected neighbors;

(2) including climate data input as an external factor,

since the development of both the sand ﬂies and the

parasites inside their guts are affected by climatic con-

ditions;

(3) hybridizing (1) and (2) with regression to form

an integrated nonlinear space-time model trained by

stochastic gradient descent on 51 months (2013-03 to

2017-08) and tested on 18 months (2017-09 to 2018-

12) in 5 highly infected regions of Sri Lanka.

The rest of the paper is organized as follows.

In section 2, we review related prior work on in-

fectious disease modeling where climate and geo-

neighbor factors have been separately modeled. In

section 3, we outline pre-processing of raw data to

remove trend, and introduce our integrated model

structure with embedding operations of climate and

time stamps (monthly) motivated by design of rec-

ommender systems. In section 4, we go over train-

ing and test data, and compare prediction results with

ARIMA as baseline. In terms of both root mean

squares error and maximum absolute error, our in-

Li, Z., Xin, J. and Zhou, G.

An Integrated Recurrent Neural Network and Regression Model with Spatial and Climatic Couplings for Vector-borne Disease Dynamics.

DOI: 10.5220/0010762700003122

In Proceedings of the 11th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2022), pages 505-510

ISBN: 978-989-758-549-4; ISSN: 2184-4313

505

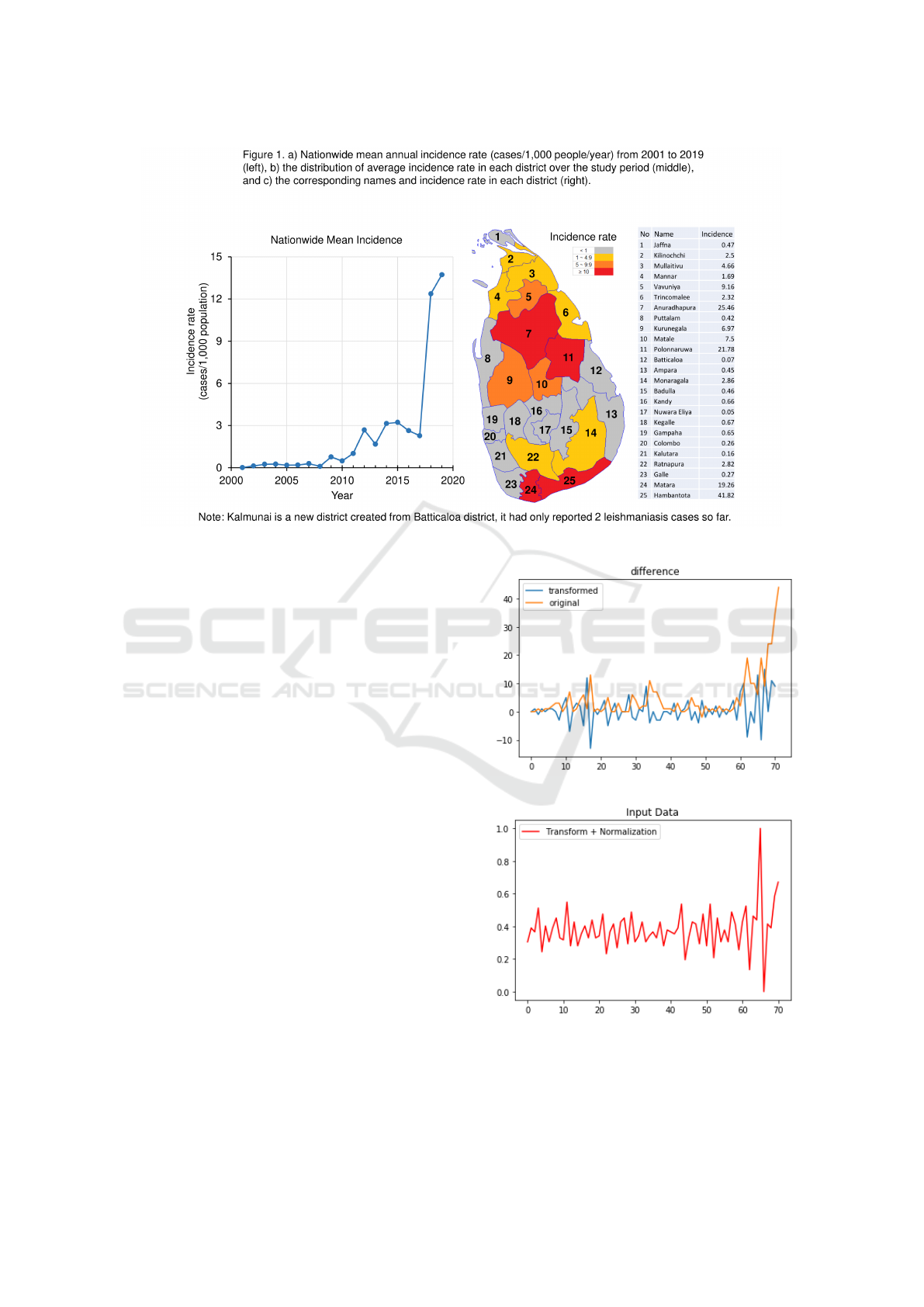
Figure 1: Sri Lanka regional map and mean incidence rate over the last two decades.

tegrated model, when applied on the difference in-

put data, out-performed ARIMA signiﬁcantly in 5 Sri

Lanka regions with high infections. Moreover, adding

climate data consistently improves prediction, which

supports climate as a strong correlate to ﬂy and para-

site mediated transmissions.

2 RELATED PRIOR WORKS

Forecasting of disease time series has gone far beyond

the traditional regression approach. External infor-

mation has been widely used in models; for example,

Yang et al. (2015) proposed Auto-Regression method

with GOogle search data (ARGO) that used google

search information as additional regressors. The

intuition of ARGO is that the amount of searches of

inﬂuenza and related key words indicate the outbreak

of inﬂuenza. Utilizing this external internet search in-

formation, ARGO outperforms auto-regressive model

and its variant ARIMA on CDC inﬂuenza data. Un-

fortunately, Google Correlate, the website where

Google provided the internet search data, has been

shut down for many years. Motivated by the infec-

tious nature of the inﬂuenza, Li et al. (2019) proposed

graph-structured recurrent neural networks (SRNN)

to learn the interaction of geographical spread of

inﬂuenza. As a result, SRNN further improves

ARGO’s accuracy on CDC data. Recently, spatio-

temporal models combining epidemic differential

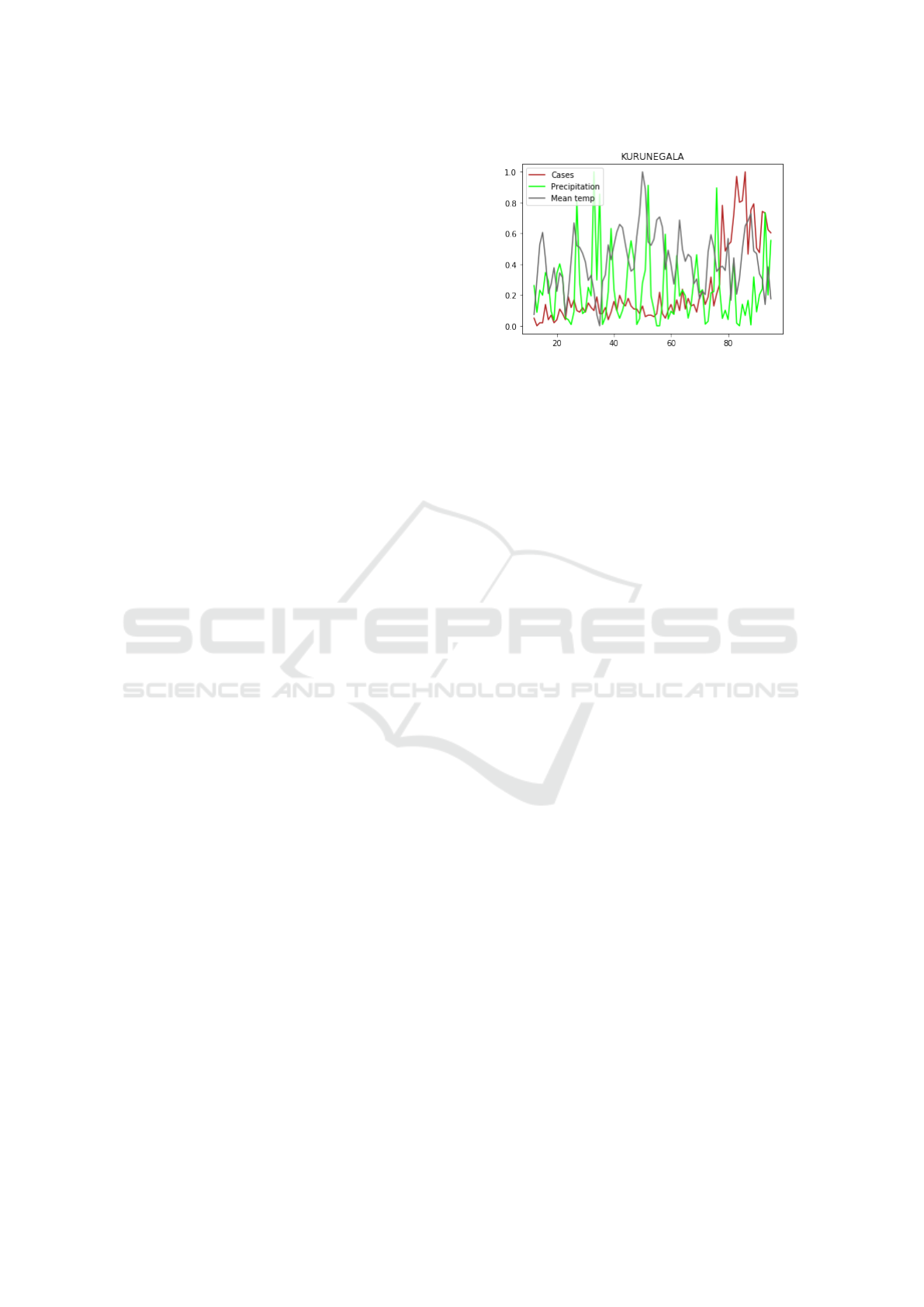
(a)

(b)

Figure 2: An example of data pre-processing for region Ku-

runegala: a) raw and transformed (differenced) data; (b)

transformed (differenced) and normalized data.

ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods

506

equations and RNNs Li et al. (2020); Zheng et al.

(2020) have been proposed for one to seven day ahead

forecasting of Covid-19 cases in Italy and the US.

For vector-borne diseases, due to the difﬁculty of

tracking ﬂy populations and evolution, mixed linear

regression-autoregression models with near-neighbor

spatial coupling has been commonly used for predic-

tion and risk analysis Kyriakidis and Journel (1999);

Elith and Leathwick (2009).

3 OUR APPROACH

3.1 Transformation of Raw Data

Since the original leishmaniasis data is highly non-

stationary Chaves and Pascual (2006), we ﬁrst trans-

form (pre-process) it to be approximately stationary.

There are several popular techniques to stationarize

data. We found that taking the ﬁrst order differ-

ence along time is effective to improve the stationar-

ity of the raw data here. In Fig. 2, panel (a) shows

how the original case data of Kurunegala region is

transformed by the difference method. As is well-

known that RNN is sensitive to normalization, panel

(b) shows the normalized-transformed data that will

be fed into our model. We remark that normalization

is a stationary-invariant process.

3.2 Basic Space-time Model

In classical space-time geological and ecological sta-

tistical modeling (Kyriakidis and Journel (1999);

Elith and Leathwick (2009) among others), the cases

of neighbors are summed as a single regressor. To

learn the impact of neighbors more at depth, we

use RNN to process such information and extract

(“edge”) features as in Li et al. (2020); Zheng et al.

(2020). Let y

e,t

= (y

t−1

, y

t−1

, y

t−1

) be a vector of

observations from the three neighbors that have the

highest cases at t − 1. Deﬁne:

= LST M(y

e,t

)

= w

where LSTM is a standard long short-term memory

network Hochreiter and Schmidhuber (1997). If a re-

gion has less than three neighbors, we pad zero into

. Let I be the set of neighbors, then the model out-

put (an estimated case number for a region of interest

at time t) is:

ˆy

= σ



αy

t−1

+ β

∑

i∈I

t−1

+ f

+ b



, (1)

where σ := max(x, 0) is the rectiﬁed linear unit

(ReLu) activation function.

Figure 3: Normalized data of cases vs. mean temperature

and precipitation in Kurunegala region of Sri Lanka.

3.3 Integrated Model

According to previous studies (Zhou et al. (2004);

Chaves and Pascual (2006) among others), leishma-

niasis outbreak is highly correlated to climate condi-

tions such as temperature, rainfalls and seasonality,

see Fig. 3 and Fig. 5 for illustrations. Hence, we

adopt climate data as an external feature to further

improve our model performance. The climate data,

denoted as v

∈ R

being part of our model input,

contains the maximum temperature, minimum tem-

perature, mean temperature, and precipitation during

month t. Unfortunately, RNN is not good at directly

learning the impact of external feature v

based on

our experiments. The temperature effect turns out

to be highly non-linear. Hence, we set out to learn

the order-2 interactions of the climate features. The

complete order-2 interactions of n features involve





+ n additional features, which are expensive to

compute and can easily lead to over-ﬁtting. Similar

problem arises in capturing high-order interactions of

user-item features in recommendation systems where

the so-called cross layer method Wang et al. (2017)

is proposed through Hadamard product and a weight

matrix and the interaction is encoded into a vector of

length n. As in Wang et al. (2017), we compute the

order 2 interaction of climate features as follows:

(W v)  v =







+ w







Once the order interaction of climate features has

been encoded in (W v  v), we use a dense layer to

map the interaction of climate data into the ﬁnal pre-

diction:

ψ(v) = ˜w

[(W v  v)].

In addition to external features, capturing season-

ality has drawn much attention in recent literature

An Integrated Recurrent Neural Network and Regression Model with Spatial and Climatic Couplings for Vector-borne Disease Dynamics

507

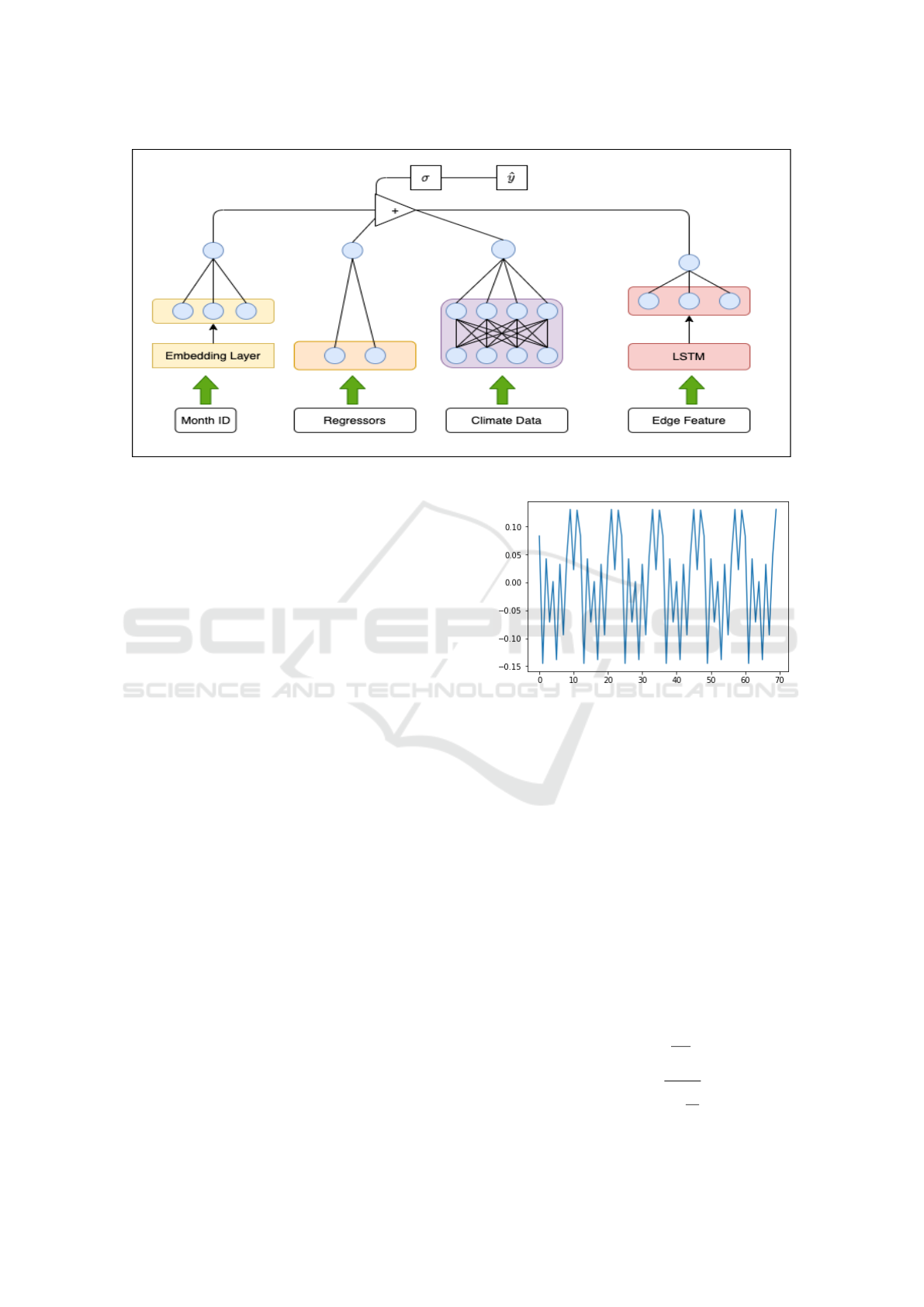
Figure 4: Illustration of our model architecture (viz. equation (2)).

Taylor and Letham (2018); Zhou et al. (2004) of time-

series forecasting. A classical analytical approach is

to use partial sums of Fourier series to represent sea-

sonality. However, the performance relies on ﬁne tun-

ing a non-trainable integer parameter (the number of

terms). Instead, in view of the personalization tech-

nique of recommendation system He et al. (2017), we

employ an embedding layer to map the month ID, 0 to

11, to a higher dimension to learn seasonality of the

data. Then, we use a dense layer to map it into the

output:

g(t) = ˆw

(embed(t)).

Integrated with the climate features and seasonality,

our model is formulated as:

ˆy

= σ



αy

t−1

+ β

∑

i∈I

t−1

+ f

+ g(t) + ψ(v

) + b



(2)

The architecture of our model is illustrated in Fig. 6.

As shown in equation (2), the ﬁnal prediction model

is written as the sum of all learned information fol-

lowed by ReLu activation function. The training loss

function is

L (Θ) =

∑

t=1

( ˆy

− y

)

which is minimized by an adaptive Adam optimizer

to arrive at an optimal value Θ

∗

4 EXPERIMENTAL RESULTS

Our clinically conﬁrmed leishmaniasis case data

came from from the national diagnostic and research

laboratory at the University of Colombo, Sri Lanka;

the epidemiology unit of the Sri Lanka Ministry

Figure 5: Seasonality component g(t) of Polonnaruwa.

of Health and through communication with medical

health ofﬁcers. The climatic data came from meteo-

rological stations in Sri Lanka in the format of max-

imum/minimum/mean temperature and precipitation.

We use 51 months (2013-03 to 2017-08) for training

and 18 months (2017-09 to 2018-12) for testing, with

ARIMA as our baseline model. We set the standard

parameters of ARIMA as (p, q, d) = (2, 1, 1) after op-

timizing. Note that with d = 1, ARIME also applied

difference transform to the original data. Meanwhile,

we compare the performance of our base model equa-

tion (1) and the integrated model equation (2). The

results are shown in Table 1 and Table 2. We evaluate

the models using both MAE and RMSE metrics. Let

e = {e

= | ˆy

− y

|, i ≤ n}, where n is the number of

data points in testing set. Then,

MAE =

∑

i=1

RMSE =

∑

i=1

ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods

508

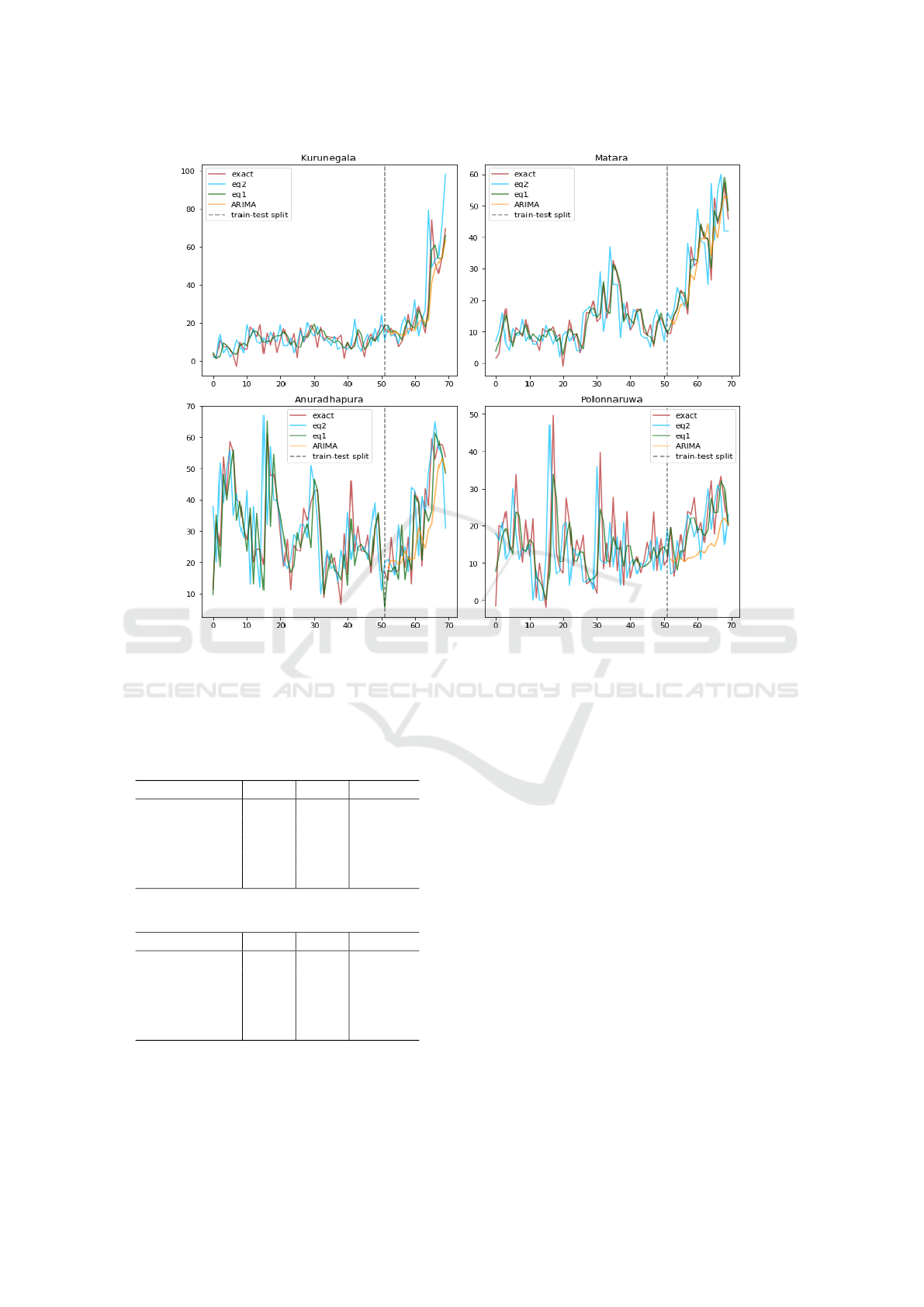
Figure 6: Training and prediction (separated by dashed line) of models (1) and (2) vs. ARIMA in 4 regions of Sri Lanka.

We note that RMSE ≥ MAE, and it can be shown that

RMSE−MAE = Var(e). We observe that equation (1)

outperforms ARIMA model in both MAE and RMSE

prediction errors.

Table 1: RMSE prediction errors of different models.

Region (1) (2) ARIMA

Matara 11.38 11.36 11.92

Anuradhapura 14.70 12.81 14.70

Polonnaruwa 8.65 8.04 8.65

Kurunegala 14.70 10.08 10.35

Hambantota 32.76 32.12 34.63

Table 2: MAE errors of different models.

Region (1) (2) ARIMA

Matara 9.33 8.62 9.54

Anuradhapura 10.25 9.88 12.2

Polonnaruwa 7.20 6.08 7.57

Kurunegala 17.50 16.80 17.50

Hambantota 41.28 39.77 41.28

Equation (2) performs the best among the three

models. Hence, the edge features in cases of

neighboring regions helped model (1) to outperform

ARIMA, which is only based on historical observa-

tions of the region of interest. The external climate

(see Fig. 5 for a seasonality illustration) information

helps model (2) to further improve prediction.

5 CONCLUSION

In this study, we integrated components of geograph-

ical spatial information, temperature, and seasonality

to build a spatio-temporal network model for predict-

ing vector-borne disease cases. We employ the cross

layer from recommendation system to compute the

order-2 interaction of climate data, and utilize embed-

ding layer to map month ID to higher dimensions to

learn seasonality. The model is successfully trained

on leishmaniasis data of several regions in Sri Lanka

with high infections (see Fig. 6).

In future work, we plan to study other vector-

borne disease data with our model (2), and also gen-

eralize RNN to an efﬁcient transformer model to ex-

plore additional non-local temporal information for

improving prediction.

As suggested in Fig. 3, the effects of climatic data

may have a latent period to induce vector growth and

subsequent case upswing. In future work, we plan

An Integrated Recurrent Neural Network and Regression Model with Spatial and Climatic Couplings for Vector-borne Disease Dynamics

509

to introduce a time delay in the climate term of our

model and learn it from the data for another improve-

ment.

ACKNOWLEDGEMENTS

This work was partially supported by NSF grants

DMS-1924548 and DMS-1952644.

REFERENCES

L. Chaves and M. Pascual. Climate cycles and forecasts

of Cutaneous Leishmaniasis, a nonstationary vector-

borne disease. PLoS Med. 3(8):e295, 2006.

J. Elith and J. Leathwick. Species distribution models: eco-

logical explanation and prediction across space and

time. Ann. Rev. Ecol. Evol. Syst., 40:677–97, 2009.

X. He, L. Liao, H. Zhang, L. Nie, X. Hu, and T.-S. Chua.

Neural collaborative ﬁltering. In Proceedings of the

26th International Conference on World Wide Web,

pages 173–182, 2017.

S. Hochreiter and J. Schmidhuber. Long short-term mem-

ory. Neural computation, 9(8):1735–1780, 1997.

N. Karunaweera, S. Ginige, S. Senanayake, H. Silva,

N. Manamperi, N. Samaranayake, and et al. Spa-

tial epidemiologic trends and hotspots of Leishmania-

sis in Sri Lanka (2001-2018). Emerg. Infect. Disease

26(1):1–10, 2018.

P. Kyriakidis and A. Journel. Geostatistical space–time

models: a review. Math Geol., 31:651–84, 1999.

Z. Li, X. Luo, B. Wang, A. L. Bertozzi, and J. Xin. A

study on graph-structured recurrent neural networks

and sparsiﬁcation with application to epidemic fore-

casting. In World Congress on Global Optimization,

pages 730–739. Springer, 2019.

Z. Li, Y. Zheng, J. Xin, and G. Zhou. A recurrent neu-

ral network and differential equation based spatiotem-

poral infectious disease model with application to

Covid-19. Proceedings of KDIR 2020; arXiv preprint

arXiv:2007.10929, 2020.

H. Siriwardana, N. Thalagala, and N. Karunaweera. Clin-

ical and epidemiological studies on the cutaneous

leishmaniasis caused by Leishmania Donovani in Sri

Lanka. Ann. Trop. Med. Parasitol. 104(3):213–223,

2010.

S. J. Taylor and B. Letham. Forecasting at scale. The Amer-

ican Statistician, 72(1):37–45, 2018.

R. Wang, B. Fu, G. Fu, and M. Wang. Deep & cross net-

work for ad click predictions. In Proceedings of the

ADKDD’17, pages 1–7. 2017.

S. Yang, M. Santillana, and S. C. Kou. Accurate estima-

tion of inﬂuenza epidemics using google search data

via argo. Proceedings of the National Academy of Sci-

ences, 112(47):14473–14478, 2015.

Y. Zheng, Z. Li, J. Xin, and G. Zhou. A spatial-temporal

graph based hybrid infectious disease model with ap-

plication to COVID-19. Proceedings of ICPRAM

2021; arXiv preprint arXiv:2010.09077, 2020.

G. Zhou, N. Minakawa, A. K. Githeko, and G. Yan. As-

sociation between climate variability and malaria epi-

demics in the east African highlands. Proceedings

of the National Academy of Sciences, 101(8):2375–

2380, 2004.

ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods

510