Deceptive AI Explanations: Creation and Detection

Johannes Schneider

, Christian Meske

and Michalis Vlachos

University of Liechtenstein, Vaduz, Liechtenstein

University of Bochum, Bochum, Germany

University of Lausanne, Lausanne, Switzerland

Keywords:

Explainability, Artiﬁcial Intelligence, Deception, Detection.

Abstract:

Artiﬁcial intelligence (AI) comes with great opportunities but can also pose signiﬁcant risks. Automatically

generated explanations for decisions can increase transparency and foster trust, especially for systems based

on automated predictions by AI models. However, given, e.g., economic incentives to create dishonest AI,

to what extent can we trust explanations? To address this issue, our work investigates how AI models (i.e.,

deep learning, and existing instruments to increase transparency regarding AI decisions) can be used to create

and detect deceptive explanations. As an empirical evaluation, we focus on text classiﬁcation and alter the

explanations generated by GradCAM, a well-established explanation technique in neural networks. Then, we

evaluate the effect of deceptive explanations on users in an experiment with 200 participants. Our ﬁndings

conﬁrm that deceptive explanations can indeed fool humans. However, one can deploy machine learning

(ML) methods to detect seemingly minor deception attempts with accuracy exceeding 80% given sufﬁcient

domain knowledge. Without domain knowledge, one can still infer inconsistencies in the explanations in an

unsupervised manner, given basic knowledge of the predictive model under scrutiny.

1 INTRODUCTION

AI can be used to increase wealth and well-being

globally. However, the potential uses of AI cause con-

cerns. For example, because of the limited modera-

tion of online content, attempts at deception prolifer-

ate. Online media struggle against the plague of “fake

news”, and e-commerce sites spend considerable ef-

fort in detecting deceptive product reviews (see (Wu

et al., 2020) for a survey). Marketing strategies ex-

ist that consider the creation of fake reviews to make

products appear better or to provide false claims about

product quality (Adelani et al., 2019).

There are multiple reasons why to provide “al-

tered” explanations of a predictive system. Truth-

ful explanations might allow to re-engineer the logic

of the AI system, i.e., leak intellectual property.

Decision-makers might also deviate from suggested

AI decisions at will. For example, a bank employee

might deny a loan to a person she dislikes claim-

ing an AI model’s recommendation as to the reason,

supported by a made-up explanation (irrespective of

the actual recommendation of the system). AI sys-

tems may perform better when using information that

should not be used but is available. For example, pri-

vate information on a person’s health condition might

be used by insurances to admit or deny applicants.

Even though this is forbidden in some countries, the

information is still very valuable in estimating ex-

pected costs of the applicant if admitted. Product sug-

gestions delivered through recommender systems are

also commonly accompanied by explanations (Fusco

et al., 2019) in the hope of increasing the likelihood

of sales. Companies have an incentive to provide ex-

planations that lure customers into sales irrespective

of their truthfulness. As such, there are incentives to

build systems that utilize such information but hide its

use. That is, “illegal” decision criteria are used, but

they are omitted from explanations requested by au-

thorities or even citizens. In Europe, the GDPR law

grants rights to individuals to get explanations of de-

cisions made in an automated manner.

The paper contributes in the area of empirical and

formal analyses of deceptive AI explanations. Our

empirical analysis, including a user study, shows in

alignment with prior work that deceptive AI explana-

tions can mislead people. Our formal analysis sets

forth some generic conditions under which detection

of deceptive explanations is possible. We show that

domain knowledge is required to detect certain forms

Schneider, J., Meske, C. and Vlachos, M.

Deceptive AI Explanations: Creation and Detection.

DOI: 10.5220/0010768300003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 2, pages 44-55

ISBN: 978-989-758-547-0; ISSN: 2184-433X

of deception that might not be available to explainees

(the recipients of explanations). Our supervised and

unsupervised detection marks one of the ﬁrst steps in

the quest against deceptive explanations. They high-

light that while detecting deception is often possible,

success depends on multiple factors such as type of

deception, availability of domain knowledge and ba-

sic knowledge of the deceptive system.

2 PROBLEM DEFINITION

We consider classiﬁcation systems that are trained us-

ing a labeled dataset D = {(X, Y )} with two sources

of deception: model decisions and explanations. A

model M maps input X ∈ S to an output Y , where

S is the set of all possible inputs. To measure the

level of deception, we introduce a reference (machine

learning (ML)) model M

∗

and a reference explana-

tion method H

∗

. In practice, M

∗

might be a deep

learning model and H

∗

a commonly used explain-

ability method such as LIME or SHAP. That is, H

∗

might not be perfect. Still, we assume that the ex-

plainee trusts it, i.e. she understands its behavior

and in what ways explanations differ from ”human”

reasoning. The model M

∗

is optimized with a be-

nign objective, i.e. maximizing accuracy. We as-

sume that M

∗

is not optimized to be deceptive. How-

ever, model M

∗

might not be fair and behave uneth-

ically. A deceiver might pursue other objectives than

those used for M

∗

leading to the deceiver’s model

. The model M

might simply alter a few de-

cisions of M

∗

using simple rules or it might be a

completely different model. A (truthful) explainabil-

ity method H(X, Y, M) receives input X, class la-

bel Y and model M to output an explanation. For

the reference explanation method H

∗

, this conforms

to provide a best-effort, ideally a truthful, reasoning,

why model M would output class Y . The deceiver’s

method H

might deviate from H

∗

using arbitrary

information. It returns H

(X), where the exact de-

ception procedure is deﬁned in context. An explainee

(the recipient of an explanation) obtains for an input

X, a decision M

(X) and an explanation H

(X).

The decision is allegedly from M

∗

and the explana-

tion allegedly from H

∗

and truthful to the model M

providing the decision. Thus, an explainee should

be lured into believing that M

∗

(X) = M

(X) and

(X) = H

∗

(X, M

(X), M

). However, the de-

ceiver’s model might not output M

(X) = M

∗

(X)

and a deceiver might choose an explainability method

that differs from H

∗

or she might explain a differ-

ent class Y . This leads to four scenarios (see Figure

1). We write H

∗

(X) := H

∗

(X, M

(X), M

The goal of a deceiver is to construct an explana-

tion so that the explainee is neither suspicious about

the decision in case it is not truthful to the model M

ie. M

(X) 6= M

∗

(X), nor about the explanation

(X) if it deviates from H

∗

(X, M

(X), M

∗

Thus, an explanation might be used to hide an un-

faithful decision to the model or it might be used to

convey a different decision-making process than oc-

curs in M

An input X consists of values for n features,

F = {i|i = 1 . . . n}, where each feature i has a sin-

gle value x

∈ V

of a set of feasible values V

. For

example, an input X can be a text document such as a

job application, where each feature i is a word speci-

ﬁed by a word id x

. Documents X ∈ S are extended

or cut to a ﬁxed length n. ML models learn (a hier-

archy of) features. Explaining in terms of learnt fea-

tures is challenging since they are not easily mapped

to unique concepts that are humanly understandable.

Thus, we focus on explanations that assign relevance

scores to features F of an input X. Formally, we con-

sider explanations H that output a value H

(X, Y, M)

for each feature i ∈ F . Where H

> 0 implies that

feature i with value x

is supportive of decision Y . A

value of zero implies no dependence of i on the deci-

sion Y . H

< 0 shows that feature i is indicative of

another decision.

3 MEASURING EXPLANATION

FAITHFULNESS

We measure faithfulness of an explanation using two

metrics, namely decision ﬁdelity and explanation ﬁ-

delity.

Decision Fidelity. It amounts to the standard no-

tion of quantifying whether input X and explanation

(X) on their own allow deriving the correct de-

cision Y = M

∗

(X) (Schneider and Handali, 2019).

Therefore, if explanations indicate multiple outputs or

an output different from Y , this is hardly possible.

Decision ﬁdelity f

can be deﬁned as the loss when

predicting the outcome using some classiﬁer g based

on the explanation only, or formally:

(X) = −L(g(X, H

(X)), Y ) (1)

The loss might be deﬁned as 0 if g(X, H

(X)) = Y

and 1 otherwise. We assume that the reference ex-

planations H

∗

(X, M

∗

(X), M

∗

) results in minimum

loss, i.e., maximum decision ﬁdelity. (Large) deci-

sion ﬁdelity does not require that an explanation con-

tains all relevant features used to derive the decision

(X). For example, in a hiring process, gender

Deceptive AI Explanations: Creation and Detection

Figure 1: Scenarios for reported predictions and explanations.

might inﬂuence the decision, but for a particular can-

didate other factors, such as qualiﬁcation, social skills

etc., are dominant and on their own unquestionably

lead to a hiring decision.

Explanation Fidelity. This refers to the overlap of

the (potentially deceptive) explanation H

(X) and

the reference explanation H

∗

(X, M

(X), M

) for

an input X and reported decision M

(X). Any mis-

match of a feature in the two explanations lowers ex-

planation ﬁdelity. It is deﬁned as:

(X) = 1 −

∗

(X, M

(X), M

) − H

(X)k

∗

(X, M

(X), M

(2)

Even if the decision M

(X) is non-truthful to the

model, i.e., M

(X) 6= M

∗

(X), explanation ﬁdelity

might be large if the explanation correctly outputs the

reasoning that would lead to the reported decision.

If the reported decision is truthful, i.e., M

(X) =

∗

(X), there seems to be an obvious correlation be-

tween decision- and explanation ﬁdelity. But any ar-

bitrarily small deviation of explanation ﬁdelity from

the maximum of 1 does not necessarily ensure large

decision ﬁdelity and vice versa. For example, assume

that an explanation from H

systematically under- or

overstates the relevance of features, i.e. H

(X)

∗

(X)

· c

with arbitrary c

> 0 and c

6= 1. For c

differing signiﬁcantly from 1, this leads to explana-

tions that are far from the truth, which is captured by

low explanation ﬁdelity. However, decision ﬁdelity

might yield the opposite picture, i.e., maximum de-

cision ﬁdelity, since a classiﬁer g (Def. 1) trained on

inputs (X, H

(X)) with labels M

(X), might learn

the coefﬁcients c

and predict labels without errors.

Explanation ﬁdelity captures the degree of decep-

tiveness of explanations from H

by aggregating the

differences of its relevances of features and those of

the reference explanations. When looking at individ-

ual features from a layperson’s perspective, deception

can arise due to over- and understating the feature’s

relevance or even fabricating features (see Figure 2).

Omission and inverting of features can be viewed as

Figure 2: Deviations from (trusted) reference explanation.

special cases of over- and understating. In this work,

we do not consider feature fabrication.

4 CREATION OF DECEPTIVE

EXPLANATIONS

We ﬁrst discuss goals a deceiver might pursue us-

ing deceptive explanations, followed by how decep-

tive explanations can be created using these goals in

mind.

Purposes of Deceptive Explanation include:

i) Convincing the explainee of an incorrect predic-

tion, i.e. that a model decided Y for input X although

the model’s output is M

(X) with Y 6= M

(X).

For example, a model M

∗

in health-care might

predict the best treatment for a patient trained on his-

torical data D. A doctor might change the prediction.

She might provide the best treatment for well-paying

(privately insured) patients and choose a treatment

that minimizes her effort and costs for other patients.

ii) Providing an explanation that does not accurately

capture model behavior without creating suspicion.

An incorrect explanation will manifest in low de-

cision ﬁdelity and explanation ﬁdelity. It involves

hiding or overstating the importance of features in the

decision process (Figure 2) with more holistic goals

such as:

a) Omission: Hiding that decisions are made based

on speciﬁc attributes such as gender or race to prevent

legal consequences or a loss in reputation.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

b) Obfuscation: Hiding the decision mechanism

of the algorithm to protect intellectual property.

The combination of (i) and (ii) leads to the four sce-

narios shown in Figure 1.

Creation: To construct deceptive explanations (and

decisions), a deceiver has access to the model M

∗

and M

, the input X and the reference explanation

∗

. She outputs a decision M

(X) in combination

with an explanation H

(X) (see Figure 3). Decep-

tive explanations are constructed to maximize the ex-

plainee’s credence of decisions and explanations. We

assume that an explainee is most conﬁdent that the

reference explanation H

∗

(X, Y, M

) and the model-

based decision Y = M

∗

(X) are correct. This en-

codes the assumption that the truth is most intuitive

since any deception must contain some reason that

can be identiﬁed as faulty.

We provide simple means for creating deceptive

explanations that are non-truthful explanations (FT

and FF). The idea is to alter reference explanations.

This approach is signiﬁcantly simpler than creating

deceptive explanations from scratch using complex

algorithms as done in other works (Aivodji et al.,

2019; Lakkaraju and Bastani, 2019; Adelani et al.,

2019), while at the same time guaranteeing high-

quality deceptive explanations since they are based

on what the explainee expects as a valid explanation.

For non-truthful explanations a deceiver aims at over-

, understating or omitting features X

⊆ X that are

problem or instance-speciﬁc. To obtain non-truthful

explanations we alter reference explanations in two

ways:

Deﬁnition 1 (Omission). Remove a ﬁxed set of values

V so that no feature i has a value x

∈ V as follows:

Omit

(X)

(

0, if x

∈ V.

∗

(X)

, otherwise.

(3)

In our context, this means denying the relevance

of some words V related to concepts such as gender

or race. The next alteration distorts relevance scores

of all features, eg. to prevent re-engineering through

obfuscation.

Deﬁnition 2 (Noise addition). Add noise in a multi-

plicative manner for any explanation H

∗

(X):

Noise

(X)

:= H

∗

(X)

· (1 + r

i,X

), (4)

where r

i,X

is chosen uniformly at random in [−k, k]

for a parameter k for each feature i and input X ∈ S.

We assume that these alterations are applied con-

sistently for all outputs. Note, that this does not imply

that all explanations are indeed non-truthful, e.g., for

noise it might be that by chance explanations are not

altered or only very little, for omission it might be that

a feature is not relevant in the decision for a particular

input X, i.e. the value of a feature H

∗

(X)

is zero

anyway.

5 DECEPTION DETECTION

To detect deception attempts, we reason using expla-

nations and decisions of multiple inputs. That is, for a

set of inputs X ∈ S

, we are given for each input X

the reported decision M

(X) and accompanying ex-

planation H

(X). Our goal is to identify if a model

outputs deceptive explanations or not. For supervised

learning, we (even) aim to identify the inputs yielding

deceptive outputs. We assume that only features that

are claimed to contribute positively to a decision are

included in explanations. Features that are claimed

to be irrelevant or even supporting of another deci-

sion outcome are ignored. The motivation is that we

aim at explanations that are as simple to understand as

possible. The omission of negatively contribution fea-

tures makes detection harder. We ﬁrst provide theo-

retical insights before looking into practical detection

approaches.

Formal Investigation: Ideally, any of the three

types of deception {T F, F T, F F } is detected using

only one or more inputs X ∈ S

and their responses

(X) and H

(X) (see Figure 3). But, without

additional domain knowledge (such as correctly la-

beled samples), metadata or context information, this

is not impossible for all deception attempts. This fol-

lows since data, such as class labels, bear no mean-

ing on their own. Thus, any form of ”consistent” ly-

ing is successful, eg. always claiming that a cat is a

dog (using explanations for class dog) and a dog is a

cat (using explanations for class cat) is non-detectable

for anybody lacking knowledge on cats and dogs, i.e.,

knowing what a cat or a dog is.

Theorem 1. There exist non-truthful reported deci-

sions M

(X) 6= M

∗

(X) that cannot be identiﬁed as

non-truthful.

Proof. Consider a model M

for dataset {(X, Y )}

for binary classiﬁcation with labels Y ∈ {0, 1} and

(X) = M

∗

(X). Assume a deceiver switches the

decision of model M

, i.e. it returns M

(X) =

1 − M

∗

(X) and H

∗

(X, M

(X), M

). Consider

a dataset with switched labels, i.e. {(X, 1 − Y )}

and a second model M

that is identical to M

except that it outputs M

(X) = 1 − Y =

1 − M

(X). Thus, reference explanations are

identical, i.e. we have H

∗

(X, M

(X), M

) =

Deceptive AI Explanations: Creation and Detection

Figure 3: Inputs and outputs for deceiver and explainee for scenario FT in Figure 1. Images by (Petsiuk et al., 2018).

∗

(X, M

(X), M

). Thus, for input X both

the deceiver and model M

report M

(X) =

1 − M

(X) and H

∗

(X, M

(X), M

). Therefore,

and M

cannot be distinguished by any detec-

tor.

A similar theorem might be stated for non-truthful

explanations H 6= H

∗

, eg. by using feature inversion

H(X) = −H

∗

(X).

The following theorem states that one cannot hide

that a feature (value) is inﬂuential if the exchange of

the value with another value leads to a change in de-

cision.

Theorem 2. Omission of at least one feature value

v ∈ V can be detected, if there are instances X, X

∈

S with decisions M

(X) 6= M

) and X

= X

except for one feature j with x

, x

∈ V and x

6= x

Proof. We provide a constructive argument. We can

obtain for each input X ∈ S, the prediction M

(X)

and explanation H

(X). By Deﬁnition of Omis-

sion, if feature values V are omitted it must hold

(X)

= 0 for all (i, X) ∈ F

S,v

and v ∈ V. Omis-

sion occurred if this is violated or there are X, X

∈ S

that differ only in the value x

∈ V for feature j and

(X) 6= M

). The latter holds because the

change in decision must be attributed to the fact that

of x

6= x

, since X and X

are identical except for

feature j with values that are deemed omitted.

Theorem 2 is constructive, meaning that it can eas-

ily be translated into an algorithm by checking all in-

puts S if the stated condition is matched. But, gen-

erally all inputs S cannot be evaluated due to com-

putational costs. Furthermore, the existence of inputs

X, X

∈ S that only differ in a speciﬁc feature is not

guaranteed. However, from a practical perspective, it

becomes apparent that data collection helps in detec-

tion, i.e. one is more likely to identify ”contradictory”

samples X, X

in a subset S

⊂ S the larger S

is.

Detection Approaches: Our formal analysis

showed that only decisions and explanations are

not sufﬁcient to detect deception involving ﬂipped

classes. That is, some knowledge on the domain

is needed. Encoding domain know-how with a

labeled dataset seems preferable to using expert rules

or the-like. Thus, not surprisingly, this approach

is common in the literature, e.g. for fake news

detection (P

erez-Rosas et al., 2017; Przybyla, 2020).

To train a detector, each sample is a triple (X,

(X), H

(X)) for X ∈ S

together with label

L ∈ {T T, F T, T F, F F } stating the scenario in

Figure 1. After the training, the classiﬁer can be

applied to the explanations and decisions of X ∈ S

to investigate. We develop classiﬁers maximizing

deception detection accuracy.

Labeling data might be difﬁcult since it requires

not only domain knowledge on the application but

also knowledge on ML, ie. the reference model and

explainability method. Thus, we also propose unsu-

pervised approaches to identify whether a model, ie.

its explanations, are truthful to the model decision.

That is, the goal is to assess if given explanations H

are true to the model M

(X) or not.

Algorithm 1: ConsistencyChecker.

Input: Untrained models M

, reference method

∗

, inputs S

with (deceptive) decisions and ex-

planations {(M

(X), H

(X)}

Output: (Outlier) Probability p

= s randomly chosen elements from S

with

s random in [c

|, |S

|] {We used: c

= 0.33}

Train each model M

∈ M

on (X, M

(X)) for X ∈

∗

(X) =

∈M

∗

(X, M

(X), M

)

s(M

) =

i∈[0,n−1],X∈S

∗

(X, M

(X), M

) − m

(X))

n|S

s(M

) =

i∈[0,n−1],X∈S

(X) − m

(X))

n|S

µ =

∈M

s(M

)

σ =

∈M

(s(M

) − µ)

p = prob



T > |s(M

) − µ|



T ∼ N (0, σ)



ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

Our approach is to check, whether the explana-

tions of H

and decisions of M

are consistent. This

would be easy, if the model M

was available, ie. we

would check if H

∗

(X, M

(X), M

) = H

(X).

Since it is not, we aim to use a model M

to approx-

imate model M

and compare the explanations H

∗

of M

with H

. Since approximation introduces an

error, we must determine if differences in the expla-

nations originate from model approximation or from

deception. To do so, we train (approximate) reference

models M

≈ M

with M

∈ M

using the provided

data (X, M

(X)) with X ∈ S

. The models might

differ, e.g. in hyperparameter settings. If explana-

tions of M

are ”outliers” relative to those of models

∈ M

explanations might be untruthful and fur-

ther investigation is needed. Otherwise, any variation

of explanation compared to H

∗

due to deception is

comparable to variation that might arise if models are

slightly varied but no deception is attempted.

Details on the model M

are unknown. But for many

common ML tasks excellent performing architectures

are publicly known. Therefore, we assume that we

can anticipate at least a well-working architecture for

the problem – the closer it is to M

the better.

Algorithm 1 (ConsistencyChecker) shows details. It

takes as input a set of untrained models M

∈ M

– ideally similar to M

. The more information is

known on M

, the more similar the models can be

chosen. If only very little information or no informa-

tion on M

is available, one might train models on

(X, M

(X)) for X ∈ S

and choose those that per-

form best.

The second unsupervised approach Algorithm 2

(UsefulnessChecker) tries to reproduce the decisions

based on explanations. If this is not possible for ex-

planations from M

but for those of approximate

models M

then explanations from M

are likely

deceptive. As before, we train multiple approximate

models M

∈ M

. For each of these models M

, we

train a classiﬁer C

using explanations from the ap-

proximate models M

as well as one on explanations

from M

. We use the same classiﬁer architecture for

all. We conduct a statistical test (as in Algorithm 1),

if accuracy is an outlier. The full pseudo-code is sim-

ilar to Algorithm 1. For the sake of completeness, it

is shown in Algorithm 2.

6 EVALUATION

We elaborate on two text classiﬁcation tasks using a

convolutional neural network (CNN) for text classi-

ﬁcation by (Kim, 2014) as our reference model M

∗

and GradCAM (Selvaraju et al., 2017) for generat-

Algorithm 2: UsefulnessChecker.

Input: Untrained models M

, reference method

∗

, inputs S

with (deceptive) decisions and expl.

{(M

(X), H

(X)}, untrained classiﬁer model C

Output: (Outlier) Probability p

= s randomly chosen elements from S

with

s random in [c

|, |S

|] {We used: c

:= 0.33}

Train each model M

∈ M

on (X, M

(X) for

X ∈ S

= random subset of S

of size c

| {We

used: c

:= 0.8}

= trained classiﬁer model C on



∗

(X, M

(X), M

), M

(X)



for X ∈ S

and

∈ M

= trained classiﬁer model C on



(X, M

(X), M

), M

(X)



for X ∈ S

Acc(C

) := Accuracy of classiﬁer C

using

X ∈ S

\ S

µ =

∈M

Acc(C

)

σ =

∈M

(Acc(C

) − µ)

p = prob



T > |Acc(C

) − µ|



T ∼ N (0, σ)



ing reference explanations H

∗

. The CNN is well-

established, conceptually simple and works reason-

ably well. GradCAM was one of the methods said

to have passed elementary sanity checks that many

other methods did not (Adebayo et al., 2018). While

GradCAM is most commonly employed for CNN im-

age recognition the mechanisms for texts are iden-

tical. In fact, (Lertvittayakumjorn and Toni, 2019)

showed that GradCAM on CNNs similar to the one

by (Kim, 2014) leads to outcomes on human tasks that

are comparable to other explanation methods such as

LIME. The GradCAM method, which serves as refer-

ence explanation H

∗

, computes a gradient-weighted

activation map starting from a given layer or neuron

within that layer back to the input X. We apply the

reference explanation method H

∗

, ie. GradCAM, on

the neuron before the softmax layer that represents

the class Y

to explain. For generating a high ﬁ-

delity explanation for an incorrectly reported predic-

tion M

(X) 6= M

∗

(X) (scenario FT in Figure 1)

we provide as explanation the reference explanation,

i.e. H

(X) = H

∗

(X, M

(X), M

). By deﬁnition

reference explanations maximize explanation ﬁdelity

Setup: We employed two datasets. The IMDB

dataset (Maas et al., 2011) consists of movie re-

views and a label indicating positive or negative sen-

timent polarity. We also utilized the Web of Science

(WoS) dataset consisting of abstracts of scientiﬁc pa-

Deceptive AI Explanations: Creation and Detection

Figure 4: Generated sample explanations for scenarios TT

(top) and FT (bottom) from Figure 1.

pers classiﬁed into 7 categories (Kowsari et al., 2017).

Our CNNs for classiﬁcation achieved accuracies of

87% for IMDB and 75% for WoS trained with 2/3 of

the samples for training and 1/3 for testing. We com-

puted explanations for test data only. For deception

using omission, we removed a randomly chosen set of

words V (see Def. 1), such that their overall contri-

bution to all explanations H

∗

is k% (with a tolerance

of 0.01k %). The contribution of a word v is given

(i,X)∈F (v,S)

∗

(X, M

∗

(X))

. For explanation

distortion parameter k (see Deﬁnitions 1 and 2) we

state values for each experiment.

ML based Detection: As detector models, we used

CNN models. For supervised learning, the model in-

put is a concatenation of three vectors: i) a text vector

of word indices, ii) a heatmap vector of values ob-

tained via GradCAM, that is a 1:1 mapping of the vi-

sual output shown to the user, and iii) a one-hot pre-

diction vector of the decision. Our ”simple” CNN de-

tector, i.e. classiﬁer, is designed as follows: we per-

form an embedding, concatenate the heatmap vector

with the word embedding before doing a 1D convo-

lution. Then we concatenate the one-hot prediction

vector and use two dense layers. The more ”com-

plex” CNN adds six more conv1D layers: two pro-

cessing the embedding, two on the heatmap vector,

and two after the ﬁrst concatenation. We used dropout

for regularization. Since labeling is difﬁcult and po-

tentially error-prone, we consider different levels of

label noise, i.e., L ∈ [0, 0.32], such that a fraction L

of all labels were replaced with a random label (dif-

ferent from the correct one). For the detection ex-

periment, we chose samples that were predicted cor-

rectly by the truthful model. For unsupervised learn-

ing, we train 35 classiﬁers M

∈ M

being varia-

tions of a CNN network (Kim, 2014), i.e., each of the

following hyperparameters was chosen uniformly at

random for each classiﬁer M

: embedding dimension

{32, 64, 128}; 1-3 linear layers; 2-6 conv layers for

the Kim network with varying number of ﬁlters. We

also varied the training sets in terms of size and ele-

ments, ie. we trained a model with a subset of T of

size 33, 50 and 100%. Any model was trained using

the Adam optimizer for 100 epochs. Train/Test data

split was 80/20 for all detector models.

Classiﬁers learning from (deceptive) explanations

as done in our unsupervised approach Usefulness-

Checker tend sometimes to focus on raw inputs X

and disregard explanation relevance scores H

(X).

That is, they often work well and show little varia-

tion in accuracy despite large variations in explana-

tions. To avoid this, we convolve also an inner repre-

sentation of the network with explanation values en-

forcing stronger entanglement. That is, in the Use-

fulnessChecker model the output of the word embed-

ding of the input is convolved with the explanations

as follows: First, we perform a low-dimensional em-

bedding (just one dimensional) and multiply the em-

bedding values with the explanation values and add

explanation values on top. This is then fed into 3

Conv1D layers followed by two dense layers.

Human-based Detection: We conducted a user

study using the IMDB dataset.

For the scenarios of

interest, we compare explanations that are aligned to

the shown prediction, i.e. TT and FT. Two samples

are shown in Figure 4. We recruited a total of 200 par-

ticipants on Amazon Mechanical Turk from the US

having at least a high-school degree. We presented

each participant with 25 predictions together with ex-

planations. They had to answer ”Is the classiﬁcation

correct?” on a scale of ﬁve ranging from strongly dis-

agree to strongly agree. We randomized the choice of

presented samples, i.e. we randomly chose a sample

of the dataset and we randomly chose between sce-

narios TT and FT in Figure 1.

7 RESULTS

Human-based Detection: Out of the 200 partici-

pants, we removed participants that spend less than 5

seconds per question, since we deemed this time too

short to provide a reasonable answer. We also ﬁltered

out participants who always gave the same answer for

all 25 questions. This left 140 participants amounting

to 3,500 answers. Demographics and answer distribu-

tions are in Figure 5 and Table 1.

A t-test of means conﬁrmed that the distributions

differ signiﬁcantly (p-value of 0.008), though the

mean scores for ”agreeing” of 3.74(TT) and 3.58(FT)

The WoS dataset seems less suited since it uses ex-

pert terminology that is often not held by the general pub-

lic from which participants originate as found in (Lertvit-

tayakumjorn and Toni, 2019).

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

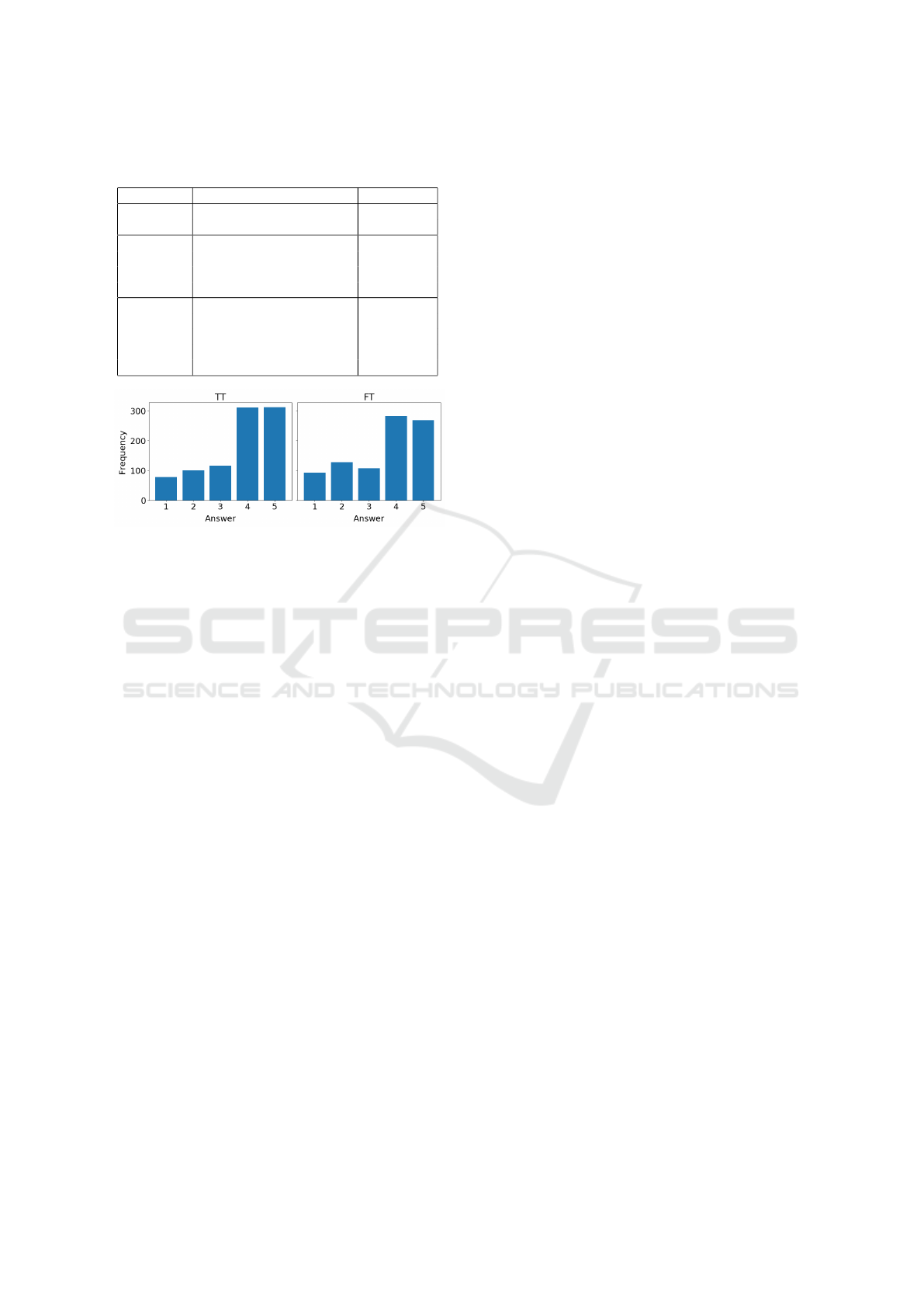
Table 1: Participants Demographics with n = 140 partici-

pants.

Variable Value Percentage

Gender Male 66%

Female 34%

Age ≤ 25 years of age 18%

from 26 to 40 years of age 62%

from 41 to 65 years of age 18%

> 65 years of age 2%

Education High School 16%

Associate Degree 11%

Bachelor’s Degree 56%

Master’s Degree 16%

Doctoral Degree 1%

Figure 5: Distributions of user replies to “The classiﬁcation

is correct” (1 = strongly disagree to 5 = strongly agree).

show that in absolute terms differences are minor.

This implies that while the majority of humans might

be fooled oftentimes, they have the capability to col-

lectively detect deceptive explanations.

Supervised ML-based Detection: Figure 6 shows

results for IMDB, those for WoS are similar, shown in

Figure 7. The plot shows that for very minor decep-

tion (small k) detection is more difﬁcult. Accuracy

rarely tops 60%, which is fairly low given that 50%

is the baseline for guessing. Accuracy is also more

volatile given label noise. Beyond some threshold

under all scenarios, accuracy exceeds 90% for cor-

rectly deciding whether a decision and/or explanation

are deceptive. Accuracy worsens with greater label

noise, though it is often better than guessing even for

a noise level of 32%. Mostly the complex CNN (with

more layers) outperforms the simple one with one ex-

ception: the scenario where the explanation is always

truthful to the model, but the decision is not. Here, a

simple function allows distinguishing deceptive (FT)

from the non-deceptive scenario (TT). We observed

that for the scenario with noise on non-truthful expla-

nations for correct decisions (TFNoise) small noise

levels can lead to very low test accuracies. Training

accuracies were larger, but mostly close to random

guessing, indicating that the network fails to learn

proper conditions what values constitute a noisy rele-

vance score and which do not.

Unsupervised ML-based Detection: For a single

model, a small probability indicates that it is unlikely

to witness such an (extreme) outcome, i.e. accuracy

or deviation from the average explanation. Thus, a

small probability such as 0.05 indicates a high like-

lihood of deception. Figure 10 shows the average as

well as maximum probability of all 35 models. Detec-

tion ability follows an S-curve, meaning that for de-

ception with parameterized strength k above a thresh-

old detection works fairly well, whereas it fails oth-

erwise. Required noise levels are somewhat higher

for the WoS dataset, as shown in Figure 7 but qualita-

tively, results are identical. The trained classiﬁer per-

forms worse on WoS than IMDB, since WoS is a more

complex dataset. Classiﬁers vary (relatively) more in

accuracy, which in turn also leads to more variance in

explanations. Looking at the mean and max indicates

that for multiplicative noise (TFNoise) all deceptive

models are reliably detected for k = 0.8, while below

that value at least for the most difﬁcult to detect model

it fails to do so. For k < 0.8, the detection methods

are still valuable to identify suspicious models, mean-

ing that such models exhibit lower probability, but are

not low enough to be certain. The same reasoning

also applies to TFOmit, though here a strong differ-

ence between methods is apparent. The Consisten-

cyChecker yields much better outcomes, highlighting

that even small omissions can be detected reliably. It

shows that statistical analysis is preferable to using a

downstream task. Our models M

are very diverse,

ie. models differ by a factor of 3 in terms of training

data and number of layers, as well as in neurons/ﬁlters

per layer. We found that reducing (or increasing) the

diversity has a profound impact on results, as shown

in Figures 8 and 9.

8 DIFFICULTY OF DECEPTION

DETECTION

We provide intuition for Algorithm Consistency-

Checker discussing the difﬁculty of detection de-

pending on noise models and deception strategy.

To compute the probability, we rely on values

s(M) as deﬁned in Algorithm 1. We are in-

terested in the gap G(H

, m

(X)) := E[(H

−

(X))

] between the mean and the relevance score

in the explanation of a feature i. For multiplicative

noise we have H

(X, M

(X), M ) = (1 + U) ·

∗

(X, M

(X), M

), where U is uniformly cho-

sen at random from [−k, k]. We shall use a

∗

(X, M

(X), M

) and m

:= m

(X) for ease of

notation. We expect that the deviation for a deceptive

explanation and the mean is:

Deceptive AI Explanations: Creation and Detection

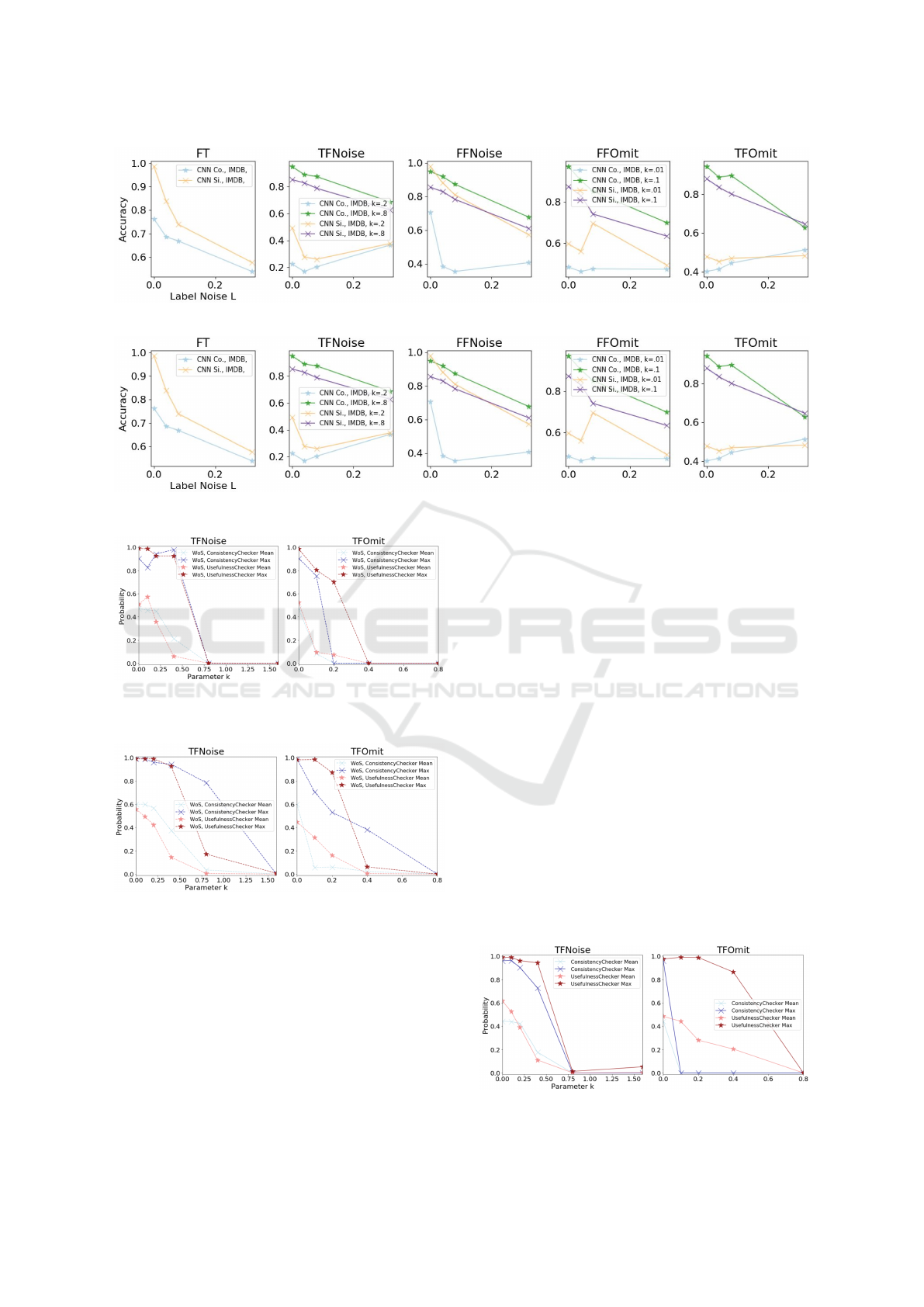
Figure 6: Supervised detection results for IMDB for scenarios in Figure 1.

Figure 7: ML-based supervised detection results for WoS for scenarios in Figure 1.

Figure 8: Unsupervised detection results for WoS where ap-

proximate models vary only in training data (but have the

same hyperparameters).

Figure 9: Unsupervised detection results for WoS where ap-

proximate models vary in training data and hyperparame-

ters. Detection is more difﬁcult compared to varying train-

ing data only (Figure 8).

G((1 + U )a

, m

) =E[((1 + U)a

− m

)

]

= E[(a

− m

)

− 2Ua

− U

]

= (a

− m

)

+ a

The overall deviation s(M) for a model is just the

mean across all features i and inputs X. Detection is

difﬁcult when

i,X

− m

)



i,X

/3 (5)

Put in words, detection is difﬁcult, when the distor-

tion due to deception (right-hand side term in Equa-

tion 5) is small compared to the one due to model

variations M

(left hand side term in Equation 5).

The closer a

and m

are and the larger k, the eas-

ier detection. For omission we get that if feature i

is omitted then G(a

, m

) = m

and G(a

, m

) =

− m

)

. Assume a set F

of features is omitted,

where the size of F

depends on the parameter k.

We get that deception is difﬁcult if

− m

)



i∈F

i /∈F

− m

)

. Clearly, the larger

the easier detection. Say we omit features with

= a

and we are given the choice of omitting two

features with mean m or one with mean 2m. The

latter is easier to detect since means are squared, ie.

+ m

= 2m

< (2m)

= 4m

. Therefore, it is

easier to detect few highly relevant omitted features

than many irrelevant ones.

Figure 10: Unsupervised detection results for IMDB.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

9 RELATED WORK

(Slack et al., 2020) showed how arbitrary explana-

tions for methods relying on perturbations can be gen-

erated for instances by training a classiﬁer with adver-

sarial inputs. (Dimanov et al., 2020) trains a classi-

ﬁer using an explainability loss term for a feature that

should be masked in explanations. (Fukuchi et al.,

2020) showed that biases in decision-making are dif-

ﬁcult to detect in an input-output dataset of a biased

model if the inputs were sampled in a way to disguise

the detector. (Lai and Tan, 2019) used ML (including

explanations) to support detection of deceptive con-

tent. The explanations were non-deceptive.

(Viering et al., 2019) are interested in manipulat-

ing the inner workings of a deep learning network to

output arbitrary explanations. Whether the explana-

tions themselves are convincing or not, is not con-

sidered, i.e., the paper shows many examples of ”in-

credible” explanations that can easily be detected as

non-genuine. (Aivodji et al., 2019) focus on manip-

ulating reported fairness based on a regularized rule

list enumeration algorithm. (Lakkaraju and Bastani,

2019) investigated the effectiveness of misleading ex-

planations to manipulate users’ trust. Decisions were

made using prohibited features such as gender and

race but misleading explanations were supposed to

disguise their usage. Both studies (Aivodji et al.,

2019; Lakkaraju and Bastani, 2019) found that users

can be manipulated into trusting high ﬁdelity but mis-

leading explanations for correct predictions. In con-

trast, we do not generate fake reviews but only gener-

ate misleading justiﬁcations for review classiﬁcations

and provide detection methods and some formal anal-

ysis.

Inspiration for detecting deceptive explanations

might be drawn from methods used for evaluating the

quality of explanations (Mohseni et al., 2021). In our

setup, quality is a relative notion compared to an ex-

isting explainability method and not to a (human) gold

standard. Papenmeier et al. (Papenmeier et al., 2019)

investigated the inﬂuence of classiﬁer accuracy and

explanation ﬁdelity on user trust. They found that

accuracy is more relevant for trust than explanation

quality though both matter.

(Nourani et al., 2019) investigated the impact of

explanations on trust. Poor explanations indeed re-

duce a user’s perceived accuracy of the model, inde-

pendent of its actual accuracy. Explanations’ helpful-

ness varies depending on task and method (Lertvit-

tayakumjorn and Toni, 2019). Explanations are more

helpful in assessing a model’s predictions compared

to its behavior. Some methods support some tasks

better than others. For instance, LIME provides the

most class discriminating evidence, while the layer-

wise relevance propagation (LRP) method (Bach

et al., 2015) helps assess uncertain predictions.

(Adelani et al., 2019) showed how to create and

detect fake online reviews of a pre-speciﬁed senti-

ment. In contrast, we do not generate fake reviews

but only generate misleading justiﬁcations for review

classiﬁcations. Fake news detection has also been

studied(P

erez-Rosas et al., 2017; Przybyla, 2020)

based on ML methods and linguistic features ob-

tained through dictionaries. (P

erez-Rosas et al., 2017;

Przybyla, 2020) use a labeled data set. Linguistic

cues (Ludwig et al., 2016) such as ﬂattery was used

to detect deception in e-mail communication. We

do not encode explicit, domain-speciﬁc detection fea-

tures such as ﬂattery.

Our methods might be valuable for the detection

of fairness and bias – see (Mehrabi et al., 2019) for

a recent overview. There are attempts to prevent ML

techniques from making decisions based on certain at-

tributes in the data, such as gender or race (Ross et al.,

2017) or to detect learnt biases based on representa-

tions (Zhang et al., 2018) or perturbation analysis for

social associations (Prabhakaran et al., 2019). In our

case, direct access to the decision-making system is

not possible — neither during training nor during op-

erations, but we utilize explanations.

In human-to-human interaction, behavioral cues

such as response times (Levine, 2014) or non-verbal

leakage due to facial expressions (Ekman and Friesen,

1969) might have some, but arguably limited im-

pact (Masip, 2017) on deception detection. In our

context, this might pertain, e.g., to computation time.

We do not use such information. Explanations to sup-

port deceptions typically suffer from at least one fal-

lacy such as ”the use of invalid or otherwise faulty

reasoning” (Van Eemeren et al., 2009). Humans can

use numerous techniques to attack fallacies (Damer,

2013), often based on logical reasoning. Such tech-

niques might also be valuable in our context. In par-

ticular, ML techniques have been used to detect lies

in human interaction, eg. (Aroyo et al., 2018).

10 DISCUSSION

Explanations provide new opportunities for deception

(Figure 1) that are expected to rise since AI is becom-

ing more pervasive, more creative (Schneider et al.,

2022), personalized (Schneider and Vlachos, 2021b).

Deceptive explanations might aim at disguising the

actual decision process, e.g., in case it is non-ethical,

or make an altered prediction appear more credible.

While faithfulness of explanations can be clearly ar-

Deceptive AI Explanations: Creation and Detection

ticulated mathematically using our proposed decision

and explanation ﬁdelity measures, determining when

an explanation is deceptive, is not always as clear,

since it includes a grey area. That is, an explanation

might be said to be deceptive, but it might also only

be judged as inaccurate or simpliﬁed. Thus, deception

detection is not an easy task: While strong deception

is well-recognizable, minor forms are difﬁcult to de-

tect. Furthermore, some form of domain or model

knowledge is necessary. This could be data similar

or, preferably, identical to the model’s training data

under investigation. Domain experts could also pro-

vide information in the form of labeled samples or de-

tection rules, i.e., they can investigate model outputs

and judge them as faithful or deceptive. Identifying

deceptive explanations becomes much easier if model

access and training or testing data are available, i.e.,

it reduces to comparing outputs from models to those

suggested by the (training) data. We recommend reg-

ulatory bodies to pass laws that ensure that auditors

have actual model access since this simpliﬁes the pro-

cess of deception detection. It is one step towards en-

suring that AI is used for the social good.

Detection methods will improve, but so will

strategies for lying. Thus, it is important to anticipate

weaknesses of detection algorithms that deceitful par-

ties might exploit, and mitigate them early on, e.g.,

with the aid of generic security methods (Schlegel

et al., ). The ﬁeld of explainability evolves quickly

with many challenges ahead (Meske et al., 2021).

This provides ample opportunities for future research

to assess methods for creation and detection of decep-

tive explanations, e.g., methods explaining features or

layers of image processing systems rather than text

(Schneider and Vlachos, 2021a).

11 CONCLUSION

Given economic and other incentives, a new cat

and mouse game between ”liars” and ”detectors” is

emerging in the context of AI. Our work provided

a ﬁrst move in this game: We structured the prob-

lem, and contributed by showing that detection of de-

ception attempts without domain knowledge is chal-

lenging. Our ML models utilizing domain knowledge

through training data yield good detection accuracy,

while unsupervised techniques are only effective for

more severe deception attempts or given (detailed) ar-

chitectural information of the model under investiga-

tion.

REFERENCES

Adebayo, J., Gilmer, J., Muelly, M., Goodfellow, I., Hardt,

M., and Kim, B. (2018). Sanity checks for saliency

maps. In Neural Information Processing Systems.

Adelani, D., Mai, H., Fang, F., Nguyen, H. H., Yamag-

ishi, J., and Echizen, I. (2019). Generating sentiment-

preserving fake online reviews using neural language

models and their human-and machine-based detec-

tion. arXiv:1907.09177.

Aivodji, U., Arai, H., Fortineau, O., Gambs, S., Hara, S.,

and Tapp, A. (2019). Fairwashing: the risk of ratio-

nalization. In Int. Conf. on Machine Learning(ICML).

Aroyo, A. M., Gonzalez-Billandon, J., Tonelli, A., Sciutti,

A., Gori, M., Sandini, G., and Rea, F. (2018). Can a

humanoid robot spot a liar? In Int. Conf. on Humanoid

Robots, pages 1045–1052.

Bach, S., Binder, A., Montavon, G., Klauschen, F., M

uller,

K.-R., and Samek, W. (2015). On pixel-wise explana-

tions for non-linear classiﬁer decisions by layer-wise

relevance propagation. PloS one.

Damer, T. E. (2013). Attacking faulty reasoning. Cengage

Learning, Boston, Massachusetts.

Dimanov, B., Bhatt, U., Jamnik, M., and Weller, A. (2020).

You shouldn’t trust me: Learning models which con-

ceal unfairness from multiple explanation methods. In

SafeAI@ AAAI.

Ekman, P. and Friesen, W. V. (1969). Nonverbal leakage

and clues to deception. Psychiatry, 32(1):88–106.

Fukuchi, K., Hara, S., and Maehara, T. (2020). Faking

fairness via stealthily biased sampling. In Pro. of the

AAAI Conference on Artiﬁcial Intelligence.

Fusco, F., Vlachos, M., Vasileiadis, V., Wardatzky, K., and

Schneider, J. (2019). Reconet: An interpretable neu-

ral architecture for recommender systems. In Proc.

IJCAI.

Kim, Y. (2014). Convolutional neural networks for sentence

classiﬁcation. In Proc. Empirical Methods in Natural

Language Processing (EMNLP).

Kowsari, K., Brown, D. E., Heidarysafa, M., Meimandi,

K. J., Gerber, M. S., and Barnes, L. E. (2017). Hdltex:

Hierarchical deep learning for text classiﬁcation. In

IEEE Int. Conference on Machine Learning and Ap-

plications (ICMLA).

Lai, V. and Tan, C. (2019). On human predictions with ex-

planations and predictions of machine learning mod-

els: A case study on deception detection. In Proceed-

ings of the Conference on Fairness, Accountability,

and Transparency, pages 29–38.

Lakkaraju, H. and Bastani, O. (2019). How do i fool you?:

Manipulating user trust via misleading black box ex-

planations. arXiv preprint arXiv:1911.06473.

Lertvittayakumjorn, P. and Toni, F. (2019). Human-

grounded evaluations of explanation methods for text

classiﬁcation. arXiv preprint arXiv:1908.11355.

Levine, T. R. (2014). Encyclopedia of deception. Sage Pub-

lications.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

Ludwig, S., Van Laer, T., De Ruyter, K., and Friedman,

M. (2016). Untangling a web of lies: Exploring au-

tomated detection of deception in computer-mediated

communication. Journal of Management Information

Systems, 33(2):511–541.

Maas, A., Daly, R., Pham, P., Huang, D., Ng, A., and Potts,

C. (2011). Learning word vectors for sentiment anal-

ysis. In Association for Computat. Linguistics (ACL).

Masip, J. (2017). Deception detection: State of the art and

future prospects. Psicothema.

Mehrabi, N., Morstatter, F., Saxena, N., Lerman, K., and

Galstyan, A. (2019). A survey on bias and fairness in

machine learning. arXiv preprint arXiv:1908.09635.

Meske, C., Bunde, E., Schneider, J., and Gersch, M. (2021).

Explainable artiﬁcial intelligence: objectives, stake-

holders, and future research opportunities. Informa-

tion Systems Management.

Mohseni, S., Zarei, N., and Ragan, E. D. (2021). A mul-

tidisciplinary survey and framework for design and

evaluation of explainable ai systems. Transactions on

Interactive Intelligent Systems.

Nourani, M., Kabir, S., Mohseni, S., and Ragan, E. D.

(2019). The effects of meaningful and meaningless

explanations on trust and perceived system accuracy

in intelligent systems. In AAAI Conference on Artiﬁ-

cial Intelligence.

Papenmeier, A., Englebienne, G., and Seifert, C. (2019).

How model accuracy and explanation ﬁdelity inﬂu-

ence user trust. arXiv preprint arXiv:1907.12652.

erez-Rosas, V., Kleinberg, B., Lefevre, A., and Mihalcea,

R. (2017). Automatic detection of fake news. arXiv

preprint arXiv:1708.07104.

Petsiuk, V., Das, A., and Saenko, K. (2018). Rise: Ran-

domized input sampling for explanation of black-box

models. arXiv preprint arXiv:1806.07421.

Prabhakaran, V., Hutchinson, B., and Mitchell, M. (2019).

Perturbation sensitivity analysis to detect unintended

model biases. arXiv preprint arXiv:1910.04210.

Przybyla, P. (2020). Capturing the style of fake news. In

Proceedings of the AAAI Conference on Artiﬁcial In-

telligence, volume 34, pages 490–497.

Ross, A. S., Hughes, M. C., and Doshi-Velez, F. (2017).

Right for the right reasons: training differentiable

models by constraining their explanations. In Int.

Joint Conference on Artiﬁcial Intelligence (IJCAI).

Schlegel, R., Obermeier, S., and Schneider, J. Structured

system threat modeling and mitigation analysis for in-

dustrial automation systems. In International Confer-

ence on Industrial Informatics.

Schneider, J., Basalla, M., and vom Brocke, J. (2022). Cre-

ativity of deep learning: Conceptualization and as-

sessment. In International Conference on Agents and

Artiﬁcial Intelligence (ICAART).

Schneider, J. and Handali, J. P. (2019). Personalized expla-

nation for machine learning: a conceptualization. In

European Conference on Information Systems (ECIS).

Schneider, J. and Vlachos, M. (2021a). Explaining neural

networks by decoding layer activations. In Int. Sym-

posium on Intelligent Data Analysis.

Schneider, J. and Vlachos, M. (2021b). Personalization of

deep learning. In Data Science–Analytics and Appli-

cations.

Selvaraju, R. R., Cogswell, M., Das, A., Vedantam, R.,

Parikh, D., and Batra, D. (2017). Grad-cam: Visual

explanations from deep networks via gradient-based

localization. In Int. Conference on Computer Vision

(ICCV).

Slack, D., Hilgard, S., Jia, E., Singh, S., and Lakkaraju, H.

(2020). Fooling lime and shap: Adversarial attacks on

post hoc explanation methods. In AAAI/ACM Confer-

ence on AI, Ethics, and Society.

Van Eemeren, F. H., Garssen, B., and Meuffels, B. (2009).

Fallacies and judgments of reasonableness: Empir-

ical research concerning the pragma-dialectical dis-

cussion rules, volume 16. Springer Science & Busi-

ness Media, Dordrecht.

Viering, T., Wang, Z., Loog, M., and Eisemann, E. (2019).

How to manipulate cnns to make them lie: the grad-

cam case. arXiv preprint arXiv:1907.10901.

Wu, Y., Ngai, E. W., Wu, P., and Wu, C. (2020). Fake online

reviews: Literature review, synthesis, and directions

for future research. Decision Support Systems.

Zhang, Q., Wang, W., and Zhu, S.-C. (2018). Examining

cnn representations with respect to dataset bias. In

AAAI Conf. on Artiﬁcial Intelligence.

Deceptive AI Explanations: Creation and Detection