ScaPMI: Scaling Parameter for Metric Importance

Ramisetty Kavya, Jabez Christopher and Subhrakanta Panda

Department of Computer Science and Information Systems, BITS Pilani, Hyderabad Campus, Telangana, India

Keywords:

Classiﬁers, Performance Metrics, Multi-criteria Decision-making.

Abstract:

Selection of an optimal classiﬁer is an important task in supervised machine learning, and it depends on per-

formance analytics, metric-importance, and domain requirements. This work considers distinct classiﬁers

as decision alternatives and various performance metrics as decision criteria. The weight for each metric

is computed by applying an Analytic hierarchy process on the proposed scaling parameter. Multi-criteria

decision-making methods consider the performance of classiﬁers along with metric-weights to generate the

ranking order of alternatives. Some typical experimental observations: Random forest is chosen as an opti-

mal classiﬁer by ﬁve MCDM methods for liver disorders dataset; Logistic regression, seems optimal for four

MCDM methods over hepatitis dataset, and to three methods over heart disease dataset; many such observa-

tions discussed in this work may enable developers to choose appropriate classiﬁer for supervised learning

systems.

1 INTRODUCTION

Classiﬁcation is the process of learning patterns from

historical data to predict the category of the unknown

instances in future. Numerous supervised machine

learning algorithms are available in literature to per-

form the classiﬁcation task (Kavya et al., 2021). Even

though various performance metrics are available in

literature to evaluate a classiﬁer, the choice of the ﬁ-

nal optimal classiﬁer is dependent on the importance

of the performance metrics. Variation in the impor-

tance of a performance metrics has signiﬁcant impact

on the optimal classiﬁer. Let us assume that accuracy

of the classiﬁer is more important than any other per-

formance metrics. The predictive model which results

in high accuracy is chosen as the optimal classiﬁer to

predict the category of the testing data. There is no

surety that the chosen classiﬁer is optimal in case high

importance is given to some other performance met-

ric instead of accuracy. Therefore, the choice of the

optimal classiﬁer is dependent on the importance of

the performance metrics whereas importance of the

performance metrics is dependent on the domain re-

quirements and user speciﬁcations.

This work focuses on analysing the relation be-

tween the choice of an optimal classiﬁer and the im-

portance of performance metrics. This work con-

siders decision tree, support vector machine, na

ıve

bayes, neural network, liner model, logistic regres-

sion, and random forest as classiﬁcation algorithms

(Osisanwo et al., 2017), and accuracy, hamming loss,

precision, true positive rate, true negative rate, false

positive rate, false negative rate, F1-score, AUC, and

cross-entropy loss as performance metrics (Naser and

Alavi, 2020).

All the chosen classiﬁcation algorithms are trained

based on the training data and evaluated over test-

ing data. The results of each performance met-

ric with respect to each classiﬁcation algorithm is

recorded for further decision-making. In this con-

text, decision-making refers to the process of choos-

ing an optimal classiﬁer based on their performance

results. Instead of providing an optimal classiﬁcation

algorithm, this work generates the preference order of

classiﬁcation algorithms based on the Multi-criteria

decision-making (MCDM) methods like Simple Ad-

ditive Weighting (SAW), Multiplicative Exponential

Weighting (MEW), Technique for Order Preference

by Similarity to Ideal Solution (TOPSIS), VIKOR,

and Preference Ranking Organisation Method for En-

riching Evaluation (PROMETHEE) (Guhathakurata

et al., 2021).

MCDM methods consider performance of each

classiﬁer with respect to each metric, and the weight

of each metric to rank the classiﬁers (Baccour, 2018).

This work introduces a Scaling Parameter, ScaPMI, Φ

to represent the importance of metrics. On the scale of

one to the number of performance metrics considered,

user can assign high Φ value to the metric to which

user want to give high importance. User assigns one

Kavya, R., Christopher, J. and Panda, S.

ScaPMI: Scaling Parameter for Metric Importance.

DOI: 10.5220/0010774600003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 3, pages 83-90

ISBN: 978-989-758-547-0; ISSN: 2184-433X

as the Φ value to the metric which is not important

compared to remaining metrics. These user-deﬁned Φ

values are considered for assigning weights to perfor-

mance metrics based on Analytic Hierarchy Process

(AHP) method (Asadabadi et al., 2019). The main

contributions of this work are as follows:

• Preference order of classiﬁers generated based on

equal weight to all the metrics serves as baseline

knowledge.

• An user-deﬁned scaling parameter (Φ) is intro-

duced to represent the importance of performance

metrics.

• A novel framework is modelled to choose an op-

timal classiﬁer based on the importance of perfor-

mance metrics, and majority ranking by various

MCDM methods.

The rest of the paper is structured as follows: Sec-

tion 2 brieﬂy describes the proposed work, Sec-

tion 3 presents the experimental analysis on medical

datasets, and Section 4 concludes the work with fu-

ture directions.

2 PROPOSED SYSTEM

The framework of the proposed decision support sys-

tem is presented as Figure 1. The three phases,

namely, model training, model testing, and decision-

making are detailed in this section.

2.1 Model Training

Computerised systems which are developed based on

the machine learning algorithms learn patterns in data

for developing predictive models as output. Predic-

tive models apply those patterns to support decision-

makers in unknown decision-making scenarios. The

seven machine learning algorithms learn patterns in

training data for developing the corresponding pre-

dictive models. Each algorithm follows different ap-

proach to learn patterns in data. By the end of the ﬁrst

phase, the proposed decision support system frame-

work is having seven predictive models which are de-

veloped based on seven different machine learning al-

gorithms.

2.2 Model Testing

Assume the dataset contains two distinct class la-

bels, namely, positive and negative; confusion ma-

trix is formed by considering the original class la-

bels as rows and the predicted class labels as columns.

Among the samples whose original class label is pos-

itive, number of correctly predicted samples are said

to be True Positive (a) and number of incorrectly

predicted samples are said to be False Negative (c).

Among the samples whose original class label is neg-

ative, number of correctly predicted samples are said

to be True Negative (d) and number of incorrectly

classiﬁed samples are said to be False Positive (b).

Table 1 presents the summary of the performance

metrics based on confusion matrix. By the end of

phase 2, all the seven predictive models are evaluated

over testing data by considering ten distinct perfor-

mance metrics.

2.3 Decision Making

Most of the existing works in literature choose an

optimal classiﬁer based on the performance metrics

(Peteiro-Barral et al., 2017). Different performance

metrics may suggest different classiﬁers as optimal.

It may not possible to choose few among the perfor-

mance metrics to select an optimal classiﬁer. Though

the evaluation focus of the metrics differ, there ex-

ist a relation among them. For example, increase in

the true positive accuracy decreases the false posi-

tive rate, decrease in the true positive rate increases

the false positive rate. All these dependencies among

the performance metrics has to be analysed and con-

sidered for selecting an optimal classiﬁer which pro-

vides signiﬁcant and domain relevant results. It is

not advisable to ignore few metrics because each of

the metric evaluates classiﬁer from different perspec-

tive. Therefore, this work focus on providing a prefer-

ence order of classiﬁers based on the user-deﬁned im-

portance parameter (Φ) for all evaluation metrics in-

stead of providing a single classiﬁer based on limited

metrics. Multi-criteria decision-making methods like

SEW, MEW, TOPSIS, VIKOR, and PROMETHEE

consider each performance metric as criterion to gen-

erate the preference (or ranking) order of classiﬁers.

Consider m classiﬁers and n performance metrics; let

i j

be the performance of i

classiﬁer with respect to

metric, and φ( j) be the importance-weight of j

metric. SAW performs the weighted sum of a

i j

and

φ( j) to assign score to i

classiﬁer.

SAW Score(i) =

∑

j=1

i j

Φ( j)

MEW performs the exponential sum of a

i j

and φ( j)

to assign score to i

classiﬁer.

MEW Score(i) =

∏

j=1

Φ( j)

i j

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

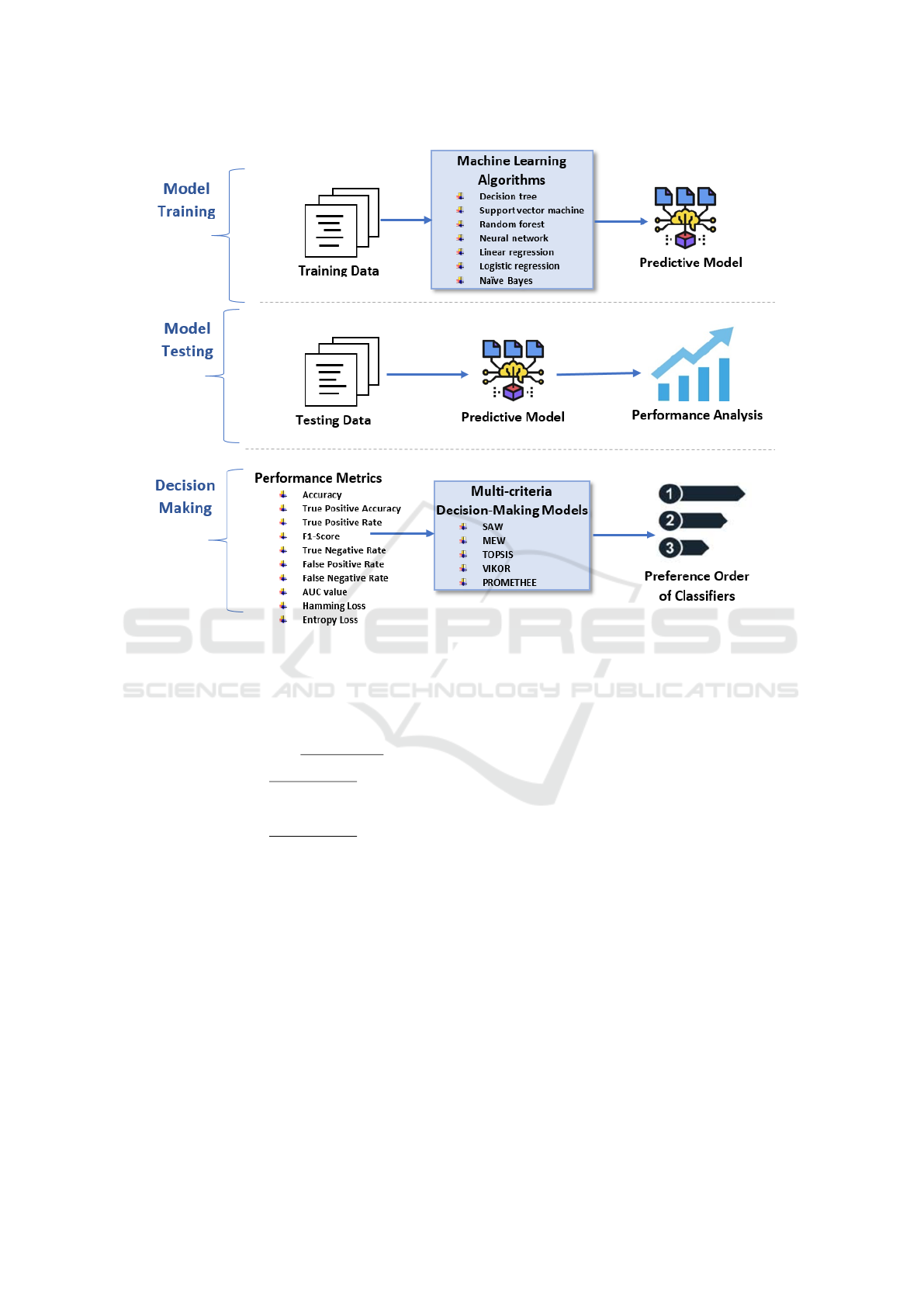
Figure 1: Framework of the proposed decision support system.

TOPSIS assigns score to i

classiﬁer based on pos-

itive ideal solution (i

) and negative ideal solution

−

TOPSIS Score(i) =

)

−

)

+ (S

)

−

)

∑

j=1

i j

− i

)

−

∑

j=1

i j

− i

−

)

i j

= a

i j

Φ( j)

VIKOR follows the same method by TOPSIS to as-

sign score for each classiﬁer. The only difference

is that VIKOR method uses L

metric with p = 1

and p = ∞ to compute weighted normalized Manhat-

tan distance (S), weighted normalized Chebyshev dis-

tance (R), and to analyse the relation with S and R as

PROMETHEE is based on pairwise comparison

among classiﬁers.

π(i,k) =

∑

j=1

(i,k)Φ( j)

where i and k are distinct classiﬁers. In-depth de-

tail about PROMETHEE can be found in (Brans and

De Smet, 2016).

Φ( j) has signiﬁcant impact on the preference or-

der of classiﬁers generated by MCDM methods. For

example, a classiﬁer can be the optimal in case accu-

racy has given high importance whereas some other

classiﬁer may be the optimal in case high importance

is given to some other metric. Hence, this work focus

on analysing the relation between (Φ) and preference

order of classiﬁers. For example, in health care do-

main, diagnosing a negative patient as positive is not

as harmful as diagnosing a positive patient as nega-

tive. Therefore, high importance has to be given to

the metrics which focus on positive class compared to

negative class. Since this work considers more than

one MCDM method, majority voting method is opted

to choose an optimal classiﬁer.

3 EXPERIMENTAL ANALYSIS

This section focus on performing a series of exper-

iments on UCI medical datasets, namely, diabetes,

liver, heart, hepatitis, and breast to verify the effec-

ScaPMI: Scaling Parameter for Metric Importance

Table 1: Summary of the performance metrics.

Performance Description Evaluation Focus

Precision It is also known as True Positive

Accuracy(TPA). TPA= a/(a + b)

It focuses on correctly predicted positive

samples among all the predicted positive

samples.

Recall/Sensitivity It is also known as True Positive

Rate(TPR). TPR= a/(a + c)

It focuses on the coverage of correctly pre-

dicted positive samples among all the actual

positive samples.

F1-score F1-Score =

(2 × T PA × T PR)

(T PA + T PR)

It focuses on the relation between the actual

positive labels and the predicted positive la-

bels.

Inverse Precision It is also known as True Negative

Accuracy (TNA). TNA= d/(d +

It focuses on the correctly predicted nega-

tive samples among all the predicted negative

samples.

Speciﬁcity It is also known as inverse re-

call or True Negative Rate(TNR).

TNR= d/(d + b)

It focuses on the correctly predicted negative

samples among all the actual negative sam-

ples.

False Positive Rate FPR= b/(a + b) It focuses on negative samples which are pre-

dicted as positive.

False Negative Rate FNR= c/(a + b) It focuses on positive samples which are pre-

dicted as negative.

Area under ROC

Curve

- This value represents how good the classiﬁ-

cation algorithm can distinguish between the

positive and negative classes. Higher the

value, higher class separability of the model

Accuracy Accuracy= (a + d)/(a + b + c +

It focuses on the correctly predicted samples

among all the test samples irrespective of pos-

itive and negative classes.

Hamming Loss HL = 1−accuracy It focuses on the incorrectly predicted sam-

ples among all the test samples irrespective

of positive and negative classes.

Cross-Entropy Loss - It focuses on the divergence between pre-

dicted probability and the actual class label.

tiveness of the proposed method in choosing an op-

timal classiﬁer. The detailed overview of the listed

datasets can be found in (Christopher, 2019). 80%

of the dataset is considered for training the classi-

ﬁers to develop the predictive models and the remain-

ing 20% of the samples are considered for evaluat-

ing the developed predictive models. This section

initially presents the performance results of predic-

tive models and then, the ranking order of classi-

ﬁers based on the MCDM methods is explained. The

complete executable ﬁles with other speciﬁcations

are available in https://github.com/pimpo9/Prefrence-

Order-of-Classiﬁers-based-on-MCDM-method.

All the seven classiﬁers develop predictive models

based on the training datasets and their performance

on the corresponding testing datasets are measured

using ten distinct metrics. Table 2 presents the perfor-

mance results of seven distinct classiﬁers on the test-

ing samples from ﬁve different datasets respectively.

If accuracy is considered as an importance metric to

choose a classiﬁer, then logistic regression achieved

82%, 70%, 80%, 86%, and 95% accuracy rate for di-

abetes, liver, heart, hepatitis, and breast datasets re-

spectively. All the remaining classiﬁers achieved ei-

ther slightly high or low accuracy rates. If the impor-

tance is changed from accuracy to some other metric,

there can be a classiﬁer other than logistic regression

which can provide better predictions.

Figure 2 to 6 presents the ROC curves for each

classiﬁer with respect to each dataset. ROC curve of

the classiﬁer which is more towards the left is bet-

ter compared to the remaining curves. However, it is

quite complex to analyse the results of various perfor-

mance metrics to choose an optimal classiﬁer. Even

after analysing the results of all the metrics, an op-

timal classiﬁer is provided to a user by considering

limited metrics.

In case, if the user comes with different argument

where importance must be given to some other then

user has to redo the entire procedure from analysing

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

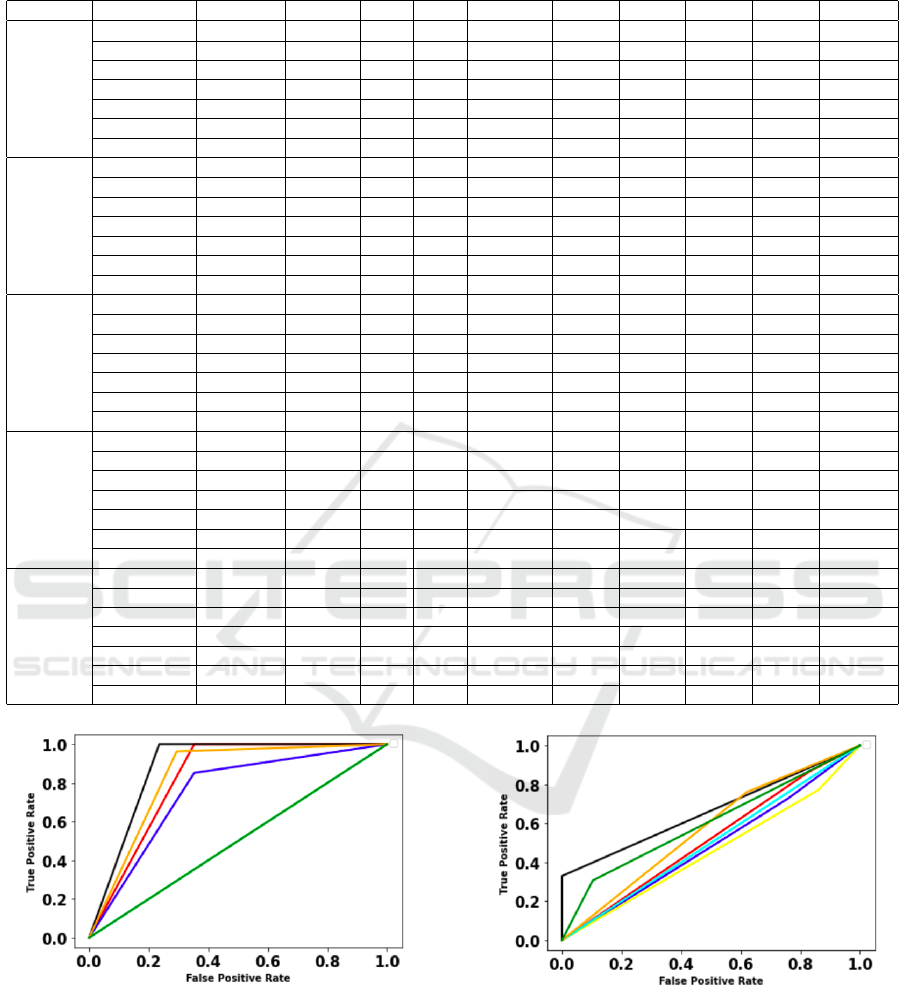
Table 2: Performance of classiﬁers on test samples of UCI datasets.

Datasets Classiﬁers Accuracy HL TPA TPR F1-Score TNR FPR FNR AUC Log loss

Diabetes

DT 0.7 0.2987 0.71 0.7 0.7 0.7572 0.2427 0.4117 0.6727 10.3169

SVM 0.48 0.5194 0.46 0.48 0.47 0.6407 0.3592 08431 0.7265 17.9424

RF 0.77 0.2272 0.77 0.33 0.76 0.8834 0.1165 0.4509 0.8229 7.8497

NN 0.7 0.2987 0.68 0.7 0.65 0.9392 0.0679 0.7647 0.6957 10.3168

LINEAR 0.33 0.6688 0.44 0.33 0.18 0.0097 0.9909 0.0196 0.4950 23.1011

LOGISTIC 0.82 0.1818 0.82 0.82 0.81 0.9320 0.0679 0.4117 0.8644 6.2798

NB 0.82 0.9029 0.82 0.82 0.82 0.9029 0.0970 0.3333 0.8850 6.0555

Liver

DT 0.61 0.3931 0.62 0.61 0.61 0.2413 0.7586 0.2727 0.4843 13.5794

SVM 0.62 0.3846 0.59 0.62 0.6 0.1379 0.8620 0.2272 0.5877 13.2843

RF 0.68 0.3162 0.72 0.68 0.7 0.5517 0.4827 0.25 0.6992 10.9226

NN 0.75 0.2478 0.57 0.75 0.65 0 1 0 0.5454 8.5610

LINEAR 0.32 0.6752 0.82 0.32 0.66 1 0 0.8977 0.5511 23.3210

LOGISTIC 0.7 0.2991 0.65 0.7 0.67 0.1724 0.8275 0.1363 0.7612 10.3322

NB 0.5 0.5042 0.83 0.5 0.5 1 0 0.6704 0.6841 17.4169

Heart

DT 0.74 0.26222 0.76 0.74 0.74 0.6470 0.3529 0.1481 0.7494 9.0595

SVM 0.44 0.5573 0.2 0.44 0.27 0 1 0 0.5664 19.2515

RF 0.8 0.1967 0.83 0.8 0.8 0.7058 0.2941 0.0740 0.8834 7.9270

NN 0.56 0.4421 0.31 0.56 0.4 1 0 1 0.3562 15.2876

LINEAR 0.69 0.3114 0.71 0.69 0.69 0.6176 0.3825 0.2222 0.6977 10.7581

LOGISTIC 0.8 0.1967 0.86 0.8 0.8 0.6470 0.3529 0 0.9498 6.7946

NB 0.87 0.1311 0.9 0.87 0.87 0.7670 0.2352 0 0.9346 4.5297

Hepatitis

DT 0.79 0.2068 0.87 0.79 0.82 0.8 0.2 0.25 0.775 7.1460

SVM 0.86 0.1379 0.74 0.86 0.8 1 0 1 0.63 4.7639

RF 0.86 0.1379 0.86 0.86 0.86 0.92 0.08 0.5 0.87 4.7639

NN 0.76 0.2413 0.73 0.76 0.74 0.88 0.12 1 0.44 4.7639

LINEAR 0.72 0.2758 0.81 0.72 0.76 0.76 0.24 0.5 0.63 4.7639

LOGISTIC 0.86 0.1379 0.89 0.86 0.87 0.88 0.12 0.25 0.86 4.7640

NB 0.83 0.1724 0.88 0.83 0.85 0.1724 0.16 0.25 0.95 5.9550

Breast

DT 0.95 0.0526 0.95 0.95 0.95 0.9 0.05 0.054 0.9479 4.7639

SVM 0.44 0.5614 0.42 0.44 0.43 0.15 0.85 0.4054 0.7557 4.7639

RF 0.98 0.0175 0.98 0.98 0.98 1 0 0.027 0.9983 4.7639

NN 0.35 0.6491 0.12 0.35 0.18 1 0 1 0.9665 4.7639

LINEAR 0.94 0.0614 0.94 0.94 0.94 0.875 0.125 0.27 0.9239 2.1208

LOGISTIC 0.95 0.0526 0.95 0.95 0.95 0.925 0.075 0.054 0.9912 4.7639

NB 0.94 0.0614 0.94 0.94 0.94 0.875 0.125 0.027 0.9888 4.7939

Figure 2: ROC for diabetes dataset.

the metrics to ﬁnalising an optimal classiﬁer. There-

fore, this work incorporates MCDM methods to rank

the classiﬁers based on the user preferences.

Figure 3: ROC for liver disorders dataset.

3.1 Analysis on the Preference Order of

Classiﬁers

The importance of the metric plays a pivotal role in

generating the preference order of classiﬁers. Though

is not advisable, this work initially assigns equal

weight to all the metrics to verify the preference or-

ScaPMI: Scaling Parameter for Metric Importance

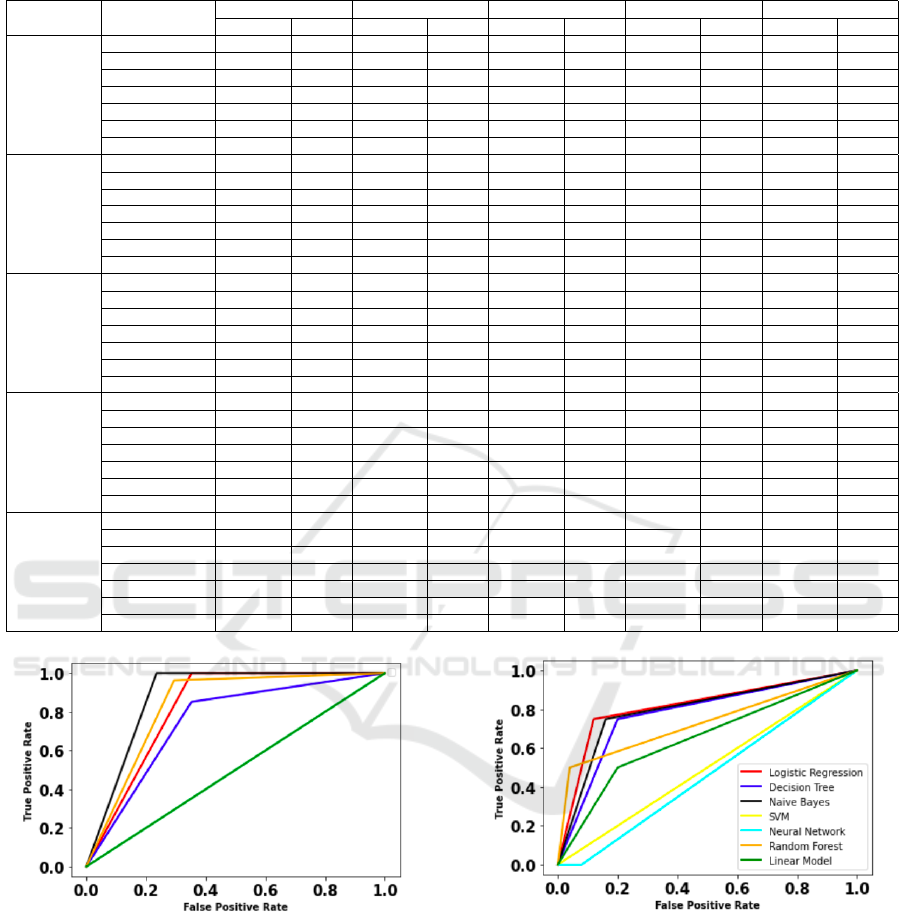
Table 3: Preference order of classiﬁers based on equal weight.

DATASET CLASSIFIERS

SAW MEW TOPSIS VIKOR PROMETHEE

VALUES RANK VALUES RANK VALUES RANK VALUES RANK VALUES RANK

DIABETES

DT 0.5377 5 0.5983 3 0.7068 4 0.2017 3 -0.1666 5

SVM 0.4877 6 0.6314 1 0.4109 6 0.8404 6 -0.5999 6

RF 0.6103 3 0.5703 4 0.8197 2 0.0964 2 0.2333 3

NN 0.5707 4 0.5674 5 0.6616 5 0.5549 5 -0.0166 4

LINEAR 0.2675 7 0.26804 7 0.2655 7 1.0 7 -0.7666 7

LOGISTIC 0.6421 2 0.5306 6 0.8629 1 0.0 1 0.7333 1

NB 0.7380 1 0.6299 2 0.7284 3 0.5545 4 0.5833 2

LIVER

DT 0.4074 6 0.5956 2 0.4671 6 0.9290 6 -0.3333 7

SVM 0.4346 4 0.5667 3 0.4869 5 0.8209 5 -0.2333 5

RF 0.5884 2 0.6404 1 0.7369 1 0.0 1 0.4333 1

NN 0.4034 7 0.0 NA 0.5568 3 0.7311 3 0.1333 3

LINEAR 0.6072 1 0.0 NA 0.4489 7 1.0 7 -0.2666 6

LOGISTIC 0.5186 4 0.5528 4 0.6249 2 0.4667 2 0.3666 2

NB 0.5713 3 0.0 NA 0.5549 4 0.7605 4 -0.0999 4

HEART

DT 0.5404 4 0.5607 2 0.7125 4 0.2200 4 -0.0666 4

SVM 0.439 7 0.0 NA 0.2677 7 1.0 7 -0.7999 7

RF 0.5804 3 0.5215 3 0.8178 2 0.1123 2 0.3666 3

NN 0.439 6 0.0 NA 0.3979 6 0.8701 6 -0.4000 5

LINEAR 0.5234 5 0.439 1 0.630 5 0.3183 5 -0.4333 6

LOGISTIC 0.5808 2 0.0 NA 0.8173 3 0.1392 3 0.4666 2

NB 0.5974 1 0.0 NA 0.9004 1 0.0 1 0.8666 1

HEPATITIS

DT 0.5647 4 0.77602 2 0.4985 5 0.8134 5 -0.2333 5

SVM 0.4896 5 0.0 7 0.6116 4 0.6571 4 0.2166 3

RF 0.5912 2 0.7328 5 0.813 1 0.0199 1 0.5 1

NN 0.3321 7 0.7605 4 0.3475 7 0.9895 6 -0.4999 6

LINEAR 0.3359 6 0.7891 1 0.3488 6 1.0 7 -0.6166 7

LOGISTIC 0.5823 3 0.7113 6 0.7969 2 0.1249 2 0.5 2

NB 0.6105 1 0.7615 3 0.6781 3 0.3765 3 0.1333 4

BREAST

DT 0.6708 4 0.4277 5 0.7319 4 0.5394 4 0.2833 3

SVM 0.419 7 0.5222 1 0.2307 7 1.0 7 -0.7166 7

RF 0.7000 1 0.0 NA 0.7500 2 0.5 2 0.8333 1

NN 0.4869 6 0.0 NA 0.3852 6 0.9197 6 -0.4499 6

LINEAR 0.578 5 0.508 2 0.8580 1 0.0098 1 -0.1833 5

LOGISTIC 0.6886 2 0.444 3 0.7375 3 0.5312 3 0.3166 2

NB 0.6806 3 0.4405 4 0.7305 5 0.5428 5 -0.0833 4

Figure 4: ROC for C-heart disease dataset.

der of classiﬁers. Table 3 presents the ranking or-

der of classiﬁers based on equal weighting. It can

be observed from Table 3 that TOPSIS and VIKOR

has assigned the ﬁrst rank to same classiﬁer for all

the ﬁve datasets. PROMETHEE has assigned ﬁrst

rank to same classiﬁer as TOPSIS and VIKOR for all

datasets other than breast. The ranking order of clas-

siﬁers based on the remaining two MCDM methods

are quite varied compared to TOPSIS and VIKOR. In

most of the cases, decision-makers may not be clear

in deciding the importance of the metrics. In such

Figure 5: ROC for hepatitis dataset.

scenarios, the ranking order based on equal weights

to all the performance metrics will serve as a baseline

knowledge to the decision-maker to assign weights to

metrics. Table 5 presents the importance value of per-

formance metrics from healthcare perspective.

In Table 5, the metrics which focus on predicting

positive class have to be given high importance com-

pared to the metrics which focus on predicting the

negative class. Both precision and recall focus more

on predicting the positive class samples correctly and

therefore a high importance value, 9 and 10, is as-

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

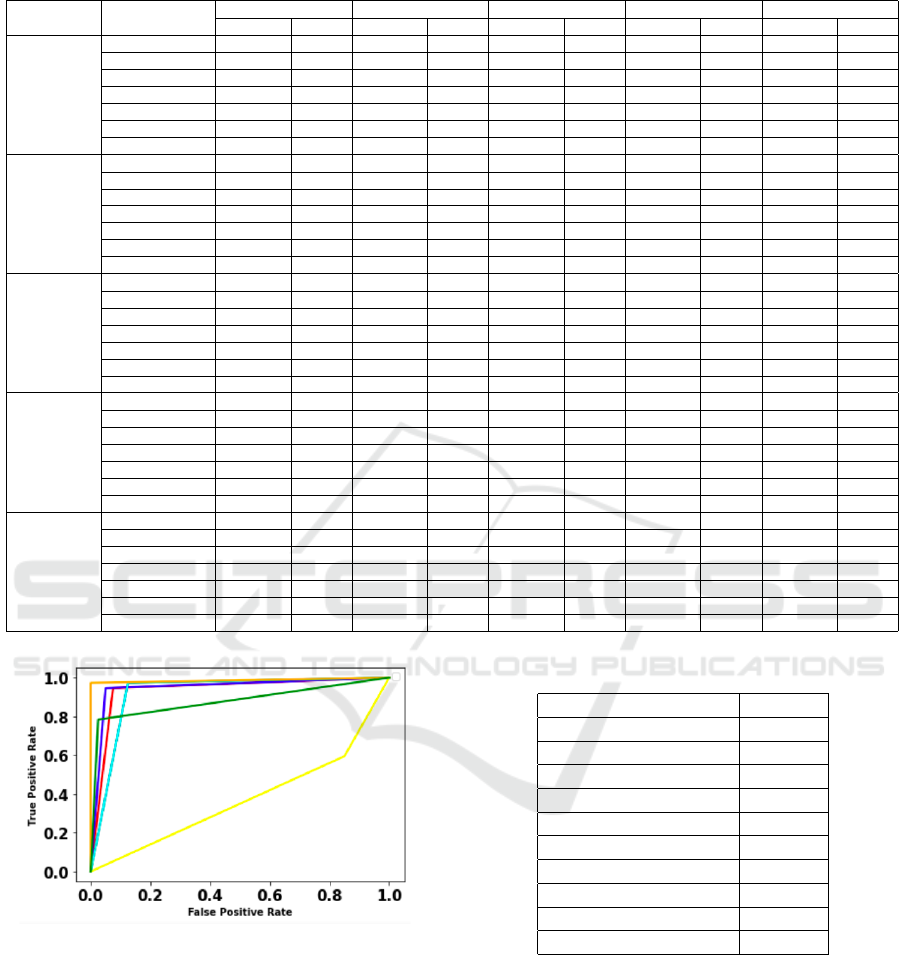
Table 4: Preference order of classiﬁers based on metric-importance.

DATASET CLASSIFIERS

SAW MEW TOPSIS VIKOR PROMETHEE

VALUES RANK VALUES RANK VALUES RANK VALUES RANK VALUES RANK

DIABETES

DT 0.61712 5 0.6995 4 0.7015 4 0.2596 4 -0.1424 4

SVM 0.4159 6 0.6258 6 0.3539 6 0.7608 6 -0.5757 6

RF 0.74149 3 0.7260 2 0.8504 2 0.0655 2 0.2848 3

NN 0.63497 4 0.6971 5 0.6623 5 0.2658 5 -0.1515 5

LINEAR 0.11594 7 0.2979 7 0.1863 7 1.0 7 -0.8242 7

LOGISTIC 0.80770 2 0.7234 3 0.9077 1 0.0 1 0.7515 1

NB 0.8998 1 0.83692 1 0.7814 3 0.2366 3 0.6575 2

LIVER

DT 0.4076 7 0.6650 3 0.4619 6 0.7193 5 -0.3878 7

SVM 0.4417 6 0.6501 4 0.4908 5 0.7552 6 -0.2424 5

RF 0.69604 1 0.7509 1 0.7736 1 0.0 1 0.4909 1

NN 0.47256 5 0.0 NA 0.5709 3 0.7552 6 0.1333 3

LINEAR 0.5496 4 0.0 NA 0.4473 7 1.0 7 -0.2818 6

LOGISTIC 0.6053 2 0.6701 2 0.6761 2 0.3065 2 0.4242 2

NB 0.57806 3 0.0 NA 0.5315 4 0.6476 3 -0.1363 4

HEART

DT 0.6245 4 0.66287 1 0.7293 4 0.2686 4 -0.0393 4

SVM 0.19052 7 0.0 NA 0.2032 7 1.0 7 -0.8363 7

RF 0.7051 3 0.6552 3 0.8590 3 0.1199 3 0.3969 3

NN 0.3454 6 0.0 NA 0.2602 6 0.7879 6 -0.5818 6

LINEAR 0.5732 5 0.6614 2 0.6373 5 0.3833 5 -0.3878 5

LOGISTIC 0.7185 2 0.0 NA 0.8688 2 0.1066 2 0.5454 2

NB 0.7742 1 0.0 NA 0.9572 1 0.0 1 0.9030 1

HEPATITIS

DT 0.5647 4 0.8116 3 0.6104 4 0.4268 4 -0.1030 5

SVM 0.5429 5 0.0 7 0.5557 5 0.6155 5 0.0727 4

RF 0.73816 2 0.8321 1 0.8656 2 0.0428 2 0.4939 2

NN 0.2694 7 0.7853 6 0.1927 7 0.9411 6 -0.7272 7

LINEAR 0.30312 6 0.8091 4 0.2726 6 0.9680 7 -0.6909 6

LOGISTIC 0.7502 1 0.8056 5 0.8966 1 0.0 1 0.6636 1

NB 0.7065 3 0.8297 2 0.8091 3 0.1161 3 0.2909 3

BREAST

DT 0.7545 4 0.5645 3 0.9047 4 0.0660 4 0.3424 3

SVM 0.3052 7 0.4920 6 0.2420 7 0.9206 6 -0.7303 7

RF 0.8000 1 0.0 NA 0.9514 1 0.0 1 0.9515 1

NN 0.34697 6 0.0 NA 0.9234 6 0.9997 7 -0.6909 6

LINEAR 0.7312 5 0.6465 1 0.8712 5 0.1225 5 -0.2515 5

LOGISTIC 0.7767 2 0.5753 2 0.9345 2 0.0280 2 0.4393 2

NB 0.7653 3 0.5597 4 0.9234 3 0.0371 3 -0.0606 4

Figure 6: ROC for W-breast cancer dataset.

signed to them respectively. If the model is having

high precision and low recall, then it is classifying

many test instances as positive but it is not classifying

most of the positive test instances as positive. If the

model is having high recall and low precision, then it

is correctly predicting the test instances of the positive

classes but it is also predicting most of the negative

classes as positive. In medical domain, sometimes di-

agnosis of a negative sample as positive is not harm-

ful. Therefore, the model with high recall is desirable

compared to high precision value. Based on this ar-

Table 5: Importance of the performance metrics.

Performance metrics Φ value

TPR 10

TPA 9

F1-SCORE 8

AUC 7

ACCURACY 6

HAMMING LOSS 5

FNR 4

TNR 3

FPR 2

LOG LOSS 1

gument, high importance value is given to recall com-

pared to precision. Since F1-Score is the harmonic

mean of precision and recall, this work assigns next

importance to F1-Score.

ROC plots are one of the best ways of presenting

how the classiﬁer is separating positive and negative

classes. Moreover, ROC plots are generated based on

true positive rate which is an important metric in med-

ical diagnosis. The classiﬁer with high AUC value

is preferred compared to remaining. Therefore, this

work assigns next importance to AUC. Though ac-

ScaPMI: Scaling Parameter for Metric Importance

curacy is a highly preferred metric in binary classiﬁ-

cation, it is subjected to be biased if there is a class-

imbalance. Therefore it is given less importance com-

pared to the metrics where true positive rate is in-

volved. The least importance is given to the metrics

which focus on negative class because they are not

so important in medical diagnosis. Table 4 presents

the ranking order of classiﬁers based on the impor-

tance weights in Table 5. It can be observed from Ta-

ble 4 that TOPSIS, VIKOR, and PROMETHEE has

assigned ﬁrst rank to same classiﬁer for all the ﬁve

datasets after assigning importance to metrics. The

ranks assigned by SAW is almost similar to TOP-

SIS, VIKOR, and PROMETHEE whereas the ranks

assigned by MEW are quite dissimilar. In between

Table 3 and 4, the consistent ranking can be observed

for the top performed classiﬁers by all the MCDM

methods in case of Table 4. By this, we can iden-

tify the fact that correctly weighting the criteria to a

particular problem will result in a similar ranking by

most of the MCDM method. In Table 4, for diabetes

dataset, logistic regression, random forest and na

ıve

bayes are the top ranked classiﬁers by various MCDM

methods, whereas random forest is followed by logis-

tic regression for both liver and breast datasets. Na

ıve

bayes is followed by logistic regression, and random

forest is followed by logistic regression for heart and

hepatitis datasets respectively.

It can observed from Table 4 that, SVM, lin-

ear model, neural network, and decision tree has not

given preference compared to random forest, logis-

tic regression and na

ıve bayes. By considered the

majority voting, this work concludes the classiﬁer

which is ranked as one by TOPSIS, VIKOR, and

PROMETHEE can be chosen as optimal for corre-

sponding datasets. Therefore, random forest classiﬁer

is chosen as the optimal for liver and breast datasets,

logistic regression for diabetes and hepatitis dataset,

and ﬁnally na

ıve bayes classiﬁer for heart dataset.

4 CONCLUSION

This work focuses on providing a preference or-

der of classiﬁers based on the importance of perfor-

mance metrics which is recorded as ScaPMI value.

A brief overview on various performance metrics and

their evaluation focus is provided so that the task of

assigning ScaPMI value to metrics becomes easier.

Moreover, the preference order of classiﬁers gener-

ated based on equal ScaPMI value to all the metrics

aid decision-maker in attaining baseline knowledge.

Decision-makers can generate the desired preference

order of classiﬁers by varying the ScaPMI value of

metrics with the knowledge attained from the prefer-

ence order by equal ScaPMI values. Since, all the

datasets in this work are from medical domain, high

ScaPMI value is given to recall and less ScaPMI value

is given to cross-entropy loss. The classiﬁer to which

most of the MCDM methods has assigned the ﬁrst

rank is considered as an optimal classiﬁer for corre-

sponding dataset.

As a further extension, this work intends to in-

corporate statistical methods to verify the signiﬁcance

of the difference among the ranking orders generated

by various MCDM methods. Moreover, an enhanced

study of the performance metrics and the evaluation

focus supports in modeling better criteria and their

weights to rank the classiﬁers precisely. A series of

experiments on non-medical datasets with multiple

weighting strategies helps in verifying the rationality

and the effectiveness of the ranking methods.

REFERENCES

Asadabadi, M. R., Chang, E., and Saberi, M. (2019). Are

mcdm methods useful? a critical review of analytic

hierarchy process (ahp) and analytic network process

(anp). Cogent Engineering, 6(1):1623153.

Baccour, L. (2018). Amended fused topsis-vikor for classi-

ﬁcation (atovic) applied to some uci data sets. Expert

Systems with Applications, 99:115–125.

Brans, J.-P. and De Smet, Y. (2016). Promethee methods.

In Multiple criteria decision analysis, pages 187–219.

Springer.

Christopher, J. (2019). The science of rule-based classiﬁers.

In 2019 9th International Conference on Cloud Com-

puting, Data Science & Engineering (Conﬂuence),

pages 299–303. IEEE.

Guhathakurata, S., Saha, S., Kundu, S., Chakraborty, A.,

and Banerjee, J. S. (2021). South asian countries are

less fatal concerning covid-19: a fact-ﬁnding proce-

dure integrating machine learning & multiple criteria

decision-making (mcdm) technique. Journal of The

Institution of Engineers (India): Series B, pages 1–15.

Kavya, R., Christopher, J., Panda, S., and Lazarus, Y. B.

(2021). Machine learning and xai approaches for al-

lergy diagnosis. Biomedical Signal Processing and

Control, 69:102681.

Naser, M. and Alavi, A. (2020). Insights into performance

ﬁtness and error metrics for machine learning. arXiv

preprint arXiv:2006.00887.

Osisanwo, F., Akinsola, J., Awodele, O., Hinmikaiye, J.,

Olakanmi, O., and Akinjobi, J. (2017). Supervised

machine learning algorithms: classiﬁcation and com-

parison. International Journal of Computer Trends

and Technology (IJCTT), 48(3):128–138.

Peteiro-Barral, D., Remeseiro, B., M

endez, R., and Penedo,

M. G. (2017). Evaluation of an automatic dry eye test

using mcdm methods and rank correlation. Medical &

biological engineering & computing, 55(4):527–536.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence