Privacy-preserving Parallel Computation of Shortest Path Algorithms

with Low Round Complexity

Mohammad Anagreh

1,2

, Peeter Laud

and Eero Vainikko

Institute of Computer Science, University of Tartu, Narva maantee 18, 51009 Tartu, Estonia

Cybernetica, M

aealuse 2/1, 12618 Tallinn, Estonia

Keywords:

Privacy-preserving Computation, Secure Multi-party Computation (SMC), Shortest Path Problem, Single-

Instruction-Multiple-Data (SIMD), Breadth-ﬁrst Search, Sharemind.

Abstract:

Reducing the round complexity in secure multiparty computation (SMC) protocols is a worthy goal due to the

latency of the network. The SIMD approach is considered an efﬁcient strategy to reduce the round complexity

of an SMC protocol. This paper studies the secure multiparty computation (SMC) protocol for the shortest

path problem in sparse and dense graphs, building upon the breadth-ﬁrst search algorithm. The sensitivity of

operations in processing the algorithms led us to produce two different structural algorithms for computing

the shortest path. We present state-of-the-art parallel privacy-preserving shortest path algorithms for weighted

and unweighted graphs based on the breadth-ﬁrst search. We have implemented the proposed algorithms on

top of the Sharemind SMC protocol set and tested it for different graphs, dense and sparse, represented as the

adjacency matrix.

1 INTRODUCTION

The shortest path algorithms are often used in dif-

ferent ﬁelds of computer science, such as social net-

work analysis, bioinformatics, geographical informa-

tion systems, transportation optimization, and other

computations. The shortest path problem requires

ﬁnding a path between two vertices in the graph such

that the sum of the weights of the edges on the path

is minimum. There are many algorithms for solving

this problem. Each of them has a somewhat different

performance proﬁle.

Among the most important algorithms for solving

the single-source shortest distance (SSSD) problem is

Bellman-Ford (Bellman, 1958) and Dijkstra (Dijkstra

et al., 1959) algorithms. The Bellman-Ford algorithm

works to ﬁnd the SSSD for a general graph with time

complexity O(nm), where n is the number of vertices

and m the number of edges of the graph. It’s also

considered the best option for sparse graphs (Black,

2019). The Dijkstra algorithm also ﬁnds shortest dis-

tances for general graphs with time complexity O(n

and it’s the best option for dense graphs (Goldberg,

1984).

There are different algorithms for All-Pairs Short-

est Distance (APSD), such as Johnson (Johnson,

1977) and Floyd-Warshall (Floyd, 1962) algorithms.

The time complexity of the Floyd-Warshall is O(n

)

while for Johnson is O(nm + n

logn). In differ-

ent cases and applications, researchers are interested

in ﬁnding efﬁcient techniques to ﬁnd the shortest

path in a privacy-preserving manner (Brickell and

Shmatikov, 2005); such a method can handle different

parties holding different private parts of the graph.

This work aims to ﬁnd the single-source shortest

distance for the weighted and unweighted graphs in

a privacy-preserving manner, using SMC protocols.

We keep the attributes of vertices and edges private,

while the number of edges and vertices is public. We

build our protocols upon the Sharemind three-party

protocol set (Bogdanov et al., 2012), which provides

passive security against one party. The protocol set

implements protocols for the arithmetic and boolean

operations that we use. The security of our proto-

cols is conveniently analyzed (Laud, 2015b) in the

Arithmetic Black box (ABB) model (Damg

ard and

Nielsen, 2003), which abstracts from the details of the

underlying SMC protocol set.

The protocols for most of the arithmetic and

boolean operations involve message exchanges be-

tween the three computing parties. Hence the latency

of the network may signiﬁcantly affect the perfor-

mance of the SSSD protocol if the algorithm imple-

mentation causes it to have a high round complexity.

Anagreh, M., Laud, P. and Vainikko, E.

Privacy-preserving Parallel Computation of Shortest Path Algorithms with Low Round Complexity.

DOI: 10.5220/0010775700003120

In Proceedings of the 8th International Conference on Information Systems Security and Privacy (ICISSP 2022), pages 37-47

ISBN: 978-989-758-553-1; ISSN: 2184-4356

 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reser ved

Consequently, the network latency in SMC protocol is

a challenge to many researchers. How can the round

complexity of private computation in the SMC plat-

form be reduced?(Katz et al., 2003; Katz and Koo,

2007; Boyle et al., 2018). One of the most efﬁcient

strategies for reducing the round complexity in secure

multiparty computation is parallel calculation (Laud,

2015a; Boyle et al., 2015; Cohen et al., 2017).

Our strategy to reduce the round complexity of

the SMC platform is to apply the Single-Instruction-

Multiple-Data (SIMD) paradigm as much as possi-

ble, using the SecreC high-level language (Bogdanov

et al., 2014) for expressing algorithms making use of

the Sharemind protocol set. We use the Breadth-First

Search (BFS) algorithm (Beamer et al., 2012) to pro-

duce the privacy-preserving shortest path algorithms

for weighted and unweighted graphs. The possibil-

ity of accelerating the BFS algorithm through paral-

lel computing in shared and distributed memory is

discussed by Murphy et al. (Murphy et al., 2010).

The container-centric and vertex-centric approaches

are two types of parallel BFS algorithms in shared

memory (Berrendorf and Makulla, 2014). The par-

allel BFS algorithm in one-dimensional distributed

memory is presented for random big graphs in (Yoo

et al., 2005). Later, the parallel BFS algorithm in

2D-partitioning is proposed with two communication

phases (Buluc¸ and Madduri, 2011). The algorithmic

structure of the conventional serial BFS algorithm is

more ﬁt to be parallelized by the SIMD approach. The

two for-loops in the serial version of the BFS algo-

rithm can also be executed in parallel by modeling the

sources and neighbors vertices as private vectors. The

new formation of vertices and their edges into vectors

can be efﬁciently processed using one single instruc-

tion with low round complexity.

The complexity of accessing memory at private

addresses has a high effect on the total running time

of the operations. This complexity led us to reduce

the processes in our proposed privacy-preserving

breadth-ﬁrst search algorithm to avoid the linear cost

of the private memory access over the private vec-

tors. This also has the effect of noticeably reduc-

ing the round complexity of the algorithm. Hence,

we introduce two structurally different algorithms for

privacy-preserving breadth-ﬁrst search for computing

the shortest path. One of the privacy-preserving short-

est path algorithms is for weighted graphs, and the

other is for unweighted graphs. Both proposed al-

gorithms have the same functionality, and both are

based on breadth-ﬁrst search. In this work, various

graphs are used to benchmark the two proposed algo-

rithms for computing the shortest path, both dense and

sparse. Regardless of the graphs’ types, all the graphs

have the same data structure as the adjacency ma-

trix. Researchers have recently proposed algorithms

for computing the shortest paths over a planar graph,

and such algorithms are adapted to privacy-preserving

computations (Henzinger et al., 1997; Fakcharoen-

phol and Rao, 2006; Klein et al., 2010; Mozes and

Wulff-Nilsen, 2010).

Motivationally, the breadth-ﬁrst search algorithm

is a basic algorithm used in various computational

graph algorithms, such as maximum ﬂow algorithms

and kernel algorithms in the Graph500 benchmark.

Accordingly, producing a privacy-preserving version

of the BFS algorithms would be usable in various al-

gorithms as a related subroutine.

The paper is organized as follows. Section 1

brieﬂy introduces the work in general. Section 2

brieﬂy presents the related work. Section 3 shows

the secure multi-party computation. Section 4 gives

an overview of the breadth-ﬁrst search. Section 5

presents the Parallel privacy-preserving BFS algo-

rithms. Section 6 presents the benchmarking results.

Finally, Section 7 concludes the paper, discussing the

results and the future work.

2 RELATED WORK

The main feature of the secure multiparty computa-

tion (SMC) protocol is the computational indistin-

guishability from some ideal functionality. The proto-

col is secure if it does not leak any information during

private computation besides what is given out by the

ideal functionality (Laud, 2015b; Canetti, 2000). Our

work in this paper does not leak any information from

the arithmetic black box (ABB). All the computations

are securely conducted in the ABB. The contribution

in this work focuses on optimizing the private com-

putation by parallel calculation to reduce the round

complexity while performing the SMC protocol over

the platform.

Recently, many researchers have been working on

optimizing the computation in the privacy-preserving

parallel computation for different combinatorial al-

gorithms. Researchers have targeted the minimum

spanning tree and shortest path algorithms in their

privacy-preserving research. The parallel privacy-

preserving minimum spanning tree algorithm for

sparse graph (Laud, 2015a) is proposed based on the

Werbach and Shiloach algorithm with time complex-

ity O(log

n). The same paper also presented an efﬁ-

cient protocol for private reads and writes.

The privacy-preserving parallel computation of

minimum spanning tree for dense graphs is proposed

based on Prim’s algorithm (Anagreh et al., 2021b).

ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy

The algorithm contains a declassiﬁcation for the ver-

tices u, but it is still secure. The algorithm securely

shufﬂes the rows and columns of their adjacency ma-

trix to mask the real identities of the vertices and their

connected edges.

In the paper (Rao and Singh, 2020), two privacy-

preserving minimum spanning tree algorithms in

the semi-honest model are proposed. The privacy-

preserving MST algorithms are implemented on top

of Yao’s protocols (Yao, 1982), which is based on

a garbled circuit (Demmler et al., 2015; Liu et al.,

2015). Both algorithms have sequential computation.

This paper focuses on a parallel privacy-

preserving shortest path algorithm for weighted and

unweighted graphs using the serial version of the

breadth-ﬁrst search. Many researchers have been

working on privacy-preserving shortest path algo-

rithms. The privacy-preserving shortest path proto-

cols based on Dijkstra and Bellman-Ford are pro-

posed in (Aly et al., 2013). Also, they proposed proto-

cols for privacy-preserving computation of the maxi-

mum ﬂow problems. Their proposed work has a high

round complexity causing a signiﬁcant running time

even on small graphs.

In the paper (Aly and Cleemput, 2017), an obliv-

ious data abstraction that improves the protocol of

computing the privacy-preserving SSSD in (Aly and

Van Vyve, 2014) is conducted. There are no more

complex cryptographic techniques such as Oblivious

RAM in this protocol, and it is secure against both

semi-honest and malicious adversaries. However, the

proposed protocol is running sequentially, and it has

high round complexity.

The privacy-preserving Dijkstra’s algorithm is im-

plemented on the sparse graph using garbled circuits

and employing oblivious priority queues to increase

efﬁciency in (Liu et al., 2015). The running time

of their proposed privacy-preserving Dijkstra’s algo-

rithm is too high, so it’s not a ﬁt for a large graph.

Blanton et al. (Blanton et al., 2013) presented sev-

eral data-oblivious algorithms, breadth-ﬁrst search,

single-source shortest path, minimum spanning tree,

and maximum ﬂow. Theoretically, they introduced

the data-oblivious algorithms without actual imple-

mentation shown.

Recently, a new parallel method for comput-

ing privacy-preserving shortest path based on the

radius-stepping algorithm was proposed (Anagreh

et al., 2021c). In general, the radius-Stepping algo-

rithm is an improved version of the ∆-Stepping algo-

rithm (Meyer and Sanders, 2003). The ∆-Stepping

and Radius-Stepping algorithms are parallel single-

source shortest path algorithms solving this problem

efﬁciently. The SIMD approach implements to efﬁ-

ciently parallelize the algorithm as the same technique

in our work. The round complexity of the SMC proto-

col is reduced into different round complexities based

on the value of radii in the algorithm. The results

show that the parallel method is efﬁcient; the speed-

up is hundreds of times faster than the standard ver-

sion of the algorithm and the results of the previous

works. In the implementations, the paper presented

the running time of the computation for sparse, dense,

and planar weighted graphs. The unweighted graph is

also implemented with the best speed-up of the algo-

rithm.

The secure multiparty computation protocol for

single-source shortest distance and All-pairs short-

est distances in sparse and dense graphs are stud-

ied (Anagreh et al., 2021a). The state-of-the-art

privacy-preserving implementations of Bellman-Ford

and Dijkstra SSSD algorithms have been presented

and Floyd-Warshall and Johnson APSD algorithms as

well. In the implementation, using single-instruction

multiple-data (SIMD) operations reduces the round

complexity of SMC protocols. In general, they copied

the vertices and edges elements of the private graph

into vectors, then performed the single instruction

for the entire vectorised data. Interestingly, using

the SIMD operations let proposed algorithms perform

the computation, which has a high round complex-

ity (with enormous vertices and edges) in low run-

ning time. This is done because of reducing the

round complexity in using SIMD. In both SSSD al-

gorithms have declassiﬁcation for some private val-

ues. To achieve privacy preservation, masking some

private values with randomness generated during the

protocol is already done. The implementation of the

Johnson ASPD algorithm is used the Laud’s Proto-

col for private reading (Laud, 2015a), the evaluation

of the ASPD algorithm is not similar to any previ-

ous work. The privacy-preserving Bellman-Ford and

Dijkstra SSSD algorithms are secure with low round

complexity but are not the lowest round complexity

than our work.

3 SECURE MULTI-PARTY

COMPUTATION

Secure Multi-party Computation (SMC) is a technol-

ogy that enables a set of n parties with their private

input x

,...,x

n−1

to jointly compute a private black

box function y

,...,y

n−1

= f (x

,...,x

n−1

), and

distribute the output to the parties, without knowing

the private inputs by other parties in the system. The

goal of this private model is that the cryptographic

techniques assure the security, the integrity of the

Privacy-preserving Parallel Computation of Shortest Path Algorithms with Low Round Complexity

storage, the operations in the black box, and the com-

munication between the participants if the adversary

has corrupted a not-too-large fraction of them.

The Arithmetic Black Box (ABB) is the con-

ﬁdential environment where the complex privacy-

preserving computation is to be securely calculated

and detailed without leaking the details of the arith-

metic operation of protocols and with private data of

the parties. The private data of the parties and the

whole arithmetic operations in the ABB are private

toward the parties themselves even if they are a par-

ticipant in this computation. In general, the ABB is

an instrumental abstraction of secure multiparty com-

putation (Laud, 2015b).

In the privacy-preserving platform, the general-

purpose model for analyzing cryptographic proto-

col with efﬁcient security properties is called the

universally composable security (UC) framework of

MPC (Canetti, 2001). The main features in UC are

guaranteeing security properties that it remains secure

if it is arbitrarily composed with other protocols se-

cure in UC. The processing of the private function

f is performed in a privacy-preserving manner (Laur

and Pullonen-Raudvere, 2021) by applying one of the

different approaches, secret-sharing (Damg

ard et al.,

2009), homomorphic encryption (Henecka et al.,

2010) or garbled circuit (Yao, 1982).

Our proposed privacy-preserving breadth-ﬁrst

search for ﬁnding the shortest path is built on the

top of the ABB. In the algorithm description below,

we use the notation JvK to denote that value v is pri-

vate, which is stored in the ABB. The notation J~vK

denotes the private vector (v

,...,v

n−1

), which is

also stored in the ABB. In our algorithms below, we

use the for-loop to denote that assign-operation in the

body of the function is performed in parallel using the

SIMD framework.

4 BREADTH-FIRST SEARCH

Let V and E refer to the sets of the vertices and edges

in private graph G respectively. The size of the vertex

set is n = |V | and the size of the edge set is m = |E|.

An undirected graph G = (V,E) is a graph that doesn’t

have directions for the edges. The edges indicate a

two-direction relationship between two vertices u ∈ V

and v ∈ V . Each edge e can traverse among two ver-

tices in both directions (from u to v and vice versa)

with the same weight w. The weight of edge is de-

noted as w(e), w(u,v) or (v,u). A Path from source

vertex u to target vertex v is a sequence of edges

),(u

),...,(u

n−1

) ∈ E, where u = u

and

v = v

. The length of the path is the sum of the

weights of the edges in the path. The shortest path

between two vertices is the path with minimum length

between them.

The undirected graph G = (V, E) can be repre-

sented in the memory as an adjacency matrix, which

is a matrix with size n × n, where the elements of the

matrix are the weights w(u,v) for the vertices u and

v. A dense graph is a graph G where the number of

edges in the graph is close to the possible maximal

number of the edges n(n − 1)/2, where n number of

the vertices |V |. A sparse graph is a graph G = (V,E)

where the number of the edges in the graph is close

to the number of vertices. A planar graph is a special

case of the sparse graph. In planar graphs, the number

of edges is at most 3n − 6. An unweighted graph is a

graph whose adjacency matrix is a symmetric matrix

of zeros and ones.

Data: Adjacency matrix G ∈ Z

n×n

Data: Source vertex s

Result: The graph distance δ(·) from s

begin

forall v ∈ V do δ(v) ← +∞

δ[s] ← 0,level ← 0

FS ← {},NS ← {}

push(s,FS)

while FS 6= {} do

foreach u ∈ FS do

foreach neighbour v of u do

if δ[v] ← ∞ then

push(v,NS)

δ[v] ← level

end

FS := NS

NS := {}

level := level + 1

end

return δ(·)

end

Algorithm 1: Serial breadth-ﬁrst search.

The serial version of the Breadth-First Search al-

gorithm is presented in Alg. 1. The main feature in

this algorithm is traversing over all vertices in the

graph using two stacks FS and NS to store the visited

vertices. The stack FS is to store the visited vertices

while the stack NS is to store the next frontier of the

visited vertices. The frontier has some distances for

vertices from the source vertex s; distances are called

level. The neighbors of this vertex have to be ex-

plored, some of which are not explored yet. The BFS

algorithm discovers these vertices and stores them in

ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy

the next frontier, and so on until all vertices in the

graph will be already stored in the stack FS. In the

outer while-loop, the number of the iterations (Iter)

is completely bounded by the distances of the longest

shortest distance from source vertex s to any vertex in

the whole graph G. The two for-loops can be executed

in parallel, either in shared or distributed memory us-

ing some parallel framework.

This work uses the same algorithmic structure of

the breadth-ﬁrst search algorithm to perform the par-

allel calculation of the BFS using Single-instruction-

multiple-data. The elements of the two sets of ver-

tices u, v ∈ V will be vectorized in two private vectors

J~vK and J~uK. Then, using the SIMD instructions, the

algorithm can traverse over all vertices in the graph

simultaneously, then update the distances, eventually

ﬁnding the shortest distances in the given graph.

5 PRIVACY-PRESERVING

SHORTEST PATHS

This section presents the privacy-preserving single-

source shortest distance algorithm that works efﬁ-

ciently for an unweighted graph. The breadth-ﬁrst

search algorithm is a good ﬁt for computing the short-

est distances in weighted and unweighted graphs,

where the graph is an undirected connected graph.

The sensitivity of the private data in secure multi-

party computation requiring several round-trips be-

tween the computing parties for each operation af-

fects the implementation. The shortest distances in

a weighted graph can be computed by applying fewer

operations than computing the shortest path for un-

weighted graphs. Therefore, we present another ver-

sion of the algorithm for computing the shortest dis-

tances in the weighted graphs that will be faster. The

ﬁrst algorithm is the privacy-preserving single-source

shortest distances for unweighted graphs (UBFS), and

the other is privacy-preserving single-source short-

est distances in weighted graphs (WBFS). The algo-

rithms are parallel, making use of the SIMD frame-

work, and based on the BFS.

5.1 Privacy-preserving UBFS

The breadth-ﬁrst search algorithm relaxes the edges

with the same starting vertex in parallel. Each iter-

ation of the algorithm relaxes the edges of the fron-

tier vertices. We use the dense representation of the

graph. The adjacency matrix gives the weights of

edges with size n × n, weight

∞

is used to denote

the lack of an edge in the adjacency matrix. Although

we use the adjacency matrix as a data structure to

ﬁt our proposed algorithm, we use different graphs

in our benchmarks, dense and sparse. Our privacy-

preserving implementation of the Breadth-ﬁrst search

for ﬁnding the shortest path in an unweighted graph

is presented in Alg. 2.

Data: Adjacency matrix JGK ∈ Z

n×n

Data: Source vertex s

Result: The graph distance δ(·) from s

begin

δ[s] ← 0

δK ← JG[s, ∗]K

forall u ∈ {0,1,..., n − 1} do

Jδ

[u]K ← JδK

end

repeat

forall v ∈ {0,1,..., n − 1} do

Jδ

[v]K ← JδK

end

CK ← (J

K 6= ∞)

MK ← (J

K + J~eK)

K := choose(J

CK, J

MK,J

δK ← min(J

K,n)

until declassify(all(JδK 6= ∞))

return Jδ(·)K

end

Algorithm 2: Privacy-preserving UBFS for un-

weighted graph.

In detail, the algorithm works as follows: the

input data is a private unweighted undirected graph

G = (V,E) represented in an adjacency matrix, and the

second input is the source vertex. The return value is

the distance J

δK which is a private vector with size n.

We vectorized the data structure of the adjacency ma-

trix to be a good ﬁt for our proposed parallel method.

Two private vectors are initialized to get the edges’

weights; both with size n

. The ﬁrst vector J

K con-

tains the rows of the matrix, and the second vector

contains J

K the columns.

The initial values are, storing the ﬁrst row in the

adjacency matrix JG[s, ∗]K into distance vector J

δK, and

source vertex. It’s important to note that the adjacency

matrix is already vectorized into a vector J~eK (the vec-

torization is column by column) with size n

. The two

vectors J

K and J

K allows to traverse over the ver-

tices in order to relax their edges via sets. Therefore,

there is no need to use the foreach-loops (in Alg 1).

This new algorithmic structure reduces the total

round complexity of the algorithm. The initial val-

ues of weights sets are given in parallel, the vector

K gets the elements of the u-row , the vector J

also gets the elements of v-column, u, v ∈ V . Getting

the indices J

K happens only once, out of the repeat-

loop, while getting the indices of J

K must take place

Privacy-preserving Parallel Computation of Shortest Path Algorithms with Low Round Complexity

at each iteration inside the repeat-loop for updates.

The algorithm has one repeat-loop, which starts by

gathering the edges’ weights of columns J

K in par-

allel.

All elements of column vector J

K will be in com-

putation, regardless if there is an edge, or there is

no edge (denoted by

∞

). To discriminate this, the

condition J

CK will be labeling the indices of existing

edges by Boolean values. The element in the vec-

tor is true if its index will be in computation. If the

value is false, this index will be ignored. The size

of the Boolean vector is n

, which is similar to the

adjacency matrix JGK. This adjacency matrix can be

vectorized easily, and then the SIMD technology can

be efﬁciently applied to the algorithm. Next step, the

elements of the columns vector J

K and the elements

of J~eK will be summed and then stored in the vector

MK. The algorithm uses the SIMD approach because

all elements are summed in a single parallel instruc-

tion.

The protocol of the vectorized operation choose

from Sharemind’s protocol set will take place in

UBFS’s algorithm. The result of this operation is a

vector, each element of which is either an element of

MK if the condition J

CK contains true in the corre-

sponding place, or an element of the rows vector J

if J

CK is false in the corresponding place. The result

of choose is stored in J

K. The currently shortest dis-

tances δ(·) from source vertex s to all vertices in the

graph are among the values stored in the vector J

The last operation is to get these minimum val-

ues (the shortest distances) for each vertex separately.

The operation min takes two arguments, the ﬁrst of

which is a vector of private values, and the second

is a public integer n. It replaces each sequence of n

elements of the input vector with a single value, the

minimum of these n values. All operations mentioned

in the UBFS’s algorithm can be applied to vectors

of values stored in the ABB. The parameters (which

are private) to the operation are required to have the

same length. This feature of the operations satisﬁes

the SIMD approach.

5.2 Privacy-preserving WBFS

The feature of the sequential breadth-ﬁrst search al-

gorithm can be ideally exploited to create a parallel

version of the BFS. The frontier’s data structure stores

the vertices at the same distance from the source ver-

tex s. This feature can be parallelized, which will

reduce the amount of layer-traversal. Therefore, the

given weighted graph can compute the shortest path a

bit easier than unweighted in the sense of fewer op-

erations. This section presents another version of the

privacy-preserving shortest path algorithm by BFS for

a weighted graph with fewer operations. This has a

positive effect on reducing the running time of the al-

gorithm. The privacy-preserving BFS’s shortest path

for the weighted graph is presented in Alg. 3.

Data: Adjacency matrix JGK ∈ Z

n×n

Data: Source vertex s

Result: The graph distance δ(·) from s

begin

δK ← JG[s, ∗]K

repeat

forall u ∈ {0,1,..., n − 1} do

Jδ

[u]K ← J

δK

end

K ← min((J

−→

K + Je(v, u)K),N(v))

DK := J

δK

δK := J

until declassify(all(J

K = J

DK))

return Jδ(·)K

end

Algorithm 3: Privacy-preserving WBFS for weighted

graph.

The data input is source vertex s, and the private

adjacency matrix has the vertices and their edges’

weights. The output data is the shortest path from the

source vertex s to all other vertices of the given graph

JGK from the source vertex s. The initial value in the

algorithm is, putting the ﬁrst row in the given graph

JGK (with source vertex s) into the shortest distances

vector J

δK that will get an update during running the

algorithm until all vertices are already handled.

The algorithm has only one repeat-loop, starts

by assigning all rows of the given graph JGK into

rows vector J

K. It’s important to note that we use

forall-loop in our algorithms to denote that all assign-

operations in that loop are already performed in paral-

lel. Later, the adjacency matrix of the given graph JGK

is already vectorized into vector J~eK, and we have vec-

torized this by storing column by column. The main

operation in the algorithm is the summation of the two

vectors J

K and J~eK, and then ﬁnding the minimum

distance for each vertex using min-operation. The last

operation in the algorithm is swapping the vectors that

will be arranged to make the updates. The aim is

to check that all vertices are already handled. The

equality check at the end of the loop returns a vec-

tor of Boolean values. The values of J

K and J

DK are

not leaked by the all-operation. This algorithm has no

speciﬁc known number of iterations. It is based on the

number of connected edges. The algorithm behaves

perfectly when the edges are close to the maximum

possible number, i.e., dense graph or like-dense.

ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy

5.3 Round Complexity

In general, our proposed algorithms reduce the round

complexity of the shortest distances computation.

Round complexity is based on the size of the adja-

cency matrix. The communication-related complex-

ities of the secure multiparty computation have two

sides, round complexity, which is the number of com-

munication among the machines of the SMC platform

and bandwidth, the number of bits that will be trans-

mitted among computation parties. Let n denote the

number of the vertices in the graph, and m is the num-

ber of the edges. Theoretically, the round complex-

ity is less than O(log n) times, but it can be realistic in

bandwidth. If the vectors’ size in computations is big-

ger than bandwidth, the actual number of rounds com-

plexity will be increased based on the number of data

packets (which split because the vector’s size is big-

ger than bandwidth). The algorithm relaxes all ver-

tices’ edges in fewer iterations if the graph is dense,

with low running time. All elements of the adjacency

matrix will be taken in computation. Regardless, ei-

ther there is an edge between two vertices or no edge

(weight is

∞

5.4 Security and Privacy

Our implementation is built on top of a universally

composable ABB of the SMC protocol. The im-

plementation is privacy-preserving if it doesn’t have

any declassiﬁcation operation. The condition of the

repeat-iteration has declassiﬁcation. Otherwise, the

declassiﬁed values cannot be directly discovered with

the public parameters of the implementation. It’s a

subset of a Boolean vector that signs unhandled ver-

tices. In other words, the arrangement of unhandled

vertices depends on the values of the shortest dis-

tances and the number of iterations. The identity of

the vertices (regardless of, it is handled or not) and

their connected edges with their weights are still pri-

vate. Such declassiﬁed values are not directly helping

the semi-honest or malicious adversaries. Our imple-

mentation of the proposed protocol with its two ver-

sions is privacy-preserving.

6 EXPERIMENTAL RESULTS

6.1 Benchmarking Results

We evaluate and benchmark our results with the best

previous results conducted on top of three-party SMC

protocols in the state of art. Recently, the benchmark-

ing results for the state-of-the-art privacy-preserving

shortest path algorithms have been reported (Aly and

Cleemput, 2017). The proposed work is an oblivi-

ous data abstraction that improves the yield in (Aly

et al., 2013) (Aly and Van Vyve, 2014). The result has

shown that the running time on a 32-vertex graph is

around 5 seconds. The permutation operation is also

used to mask the real identity of the vertices, which

will increase the total running time. It is an efﬁcient

way to keep privacy, but at the same time, it’s an extra

operation that will increase the whole running time of

computation. The presented result doesn’t show the

scalability, or it has more running time. The size of

the graph used in their experimentation is small.

In contrast, our work has no extra operations for

permutation or other steps. As well as, our proto-

col is scalable; we used different sizes of graphs in

our benchmarking. The result shows that our work is

faster than the previous work, around 50 times.

The most state of the art conducted work for

privacy-preserving SSSD is based on the radius-

stepping algorithm (Anagreh et al., 2021c). The re-

sult shows that the algorithm is more efﬁcient than

the previous work and others, and because of the nov-

elty in this work, we use it to evaluate our work with

it. This algorithm also has an extra operation, radii,

which does not exist in classical shortest path algo-

rithms. Thus, our proposed protocol has pure pro-

cesses for ﬁnding the shortest distances without any

extra operations. The empirical tests for our protocol

show that the acceleration is 3 to 4 times more than in

the best radii case of the radius-stepping algorithm.

Extensive benchmarking results for privacy-

preserving SSSD Dijkstra and bellman-Ford algo-

rithms are documented in (Anagreh et al., 2021a).

These results are benchmarked with our BFS’s results

in Section 6.2.

6.2 Breadth-ﬁrst Search Experiments

In this work, we have implemented our proposed

protocol of the privacy-preserving shortest distances

with its two versions on the Sharemind SMC plat-

form (Bogdanov et al., 2008; Bogdanov et al., 2012).

The computation was performed on the Sharemind

Cluster of three computers connected with a three-

party protocol set secure against one passively cor-

rupted party. The SIMD framework under SecreC

high-level language is used to write the code of all

implementations. The three workstations of the clus-

ter have a 12-core 3 GHz CPU with Hyper-Threading

running Linux and 48 GB of RAM. An Ethernet lo-

cal area network connects the workstations with a link

speed of 1 Gbps. Although our algorithm ﬁts dense

graphs, we use different graphs in the implementa-

Privacy-preserving Parallel Computation of Shortest Path Algorithms with Low Round Complexity

tions on the top of the SMC protocol set, sparse and

dense ones, with varying sizes. Among the sparse

graphs, we consider graphs whose number of edges is

similar to planar graphs, i.e., either two or three times

the number of the vertices. Using different kinds of

graphs is for the benchmarking of the two versions of

our privacy-preserving BFS algorithm. We reported

the running time of our experiments in seconds. Suf-

ﬁx K denotes the multiplication by 1000, while the M

denotes the multiplication by 1000000. The paral-

lel codes of the implementation are written using the

SIMD framework; after vectorization of the given ad-

jacency matrices, there is no use of the multiple cores

of the Sharemind SMC platform. Among the three

workstations of the Sharemind cluster, the adjacency

matrix data is represented in secret-shared manners

for both inputs and outputs.

Table 1: Running times (in seconds) of privacy-preserving

WBFS and radius-stepping algorithms for various graphs.

Graphs Parallel Radius Parallel WBFS Speed-up

Radii = rnd Radii = ∞ BFS vs.

k n m Iter. Time Iter. Time Iter. Time rnd ∞

25 100 8 0.33 6 0.24 5 0.07 5.0x 3.6x

50 400 7 0.78 5 0.52 4 0.13 6.1x 4.1x

100 900 14 4.67 6 2.05 5 0.47 10.0x 4.4x

200 1k 33 41.4 11 13.8 10 2.98 13.9x 4.6x

500 5k 38 275 12 86.9 11 21.5 12.8x 4.1x

750 10k 58 916 9 142 8 35.4 25.9x 4.0x

1k 10k 94 2620 14 392 13 98.9 26.5x 4.0x

1k 40k 41 1141 8 224 7 56.6 20.2x 4.0x

Sparse

3k 100k 147 36.4k 11 2724 10 685 53.0x 4.0x

3k 1M 44 10.9k 7 1733 6 429 25.4x 4.0x

5k 1M 95 41.8k 7 4778 6 1198 34.8x 4.0x

5k 5M 31 14.1k 5 3459 4 852 16.5x 4.1x

10k 15M 51 91.3k 6 16.5k 5 4090 22.2x 4.0x

50 1225 5 0.56 4 0.43 3 0.11 5.0x 3.8x

100 4950 8 2.67 6 1.99 5 0.44 6.0x 4.5x

200 19.9k 9 11.3 5 6.35 4 1.45 7.8x 4.4x

750 280k 16 254 6 94.9 5 23.5 10.8x 4.0x

1k 499k 20 560 5 140 4 35.3 15.9x 4.0x

Dense

5k 12.4M 21 14.4k 5 3419 4 852 16.9x 4.4x

6k 17.9M 28 17.7k 6 5953 5 1465 12.0x 4.1x

10k 49.9M 27 48.9k 5 13.7k 4 3377 11.9x 4.1x

50 100 11 1.14 9 1.01 8 0.24 4.8x 4.3x

50 150 11 0.98 7 0.69 5 0.16 6.2x 4.4x

100 200 21 6.93 10 3.31 9 0.72 9.6x 4.6x

100 300 21 7.08 8 2.72 7 0.61 11.7x 4.5x

500 1k 146 1056 11 79.9 10 19.8 53.0x 4.0x

Like-Planar

500 1500 105 759 15 108 14 26.9 28.2x 4.0x

1k 2k 245 6834 14 271 13 61.5 111x 4.4x

1k 3K 169 4713 15 285 13 61.6 77.3x 4.6x

We report the running times of the privacy-

preserving WBFS’s algorithm for different kinds of

weighted graphs, sparse dense and like-planar, with

various sizes in Table. 1. This table presents the

benchmark for the privacy-preserving parallel ver-

sions of the WBFS and Radius-stepping algorithms.

In the implementations of the radius-stepping algo-

rithm, we use the best two cases of the radii, which

are random (rnd) and inﬁnity (

∞

). The table shows

the number of possible iterations (Iter) for each al-

gorithm with their total running time. It is impor-

tant to note that we use a function to generate ran-

dom graphs. Therefore, the number of iterations in

all implementations can differ based on the weights

of edges and which vertices are connected by edges.

Anyway, the number of iterations in WBFS’s algo-

rithms is smaller than in both versions of the radius-

steeping algorithm in all experiments. The empiri-

cal test clearly shows that WBFS’s algorithm is faster

than the radius-stepping algorithm in two considered

cases of radii. Moreover, the efﬁciency shows how

much WBFS’s algorithm is faster than the best case

of radii (which is

∞

) — between 3 and 5 times.

Although, the number of Iter in WBFS is one time

less than the number of Iter in the ∞-radii version

(with some exceptions). For rnd-radii, the speed-up

of WBFS is 50 times or more. Lastly, we note that the

number of iterations in running the algorithm using

dense graphs (regardless of the sizes) is less than the

number of iterations in running the algorithm using

sparse graphs. The number of iterations is decreased

by increasing the number of edges in the given graphs.

Thus, the BFS algorithm is an efﬁcient algorithm over

dense graphs with low running time. The algorithm

is still more efﬁcient for other graphs than radius-

stepping and other algorithms in previous works. The

implementations of our proposed privacy-preserving

parallel computation of UBFS’s algorithm for an un-

weighted graph are presented in Table. 2.

Table 2: Running times (in seconds) of privacy-preserving

radius-stepping and UBFS algorithms over Sharemind.

Size Parallel Radius Parallel UBFS

Level Efﬁciency

n m Iter Time Iter Time

50 400 3 0.32 1 0.07 3 4.8x

100 2k 3 1.02 1 0.21 3 4.9x

150 750 5 3.59 3 0.71 4 5.1x

200 1k 5 6.28 3 1.25 4 5.0x

500 20k 3 21.9 1 4.02 3 5.5x

Sparse

750 10k 4 63.5 2 13.1 4 4.8x

1k 20k 4 113 2 23.5 4 4.8x

1k 100k 3 84.9 1 15.5 3 5.5x

3k 5k 3 762 1 136 3 5.6x

10K 15M 3 8425 1 1524 3 5.5x

50 1225 3 0.33 1 0.06 3 5.2x

100 4950 3 1.04 1 0.21 3 5.5x

200 19.9k 3 3.78 1 0.69 3 5.5x

500 124k 3 22.1 1 3.96 3 5.6x

750 280k 3 48.5 1 9.01 3 5.4x

Dense

1k 499k 3 85.1 1 15.7 3 5.4x

3k 4.49M 3 758 1 135 3 5.6x

5k 12.4M 3 2091 1 374 3 5.6x

10k 49.9M 3 8312 1 1490 3 5.6x

50 100 6 0.62 4 0.15 6 4.2x

50 150 5 0.55 3 0.11 5 5.0x

100 200 6 1.95 4 0.41 6 4.7x

100 300 5 1.72 3 0.36 6 4.8x

500 1k 10 72.6 8 18.1 10 4.0x

Like-Planar

500 1500 6 43.5 4 10.0 6 4.0x

1k 2k 9 250 7 62.4 9 4.0x

1k 3k 7 195 5 49.9 7 4.2x

We have benchmarked our algorithm with a

privacy-preserving radius-stepping algorithm for un-

weighted graphs. Different kinds of graphs were

used in the implementations, sparse, dense, and like-

planar, with various sizes. The running time in sec-

onds is reported for both algorithms. The benchmark

of the radius-stepping algorithm is noted for the ∞-

ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy

radii case, which is considered the most efﬁcient case

of radii. In both algorithms, the result shows the pos-

sible iterations (Iter) based on the number of given

edges. The results also show the number of vertices

with the exact distances (levels) for both algorithms.

In general, the results show the running times of the

UBFS’s algorithm and its speed-up in comparison to

the radius-stepping algorithm. This speed-up is be-

tween 4 and 5.6 times.

The algorithm has the lowest possible number of

iterations in experiments with dense graphs, regard-

less of the size. The number of iterations is decreased

by increasing the number of edges in the given graph.

Thus, until reaching the maximal possible number of

edges in the dense graph. Indeed, the number of it-

erations will be only one. This is the signiﬁcance of

our work, that’s, for the maximal possible number of

edges, the round complexity is constant.

Table 3: Running times (in seconds) and Bandwidth of dif-

ferent rounds for the privacy-preserving versions of BFS.

K Size WBFS UBFS

n m r / Iter. Time Band. r / Iter Time Band.

50 400 1/4 0.07 0.8 MB 1/1 0.08 0.7 MB

50 400 2/4 0.09 1.3 MB - - -

50 400 3/4 0.12 1.7 MB - - -

50 400 4/4 0.14 2.1 MB - - -

500 5k 1/11 3.9 43.9 MB 1/3 4.20 49.3 MB

500 5k 2/11 5.7 83.3 MB 2/3 6.11 102.7 MB

500 5k 3/11 7.42 109.0 MB 3/3 8.31 146.2 MB

Sparse

500 5k 7/11 14.4 277.9 MB - - -

500 5k 11/11 21.5 429.4 MB - - -

1k 40k 1/7 14.9 176.1 MB 1/2 16.2 197.7 MB

1k 40k 2/7 22.0 319.2 MB 2/2 24.5 399.1 MB

1k 40k 3/7 28.9 492.0 MB - - -

100 4950 1/4 0.20 2.0 MB 1/1 0.21 2.6 MB

100 4950 4/4 0.41 7.2 MB - - -

500 124k 1/4 3.87 49.7 MB 1/1 4.24 55.8 MB

500 124k 2/4 5.73 90.7 MB - - -

500 124k 4/4 9.32 164.4 MB - - -

Dense

1k 499k 1/5 14.7 190.8 MB 1/1 15.6 226 MB

1k 499k 5/5 43.4 562.7 MB - - -

2k 1.9M 1/5 56.9 753 MB 1/1 61.2 899 MB

2k 1.9M 5/5 164 3.2 GB - - -

5k 12.4M 1/4 362 4.5 GB 1/1 391 5.6 GB

5k 12.4M 4/4 868 16.0 GB - - -

50 100 1/7 0.07 0.5 MB 1/4 0.07 0.8 MB

50 100 2/7 0.10 1.0 MB 2/4 0.10 1.2 MB

50 100 7/7 0.22 3.1 MB 4/4 0.16 2.3 MB

50 150 1/5 0.07 0.8 MB 1/3 0.07 0.8 MB

100 200 1/9 0.21 1.9 MB 1/4 0.22 2.0 MB

Like-Planar

100 300 1/7 0.21 2.2 MB 1/3 0.22 2.2 MB

500 1k 1/12 3.84 44.7 MB 1/8 4.04 50.5 MB

500 1k 12/12 23.1 471.8 MB 8/8 17.9 391 MB

1k 2k 1/12 14.7 158.8 MB 1/9 15.8 200 MB

1k 2k 12/12 91.6 1.8 GB 9/9 76.4 1.7 GB

The performance of the secure multiparty compu-

tation protocols feature is measured by two parame-

ters — the round complexity and the bandwidth. Ta-

ble. 3 presents the running time and the bandwidth

for two versions of the algorithm with different data

inputs. We performed the computation over the pre-

ferred network, which has high bandwidth and low

latency. The table shows the running time and band-

width for each number of rounds (r) separately and

how many possible iterations there are for the entire

computation, given by r/Iter. In general, the number

of Iter is somewhat larger. These cause a higher band-

width and running time. The running time and band-

width for ﬁrst-round r = 1 is similar in both dense and

sparse graphs (those have the same number of ver-

tices). When the number of rounds r starts increas-

ing, both running time and bandwidth scalably in-

creased. Thus, until computation reach the last round

(r = Iter). In the dense graph, the computation ﬁn-

ishes early, while in the sparse graph, iterating un-

til the last round in computation. This causes round

complexity and bandwidth for a given graph.

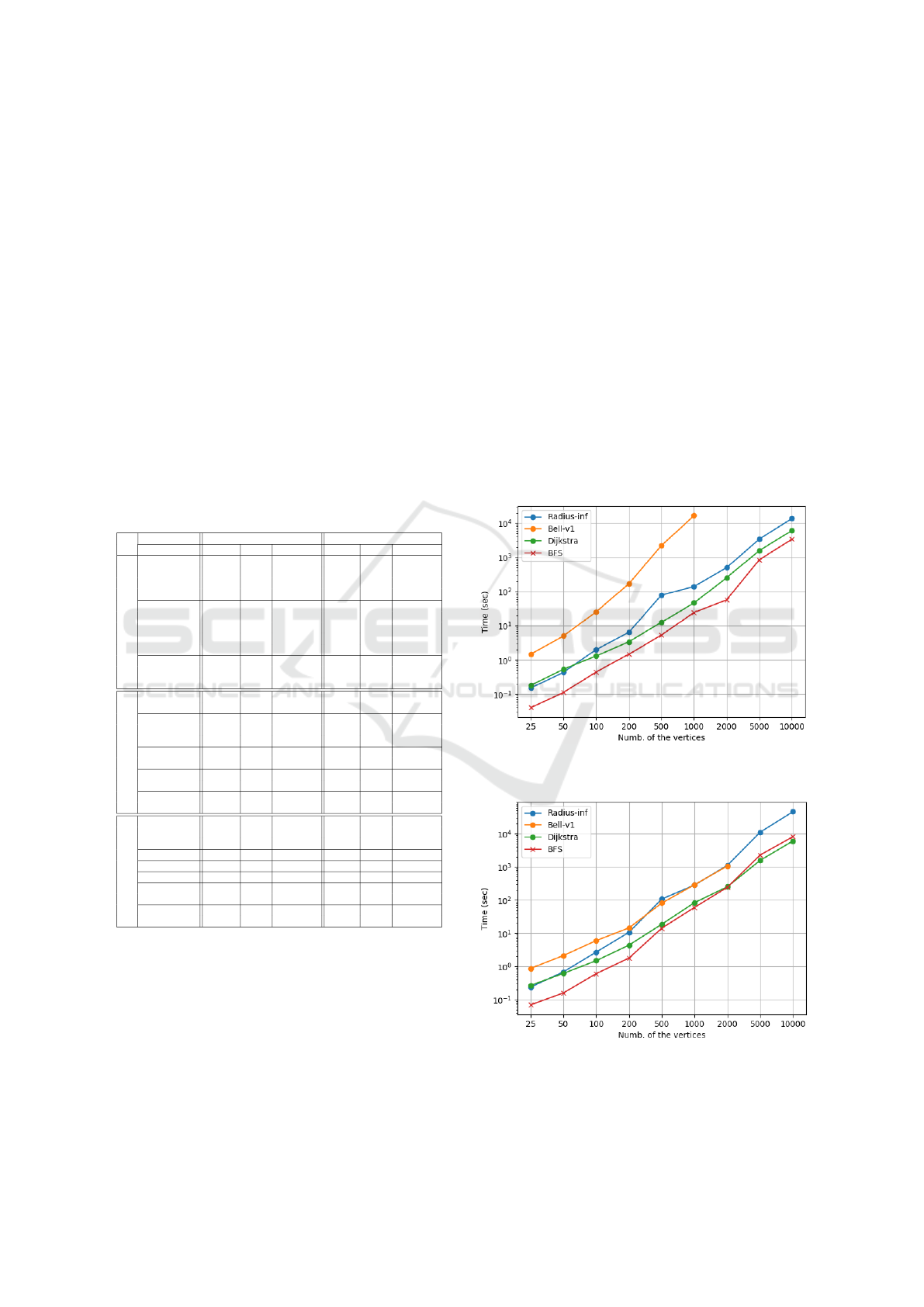
In Figure. 1, the benchmark results for the four

SSSD algorithms in privacy preservation over dense

graphs are presented. In contrast, the privacy-

preserving SSSD Algorithms for the sparse graph is

presented in Figure. 2. The number of the edges in

the sparse graphs is three times number of the ver-

tices, given by m = 3n.

Figure 1: Running time of the privacy-preserving SSSD al-

gorithms over the dense graphs in different sizes.

Figure 2: Running time of the privacy-preserving SSSD al-

gorithms over the sparse graphs in different sizes.

Privacy-preserving Parallel Computation of Shortest Path Algorithms with Low Round Complexity

7 CONCLUSIONS

We have presented the state-of-the-art privacy-

preserving computation of the single-source shortest

distances for the weighted and unweighted graphs.

The proposed protocol is built based on a breadth-

ﬁrst search algorithm. We have designed our proto-

col using SIMD to reduce the round complexity of

the SMC protocol. The protocol perfectly processes a

subset of the vertices and their edges in the possible

lower number of iterations, thus relaxing all edges.

We have benchmarked this protocol using different

graphs of various sizes. As well as, we evaluated our

work with a privacy-preserving shortest path by the

radius-stepping algorithm with its the best two cases

of radii. The result shows that our protocol is efﬁcient.

Its running time was never achieved before by other

such work, especially for the dense graph. The fu-

ture work is studying other classical SSSD and APSD

algorithms in privacy and using different techniques

for ﬁnding the shortest path like path algebra com-

putation. As well as the ability to use our proposed

method as related work in other techniques in com-

binatorial graph algorithms such as maximum follow

algorithms. In general, our work can be considered

an example of how using SIMD is beneﬁcial in de-

signing new computational protocols with low round

complexity. Such work using such a parallel strat-

egy makes the whole privacy-preserving computation

more usable due to reducing network latency, which

is considered the most critical challenge of the SMC

protocol set.

ACKNOWLEDGEMENT

We want to thank Dr Alisa Pankova from Cybernetica

for her constructive suggestions on bandwidth issues.

This research received funding from the European Re-

gional Development Fund through the Estonian Cen-

tre of Excellence in ICT Research-EXCITE.

REFERENCES

Aly, A. and Cleemput, S. (2017). An improved protocol for

securely solving the shortest path problem and its ap-

plication to combinatorial auctions. Cryptology ePrint

Archive, Report 2017/971. https://ia.cr/2017/971.

Aly, A., Cuvelier, E., Mawet, S., Pereira, O., and Van Vyve,

M. (2013). Securely solving simple combinatorial

graph problems. In International Conference on Fi-

nancial Cryptography and Data Security, pages 239–

257. Springer.

Aly, A. and Van Vyve, M. (2014). Securely solving classi-

cal network ﬂow problems. In International Confer-

ence on Information Security and Cryptology, pages

205–221. Springer.

Anagreh, M., Laud, P., and Vainikko, E. (2021a). Parallel

privacy-preserving shortest path algorithms. Cryptog-

raphy, 5(4):27.

Anagreh, M., Vainikko, E., and Laud, P. (2021b). Paral-

lel privacy-preserving computation of minimum span-

ning trees. In ICISSP, pages 181–190.

Anagreh, M., Vainikko, E., and Laud, P. (2021c). Parallel

privacy-preserving shortest paths by radius-stepping.

In 2021 29th Euromicro International Conference on

Parallel, Distributed and Network-Based Processing

(PDP), pages 276–280. IEEE.

Beamer, S., Asanovic, K., and Patterson, D. (2012).

Direction-optimizing breadth-ﬁrst search. In SC’12:

Proceedings of the International Conference on High

Performance Computing, Networking, Storage and

Analysis, pages 1–10. IEEE.

Bellman, R. (1958). On a routing problem. Quarterly of

applied mathematics, 16(1):87–90.

Berrendorf, R. and Makulla, M. (2014). Level-synchronous

parallel breadth-ﬁrst search algorithms for multicore

and multiprocessor systems. In Nygard, T., editor, Fu-

ture Computing 2014, The Sixth International Confer-

ence on Future Computational Technologies and Ap-

plications. Venice, Italy, May 25-29, 2014, pages 26 –

31. ThinkMind.

Black, P. E. (2019). Bellman-ford algorithm. in Dictionary

of Algorithms and Data Structures (online), Paul E.

Black, ed.

Blanton, M., Steele, A., and Alisagari, M. (2013). Data-

oblivious graph algorithms for secure computation

and outsourcing. In Proceedings of the 8th ACM

SIGSAC symposium on Information, computer and

communications security, pages 207–218.

Bogdanov, D., Laud, P., and Randmets, J. (2014). Domain-

polymorphic programming of privacy-preserving ap-

plications. In Proceedings of the Ninth Workshop on

Programming Languages and Analysis for Security,

pages 53–65.

Bogdanov, D., Laur, S., and Willemson, J. (2008). Share-

mind: A framework for fast privacy-preserving com-

putations. In European Symposium on Research in

Computer Security, pages 192–206. Springer.

Bogdanov, D., Niitsoo, M., Toft, T., and Willemson, J.

(2012). High-performance secure multi-party com-

putation for data mining applications. International

Journal of Information Security, 11(6):403–418.

Boyle, E., Chung, K.-M., and Pass, R. (2015). Large-

scale secure computation: Multi-party computation

for (parallel) ram programs. In Annual Cryptology

Conference, pages 742–762. Springer.

Boyle, E., Jain, A., Prabhakaran, M., and Yu, C.-H. (2018).

The bottleneck complexity of secure multiparty com-

putation. In 45th International Colloquium on Au-

tomata, Languages, and Programming (ICALP 2018).

Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik.

ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy

Brickell, J. and Shmatikov, V. (2005). Privacy-preserving

graph algorithms in the semi-honest model. In Inter-

national Conference on the Theory and Application of

Cryptology and Information Security, pages 236–252.

Springer.

Buluc¸, A. and Madduri, K. (2011). Parallel breadth-ﬁrst

search on distributed memory systems. In Proceed-

ings of 2011 International Conference for High Per-

formance Computing, Networking, Storage and Anal-

ysis, pages 1–12.

Canetti, R. (2000). Security and composition of multiparty

cryptographic protocols. Journal of CRYPTOLOGY,

13(1):143–202.

Canetti, R. (2001). Universally composable security: A new

paradigm for cryptographic protocols. In Proceedings

42nd IEEE Symposium on Foundations of Computer

Science, pages 136–145. IEEE.

Cohen, R., Coretti, S., Garay, J., and Zikas, V.

(2017). Round-preserving parallel composition of

probabilistic-termination cryptographic protocols. In

44th International Colloquium on Automata, Lan-

guages, and Programming (ICALP 2017). Schloss

Dagstuhl-Leibniz-Zentrum fuer Informatik.

Damg

ard, I., Geisler, M., Krøigaard, M., and Nielsen, J. B.

(2009). Asynchronous multiparty computation: The-

ory and implementation. In International workshop

on public key cryptography, pages 160–179. Springer.

Damg

ard, I. and Nielsen, J. B. (2003). Universally com-

posable efﬁcient multiparty computation from thresh-

old homomorphic encryption. In Annual International

Cryptology Conference, pages 247–264. Springer.

Demmler, D., Schneider, T., and Zohner, M. (2015). Aby-

a framework for efﬁcient mixed-protocol secure two-

party computation. In NDSS.

Dijkstra, E. W. et al. (1959). A note on two problems

in connexion with graphs. Numerische mathematik,

1(1):269–271.

Fakcharoenphol, J. and Rao, S. (2006). Planar graphs, nega-

tive weight edges, shortest paths, and near linear time.

Journal of Computer and System Sciences, 72(5):868–

889.

Floyd, R. W. (1962). Algorithm 97: shortest path. Commu-

nications of the ACM, 5(6):345.

Goldberg, A. V. (1984). Finding a maximum density sub-

graph. University of California Berkeley.

Henecka, W., K

ogl, S., Sadeghi, A.-R., Schneider, T., and

Wehrenberg, I. (2010). Tasty: tool for automating se-

cure two-party computations. In Proceedings of the

17th ACM conference on Computer and communica-

tions security, pages 451–462.

Henzinger, M. R., Klein, P., Rao, S., and Subramanian,

S. (1997). Faster shortest-path algorithms for pla-

nar graphs. journal of computer and system sciences,

55(1):3–23.

Johnson, D. B. (1977). Efﬁcient algorithms for shortest

paths in sparse networks. Journal of the ACM (JACM),

24(1):1–13.

Katz, J. and Koo, C.-Y. (2007). Round-efﬁcient secure

computation in point-to-point networks. In Annual

International Conference on the Theory and Appli-

cations of Cryptographic Techniques, pages 311–328.

Springer.

Katz, J., Ostrovsky, R., and Smith, A. (2003). Round ef-

ﬁciency of multi-party computation with a dishonest

majority. In International Conference on the Theory

and Applications of Cryptographic Techniques, pages

578–595. Springer.

Klein, P. N., Mozes, S., and Weimann, O. (2010). Shortest

paths in directed planar graphs with negative lengths:

A linear-space o (n log2 n)-time algorithm. ACM

Transactions on Algorithms (TALG), 6(2):1–18.

Laud, P. (2015a). Parallel oblivious array access for secure

multiparty computation and privacy-preserving mini-

mum spanning trees. Proc. Priv. Enhancing Technol.,

2015(2):188–205.

Laud, P. (2015b). Stateful abstractions of secure multi-

party computation. In Laud, P. and Kamm, L., edi-

tors, Applications of Secure Multiparty Computation,

volume 13 of Cryptology and Information Security Se-

ries, pages 26–42. IOS Press.

Laur, S. and Pullonen-Raudvere, P. (2021). Foundations

of programmable secure computation. Cryptography,

5(3):22.

Liu, C., Wang, X. S., Nayak, K., Huang, Y., and Shi, E.

(2015). Oblivm: A programming framework for se-

cure computation. In 2015 IEEE Symposium on Secu-

rity and Privacy, pages 359–376. IEEE.

Meyer, U. and Sanders, P. (2003). δ-stepping: a paralleliz-

able shortest path algorithm. Journal of Algorithms,

49(1):114–152.

Mozes, S. and Wulff-Nilsen, C. (2010). Shortest paths in

planar graphs with real lengths in o (nlog 2 n/loglogn)

time. In European Symposium on Algorithms, pages

206–217. Springer.

Murphy, R. C., Wheeler, K. B., Barrett, B. W., and Ang,

J. A. (2010). Introducing the graph 500. Cray Users

Group (CUG), 19:45–74.

Rao, C. K. and Singh, K. (2020). Securely solving pri-

vacy preserving minimum spanning tree algorithms in

semi-honest model. International Journal of Ad Hoc

and Ubiquitous Computing, 34(1):1–10.

Yao, A. C. (1982). Protocols for secure computations. In

23rd annual symposium on foundations of computer

science (sfcs 1982), pages 160–164. IEEE.

Yoo, A., Chow, E., Henderson, K., McLendon, W., Hen-

drickson, B., and Catalyurek, U. (2005). A scal-

able distributed parallel breadth-ﬁrst search algorithm

on bluegene/l. In SC’05: Proceedings of the 2005

ACM/IEEE Conference on Supercomputing, pages

25–25. IEEE.

Privacy-preserving Parallel Computation of Shortest Path Algorithms with Low Round Complexity