Study of Three WFS for the Modular System in a Portable AO

Instrument: ALIOLI

Esther Soria

1,2 a

and Roberto L

opez

1,2 b

Instituto de Astrof

ısica de Canarias, C/V

ıa L

actea s/n, La Laguna, E-38205, Spain

Departamento de Astrof

ısica, Universidad de La Laguna, La Laguna, E-38200, Spain

Keywords:

Adaptive Optics, High Resolution, Wavefront Sensor, Wavefront Corrector, Medium Sized Telescopes.

Abstract:

Adaptive optics (AO) systems correct atmospheric turbulence in real time and they are normally designed for

large telescopes but not for modest due to their cost. In this paper, we propose a portable AO instrument,

named ALIOLI, capable of be installed in different medium and small-sized telescopes. The novelty of this

new instrument is the modularization of its components which allows great ﬂexibility in the design, being

possible easily adapt the instrument to the working telescope or observing technique by adjusting each module

independently. Here we present the instrument concept and a preliminary design for its installation in the

Carlos Sanchez Telescope ( 1.5m, Teide Observatory (Canary Islands)). The Wavefront Sensor (WFS)

module is intended to be used with three different WS, Shack-Hartmann, Two Pupil Plane Position and non-

modulated Pyramidal, allowing a joint conﬁguration for comparative studies. A comparison of the response of

these sensors has been carried out by simulating the instrument in Python. The simulation results demonstrate

the goodness of the applied algorithms and the higher linearity and precision of the SH WFS in comparison

with the others two.

1 INTRODUCTION

The wavefront (WF) of light coming from a distant

source such as an astronomical object can be consid-

ered ﬂat when it propagates through the void. How-

ever, when this WF cross through the turbulent and

variable atmosphere, it is distorted due to ﬂuctuations

in the refractive index and the result is a blur in the

image of the object that is being observed (Hickson,

2014).

Adaptive optics (AO) is a technique that charac-

terizes and corrects atmospheric turbulence in real

time using a Wavefront Sensor (WFS). The WFS must

measure the incoming wavefront to allow the correc-

tion with an active element, located along the opti-

cal path, being the most common a Deformable Mir-

ror (DM). The wavefront reconstructor is in charge of

translating the wavefront signal into DM language.

The construction of large telescopes requires

the development of increasingly sensitive and faster

Adaptive Optics systems, leaving behind the large

number of telescopes, smaller and still crucial in

many observation campaigns. Therefore, improving

https://orcid.org/0000-0003-2486-7998

https://orcid.org/0000-0002-6491-5555

the spatial resolution would open the possibility of

equipping them with scientiﬁc instrumentation such

as an spectrograph or coronagraph, which multiplies

observers’ options.

It is in this context that the concept of ALIOLI

emerges. This is an evolution of AOLI instrument

(Adaptive Optics and Lucky Imager) (Colodro-Conde

and others., 2018) towards a Lightweight Instrument

customised for small telescopes, constituting a thesis

project. For this approach, the LI was put aside and

the main effort is concentrated on selecting the most

appropriate WFS, as well as on undertaking a study of

the behaviours of different WFS approaches depend-

ing on the telescope, the atmospheric conditions or

even the science instrument we work with.

As a WF propagates, it is possible to predict the

WF geometry using ray optics because the light at

each point in the WF travels perpendicularly to that

point. We wish to determine the shape of the incom-

ing WF, thus if we divide the WF surface into area dif-

ferentials, we could know the slope distribution mea-

suring the mean slope in each zone. This linear rela-

tionship between beam slopes and light displacement

underlies most wavefront sensing techniques, and it

is the underlying principle of operation of the 3 sen-

Soria, E. and López, R.

Study of Three WFS for the Modular System in a Portable AO Instrument: ALIOLI.

DOI: 10.5220/0010778000003121

In Proceedings of the 10th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2022), pages 17-25

ISBN: 978-989-758-554-8; ISSN: 2184-4364

 2022 by SCITEPRESS – Science and Technology Publications, Lda. All r ights reserved

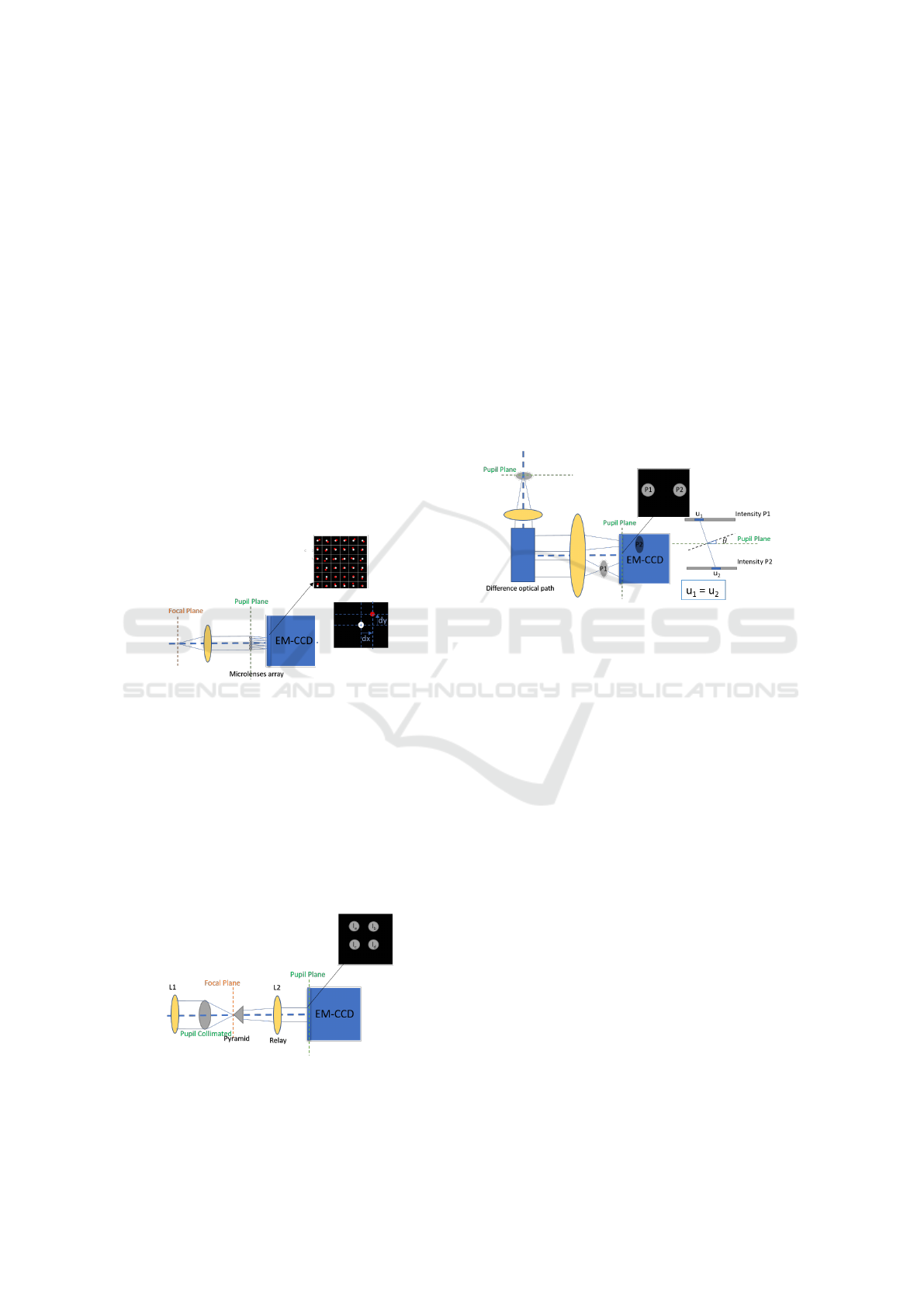
sors with which we are going to work, the Shack-

Hartmann (S-H,) the Two Pupil Plane (TP3) and the

non-modulated Pyramidal (nm-PYR).

A wavefront sensor uses optical elements to trans-

form readable intensity distribution on a detector into

wavefront deformations. It consists in a hardware

part, the optical elements and the detector, and a soft-

ware part, the signal processing. The computation

must be fast enough, which means, practically, that

only linear reconstructors are useful. A linear recon-

structor typically performs matrix multiplication.

The S-H WFS was developed in the late 1960s,

evolving from the Hartmann screen test (Thibos,

2000). It works by subdividing the complex ﬁeld in

the plane of the telescope’s pupil, the hardware part

is a lenslet array that generates low resolution images

of the object. See ﬁgure 1. The integrated gradient of

the wavefront across the lenslet is proportional to the

displacement of the centroid (dx,dy). Consequently,

any phase aberration can be approximated by a set of

discrete tilts.

Figure 1: Shack-Hartmann WFS scheme.

The nm-PYR WFS was ﬁrst introduced in 1996

by Ragazzoni (Ragazzoni, 1996). For this sensor the

hardware part is a pyramid, which is placed on the fo-

cal plane of the telescope and the light is focused on

the apex of the pyramid. This element subdivides the

focal plane of the telescope into four quadrants. The

output of the prism is collimated obtaining four aper-

ture images in the focal plane of the lens. From the

intensity distribution in the four pupils we can calcu-

late local slopes.

Figure 2: Pyramid WFS scheme.

The TP3 WFS was conceived by van Dam and

Lane in 2002, and was ﬁrst used in a closed-loop AO

system in 2017 (Colodro-Conde and others., 2017).

It is based on the derivation of the wavefront aberra-

tions from two defocused intensity images (van Dam

and Lane, 2002). For this sensor the hardware part

will be an optical element which generates an optical

path difference. It working principle is based on the

divergences and convergences of the rays in an aber-

rated WF, which create ﬂuctuations intensity maps.

The total intensity must be constant between the ray

path due to the principle of conservation of energy.

Thus, an area of light divergent in one image will have

the same total intensity as its respective convergent

area in the other image. The ray tracing is performed

by measuring the displacement of the corresponding

light and dark regions in the defocused images, see

ﬁgure 3.

Figure 3: Two Pupil Plane WFS scheme.

This paper presents the ﬁrst work carried out to

determine the best WFS to couple ALIOLI to differ-

ent scientiﬁc instruments in medium-sized telescopes.

The ﬁnal purpose is to develop simulations, labora-

tory tests and telescopic operation of a prototype that

offers the possibility of using one type or another ac-

cording to the observing conditions.

2 MODULAR CONCEPT

The ultimate purpose of this project is to have a

portable instrument that could be mated and removed

in different telescopes. For this reason, a modular sys-

tem has been proposed. The modules in the ALIOLI

instrument are as follows:

• Telescope Simulator. An optical ﬁber has been

used as a reference star. This block has been ini-

tially developed for the TCS. To simulate the TCS

aperture, two achromatic doublets and a physical

pupil have been used. See Figure 4 blue beam.

• Wavefront Corrector. This block consisting of a

DM placed on the conjugated pupil plane of the

telescope that act as a phase modulator. It was

decided for the simplest design using commercial

achromatic doublets. The collimating lens images

PHOTOPTICS 2022 - 10th International Conference on Photonics, Optics and Laser Technology

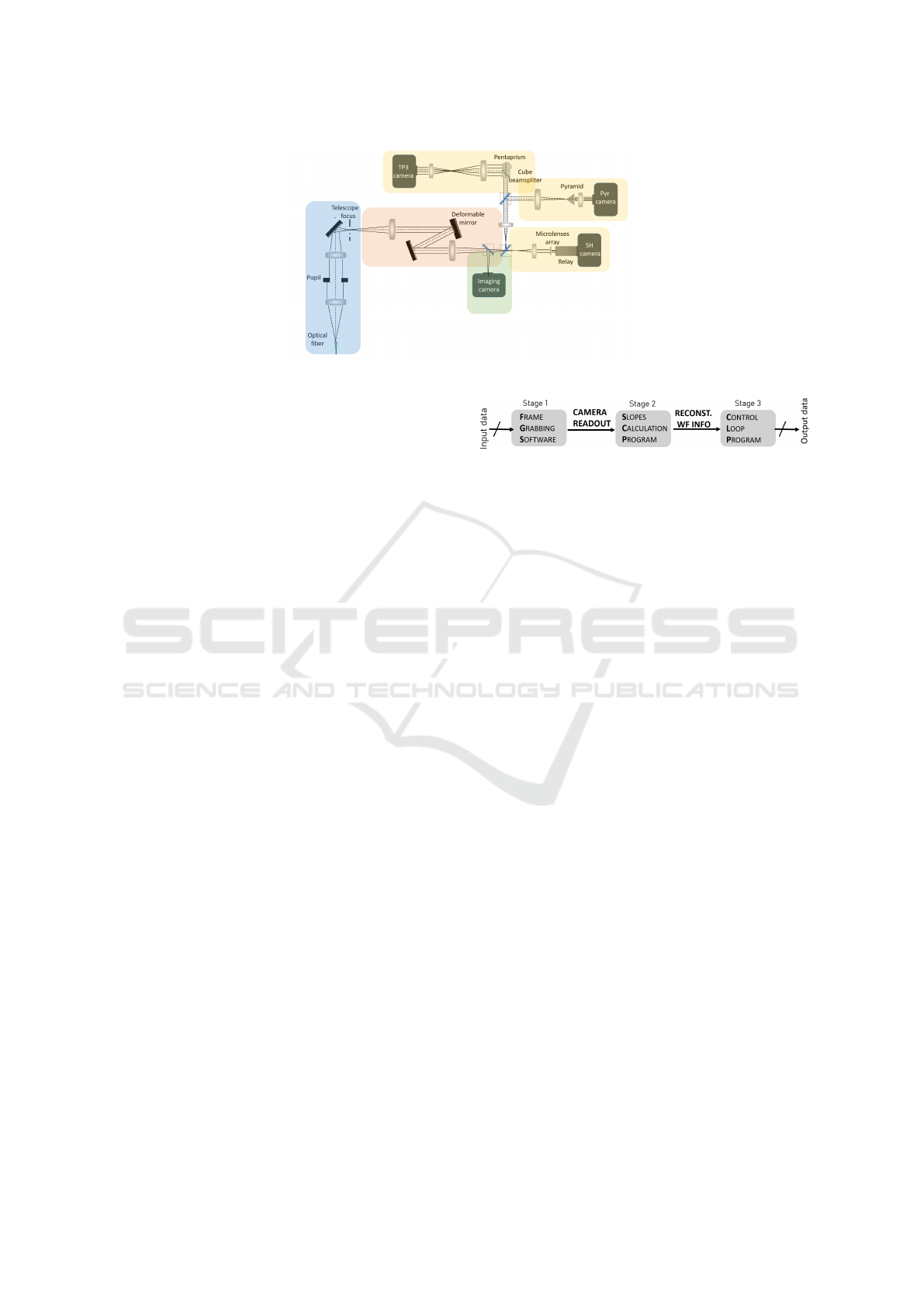
Figure 4: Mounting proposals for each module of the ALIOLI instrument.

the entrance pupil on the DM, and a second lens

refocuses the object. The DM is an ALPAO de-

vice with 88 actuators and a pupil diameter of

20mm. This compact design will allow to incor-

porate a Tip Tilt Mirror (TTM) along the optical

path, but due to the tip/tilt stroke of this DM is

40µm, in the actual design the tip-tilt corrections

could be assumed by the DM. See Figure 4 red

beam.

• Wavefront Sensor. A WFS with interchangeable

S-H, TP3, PYR modules. The optical design for

each wavefront is done and it is widely reported

in Section 3. The sensor camera, an Andor Ixon

DU-897 camera, which is based on a sub-photon

noise 512x512 e2v EMCCD (Electron Multiply-

ing Charge-Coupled Device) detector, and the col-

limating lenses are common for the three ap-

proaches. See Figure 4 yellow beam. Each WFS

carries an image analysis program for calculat-

ing the slopes, Slopes Calculation Program (SCP),

that reproduce the incident wavefront.

• Control Software. The same modular strategy

has been proposed for the Control Software. See

Figure 5. Here, we will distinguish three mod-

ules. The ﬁrst one is the Frame Grabbing Soft-

ware (FGS) whose objective is to continuously

acquire images from the WFS camera, the input

data, using an appropriate conﬁguration depend-

ing on the post processing. This part send the

images to the next level. The second ones is the

Slope Calculation Program (SCP) which receives

the images and processes them according to each

algorithm. The information collected after pro-

cessing is sent in terms of slopes or Zernike coef-

ﬁcients to the next level. The last module is the

Control Loop Program (CLP). The base of this

prototype is to use resources of previous projects,

so the CLP used is the one developed for AOLI,

whose description is widely reported in (Colodro-

Conde and others., 2017).

Figure 5: Pipeline for the Analysis + Control Software.

• Graphics Manager. A python application has been

developed to manage the graphics produced dur-

ing the AO process, such as the reconstruction of

the wavefront, the DM geometry or the WFS cam-

era readout. This application allows view real-

time information relevant to the sensing and close

loop process, as well as save the information in

the appropriate format.

• A Science System: the initial approach is to place

directly an imaging camera. Since our WFC

maintains the telescope’s F#, we have decided to

attach the lenses of FastCam instrument, based

on Lucky Imaging technique, (Alejandro Oscoz,

2008) to our science arm. See Figure 4 green

beam. Using an adaptive optics system prior

to a lucky imaging detector, ﬁrst tested in 2007

(Gladysz et al., 2007), allows obtain a higher

number of images minimally affected by turbu-

lence. The lucky imaging system averages the

best images taken during the AO process to get a

ﬁnal image with higher resolution than it is possi-

ble with a regular long exposure AO camera. The

EMCCD camera is an iXon 888 from Andor, with

sensor diagonal size 18.8 mm and pixel size 13

µm.

3 WAVEFRONT SENSORS

DESIGN

Throughout this section we will explain the design

of each one of the wavefront sensors, at the concept

level, the selection of the optical components as well

as the outlook of the Slopes Calculation Program.

Study of Three WFS for the Modular System in a Portable AO Instrument: ALIOLI

3.1 Shack Hartmann

In the operation of a wavefront sensor type SH there

are three basic steps in the analysis process: determi-

nation of the spot positions, conversion to wavefront

slopes, and the wavefront reconstruction.

In the design, the deformable mirror and the mi-

crolenses array (MA) are in a pupil conjugate plane,

we are looking for the simplest setup, so our choice

was to select a commercial MA. The ﬁrst design was

carried out using the MLA300-14AR(-M) Thorlabs

model Square Grid with size 10mm x 10mm and

lenslet pitch 300µm.

The higher the number of lenslets sampling the

pupil, the higher is the spatial resolution of the mea-

surements. However, this will lead to a lower sig-

nal to noise ratio since we reduce the amount of light

by lenslet, so we have to ﬁnd a balance between

these two parameters. Our idea is to control the sam-

pling varying the pupil size over the MA, and this

is achieved by modifying the collimation lens that

projects the pupil on the MA.

We need to know the minimum number of mi-

crolenses required to accurately sample the tele-

scope’s pupil. The seeing for a good night at the TCS

in the Teide Observatory is r

= 0.15m. Therefore,

the area of the telescope’s pupil must be divided by

the area of the atmospheric cell to know the regions in

which our pupil has to be divided and, consequently,

the minimum number of microlenses across our pupil:

Number of regions =

(1.52)

(0.15)

∼ 103 regions.

Two different designs have been tested. The ﬁrst

one assumed a 5.4mm pupil, and therefore an over-

sampling of 20 x 20 microlenses. The results obtained

both in laboratory and in the telescope are summa-

rized in (Soria et al., 2020).

To improve the signal per microlense a second design

was proposed. In this case we generate a pupil of 3.6

mm and therefore an sampling of 12 x 12 microlenses.

The conﬁguration of the detector camera is conﬁgured

to read only the area in which the light falls, to reduce

the sampling time.

A reference image whose spots falls in the cen-

tre of the microlenses areas is needed. To obtain this

image, a reference beam is inserted placing an opti-

cal ﬁber in the focus of the telescope (Telescope Fo-

cus Figure 4). In this conﬁguration, the only optical

element that can introduce aberrations in the system

is the DM, since without voltage the surface is not

ﬂat. For ﬂattening, a commercial wavefront sensor

(Thorlabs WFS40-7AR) placed after the collimating

lens of the WFS beam. The readout has been con-

nected to the control system and after the Static Char-

acterization we have closed the loop and therefore the

DM surface has been corrected until obtaining a ﬂat

wavefront. This ﬂattening can be veriﬁed with the

science image in the event that both optical paths are

equal, if not, the dreaded Non Common Path Aber-

ration (NCPA) will appear. This wavefront will be

our objective readout throughout the test. This step is

common for all the WFS.

3.2 Pyramidal

The operating principle of our Pyramidal WFS consist

of focusing the distorted WF on the vertex of a pyra-

mid by L1 and split into four beams by four facets of

pyramid, and then four conjugated images of the pupil

are produced on the detector camera by L2, see ﬁgure

2. I1, I2, I3 and I4 denote their respective intensity.

For the optical design, the PAM2R.dll dynamic

linked library that deﬁne a user surface for ZEMAX

has been used as a resource, describing a pyramid

as an optical element for geometrical ray-tracing pur-

poses developed by Arcetri (Antichi et al., 2016). One

of the main problems in the manufacture of a pyra-

mid by polishing is the roof-shaped tip, especially for

small angles, which produce not evenly spread into

four parts. The angle is limited by the area of the de-

tector so two different pyramids have been proposed.

A simple one with a base angle of 8 degrees, and a

double one with 20 and 12 degrees. The use of a dou-

ble pyramid allows to select a base angle greater than

with a single pyramid conﬁguration which results in

an easier polishing process (Tozzi et al., 2008b). Nev-

ertheless, because of the higher thickness, it creates

another problem: the appearance of chromatic aber-

ration. For this reason, a design with two different

glasses is needed (Tozzi et al., 2008a). Both pyramids

are still in the design process.

Due to the group’s lack of experience with this

sensor, the Slope Calculation Program will have to be

developed. To date, the algorithm has been veriﬁed

through different simulations, but it must be imple-

mented in real time, and its output must be compatible

with our Control Loop Program.

3.3 Two Pupil Plane Positions

This was the WFS used in the previous instrument

AOLI. For this task, the optical design had to be

changed because a much more compact instrument is

needed, so to generate a sufﬁcient difference in the

optical path it was not possible to use a Lateral Prism.

There are two Lateral Prisms available: 10mm and

20mm. The large one induces an excessive separa-

tion of the pupils on the detector, while the smaller

PHOTOPTICS 2022 - 10th International Conference on Photonics, Optics and Laser Technology

one generates an optical path difference less than the

depth of focus of the telescope, so the selected optical

element to introduce the optical difference path is a

pentaprism.

As we have mentioned, the greater the projection

of the wavefront, the greater the resolution of our sen-

sor, so the difference in the optical path that we intro-

duce is proportional to it. This optical element in-

duces two potential problems, the decrease in the in-

tensity due to the absorption of the pentaprism and the

inversion in the pupil. Therefore, some adjustments

have been made in the slope calculation program. To

solve the problem related to the differences in the il-

lumination, it is carried out a normalization of each

pupil, and for the inversion a X-ﬂip is done in one of

the pupils before applying the algorithm.

The steps to apply the Van Damm algorithm are ex-

plained in the simulation section. The real time SCP

works in real time thanks to its GPU-accelerated im-

plementation (Fern

andez-Valdivia et al. 2013)

4 PYTHON SIMULATIONS

We have been developing simulators for the 3 WFS

to test the algorithm of each SCP. This study helps

us better understand our system and be able to make

sensor comparisons in a theoretical way. To carry out

the simulations we used Python as programming lan-

guage.

The setup components have been simulated using

the High Contrast Imaging for Python (HCIPy) mod-

ule developed by a group of astronomers at Leiden

Observatory (Por et al., 2018), see table 1.

The phase proﬁle of the deformable mirror

(x, y) can be described by two different ways:

through a Gaussian proﬁle of inﬂuence of each ac-

tuator c

act

or set of modal functions f

(x, y) deﬁned

by:

(x, y) =

∑

(x, y) (1)

Modal reconstruction involves the estimation of

the actuator state c

act

or the modal coefﬁcients c

that

compensate the incident aberration. Throughout this

paper, the actuator modes will be used in Zernike

mode.

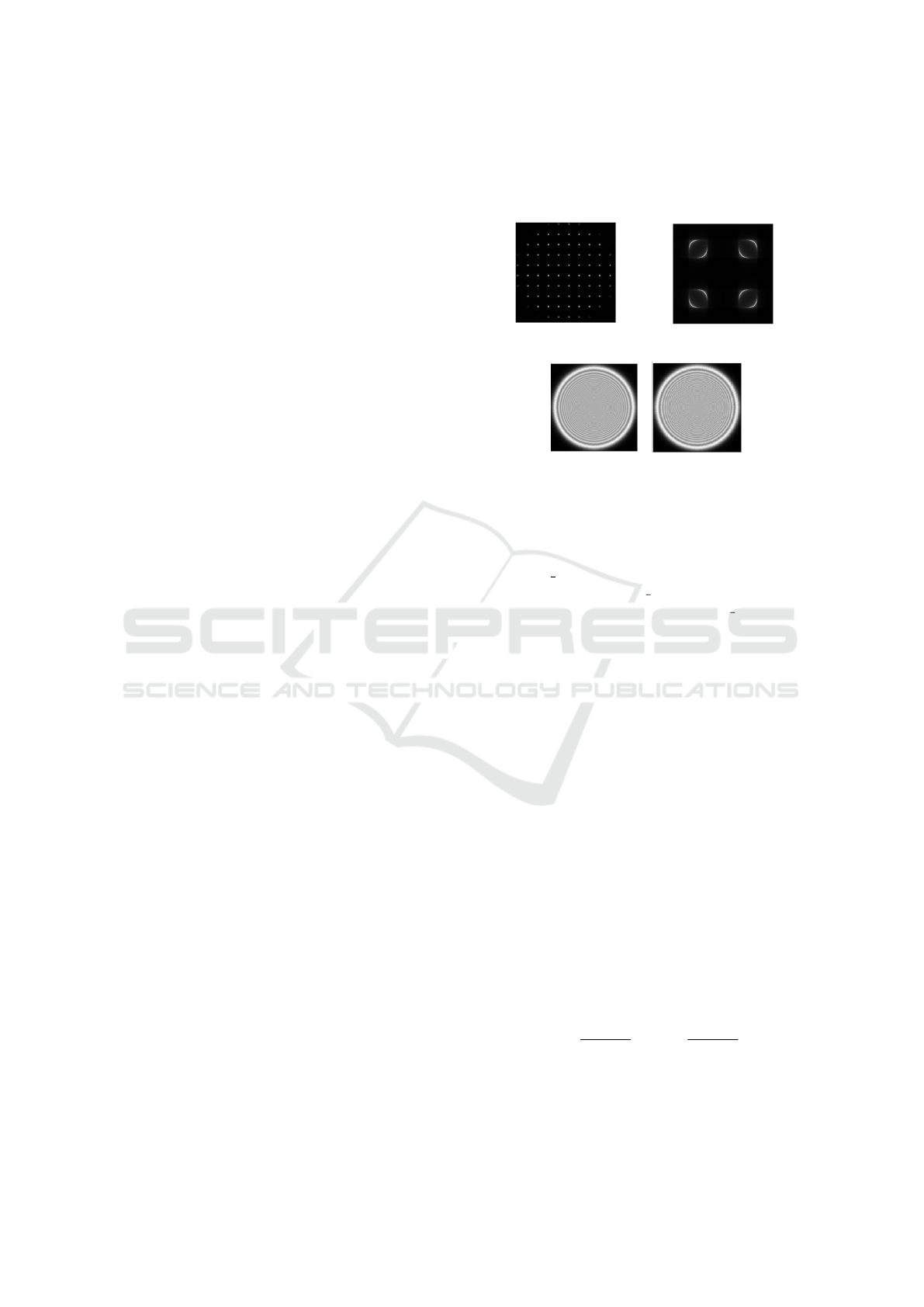
For the reference image, the DM is ﬂattened and

a perfect ﬂat wavefront that passes through the pupil

of the telescope is generated. This WF passes through

the different components, the pupil reducer, the DM

and the different optical elements of each WFS, mi-

crolenses array (MA) for the SH, the pyramid for the

PYR and 2 Fresnel propagator surfaces for the TP3.

After that, the signal is read on the detector camera

and the image is normalized. Once the camera is

read out, each image is analysed though functions that

carry out the algorithms explained in the section 3.

(a) Reference image for the

SH.

(b) Reference image for the

Pyr.

Figure 6: Reference image for each WF.

For the SH, the simulation of the MA is deﬁned

though the HCIPy function:

MicroLensArray(pup_grid,mla_grid,focal_length)

Where pup grid deﬁnes the area in which the light

will fall over the MA, mla grid deﬁnes the positions

of the centre of the micolenses, and focal length is the

value of the focal of the microlenses.

We use the reference image to select the lenslet

area in which to measure each centroid (microlens

pitch) and the ideal position of the spots, in the case

of the simulation this points will be the same that the

coordinates that deﬁne the pupil grid, see Figure 6a.

To carry out this task we have implemented a func-

tion that from an input value of the spots distance,

that we mark over the reference image, it performs a

peak detection algorithm, and in the last iteration it

saves the position of the centroid of each microlens

and the parameter that characterize the readout area.

This method allows us to apply the algorithm to dif-

ferent assemblies that we could use. From the refer-

ence we generate a mask that selects the areas of the

detector in which the software has to measure the po-

sition of the centroids. To know which pixels we have

to take into account, in this point, we apply a dynamic

threshold which is proportional to the maximum pixel

value in the cell. The localization of the spot behind

each lenslet area is determined using a centre of mass

algorithm. The x and y location are given by:

∑

i=1

∑

i=1

, C

∑

i=1

∑

i=1

. (2)

This calculus are involve in the following imple-

mented function:

SH_estimator(det,regx,regy,regh,regw,refx,refy)

Study of Three WFS for the Modular System in a Portable AO Instrument: ALIOLI

Table 1: Characteristics of simulated elements.

Parameter Value

Telescope Diameter 1.5 m

Pupil diameter over the DM 18.11 mm

WFS Wavelength 700 nm

SH: Subapertures 12 x 12

SH: Focal 14.6mm

SH: Lenslet diameter 300 µm

Pyramid separation 0.04

TP3 optical path difference 10mm

DM: Actuators across pupil 9

DM inﬂuence Zernike polynomails

Science camera Noiseless detector 1024 x 1024 px

WFS camera Noiseless detector 256 x 256 px

Number of Zernike reconstruct coefﬁcients 30

Being det the image we want to process, and the rest

of the inputs the parameters that mark the readout

area.

From that moment, the SCP will measure the position

of the centroids in each of the regions that we have

deﬁned on the detector and will compare the results

with those of the reference image to calculate the dis-

placements in x and y for each subaperture.

For the PYR WFS the pyramid is simulated

though the HCIPy function:

PyramidWavefrontSensorOptics(pupil_grid,sep,wl_0)

Where pup grid deﬁnes the area in which the light

will fall, sep, separation, is related to the angle of

the pyramid root, and wl 0 is the wavelength used for

sensing. To know the detector readout area, we have

implemented a circle detection function:

Detect_circle(direction_image,minR,maxR)

Where direction image point to the folder where the

reference image has been saved, and minR,maxR de-

limit the expected range of the radius of the circle we

are looking for in pixels. This function applied an

Hough ﬁlter to the binarized reference image using

the OpenCV library, and it returns the x and y coordi-

nates of each detected circle and its radius. Using this

parameters we could create a square mask that extract

the pixel values of the detector which correspond to

the pupils areas. To avoid edge effects, that we have

veriﬁed to have a great weight in the reading of the

WF, the readout area is 2 pixel smaller than the size

of the detected circle. This approach allows operate

with the pupils as simple matrices. Finally, we apply

the algorithm to calculate the deviations in the x and

y direction:

+ I

−I

)

norm

(3)

−I

+ I

)

norm

(4)

The normalization factor could be calculated using

different methods (Bond et al., 2015). For this ap-

proach we have chosen the classical normalisation for

a pyramidal WFS, a pixel-wise normalization. Ev-

ery pixel intensity is normalised by the total intensity

in that pixel position, summed across the four pupils.

The algorithm has been implemented in the function:

Proc_pupil(aberr,pupils)

Where aberr is the detector frame that we want

to analyse, and pupils contains the information re-

garding the areas of the detector that we have to

read, namely, the output of the previous function

Detect circle.

In the case of the TP3 WFS, the optical path dif-

ference between the pupils has been generated adding

to the beam two Fresnel surfaces deﬁned in the HCIPy

library:

F1=FresnelPropagator(pupil_grid,z,num_oversamp,n)

F2=FresnelPropagator(pupil_grid,-z,num_oversamp,n)

Once again pupil grid marks the area in which the

light will fall, z is half of the distance generated be-

tween the pupils, oversamp is the number of times the

transfer function is oversampled, and n is the refrac-

tive index in which the light spreads. To simplify the

process each pupil is read out in its own detector, so it

is not necessary to extract the pupils. We use the ref-

erence image to delimiter the size of the pre-calculus

polynomial slopes matrix and the coefﬁcients read for

the reference image are used as a baseline. Figure

6c. Following the Vam Dam article, the ﬁrst step is to

calculate the mean slope of the polynomials in the or-

thogonal direction to the projection. For every angle,

α, and a circle of radius R this quantity is given by:

(u, Z

) =

√

−u

× .



∂Z

(x, y)

∂x

cos(θ) +

∂Z

(x, y)

∂y

sen(θ)



(5)

PHOTOPTICS 2022 - 10th International Conference on Photonics, Optics and Laser Technology

Being R the Radon Transform and u the coordinates.

The calculation of the Radon Transform has been

implemented in python based on the code of Justin

K. Romberg, making a small modiﬁcation so that

it returns the reference coordinates of the calculated

sinogram, that we need to use in this algorithm.

The derivatives of the Zernike polynomials can be

computed directly from their mathematical deﬁnition.

These calculations have been implemented within the

following function:

H = g_wfs_precalc(modes, angles, x, y)

Whose inputs are modes, a vector with the modes

used for the reconstruction, angles a vector with the

projection angles for the Radon Transform, and the

horizontal size, x, and vertical size, y, of the readout

area. This function returns a 3D matrix H whose size

is H[number of coords, number of angles, number of

modes.

The Zernike coefﬁcients a

are then calculated

through a least squares ﬁt:

= [Hα(u, Z

)

(u, Z

)]

−

(u, Z

)

(u) (6)

Being [Hα(u, Z

)

(u, Z

)]

−

(u, Z

)

the expres-

sion of the Moore-Penrose pseudo-inverse, a general-

ization of the inverse. The ﬁrst step is to convert our

3D matriz in an 2D matrix to operate with it, for this

task a simple reshape was applied. The second step

is to carry out the pseudoinverse. To avoid degrada-

tion of the reconstruction by small singular values, we

have used the Thicknov regularization that is imple-

mented in the HCIPy library. We choose a tolerance

of 10

−3

The next step is to calculate the sinogram, by

means of the Radon transform, of each of the unfo-

cused pupils, and then relate the intensities by means

of an histogram matching. Once I know the coordi-

nates of each sinogram that have the same light in-

tensity (u

and u

), I can calculate the slope of the

incident wavefront by:

∂W

r∂u

−u

2 ·z

(7)

Finally, to calculate the slope along the pupil we

have to perform an interpolation of the measured val-

ues. The function chosen to carry out the interpolation

has been InterpolatedUnivariateSpline from Scipy li-

brary. All these calculations have been implemented

within the following function:

g_wfs(i1, i2, nangles, z ,H_pinv)

Where i1 and i2 are the detector images of each blur

pupil, nangles the number of angles projected, z the

distance in meters between each pupil and the pupil

focus plane, and H pinv the pseudo-inverse of the H

matrix. This function returns the slopes calculated

if H pinv is NONE or otherwise the reconstructed

Zernike coefﬁcients.

Up to here we would have completed the simula-

tion of the WFS module, the next phase will be the

simulation of the calibration of our instrument.

For the linear reconstructor we need to now the

Inﬂuence Matrix, which tells us how each wavefront

sensor responds to each movement of the deformable

mirror. We are working in Zernike mode basic for

the DM characterization so the modal characteriza-

tion can be build by sequentially applying a positive

and negative single mode on the deformable mirror

surface and reading the measurement on each WFS.

The difference between the two WFS readouts gives

us the DM response. The most common technique

of wavefront reconstruction is to assume a linear rela-

tion between the measurement vector s and the modal

coefﬁcients c. The forward model is then given by:

s = M

in f lu

·c + N (8)

Where M

in f lu

is the Inﬂuence Matrix, s the WFS mea-

surement, c the incoming perturbation and N some

measurement noise from the WFS. The Inﬂuence Ma-

trix can be calibrated by measuring the actuator re-

sponse within the linearity range of the WFS. The

inverse operation of reconstructing the WF from the

slope measurements involves the estimation of the

Actuation Matrix, M

act

. This estimation requires in-

version of the Inﬂuence Matrix. M

in f lu

is not a square

matrix so to apply the least-squares a pseudo-inverse

in needed. Again we use the pseudo-inverse of Thic-

knov.

For each WFS we have implemented a function

responsible of calculate M

in f lu

. In addition to the re-

quested parameters that characterize each WFS oper-

ation, there are some common inputs that indicates the

number of DM actuators poke, the number of mea-

surements and the number of modes that we apply to

the DM.

Once we have completed the calibration process,

we could reconstruct the shape of the incoming WF

just multiplying the WFS lecture by the Actuation

Matrix:

c = M

act

·s (9)

4.1 Results

As our objective is to verify the reliability of the algo-

rithm under different conditions, it is more useful to

generate a controllable wavefront and check whether,

after the analysis and reconstruction, the wavefront

corresponds to the simulated one. It is a static mea-

surement, so for simplicity we are going to resort

leaving the deformable mirror in a random position

and checking the reconstruction of its surface with

each of the sensors. The results are shown in ﬁgures

7, 8 and 9:

Study of Three WFS for the Modular System in a Portable AO Instrument: ALIOLI

Figure 7: Reconstruction process for the SH module simu-

lation.

Figure 8: Reconstruction process for the TP3 module simu-

lation.

The ﬁrst image shows the DM surface when we

send it a random signal, the second shows the recon-

struction of the WF with each WFS, and the third

ﬁgure shows an histogram with the generated modes

(blue), the reconstructed modes (orange), as well as

the difference between them (green).

On ﬁrst thought, if we compare the ﬁrst and the

second ﬁgure, we see as the reconstruction algorithm

used for the SH WFS and the TP3 WFS reconstruct

the incident wavefront in a more faithful way than the

algorithm used with the nm-PYR module showing the

non-linear behaviour of this sensor referenced in the

bibliography (Hutterer et al., 2019).

For a statistic study, we generate 90 random positions

for the DM, working with 30 Zernike coefﬁcient and

leaving aside the mode 0 corresponding to the pis-

ton. Then, we perform the reconstruction process

with each WFS and calculate the Root Mean Square

(RMS) of the difference vector. Results obtained are

summarized in table 2.

Table 2: Differences between the incoming WF and the re-

constructed WF for each WFS.

RMS (u.a.)

SH wfs (1.58 ±0.03) ·10

−02

Pyr wfs (2.1 ±0.6) ·10

−01

TP3 wfs (5 ±4) ·10

−02

In the absence of noise, the goodness of the re-

construction process differs by an order of magni-

tude between the PYR WFS and the others. SH WFS

shows better results, with the smallest RMS. More-

over, the error associate to the RMS measurement in-

dicates that the SH WFS is more precise.

To analyse the behaviour of the sensors under real

Figure 9: Reconstruction process for the Pyr module simu-

lation.

conditions, we are going to carry out a study of the

reconstruction process when the input signal is not

clear. For this task we are going to add random noise

to the detector camera, whose medium value is zero

and the Standard Deviation (SD) will vary. This sit-

uation would reﬂects the observation with different

reference stars magnitudes. The results in Figure 10

summarize the performance of the sensors, and error

bars show the SD (over maximum and minimum val-

ues) of the measured RMS value for each noise value.

See ﬁgure 10.

Figure 10: WFS response comparison for different SN ra-

tios.

The same trend is followed when the measure-

ments have noise. The high SD for the PYR WFS

in the last point shows that this WFS is not capable

of reconstruct the incident WF under this conditions

while the SH and the TP3 get good results.

5 CONCLUSIONS

In the WFS comparison there are many requirements

that we have to balance for the AO system design.

• Accuracy

• Efﬁciency (good use of photons)

• Speed (related with linearity)

• Robustness (chromaticity, ability to work on ex-

tended sources, etc ...)

• Other parameters (price, assembly-friendly..)

PHOTOPTICS 2022 - 10th International Conference on Photonics, Optics and Laser Technology

These simulations have given us the chance to test

the implemented algorithm for the three WFS. Results

show that the SH WFS is the most accurate and pre-

cise. The same efﬁciency has been obtained for the

TP3 and the SH WFS.

Other requirements such as speed will have to be

rated when the real time implementation will be ﬁn-

ished for the three WFS. To compare others parame-

ters speciﬁc test will be designed.

Furthermore, these simulations have allowed us to

discard the nm-PYR for our instrument, opening the

possibility of design a modulated one to increase lin-

earity.

ACKNOWLEDGEMENTS

The research leading to these results received the sup-

port of the Spanish Ministry of Science and Inno-

vation under the FEDER Agreement INSIDE-OOCC

(ICTS-2019-03-IAC-12) and managed by the Insti-

tuto de Astrof

ısica de Canarias (IAC).

REFERENCES

Alejandro Oscoz, a. o. (2008). FastCam: a new lucky

imaging instrument for medium-sized telescopes. In

McLean, I. S. and Casali, M. M., editors, Ground-

based and Airborne Instrumentation for Astronomy II,

volume 7014, pages 1447 – 1458. International Soci-

ety for Optics and Photonics, SPIE.

Antichi, J., Munari, M., Magrin, D., and Riccardi, A.

(2016). Modeling pyramidal sensors in ray-tracing

software by a suitable user-deﬁned surface. Journal of

Astronomical Telescopes, Instruments, and Systems,

2(2):1 – 7.

Bond, C., El Hadi, K., Sauvage, J. F., Correia, C., Fau-

varque, O., Rabaud, D., Neichel, B., and Fusco, T.

(2015). Experimental implementation of a Pyramid

WFS: Towards the ﬁrst SCAO systems for E-ELT. In

Adaptive Optics for Extremely Large Telescopes IV

(AO4ELT4), page E6.

Colodro-Conde, C. and others. (2017). Laboratory and tele-

scope demonstration of the TP3-WFS for the adaptive

optics segment of AOLI. Monthly Notices of the Royal

Astronomical Society, 467(3):2855–2868.

Colodro-Conde, C. and others. (2018). The TP3-WFS: a

new guy in town. page arXiv:1811.05607.

Gladysz, S., Christou, J. C., and Redfern, M. (2007). “lucky

imaging” with adaptive optics. In Adaptive Optics:

Analysis and Methods/Computational Optical Sensing

and Imaging/Information Photonics/Signal Recovery

and Synthesis Topical Meetings on CD-ROM, page

ATuA7. Optical Society of America.

Hickson, P. (2014). Atmospheric and adaptive optics. The

Astronomy and Astrophysics Review, 22:1–38.

Hutterer, V., Ramlau, R., and Shatokhina, I. (2019). Real-

time adaptive optics with pyramid wavefront sensors:

part i. a theoretical analysis of the pyramid sensor

model. Inverse Problems, 35(4):045007.

Por, E. H., Haffert, S. Y., Radhakrishnan, V. M., Doel-

man, D. S., Van Kooten, M., and Bos, S. P. (2018).

High Contrast Imaging for Python (HCIPy): an open-

source adaptive optics and coronagraph simulator. In

Adaptive Optics Systems VI, volume 10703 of Proc.

SPIE.

Ragazzoni, R. (1996). Pupil plane wavefront sensing with

an oscillating prism. Journal of Modern Optics,

43(2):289–293.

Soria, E., L

opez, R. L., Oscoz, A., and Colodro-Conde,

C. (2020). ALIOLI: presentation and ﬁrst steps. In

Schreiber, L., Schmidt, D., and Vernet, E., editors,

Adaptive Optics Systems VII, volume 11448, pages

517 – 525. International Society for Optics and Pho-

tonics, SPIE.

Thibos, L. N. (2000). Principles of hartmann-shack aber-

rometry. In Vision Science and its Applications, page

NW6. Optical Society of America.

Tozzi, A., Stefanini, P., Pinna, E., and Esposito, S. (2008a).

The double pyramid wavefront sensor for lbt. In Hu-

bin, N., Max, C. E., and Wizinowich, P. L., editors,

Adaptive Optics Systems, volume 7015, pages 1454 –

1462. International Society for Optics and Photonics,

SPIE.

Tozzi, A., Stefanini, P., Pinna, E., and Esposito, S. (2008b).

The double pyramid wavefront sensor for LBT. In

Hubin, N., Max, C. E., and Wizinowich, P. L., editors,

Adaptive Optics Systems, volume 7015, pages 1454 –

1462. International Society for Optics and Photonics,

SPIE.

van Dam, M. A. and Lane, R. G. (2002). Wave-front sensing

from defocused images by use of wave-front slopes.

Appl. Opt., 41(26):5497–5502.

Study of Three WFS for the Modular System in a Portable AO Instrument: ALIOLI