
Utility of Anonymised Data in Decision Tree Derivation
Jack R. Davies and Jianhua Shao
School of Computer Science & Informatics, Cardiff University, U.K.
Keywords:
Data Anonymisation, Data Utility, Decision Tree.
Abstract:
Privacy Preserving Data Publishing (PPDP) is a practice for anonymising microdata such that it can be publicly
shared. Much work has been carried out on developing methods of data anonymisation, but relatively little
work has been done on examining how useful anonymised data is in supporting data analysis. This paper eval-
uates the utility of k-anonymised data in decision tree derivation and examines how accurate some commonly
used metrics are in estimating this utility. Our results suggest that whilst classification accuracy loss is mini-
mal in most common scenarios, using a small selection of simple metrics when calibrating a k-Anonymisation
could help significantly improve decision tree classification accuracy for anonymised data.
1 INTRODUCTION
With the increase in personal data collection, storage
and use by a growing number of corporations and or-
ganisations, there has been a corresponding rise in the
population’s concern for their privacy. To alleviate
these concerns, governments require that individuals’
privacy is protected in the sharing of sensitive data. To
comply with these requirements, data publishers use
a process known as Privacy Preserving Data Publish-
ing (PPDP) (Fung et al., 2010). The major challenge
with PPDP is to ensure that the privacy of individu-
als is maintained, whilst also retaining the usefulness
of the original data. Na
¨
ıve approaches such as sim-
ply removing explicit identifiers (e.g., driving license
number) from the data set, or redacting contextual in-
formation, are not sufficient. A more sophisticated
approach is needed whereby the data satisfies given
privacy requirements defined in a privacy model, to
protect against potential attacks.
One such model is k-Anonymity (Samarati and
Sweeney, 1998). k-Anonymity requires each record
in a data set to be indistinguishable from at least k −1
other records over the set of quasi-identifiers (QIDs).
QIDs are attributes in the data set that are externally
available and can be used to link a record to a spe-
cific individual – an attack known as Record Link-
age. For example, Age and Occupation are possible
QIDs that could be used to identify a specific per-
son in a data set if there is a unique combination of
their values within. A given data set will rarely sat-
isfy k-Anonymity, thus the data will need to be mod-
ified through anonymisation operations. For exam-
ple, if the Occupation values ‘Lawyer’ and ‘Doctor’
do not appear k times in a data set individually, we
can choose to generalise both into ‘Professional’ or
simply ’{Lawyer, Doctor}’. The data set will publish
at least k records with the generalised value instead,
thereby satisfying k-Anonymity.
Whilst k-Anonymity ensures anonymity in the
data, it must retain utility for recipients of the data
too. The degree to which this utility is maintained
is something that has not been comprehensively stud-
ied; this paper attempts to study this in the context
of one particular area of data analysis – classification
using decision trees. We adapt the basic ID3 algo-
rithm (Quinlan, 1986) to derive decisions trees from
anonymised data and we then use this adapted algo-
rithm to train and test decision trees in four differ-
ent scenarios, comparing and evaluating the results
from each scenario to measure the data utility in terms
of classification accuracy. In addition, we measure
the utility of the anonymised data using some metrics
commonly found in the literature and compare these
measures to classification accuracy. This grants in-
sight into the reliability of these metrics in estimating
the utility of anonymised data in decision tree classi-
fication.
The rest of the paper is organised as follows: In
Section 2, we briefly discuss some related work; Sec-
tion 3 presents essential background information; in
Section 4, we present our experiments and report our
results in Section 5; finally, in Section 6, we conclude
the paper.
Davies, J. and Shao, J.
Utility of Anonymised Data in Decision Tree Derivation.
DOI: 10.5220/0010778300003120
In Proceedings of the 8th International Conference on Information Systems Security and Privacy (ICISSP 2022), pages 273-280
ISBN: 978-989-758-553-1; ISSN: 2184-4356
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All r ights reserved
273

2 RELATED WORK
Much of the work done on evaluating the utility of
anonymised microdata has been performed in order to
evaluate a novel algorithm or method for achieving a
certain privacy model (LeFevre et al., 2006; Li et al.,
2011; Tang et al., 2010). There has been much less
work performed on comprehensively evaluating the
utility of data anonymised using existing methods.
Ayala-Rivera et al. (Ayala-Rivera et al., 2014)
performed experiments on several k-Anonymity al-
gorithms, including the Mondrian algorithm used
for this paper, to measure the efficiency and utility
retention of the different algorithms for practition-
ers. However, the experiments performed only utilise
general-purpose metrics, as such it lacks the depth of
investigation proposed in this paper. Primarily basing
evaluation of utility on measurements of metrics is a
common theme among much of the related work. In
contrast, this paper attempts to link the measurements
of these metrics to concrete experimental results.
Shao & Beckford (Shao and Beckford, 2017) eval-
uated the decision tree classification accuracy of data
anonymised using the Mondrian algorithm. They did
so by performing a series of experiments using the
ADULT data set to train and test an ID3 decision tree.
It shows that whilst there is a degradation of classi-
fication accuracy for anonymised data sets compared
to non-anonymised, the degradation is minimal. This
is a similar study to the one described in this paper.
However, it differs in that this paper considers multi-
ple possible scenarios for training and testing of the
ID3 decision tree. It also differs in the implemen-
tation of the ID3 algorithm, and in the utilisation of
the two modes of Mondrian algorithm. Furthermore,
their work does not examine metrics in relation to the
utility results as this paper proposes.
It is notable that the majority of related work uses
metrics as part of the evaluation in some capacity. It is
clear that these metrics are heavily relied upon in eval-
uation of anonymised data, providing obvious motiva-
tion for the work described in this paper.
3 BACKGROUND AND
METHODS
3.1 k-Anonymity
k-Anonymity is a privacy model first introduced by
Samarati & Sweeney (Samarati and Sweeney, 1998).
A data table is said to provide k-Anonymity “if at-
tempts to link explicitly identifying information to its
contents ambiguously map the information to at least
k entities” (Samarati and Sweeney, 1998). This can be
achieved by ensuring that each unique record is iden-
tical to at least k −1 other records over the QIDs. This
set of identical records is referred to as an equivalence
class (EC).
3.2 The Mondrian Algorithm
The algorithm we use to anonymise a raw data set
in this paper is the Mondrian Multidimensional algo-
rithm (LeFevre et al., 2006). The algorithm is imple-
mentable in two modes: Strict or Relaxed. The pseu-
docode for the Strict algorithm can be seen in Algo-
rithm 1.
Algorithm 1: Mondrian - Strict.
1: function Anonymise(D)
2: if D cannot be partitioned then
3: return D
4: else
5: X
i
← chooseAttribute(D)
6: F ← f requencySet(D, X
i
)
7: pv ← median(F)
8: lhs ← {t ∈ D|t.X
i
≤ pv}
9: rhs ← {t ∈ D|t.X
i
> pv}
10: end if
11: return Anonymise(lhs) ∪ Anonymise(rhs)
12: end function
The Mondrian algorithm is recursive. The data set
D used as input is initially the entire data set requir-
ing anonymisation. The algorithm in both Strict and
Relaxed modes will first determine if D can be par-
titioned (line 2) by ensuring D is large enough to be
split into two subsets of minimum size k. X
i
in this
implementation is simply the QID attribute with the
widest normalised range of values (line 5). The fre-
quency of each unique value in X
i
is counted and val-
ues ordered in a frequency set F (line 6). For this im-
plementation, the ordering used was alphabetical for
categorical values and ascending for numerical. Par-
titioning of records is then performed based on the
position of the values of X
i
in F relative to the me-
dian value of F, or the ”pivot value” pv ∈ X
i
(line 7).
The Strict and Relaxed algorithms differ in how the
partitioning is performed. A Strict partitioning does
not allow intersecting values between the two subsets
of D resulting from a cut (lhs & rhs); whereas, the
Relaxed algorithm allows this by modifying the parti-
tioning (lines 8-9) to that shown below:
lhs ← {t ∈ D|t.X
i
< pv}
ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy
274

med ← {t ∈ D|t.X
i
= pv}
rhs ← {t ∈ D|t.X
i
> pv}
The records in med are then distributed into lhs
and rhs such that neither exceeds the median count of
values in F.
Following this, recursive calls are made to the al-
gorithm with lhs & rhs as input D (line 11), result-
ing in a partition of the initial data set with minimally
sized subsets. All that remains is the generalisation
of the values in each subset for all selected QIDs.
The generalised subsets are our equivalence classes,
the union of which is a k-Anonymisation of the initial
data set.
3.3 ID3 Decision Trees and Induction
The ID3 algorithm (Quinlan, 1986) was selected as
the method of building decision trees in this pa-
per. The implementation is as described in (Mitchell,
1997), with some modifications.
The first modification relates to the calculation of
entropy. The entropy of a set of records D with an ar-
ray of different classification values in class attribute
φ is given by the following:
Entropy(D) =
∑
i∈φ
−P
i
log
2
P
i
Where P
i
is the proportion of D with class i in class
attribute φ.
The entropy can then be used in the following cal-
culation of Information Gain (IG):
IG(D, A) = Entropy(D) −
∑
v∈A
|D
v
|
|D|
Entropy(D
v
)
Where A is the selected attribute and D
v
is the subset
of records with value v in A.
We must consider how to deal with generalised
values when calculating entropy. P
i
can be written
|D
φ=i
|
|D|
where D could be the entire data set or sub-
set, which poses no issue where generalised values
are concerned. However, in the information gain cal-
culation, we need to also find the entropy of D
v
. In
an anonymised data set, for any given record, value
v may be generalised. To deal with this, we use the
same method as in Shao & Beckford (Shao and Beck-
ford, 2017). Each value in a generalisation value-set
is equally likely to be the true value. In a generalisa-
tion containing r values, we can consider each value
in the generalisation to be worth
1
r
.
An example of this is shown below. The table
shows records for a generic attribute and correspond-
ing class, followed by entropy calculations for each
attribute value.
Attribute Class
A X
B X
B Y
{A, B} Y
{A, B} Y
{A, B} X
Entropy(Attrib
A
) = −
1.5
2.5
log
2
1.5
2.5
−
1
2.5
log
2
1
2.5
Entropy(Attrib
B
) = −
1.5
3.5
log
2
1.5
3.5
−
2
3.5
log
2
2
3.5
In addition to the calculation of entropy, we also
need to consider how to integrate generalised values
as branches in the decision tree. We cannot simply use
the generalised value itself. Consider the generalised
value {Doctor, Lawyer} used as a branch in a tree.
This implies that we are posing the logical question
“is the Occupation value Doctor or Lawyer?” when
classifying a record. This may seem fine, but if there
exists another branch at the same level of the tree la-
belled with {Doctor, Mechanic}, how would we de-
cide which branch to traverse when the record being
classified has the value ”Doctor”? Further problems
are encountered if the record being classified itself has
generalised values.
It would be much simpler to have exclusively spe-
cific values as branches in the tree. To do this, we map
back the generalisations using two different methods:
• Random: We take a specific value from the gen-
eralised value-set at random and use this as the
branch value in the tree.
• Statistical: We consider the possibility of re-
leasing anonymisations with a frequency distri-
bution of the QID values from the original data.
This statistical information could then be used
to potentially recreate the original data more ac-
curately, providing better classification accuracy.
We weight each value by its frequency in the orig-
inal data. This does not guarantee the correct
value will be mapped back, however, this is to be
expected as otherwise anonymisation would be re-
dundant.
In this paper, we examine both methods to deter-
mine if there is any utility in releasing statistical in-
formation with an anonymisation.
The final modification we make to the ID3 algo-
rithm regards numerical values. The data set we use
in our experiments includes numerical values as im-
portant determiners. The standard ID3 algorithm does
not deal with numerical values, so we use the method
Utility of Anonymised Data in Decision Tree Derivation
275

suggested in (Mitchell, 1997) to allow for them to be
considered.
4 EXPERIMENTS DESIGN
4.1 Experimental Setup
We want to evaluate how useful an anonymised data
set is in decision tree classification. To do this, we
first find classification accuracy results from the four
possible scenarios:
1. Classification of Non-Anonymised data using a
decision tree trained on Non-Anonymised data
2. Classification of Anonymised data using a deci-
sion tree trained on Anonymised data
3. Classification of Non-Anonymised data using a
decision tree trained on Anonymised data
4. Classification of Anonymised data using a deci-
sion tree trained on Non-Anonymised data
For brevity, we refer to each scenario in the rest of
this paper by its numbering. We use Scenario 1 as
the baseline for our experiments; it is the scenario in
which maximal information is available to the clas-
sifier. Comparisons between these scenarios should
provide insight into how much information is lost
through anonymisation, allowing an evaluation on
utility.
In this paper, we use the ADULT data set (Dua and
Graff, 2017) for all experiments to train and test deci-
sion trees and classify records. It is the de-facto stan-
dard for the evaluation of anonymisation algorithms.
Of the 15 attributes in the data set, the income at-
tribute is the class attribute. We omit the attributes fnl-
wgt (not useful for our purpose) and education-num
(enumeration of education). This leaves us with 12
attributes that can be used to classify a record. We
also remove records with missing values, resulting in
45,222 records for our experiments.
We run a series of experiments using the following
process:
1. k-Anonymise ADULT data set with given QIDs &
k-value.
2. Train and test the data according to one of the four
scenarios explained above.
3. Use 6-fold cross-validation testing to measure
classification accuracy.
We repeat this process for the two modes of Mon-
drian algorithm and for the two types of generalisa-
tion mapping. Note that this means that the Scenario
1 experiment will only be performed once as there is
no anonymisation to vary the k-value, and no require-
ment to change the algorithm mode or mapping type.
Furthermore, the Scenario 4 experiments will not be
repeated for the two mapping types as training of the
decision tree is done on Non-Anonymised data.
4.2 Metric Correlations
Once results have been collected from the utility eval-
uation, we try to find a correlation between those re-
sults and a selection of relevant metrics. The metrics
chosen for this paper include Discernability Metric,
ILoss and Classification Metric.
Discernability Metric (DM) (Slowinski, 1992) is
almost ubiquitous in the related literature. It assigns
a penalty to an anonymisation based on the size of
equivalence classes; a higher penalty suggests that
records are less discernible. The penalty is given by
the following formula:
DM =
∑
E∈T
|E|
2
where E is an equivalence class and T is the data table
being evaluated.
ILoss (Tao and Xiao, 2008) is a metric that tries
to consider the information loss from the generalisa-
tion of values. Fung et al. (Fung et al., 2010) states:
”ILoss measures the fraction of domain values gener-
alized by [a generalised value] v
g
.” The ILoss mea-
surement for a specific generalised value is given by:
ILoss(v
g
) =
|v
g
| − 1
|D
A
|
where A is the attribute of the value v
g
, |v
g
| is the num-
ber of values within the domain of A that are descen-
dants of v
g
, and |D
A
| is the total number of values in
the domain of A. The total ILoss for a given table can
then be found by simply summing the measurements
for each generalised value in the table.
Finally, we examined Classification Metric (CM)
(Iyengar, 2002). This is a specialised metric designed
specifically for measuring utility regarding classifica-
tion. The metric is defined:
CM =
∑
r∈T
penalty(r)
N
where r is a row in the table T , N is the total number
of rows, and the penalty function is defined:
penalty(r) =
1, if r is suppressed
1, if class(r) 6= majority(E(r))
0, all other cases
Here E(r) is the equivalence class record r belongs to.
In this paper, we can ignore the first penalty case as
ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy
276
suppression, another method of anonymisation differ-
ent to generalisation, is not used. The case where the
class of record r is not the majority of its EC adds a
penalty if we have an EC that is not homogeneous in
its classification.
5 EXPERIMENTAL RESULTS
As mentioned, we get our baseline from the Scenario
1 experiment. We found the classification accuracy in
this case to be 81.82%. It is expected that this will be
the highest measured accuracy, as maximal informa-
tion is available to the classifier.
5.1 Classification Accuracy
We now discuss the effect of k-anonymisation on clas-
sification accuracy by analysing the results for other
scenarios.
Classification Accuracy Degradation
Here, we view the results of the reduction in classi-
fication accuracy from the measured baseline in each
scenario involving anonymisation. The results were
averaged over all QID counts, mapping and algorithm
types. For Scenarios 2 & 3 we saw similar results to
those measured in Shao & Beckford (Shao and Beck-
ford, 2017), that is, degradation in classification ac-
curacy from the baseline increases with the k-value.
The fall for these two scenarios ranged from 2.15%
to 19.15%, with an average for the more commonly
used values of k (2-10) (Emam and Dankar, 2008) be-
ing 11.72%.
For Scenario 4, we saw the fall in classification ac-
curacy stabilise across the board, with the measured
fall ranging from 5.51% to 8.01%. This would sug-
gest that anonymisation in the training phase of deci-
sion tree classification has a greater impact on classi-
fication accuracy than during the testing phase. Also,
echoing the conclusions from Shao & Beckford (Shao
and Beckford, 2017), it would be beneficial to re-
searchers performing decision tree classification for
data publishers to keep the k-value in the range 2-10,
regardless of applicable scenario.
Mapping Type Comparison
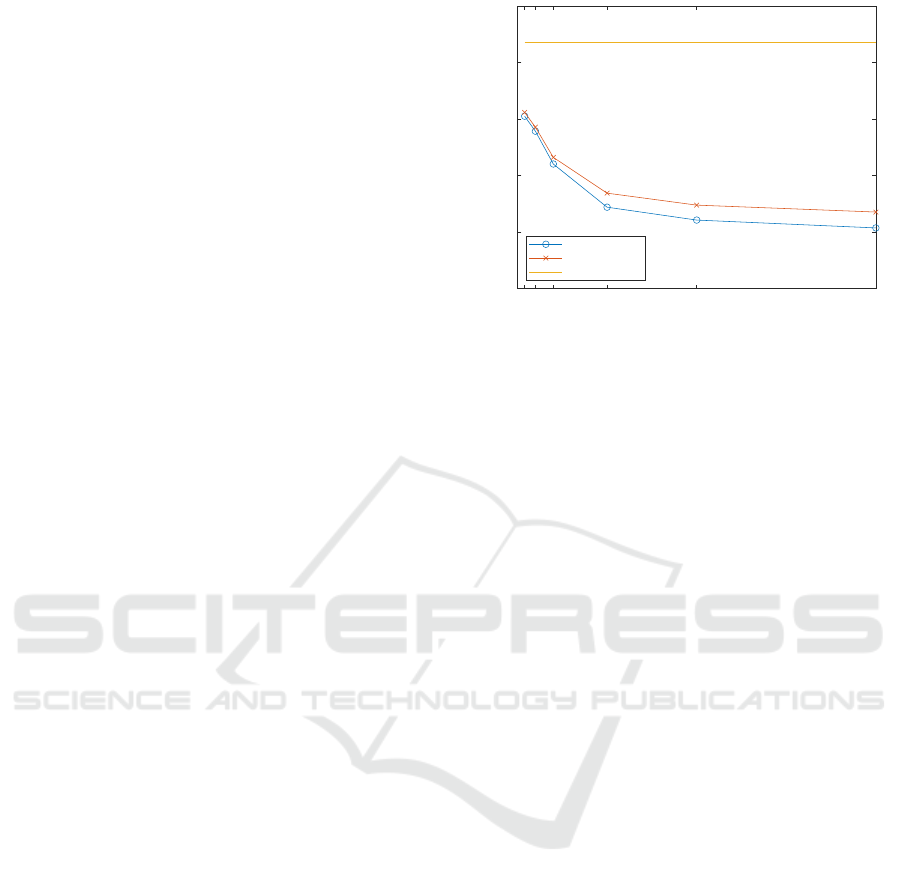
Figure 1 shows the classification accuracy compari-
son between the two types of generalisation mapping
used in this paper. These results are for Scenario 2,
with the result from Scenario 1 shown for compari-
son.
2 5 10 25 50 100
k
60
65
70
75
80
85
Classification Accuracy %
Random
Statistical
Non-Anonymised
Figure 1: Generalisation Mapping Comparison - Scenario
2.
We can see a slight improvement in classification
accuracy for the statistical method of generalisation
mapping compared to the random method. However,
this increase is minimal with an improvement of just
1.4% in the best case. Furthermore, in the commonly
used k-value range (2-10), the improvement is neg-
ligible. The expectation was that the statistical ap-
proach would show an improvement in classification
accuracy over the random approach; these results are
in line with that, but the increase is so small that it
would be better for the data publisher not to provide
frequency statistics with their anonymised data so that
it is better protected. We found similar results for Sce-
nario 3.
Algorithm Comparison
Here, we compare the results for the two modes of
the Mondrian algorithm. These results are compiled
from average classification accuracy over all QID
counts for the given k-value, disregarding the map-
ping method.
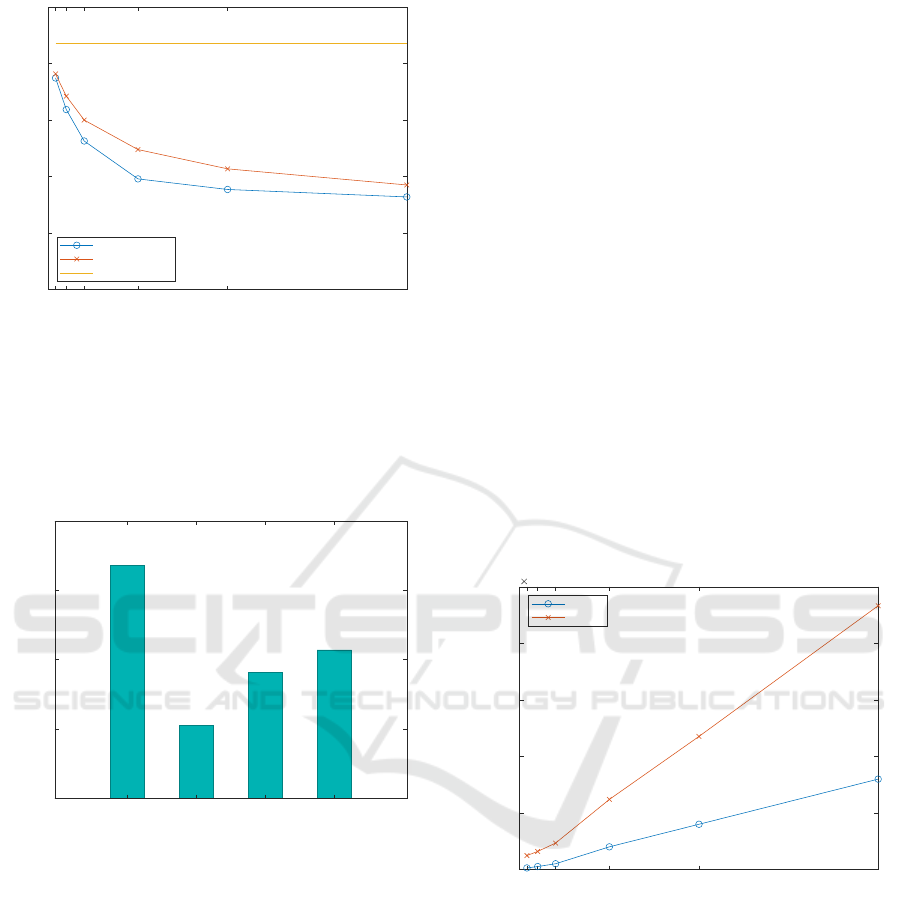
Figure 2 shows the comparison of algorithm
modes for Scenario 3. We see a minor improve-
ment for the strict algorithm over the relaxed. The
relaxed algorithm tends to result in anonymisations
with smaller ECs. Hence, for decision tree classifica-
tion, the size of ECs seem less of a factor than the size
and number of generalisations within.
The results for Scenarios 2 & 4 showed a negli-
gible difference between the two algorithm modes re-
garding classification accuracy. It would appear to be
a better choice for the publisher to opt for the strict
algorithm when the known use of the data is decision
tree classification.
Utility of Anonymised Data in Decision Tree Derivation
277
2 5 10 25 50 100
k
60
65
70
75
80
85
Classification Accuracy %
Relaxed
Strict
Non-Anonymised
Figure 2: Algorithm Mode Comparison - Scenario 3.
Scenario Comparison
To complete the classification accuracy results, we
compare the average classification accuracy of all
given scenarios described in Section 4.1.
1 2 3 4
Scenario
65
70
75
80
85
Avg. Classification Accuracy %
Figure 3: Scenario Classification Accuracy Comparison.
Figure 3 shows the average classification accuracy
by scenario, all else being equal. We can see more
clearly here the degradation in accuracy from classi-
fication where no anonymisation is used. These re-
sults highlight that degradation is expected when us-
ing anonymised data in decision tree classification;
however, it can be limited by restricting the use of
anonymised data to either the training or classifica-
tion phase only. This is particularly so in the case
described in Scenario 4.
5.2 Metric Correlation
This section will analyse the results from measure-
ments of the three well-established metrics tradition-
ally used in the literature to measure the effectiveness
and utility of anonymisations. As stated, the three
metrics measured were Discernability Metric, ILoss,
and Classification Metric. We took measurements for
each of these metrics on the same anonymised data
sets as used in the previous experiments, then tried to
establish a correlation between the metric measure-
ments and the corresponding classification accuracy
measurements.
Discernability Metric
Firstly, as an aside from the correlation results, Fig-
ure 4 shows a comparison of the Discernability Met-
ric (DM) penalty for the two modes of Mondrian al-
gorithm. It is notable that the strict algorithm showed
a much higher measured DM in all cases. As estab-
lished, DM is a measure of the size of equivalence
classes in an anonymisation. These measurements
provide evidence to show that the relaxed algorithm
results in smaller equivalence classes on average, ev-
erything else being equal. It is worth noting that the
disparity here is in contrast with Figure 2, where the
two modes of Mondrian were found showing only a
small difference in accuracy.
2 5 10 25 50 100
k
0
0.5
1
1.5
2
2.5
Discernability Penalty
10
7
Relaxed
Strict
Figure 4: Discernability Penalty - Algorithm Comparison.
Figure 5 shows a scatter graph illustrating the cor-
relation between the classification accuracy and the
DM for each scenario involving anonymisation. We
can see from these results that the correlation between
DM and classification accuracy is relatively mediocre
in all cases; ILoss and the Classification Metric show
much stronger correlations. Notably, the correlation
is clearly negative, indicating that an increase in DM
suggests a decrease in classification accuracy. How-
ever, the correlation is not strong enough for DM to be
considered a reliable estimator for classification accu-
racy in decision tree classification.
ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy
278
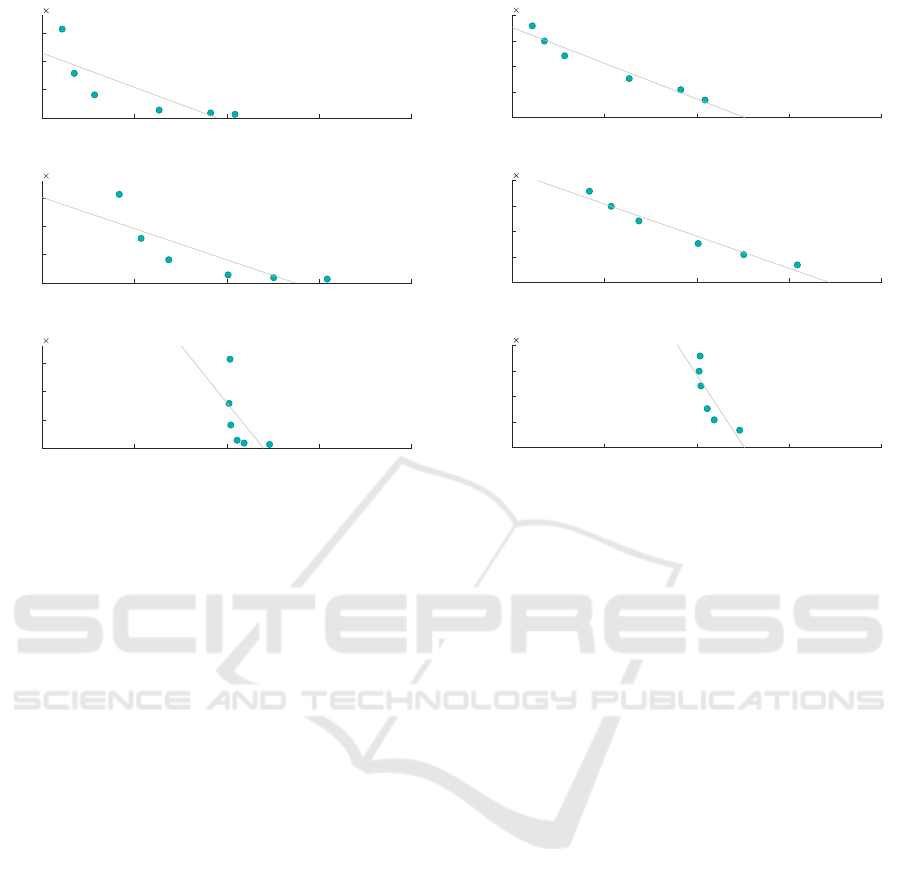
65 70 75 80 85
Classification Accuracy %
5
10
15
Discernability Penalty
10
6
Scenario 2
r = -0.81
65 70 75 80 85
Classification Accuracy %
5
10
15
Discernability Penalty
10
6
Scenario 3
r = -0.83
65 70 75 80 85
Classification Accuracy %
5
10
15
Discernability Penalty
10
6
Scenario 4
r = -0.58
Figure 5: Discernability Penalty / Classification Accuracy
Correlation.
ILoss
Similar to the previous subsection, Figure 6 shows the
correlation between the classification accuracy and
the ILoss.
In comparison to DM, we can see a much stronger
correlation between this metric and the measured
classification accuracy, with Scenarios 2 & 3 showing
an impressive correlation coefficient r of 0.98. This
would suggest that ILoss is a good estimator for clas-
sification accuracy in decision tree classification.
As discussed, ILoss considers individual records
when calculating the penalty, unlike DM which sim-
ply considers the size of the ECs containing said
records. Specifically, ILoss considers the size of gen-
eralisations in a given attribute compared to the do-
main of that attribute. The strong correlation shown
here would suggest that the number and relative size
of generalisations in an anonymisation has a greater
effect on classification accuracy than the size of ECs.
Classification Metric
Finally, we consider the Classification Metric (CM).
Figure 7 shows the correlation between the classifica-
tion accuracy and the CM penalty.
CM is a special purpose metric, designed to give
insight into the utility of an anonymisation in classi-
fication tasks. Therefore, we expected the correlation
shown here to be the strongest of the three metrics.
This is indeed the case, with the lowest correlation
65 70 75 80 85
Classification Accuracy %
0.5
1
1.5
2
ILoss
10
5
Scenario 2
r = -0.98
65 70 75 80 85
Classification Accuracy %
0.5
1
1.5
2
ILoss
10
5
Scenario 3
r = -0.98
65 70 75 80 85
Classification Accuracy %
0.5
1
1.5
2
ILoss
10
5
Scenario 4
r = -0.82
Figure 6: ILoss / Classification Accuracy Correlation.
coefficient being 0.95 in Scenario 4 - much higher
than with the other metrics tested. As with ILoss, CM
would appear to be a very reliable metric for estimat-
ing classification accuracy in decision tree classifica-
tion.
It is notable that for each metric, the correlation
in Scenario 4 is the weakest. This would seem to
be evidence for the suggestion that classification ac-
curacy is affected to a greater degree by anonymisa-
tion in the training of the decision tree, compared to
the classification of values using it. In Scenario 4,
anonymisation in the training part of the algorithm is
eliminated, and the classification results became more
stable whilst the metric measures showed a dispropor-
tionate change.
6 CONCLUSIONS
We can see from these results that you can expect the
anonymisation of data to be detrimental to the utility
regarding decision tree classification, but the magni-
tude of that detriment is minimal in most cases. Of
course, these results only relate to the ID3 decision
tree algorithm; more research is necessary to draw
general conclusions on machine learning tasks.
There are clear factors that affect the loss of util-
ity from anonymisation. Primarily, the scenario in
which the data is used and the value of k. We saw
that, generally, Scenario 4 had the best results in this
regard, although Scenario 3 was similar for the more
Utility of Anonymised Data in Decision Tree Derivation
279
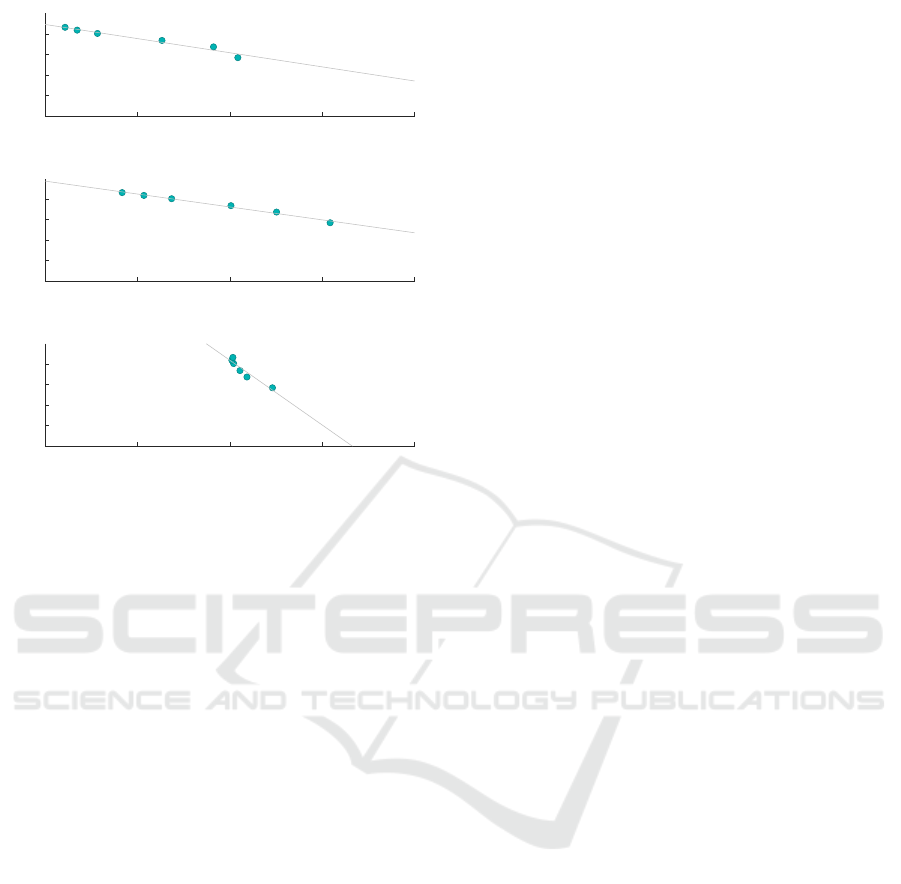
65 70 75 80 85
Classification Accuracy %
0
0.05
0.1
0.15
0.2
CM Penalty
Scenario 2
r = -0.98
65 70 75 80 85
Classification Accuracy %
0
0.05
0.1
0.15
0.2
CM Penalty
Scenario 3
r = -0.99
65 70 75 80 85
Classification Accuracy %
0
0.05
0.1
0.15
0.2
CM Penalty
Scenario 4
r = -0.95
Figure 7: Classification Metric / Classification Accuracy
Correlation.
commonly used values of k. Limiting the amount of
anonymisation where possible is therefore endorsed.
In addition, a value of k between 2 and 10 is generally
recommended based on these results. In most cases,
a value in this range would provide sufficient privacy,
whilst maintaining utility.
There appeared to be no benefit to using frequency
statistics to aid the mapping of generalised values
when building decision trees. Furthermore, there was
very little difference between the two modes of Mon-
drian algorithm – although the Strict mode performed
slightly better in some cases.
Data publishers who want to maximise the util-
ity of their data for classification could consider the
use of the ILoss Metric and Classification Metric to
provide an estimation of decision tree classification.
These metrics are easily calculated, and the evidence
provided in this paper suggests that they are reliable
estimators. By utilising these metrics to calibrate their
anonymisation parameters, data publishers can cer-
tainly provide more useful data to researchers without
compromising privacy.
REFERENCES
Ayala-Rivera, V., McDonagh, P., Cerqueus, T., and Murphy,
L. (2014). A systematic comparison and evaluation of
k-anonymization algorithms for practitioners. Trans-
actions on Data Privacy, 7(3):337–370.
Dua, D. and Graff, C. (2017). UCI machine learning repos-
itory. [http://archive.ics.uci.edu/ml]. Irvine, CA: Uni-
versity of California, School of Information and Com-
puter Science.
Emam, K. and Dankar, F. (2008). Protecting privacy using
k-anonymity. Journal of the American Medical Infor-
matics Association, 15:627–37.
Fung, B. C. M., Wang, K., Chen, R., and Yu, P. S. (2010).
Privacy-preserving data publishing: a survey of recent
developments. ACM Computing Surveys, 42(4):14:1–
14:53.
Iyengar, V. S. (2002). Transforming data to satisfy pri-
vacy constraints. In Proceedings of the Eighth
ACM SIGKDD International Conference on Knowl-
edge Discovery and Data Mining, page 279–288.
LeFevre, K., DeWitt, D. J., and Ramakrishnan, R. (2006).
Mondrian multidimensional k-anonymity. In Proceed-
ings of the 22nd International Conference on Data En-
gineering, pages 25–25.
Li, J., Liu, J., Baig, M. M., and Wong, R. C.-W. (2011).
Information based data anonymization for classifi-
cation utility. Data & Knowledge. Engineering.,
70(12):1030–1045.
Mitchell, T. (1997). Machine Learning, chapter 3. McGraw
Hill.
Quinlan, J. R. (1986). Induction of decision trees. Machine
Learning, 1:81–106.
Samarati, P. and Sweeney, L. (1998). Protecting privacy
when disclosing information: k-anonymity and its
enforcement through generalization and suppression.
Technical report.
Shao, J. and Beckford, J. (2017). Learning decision trees
from anonymized data. In 8th Annual International
Conference on ICT: Big Data, Cloud and Security.
Slowinski, R. (1992). Intelligent decision support: Hand-
book of applications and advances of the rough sets
theory.
Tang, Q., Wu, Y., Liao, S., and Wang, X. (2010). Utility-
based k-anonymization. In The 6th International Con-
ference on Networked Computing and Advanced In-
formation Management, pages 318–323.
Tao, Y. and Xiao, X. (2008). Personalized Privacy Preser-
vation, pages 461–485.
ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy
280
