
Semantic Attack on Disassociated Transactions
Asma AlShuhail and Jianhue Shao
Cardiff University, U.K.
Keywords:
Data Privacy, Semantic Attack, Transaction Data, Disassociation.
Abstract:
Publishing data about individuals is a double-edged sword; it can provide a significant benefit for a range
of organisations to help understand issues concerning individuals and improve services they offer. However,
it can also represent a serious threat to individuals’ privacy. To deal with these threats, researchers have
worked on anonymisation methods. One such method is disassociation which protects transaction data by
dividing them into chunks to hide sensitive links between data items. However, this method does not take into
consideration semantic relationships that may exist among data items, which can be exploited by attackers to
expose protected data. In this paper, we propose a de-anonymisation approach to attacking transaction data
anonymised by the disassociation method. Our approach attempts to re-associate disassociated transaction data
by exploiting semantic relationships among data items, and our findings show that the disassociation method
may not protect transaction data effectively: up to 60% of the disassociated items can be re-associated, thereby
breaking the privacy of nearly 70% of protected itemsets in disassociated transactions.
1 INTRODUCTION
Transaction data consists of a set of records, each
containing a set of terms or items. One example of
transaction data is given in Table 1, which contains
four records or transactions, each describing a set of
medical diagnoses and treatments for a patient.
Table 1: An Example of Transaction Data.
TID Items
1 vessel, blood, treatment, lung, catheterisation
2 cancer, radiotherapy, lung, treatment
3 cancer, lung, blood, tumor, biopsy
4 cancer, blood, treatment, tumor, biopsy
Transaction data can be collected from different
sources, such as social networks, e-commerce web-
sites or healthcare systems, and these data are often
published to third-party research and business organ-
isations to enable a wide range of data analyses. Al-
though this type of data publishing can help improve
service provisions by organisations and develop new
solutions that are otherwise not possible, one issue
must be addressed in doing so is the protection of pri-
vate and confidential information contained within the
datasets to be published. However, removing iden-
tifying information such as one’s national insurance
number from a dataset may not be sufficient to protect
individuals’ privacy because a combination of other
information available in de-identified data can still be
used to identify individuals.
Over the last two decades, much work has been
carried out by the research community to understand
how individuals’ privacy can be protected when the
data associated with them need to be published (Fung
et al., 2010). A range of methods have been pro-
posed to protect data privacy through anonymisation.
These methods aim to prevent intentional or uninten-
tional misuse of data by altering the data in such a
way that individuals and the sensitive information as-
sociated with them can no longer be identified directly
or indirectly (Rubinstein and Hartzog, 2016). Differ-
ent anonymisation methods exist, such as generalisa-
tion, suppression and perturbation, and they can be
applied to different types of data, for example, rela-
tional (El Emam and Dankar, 2008), text (Hedegaard
et al., 2009), graph (Cormode et al., 2010b) and trans-
action (Terrovitis et al., 2008)) data.
Transaction data is difficult to protect due to its
high dimensional nature. Using anonymisation meth-
ods such as generalisation or suppression to protect
them is likely to result in substantial information loss
(Terrovitis et al., 2012). The disassociation method
achieves protection for transaction data by break-
ing privacy threatening associations among the items,
rather than by generalising or suppressing them. It is
built on the k
m
-anonymity privacy model that states
that if an attacker has knowledge up to m items, they
cannot match their knowledge to fewer than k trans-
60
AlShuhail, A. and Shao, J.
Semantic Attack on Disassociated Transactions.
DOI: 10.5220/0010780500003120
In Proceedings of the 8th International Conference on Information Systems Security and Privacy (ICISSP 2022), pages 60-72
ISBN: 978-989-758-553-1; ISSN: 2184-4356
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

actions. In other words, the disassociation method
ensures that each combination of m items appears at
least k times in the released dataset. Using the disas-
sociation method, items in transactions are protected
by dividing them into groups such that the items in
each group satisfies the k
m
-anonymity requirement.
In this paper, we present a de-anonymisation ap-
proach to attacking transaction data anonymized by
the disassociation method, and we do so by exploit-
ing semantic relationships among the data items to
expose hidden links between them. We use some
well-established measures to score semantic relation-
ships and we heuristically re-construct original trans-
actions from disassociated ones. Our findings show
that the disassociation method may not protect trans-
action data effectively: up to 60% of the disassociated
items can be re-associated, thereby breaking the pri-
vacy of nearly 70% of protected itemsets in disasso-
ciated transactions.
The rest of the paper is organised as follows. In
Section 2, we discuss the work related to this paper. In
Section 3, we give a brief introduction to the disasso-
ciation method. In Section 4, we present our approach
to semantic attack and explain the two key steps of
our attacking approach. In Section 5, we illustrate
how chunks in disassociated dataset can be attacked
by proposing three hueristic strategies to re-construct
original transactions based on semantic relationships.
In Section 6, we report the experimental results. Fi-
nally, in Section 7, we conclude the paper.
2 RELATED WORKS
In recent years, privacy threats associated with releas-
ing data concerning individuals have been extensively
investigated, leading to identifying a variety of possi-
ble attacks on published data. One well-publicised
potential attack is linkage attack where an attacker
is assumed to be able to link a record in a dataset to
the record owner by using some external knowledge.
Sweeney (Sweeney, 2002) described an example of
linkage attack where records in a medical dataset pub-
lished by the Group Insurance Commission in Mas-
sachusetts were matched with the voters registration
list for Cambridge, Massachusetts. Despite the fact
that all the explicit identifiers in the medical dataset
have been removed, she was able to re-identify the
Governor of Massachusetts, William Weld, by link-
ing his data in the voters registration list to that in the
medical dataset.
Published data can also be attacked by inferences.
This type of attack occurs when an attacker can
deduce sensitive information that they do not have
access to from accessible non-sensitive information
published in the dataset by using a range of techniques
(Farkas and Jajodia, 2002). For example, data analy-
sis or data mining tools can be used to discover sen-
sitive patterns or correlations within data that violate
the privacy of individuals (Turkanovic et al., 2015),
(Clifton and Marks, 1996).
One advanced inference attack is the minimality
attack. In this type of attack, an attacker is assumed
to have knowledge of the anonymisation mechanism
used and the privacy requirements set to anonymise
a dataset. The attacker may obtain this knowledge
by examining the published dataset and the documen-
tation about the anonymisation algorithm, and then
uses this knowledge to break anonymity (Fung et al.,
2010), (Wong et al., 2007), (Cormode et al., 2010a),
(Zhang et al., 2007).
All types of attack described above rely on data
frequency to identify individuals and their associated
sensitive information from a published dataset. They
do not, however, exploit semantic relationships that
may exist among data items when attacking data pri-
vacy. Shao and Ong proposed a method for attacking
set-generalised transactions based on semantic rela-
tionships (Shao and Ong, 2017). To illustrate this type
of attack, consider the example given in Figure 1.
The original transactions in Figure 1 (a) have been
anonymised by a set-based generlisation (Loukides
et al., 2011) to produce the result shown in Figure
1 (b), where an item that does not occur frequent
enough is replaced by a set of items. Assuming that in
this case insulin, sneezing and petechiae are sensitive
items that need protection, they are generalised into
a set as shown in Figure 1 (b). As such, an attacker
will not know which sensitive item belongs to which
transaction. However, by exploiting semantic rela-
tionships, an attacker may establish that insulin has
stronger relationship with diabetes than other items in
transaction (1), hence it is more likely to be the orig-
inal item. This type of semantic attack can reduce
the “cover” through generalisation by removing some
items, as shown in Figure 1 (d), thereby violating in-
dividuals’ privacy.
This type of semantic attack depends on effective
assessment of the likelihood that two or more items
will occur together in a given context. A number of
tools in natural language processing (NLP) can be
used to understand and interpret semantic relation-
ships. For example, Sanchez et al. (Sánchez et al.,
2013) measure the semantic distance between terms
using point-wise mutual information (PMI) and use
the World Wide Web (WWW) as a corpus to find re-
lated terms (Bouma, 2009), (Sánchez et al., 2012),
(Staddon et al., 2007), (Chow et al., 2009). Chow
Semantic Attack on Disassociated Transactions
61

Figure 1: An example of semanitc attack.
et al. (Chow et al., 2008) use word co-occurrences on
the web as a part of their inference detection model to
predict what an attacker can infer and to detect unde-
sired inferences that may be derived from text.
3 DISASSOCIATION METHOD
To understand how our proposed de-anonymisation
method works, we briefly describe the Disassociation
method in this section. The disassociation method
is an anonymisation method that is designed to pro-
tect identities and sensitive information of individuals
contained in a published transaction dataset (Terrovi-
tis et al., 2012). Disassociation preserves the original
terms, but hides the fact that two or more infrequent
terms appear in the same transaction. In other words,
it protects the individuals’ privacy by disassociating
the transaction’s terms that participate in identifying
combinations to prevent an attacker from using those
infrequent combinations to identify individuals within
a published dataset.
Let W = {w
1
,... ,w
m
} be a finite set of words
called terms. A transaction T over W is a set of terms
T = {t
1
,t
2
,. .. ,t
k
}, where t
j
,1 ≤ j ≤ k, is a distinct
term in W . A transaction dataset D = {T
1
,T
2
,. .. ,T
v
}
is a set of transactions over W .
Definition 1 (k
m
-anonymity). If an adversary knows
up to m terms of a record, but cannot use this knowl-
edge to identify less than k candidate records in a
dataset, then the dataset is said to be k
m
-anonymous.
In other words, the k
m
-anonymity model guarantees
that each combination of m terms appears at least k
times in the dataset.
For example, if an attacker knows that a person
suffers from cancer and diabetes and this person’s
record is released in a 2
3
-anonymous dataset, then
the attacker will not be able to identify this person’s
record from less than 2 records.
Definition 2 (Disassociated transactions). Let D =
{T
1
,T
2
,. .. ,T
n
} be a set of transactions. Disassocia-
tion takes as an input D and results in an anonymised
dataset
ˆ
D, which groups transactions into clusters
ˆ
D = {P
1
,. .. ,P
z
}. Each cluster divides the terms
of the transactions into a number of record chunks
{C
1
,. .. ,C
s
} and a term chunk C
T
. The record chunks
contain the terms in an itemset form called sub-record
{SR
1
,SR
2
,. .. ,SR
v
} that satisfy k
m
-anonymity, while
the term chunk contains the rest of the terms of the
transactions.
The disassociation of transactions is achieved
through three steps:
Horizontal Partitioning. Transactions are separated
into groups called clusters. Horizontal partitioning
uses a recursive method to perform binary partition-
ing of the data into groups based on the frequency of
term occurrence in the dataset. The aim of the hor-
izontal partitioning step is to minimise information
loss: each cluster resulted from the partitioning will
have as few transactions and as many similar terms as
possible. This will lead to less disassociation among
the terms in the next step and enhance data utility.
Vertical Partitioning. The purpose of vertical parti-
tioning is to hide combinations of infrequent terms in
a cluster by disassociating them into chunks. It is per-
formed on each cluster independently. A cluster is di-
vided vertically into two types of chunks: record and
term chunks. The record chunks contain sub-records
of the original transactions and these sub-records sat-
isfy the k
m
-anonymity condition. This means that
each m-sized combination of terms needs to appear
at least k times in a record chunk. The term chunks
contain the terms that have not been placed in record
ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy
62

chunks. Each cluster can have a number of record
chunks but only one term chunk.
Refining. The aim of the refining step is to en-
hance the utility of published data while preserving
anonymisation. It targets term chunks and examines
the possibility of reducing the number of terms in the
term chunks by introducing joint clusters which are
shared across several clusters.
The reader is referred to (Terrovitis et al., 2012)
for more detailed description of the Disassociation
method. The example given in Tables 2 and 3 be-
low show the anonymised transactions produced by
the Disassociation method.
Table 2: Original Transactions.
ID Transactions
1
2
3
4
{vessel, blood, treatment, lung, catheterisation}
{cancer, radiotherapy, lung, treatment}
{cancer, lung, blood, tumor, biopsy}
{cancer, blood, treatment, tumor, biopsy}
Table 3: Disassociated Transactions.
Record Chunks Term Chunk
ID C1 C2 CT
1
2
3
4
{blood, treatment, lung}
{cancer, lung, treatment}
{cancer, lung, blood}
{cancer, blood, treatment}
{tumor, biopsy}
{tumor, biopsy}
{vessel,
catheterisation,
radiotherapy}
4 PROPOSED APPROACH
Our approach takes transactions anonymised by the
Disassociation method as input, and attempts to re-
construct original transactions by exploiting seman-
tic relationships that may exist among the data items.
Our attack consists of two steps. The first step, the
Scoring step, is to measure the semantic relation-
ships among the terms in a disassociated transactions.
The second step, the Selection step, uses the seman-
tic scores obtained from the first step to determine
heuristically which terms should be re-associated to
reconstruct original transactions.
4.1 Scoring Step
We use two measures, Normalised Google Distance
(NGD) (Cilibrasi and Vitanyi, 2007) and Word Em-
beddings (WE) (Pennington et al., 2014) in the Scor-
ing step to establish the strength of semantic rela-
tionships that exist among various groups of terms.
More specifically, we use the sub-records in the first
record chunk as an anchoring chunk, and measure
the semantic relationships between the terms in other
chunks and the terms in this anchoring chunk. The
pseudo code for the scoring step is provided in Algo-
rithm 1.
Algorithm 1: Scoring Step.
Input: Disassociated transactions
Output: Semantic relationship scores
1 for each cluster P do
2 for each record chunk RC of P do
3 for each sub-record SR of RC do
4 Calculate the semantic score
between SR and all sub-records in
C
1
by NGD or WE
5 scores
P
= scores
P
∪ scores
6 end
7 for each term t
i
in C
T
do
8 Calculate the semantic score
between t
i
and all sub-records in
C
1
9 scores
P
= scores
P
∪ scores
10 end
11 end
12 end
13 return scores
P
The algorithm is performed for each cluster P in
the disassociated dataset
ˆ
D. There are two different
types of chunks in a disassociated dataset: record
chunks (C
1
,C
2
,. .. ,C
n
) and a term chunk (C
T
), as
shown in Table 3. Each record chunk contains a num-
ber of sub-records (SR
1
,SR
2
,. .. ,SR
v
) and the term
chunk contains terms (t
1
,t
2
,. .. ,t
j
). For each sub-
record SR in record chunks from C
2
to C
n
and for each
term in C
T
, the algorithm uses NGD or WE to cal-
culate its semantic relationships with each sub-record
ASR in C
1
. All resulting scores are stored in scores
P
.
For example, for Table3, to calculate the semantic
score between the first sub-record (tumor, biopsy) in
C
2
and the first sub-record (blood, treatment, lung)
in C
1
using WE, we obtain three scores [0.47, 0.61,
0.84]. This step will be repeated for the other three
sub-records in C
1
, followed by calculating the seman-
tics scores between each term vessel, catheterisation,
radiotherapy in C
T
and the four sub-records in C
1
.
4.2 Selection Step
The Selection step aims to reconstruct original trans-
actions from disassociated ones by re-associating the
sub-records in the record chunk and the terms in the
term chunk based on the semantic scores obtained
from the Scoring step. Algorithm 2 shows how the
Selection step is performed, and we defer the discus-
Semantic Attack on Disassociated Transactions
63

sion on the three heuristic reconstruction methods we
propose to the following section.
Algorithm 2: Selection Step.
Input: Disassociated transactions, Semantic
relationship scores
Output: Reconstructed transactions
1 for each cluster P do
2 for each record chunk RC do
3 for each sub-record SR
i
in RC do
4 ASR
k
= Reconstruction (SR
i
)
5 Update ASR
k
in C
1
with RS
i
6 end
7 end
8 for each Term t
i
in C
T
do
9 ASR
k
= Reconstruction (t
i
)
10 Update ASR
k
in C
1
with t
i
11 end
12 Rec
P
= Reconstructed transactions of P
13 end
14 return Rec
P
The algorithm is applied to each cluster P inde-
pendently. For each record chunk from C
2
to C
n
in P,
a reconstruction method is preformed for each sub-
record RS
i
in a record chunk (steps 3 and 4). This will
find the best ASR
i
in C
1
for RS
i
, and the correspond-
ing sub-record in C
1
will then be extended with RS
i
(step 5). The reconstruction for the terms in the term
chunk C
T
is performed similarly (steps 8-10). After
all the sub-records in record chunks and the terms in
the term chunk have been processed, the transactions
are deemed to be reconstructed, and the reconstructed
transactions returned in step 14.
5 RECONSTRUCTION METHODS
In this section, we illustrate how record and
term chunks can be attacked. We propose three
heuristic strategies, averaging-based attack (ABA),
most-related attack (MRA) and related-group attack
(RGA), that use semantic scores to reconstruct the
original transactions from the terms and sub-records
in disassociated transactions.
In disassociated transactions, each sub-record
ASR
i
in the anchoring chunk needs to be completed
by combining its terms from other chunks to recon-
struct the original transaction. Hence, the terms in the
sub-records in the anchoring chunk are used as a base
to assemble the original transactions. In the follow-
ing, we explain how the record and term chunks will
be attacked.
• Attacking Record Chunks
In general, to perform an attack on record chunks,
the scoring step is executed first for each cluster P
of the dataset, where a semantic relationship cal-
culation is performed on the anchoring chunk C
1
and a chunk from C
2
to C
n
. After that, the se-
lection step is applied. To attack record chunks,
only the ABA method is used. This is because the
sub-records in record chunks usually have more
than one term. Each term in one sub-record could
have different levels of semantic relatedness with
another sub-record. Therefore, using the MRA
and RGA strategies may not capture the seman-
tic score properly between two sub-records. As a
result, the MRA and RGA strategies are not used
in attacking record chunks.
• Attacking Term Chunk
Unlike record chunks, the term chunk of a cluster
contains single terms. These terms have support
of less than k, and they are protected by placing
them in the term chunk so that no terms can be
linked to fewer transactions than the size of the
cluster. To perform the attack on the term chunk,
the scoring step is first executed for each cluster P
in the disassociated dataset between each term in
the term chunk and all sub-records in the anchor-
ing chunk. After that, the selection step is applied.
For term chunks that are attacked, all strategies
are used.
5.1 Averaging-Based Attack (ABA)
This strategy assumes that all the terms in one trans-
action are about the same context, which means that
they should have similar semantic relatedness. There-
fore, all the terms in the sub-records from the anchor-
ing chunk should be included in the selection step.
In other words, to find the correct sub-record ASR in
C
1
for a sub-record SR or term t in other chunks, the
semantic scores for all terms in ASR
i
are considered.
That is, this strategy selects the best semantically re-
lated sub-record based on the average of the terms in
ASR.
The pseudocode of the ABA strategy is provided
in Algorithm 3. The algorithm is run for each input
sub-record or term that needs to be re-associated. For
each sub-record ASR in the anchoring chunk, the aver-
age score of all the semantic relationships scores be-
tween the terms in SR or t and all the terms in ASR
is calculated (steps 1 and 2). After this, based on the
averages, the sub-records in the anchoring chunk are
arranged from the most to least related in N (step 4). If
the input is a sub-record SR, then the algorithm calcu-
lates the count of how many sub-records there are in
ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy
64
a record chunk (step 6). Based on the count, the algo-
rithm returns the number of most related sub-records
ASR (step 8). If the input is a term t, then the algo-
rithm can return k − 1 of the most related sub-records
ASR from the list (steps 11 to 13).
Algorithm 3: ABA.
Input: C
1
, SR or t, k
Output: Chosen ASR
i
1 for each sub-record ASR
i
in C
1
do
2 Calculate the average score of the total
semantic relationships scores for SR or t
3 end
4 Arrange sub-records of C
1
based on the average
in list N
5 if the input is SR then
6 Find the SR count
7 for i = 1 to count do
8 return The top ASR
i
in N
9 end
10 end
11 if the input is t then
12 for i = 1 to k − 1 do
13 return The top ASR
i
in N
14 end
15 end
To illustrate this type of attack, consider the exam-
ple of disassociated transactions in Table 3. The ex-
ample in Table 3 contains one cluster with two record
chunks and a term chunk. To attack this cluster, the
sub-records SR in the second record chunk C2 and
each term in the term chunk need to be re-associated
with C
1
. As a first step, the attack applies the scoring
step to obtain all the semantic relationship scores be-
tween the terms in different chunks by the WE seman-
tic measure. Table 4 is the resulting semantic scores
from the scoring step for the cluster in Table 3.
Table 4: The semantic scores.
Terms in C1 Terms in C2 Terms in CT
tumor biopsy vessel catheterisation radiotherapy
blood 0.20 0.27 0.17 0.25 0.08
treatment 0.27 0.34 0.16 0.37 0.48
lung 0.48 0.36 0.18 0.36 0.33
cancer 0.63 0.44 0.11 0.20 0.51
The ABA method considers the terms in a trans-
action to be semantic related to each other, for ex-
ample, the terms in a transaction describing one dis-
ease. Therefore, the ABA calculates the average of
the semantic relationship scores between a term or
sub-record from different chunks and all the terms of
the sub-records in the anchoring chunk by applying
Equation 1.
ABA(ASR, SR) =
∑
n
i=1
∑
x
i=1
(SC)
|x|
|n|
(1)
where SC is the semantic scores between ASR and SR,
x is the number of terms in SR, and n is the number of
terms in ASR.
For example, to find the the average semantic
score between the two sub-records ASR (blood, treat-
ment, lung) and SR (tumor, biopsy), ABA will calcu-
late its semantic relatedness as follows.
ABA(ASR, SR) =
(0.27 + 0.61 + 0.84)/6
3
= 0.316
The similarity scores obtained by the ABA dis-
tances for all chunks are shown in Table 6, and the
reconstructed transactions are given in Table 5.
Table 5: Reconstructed transactions (ABA).
ID Transactions
1
2
3
4
{blood, treatment, lung, vessel, catheterisation}
{cancer, lung, treatment, tumor, biopsy, radiotherapy}
{cancer, lung, blood, tumor, biopsy}
{cancer, blood, treatment}
As can be seen, ABA reconstructed the original
transactions correctly, except for the last transaction.
This means that some combinations terms, such as
(vessel, catheterisation), are exposed. It is worth not-
ing however that although ABA is effective in recon-
structing transactions as shown in this example, the
assumption that all terms in a single transaction are
semantically connected to each other may not hold
true for all transactions.
5.2 Related-Group Attack (RGA)
In some datasets, a transaction may contain more than
one context. For example, a patient’s medical record
may describe two unrelated diseases. In such cases,
considering all the terms of ASR from C
1
may include
unrelated terms in semantic calculation, which can af-
fect the accuracy of final score, resulting in the term t
or sub-record SR being added to a wrong transaction.
The RGA strategy considers a situation where
terms may come from multiple contexts in the selec-
tion step. In other words, a term t or sub-record SR
from different chunks can be closely related only to
some terms, but not others, in a sub-record ASR in the
anchoring chunk. This makes it unreasonable to treat
all terms equally when determining which transaction
is the best for combination in the selection step.
In the RGA strategy, we assume that the terms
of one sub-record ASR in the anchoring chunk can
Semantic Attack on Disassociated Transactions
65

Table 6: ABA results for Example 3.
Record Chunks Term Chunk
ID C1 C2 CT
tumor, biopsy vessel catheterisation radiotherapy
1 blood, treatment, lung 0.316 0.170 0.326 0.296
2 cancer, lung, treatment 0.416 0.150 0.310 0.440
3 cancer, lung, blood 0.393 0.153 0.270 0.306
4 cancer, blood, treatment 0.353 0.146 0.273 0.356
be divided into at least two contexts. Therefore, af-
ter applying the scoring step, the RGA strategy finds
the median semantic relationship score between each
t or SR that needs to be associated and the sub-record
ASR in the anchoring chunk, and uses this value as
a division indicator. Based on this division indica-
tor, the terms in each ASR in the anchoring chunk are
divided into two groups. The first group is the re-
lated group which contains the terms that are seman-
tically close to the disassociated t or SR, while the
other group is the unrelated group which contains the
rest of the terms. After that, only the semantic rela-
tionship scores for the terms in the related group will
be considered when conducting the selection step.
The pseudocode for the RGA strategy is illus-
trated in Algorithm 4. The algorithm is executed to re-
combine disassociated terms or sub-records. For each
sub-record ASR in the anchoring chunk, the division
indicator between terms in SR or t and all the terms
in ASR are calculated (steps 1 and 2). Based on the
division indicator, the terms in ASR in the anchoring
chunk are divided into two groups: related group RG
and unrelated NG (line 3). Only the terms in the re-
lated group RG are included in the semantic calcula-
tion for ASR, and the average of the semantic relation-
ship scores for terms in RG will be calculated (step 4).
After that, based on the averages, the sub-records in
the anchoring chunk are arranged from the most to
least related in a list N (step 6). For sub-records SR,
the algorithm returns the number of most related sub-
records ASR (step 10). For term t, the algorithm can
return k− 1 most related sub-records ASR (steps 13 to
15).
To illustrate how the RGA strategy works, we ap-
ply it to Example 3. To find the division indicator, we
use Equation 2.
Div
i
(SC) =
(
SC
n+1
2
if n is odd
(
SC
[
n
2
]
+SC
[
n
2
+1
])
2
if n is even
(2)
where SC is the ordered list of semantic scores for
terms of ASR and n is the number of terms in ASR.
For example, to find the division indicator of the
semantic scores SC (0.08, 0.33, 0.48) for the first ASR
(blood, treatment, lung) and t (radiotherapy), RGA
Algorithm 4: RGA.
Input: C
1
, SR or t, k
Output: Chosen ASR
i
1 for each sub-record ASR
i
in C
1
do
2 Calculate the division indicator for SR or t
3 Divide terms into RG and NG based on the
division indicator value
4 Calculate the average semantic score for
RG
5 end
6 Arrange sub-records of C
1
based on the average
in list N
7 if the input is SR then
8 Find the SR count
9 for i = 1 to count do
10 return The top ASR
i
in N
11 end
12 end
13 if the input is t then
14 for i = 1 to k − 1 do
15 return The top ASR
i
in N
16 end
17 end
performs the calculation shown in Equation 3.
Div
i
(SC) = SC
3 + 1
2
= 0.33 (3)
As the division indicator for the first SR is 0.33, the
term blood is excluded from the semantic score calcu-
lation because the semantic score between blood and
radiotherapy is 0.08, which is less than the division
indicator. Consequently, blood is placed in the unre-
lated group. Based on the related group, we obtain the
resulting average semantic scores between chunks as
shown in Table 7.
Based on the semantic scores, the reconstructed
transactions are produced as shown in Table 8. As can
be seen, RGA reconstructed the original transactions
correctly, except for transaction 4, where separating
terms into two contexts did not help. Therefore, this
strategy would work better with sub-records that con-
tain many terms which are likely to include more than
one context.
ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy
66
Table 7: RGA results for example 3.
Record Chunks Term Chunk
ID C1 C2 CT
tumor, biopsy vessel catheterisation radiotherapy
1 blood, treatment, lung 0.360 0.175 0.365 0.405
2 cancer, lung, treatment 0.475 0.170 0.365 0.495
3 cancer, lung, blood 0.475 0.175 0.305 0.420
4 cancer, blood, treatment 0.415 0.165 0.31 0.490
Table 8: Reconstructed transactions (RGA).
ID Transactions
1
2
3
4
{blood, treatment, lung, vessel, catheterisation}
{cancer, lung, treatment, tumor, biopsy, radiotherapy}
{cancer, lung, blood, tumor, biopsy}
{cancer, blood, treatment}
5.3 Most-Related Attack (MRA)
The MRA strategy focuses on the strongest semantic
relationship between two sets of terms. With the RGA
strategy, the terms in the related group may not have
the same semantic relationship strength for a term or
sub-record. This is because the terms in that trans-
action can describe more than one context. Hence,
the MRA strategy finds the term with the strongest
semantic relationship to determine which ASR is the
most related one for combining a term t or sub-record
SR. In highly sparse datasets, the semantic relation-
ships between terms become more distinct, increas-
ing the chance to have more distinct semantic scores.
Therefore, for each term t or sub-record SR, the MRA
strategy arranges the terms of ASR from the most re-
lated to the least in a list. Then, it will include only the
most related term in each ASR. After that, the strategy
will add t or SR that has have the best semantic score
to ASR.
The pseudocode for the MRA strategy is provided
in Algorithm 5. For each sub-record ASR in the an-
choring chunk, the MRA finds the best score from all
the semantic relationships between the terms in SR or
t and all the terms in ASR (steps 1 and 2). After that,
based on the best score in each sub-record in the an-
choring chunk, the sub-records are arranged from the
most to least related in a list (step 4). For sub-records
SR, the algorithm returns the number of most related
sub-records ASR (steps 5 to 8) based on the count of
how many of this sub-record SR is in a record chunk.
For term t, the algorithm can return k −1 most related
sub-records ASR from the list N (steps 11 to 13).
To illustrate how MRA works, Table 10 shows the
semantic scores between chunks after applying it to
example 3. The MRA strategy includes just the term
with the closest semantic relationship to determine the
best ASR for combining the term t or sub-record SR.
For example, when using MRA to determine term ra-
Algorithm 5: MRA.
Input: C
1
, SR or t, k
Output: Chosen ASR
i
1 for each sub-record ASR
i
in C
1
do
2 Find the best score in the semantic
relationships for SR or t
3 end
4 Arrange sub-records of C
1
based on the best
scores in list N
5 if the input is SR then
6 Find the SR count
7 for i = 1 to count do
8 return The top ASR
i
in N
9 end
10 end
11 if the input is t then
12 for i = 1 to k − 1 do
13 return The top ASR
i
in N
14 end
15 end
diotherapy from the term chunk, the term treatment in
C
1
has the strongest semantic relationship with it. so
the sub-records that contain treatment will be consid-
ered for adding radiotherapy to them.
The result of the MRA attack is shown in Table 9.
Most of original transactions have been reconstructed
correctly. This method works well when there is a
clear pair of terms that can determine the semantic re-
lationship between parts of disassociated transactions,
effectively cancelling noise from other terms.
Table 9: Reconstructed transactions (MRA).
ID Transactions
1
2
3
4
{blood, treatment, lung, vessel, catheterisation}
{cancer, lung, treatment, tumor, biopsy, radiotherapy}
{cancer, lung, blood, tumor, biopsy}
{cancer, blood, treatment}
Semantic Attack on Disassociated Transactions
67

Table 10: MRA results for Example 3.
Record Chunks Term Chunk
ID C1 C2 CT
tumor, biopsy vessel catheterisation radiotherapy
1 blood, treatment, lung 0.42 0.18 0.37 0.48
2 cancer, lung, treatment 0.53 0.18 0.37 0.51
3 cancer, lung, blood 0.53 0.18 0.36 0.51
4 cancer, blood, treatment 0.53 0.17 0.37 0.51
6 EXPERIMENTAL EVALUATION
6.1 Experimental Settings
Datasets. In our experments, we use real-world
datasets collected from Ezinearticles.com. This
source contains hundreds of thousands of articles. To
construct our datasets, we have chosen about 1000
articles in different topics with a varying number of
keywords to form transactions.
Parameters. We tested the performance of our
methods by varying the following parameters: (a) the
k value from 2 to 5, (b) data density ranging from 0.2
to 0.7, and (c) the max cluster size from k
2
to k
6
.
Evaluation Measures. We used two measures in
our experiments. The first one measures transaction
breakage and k
m
-anonymity breakage. In transaction
breakage, we calculate how many transactions’ pro-
tection is broken by correctly re-associating at least
one correct term to them. k
m
-anonymity breakage
calculates how many infrequent itemsets (i.e. hav-
ing a support of less than k) are exposed after re-
association. The second measurement assesses how
much of the original transactions are correctly re-
constructed from the disassociated dataset. We used
accuracy and Word Mover’s distance for this. The
accuracy measures the proportion of correct recon-
structions, and the Word Mover’s Distance measures
the quality of reconstruction by finding the semantic
distance between the original dataset and the recon-
structed dataset as a whole.
6.2 Experimental Results
In Figure 2a, we show the efficacy of our algorithms
with varying k values with the max cluster size fixed
at 5
2
. k is used as a privacy constraint that needs to
be satisfied in the disassociated dataset. Increasing k
means increasing the level of protection, which usu-
ally results in pushing more terms into term chunks
and sub-records in the record chunks become more
indistinguishable. In terms of accuracy, the effect
of increasing k makes the anonynisation more break-
able. This is due to two reasons. First, because the
number of transactions in a cluster is increased in
order to satisfy the k
m
-anonymity requirement, the
number of sub-records in the anchoring chunks that
have the same semantic relationship scores increase
as well. This reduces the chance of choosing a wrong
sub-record when associating a term. Second, when
there is a large number of identical sub-records in
the anchoring chunk is, any sub-record that is cho-
sen for adding a term to it will be correct. Note
that when increasing k, the difference between our
methods and the random attack (which is our baseline
method that re-construct the transactions randomly)
becomes smaller. This is because the sub-records in
the anchoring chunk become almost identical, so the
difference between semantic relationships scores be-
comes insignificant.
In Figure 2a we can see a clear upward trend in
accuracy percentage, reaching over 90% of the re-
constructed sub-records and the terms being correct.
The algorithm’s effectiveness in re-associating sub-
records and terms increases with k, even for the ran-
dom attack. Also, it can be seen in Figure 2a that
ABA with both NGD and WE measures has the best
performance with different k values; this is because
of the density level of the dataset. The density level
is fixed at 0.30 in this experiment, which is relatively
dense. With a dense dataset, considering all the terms
from the anchoring chunk in the selection step is more
effective in determining the semantic relatedness be-
tween chunks.
Figure 2b illustrates the reconstruction extent in
terms of reconstructing the entire transactions cor-
rectly from original dataset. In general, the semantic
distance between the reconstructed and the original
transaction is increased with an increasing k value for
the random attack, while it is slightly decreased for
other semantic attack methods when k ≤ 4. The num-
ber of terms in the anchoring chunk can affect the
WMD measure: larger numbers mean less terms in
different chunks that need to be re-associated and that
less semantic distance is needed between the terms
in both the original and reconstructed transactions.
ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy
68
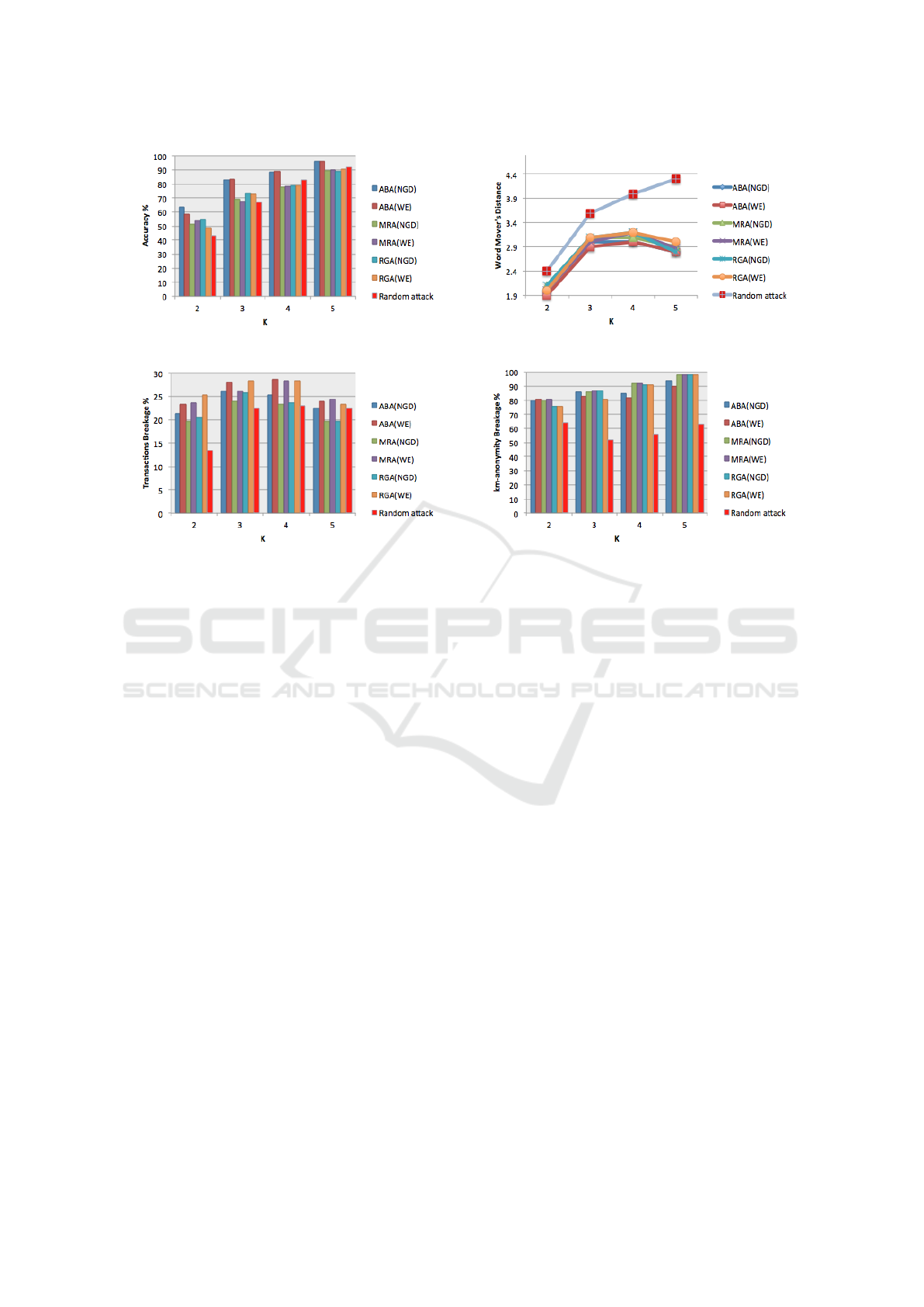
(a) Accuracy (b) WMD
(c) Transaction breakage (d) k
m
-anonymity breakage
Figure 2: The effect of k on attacking methods.
Therefore, when k is increased, the number of terms
in the anchoring chunk decreased and the semantic
distance started to increase. However, semantic at-
tack methods maintained a low WMD with increasing
k compared with the random attack attack.
In Figure 2c we can see the effectiveness of our
algorithms in terms of transaction breakage. Overall,
the breakage rate is around 25% for all k values. How-
ever, an increasing value of k has a different effect on
attacking record chunks and term chunks. Attacks on
record and term chunks have opposite trends for trans-
action breakage when k increases. This explains the
fluctuating trend of the overall transaction breakage
with different k values.
Figure 2d shows the impact of increasing k val-
ues on attacking the protected infrequent itemsets in
the disassociated dataset. It can be seen that the
breakage percentage increases with k. In general, a
higher k means that more infrequent itemsets would
have been protected. However, because we associate
terms based on the semantic relationships in our se-
mantic attack methods, the increase in the number of
protected itemsets means a greater chance of finding
more infrequent itemsets.
The result in Figure 3a compares the accuracy of
our algorithms when applied to datasets with differ-
ent density levels: a dataset with a higher density will
have less distinct terms in it. In general, the accu-
racy greatly increases as the density level decreases
for most attacking methods. This is because decreas-
ing density would increase sparsity for a dataset, i.e.
there will be more distinct terms and more varied se-
mantic relationships in a dataset. Note also that NGD
uses the WWW as a corpus to find the semantic rela-
tionships. Therefore, the NGD measure can find the
semantic score for any term in a dataset. On the con-
trary, the WE measure will be limited by the trained
corpus. This shows that when increasing the sparsity
level, the methods using NGD as a semantic measure
perform better than the same methods that using the
WE measure in Figure 3a.
Figure 3b describes the reconstruction of correct
transactions. For our semantic attack methods, the
density level does not have a strong effect on the full
reconstruction, and the results fluctuated between 2.5
and 3.
The results of transaction breakage are presented
in Figure 3c. The breakage level for all attacking
methods improves when the sparsity level increases
until 0.5, at which point it starts to decrease. This is
because after 0.5, the number of sub-records or terms
that have a frequency greater than k drops. In other
words, the number of terms inside the record chunks
decreased.
Figure 3d shows the overall k
m
-anonymity break-
age for the attacking methods with different data den-
Semantic Attack on Disassociated Transactions
69
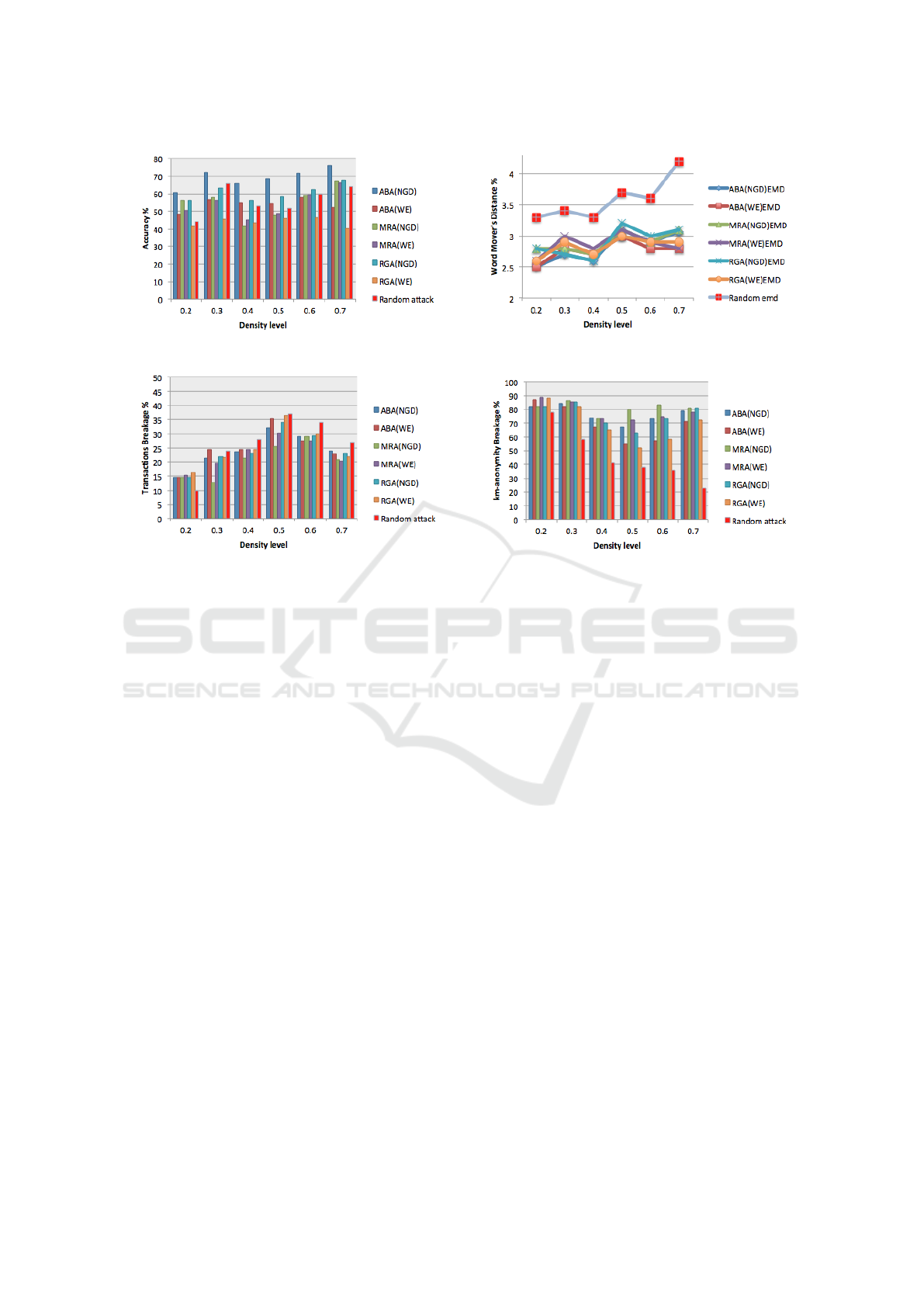
(a) Accuracy (b) WMD
(c) Transaction breakage (d) k
m
-anonymity breakage
Figure 3: The effect of data density on attacking methods.
sity levels. In general, the difference between the
performances of attacking methods becomes clearer
when the density is lower. This is because sparse
datasets will have more diversity of semantic relation-
ships, hence it helps to determine which terms need to
be included from anchoring chunks, and which has an
effect on the total semantic scores, thereby affecting
the reconstruction.
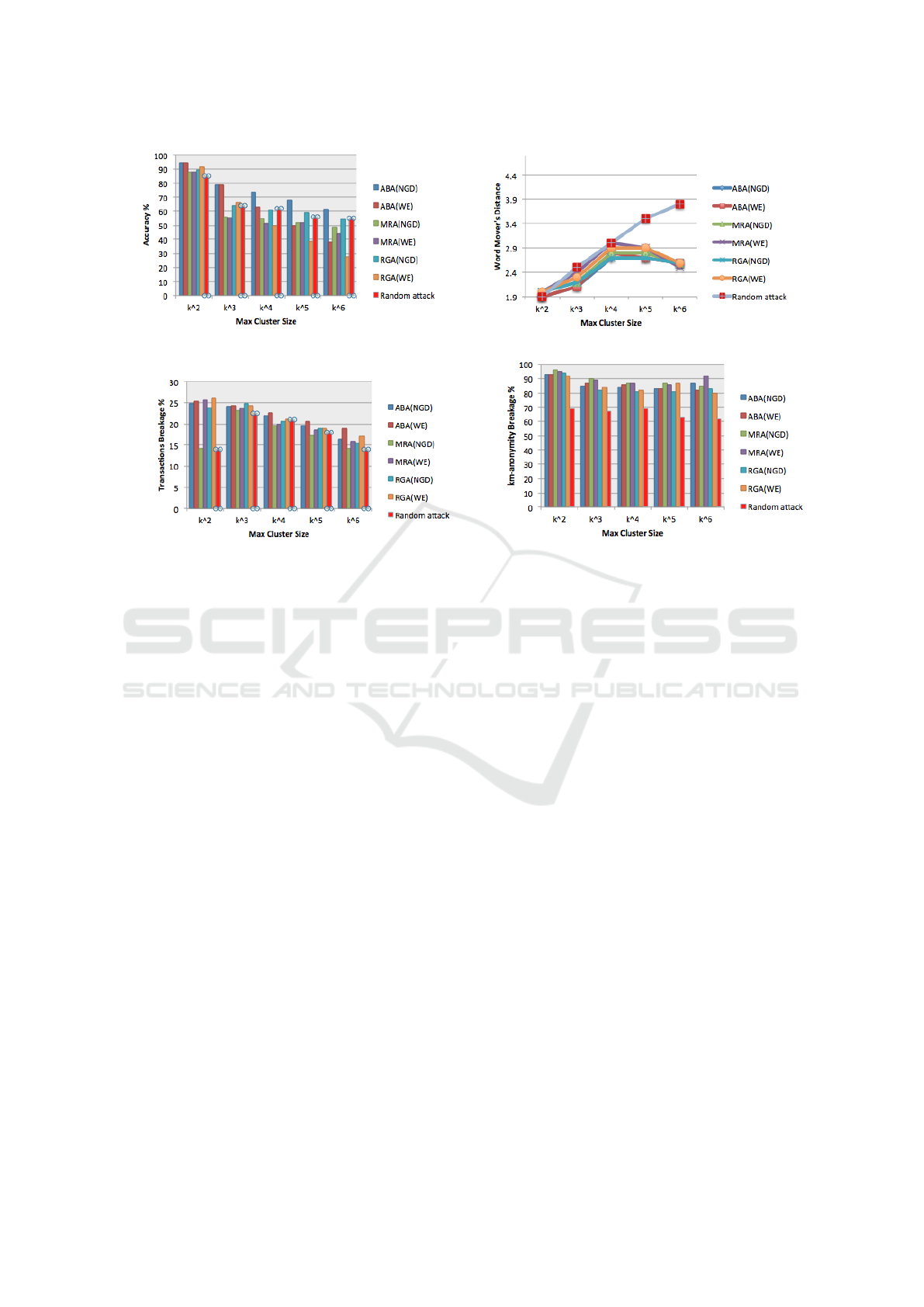
Figure 4a compares the accuracy of our algo-
rithms with various max cluster sizes. In general,
larger sizes allow for more transactions in a cluster,
and this negatively affects the accuracy of all attack-
ing methods. This is because the chance to associate
terms with wrong sub-records increases.
The extent of reconstruction in terms of propor-
tion of reconstruction for the original transactions is
illustrated in Figure 4b. With an increase in cluster
size, the reconstructed transactions become semanti-
cally less similar to the original transactions. In larger
clusters, the number of transactions is large, increas-
ing the possibility of incorrectly combining terms into
sub-records.
In Figure 4c, we evaluate the effectiveness of our
attacking methods on transaction breakage. Note that
increasing clusters size has different impacts on at-
tacking record chunks and term chunks.
Figure 4d illustrates the overall k
m
-anonymity
breakage of the attacking methods with different max
cluster sizes. As mentioned earlier, larger sizes allow
for more transactions in a cluster, hence affecting the
performance of all methods, and we observe that the
breakage percentage decreases slightly as the cluster
size increases.
7 CONCLUSIONS
In this paper, we have studied the effectiveness of
the Disassocation method when used to protect trans-
action data. We have proposed a de-anonymisation
approach that aims to expose the hidden links be-
tween items in a disassociated dataset. In our attack
approach, we have exploited semantic relationships
between items in a anonymised transaction dataset
and have used such semantic information to recon-
struct the original transactions. Our semantic at-
tack approach can reconstruct different chunks with
around 60% accuracy and can break over 70% of pro-
tected itemsets. This illustrates that the disassociation
method may not be safe enough to protect transac-
tion data if semantic relationships among the terms
are considered.
ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy
70
(a) Accuracy (b) WMD
(c) Transaction breakage (d) k
m
-anonymity breakage
Figure 4: The effect of max cluster size on attacking methods.
REFERENCES
Bouma, G. (2009). Normalized (pointwise) mutual in-
formation in collocation extraction. Proceedings of
GSCL, pages 31–40.
Chow, R., Golle, P., and Staddon, J. (2008). Detecting pri-
vacy leaks using corpus-based association rules. In
Proceedings of the 14th ACM SIGKDD international
conference on Knowledge discovery and data mining,
pages 893–901.
Chow, R., Oberst, I., and Staddon, J. (2009). Sanitization’s
slippery slope: the design and study of a text revision
assistant. In Proceedings of the 5th Symposium on
Usable Privacy and Security, pages 1–11.
Cilibrasi, R. L. and Vitanyi, P. M. (2007). The google simi-
larity distance. IEEE Transactions on knowledge and
data engineering, 19(3):370–383.
Clifton, C. and Marks, D. (1996). Security and privacy im-
plications of data mining. In ACM SIGMOD Work-
shop on Research Issues on Data Mining and Knowl-
edge Discovery, pages 15–19. Citeseer.
Cormode, G., Srivastava, D., Li, N., and Li, T. (2010a).
Minimizing minimality and maximizing utility: an-
alyzing method-based attacks on anonymized data.
Proceedings of the VLDB Endowment, 3(1-2):1045–
1056.
Cormode, G., Srivastava, D., Yu, T., and Zhang, Q. (2010b).
Anonymizing bipartite graph data using safe group-
ings. the VLDB Journal, 19(1):115–139.
El Emam, K. and Dankar, F. K. (2008). Protecting privacy
using k-anonymity. Journal of the American Medical
Informatics Association, 15(5):627–637.
Farkas, C. and Jajodia, S. (2002). The inference problem:
a survey. ACM SIGKDD Explorations Newsletter,
4(2):6–11.
Fung, B. C., Wang, K., Chen, R., and Yu, P. S. (2010).
Privacy-preserving data publishing: A survey of re-
cent developments. ACM Computing Surveys (Csur),
42(4):1–53.
Hedegaard, S., Houen, S., and Simonsen, J. G. (2009). Lair:
A language for automated semantics-aware text saniti-
zation based on frame semantics. In 2009 IEEE Inter-
national Conference on Semantic Computing, pages
47–52. IEEE.
Loukides, G., Gkoulalas-Divanis, A., and Malin, B.
(2011). Coat: Constraint-based anonymization of
transactions. Knowledge and Information Systems,
28(2):251–282.
Pennington, J., Socher, R., and Manning, C. D. (2014).
Glove: Global vectors for word representation. In
Proceedings of the 2014 conference on empirical
methods in natural language processing (EMNLP),
pages 1532–1543.
Rubinstein, I. S. and Hartzog, W. (2016). Anonymization
and risk. Wash. L. Rev., 91:703.
Sánchez, D., Batet, M., and Viejo, A. (2012). Detect-
ing sensitive information from textual documents: an
information-theoretic approach. In International Con-
Semantic Attack on Disassociated Transactions
71

ference on Modeling Decisions for Artificial Intelli-
gence, pages 173–184. Springer.
Sánchez, D., Batet, M., and Viejo, A. (2013). Detecting
term relationships to improve textual document sani-
tization. In PACIS, page 105.
Shao, J. and Ong, H. (2017). Exploiting contextual in-
formation in attacking set-generalized transactions.
ACM Transactions on Internet Technology (TOIT),
17(4):40.
Staddon, J., Golle, P., and Zimny, B. (2007). Web-based
inference detection. In USENIX Security Symposium.
Sweeney, L. (2002). k-anonymity: A model for protecting
privacy. International Journal of Uncertainty, Fuzzi-
ness and Knowledge-Based Systems, 10(05):557–570.
Terrovitis, M., Liagouris, J., Mamoulis, N., and Skiadopou-
los, S. (2012). Privacy preservation by disassociation.
arXiv preprint arXiv:1207.0135.
Terrovitis, M., Mamoulis, N., and Kalnis, P. (2008).
Anonymity in unstructured data. In Proc. of Interna-
tional Conference on Very Large Data Bases (VLDB).
Turkanovic, M., Druzovec, T. W., and Hölbl, M. (2015).
Inference attacks and control on database structures.
TEM Journal, 4(1):3.
Wong, R. C.-W., Fu, A. W.-C., Wang, K., and Pei, J. (2007).
Minimality attack in privacy preserving data publish-
ing. In Proceedings of the 33rd international confer-
ence on Very large data bases, pages 543–554.
Zhang, L., Jajodia, S., and Brodsky, A. (2007). Informa-
tion disclosure under realistic assumptions: Privacy
versus optimality. In Proceedings of the 14th ACM
conference on Computer and communications secu-
rity, pages 573–583.
ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy
72
