
Expert-guided Symmetry Detection in Markov Decision Processes
Giorgio Angelotti,
1,2
Nicolas Drougard
1,2 a
and Caroline P. C. Chanel
1,2 b
1
ISAE-SUPAERO, University of Toulouse, France
2
ANITI, University of Toulouse, France
Keywords:
Offline Reinforcement Learning, Batch Reinforcement Learning, Markov Decision Processes, Symmetry
Detection, Homomorphism, Density Estimation, Data Augmenting.
Abstract:
Learning a Markov Decision Process (MDP) from a fixed batch of trajectories is a non-trivial task whose
outcome’s quality depends on both the amount and the diversity of the sampled regions of the state-action
space. Yet, many MDPs are endowed with invariant reward and transition functions with respect to some
transformations of the current state and action. Being able to detect and exploit these structures could benefit
not only the learning of the MDP but also the computation of its subsequent optimal control policy. In this
work we propose a paradigm, based on Density Estimation methods, that aims to detect the presence of some
already supposed transformations of the state-action space for which the MDP dynamics is invariant. We tested
the proposed approach in a discrete toroidal grid environment and in two notorious environments of OpenAI’s
Gym Learning Suite. The results demonstrate that the model distributional shift is reduced when the dataset
is augmented with the data obtained by using the detected symmetries, allowing for a more thorough and
data-efficient learning of the transition functions.
1 INTRODUCTION
Model-based Offline Reinforcement Learning (ORL)
is the branch of Machine Learning that first fits a dy-
namical model and then obtains a behavioural (opti-
mal) system control policy with the aim of maximiz-
ing a predetermined utility function (Sutton, 1990).
The model learning phase is usually based on a fi-
nite batch of trajectories followed by the system. Al-
though it is always possible to compute confidence
intervals on the parameters of the learnt categorical
distribution, it is hard to determine the amount of data
needed for the model optimisation to return a suffi-
ciently improved policy.
Following (Levine et al., 2020) the statistical dis-
tance between reality and the learnt model is de-
fined as distributional shift. Thus, in order to be
able to compute reliable strategies that can be applied
to real world scenarios (e.g. planning in healthcare,
autonomous driving) the distributional shift must be
minimal. Consequently, limiting it by considering
strategies close to the one used for data collection, is
the main challenge of ORL (Levine et al., 2020). In-
deed, such strategies are more likely to drive the sys-
a
https://orcid.org/0000-0003-0002-9973
b
https://orcid.org/0000-0003-3578-4186
tem into areas of the state-action space whose transi-
tions have been thoroughly explored in the batch, al-
lowing a better estimation of the model than in other
areas.
Interestingly, the detection of symmetries in
physics has always provided greater representability
and generalization power to the learnt models (Gross,
1996). Moreover, symmetry detection can potentially
provide knowledge about what will be the time evo-
lution of a system state that has never been explored
before. Such an idea can be explored to allow a more
data efficient model learning phase for ORL taking
advantage of the knowledge of regularities in the sys-
tem dynamics that repeat themselves in different situ-
ations, independently of the initial conditions.
In this context, a method to detect symmetries for
ORL relying on expert guidance is presented. The
described method is built in the classical framework
of discrete time Markov Decision Processes (MDPs)
for both discrete and continuous state-action spaces
(Mausam and Kolobov, 2012).
1.1 Illustrative Example
One of the most emblematic examples is checking
whether or not a dynamical system is symmetric with
88
Angelotti, G., Drougard, N. and Chanel, C.
Expert-guided Symmetry Detection in Markov Decision Processes.
DOI: 10.5220/0010783400003116
In Proceedings of the 14th International Conference on Agents and Artificial Intelligence (ICAART 2022) - Volume 2, pages 88-98
ISBN: 978-989-758-547-0; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
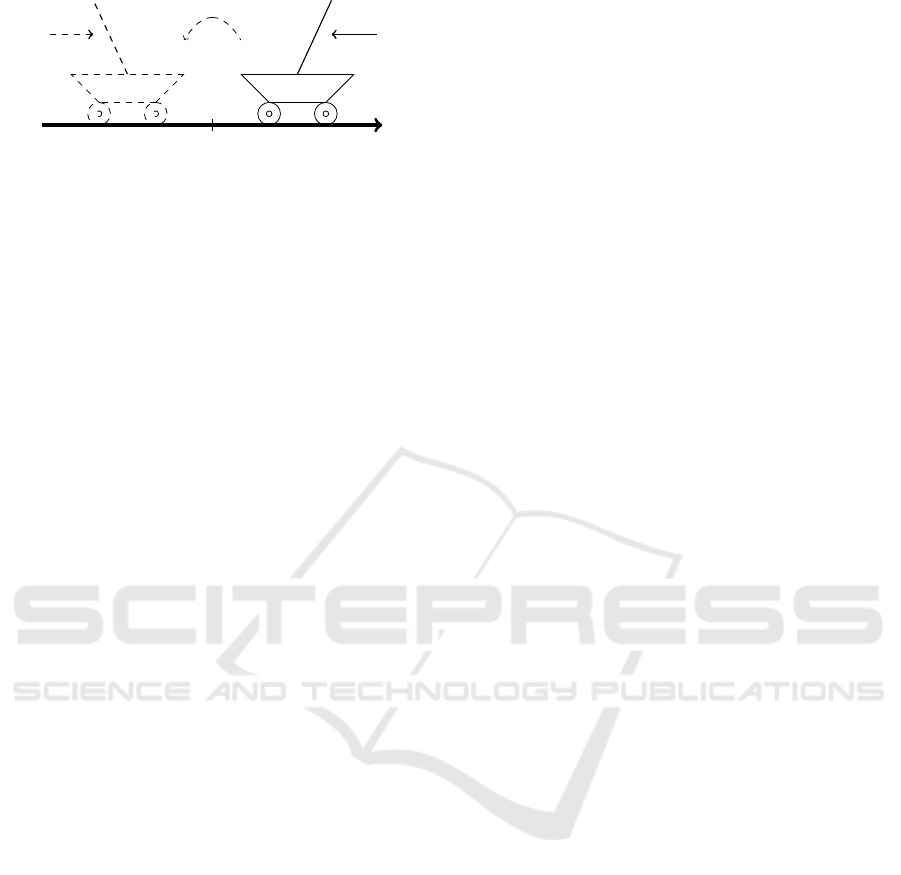
x
x = 0
a
h
g(a)
Figure 1: The cart in the right is a representation of a Cart-
Pole’s state s
t
with x
t
> 0 and action a
t
=←. The dashed
cart in the left is the image of (s
t
, a
t
) under the transforma-
tion h which inverses state f (s) = −s and action g(a) = −a.
respect to some particular transformation of the sys-
tem of reference. For instance, consider the well-
known CartPole Reinforcement Learning (RL) do-
main of the OpenAI’s Gym Learning Suite (Brock-
man et al., 2016). In CartPole the purpose of the au-
tomated agent is to avoid a rotating pole situated on
a sliding cart falling down due to gravity. The state
of the system is expressed as a tuple s = (x, v, α, ω)
where x is the position of the cart with respect to a
horizontal track upon which it can slide, v is its lon-
gitudinal velocity, α is the angle between the rotating
pole and the axis pointing along the direction of the
gravitational acceleration, and ω the angular velocity
of the pole. The agent can push the cart left (←) or
right (→) at every time step (in the negative or posi-
tive direction of the track) providing to the system a
fixed momentum |p|. A pictorial representation of a
state-action pair (s
t
, a
t
) can be found in Figure 1.
Let us suppose there exists a function h : S ×
A → S × A that maps a state-action pair (s
t
, a
t
) to
f (s
t
), g(a
t
)
, where f : S → S and g : A → A, such
that the dynamics of the pair (s, a) is the same as the
one of h(s, a). Note that in this example, the system
dynamics is symmetric with respect to a flip around
the vertical axis. In other words, its dynamics is in-
variant by multiplication by minus one, assuming that
if a =← then g(a) = −a =→ and vice versa. Indeed,
if the state-action pair (s
t
, a
t
) leads to the state s
t+1
,
this property will imply that h(s
t
, a
t
) = (−s
t
, −a
t
)
leads to f (s
t+1
) = −s
t+1
.
When learning the dynamics from a finite batch
of experiences (or trajectories), resulting in a set of
transitions D =
(s
i
, a
i
, s
0
i
)
n
i=1
with n ∈ N the size of
the batch, we might for instance fit a function ˆs(s, a) =
s
0
with the aim of minimizing a loss, e.g. the Mean
Squared Error. However, imagine that in the batch D
there were many transitions regarding the part of the
state-action space with x > 0 and very few with x < 0.
Unfortunately, we may learn a good model to forecast
what will happen when the cart is at the right of the
origin and a very poor model at its left side. We can
then suppose that also the optimal control policy will
perform well when x > 0 and poorly when x < 0.
Nevertheless, if it were possible to be confident of
the existence of the symmetry f (s) = −s and g(a) =
−a (where the opposite of the action a is the trans-
formation stated above), we might extend the batch
of experiences without additional interaction with the
system, and then improve the accuracy of the model
also to the regions where x < 0.
1.2 Definition of the Problem and
Related Work
How can we automatically detect these sorts of sym-
metries in the batch of experiences?
In this work we propose a paradigm to check
whether a pre-alleged structure of this kind is present
in the batch and consequently utilize it to augment the
data.
Data augmentation is a common practice in Ma-
chine Learning to improve performances in data-
limited regimes. For example, it has been used in
recent Computer Vision DNN architectures (Shorten
and Khoshgoftaar, 2019) where, if the purpose is to
detect an object in an image independently of its po-
sition or orientation the original data set gets aug-
mented with several copies of the images providing
the object translated or rotated.
We build our approach upon the Markov Decision
Process (MDP) framework (Mausam and Kolobov,
2012), whether discrete or continuous state and action
spaces can be considered, although hypothesizing a
non stochastic dynamics.
The detection of structures and abstractions in
MDPs has been widely studied in the literature. In
(Dean and Givan, 1997; Givan et al., 2003) the no-
tions of MDP homomorphism (structure-preserving
maps between the original MDP and one charac-
terized by a factored representation) and stochastic
bisimulation (are introduced and used to automati-
cally partition the state space of an MDP and to find
aggregated and factored representations. In (Ravin-
dran and Barto, 2001) the previous works on state ab-
stractions have been extended to include the concept
of symmetry, and in (Ravindran and Barto, 2004) ap-
proximate homomorphisms are considered.
Later on, (Narayanamurthy and Ravindran, 2008)
showed that the fully automatic discovery of symme-
tries in a discrete MDP is as hard as verifying whether
two graphs are isomorphic. Concurrently, (Taylor
et al., 2009) relaxed the notion of bisimulation to al-
low for the attainment of performance bounds for ap-
proximate MDP homomorphisms. Approximate ho-
momorphisms are of particular interest in continuous
state MDPs where a hard mapping to an aggregated
representation could be impractical. In this context,
Expert-guided Symmetry Detection in Markov Decision Processes
89

(Ferns et al., 2004) developed a bisimulation pseu-
dometric to extend the concept of bisimulation rela-
tion. The automatic discovery of representations us-
ing the bisimulation pseudometric has been investi-
gated in recent years using Deep Neural Networks and
obtaining theoretical guarantees for such a method-
ology (Ruan et al., 2015; Castro, 2020; Abel et al.,
2020).
From a more theoretical perspective (Li et al.,
2006) classified different kinds of possible state ab-
stractions, showing for each one of them which func-
tion would be preserved under the new refinement:
the value function, the Q-value function, the optimal
policy, and so on. From a different perspective (Man-
del et al., 2016) developed an algorithm that aims
to cluster MDPs states in a Bayesian sense in or-
der to solve the MDP in a more data efficient way,
even when an underlying homomorphic or symmetric
structure is not present.
Recently, (van der Pol et al., 2020a) used a con-
trastive loss function that enforces action equivariance
on a to be learnt representation of an MDP. Their ap-
proach resulted in the automatic learning of a struc-
tured latent space which can be used to plan in a more
data efficient fashion. Finally, (van der Pol et al.,
2020b) introduced MDP Invariant Networks, a spe-
cific class of Deep Neural Network (DNN) architec-
tures that guarantees by construction that the opti-
mal MDP control policy obtained through other Deep
RL approaches will be invariant under some set of
symmetric transformations and hence providing more
sample efficiency to the baseline when the symmetry
is actually present.
1.3 Contribution
In summary, the literature can be divided in two cate-
gories: 1) learning a representation using only or the
data contained in the batch or some a priori knowl-
edge about the environment; 2) exploiting an alleged
symmetry to obtain a behavioural policy that con-
verges faster to the optimal one.
The present work gets inspiration from all the re-
ported literature, but rather than automatically look-
ing for a state space abstraction or directly exploiting
a symmetry to act in the world it focuses on checking
whether the dynamical model to be learnt is symmet-
ric with respect to some transformation that is pre-
sumed by other means. In other words, such transfor-
mation can be given by external expert knowledge or
proposed by the user insight and its existence is ver-
ified by estimating the chance of its occurrence with
machine learning tools.
In order to verify the presence of a symmetry,
a preliminary estimate of the transition model is
needed. More specifically, we first perform a prob-
ability mass function (pmf) estimation or a proba-
bility density function (pdf) estimation of the transi-
tions in the batch D depending on the typology of the
MDP we are tackling (respectively discrete or con-
tinuous). In the discrete case this amounts to learn-
ing a set of categorical distributions. In the continu-
ous case we opt for using Normalizing Flows (Dinh
et al., 2015; Kobyzev et al., 2020), a Deep neural net-
work architecture that allows to adapt and estimate a
pdf while being always able to exactly compute the
density value for new samples. In this way, once a
pmf/pdf has been estimated from the batch of transi-
tions D we can compute the probability of an alleged
symmetric transition that is supposed to be sampled
from the same distribution.
When the probability (or the density in the contin-
uous case) is bigger than a given threshold for a high
fraction of samples, we decide to trust in the presence
of this alleged symmetry and hence augment the batch
by including the symmetric transitions.
In the end the dynamics of the model is learnt over
the augmented data set. When the approach detects a
symmetry that is really present in the true environ-
ment then the accuracy of the learnt model increases,
otherwise the procedure could also result in detrimen-
tal effects.
The paper is organized as follows: in Section 2
we provide the definitions of MDP, MDP homomor-
phism, symmetric transformation and pmf/pdf esti-
mation; next, in Section 3 the two algorithms for
expert-guided detection of symmetries are presented
along with a discussion of the limitations of both
(these are the main contributions); results in proof-of-
concept environments are shown in Section 4; conclu-
sion and future perspective are illustrated in Section
5.
2 BACKGROUND
In this section, we introduce the basic concepts about
MDPs, homomorphisms and symmetries.
Definition 2.1 (Markov Decision Process). A
discrete-time MDP (Bellman, 1966) is a tuple M =
(S, A, R,T, γ), where S is the set of states, A is the
set of actions, R : S × A → R is the reward function,
T : S × A → Dist(S) is the transition pdf, and γ ∈ [0, 1)
is the discount factor. At each time step, the agent ob-
serves a state s = s
t
∈ S, takes an action a = a
t
∈ A
drawn from a policy π : S ×A → [0, 1], and with prob-
ability T (s
0
|s, a) transits to a next state s
0
= s
t+1
, earn-
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
90

Estimate
transitions
Transform
data with k
Evaluate
probabilities
Augment
or not D
ν
k
> ν?
Figure 2: Pseudo flow chart of Algorithms 1 and 2.
ing a reward R(s
t
, a
t
). The value function of the policy
π is defined as: V
π
(s) = E
π
∑
∞
t=0
γ
t
R(s
t
, a
t
)|s
0
= s
.
The optimal value function V
∗
is the maximum of
the previous expression over every possible policy π.
When ∀(s, a) ∈ S × A, T dictates the transition to one
and only state s
0
∈ S the MDP is said to be determin-
istic or non stochastic.
A homomorphism from a dynamic system M to a
dynamic system M
0
is a mapping that preserves M ’s
dynamics, while in general eliminating some of the
details of the full system M .
Definition 2.2 (MDP Homomorphism). An MDP ho-
momorphism h (Ravindran and Barto, 2004) from
an MDP M = (S, A, T, R, γ) to an MDP M
0
=
(S
0
, A
0
, T
0
, R
0
, γ) is a surjection from S × A to S
0
× A
0
,
defined by a tuple of surjections ( f , g), with h(s,a) =
f (s), g(a)
, where f : S → S
0
and g : A → A
0
such that
∀(s, s
0
) ∈ S
2
, a ∈ A:
T
0
f (s), g(a), f (s
0
)
=
∑
s
00
∈[s
0
]
f
T (s,a, s
00
), (1)
R
0
f (s), g(a)
= R(s, a). (2)
where [s
0
]
f
= f
−1
f (s
0
)
, i.e. [s
0
]
f
is the set of
states for which the application of f results in the state
f (s
0
) ∈ S
0
.
Definition 2.3 (MDP Symmetry). Let k be a a sur-
jection from an MDP M to itself defined by the tu-
ple of surjections ( f , g, l) where f : S → S, g : A → A
and l : S → S. The transformation k is a symmetry
if ∀(s, s
0
) ∈ S
2
, a ∈ A both the dynamics T and the
reward R are invariant with respect to the transforma-
tion induced by k:
T
f (s), g(a), l(s
0
)
= T (s, a, s
0
), (3)
R
f (s), g(a)
= R(s, a). (4)
If M
0
= M and l = f then an MDP symmetry is
also an MDP homomorphism.
In this work we will focus only on symmetries
with respect to the dynamics and not the reward. In
particular, we will check for transformations k that
map a whole transition k(s, a, s
0
) →
f (s), g(a), l(s
0
)
.
Therefore the only condition that will be examined
and fulfilled is Equation 3. Detecting the said struc-
ture will help reduce the distributional shift between
the true environment dynamics and the one learnt
from experience.
Probability Mass Function Estimation for Dis-
crete MDPs. Let D = {(s
i
, a
i
, s
0
i
)}
n
i=1
be a batch
of recorded transitions. Performing mass estimation
over D amounts to compute the probabilities that de-
fine the unknown categorical transition distribution T
by estimating the frequencies of transition in D. In
other words we compute:
ˆ
T (s, a, s
0
) =
n
s,a,s
0
∑
s
0
n
s,a,s
0
if
∑
s
0
n
s,a,s
0
> 0,
|S|
−1
otherwise;
(5)
where n
s,a,s
0
is the number of times the transition (s
t
=
s, a
t
= a, s
t+1
= s
0
) ∈ D.
Probability Density Function Estimation for Con-
tinuous MDPs. Performing density estimation over
D amounts to finding an analytical expression for the
probability density of a transition (s, a, s
0
) given D:
L(s, a, s
0
|D). Normalizing flows (Dinh et al., 2015;
Kobyzev et al., 2020) allow defining a parametric flow
of continuous transformations that reshapes a known
pdf (e.g. a multivariate gaussian) to one that best fits
the data. Since the transformations are known, the Ja-
cobians are computable at every step and the probabil-
ity value can always be assessed. (Dinh et al., 2015).
3 EXPERT-GUIDED DETECTION
OF SYMMETRIES
We propose a paradigm to check whether the dynam-
ics of a to-be-learnt (i) deterministic discrete MDP
(see Algorithm 1) or (ii) a deterministic continuous
MDP (see Algorithm 2) is endowed with the invari-
ance of the dynamics with respect to some transfor-
mation. A pseudo representation of the flow chart of
both algorithms is shown in Figure 2.
Let M be a deterministic MDP, let D be a batch of
pre-collected transitions and let k be an alleged sym-
metric transformation of M ’s dynamics.
In order to check whether k can be considered or
not as a symmetry of the dynamics, in the discrete
case we will first estimate the most likely set of tran-
sition categorical distributions
ˆ
T given the batch of
transitions (Line 1, Algorithm 1) while in the con-
tinuous case we will estimate the density of tran-
sition in the batch obtaining the probability density
L(s, a, s
0
|D) (Line 1, Algorithm 2). In the continuous
Expert-guided Symmetry Detection in Markov Decision Processes
91
Algorithm 1: Symmetry detection and data aug-
menting in a deterministic discrete MDP.
Input: Batch of transitions D, ν ∈ (0, 1)
percentage threshold, k alleged
symmetry
Output: Possibly augmented batch D ∪ D
k
1
ˆ
T ← Most Likely Categorical pmf from (D)
2 D
k
= k(D)
3 ν
k
=
1
|D
k
|
∑
(s,a,s
0
)∈D
k
1
{
ˆ
T (s
0
|s,a)=1}
4 if ν
k
> ν then
5 return D ∪ D
k
6 else
7 return D
8 end
case we will then compute the density value of every
transition (s, a, s
0
) ∈ D, resulting in a set of real values
from L denoted by Λ (Line 2, Algorithm 2). We will
select the q-order quantile of Λ to be a threshold θ ∈ R
(Line 3, Algorithm 2) that will determine whether
we can trust the symmetry to be present, and hence
to augment or not the starting batch. Next, we will
map any (s, a, s
0
) ∈ D to its alleged symmetric image
f (s), g(a), l(s
0
)
(Line 4, Algorithm 2). The map of
D under the transformation k will be denoted as D
k
.
Let then, ∀(s, a, s
0
) ∈ D
k
, L(s, a, s
0
|D) be the probabil-
ity density of the symmetric image of a transition in
the batch. We will assume that the system dynamics
is invariant under the transformation k if ν
k
, the per-
centage of transitions whose density is greater than
θ, is bigger than the percentage threshold ν (Lines 5-
10, Algorithm 2). In the discrete case we will just
count how many images of the symmetric transfor-
mation D
k
are present in the batch (Line 3, Algorithm
1) and then decide whether to perform data augment-
ing according to both ν
k
and the threshold ν (Lines
4-8, Algorithm 1). If data augmenting is performed,
the boosted batch D ∪ D
k
will be returned as output.
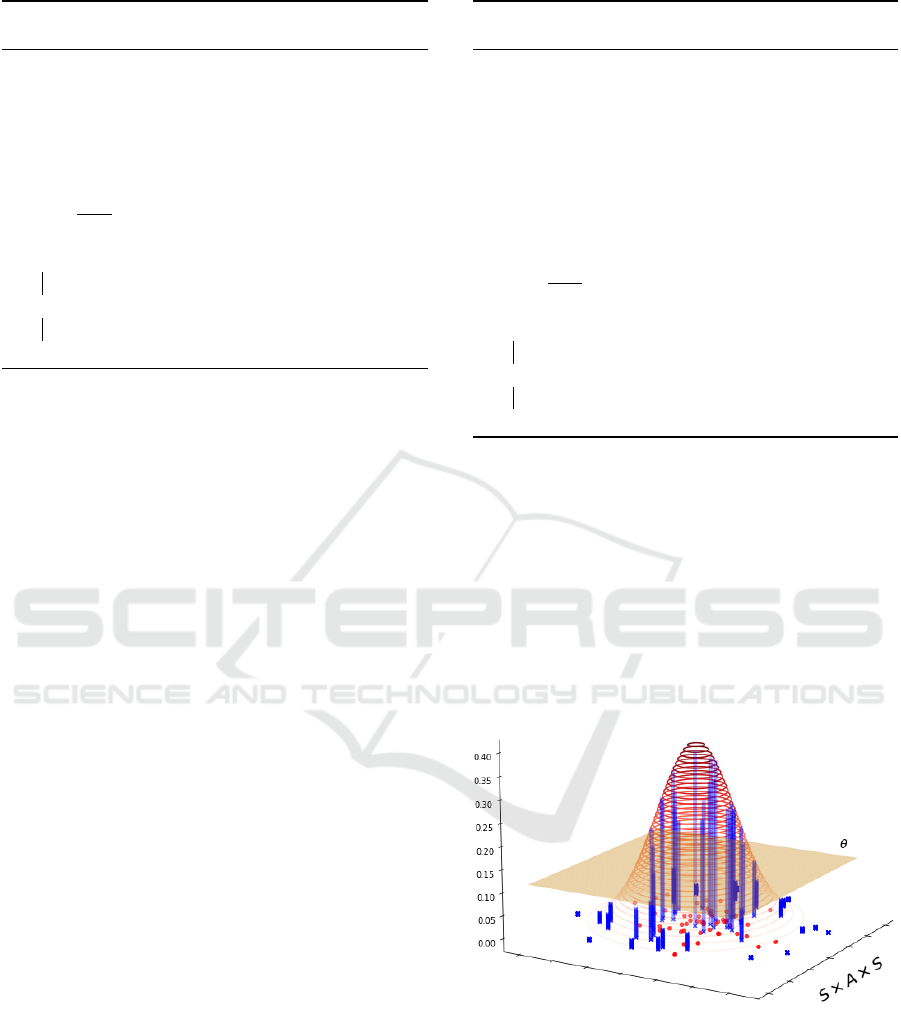
Figure 3 provides an intuition about Algorithm 2.
3.1 Intuition for the Discrete Case
In the discrete case we are performing a sort of “proof
by induction“. If the majority of symmetric transi-
tions (with respect to the threshold ν) were already
sampled, then we can imagine that the other ones
were not sampled just because our data set is not big
enough. Therefore we trust that the dynamics is sym-
metric with respect to k and augment the batch.
Algorithm 2: Symmetry detection and data aug-
menting in a deterministic continuous MDP.
Input: Batch of transitions D, q ∈ [0, 1)
order of the quantile, ν ∈ (0, 1)
percentage threshold, k alleged
symmetry
Output: Possibly augmented batch D ∪ D
k
1 L ← Density Estimate (D)
2 Λ ← Distribution L(D) (L evaluated over D)
3 θ = q-order quantile of Λ
4 D
k
= k(D)
5 ν
k
=
1
|D
k
|
∑
(s,a,s
0
)∈D
k
1
{L(s,a,s
0
|D)>θ}
6 if ν
k
> ν then
7 return D ∪ D
k
8 else
9 return D
10 end
3.2 Intuition for the Continuous Case
The intuition behind the approach in the continuous
case is that if in the original batch D the density of
transitions that are “not so different” from some of
the symmetric images D
k
of D , then L(D
k
|D) will
not be “too small”. How small is small when we
are considering real valued, continuous pdf? In or-
der to insert a comparable scale we take the threshold
θ to be a q-quantile of the set of the estimated density
values of the transitions in the original batch D , i.e.
Figure 3: Intuition for the continuous case. The xy plane is
the space of transitions S×A×S, the z axis is L, the value of
the probability density of a given transition. The red points
represent D, the blue crosses D
k
for a given transformation
k. We display as a red contour plot the pdf L learnt in Line 1
of Algorithm 2. The orange hyperplane has height θ which
is the threshold computed in Line 3 of Algorithm 2. The
blue vertical bars have as height the value of L evaluated for
that specific transition. The algorithm counts the fraction ν
k
of samples (blue crosses) which have a vertical bar higher
than the hyperplane.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
92

L(s, a, s
0
| D) | (s, a, s
0
) ∈ D
. It goes without say-
ing that since the purpose of Algorithm 2 is to perform
data augmentation, it is necessary to select a small q-
order quantile, otherwise the procedure would bear no
meaning: it would be pointless to augment the batch
with transitions that are already very likely in the orig-
inal one (see Figure 4). In this case we won’t insert
any new information.
D
D
k
1
D
k
2
S × A × S
Figure 4: Representation of the support in S
2
× A of the
of D, D
k
1
and D
k
2
. k
1
and k
2
are two different alleged
transformations. The shape and the position of the sets is
decided according to the value of the log likelihood of the
density estimate L and quantile threshold θ. D
k
1
∩ D 6= ∅
and D
k
2
∩ D = ∅. Depending on the user chosen percent-
age threshold ν, k
1
could be a symmetry while k
2
no. If k
1
is detected as a symmetry then data augmenting D with D
k
1
means training the model over D ∪D
k
1
. Notice that the data
contained in D
k
1
\D are not present in the original batch D.
3.3 Limitations
Both in the discrete and in the continuous case the
approach is limited by the size and the variety of the
data set. It is hard to tell how good an initial batch
is, but this aspect could non negligibly affect the out-
put of the paradigm. The approach in the continuous
case is also limited by the impact that the transforma-
tion has on the representation of the transition. More
in detail, if the distance in Euclidean space between
(s, a, s
0
) and k(s, a, s
0
) is small, or if only a small frac-
tion of the total number of components that represent
the transition is affected by the transformation then
the probability of the image of the alleged symme-
try will be high, resulting in a false positive detec-
tion. With this in mind, appropriately preprocessing
the data before density estimation could enormously
affect the outcome of the procedure.
4 EXPERIMENTS
We test the algorithm in one discrete grid environ-
ment with periodic boundary conditions and in two
famous environments of OpenAI’s Gym Learning
Suite: CartPole and Acrobot.
4.1 Setup
We first collect a batch of transitions D by acting in
the environment with a uniform random policy. We
suppose the presence of a symmetry k and we try
to detect it using Algorithm 1 or Algorithm 2. We
report ν
k
, the average value plus or minus the stan-
dard deviation of the quantity ν
k
computed over an
ensemble of N different iterations of the procedure
(with N different batches D). We do not consider any
threshold ν, thus limiting the analysis at the phase of
the calculation of ν
k
since the detection or not of a
symmetry is highly dependent of an expert-wise do-
main dependent choice of ν. In the end we show that
detecting the right symmetry really results in learn-
ing more accurate models by computing ∆, the aver-
age of an estimate of the distributional shift ∆ over
the various simulations. Since ∆ is measured differ-
ently depending on the typology of the environment
(discrete or continuous) more details about the per-
formances are illustrated in the next subsections and
the results are reported in Table 4. In Tables 1, 2,
3 we adopted the following contracted notation: let
a
1
, a
2
, a
3
, a
4
be some actions ∈ A, for space’s sake we
will use the notations g(a
1
, a
2
, . . . ) = (a
3
, a
4
, . . . ) to
indicate g(a
1
) = a
3
, g(a
2
) = a
4
, . . . , etc.
4.2 Grid (Discrete)
In this environment the agent can move along fixed
directions over a torus by acting with any a ∈ A =
{
↑, ↓, ←, →
}
. The positions on the torus are the states
s = (i, j) and the set S is represented as a grid of fixed
size l and periodic boundary conditions (see Figure
5). Since there are no obstacles and the dynamics is
deterministic this environment is endowed of many
symmetric transformations and therefore can serve as
an useful proof-of-concept.
We tested Algorithm 1 with six different alleged
transformations k in a Grid with size l = 100 over N =
Figure 5: Representation of the Grid Environment. The red
dot is the position of a state s on the torus. The displacement
obtained by acting with action a =↑ is shown as a red arrow.
Expert-guided Symmetry Detection in Markov Decision Processes
93

50 different simulations.
1. Time Reversal Symmetry with Action Inver-
sion (TRSAI). Assuming that ↓ is the reverse of
↑ and ← is the reverse of → we proposed the fol-
lowing transformation: k =
f (s) = s
0
, g(↑, ↓, ←
, →) = (↓, ↑, →, ←), l(s
0
) = s
. The symmetric
transformation is present in the batch with a per-
centage ν
k
= 0.6 ± 0.1.
2. Same Dynamics with Action Inver-
sion (SDAI). When k =
f (s) = s,
g( ↑, ↓, ←, → ) = ( ↓, ↑, →, ← ), l(s
0
) = s
0
the results clearly show that this transforma-
tion is not a symmetry. Indeed in this case
ν
k
= 0.0 ± 0.0.
3. Opposite Dynamics and Action Inversion
(ODAI): k =
f (s) = s, g( ↑, ↓, ←, → ) =
(↓, ↑, →, ←), l(s
0
) = s
0
∓ (2, 0) ∨ (0, 2)
. In other
words we revert the action but also the final state is
changed in order to reproduce the correct destina-
tion. ν
k
= 0.4 ± 0.1 showing that the latter could
be a symmetry of the environment.
4. Opposite Dynamics but Wrong Action
(ODWA). The alleged transformation is like the
one of Point 3, but the action is switched on the
wrong axis (e.g. g(↑) =→). Here ν
k
= 0.0 ± 0.0
and not a symmetry.
5. Translation Invariance (TI). k =
f (s) =
s
0
, g ( ↑, ↓, ←, →) = (↑, ↓, ←, →), l(s
0
) = s
0
±
(1, 0) ∨ (0, 1)
. The proposed transformation pro-
poses a displacement with similar effects when
the same action is applied to the next state. ν
k
=
0.5 ± 0.1. k could be a symmetry.
6. Translation Invariance with Opposite Dynam-
ics (TIOD). In this case the action is the same as
Point 5 but the agent returns to the previous state.
With ν
k
= 0.0 ± 0.0 the latter is not a symmetry.
The said transformations are resumed in the Table 1
along with the results in Table 4.
With the scope of showing that augmenting the
data set with the image of the symmetry k leads to
better model we compute the distributional shift be-
tween the true model T and
ˆ
T , the one learnt from D,
as the sum over every possible state-action pair of the
Total Variation Distance for each transition.
In other words let
d(T,
ˆ
T ) =
1
2
∑
(s,s
0
)∈S
2
,a∈A
|T (s, a, s
0
) −
ˆ
T (s, a, s
0
)| (6)
be the distance between T and
ˆ
T and let
d(T,
ˆ
T
k
) =
1
2
∑
(s,s
0
)∈S
2
,a∈A
|T (s, a, s
0
) −
ˆ
T
k
(s, a, s
0
)| (7)
Table 1: Grid. Proposed transformations and label.
k Label
f (s) = s
0
g(↑, ↓, ←, →) = (↓, ↑, →, ←) TRSAI
l(s
0
) = s
f (s) = s
g(↑, ↓, ←, →) = (↓, ↑, →, ←) SDAI
l(s
0
) = s
0
f (s) = s
g(↑, ↓, ←, →) = (↓, ↑, →, ←) ODAI
l(s
0
) = s
0
∓ (2, 0) ∨ (0, 2)
f (s) = s
g(↑, ↓, ←, →) = (→, ←, ↑, ↓) ODWA
l(s
0
) = s
0
∓ (2, 0) ∨ (0, 2)
f (s) = s
0
g(↑, ↓, ←, →) = (↑, ↓, ←, →) TI
l(s
0
) = s
0
± (1, 0) ∨ (0, 1)
f (s) = s
0
g(↑, ↓, ←, →) = (↑, ↓, ←, →) TIOD
l(s
0
) = s
where
ˆ
T
k
is the dynamics inferred from A
k
, we report
∆ in Table 4: the difference
∆ = d(T,
ˆ
T ) − d(T,
ˆ
T
k
) (8)
averaged over N = 50 simulations, showing that when
k is a true symmetry of the dynamics the said quantity
is positive (d(T,
ˆ
T
k
) < d(T,
ˆ
T )) and when k is not a
real symmetry it is negative. Hence, augmenting the
data set after having detected a true symmetry leads
to better model learning, but the false detection of
a symmetric transformation could also result in less
representative models.
4.3 CartPole (Continuous)
As stated in the Introduction, the dynamics of Cart-
Pole is invariant with respect to the transformation
k = ( f (s) = −s, g(a) = −a, l(s
0
) = −s)∀(s, s
0
) ∈ S
2
.
In order to use Algorithm 2 we first map the actions
to real numbers: ←= −1.5 and →= 1.5. We then nor-
malize every state feature in the range [−1.5,1.5]. We
tested Algorithm 2 with four different alleged trans-
formations h over N = 5 different simulations, a batch
of size |D| = 10
3
collected with a random policy,
quantile order to compute the thresholds q = 0.1.
1. State and Action Reflection with Respect to an
Axis in x = 0 (SAR). Assuming that ← is the re-
verse of → we proposed the following transforma-
tion: k =
f (s) = −s, g(←, →) = (→, ←), l(s
0
) =
−s
0
. The symmetric transformation is present in
the batch with a percentage ν
k
= 0.80 ± 0.05.
2. Initial State Reflection (ISR). We then tried the
same transformation as before but without reflect-
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
94

ing the next state s
0
: k =
f (s) = −s, g(←, →) =
(→, ←), l(s
0
) = s
0
. This is clearly not a symme-
try because ν
k
= 0.00 ± 0.00.
3. Action Inversion (AI). What about reversing
only the actions? k =
f (s) = s, g(←, →) =
(→, ← ), l(s
0
) = s
0
and ν
k
= 0.00 ± 0.00. There-
fore this is not a symmetry of the environment ac-
cording to our criterion.
4. Single Feature Inversion (SFI). We also tried
to reverse only one single feature of the start-
ing state: k =
f (x, v, α, ω) = (−x, v, α, ω),
g( ←, → ) = (←, → ), l(s
0
) = s
0
. In this case
ν
k
= 0.05 ± 0.03.
5. Translation Invariance (TI). We translated the
position of the initial state x and that of
the final state x
0
by an arbitrary value (0.3):
k =
f (x, v, α, ω) = (x + 0.3, v,α, ω), g(←, →) =
(←, → ), l(x
0
, v
0
, α
0
, ω
0
) = (x
0
+ 0.3, v
0
, α
0
, ω
0
)
.
The percentage ν
k
= 0.25 ± 0.23. Given the high
variance this could be detected as a symmetry or
not depending on the simulation.
The proposed transformations are resumed in Table 2
along with the results in Table 4.
Table 2: CartPole. Proposed transformations and label.
k Label
f (s) = −s
g(←, →) = (→, ←) SAR
l(s
0
) = −s
0
f (s) = −s
g(←, →) = (←, →) ISR
l(s
0
) = s
0
f (s) = s
g(←, →) = (→, ←) AI
l(s
0
) = s
0
f ((x, ...)) = (−x, ...)
g(←, →) = (←, →) SFI
l(s
0
) = s
0
f ((x, ...)) = (x + 0.3, ...)
g(←, →) = (←, →) TI
l((x
0
, ...)) = (x
0
+ 0.3, ...)
With the aim of computing the distributional shift
we fit over D the evolution ˆs
0
(s, a) with a Multi Layer
Perceptron by minimizing the Mean Squared Error
(MSE) between ˆs
0
and s. We reiterate the same proce-
dure over D ∪ D
k
obtaining a next state ˆs
0
k
(s, a). We
then randomly generate 10
6
other transitions building
up an evaluation batch D
ev
from the environment and
we evaluate with respect to the MSE these two mod-
els over the new data set. We report in Table 4 the
α
1
> 0
α
2
< 0
Figure 6: Representation of a state of the Acrobot environ-
ment.
difference:
∆ = MSE
D
ev
(s
0
, ˆs
0
(s, a)) − MSE
D
ev
(s
0
, ˆs
0
k
(s, a)) (9)
Again, when ∆ > 0 augmenting the data set leads to
better models ˆs
0
k
, but when ∆ < 0 exploiting the trans-
formation h is detrimental to the dynamics.
4.4 Acrobot (Continuous)
The Acrobot environment consists of two poles
linked with a rotating joint at one end. One of the
poles is pinned to a wall with a second rotating joint
(see Figure 6). The system is affected by gravity and
hence the poles are hanging down. An agent can
apply a negative torque to the lower pole (a = −1), a
positive one (a = 1) or do nothing (a = 0). The goal is
to push the lower pole as high as possible. The state
consists of the sine and cosine of the two rotational
joint angles (α
1
, α
2
) and the joint angular velocities
(ω
1
, ω
2
) : s = (sinα
1
, cos α
1
, sin α
2
, cos α
2
, ω
1
, ω
2
).
The dynamics is invariant under the transformation
k = ( f ((α
1
, α
2
, ω
1
, ω
2
)) = (−α
1
, −α
2
, −ω
1
, −ω
2
)
and g(a) = −a, l((α
0
1
, α
0
2
, ω
0
1
, ω
0
2
)) =
(−α
0
1
, −α
0
2
, −ω
0
1
, −ω
0
2
))∀(s, s
0
) ∈ S
2
. In order to
apply Algorithm 2 we first normalize the state
features and the action in the interval [−3, 3]. We
tested Algorithm 2 with four different alleged trans-
formations k over N = 5 different simulations, a batch
of size |D| = 10
3
collected with a random policy,
quantile order to compute the thresholds q = 0.1. The
label of the transformations here after explained are
resumed in Table 3.
1. Angles and Angular Velocities Inversion
(AAVI).
k =
f (sin α
1
, sin α
2
, cos α
1
, cos α
2
, ω
1
, ω
2
) =
(−sin α
1
, −sin α
2
, cos α
1
, cos α
2
, −ω
1
, −ω
2
),
g(a) = −a, l(sinα
0
1
, sin α
0
2
, cos α
0
1
, cos α
0
2
, ω
0
1
, ω
0
2
)
= (−sinα
0
1
, −sin α
0
2
, cos α
0
1
, cos α
0
2
, −ω
0
1
, −ω
0
2
)
.
This transformation could be a symmetry since
the percentage of images with a probability
higher than the threshold is
ν
k
= 0.86 ± 0.03.
2. Cosines and Angular Velocities Inversion
(CAVI).
k =
f (sin α
1
, sin α
2
, cos α
1
, cos α
2
, ω
1
, ω
2
) =
(sinα
1
, sin α
2
, −cos α
1
, −cos α
2
, −ω
1
, −ω
2
),
Expert-guided Symmetry Detection in Markov Decision Processes
95

Table 3: Acrobot. Proposed transformations and label.
k Label
f ((s
1
, s
2
, ω
1
, ω
2
, . . . )) = −(s
1
, s
2
, ω
1
, ω
2
, . . . )
g(−1, 0, 1) = (1, 0, −1) AAVI
l((s
0
1
, s
0
2
, ω
0
1
, ω
0
2
, . . . )) = −(s
0
1
, s
0
2
, ω
0
1
, ω
0
2
, . . . )
f ((c
1
, c
2
, ω
1
, ω
2
, . . . )) = −(c
1
, c
2
, ω
1
, ω
2
, . . . )
g(−1, 0, 1) = (1, 0, −1) CAVI
l((c
0
1
, c
0
2
, ω
0
1
, ω
0
2
, . . . )) = −(c
0
1
, c
0
2
, ω
0
1
, ω
0
2
, . . . )
f (s) = s
g(−1, 0, 1) = (1, 0, −1) AI
l(s
0
) = s
0
f (s) = −s
g(−1, 0, 1) = (−1, 0, 1) SSI
l(s
0
) = s
0
g(a) = −a, l(sinα
0
1
, sin α
0
2
, cos α
0
1
, cos α
0
2
, ω
0
1
, ω
0
2
)
= (sinα
0
1
, sin α
0
2
, −cosα
0
1
, −cos α
0
2
, −ω
0
1
, −ω
0
2
)
.
This is not a symmetry since
ν
k
= 0.00 ± 0.00.
3. Action Inversion (AI). k =
f (s) = s, g(a) =
−a, l(s
0
) = s
0
. In this case the results are not so
indicative because ν
k
= 0.35 ± 0.09 and therefore
the transformation could be falsely detected as a
symmetry if a low threshold ν is chosen.
4. Starting State Inversion (SSI). k =
f (s) =
−s, g(a) = a, l(s
0
) = s
0
. This is clearly not a sym-
metric transformation because ν
k
= 0.00 ± 0.00.
The results can be found in Table 4 along with
model performance. Using the said metrics ∆ to eval-
uate the gains of data augmentation, we notice that
in this case the high dimensionality of the state space
makes it harder for the MLP to reconstruct the next
state and that even the discovery of the true symmetry
k = ( f ((α
1
, α
2
, ω
1
, ω
2
)) = −(α
1
, α
2
, ω
1
, ω
2
), g(a) =
−a, l((α
0
1
, α
0
2
, ω
0
1
, ω
0
2
)) = −(α
0
1
, α
0
2
, ω
0
1
, ω
0
2
)) seems to
not lead to the expected results because the confidence
interval of ∆ also falls on the negative part of the real
axis.
4.5 Discussion
In the light of the results we can state that, when used
with care, the proposed approaches manage to detect
the alleged transformations of the transitions which
are symmetries of the dynamics.
However, note that the present experiments in
the continuous environments were performed with a
quantile of order q = 0.1. The outcomes can greatly
be affected by the choice of q and further studies
should be carried out in the next future to address this
limitation.
Moreover, the expert choice of ν can also have a
huge impact on the final detection. Indeed, ν = 0.30
in the Acrobot environment could lead to the misde-
tection of AI as a symmetry, while the TI symmetry
of CartPole requires a very low (ν < 0.20) in order to
be detected (Table 4).
5 CONCLUSIONS
The present work proposed an expert-guided ap-
proach to data augment the batch of trajectories used
to learn a model in Offline Model Based RL. More
specifically, new information is created assuming
that the dynamics of the system is invariant with
respect to some symmetric transformation of the state
and action representations. The alleged symmetry is
detected exploiting both expert knowledge and the
fulfillment of an a priori established criterion. Ex-
perimental results in proof-of-concepts deterministic
environments suggest that the proposed method could
be an useful tool for the developer of Reinforcement
Learning algorithms when he is ought to apply them
to real world scenarios. Nevertheless, the strong
dependency from preprocessing, from neural network
hyperparameters to be fine tuned before training and
the from the choice of the quantile order q and of
the percentage threshold ν impose that Algorithms
1 and 2 should be handled with care. Indeed, the
false detection of a symmetry and the following data
augmenting could lead to catastrophic aftermaths
when the retrieved optimal policy is going to be
applied to the real environment.
An immediate next step consists in estimating to
what extent the solution to an MDP learnt offline ben-
efits from the reduction in distributional shift obtained
with the proposed paradigm.
Future research perspectives involve (1) using
more recent Normalizing Flows approaches to per-
form density estimation, e.g. we do not exclude that
state-of-the art continuous time Normalizing Flows
who exploit ODE solvers like FFJORD (Grathwohl
et al., 2019) might yield even better results; (2) ex-
tending the approach to also tackle stochastic envi-
ronments.
ACKNOWLEDGEMENTS
This work was carried out during a visit at the Pompeu
Fabra University (UPF) in Barcelona and was funded
by the Artificial and Natural Intelligence Toulouse In-
stitute (ANITI) - Institut 3iA (ANR-19-PI3A-0004).
We thank Hector Geffner, Anders Jonsson and the Ar-
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
96
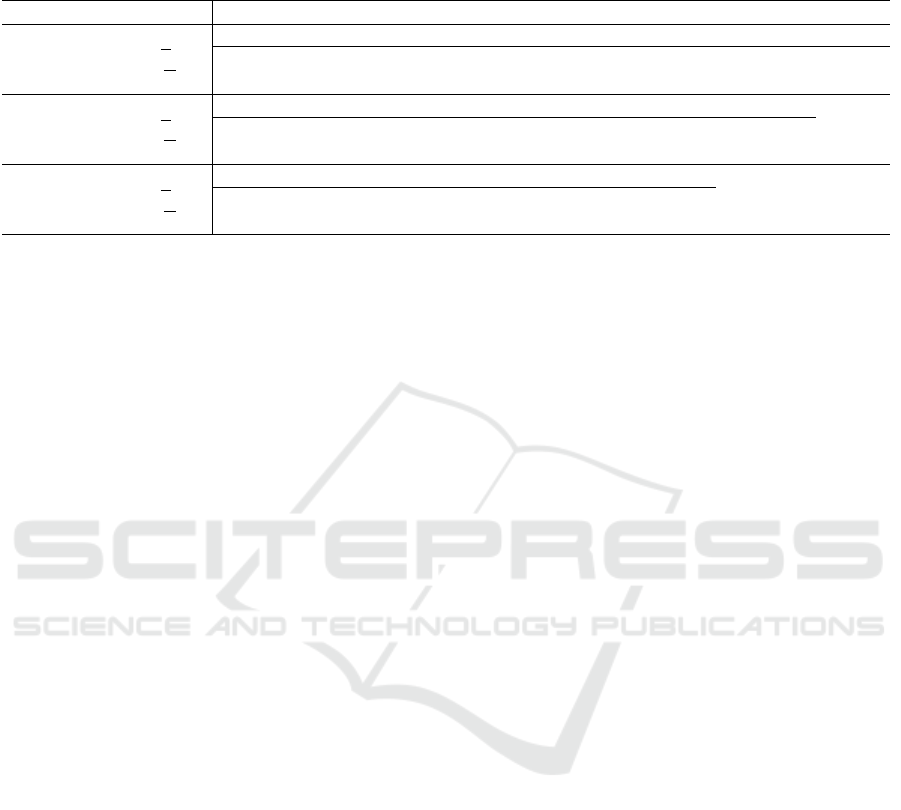
Table 4: Results of the algorithms in all environments. The columns on the right point to the tested alleged symmetry, indexed
by its label as reported in Table 1 for the toroidal Grid, Table 2 for CartPole and Table 3 for Acrobot. All experiments were
performed with q = 0.1. The true symmetries are displayed in bold.
Environment Metrics Alleged Transformation
TRSAI SDAI ODAI ODWA TI TIOD
Grid
ν
k
0.6 ± 0.1 0.0 ± 0.0 0.4 ± 0.1 0.0 ± 0.0 0.5 ± 0.1 0.0 ± 0.0
∆ 27 ± 9 -14 ± 3 47 ± 12 -14 ± 3 39 ± 9 -17 ± 2
SAR ISR AI SFI TI
CartPole
ν
k
0.80 ± 0.05 0.00 ± 0.00 0.00 ± 0.00 0.05 ± 0.03 0.25 ± 0.23
∆ 4 ± 2 ×
×
×1
1
10
0
0
−4
-10 ± 1 × 10
−2
-8 ± 1 × 10
−3
-4 ± 3 × 10
−3
3 ± 2 ×
×
×1
1
10
0
0
−4
AAVI CAVI AI SSI
Acrobot
ν
k
0.86 ± 0.03 0.00 ± 0.00 0.35 ± 0.09 0.00 ± 0.00
∆ 3.3 ± 6.6 ×
×
×1
1
10
0
0
−3
−3.9 ± 1.9 × 10
−2
−0.6 ± 1.3 × 10
−2
−9.5 ± 4.3 × 10
−2
tificial Intelligence and Machine Learning group of
the UPF for their warm hospitality.
REFERENCES
Abel, D., Umbanhowar, N., Khetarpal, K., Arumugam, D.,
Precup, D., and Littman, M. (2020). Value Preserv-
ing State-Action Abstractions. In International Con-
ference on Artificial Intelligence and Statistics, pages
1639–1650. PMLR.
Bellman, R. (1966). Dynamic Programming. Science,
153(3731):34–37.
Brockman, G., Cheung, V., Pettersson, L., Schneider, J.,
Schulman, J., Tang, J., and Zaremba, W. (2016). Ope-
nAI Gym. arXiv preprint arXiv:1606.01540.
Castro, P. S. (2020). Scalable Methods for Computing
State Similarity in Deterministic Markov Decision
Processes. In Proceedings of the AAAI Conference
on Artificial Intelligence, volume 34, pages 10069–
10076.
Dean, T. and Givan, R. (1997). Model Minimization in
Markov Decision Processes. In AAAI/IAAI, pages
106–111.
Dinh, L., Krueger, D., and Bengio, Y. (2015). NICE: Non-
linear Independent Components Estimation. In Ben-
gio, Y. and LeCun, Y., editors, 3rd International Con-
ference on Learning Representations, ICLR 2015, San
Diego, CA, USA, May 7-9, 2015, Workshop Track Pro-
ceedings.
Ferns, N., Panangaden, P., and Precup, D. (2004). Metrics
for Finite Markov Decision Processes. In UAI, vol-
ume 4, pages 162–169.
Givan, R., Dean, T., and Greig, M. (2003). Equivalence
Notions and Model Minimization in Markov Decision
Processes. Artificial Intelligence, 147(1-2):163–223.
Grathwohl, W., Chen, R. T. Q., Bettencourt, J., Sutskever, I.,
and Duvenaud, D. (2019). FFJORD: Free-Form Con-
tinuous Dynamics for Scalable Reversible Generative
Models. In 7th International Conference on Learning
Representations, ICLR 2019, New Orleans, LA, USA,
May 6-9, 2019. OpenReview.net.
Gross, D. J. (1996). The role of symmetry in fundamen-
tal physics. Proceedings of the National Academy of
Sciences, 93(25):14256–14259.
Kobyzev, I., Prince, S., and Brubaker, M. (2020). Normal-
izing Flows: An Introduction and Review of Current
Methods. IEEE Transactions on Pattern Analysis and
Machine Intelligence.
Levine, S., Kumar, A., Tucker, G., and Fu, J. (2020). Offline
reinforcement learning: Tutorial, review, and perspec-
tives on open problems. ArXiv, abs/2005.01643.
Li, L., Walsh, T. J., and Littman, M. L. (2006). Towards
a Unified Theory of State Abstraction for MDPs.
ISAIM, 4:5.
Mandel, T., Liu, Y.-E., Brunskill, E., and Popovic, Z.
(2016). Efficient Bayesian Clustering for Reinforce-
ment Learning. In IJCAI, pages 1830–1838.
Mausam and Kolobov, A. (2012). Planning with Markov
Decision Processes: An AI Perspective. Morgan &
Claypool Publishers.
Narayanamurthy, S. M. and Ravindran, B. (2008). On the
Hardness of Finding Symmetries in Markov Decision
Processes. In Proceedings of the 25th international
conference on Machine learning, pages 688–695.
Ravindran, B. and Barto, A. G. (2001). Symmetries and
Model Minimization in Markov Decision Processes.
Technical report, USA.
Ravindran, B. and Barto, A. G. (2004). Approximate Ho-
momorphisms: A Framework for Non-exact Mini-
mization in Markov Decision Processes.
Ruan, S. S., Comanici, G., Panangaden, P., and Precup, D.
(2015). Representation Discovery for MDPs Using
Bisimulation Metrics. In Twenty-Ninth AAAI Confer-
ence on Artificial Intelligence.
Shorten, C. and Khoshgoftaar, T. M. (2019). A survey on
Image Data Augmentation for Deep Learning. Jour-
nal of Big Data, 6(1):1–48.
Sutton, R. S. (1990). Integrated Architectures for Learning,
Planning, and Reacting Based on Approximating Dy-
namic Programming. In Porter, B. and Mooney, R.,
editors, Machine Learning Proceedings 1990, pages
216–224. Morgan Kaufmann, San Francisco (CA).
Taylor, J., Precup, D., and Panagaden, P. (2009). Bound-
ing Performance Loss in Approximate MDP Homo-
morphisms. In Koller, D., Schuurmans, D., Bengio,
Expert-guided Symmetry Detection in Markov Decision Processes
97

Y., and Bottou, L., editors, Advances in Neural Infor-
mation Processing Systems, volume 21. Curran Asso-
ciates, Inc.
van der Pol, E., Kipf, T., Oliehoek, F. A., and Welling,
M. (2020a). Plannable Approximations to MDP Ho-
momorphisms: Equivariance under Actions. In Pro-
ceedings of the 19th International Conference on Au-
tonomous Agents and MultiAgent Systems, AAMAS
’20, page 1431–1439, Richland, SC. International
Foundation for Autonomous Agents and Multiagent
Systems.
van der Pol, E., Worrall, D., van Hoof, H., Oliehoek, F.,
and Welling, M. (2020b). MDP Homomorphic Net-
works: Group Symmetries in Reinforcement Learn-
ing. In Larochelle, H., Ranzato, M., Hadsell, R., Bal-
can, M. F., and Lin, H., editors, Advances in Neu-
ral Information Processing Systems, volume 33, pages
4199–4210. Curran Associates, Inc.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
98
