
A Simple and Effective Convolutional Filter Pruning based on Filter
Dissimilarity Analysis
F. X. Erick
1
, Shrutika S. Sawant
1
, Stephan Göb
1
, N. Holzer
1
, E. W. Lang
2
and Th. Götz
1,2,3
1
Fraunhofer Institute of integrated Circuits, 91054 Erlangen, Germany
2
CIML Group, Biophysics, University of Regensburg, 3040 Regensburg, Germany
3
Clinic of Rheumatology, University Hospital Erlangen, 91054 Erlangen, Germany
Keywords: Convolutional Neural Network, Deep Learning, Filter Pruning.
Abstract: In this paper, a simple and effective filter pruning method is proposed to simplify the deep convolutional
neural network (CNN) and accelerate learning. The proposed method selects the important filters and discards
the unimportant ones based on filter dissimilarity analysis. The proposed method searches for filters with
decent representative ability and less redundancy, discarding the others. The representative ability and
redundancy contained in the filter is evaluated by its correlation with currently selected filters and left over
unselected filters. Moreover, the proposed method uses an iterative procedure, so that less representative
filters can be discarded evenly from the entire model. The experimental analysis confirmed that a simple filter
pruning method can reduce floating point operations (FLOPs) of TernausNet by up to 89.65% on an INRIA
Aerial Image Labeling dataset with an only marginal drop in the original accuracy. Furthermore, the proposed
method shows promising results in comparison with other state-of-the-art methods.
1 INTRODUCTION
When deep CNN is adopted for computer vision
tasks, the input image is convolved with many filters,
extracting meaningful features from the input image.
As the network grows deeper and wider, deep feature
extraction plays a significant role in demonstrating
excellent performance in the field of computer vision
(Ahmadi et al. 2020; N. Liu et al. 2018; X. Liu et al.
2017; Liao et al. 2020; Lunga et al. 2018; Xu et al.
2018). However, the success of deep CNN comes
with an over-parameterized model that hampers their
applicability while deploying them on embedded
devices due to difficulties, such as, large number of
parameters, expensive computational cost, slow
convergence and so on. Therefore, network pruning
has become an essential process to compress the
model and accelerate its training (C. T. Liu et al.
2019; Torfi et al. 2018; Wang et al. 2019; Wen et al.
2020). Network pruning can be performed by either
weight pruning or filter pruning. Weight pruning
removes unimportant connections (parameters) and
results in an unstructured network (Han, Mao, and
Dally 2016; Ma et al. 2021). This necessitates
specialized software and hardware to recover the
performance of damaged networks. Moreover,
weight pruning offers only limited speedup, as most
parameters of the model lie in fully connected layers
and weight pruning simply reduces the number of
parameters, but fails to reduce Floating Point
Operations (FLOPs) significantly. For instance, the
VGG16 network has 90% of its parameters in a fully
connected layer, which account for 10% of
computations, whereas the remaining 90% of
computations is due to 10% of parameters in the
convolutional layer. This has encouraged the research
community to focus on exploring the filter pruning.
Filter pruning cuts out unimportant filters entirely
instead of connections, resulting in structured sparsity
(Shi et al. 2021; Jang, Lee, and Kim 2021; Zuo et al.
2020; Zeng et al. 2021). Here the idea is to rank the
filters using a specific criteria and preserve only top
ranked filters. In the past decade, numerous methods
have been suggested to evaluate the filter importance,
including, 𝑙
norm, 𝑙
norm, entropy measure,
geometric mean, Taylor expansion and many more
(Han et al. 2015; Luo and Wu 2017; He et al. 2019;
Molchanov et al. 2017). These magnitude based
pruning methods calculate the importance based on
filter itself, but do not take filter correlation into
account. Intuitively, the filters of the convolutional
neural networks are not independent. Even though
Erick, F., Sawant, S., Göb, S., Holzer, N., Lang, E. and Götz, T.
A Simple and Effective Convolutional Filter Pruning based on Filter Dissimilarity Analysis.
DOI: 10.5220/0010786400003116
In Proceedings of the 14th International Conference on Agents and Artificial Intelligence (ICAART 2022) - Volume 3, pages 139-145
ISBN: 978-989-758-547-0; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
139

different filters try to learn different features, there
exists potential similarity/correlation among them
leading to performance degradation of deep CNN.
Therefore, we believe that filters could be removed
by taking correlation among them into account.
Despite the success of the existing filter pruning
approaches, we have identified a major shortcoming:
filter importance is measured independently while
totally ignoring the redundancy among filters. Any
convolutional layer generally consists of many
similar/redundant filters. From an information theory
point of view, these correlated filters do not provide
additional discriminant information. Instead, they
increase the computational burden. Therefore, in this
paper, we propose a simple and efficient approach to
obtain compact deep CNNs by selecting important
filters and eliminating the unimportant ones based on
filter correlation analysis. The proposed method
adopts a sequential search process to obtain the final
subset of important filters. The major contributions of
this work are as follows:
1. A simple and efficient approach to simplify deep
CNN architectures, which is based on filter
dissimilarity analysis.
2. The importance of a filter is decided by
measuring its distance with other selected and
unselected filters.
3. The selected filters show better representative
ability and less redundancy.
4. Experimental analysis on the TernausNet and U-
Net model trained with the INRIA dataset
demonstrate the effectiveness of the proposed
approach.
The remaining sections of the paper are organized as
follows: The proposed OSFP approach is introduced
in Section 2. Section 3 discusses the experiments and
presents the results. Finally, we conclude this paper
in Section 4.
2 PROPOSED FILTER PRUNING
APPROACH
The proposed method compresses the CNN model by
selecting the important filters while discarding the
remaining ones. The method starts with an empty set
and adds a filter sequentially to it. A filter is added to
the final set by determining its filter priority index
(FPI) which indicates the contribution of the selected
filter. The FPI of the filter is computed by measuring
its representative ability and redundancy with other
selected and unselected filters. The filter is said to be
representative if it is highly correlated (similar) with
other unselected filters of the CNN model, whereas
the filter is said to be less redundant if it is only
marginally correlated (dissimilar) with other selected
filters.
Let us consider a CNN model with L
convolutional layers and each i
th
layer is denoted as
𝐿
. Each 𝐿
consists of N filters indicated as 𝐹
=
𝑓
,𝑓
,𝑓
,…,𝑓
. The dissimilarity matrix D of the
filters of 𝐹
can be expressed as:
𝐷=
⎣
⎢
⎢
⎡
𝑑
,
𝑑
,
𝑑
,
𝑑
,
⋯
𝑑
,
𝑑
,
⋮⋱⋮
𝑑
,
𝑑
,
⋯𝑑
,
⎦
⎥
⎥
⎤
(1)
Here, 𝑑
,
is the dissimilarity between i
th
and j
th
filter. The value of 𝑑
,
depends on the type of metric
used for calculating the dissimilarity between two
filters. For instance, in case of the Manhattan distance
(𝑙
norm), the smaller the value of 𝑑
,
, the higher the
correlation is (two filters are similar to each other).
Correspondingly, in case of the Pearson correlation
coefficient (PCC), the larger the value of 𝑑
,
, the
higher the correlation is. Due to simplicity and ease
of implementation, we will use Manhattan distance to
compute the correlation between two filters.
Moreover, it is less expensive in terms of
computational costs than PCC as well as Euclidean
distance (𝑙
norm).
The proposed method assigns FPI to each
filter and selects the set of important filters,
discarding the unimportant ones. The process selects
one filter each time resulting in a sequential search. It
starts with an empty subset 𝜑. To add the filter into
the set, we need to evaluate its representative ability
by measuring the relative correlation with remaining
unselected filters and by measuring its redundancy.
Let us assume, 𝜑
and 𝜑
be the set of selected and
unselected filters. Consider that we need to select 𝑚
filters out of 𝑁 filters in total and have found 𝑛 filters
𝑛∈
0,𝑚
. To find the
𝑛+1
filter, the relative
correlation of 𝑓
can be evaluated as,
𝐼
=
∑
𝑑
,∈
(2)
Where, 𝐼
indicates the relative correlation of 𝑓
with respect to the remaining unselected filters. The
smaller the value of 𝐼
, the more representative the
filter is. The redundancy of 𝑓
can be calculated as,
𝐼
=
∑
𝑑
,∈
(3)
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
140

Where, 𝐼
indicates the redundancy of 𝑓
with
respect to currently selected filters. Clearly, the larger
the value of 𝐼
, the lesser the redundancy is. Then, the
priority index 𝐼
of the filter 𝑓
can be computed as,
𝐼
=
𝐼
𝐼
(4)
Once the priority index of all filters has been
computed, the filter with maximum index will be
selected and added to the set of important filters. This
process is repeated until the desired set of filters is
obtained. Algorithm 1 gives the overall procedure of
the proposed method for representative filter
selection and pruning of remaining (weak) filters.
Algorithm 1: The proposed method for representative filter
selection and pruning of weak filters.
Input: Original model M, Set of filters of 𝐹
from
each layer 𝐿
, m number of filters to be retained
1. For i=1:L
2. Compute the dissimilarity matrix D. Set 𝜑
=
1, 𝜑
=𝑁, n=1.
3. while 𝑛<𝑚+1 do
4. Compute priority index of each filter using
equation (4).
5. Add the filter with the lowest value in 𝜑
.
6. 𝑛←𝑛+1
7. end while
8. End For
9. Output: Compressed model M’
3 EXPERIMENTS
To assess the effectiveness of the proposed approach,
several tests were conducted on the INRIA Aerial
Image Labeling dataset (Maggiori et al. 2017). The
INRIA dataset consists of training images and test
images. We have used two widely known deep CNN
models for segmentation purposes, namely,
TernausNet (Iglovikov and Shvets 2018) and a
standard U-Net. All the experiments were performed
on Intel Xeon CPU E5-2680 with four cores and
NVIDIA P100 GPU. Both TernausNet and standard
U-Net were trained using the deep learning
framework Pytorch. The hyper-parameter setting
used in the experiments is shown in Table 1. To get
the baseline accuracies for each network, we train
each model from scratch on INRIA dataset and follow
the same data processing as TernausNet (Iglovikov
and Shvets 2018). After the pruning stage, to recover
the performance of the pruned model, fine-tuning is
performed by training the pruned model for 15
epochs. We have used three metrics to evaluate the
performance of the segmentation task, such as,
validation accuracy (Val. Acc.), validation loss and
Jaccard index (also known as Intersection over Union
(IoU)). In order to assess the performance of the
compressed model, the number of parameters and
FLOPs are reported. We evaluated the proposed
method on the INRIA dataset with TernausNet and U-
Net by varying pruning rates and results are discussed
in following subsections.
Table 1: Hyper-parameter setting re-training/ fine-tuning of
pruned network.
Hyper-parameter Value
Number of epochs 15
O
p
timize
r
Adam
Optimizer learning rate 0.0001
Optimizer betas (0.9, 0.999)
Loss function Binar
y
cross entro
py
Batch size 64
3.1 TernausNet on INRIA
The experimental results for the TernausNet are
reported in Table 2 and Table 3. Table 2 shows the
overall performance of the proposed approach under
different pruning ratios. As shown in Table 2, the
baseline model achieved lowest Val. loss (0.1031),
but had an enormous amount of memory (22.9
Million parameters) and a slow inference speed (23.5
Billion FLOPs). Note that the proposed approach
demonstrated a significantly better performance than
the unpruned model, even at higher pruning rates.
Especially, at 70% pruning rate, the proposed method
reduced the FLOPs by 69.75% with only 0.64% drop
in the Val. Acc., which is quite negligible. As the
pruning amount exceeded 70%, the performance
started to degrade. TernausNet has many redundant
filters. So, even when more filters were pruned, the
performance degradation was still negligible in
general. We can conclude that when a large amount
of FLOPs and parameters are reduced, the proposed
approach still achieves comparable performance.
This means the proposed method effectively retains
the filters, which exhibit great generalization ability.
To validate the effectiveness of the proposed
approach, the performance of the proposed approach
is compared with two other state-of-the-art methods,
such as, magnitude based filter pruning- 𝑙
similarity
(Li et al. 2017) and random pruning (Mittal et al.
2019). 𝑙
similarity based method removes the filters
with smaller weight, whereas a random pruning
method prunes the filters randomly. Furthermore, we
have tested other dissimilarity metrics namely, PCC
A Simple and Effective Convolutional Filter Pruning based on Filter Dissimilarity Analysis
141
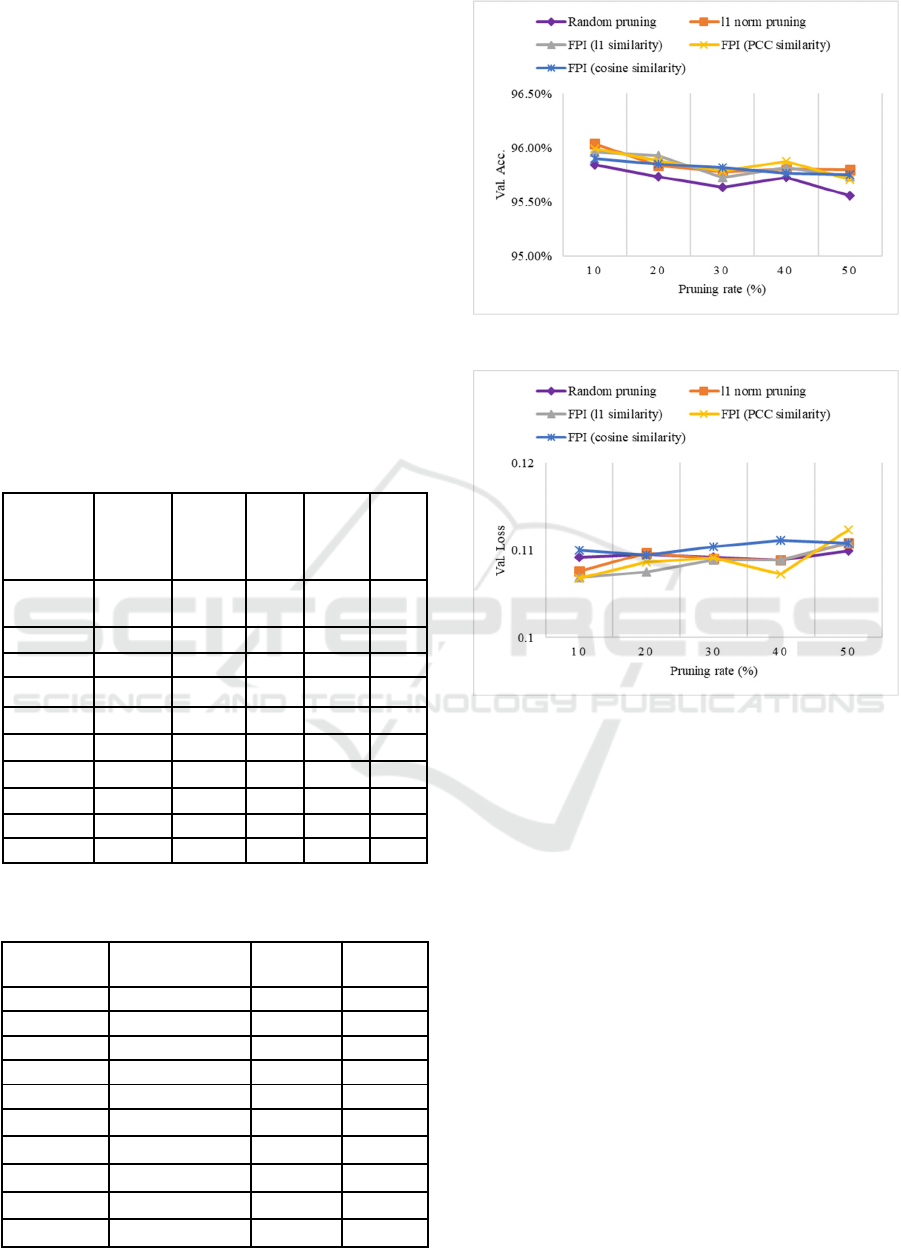
and cosine dissimilarity. The performance in terms of
Val. Acc. and Val. loss after fine-tuning is recorded
in Fig. 1. All approaches have shown lower
performance before fine-tuning. Therefore, accuracy
is restored by fine-tuning the pruned model for
several epochs. Though, random pruning shows
almost equal performance, it is not a robust method in
practice and may lead to unstable accuracies when
applied to a larger model. Compared to state-of-the-
art methods, the proposed approach performs at a
moderate level and shows acceptable error.
Moreover, when PCC is used as a dissimilarity
measure, it reduces the redundancy better and
performs comparably better than state-of-the-art
methods as well as other metrics. This analysis
completely confirms effectiveness of different
metrics in dissimilarity measures of convolutional
filters and flexibility for filter pruning.
Table 2: Overall Performance of our approach on
TernausNet with different pruning rate.
Pruning
rate
(%)
Number
of
Param.
(Million)
FLOPs
(Billion)
Val.
Acc.
(%)
Val.
loss
IoU
Baseline
(unpruned)
22.9 23.5 96.02 0.1031
0
.4599
10
21.0
21.2 95.95 0.1069 0.4653
20 19.0 18.9 95.92 0.1075 0.4602
30
17.0
16.6 95.72 0.1109 0.4566
40
15.0
14.2 95.81 0.1089 0.4567
50
13.0
11.8 95.73 0.1109 0.4539
60
11.1
9.48 95.46 0.1173 0.4397
70
9.09
7.12 95.38 0.1193 0.4338
80 7.12 4.79 94.90 0.1314 0.4122
90 5.15 2.43 94.20 0.1465 0.3759
Table 3: Pruning statistics for TernausNet on Inria dataset
under different pruning rates.
Pruning rate
(
%
)
Reduction in
number of Param.
Reduction
in FLOPs
Change in
Val. Acc.
Baseline 0% 0% --
10 8.57% 9.73% -0.06%
20 17.19% 19.75% -0.10%
30 25.77% 29.65% -0.30%
40 34.39% 39.66% -0.21%
50 43.15% 50.00% -0.29%
60 51.73% 59.73% -0.57%
70 60.34% 69.75% -0.64%
80 68.93% 79.65% -1.13%
90 77.54% 89.66% -1.82%
(a)
(b)
Figure 1: Performance of different filter pruning
approaches on TernausNet under different pruning rate. The
model was trained, fine-tuned and validated on a cropped
image of 256 256 resolution. (a) Val. Acc. vs pruning
rate (b) Val. loss vs. pruning rate.
3.2 U-Net on INRIA
Table 4 and 5 show the experimental results for a U-
Net. As shown in Table 4, the baseline model
achieved lowest Val. loss (0.1054), but had an
enormous amount of memory (31 Million
parameters) and a slow inference speed (46 Billion
FLOPs). At 70% pruning rate, the Val. Acc. of the
proposed method was reduced by 0.95% in
comparison with the baseline model, but the number
of parameters was reduced by 63.62% and the
necessary FLOPs were also significantly reduced by
69.60%. In other words, the proposed method offers
excellent performance in terms of Val. Acc., FLOPs
and number of parameters over different pruning
rates. This excellent performance is in line with the
results of the TernausNet. We can conclude that when
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
142
a large amount of FLOPs and parameters are reduced,
the proposed approach still obtains comparable
performance. This means the proposed method
effectively retains the filters which exhibit great
generalization ability. Moreover, both the models are
trained from scratch instead of using pre-trained
weights and results show that the proposed approach
is independent of the pre-trained model’s
performance and helps filters to learn their
responsibility.
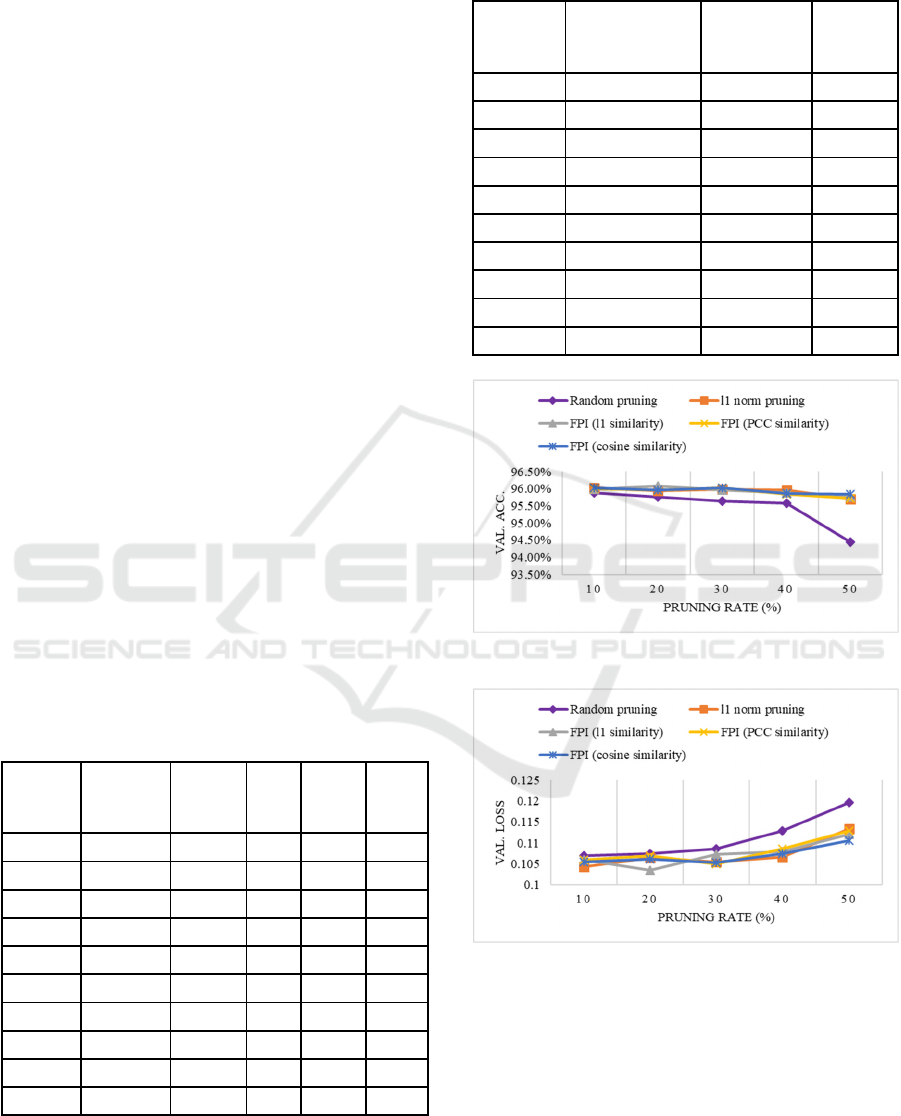
To validate the effectiveness of the proposed
approach, the performance of the proposed approach
is compared with two other state-of-the-art methods,
such as, magnitude based filter pruning- 𝑙
similarity
and random pruning. Furthermore, we have tested
other dissimilarity metrics namely, PCC and cosine
dissimilarity. The performance in terms of Val. Acc.
and Val. loss after fine-tuning is recorded in Fig. 2.
All approaches have shown lower performance
before fine-tuning. Therefore, accuracy is restored by
fine-tuning the pruned model for several epochs.
Random pruning method has achieved lowest Val.
Acc. at all pruning rates among all methods.
Compared to state-of-the-art methods, the proposed
approach performs at a moderate level and shows
acceptable error. Moreover, when PCC is used as a
dissimilarity measure, it reduces the redundancy
better and performs comparably better than state-of-
the-art methods as well as other metrics. This analysis
completely confirms effectiveness of different
metrics in dissimilarity measures of convolutional
filters and flexibility for filter pruning.
Table 4: Overall Performance of our approach on U-Net
with different pruning rate.
Pruning
rate
(%)
Number
of Param.
(Million)
FLOPs
(Billion)
Val.
Acc.
(%)
Val.
loss
IoU
Baseline 31.0 46.0 96.13 0.1054 0.4714
10 28.2 41.6 96.04 0.1043 0.4647
20 25.4 37.0 95.98 0.1056 0.4633
30 22.6 32.3 95.98 0.1065 0.4648
40 19.8 27.8 95.87 0.1088 0.4541
50 16.9 23.0 95.64 0.1142 0.4486
60 14.1 18.6 95.39 0.1212 0.4361
70 11.3 14.0 95.27 0.1217 0.4292
80 8.47 9.32 94.82 0.1337 0.4144
90 5.65 4.75 92.97 0.1721 0.3203
Table 5: Pruning statistics for U-Net on Inria dataset under
different pruning rates.
Pruning
rate
(%)
Reduction in
number of
Param.
Reduction in
FLOPs
Change in
Val. Acc.
Baseline 0% 0% --
10 9.03% 9.66% -0.09%
20 18.03% 19.58% -0.15%
30 27.10% 29.86% -0.15%
40 36.13% 39.63% -0.26%
50 45.48% 50.05% -0.49%
60 54.52% 59.61% -0.74%
70 63.55% 69.60% -0.86%
80 72.68% 79.76% -1.31%
90 81.77% 89.68% -3.16%
(a)
(b)
Figure 2: Performance of different filter pruning
approaches on U-Net under different pruning rate. The
model was trained, fine-tuned and validated on a cropped
image of 256 256 resolution. (a) Val. Acc. vs pruning
rate (b) Val. loss vs. pruning rate.
A Simple and Effective Convolutional Filter Pruning based on Filter Dissimilarity Analysis
143

4 CONCLUSION AND FUTURE
WORK
In this paper, a simple and effective filter pruning
method based on filter correlation analysis is
proposed. The new method searches for a subset of
filters that can reliably and adequately represent the
structure of the original model. The proposed method
iteratively adds filters with better representative
ability and less redundancy into the final set of
retained filters, discarding the others. Unlike the
existing norm based criterion, the proposed method
explicitly considers the correlation among filters. The
pruned model with the proposed method learns
effectively with few filters. Thus, when pruning a
TernausNet trained on the INRIA dataset by the
proposed method, FLOPs reduction rates are as high
as 89.65% accompanied by a negligible drop in the
Val. Acc. ( <2% ). The experimental analysis on
TernausNet and U-Net confirms the robustness of the
proposed approach. However, iterative searching for
the representative filters takes some good amount of
time. Therefore, it will be our future work to explore
a way to render the method faster.
ACKNOWLEDGEMENTS
The authors would like to thank the Fraunhofer
Institute for Integrated Circuits for providing
infrastructure for carrying out this research work and
the European Research Consortium for Informatics
and Mathematics (ERCIM) for the award of Research
Fellowship.
REFERENCES
Ahmadi, Mahdi, Alireza Norouzi, Nader Karimi, Shadrokh
Samavi, and Ali Emami. 2020. “ReDMark : Framework
for Residual Diffusion Watermarking Based on Deep
Networks” 146. https://doi.org/10.1016/j.eswa.2019.11
3157.
Han, Song, Huizi Mao, and William J. Dally. 2016. “Deep
Compression: Compressing Deep Neural Networks
with Pruning, Trained Quantization and Huffman
Coding.” 4th International Conference on Learning
Representations, ICLR 2016 - Conference Track
Proceedings, 1–14.
Han, Song, Jeff Pool, John Tran, and William J. Dally.
2015. “Learning Both Weights and Connections for
Efficient Neural Networks.” Advances in Neural
Information Processing Systems 2015-Janua: 1135–43.
He, Yang, Ping Liu, Ziwei Wang, Zhilan Hu, and Yi Yang.
2019. “Filter Pruning via Geometric Median for Deep
Convolutional Neural Networks Acceleration.”
Proceedings of the IEEE Computer Society Conference
on Computer Vision and Pattern Recognition 2019-
June: 4335–44. https://doi.org/10.1109/CVPR.2019.0
0447.
Iglovikov, Vladimir, and Alexey Shvets. 2018.
“TernausNet: U-Net with VGG11 Encoder Pre-Trained
on Imagenet for Image Segmentation.” ArXiv.
Jang, Yunseok, Sangyoun Lee, and Jaeseok Kim. 2021.
“Compressing Convolutional Neural Networks by
Pruning Density Peak Filters.” IEEE Access 9: 8278–
85. https://doi.org/10.1109/ACCESS.2021.3049470.
Li, Hao et al. 2017. “Pruning Filters for Efficient
Convnets.” 5th International Conference on Learning
Representations, ICLR 2017 - Conference Track
Proceedings (2016): 1–13.
Liao, Xin, Kaide Li, Xinshan Zhu, and K. J.Ray Liu. 2020.
“Robust Detection of Image Operator Chain with Two-
Stream Convolutional Neural Network.” IEEE Journal
on Selected Topics in Signal Processing 14 (5): 955–
68. https://doi.org/10.1109/JSTSP.2020.3002391.
Liu, Chih Ting, Tung Wei Lin, Yi Heng Wu, Yu Sheng Lin,
Heng Lee, Yu Tsao, and Shao Yi Chien. 2019.
“Computation-Performance Optimization of
Convolutional Neural Networks with Redundant Filter
Removal.” IEEE Transactions on Circuits and Systems
I: Regular Papers 66 (5): 1908–21. https://doi.org/
10.1109/TCSI.2018.2885953.
Liu, Na, Lihong Wan, Yu Zhang, Tao Zhou, Hong Huo, and
Tao Fang. 2018. “Exploiting Convolutional Neural
Networks With Deeply Local Description for Remote
Sensing Image Classification.” IEEE Access 6 (c):
11215–27. https://doi.org/10.1109/ACCESS.2018.279
8799.
Liu, Xuefeng, Qiaoqiao Sun, Bin Liu, Biao Huang, and Min
Fu. 2017. “Hyperspectral Image Classification Based
on Convolutional Neural Network and Dimension
Reduction,” no. 61401244: 1686–90.
Lunga, Dalton, Hsiuhan Lexie Yang, Andrew Reith,
Jeanette Weaver, Jiangye Yuan, and Budhendra
Bhaduri. 2018. “Domain-Adapted Convolutional
Networks for Satellite Image Classification: A Large-
Scale Interactive Learning Workflow.” IEEE Journal of
Selected Topics in Applied Earth Observations and
Remote Sensing 11 (3): 962–77. https://doi.org/10.11
09/JSTARS.2018.2795753.
Luo, Jian Hao, and Jianxin Wu. 2017. “An Entropy-Based
Pruning Method for CNN Compression.” ArXiv.
Ma, Xiaolong, Sheng Lin, Shaokai Ye, Zhezhi He, Linfeng
Zhang, Geng Yuan, Sia Huat Tan, et al. 2021. “Non-
Structured DNN Weight Pruning--Is It Beneficial in
Any Platform?” IEEE Transactions on Neural
Networks and Learning Systems, 1–15. https://doi.org/
10.1109/TNNLS.2021.3063265.
Maggiori, Emmanuel, Yuliya Tarabalka, Guillaume
Charpiat, and Pierre Alliez. 2017. “Can Semantic
Labeling Methods Generalize to Any City? The INRIA
Aerial Image Labeling Benchmark.” International
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
144

Geoscience and Remote Sensing Symposium (IGARSS)
2017-July: 3226–29. https://doi.org/10.1109/IGARSS.
2017.8127684.
Mittal, Deepak, Shweta Bhardwaj, Mitesh M. Khapra, and
Balaraman Ravindran. 2019. “Studying the Plasticity in
Deep Convolutional Neural Networks Using Random
Pruning.” Machine Vision and Applications 30(2): 203–
16. https://doi.org/10.1007/s00138-018-01001-9.
Molchanov, Pavlo, Stephen Tyree, Tero Karras, Timo Aila,
and Jan Kautz. 2017. “Pruning Convolutional Neural
Networks for Resource Efficient Inference.” 5th
International Conference on Learning Representations,
ICLR 2017 - Conference Track Proceedings, no. 2015:
1–17.
Shi, Jun, Jianfeng Xu, Kazuyuki Tasaka, and Zhibo Chen.
2021. “SASL: Saliency-Adaptive Sparsity Learning for
Neural Network Acceleration.” IEEE Transactions on
Circuits and Systems for Video Technology 31 (5):
2008–19. https://doi.org/10.1109/TCSVT.2020.3013
170.
Torfi, Amirsina, Rouzbeh A. Shirvani, Sobhan Soleymani,
and Nasser M. Nasrabadi. 2018. “Attention-Based
Guided Structured Sparsity of Deep Neural Networks.”
ArXiv, no. 1: 1–5.
Wang, Zongyue, Shaohui Lin, Jiao Xie, and Yangbin Lin.
2019. “Pruning Blocks for CNN Compression and
Acceleration via Online Ensemble Distillation.” IEEE
Access 7: 175703–16. https://doi.org/10.1109/
ACCESS.2019.2957203.
Wen, Liangjian, Xuanyang Zhang, Haoli Bai, and Zenglin
Xu. 2020. “Structured Pruning of Recurrent Neural
Networks through Neuron Selection.” Neural Networks
123: 134–41. https://doi.org/10.1016/j.neunet.2019.
11.018.
Xu, Xiaodong, Wei Li, Qiong Ran, Qian Du, Lianru Gao,
and Bing Zhang. 2018. “Multisource Remote Sensing
Data Classification Based on Convolutional Neural
Network.” IEEE Transactions on Geoscience and
Remote Sensing 56 (2): 937–49. https://doi.org/
10.1109/TGRS.2017.2756851.
Zeng, Junying, Boyuan Zhu, Yujie Huang, Chuanbo Qin,
Jingming Zhu, Fan Wang, Yikui Zhai, et al. 2021.
“Real-Time Segmentation Method of Lightweight
Network for Finger Vein Using Embedded Terminal
Technique.” IEEE Access 9: 303–16. https://doi.org/
10.1109/ACCESS.2020.3046108.
Zuo, Yuding, Bo Chen, Te Shi, and Mengfan Sun. 2020.
“Filter Pruning without Damaging Networks
Capacity.” IEEE Access 8: 90924–30. https://doi.org/
10.1109/ACCESS.2020.2993932.
A Simple and Effective Convolutional Filter Pruning based on Filter Dissimilarity Analysis
145
