Taking Advantage of Typical Testor Algorithms for Computing

Non-reducible Descriptors

Manuel S. Lazo-Cortés

1 a

, José Fco. Martínez-Trinidad

2 b

, J. Ariel Carrasco-Ochoa

2 c

Ventzeslav Valev

3 d

, Mohammad Amin Shamshiri

4 e

and Adam Krzy

zak

4 f

TecNM/Instituto Tecnológico de Tlalnepantla, Edo. de Mexico 54070, Mexico

Instituto Nacional de Astrofísica, Óptica y Electrónica, Puebla 72840, Mexico

Institute of Mathematics and Informatics, Bulgarian Academy of Sciences, 1113 Soﬁa, Bulgaria

Department of Computer Science and Software Engineering, Concordia University, Montreal, H3G 1M8, Canada

Keywords:

Non-reducible Descriptor, Typical Testor, Feature Selection.

Abstract:

The concepts of non-reducible descriptor (NRD) and typical testor (TT) have been used for solving quite

different pattern recognition problems, the former related to feature selection problems and the latter related to

supervised classiﬁcation. Both TT and NRD concepts are based on the idea of discriminating objects belonging

to different classes. In this paper, we theoretically examine the connection between these two concepts. Then,

as an example of the usefulness of our study, we present how the algorithms for computing typical testors can

be used for computing non-reducible descriptors. We also discuss several future research directions motivated

by this work.

1 INTRODUCTION

In pattern recognition, both feature selection and pat-

tern discovery provide useful information for object

classiﬁcation. Although they are quite different prob-

lems they often deal with similar topics and involve

the same data properties into their formalism. An

example of this occurs with the concepts of typical

testors (TTs) and non-reducible descriptors (NRDs).

Some supervised pattern recognition applications

deal with binary features like in medicine, namely,

presence or absence of a given symptom. Hence,

the information needed for pattern classiﬁcation is

generally included in various combinations of binary

features. The mathematical model that uses binary

features for describing patterns is based on learning

Boolean formulas. An NRD is a descriptor with min-

imal length and hence, different NRDs for a given

object may have different lengths. The length of the

https://orcid.org/0000-0001-6244-2005

https://orcid.org/0000-0001-7973-9075

https://orcid.org/0000-0002-9982-7758

https://orcid.org/0000-0002-1084-3605

https://orcid.org/0000-0001-8231-3972

https://orcid.org/0000-0003-0766-2659

NRD is obtained during the process of its construc-

tion. General approach to feature selection based on

mutual information is described in (Kwak and Choi,

2002).

Typical testors derive from the test theory

(Cheguis and Yablonskii, 1955; Chikalov et al.,

2012). A typical testor is a feature subset where fea-

tures are jointly sufﬁcient and each feature is nec-

essary to discriminte among object descriptions be-

longing to different classes. Thus, typical testors are

commonly used for feature selection, see, e.g., (Pons-

Porrata et al., 2007). On the other hand, a non-

reducible descriptor (Valev, 2014; Valev and Sankur,

2004) for a certain object in a particular class is a se-

quence of values of its features that makes this ob-

ject different from the descriptions of objects in the

remaining classes. Thus, descriptors refer to the in-

formation needed for classifying an object, which

may be contained in some combinations of several

of its features. The assumption that these concepts

are closely related is based on the fact that both con-

cepts focus in discriminating objects belonging to dif-

ferent classes. The complexity of computing all typ-

ical testors of a training matrix grows exponentially

with respect to the number of features. Several meth-

188

Lazo-Cortés, M., Martínez-Trinidad, J., Carrasco-Ochoa, J., Valev, V., Shamshiri, M. and Krzy

zak, A.

Taking Advantage of Typical Testor Algorithms for Computing Non-reducible Descriptors.

DOI: 10.5220/0010797300003122

In Proceedings of the 11th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2022), pages 188-194

ISBN: 978-989-758-549-4; ISSN: 2184-4313

ods that speed up the calculation of the set of all

typical testors have been developed, see, e.g., (Lias-

Rodríguez and Pons-Porrata, 2009).

In this paper, we theoretically examine the con-

nection between these two concepts. Additionally,

as a result of this study, we introduce a way for tak-

ing advantage of the algorithms for computing typical

testors to compute non-reducible descriptors.

The rest of the paper is organized as follows. In

Section 2, we provide the theoretical foundations of

typical testors and non-reducible descriptors. Sec-

tion 3 presents the connection between both concepts

as well as an example of its use for applying algo-

rithms for computing typical testors, but for comput-

ing non-reducible descriptors. An illustrative exam-

ple for showing the usefulness of our study is pre-

sented in Section 4. Finally, in Section 5 some con-

cluding remarks are discussed.

2 THEORETICAL

FOUNDATIONS

Let us consider a supervised pattern recognition prob-

lem. We denote by U the set of all objects, U is the

union of a ﬁnite number of subsets C

, C

, . . . , C

which are called classes. We assume that these classes

are disjoint.

Each object Q

∈ U is described in terms of n fea-

tures R={x

,..., x

} as an n-tuple (x

),x

... , x

)). However, the known information corre-

sponds only to a reduced subset, TS ⊆ U called the

training set. We assume that |T S| = m; i. e., there

are m objects in T S, which are distributed into the r

classes; it means that all classes are represented by at

least one object in the training set. We will denote by

the number of objects in TS belonging to the class

. Thus, m

+... +m

= m. This information is

organized in a matrix called training matrix, denoted

by TM

m,n,r

. When this does not generate confusion,

we will use only TM.

For the purposes of this work, we will restrict the

problem to the case in which objects are described by

only binary features. A typical example of a pattern

recognition problem with binary features would be a

medical diagnosis based on the presence or absence

of several symptoms. Table 1 shows an example of

a training matrix with six objects, seven features and

two classes. The last column contains the class each

object belongs to.

The supervised pattern recognition problem is for-

mulated as follows. Using the training matrix and

the description of an unseen object Q ∈ U\TS, the

problem consists in assigning Q to one of the classes

Table 1: An example of TM.

6,7,2







class

0 0 1 1 0 1 0 C

1 0 0 0 0 1 0 C

0 1 0 0 1 0 0 C

0 0 0 1 0 1 1 C

0 0 1 1 1 0 0 C

1 0 1 1 0 0 1 C







, ...C

. The descriptions of objects in T M are as-

sumed to be in terms of Boolean features. Thus, for

the object Q each entry with “1” is equivalent to the

presence of the respective binary feature, while a “0”

means that the respective feature is absent, this can

be expressed as the negation of the respective binary

feature.

2.1 Typical Testors

The concept of testor was originally formulated by

Cheguis and Yablonskii (Cheguis and Yablonskii,

1955), after that, Zhuravlev (Dmitriev et al., 1966)

introduced this concept into the framework of pattern

recognition theory. And then the concept has been ex-

tended in several directions (Lazo-Cortes et al., 2001).

Below, we formulate the deﬁnitions of testor and typ-

ical testor.

Deﬁnition 1. T ⊆ R is a testor for TM if in the sub-

matrix of the training matrix T M, containing only

columns associated to features in T , all rows corre-

sponding to objects belonging to different classes are

different.

It means that if T is a testor, and in the correspond-

ing sub-matrix of T M there are two equal rows, they

are sub-descriptions of two objects that belong to the

same class. Among testors, there are some of them

where all their features are essential for discriminat-

ing objects from different classes. Such testors are

called typical testors and are deﬁned as follows.

Deﬁnition 2. If T ⊆ R is a testor such that none of

its proper subsets is a testor, then we call T a typical

testor.

These deﬁnitions mean that features belonging to

a testor are jointly sufﬁcient to discriminate between

any pair of objects belonging to different classes. If

a testor is typical, each feature is individually neces-

sary.

For the training matrix in Table 1, the following

subsets of features {x

, x

}, {x

, x

}, {x

, x

}

are examples of testors. It is not difﬁcult to observe

that if we reduce this training matrix considering only

the columns corresponding to one of these sets of fea-

tures, none of the ﬁrst four rows (corresponding to

Taking Advantage of Typical Testor Algorithms for Computing Non-reducible Descriptors

189

class C

) is confused with the last two rows (corre-

sponding to class C

). Since {x

, x

} is a subset of

, x

}, then {x

, x

} is not a typical testor, but

, x

} is a typical testor. We can easily corrobo-

rate it, since if we eliminate x

from {x

, x

} then

the rows 3 and 5 in Table 1 are indistinguishable (the

same happens with rows 3 and 6); if we eliminate x

from {x

, x

}, the rows 1 and 5 in Table 1 are also

indistinguishable (the same happens with rows 1 and

6). For Table 1, the whole set of typical testors is

{{x

, x

} , {x

, x

} , {x

, x

}, {x

, x

} , {x

, x

} , {x

, x

}}.

Several algorithms for computing all typical

testors have been proposed, for example (Lias-

Rodríguez and Pons-Porrata, 2009; Piza-Davila et al.,

2018; Sanchez-Díaz and Lazo-Cortés, 2007).

2.2 Non-reducible Descriptors

The concept of non-reducible descriptor was intro-

duced in (Djukova, 1989). This concept has been ex-

tended in several directions (Valev and Radeva, 1996;

Valev and Sankur, 2004).

Below, we introduce the concept of non-reducible

descriptor using the notations previously presented.

Deﬁnition 3. Let Q

= (x

), x

), ... , x

))

be an object in TS. The subsequence (x

), ... , x

)), j

≤ n, is called a descrip-

tor of object Q

, if there does not exist any object in

TS, belonging to a class different from the class of Q

with the same subsequence of values.

Deﬁnition 4. A descriptor is called a Non-Reducible

Descriptor (NRD) if none of its proper sub-sequences

is a descriptor.

Deﬁnition 4 means that if an arbitrarily chosen

feature is removed from a non-reducible descriptor,

then this subsequence loses its property of descriptor.

Therefore, an NRD is a descriptor of minimal length.

Being T ⊆ R a subset of features, Q|

denotes the

partial description of Q considering only features be-

longing to T. For simplicity, in the representation of

as an n-tuple we will use a dot “.” in the respec-

tive entry of the n-tuple for indicating that the corre-

sponding feature is not being taken into account.

In Table 1, if we consider, for example, the

ﬁrst object Q

, then (0, 0, ., ., 0, ., 0) (i.e. x

= x

= 0) is a descriptor since the object Q

be-

longs to class C

and that combination does not ap-

pear in any object of class C

, however this descrip-

tor does not fulﬁl being a non-reducible descriptor,

since (0, ., ., ., 0, ., .) (x

= x

= 0) is also a descrip-

tor of the object Q

, and in this case, the descrip-

tor (0, ., ., ., 0, ., .) is non-reducible. The descriptor

(., ., ., ., ., 1, .) is also a non-reducible descriptor for the

object Q

of Table 1, since x

6= 1 for all objects of

class C

Algorithms for construction of NRDs based on the

dissimilarity matrix concept following a combinato-

rial approach have been proposed in (Valev, 2014) and

(Valev and Sankur, 2004).

3 OUR THEORETICAL STUDY

A very important aspect to highlight in any analy-

sis that involves typical testors and non-reducible de-

scriptors, is that the former are relative to a training

sample as a whole, that is, all classes are considered

together. Notice that a testor is a combination of fea-

tures that allows differentiating any pair of objects

that belong to different classes, and a testor is typ-

ical if all its features are essential for this purpose;

however, when we refer to a non-reducible descrip-

tor, we are referring speciﬁcally to an object in the

training set, a descriptor is a combination of values

of certain features, which characterizes that speciﬁc

object in the training set and distinguishes this object

from all the objects belonging to the other classes.

With this perspective, let us analyze the connec-

tion between testors and descriptors.

Proposition 1. Let TM be a training matrix. If T ⊆ R

is a testor for TM then each combination of values of

the features in T is a descriptor for the object in which

this combination appears.

Corollary 1. Let T M be a training matrix. If T ⊆ R

is a typical testor in T M then each combination of

values of the features in T is a descriptor (not neces-

sarily non-reducible) for the object in which the com-

bination appears.

We can see, by using Table 1, that a combination

of values associated with a typical testor does not nec-

essarily become a non-reducible descriptor.

For example, {x

, x

} is a typical testor for T M.

Then (., 0, ., ., ., 1, .) is a descriptor for Q

, Q

and

, but this descriptor is not an NRD because the de-

scriptor (., ., ., ., ., 1, .) is also a descriptor for Q

, Q

and Q

. The descriptor (., 1, ., ., ., 0, .) is a descriptor

for Q

but it is not an NRD, because the descriptor

(., 1, ., ., ., ., .) is also a descriptor for Q

. On the other

hand, the descriptor (., 0, ., ., ., 0, .) is an NRD for Q

and Q

Let us now consider an object in the training ma-

trix TM that appears in Table 1, for example Q

be-

longing to class C

. We build a new two class (C

, C

)

training matrix TM

m−m

+1,n,2

from T M by consider-

ing Q

as the only object in the class C

of the new

ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods

190

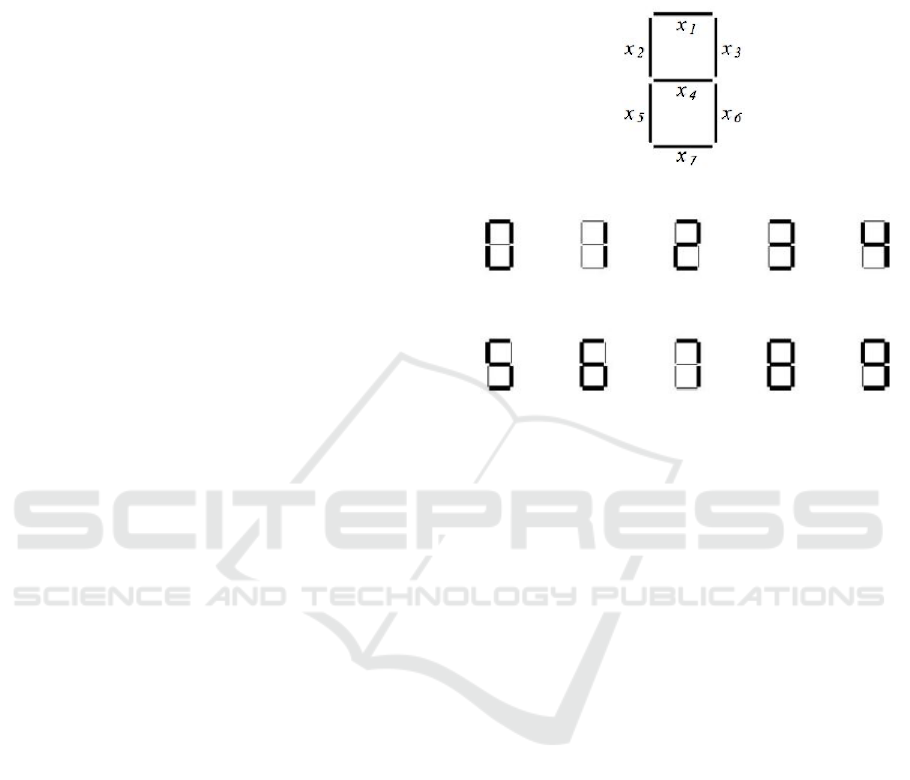
Table 2: Training matrix corresponding to object Q

regard-

ing TM in Table 1.

TM(Q

) =





0 0 1 1 0 1 0 C

0 0 1 1 1 0 0 C

1 0 1 1 0 0 1 C





TM(Q

) = TM

3,7,2

training matrix, while those objects belonging to the

other classes in TM, different from C

, will belong to

the class C

in the new training matrix. From Table

1, by applying the procedure above described for Q

we get the training matrix shown in Table 2.

Let us denote the training matrix derived from this

procedure, for object Q

TM(Q

Proposition 2. Let T = {x

, x

, ..., x

} be a typi-

cal testor in

TM(Q

), then the subsequence (x

),..., x

)) is a non-reducible descriptor for

Proposition 3. Let the subsequence (x

), ..., x

)) be a non-reducible descriptor

for Q

, then T = {x

, x

, ..., x

} is a typical testor

TM(Q

Corollary 2. Let TM be a training matrix and let

NRD(Q

) be the set of all non-reducible descrip-

tors for Q

, then NRD(Q

) = {(x

), x

), ...

)) such that {x

, x

, ... , x

} is a typical

testor in

TM(Q

)}.

Corollary 2 allows us to deﬁne a strategy for com-

puting all NRDs for a TM by computing typical

testors as follows:

For each object Q

of TM:

Obtain

TM(Q

Compute the set Ψ

∗

(

TM(Q

) of all typical

testors in the matrix

TM(Q

For each typical testor T =

, x

, ..., x

} ∈ Ψ

∗

(

TM(Q

Generate the subsequence (x

), ..., x

)).

Save the subsequence as an NRD for Q

4 ILLUSTRATIVE EXAMPLE

In order to illustrate our proposed strategy for com-

puting all NRDs by the algorithm for computing typ-

ical testors let us consider the problem of Arabic nu-

merals recognition as discussed in (Valev, 9962). In

this example, each digit is represented by a 7-segment

display as shown in Figure 1. Each display segment

is a feature useful for describing a digit. The Arabic

numerals be represented as in Figure 2. Considering

the features ordered from x

to x

as in Figure 1, we

obtain the training matrix shown in Table 3. Notice

that in TM

10,7,10

each row represents a class.

Figure 1: Features describing Arabic numerals.

Figure 2: The Arabic numerals represented by a 7-segment

display.

Table 3: Training matrix for the Arabic numerals in Fig.2.

10,7,10







class

1 1 1 0 1 1 1 0

0 0 1 0 0 1 0 1

1 0 1 1 1 0 1 2

1 0 1 1 0 1 1 3

0 1 1 1 0 1 0 4

1 1 0 1 0 1 1 5

1 1 0 1 1 1 1 6

1 0 1 0 0 1 0 7

1 1 1 1 1 1 1 8

1 1 1 1 0 1 1 9







In the ﬁrst column of Table 4 appears each Ara-

bic numeral, the second column shows all the non-

reducible descriptors of these Arabic numerals (the

non-reducible descriptors that appear in this column

are those reported in [15]), while in the third column

the corresponding typical testors are shown. For ex-

ample, if we look at the third row, we notice that there

are two typical testors, namely, {x

} and {x

, x

};

this means that if we take the values corresponding

to these features for the Arabic numeral “2”, that is,

= 0, or x

= 0 and x

= 1, we obtain the two non-

reducible descriptors corresponding to the Arabic nu-

meral “2”, as it can be seen in the second column of

Table 4. In Figure 2, it can be seen that the Arabic nu-

meral “2” is the only digit that does not have the lower

right vertical segment. Likewise, the Arabic numeral

“2” is the only digit for which the upper left vertical

Taking Advantage of Typical Testor Algorithms for Computing Non-reducible Descriptors

191

Table 4: Non-reducible descriptors and typical testors for Arabic numerals.

Non-reducible descriptors Corresponding features

0 {., 1, ., 0, ., ., .}, {., ., ., 0, 1, ., .}, {., ., ., 0, ., ., 1} {x

, x

},{x

, x

},{x

, x

}

1 {0, ., ., 0, ., ., .}, {0, 0, ., ., ., ., .} {x

, x

},{x

, x

}

2 {., ., ., ., ., 0, .}, {., 0, ., ., 1, ., .} {x

},{x

, x

}

3 {., 0, ., ., ., 1, 1}, {., 0, ., 1, 0, ., .}, {., 0, ., 1, ., 1, .}, {., 0, ., ., 0, ., 1} {x

, x

},{x

, x

},{x

, x

},{x

, x

}

4 {0, 1, ., ., ., ., .}, {0, ., ., 1, ., ., .}, {., 1, ., ., ., ., 1}, {., ., ., 1, ., ., 0} {x

, x

},{x

, x

},{x

, x

},{x

, x

}

5 {., ., 0, ., 0, ., .} {x

, x

}

6 {., ., 0, ., 1, ., .} {x

, x

}

7 {1, 0, ., 0, ., ., .}, {1, ., ., 0, 0, ., .}, {1, ., ., ., ., ., 0} {x

, x

},{x

, x

},{x

, x

}

8 {., 1, 1, 1, 1, ., .}, {., ., 1, 1, 1, 1, .} {x

, x

}, {x

, x

}

9 {1, 1, 1, ., 0, ., .}, {., 1, 1, ., 0, ., 1} {x

, x

}, {x

, x

}

segment is omitted and the lower left vertical segment

is present.

The only typical testor for Table 3 is

, x

}. From the training matrix shown

in Table 3, we build the training matrices

TM(0),

TM(1),...,

TM(9) accordingly to the strategy for

computing all NRDs explained above in Section 3.

Thus, we have ten two-class problems, one for each

digit. For each matrix, typical testors were computed

by using the YYC algorithm (Piza-Davila et al.,

2018), here it is convenient to remember that any

other algorithm for computing typical testors could be

used. All calculations were carried out on an Intel(R)

Core(TM) Duo CPU T5800 @ 2.00 GHz 64-bit

system with 4 GB of RAM running on Windows 10.

For each matrix less than one second was required

for computing all typical testors. This illustrative

example shows that our proposed strategy based on

typical Testors for computing NDRs, introduced in

section 3, obtains the same NRDs reported in (Valev,

2014).

We also derive NRDs for problem with faulty dis-

plays, where we distinguish Arabic numerals from

non-numeral patterns. The data matrix is given in Ta-

ble 5 and the corresponding NRDs and features in Ta-

ble 6. These calculations were carried out on an In-

tel(R) Core(TM) i7-3630QM CPU @ 2.40 GHz 64-

bit system with 8 GB of RAM running on Windows

10.

5 CONCLUSIONS

The main purpose of the research reported in this pa-

per is presenting a theoretical study of the connec-

tion between the concepts of typical testor and non-

reducible descriptor, which come from two different

problems of pattern recognition.

Table 5: Training matrix for the Arabic numerals in Fig.2

and non-numeral patterns.

128,7,2







class

1 1 1 0 1 1 1 0

0 0 1 0 0 1 0 1

1 0 1 1 1 0 1 2

1 0 1 1 0 1 1 3

0 1 1 1 0 1 0 4

1 1 0 1 0 1 1 5

1 1 0 1 1 1 1 6

1 0 1 0 0 1 0 7

1 1 1 1 1 1 1 8

1 1 1 1 0 1 1 9

0 0 0 0 0 0 0 non-digit

. . . . . . .

1 1 1 1 1 1 0 non-digit







Given a training matrix where the objects are de-

scribed by Boolean features, in this paper, we charac-

terize under what conditions a testor is a descriptor.

Even more, we provide a procedure to build a sub-

matrix of the training matrix that allows characteriz-

ing when a typical testor is a non-reducible descrip-

tor. As an example of the usefulness of the relation

found, we provide a typical-testor-based strategy for

computing all the non-reducible descriptors of a train-

ing matrix. We illustrate the usefulness of the pro-

posed strategy by applying it in the problem of Ara-

bic numerals recognition and we show that the results

obtained by our approach are the same that those pre-

viously reported by applying an algorithm for com-

puting NRDs.

From this study, we conclude that indeed there is

a relation between the concepts of typical testor and

non-reducible descriptor. Moreover, we show that this

relation is useful, in ﬁrst instance, for taking advan-

tage of typical testor algorithms for computing non-

reducible descriptors. However, our study opens sev-

ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods

192

Table 6: Non-reducible descriptors and corresponding features for Arabic numerals and non-numerals.

Non-reducible descriptors Corresponding features

0 {1, 1, 1, ., 1, 1, 1} {x

, x

}

1 {., 0, 1, 0, 0, 1, 0} {x

, x

}

2 {1, 0, 1, 1, 1, 0, 1} {x

, x

}

3 {1, ., 1, 1, 0, 1, 1} {x

, x

}

4 {0, 1, 1, 1, 0, 1, 0} {x

, x

}

5 {1, 1, ., 1, ., 1, 1} {x

, x

}

6 {1, 1, ., 1, ., 1, 1} {x

, x

}

7 {., 0, 1, 0, 0, 1, 0} {x

, x

}

8 {1, 1, 1, ., 1, 1, 1}, {1, 1, ., 1, ., 1, 1} {x

, x

}, {x

, x

}

9 {1, 1, ., 1, ., 1, 1}, {1, ., 1, 1, 0, 1, 1} {x

, x

}, {x

, x

}

non-digit each non-digit string is NRD itself {x

, x

}

eral other study possibilities to research.

Among open problems we can mention, for ex-

ample, comparison of computational cost of the algo-

rithms for computing NDRs with the algorithm pro-

posed by us for computing NRDs by means of all typ-

ical testors. Since any algorithm for computing typ-

ical testors can be used in our algorithm for comput-

ing NDRs, determining the best one in terms of efﬁ-

ciency is another interesting future work. The design

of algorithms for computing all the NRDs of a train-

ing matrix with a new perspective based on the con-

cept of typical testor is another interesting problem

worth considering. Another research problem that

deserves close scrutiny is an extension of the results

presented in this paper to non-Boolean training matri-

ces or other types of descriptors, e.g., visual descrip-

tors (Ohm et al., 2000). Finally, we conclude that all

research directions mentioned above and some oth-

ers, can lead to interesting theoretical developments

in which both concepts, in a synergic manner, could

be applied to solve practical pattern recognition prob-

lems.

ACKNOWLEDGEMENTS

M. A. Shamshiri and A. Krzy

zak were partially sup-

ported by the Natural Sciences and Engineering Re-

search Council of Canada.

REFERENCES

Cheguis, I. and Yablonskii, S. (1955). On tests for electric

circuits. Uspieji matematiceskij Nauk, 4(10):182–184

(in Russian).

Chikalov, I., Lozin, V., Lozina, I., Moshkov, M., Nguyen,

H. S., Skowron, A., and Zielosko, B. (2012). Three

approaches to data analysis: Test theory, rough sets

and logical analysis of data, volume 41. Springer Sci-

ence & Business Media.

Djukova, E. (1989). Pattern recognition algorithms of

the kora type. Pattern recognition, classiﬁcation,

forecasting-Mathematical techniques and their appli-

cations, (2):99.

Dmitriev, A., Zhuravlev, Y. I., and Krendelev, F. (1966). On

mathematical principles for classiﬁcation of objects

and phenomena. Diskret. Analiz, 7:3–15, (in Russian).

Kwak, N. and Choi, C.-H. (2002). Input feature selection

for classiﬁcation problems. IEEE transactions on neu-

ral networks, 13(1):143–159.

Lazo-Cortes, M., Ruiz-Shulcloper, J., and Alba-Cabrera, E.

(2001). An overview of the evolution of the concept

of testor. Pattern recognition, 34(4):753–762.

Lias-Rodríguez, A. and Pons-Porrata, A. (2009). Br:

A new method for computing all typical testors.

In Iberoamerican Congress on Pattern Recognition,

pages 433–440. Springer.

Ohm, J.-R., Bunjamin, F., Liebsch, W., Makai, B., Müller,

K., Smolic, A., and Zier, D. (2000). A set of visual

feature descriptors and their combination in a low-

level description scheme. Signal Processing: Image

Communication, 16(1-2):157–179.

Piza-Davila, I., Sanchez-Diaz, G., Lazo-Cortes, M. S., and

Noyola-Medrano, C. (2018). Enhancing the perfor-

mance of yyc algorithm useful to generate irreducible

testors. International Journal of Pattern Recognition

and Artiﬁcial Intelligence, 32(01):1860001.

Pons-Porrata, A., Gil-García, R., and Berlanga-Llavori, R.

(2007). Using typical testors for feature selection in

text categorization. In Iberoamerican Congress on

Pattern Recognition, pages 643–652. Springer.

Sanchez-Díaz, G. and Lazo-Cortés, M. (2007). Ct-

ext: an algorithm for computing typical testor set.

In Iberoamerican Congress on Pattern Recognition,

pages 506–514. Springer.

Valev, V. (19962). Construction of boolean classiﬁcation

rules and their applications in computer vision prob-

lems. Machine Graphics and Vision, 5(2):5–23.

Taking Advantage of Typical Testor Algorithms for Computing Non-reducible Descriptors

193

Valev, V. (2014). From binary features to non-reducible de-

scriptors in supervised pattern recognition problems.

Pattern Recognition Letters, 45:106–114.

Valev, V. and Radeva, P. (1996). Construction of boolean

decision rules for ecg recognition by non-reducible

descriptors. In Proceedings of 13th International Con-

ference on Pattern Recognition, volume 2, pages 111–

115. IEEE.

Valev, V. and Sankur, B. (2004). Generalized non-reducible

descriptors. Pattern Recognition, 37(9):1809–1815.

ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods

194