On Learning-free Detection and Representation of Textline Texture in

Digitized Documents

Dominik Hauser, Christoffer Kassens and H. Siegfried Stiehl

Department of Informatics, Universit

at Hamburg, Germany

Keywords:

Document Analysis, Feature Selection and Extraction.

Abstract:

Textline detection and extraction is an integral part of any document analysis and recognition (DAR) system

bridging the signal2symbol gap in order to relate a raw digital document of whatever sort to the computational

analysis up to understanding of its semantic content. Key is the computational recovery of a rich representation

of the salient visual structure which we conceive texture composed of periodic and differently scaled textlines

in blocks with varying local spatial frequency and orientation. Our novel learning-free approach capitalizes on

i) a texture model based upon linear system theory and ii) the complex Gabor transform utilizing both real even

and imaginary odd kernels for the purpose of imposing a quadrilinear representation of textline characteristics

as in typography. The resulting representation of textlines, be they either linear, curvilinear or even circular,

then serves as input to subsequent computational processes. Via an experimental methodology allowing for

controlled experiments with a broad range of digital data of increasing complexity (e.g. from synthetic 1D data

to historical newspapers up to medieval manuscripts), we demonstrate the validity of our approach, discuss

success and failure, and propose ensuing research.

1 INTRODUCTION

Textline detection – and extraction as a related prob-

lem e.g. in the context of layout analysis – is a well-

researched DAR topic since decades. The known

methods span the range from bottom-up learning-free

to machine learning methods and the latemost ICDAR

competition (Diem et al., 2019) convincingly eluci-

dates the attained performance level. However, as

yet the DAR focus was mainly set on baseline de-

tection, whereas our novel approach goes well be-

yond since we detect four lines related to the typo-

graphical line system for quadrilinear scripts: base-

and top-lines as well as mid-lines of both the textline

itself and the space between textlines. Such lines

with a unique semantics are important for the mea-

surement of saliency of quadrilinear scripts: Whereas

the mid-line of the textline itself is self-explanatory,

the base- and top-lines are delimiters of minuscule

scripts while the mid-line of the interspace along with

the neighbouring base- and topline index the poten-

tial margin space for appearance of descenders, as-

cenders, majuscules and/or even diacritics. Note that

the distance between descender and ascender margins

in two consecutive textlines is coined lead(ing) or

slug though no standard deﬁnition exists. Moreover

the distance between mid-lines of textlines in a regu-

lar textblock is related to the local spatial frequency

while the distance between base-lines renders possi-

ble the typographical classiﬁcation of normal, com-

press, and splendid. Hence the four lines, to be un-

derstood as a local semantically rich representation

system, serve as local search space for visually salient

textline features or, in other words, as a local signage

system for subsequent computational processes in a

task-oriented DAR system (see (Diem et al., 2013) for

an epitome of a potential real-world use case drawing

on word-signaling proﬁle boxes).

As already mentioned, differently scaled textlines

with blockwise varying local spatial frequency and

orientation are conceived visual texture relating

textline detection to texture detection. Visual tex-

ture is a multi-facetted phenomenon tackled by ﬁnd-

ings from visual neurosciences, visual psychophysics

of e.g. arbitrary gratings, cognitive reading sci-

ence, Gabor transform from linear system theory,

photogrammetry-based remote sensing and scene

analysis – you name it. Non-surprisingly past

DAR research exploited the treasure trove of bottom-

up approaches and – given the plethora (see (Bin-

makhashen and Mahmoud, 2019) for a recent survey)

– in particular the well-understood Gabor transform

Hauser, D., Kassens, C. and Stiehl, H.

On Learning-free Detection and Representation of Textline Texture in Digitized Documents.

DOI: 10.5220/0010801300003122

In Proceedings of the 11th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2022), pages 203-212

ISBN: 978-989-758-549-4; ISSN: 2184-4313

203

made it into the DAR toolbox (see Chpt. 2 for some

seminal work). However, to the best of our knowl-

edge, past work drew upon the energy and/or the ker-

nel orientation of the Gabor transform only thus ig-

noring the potential of the complex (real even and

imaginary odd) notation. While energy (with its ori-

entation) alone was proven to be successful in textline

detection and even layout analysis, it lacks the ca-

pability of computational measurement of the above

mentioned system of lines. Even more, the tacit as-

sumption was textline regularity in terms of both spa-

tial frequency within a horizontally aligned text block

(e.g. main text in an Arab manuscript) and orientation

(e.g. in the case of rotated commentaries). Regular-

ity evidently is the ideal case (e.g. historical newspa-

pers) while irregularities are prevalent due to varying

cultural epoch, script, writing school, hand, produc-

tion etc. thus posing challenges to DAR systems for

OCR up to hand identiﬁcation. Typically regularity

is bound to height, contrast, distance, and orientation

of textlines in digital documents. In contrast, irregu-

larity is any deviation but also implies deviation from

the ideal linear case of textlines which may be bended

due to e.g. a hand’s purpose or by accident during

digitization (let alone the range of document degrada-

tions). As a consequence past research also focused

on computational methods being tolerant to local ir-

regularities (see seam carving as prominent example

(Arvanitopoulos and S

usstrunk, 2014)) but as yet no

all-in-one solution exists due to the variety of irregu-

larities in the document domain.

With the revival of machine (and particularly the

advent of deep) learning came along a paradigm shift

from bottom-up computational vision e.g. for vi-

sual feature detection – disparaged as hand-crafted

while ignoring the formal grounding – and represen-

tation to, say, empiricism-driven learning algorithms.

Whilst achievements and breakthroughs – particularly

in object classiﬁcation for still images as for certain

DAR tasks – have to be acknowledged, the sober-

ing limits also came to surface, to name a few chal-

lenges (see e.g. (Yuille and Liu, 2021), (Drummond,

2006) and (Guidotti et al., 2018)): capability of adap-

tion to a grand variety of data and tasks in DAR,

sparseness and imbalance of training data, lack of

ground truth, experimental methodology beyond cur-

rent scalar-based metrics, dependency on tramontane

platform providers as well as the black-box issue –

let alone the evenly critical issue of complexity mas-

tering by developers or non-tech-savvy users with de-

mand for workﬂow support in their daily, e.g. schol-

arly or routine, work with DAR systems. As one

consequence, current research on interactive machine

learning aims at bringing the user with her/his intelli-

gence back in the loop and in control. Our learning-

free approach to textline detection and representation

thus is guided by the heretical question ”Why should

we ﬁrst learn what we already know?” – simply since

in our case it is well known that in the ﬁrst layers of

some deep nets primarily ”Gaborish” ﬁlter kernels are

arduously learned ((Zeiler and Fergus, 2014), (Sprin-

genberg et al., 2015), (Krizhevsky et al., 2017)), but

devoid of theoretical grounding as common in low-

level computer vision. In the chapters to follow we

outline the theory behind our learning-free approach,

illustrate the validity via our 1D model of textlines as

texture, describe our OpenCV-based 2D implementa-

tion and present experimental results

as a conclusive

proof-of-concept for the cases of linear and curvilin-

ear textlines in retro-digitized documents as well as of

even circular epigraphic textlines in digital images of

ancient bowls. Eventually we attempt to surmount the

dichotomy of neat math and DARing needs of users as

posed by Lopresti and Nagy one decade ago in their

inﬂuential paper ”When is a Problem Solved?” (Lo-

presti and Nagy, 2011).

2 RELATED WORK

As mentioned above, much work has been done on

textline extraction and particularly baseline detection

(see (Diem et al., 2019) for state-of-the art results of

the 2019 cBAD competition) as such but – apart from

lack of space – due to our focus on the texture-side

of textlines in digital documents we here only review

matching papers. The fact that the Gabor transforma-

tion plays a key role in computational texture analysis

per se (see (Humeau-Heurtier, 2019) for a recent com-

prehensive survey) was early recognized in the DAR

community (see recent reviews by (Mehri et al., 2017)

and (Eskenazi et al., 2017)).

As a two-fold summary, ﬁrst, despite the popu-

larity of the Gabor transform in the DAR domain so

far only local and/or directional ﬁlter energy measures

have been used for, e.g. more recently, texture-based

textline segmentation (Chen et al., 2014) and texture-

exploiting binarization (Sehad et al., 2019). Second,

the bulk of line detection approaches was tailored to

baselines and, again to the best of our knowledge, in

DAR no machine learning approach (see surveys in

Please note that due to our University’s pandemic-

driven lab access restrictions since more than one year

the planned number of joint experiments in our lab had

to be trimmed. Further results of our web-based ex-

perimentation beyond the reported proof-of-concept are

made available via https://www.inf.uni-hamburg.de/en/inst/

ab/bv/publications.html

ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods

204

(Liwicki and Liwicki, 2020), (Lombardi and Mari-

nai, 2020) and (Subramani et al., 2020)) to visual tex-

ture detection in digital documents aiming at compu-

tational measurement of textline features in a quadri-

linear reference system is available as yet.

Interestingly, already in 2007 Likforman-Sulem et

al. (Likforman-Sulem et al., 2007) in their early sur-

vey stressed the importance of visual characteristics

as well as representation of text lines, e.g. baseline,

median line, upper line, and lower line in their nota-

tion, for textline segmentation. In their vein, recent

research has been reported on learning-free beyond-

baseline detection drawing upon computational vision

milestones. Manmatha and Srimal (Manmatha and

Srimal, 1999) at ﬁrst applied the then well-established

scale space theory to segmentation of hand-written

words via i) scaled anisotropic Laplacian-of-Gaussian

operators and ii) scale selection for blob detection re-

sulting in bounding boxes for words. Later on, Cohen

et al. (Cohen et al., 2014) also used the anisotropic

directional Gaussian kernel G(σ) along with its 2

order derivatives at multiple scales for textline extrac-

tion by scaling G(σ) to the average textline height.

On this basis, Saabni et al. (Saabni et al., 2014)

proposed an approach to impose so-called seams on

binary/gray-scale images (inter alia using an energy

map derived from a signed distance transform) pass-

ing across/between textlines thus approximating their

upper/lower boundaries.

In a recent follow-up paper on language-

independent - though computationally expensive -

text line extraction for handwritten gray-scale docu-

ments with near-horizontal or ﬂuctuating lines, Azran

et al. (Azran et al., 2021) proposed a combination of

two known CNNs resulting in an energy map. In a

second step, minimal energy sub-seams are tracked

and accumulated ”. . . to perform a full local mini-

mal/maximal separating and medial seam deﬁning the

text baselines and the text line regions.” (trilinear rep-

resentation).

In like manner to (Cohen et al., 2014), Aldav-

ert and Rusinol (Aldavert and Rusi

nol, 2018) at-

tempted streak-like representations of textlines (vary-

ing in height, orientation and bending) utilizing scaled

oriented 2

order Gaussian derivatives again with σ

proportional to line height.

Current work by Barakat et al. (2020) (Barakat

et al., 2020) described a method based upon 2

or-

der derivatives of anisotropic Gaussian ﬁlters (with

automatic scale selection), energy minimization and

graph cuts for detecting so-called blob lines that strike

through text lines with an admissible skew and bend-

ing (see also their companion paper linking their pre-

vious work to CNN (Barakat et al., 2021)).

Lately, Mechi et al. (Mechi et al., 2021) pro-

posed a complex two-step framework for text line seg-

mentation (for Arabic and Latin manuscripts) which

comprises both a deep FCN model and a post-

processing based on topological structural analysis.

Through copious FCN benchmarking, they experi-

mentally demonstrated superiority of the adaptive U-

Net model which yields a two-line (namely base- and

top-line, or synonymously, X-height) representation

enhanced by a rather sophisticated post-processing

step for extraction of complete text lines (including

both the ascender and descender components). Exper-

imental results of the two-step architecture revealed a

97/99% correctness of text lines given ANT-A/ANT-

L datasets

Taken together, so far learning-free line detec-

tion as well as representation in the ﬁrst place cap-

italized on scaled anisotropic – ergo oriented – 2

order Gaussian derivatives matching textline height

whereas - as will be elucidated below - the complex

Gabor transform renders possible both bottom-up de-

tection of line-line texture and its quadri-linear repre-

sentation borrowed from typography/paleography.

3 OUR APPROACH

As sketched above, we ground our approach on linear

(LTI) system theory in order to i) model the structure

of visual texture at hand and ii) derive convolution

kernels via the complex Gabor transform. For reason

of convenience we brieﬂy introduce the 1D case only

since generalization to 2D is straightforward (see also

below).

Let I(x, y) be a digital document (or, tout court,

image I with x/y for columns/rows and its origin in

the upper left corner) and I(x = const, y) ≡I(y) a ver-

tical section. Then an idealized, viz binary, 1D model

of both a black-inked textline and a white interspace

is a rectangular pulse P(y) with either negative or

positive polarity. Since for the latter case P(y) can

be composed from two shifted Heaviside functions

H(.), P(y) = H(y) −H(y −w) holds with w as pulse

width (see ﬁg 1). Note that for modeling of varying

contrast, constants can easily be included. Since a

pulse of whatever polarity has two Heaviside ﬂanks

of inverse polarity and a mid-point at its center, four

salient visual features are deﬁned: Points of ascend-

ing/descending ﬂanks of a pulse and mid-points of a

positive/negative pulse – which in 2D generalize to

the above mentioned four lines: base-/top-lines and

textline/interspace midlines.

http://www.archives.nat.tn/

On Learning-free Detection and Representation of Textline Texture in Digitized Documents

205

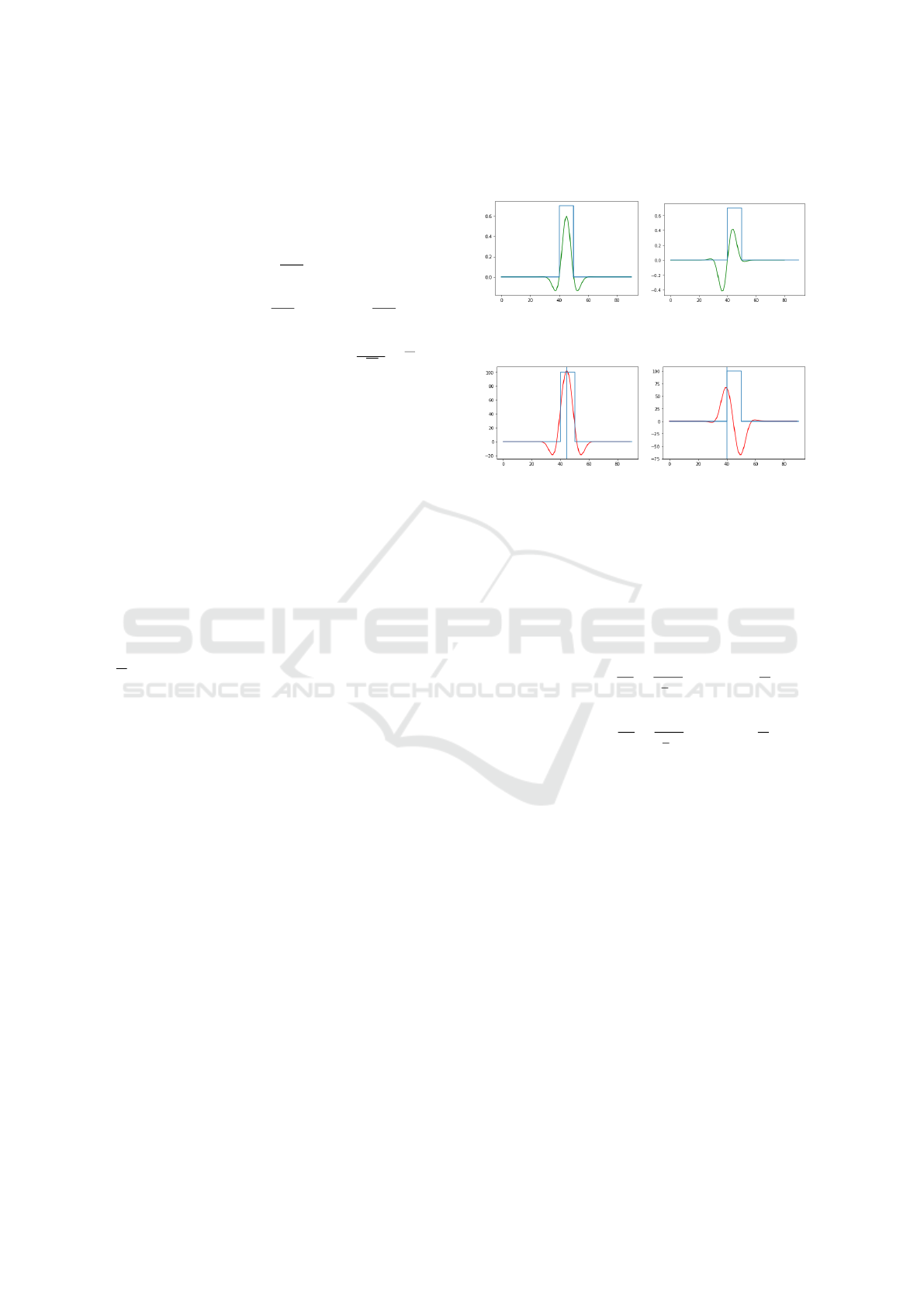
Since the mentioned ﬂanks of a pulse are of odd

nature with inverse polarity whereas the pulse (be it

of positive or negative polarity) is even, the complex

Gabor transform comes into play with both even and

odd kernel

G (y) = G(y; σ) ·exp



j ·

2πy



= G(y;σ) ·



cos



2πy



+ j ·sin



2πy



(1)

with the Gaussian envelope G(y; σ) =

√

2πσ

−

2σ

and

λ as the wavelength of the sinusoidals. The Gabor

transform as convolution then reads as T (G (y)) =

I(y) ⊗G (y) with its result coined response map R(y).

Note that the convolution kernels map to ﬁlters in

the frequency domain with tunable mid frequency and

bandwidth rendering possible a best match with local

spatial frequency content.

Evidently both the real even and the imaginary

odd parts are required as convolution kernels (in the

sense of matched ﬁlters) in order to detect the above

mentioned four salient features. Moreover, as a more

than welcome side effect, each kernel with a speci-

ﬁcity for just one of the four salient points bears

an implicit semantics yielding four pre-classiﬁed re-

sponse maps (or feature channels). For the detec-

tion of the extrema in the response maps, the criterion

R(y)

= 0 must hold. In ﬁg. 1c and 1d the local

extrema are indicated by the vertical lines, which rep-

resent the mid- and top-line of the interline space.

Since the implicit convolution of both the Heav-

iside functions and the rectangular pulse (being dis-

tributions not functions in the common sense) with

a Gaussian kernel implies their regularization, result-

ing extrema at the mentioned points can easily be de-

tected. However, as pointed out below, in the case of

the rectangular pulse the kernel width of the even Ga-

bor kernel has to match the pulse width for an unique

extrema giving rise to the necessity of appropriately

selecting the scale σ of the Gaussian.

Line texture now can trivially be modeled in 1D

by a linear combination of rectangular pulses with de-

grees of freedom allowing for varying local frequency

via a change of the width of neighboring pulses of op-

posite polarity (forming an antisymmetric pair mod-

eling textline and interspace in 1D). Clearly the ideal

case in terms of texture regularity is a linear combi-

nation of antisymmetric pairs of pulses for which the

four salient line features can easily be detected via the

above mentioned two kernels of the complex Gabor

transform. In the case of texture irregularity, how-

ever, a careful analysis of the Fourier phase space is

required.

For the case of 1D regularity in I(y), the following

ﬁg. 1a and 1b illustrate the core of our approach.

(a) Positive pulse with

width-matching even Gabor

kernel.

(b) Positive pulse with ﬂank-

matching odd Gabor kernel.

with extremum at mid-point

of pulse.

(d) Response map for (b)

with extrema at ﬂank of

pulse.

Figure 1: Principle of detecting salient points at positive

pulse (aka interline space model).

As known the 1D Gabor kernel generalize to 2D

without ado (Henriksen, 2007) for both the real even

and imaginary odd part:

Real

(p) = exp

−



(

)



cos



2π



(2)

Img

(p) = exp

−



(

)



sin



2π



(3)

where

p := (x, y; λ, θ, σ, γ)

= x cosθ + y sin θ

= −x sin θ + y cos θ

and λ as the wavelength of the wavefronts, θ as the

orientation of the kernel, σ as the standard deviation

along x’ and γ steering the anisotropy of the Gaus-

sian along y’. However it is worth recalling that in

2D two more degrees of freedom have to be consid-

ered, viz the orientation of line-like texture and the

anisotropy of the Gaussian determined by its covari-

ance matrix or, respectively, the aspect ratio (imply-

ing a tradeoff between frequency and orientation sen-

sitivity). Having said that, the 2D complex Gabor

transform reads as T (G (x, y)) = I(x, y) ⊗G

, where

∈ {G

Real

, G

Img

In other words, a fully-ﬂedged 2D Gabor trans-

form spans a solution space S(λ, θ, σ, γ) for 2D vi-

sual texture with dimensions anisotropy/orientation

ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods

206

of Gaussian and frequency/orientation of sinusoidal

wave fronts. As a consequence, S(λ, θ, σ, γ) has to be

explored for extrema in order to detect spatially vary-

ing local texture with high precision which relates to

both Gaussian scale-space and wavelet theory. How-

ever, as laid out with acuity in (Lee, 1996), although

the 2D Gabor transform with the Gabor kernels from

Equ. 2 and 3 achieves the resolution limit, it does

not fully satisfy wavelet theory due to an existing d.c.

component of the even kernel (see (Lee, 1996) sec. 2

for details and a derivation of – still nonorthogonal –

Gabor wavelets).

In our case, since the Gabor transform utilized

is the standard complex one (with kernels provided

by OpenCV for the sake of convenience; see also

below), a solution to our visual texture detection

problem in digital documents requires some further

thoughts. First, in terms of regularity, we assume dig-

ital document images (or, synonymously, pages from

e.g. manuscripts, codices or newspaper collections) to

obey block-wise texture regularity due to constancy in

writing school, hand or print typeface barring admis-

sible deviation. Thus, secondly, as yet we only allow

for spatially regular composition of textlines varying

in height, interline spacing, orientation but also cur-

vature of rather arbitrary radius. In order to constrain

the mentioned full solution space S(.), in the follow-

ing a pragmatic approach will be presented which i)

capitalizes on prior domain/task knowledge embed-

ded in an interactive scenario and ii) serves as proof-

of-concept.

4 EXPERIMENTS AND RESULTS

In brief, our experimental strategy for the 2D case

complies with the methodology in (Neumann and

Stiehl, 1987) for controllable experimentation (see

also (Alberti et al., 2018) as well as the in-depth

treatise in (Thacker et al., 2008)) proposing the use

of a well-deﬁned range of test images with increas-

ing visual complexity. Hence synthetic images of bi-

nary line texture (subject to e.g. scaling, orientation,

curvilinearity and Gaussian noise) allow for basal per-

formance characterization whereas digital documents

with increasing line texture complexity – due to e.g.

spatial frequency, orientation, and curvilinearity – do

so for task-speciﬁc problems. Along the graded range

our experiments also reveal the tolerance of certain

Gabor kernels to deviation from whatever regularity

assumption. As yet no consideration was given to typ-

ical degradations in ancient/historical documents such

as bleed-through, stains, etc. (except for intensity gra-

dients due to scanning).

As mentioned above, for the sake of both brevity

and simplicity we utilized the current OpenCV imple-

mentation of the Gabor kernels (see (OpenCV, 2021a)

and (Henriksen, 2007)) for our 2D experiments al-

though we found through careful late-minute code

scrutiny that neither the normalization of the Gaus-

sian nor the d.c. compensation for the even Gabor

kernel (see below) have been implemented. Although

the numerical results have a known bias, we decided

not to correct for it now in favor of reproducibility by

other research groups.

Moreover we have to point out that due to the lack-

ing d.c. compensation the even kernel does not obey

the wavelet criterion ψ(.) = 0 (Lee, 1996) hence the

full complex Gabor transform is not a wavelet trans-

form yet. Apart from that, given that the real even and

imaginary odd part resemble scaled differential oper-

ators like the seminal ones by e.g. (Hildreth, 1983)

and (Canny, 1986) and later on by e.g. (Florack et al.,

1993), for the purpose of a full scale-space integra-

tion (with degrees-of-freedom like scale/aspect ratio

of the Gaussian, local frequency range of the sinu-

soidal waves, and their orientation) w.r.t. the solution

space S(.) from above, both kernels need to be further

normalized according to milestone research by (Lin-

deberg, 1990). To this end of our knowledge no val-

idated and reliable open source tools have been pro-

vided in order to fully falsify the theory thru experi-

ments.

As a pragmatic consequence of the lack, in order

to constrain the above mentioned full solution space,

we adopt the “keep-the-user-in-the-loop” paradigm

behind interactive document exploration (see (Pandey

et al., 2020) for a recent use case) as follows: Given

sets of document images with a minimally required

and persistent regularity e.g. in a collection (which

is safe to assume), a user is provided with an inter-

active tool for measuring the prevalent visual texture

properties thus tailoring speciﬁc sets of Gabor kernels

(as feature channels) to the texture detection problem

at hand. In this vein of experimentation, the follow-

ing results for linear, curvilinear and circular textlines

have been attained so far (see below).

Since the convolution of a digital document with

Gabor kernels alone will not yield the quadrilinear

textline representation, post-processing was neces-

sary also in order to visualize the detected lines as

brieﬂy described next. First, the gray-value docu-

ment image as well as the texture parameters such

as the height and orientation of the lines are up-

loaded and convolved with the respective even/odd

Gabor kernels. Second, our post-processing entails

global/local thresholding on the response maps as

well as local extrema detection. The resulting points

On Learning-free Detection and Representation of Textline Texture in Digitized Documents

207

are then grouped into lines via a connected com-

ponent labeling algorithm which is available thru

OpenCV (OpenCV, 2021b). The four lines are col-

ored (red/blue as below) and overlaid with the up-

loaded image. Note that our rough-and-ready post-

processing was not a research topic by itself and thus

can be varied at each step in order to further improve

the results.

(a) Detected top-/baselines

(blue/red) in odd-Gabor

response map.

(b) Detected textline/inter-

space midlines (red/blue)

in even-Gabor response

map.

Figure 2: Quadrilinear representation of synthetic textlines

(height: 10 pixels).

Following our experimental strategy, we ﬁrst con-

verted the 1D rectangular pulses into 2D straight bars,

which can be considered as a regular textline model.

Similar to ﬁg. 1 these synthetic textlines have each a

height of 10 pixels. Based on this and the given hor-

izontal orientation as pre-knowledge, the Gabor ker-

nels from Equ. 2 and 3 are used with λ = 20, σ = 10,

γ = 0.5 and θ = 0. Both λ and σ are directly derived

from the line height while γ is a ﬁxed value hence the

solution space S(.) is reduced by three dimensions.

By convolving the synthetic image with even and

odd Gabor kernels, the response maps will yield ex-

trema along the quadrilinear lines as shown in ﬁg. 2.

Because of the elongation of the (anisotropic) Gabor

kernels along the textline, there are still relatively high

responses at the end of textlines, which are not sup-

pressed by the thresholding. Note that Gabor-based

line end detection is work in progress.

(a) Detected top/baselines in

regular text block.

(b) Detected midlines in reg-

ular text block.

Figure 3: Quadrilinear representation of newspaper

textblock

Applying our approach to real documents faces

noise as a result of imperfect imaging barring low

resolution and further degradation. Hence efﬁcient

thresholding of the response maps as one way to lower

the sensitivity to noise is all-important. Fig. 3 depicts

Courtesy: Content Conversion Specialists GmbH,

Hamburg https://content-conversion.com/

our results for a low-noise document with small irreg-

ularity due to different font size.

The horizontally aligned anisotropic Gabor ker-

nels used here were parametrized to a line height of

19 pixels thus ﬁtting the text block. Since the word

”Kantone” is larger than the textlines in the textblocks

below, some false-positives result occur though the

kernel setting is quite tolerant against height devia-

tion.

(a) Detected top/baselines in

irregular text block.

(b) Detected midlines in ir-

regular text block.

Figure 4: Quadrilinear representation of irregular

manuscript text block (Islamic Manuscripts, 2021).

In contrast, results for a cropped Arab manuscript

with irregularity are given in ﬁg. 4. Despite the par-

ticular language and writing style, the lower contrast

and some irregularities w.r.t. line height, spacing and

orientation, the response maps still expose extrema as

in the use cases above. Here the Gabor kernels are

tailored to a line height of 21 pixels, due to ascen-

ders/descenders and diacritics, and the results do well

approximate a quadrilinear reference systems. Note

that spurious detections can easily be suppressed by

imposing task-speciﬁc geometric constraints.

(a) Detected top/baselines in index card.

(b) Detected textline/interspace midlines in index card.

Figure 5: Quadrilinear representation of index card

A different case of historic documents is a form or

index card as shown in ﬁg. 5. Using Gabor kernels

tailored to a line height of 11 pixels, the approach is

able to detect form ﬁelds as well as most of the hand-

Courtesy: Archive of Universit

at Hamburg

ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods

208

writing. The increased spacing between the lines pre-

vents the detection of the inter lines with the same

Gabor Kernel and requires a different scale. Fitting

the Gabor kernel to a line height of 17 pixels will im-

prove the detection of the inter lines, which is shown

in ﬁg. 6, but on the other hand the mid lines are not as

narrow as in ﬁg. 5, which means bigger gaps between

words are connected as shown in the last textline.

Figure 6: Detected interlines in index card

(a) Detected textline/interspace midlines.

(b) Detected top/baselines.

Figure 7: Quadrilinear representation of a Latin manuscript

from DIVA-HisDB (Courtesy: https://diuf.unifr.ch/main/

hisdoc/diva-hisdb).

We also tested our approach on some manuscripts

from the DIVA-HisDB dataset in comparison to

(Mechi et al., 2021, ﬁg. 10). The shown manuscript

page in particular stands out w.r.t. an overall differ-

ence – or moderate irregularity – in textline height and

spacing. As parameter constraint for the Gabor ker-

nels, in our experiment we interactively estimated the

page-averaged line height at 67 pixels, which yields

a result as shown in ﬁg. 7. Similar to the results

from ﬁg. 6, due to the estimated line height the top-

and baselines cannot perfectly represent the textline

margins but expose tolerance to such irregularity. On

the other hand, however, both lines encase descenders

and ascenders, which reveals their usability for de-

termining a bounding box in a subsequent processing

step.

As mentioned above, our Gabor-based proof-of-

concept and the post-processing step include a sim-

ple global thresholding to reduce noise. As a result

we have some small gaps even though the response

map does have local extrema. For illustration pur-

pose ﬁg. 8 displays the response maps of the convo-

lution of data in ﬁg. 7 with even/odd Gabor kernels.

Fig. 8 display absolute values to make the extrema

more visible, which is why both minima und max-

ima are shown as high values. The response maps

indicate that the gaps are results of the global thresh-

olding, which can be improved with more advanced

algorithms.

Since 2D Gabor kernels are both selective and sen-

sitive to texture orientation, detection of textlines with

varying curvature is not far to seek (ﬁg. 9). However,

in the case of curvilinear or even circular textlines,

two questions arise: First, how to discretize the angu-

lar range and, second, how to match the scale of an

anisotropic Gabor kernel to the textline curvature. As

shown below, our experiments demonstrate that one

set of Gabor kernels is quite tolerant against deviation

from textline linearity (ﬁg.9a) but a combination of

multiple kernels is required for imposing a quadrilin-

ear reference system on textlines beyond a lower cur-

vature limit. In ﬁg. 9a, with parabola-like textlines

having slight curvature of 0.0018, just one even ker-

nel set (for midlines) with an orientation of θ = 0.5π

does not sufﬁce.

The midlines are cut-off because the responses

were too low and also false-positives are prominent at

the line end. Evidently, to detect curvilinear or even

circular textlines, a set of Gabor kernels with multiple

orientations - depending on the present curvature - is

in order.

Our experiments reveal that only three kernels of

different orientation are sufﬁcient for fully detecting

the mid-lines in ﬁg. 9b. For fusion of the response

maps, the arithmetic mean of the responses for each

pixel is calculated. However, the responses will be di-

minished such that the difference between responses

On Learning-free Detection and Representation of Textline Texture in Digitized Documents

209

(a) Response map of textline/interspace midlines.

(b) Response map of top/baselines.

Figure 8: Reponse map of the quadrilinear representation of

a Latin manuscript from DIVA-HisDB.

(a) Detected midlines via one

even kernel θ = 0.5π.

(b) Detected midlines via

combination of 3 even ker-

nels θ

1,2,3

= (0.2π, 0.5π,

0.8π).

Figure 9: Detection of midlines in synthetic curvilinear text

block.

from textlines and noise will be less plainly. To cir-

cumvent this effect, which gets worse the more ker-

nels are used, kernels may only contribute to pixels

that lay in their respective orientation of detection.

Here two assumptions have to be made for our current

experimental system: i) the circular textlines have

only one center and ii) its coordinates must be prior

given. From this center the angle between a pixel and

each kernel can be derived to let a kernel only con-

tribute if this angle is within its orientation. Adopting

the ”keep-the-user-in-the-loop” paradigm, the center

is interactively determined and aligned with the cen-

ter of the cropped image. Ellipse detection using two

focal points is ongoing work.

In our experiments 16 kernels are used with orien-

tations equally distributed between 0π and (2 −

)π

with a step size of

. Two exemplary results for cir-

cular textlines with a moderate but observable irregu-

larity are presented in ﬁg. 10.

(a) Mid and inter lines with

line height of 10 pixels

(Tilemahos Efthimiadis,

2010).

(b) Top and base lines with

line height of 10 pixels

(Tilemahos Efthimiadis,

2010).

line height of 12 pixels

(Daderot, 2011).

(d) Top and base lines with

line height of 12 pixels

(Daderot, 2011).

Figure 10: Detection of epigraphy midlines in bowl images.

Note that in ﬁg. 10a the bleeding glaze of the bowl

leads to an irregularity that has not much affected the

midline detection whereas in ﬁg. 10c only midlines

for the epigraphy are detected while the low responses

for the drawn rectangles were removed due to thresh-

olding. The entire set of the quadrilinear line repre-

sentation for each bowl will be made public via the

given footnote link 1. In summary our experiments

provide strong evidence of both validity and feasibil-

ity of our approach and its proof-of-concept imple-

mentation.

5 CONCLUSION

In our theoretically well-grounded research we i) de-

ﬁned repetitive textlines with varying properties (e.g.

height, spatial frequency, orientation and curvature)

ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods

210

as visual texture in documents, ii) derived an explicit

LTI-based model for textlines of varying regularity

and their detection via even/odd Gabor kernels with

implicit semantics, iii) bridged a speciﬁc gap between

complex-valued Gabor theory and DAR practice in

order to not only detect text(base)lines but to impose a

quadrilinear reference system (or ”textural stave”) as

a signage for further computational processes such as

Hough transform, textline extraction, word spotting,

machine learning, OCR etc., iv) demonstrated the va-

lidity of our approach thru controlled experimentation

with a variety of documents as a proof-of-concept (see

footnote 1) and v) linked our learning-free approach

to the “human-in-the-loop-and-control” paradigm.

Needless to say that our current research couldn’t

reach the top end of the ﬂagpole in DAR practice

as pointed out above: Apart from known theoretical

blank spots for computationally exploring the solu-

tion space solely for the case of texture regularity, in

the case of irregularity the role of the Fourier/Gabor

phase space – being inherent to the pair of real even

and odd imaginary kernels and indicating deviation

from textline regularity in the spatial domain – has

to be given proper attention in future work. In ad-

dition, given the rich quadrilinear text line represen-

tation derived so far, Gabor-based texture analysis

of text blocks is a next logical step in a processing

chain. Moreover, in terms of algorithmic time com-

plexity of multi-scale ﬁlter banks, recent GPU hard-

ware progress up to hundreds of TOPS will alleviate

computational burden. Taken all together such issues

will be part of our research road map to further deepen

the transdisciplinary understanding of line texture in

documents - in the end probably yielding a theoreti-

cally grounded, generic, and bottom-up thus learning-

free tool for computation of rich visual representa-

tions to be fed into higher-level modules of a fully-

ﬂedged DAR system.

REFERENCES

Alberti, M., Pondenkandath, V., W

ursch, M., Ingold, R.,

and Liwicki, M. (2018). Deepdiva: A highly-

functional python framework for reproducible experi-

ments. In 16th International Conference on Frontiers

in Handwriting Recognition, ICFHR 2018, Niagara

Falls, NY, USA, August 5-8, 2018, pages 423–428.

IEEE Computer Society.

Aldavert, D. and Rusi

nol, M. (2018). Manuscript text

line detection and segmentation using second-order

derivatives. In 2018 13th IAPR International Work-

shop on Document Analysis Systems (DAS), pages

293–298.

Arvanitopoulos, N. and S

usstrunk, S. (2014). Seam carving

for text line extraction on color and grayscale histor-

ical manuscripts. In 2014 14th International Confer-

ence on Frontiers in Handwriting Recognition, pages

726–731.

Azran, A., Schclar, A., and Saabni, R. (2021). Text line ex-

traction using deep learning and minimal sub seams.

In Proceedings of the 21st ACM Symposium on Docu-

ment Engineering, DocEng ’21, pages 1–4, New York,

NY, USA. Association for Computing Machinery.

Barakat, B. K., Cohen, R., Droby, A., Rabaev, I., and El-

Sana, J. (2020). Learning-free text line segmentation

for historical handwritten documents. Applied Sci-

ences, 10(22). 8276.

Barakat, B. K., Droby, A., Alaasam, R., Madi, B., Rabaev,

I., and El-Sana, J. (2021). Text line extraction us-

ing fully convolutional network and energy minimiza-

tion. In Del Bimbo, A., Cucchiara, R., Sclaroff,

S., Farinella, G. M., Mei, T., Bertini, M., Escalante,

H. J., and Vezzani, R., editors, Pattern Recognition.

ICPR International Workshops and Challenges - Vir-

tual Event, January 10-15, 2021, Proceedings, Part

VII, pages 126–140, Cham. Springer International

Publishing.

Binmakhashen, G. M. and Mahmoud, S. A. (2019). Docu-

ment layout analysis: A comprehensive survey. ACM

Comput. Surv., 52(6):1–36.

Canny, J. F. (1986). A computational approach to edge

detection. IEEE Trans. Pattern Anal. Mach. Intell.,

8(6):679–698.

Chen, K., Wei, H., Liwicki, M., Hennebert, J., and Ingold,

R. (2014). Robust text line segmentation for historical

manuscript images using color and texture. In 2014

22nd International Conference on Pattern Recogni-

tion, pages 2978–2983.

Cohen, R., Dinstein, I., El-Sana, J., and Kedem, K. (2014).

Using scale-space anisotropic smoothing for text line

extraction in historical documents. In Campilho, A.

and Kamel, M., editors, Image Analysis and Recog-

nition, pages 349–358, Cham. Springer International

Publishing.

Daderot (2011). https://commons.wikimedia.org/w/index.

php?title=File:Bowl with incantation for Buktuya

and household, Mandean in Mandaic language and

script, Southern Mesopotamia, c. 200-600 AD -

Royal Ontario Museum - DSC09714.JPG&oldid=

486031305 [Online; accessed 23-07-2021].

Diem, M., Kleber, F., and Sablatnig, R. (2013). Text line de-

tection for heterogeneous documents. In 12th ICDAR,

pages 743–747. IEEE.

Diem, M., Kleber, F., Sablatnig, R., and Gatos, B. (2019).

cbad: Icdar2019 competition on baseline detection. In

2019 International Conference on Document Analysis

and Recognition (ICDAR), pages 1494–1498.

Drummond, C. (2006). Machine learning as an experimen-

tal science (revisited). In AAAI Workshop on Evalua-

tion Methods for Machine Learning, pages 1–5.

Eskenazi, S., Gomez-Kr

amer, P., and Ogier, J.-M. (2017).

A comprehensive survey of mostly textual document

segmentation algorithms since 2008. Pattern Recog-

nition, 64:1–14.

On Learning-free Detection and Representation of Textline Texture in Digitized Documents

211

Florack, L., ter Haar Romeny, B., Koenderink, J., and

Viergever, M. (1993). Cartesian differential invariants

in scale-space. Journal of Mathematical Imaging and

Vision, 3:327–348.

Guidotti, R., Monreale, A., Ruggieri, S., Turini, F., Gian-

notti, F., and Pedreschi, D. (2018). A survey of meth-

ods for explaining black box models. ACM Comput.

Surv., 51(5).

Henriksen, J. J. (2007). 3d surface tracking and approxima-

tion using gabor ﬁlters. pages 5–8. South Denmark

University. https://www.yumpu.com/en/document/

view/44234347/ [Online; accessed 23-07-2021].

Hildreth, E. C. (1983). The detection of intensity changes

by computer and biological vision systems. Comput.

Vis. Graph. Image Process., 22(1):1–27.

Humeau-Heurtier, A. (2019). Texture feature extraction

methods: A survey. IEEE Access, 7:8975–9000.

Islamic Manuscripts (2021). https://www.

islamic-manuscripts.net/receive/IslamHSBook

islamhs 00000626 [Online; accessed 23-07-2021].

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2017). Im-

agenet classiﬁcation with deep convolutional neural

networks. Commun. ACM, 60(6):84–90.

Lee, T. S. (1996). Image representation using 2d gabor

wavelets. IEEE Trans. Pattern Anal. Mach. Intell. ,

18(10):959–971.

Likforman-Sulem, L., Zahour, A., and Taconet, B. (2007).

Text line segmentation of historical documents: a sur-

vey. International Journal of Document Analysis and

Recognition (IJDAR), 9(2):123–138.

Lindeberg, T. (1990). Scale-space for discrete signals. IEEE

Trans. Pattern Anal. Mach. Intell., 12(3):234–254.

Liwicki, F. S. and Liwicki, M. (2020). Deep learning for

historical document analysis. In Handbook of Pattern

Recognition and Computer Vision, chapter 2.6, pages

287–303.

Lombardi, F. and Marinai, S. (2020). Deep learning for his-

torical document analysis and recognition—a survey.

Journal of Imaging, 6(10).

Lopresti, D. P. and Nagy, G. (2011). When is a problem

solved? In 2011 International Conference on Docu-

ment Analysis and Recognition, ICDAR 2011, Beijing,

China, September 18-21, 2011, pages 32–36. IEEE

Computer Society.

Manmatha, R. and Srimal, N. (1999). Scale space technique

for word segmentation in handwritten documents. In

Nielsen, M., Johansen, P., Olsen, O. F., and Weickert,

J., editors, Scale-Space Theories in Computer Vision,

pages 22–33, Berlin, Heidelberg. Springer Berlin Hei-

delberg.

Mechi, O., Mehri, M., Ingold, R., and Amara, N. E. B.

(2021). A two-step framework for text line seg-

mentation in historical arabic and latin document im-

ages. International Journal on Document Analysis

and Recognition (IJDAR) volume, 24(3):197–218.

Mehri, M., H

eroux, P., Gomez-Kr

amer, P., and Mullot, R.

(2017). Texture feature benchmarking and evaluation

for historical document image analysis. International

Journal on Document Analysis and Recognition (IJ-

DAR), 20.

Neumann, H. and Stiehl, H. S. (1987). Toward a testbed for

evaluation of early visual processes. Proceedings of

the 2nd International Conference on Computer Analy-

sis of Images and Patterns (CAIP’87), pages 256–263.

OpenCV (2021a). Open source computer vision li-

brary. https://github.com/opencv/opencv/blob/master/

modules/imgproc/src/gabor.cpp [Online; accessed 23-

07-2021].

OpenCV (2021b). Open source computer vision library

- function connected components with stats. https:

//docs.opencv.org/3.4/d3/dc0/group imgproc shape.

html#ga107a78bf7cd25dec05fb4dfc5c9e765f [On-

line; accessed 25-11-2021].

Pandey, P. S., Rajan, V., Stiehl, H. S., and Kohs, M. (2020).

Visual programming-based interactive analysis of an-

cient documents: The case of magical signs in jewish

manuscripts. In et al., A. D. B., editor, Pattern Recog-

nition. ICPR International Workshops and Challenges

- Virtual Event, January 10-15, 2021, Proceedings,

Part VII, volume 12667 of Lecture Notes in Computer

Science, pages 156–170. Springer.

Saabni, R., Asi, A., and El-Sana, J. (2014). Text line extrac-

tion for historical document images. Pattern Recogni-

tion Letters, 35:23–33. Frontiers in Handwriting Pro-

cessing.

Sehad, A., Chibani, Y., Hedjam, R., and Cheriet, M. (2019).

Gabor ﬁlter-based texture for ancient degraded docu-

ment image binarization. Pattern Analysis and Appli-

cations, 22(1):1–22.

Springenberg, J. T., Dosovitskiy, A., Brox, T., and Ried-

miller, M. A. (2015). Striving for simplicity: The all

convolutional net. In Bengio, Y. and LeCun, Y., ed-

itors, 3rd International Conference on Learning Rep-

resentations, ICLR 2015, San Diego, CA, USA, May

7-9, 2015, Workshop Track Proceedings.

Subramani, N., Matton, A., Greaves, M., and Lam, A.

(2020). A survey of deep learning approaches

for OCR and document understanding. CoRR,

abs/2011.13534.

Thacker, N. A., Clark, A. F., Barron, J. L., Beveridge, J. R.,

Courtney, P., Crum, W. R., Ramesh, V., and Clark,

C. (2008). Performance characterization in computer

vision: A guide to best practices. Comput. Vis. Image

Underst., 109(3):305–334.

Tilemahos Efthimiadis (2010). Egyptian antiquities - clay

magic bowl with aramaic writing. national archaeo-

logical museum, athens, greece. https://www.ﬂickr.

com/photos/telemax/4334582134/ [Online; accessed

23-07-2021].

Yuille, A. L. and Liu, C. (2021). Deep nets: What have they

ever done for vision? Int. J. Comput. Vis., 129(3):781–

802.

Zeiler, M. D. and Fergus, R. (2014). Visualizing and un-

derstanding convolutional networks. In Fleet, D. J.,

Pajdla, T., Schiele, B., and Tuytelaars, T., editors,

Computer Vision - ECCV 2014 - 13th European Con-

ference, Zurich, Switzerland, September 6-12, 2014,

Proceedings, Part I, volume 8689 of Lecture Notes in

Computer Science, pages 818–833. Springer.

ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods

212