Discrete Mother Tree Optimization and Swarm Intelligence for

Constraint Satisfaction Problems

Wael Korani and Malek Mouhoub

University of Regina, 3737 Wascana Parkway, Regina, Canada

Keywords:

Constraint Satisfaction, Swarm Intelligence, Nature Inspired Techniques, Metaheuristics.

Abstract:

The Constraint Satisfaction Problem (CSP) is a powerful framework for a wide variety of combinatorial prob-

lems. The CSP is known to be NP-complete, and many algorithms have been developed to tackle this challenge

in practice. These algorithms include the backtracking technique, improved with constraint propagation and

variable ordering heuristics. Despite its success, backtracking still suffers from its exponential time cost, es-

pecially for large to solve problems. Metaheuristics, including local search and nature-inspired methods, can

be an alternative that trades running time for the quality of the solution. Indeed, these techniques do not

guarantee to return a complete solution, nor can they prove the inconsistency of the problem. They are, how-

ever time-efﬁcient, thanks to their polynomial running time. In particular, nature-inspired techniques can be

very effective if designed with a good exploitation/exploration balance during the search. To solve CSPs, we

propose two discrete variants of two known nature-inspired algorithms. The ﬁrst one is an adaptation of the

Mother Tree Optimization (MTO). In contrast, the second is an extension of the Particle Swarm Optimization

(PSO) with a new operator that we propose. Both variants rely on a heuristic that gathers information about

constraints violations during the search. The latter will then be used to update candidate solutions, follow-

ing a given topology for MTO, and position/velocity equations for PSO. To assess the performance of both

methods, we conducted several comparative experiments, considering other known systematic methods and

metaheuristics. The results demonstrate the effectiveness of both methods.

1 INTRODUCTION

Many combinatorial problems are known to be NP-

hard and require powerful solving models and tech-

niques. In this regard, the Constraint Satisfaction

Problems (CSPs) (Dechter et al., 2003; Carbonnel

and Cooper, 2016; Gutin and Yeo, 2012; Apt, 2003)

has been proposed to tackle a wide variety of deci-

sion problems. The CSP is the cornerstone of many

industrial real-world and academic applications such

planning (Do and Kambhampati, 2001), scheduling

(Apt, 2003), vehicle routing and timetabling (Hmer

and Mouhoub, 2016; Roos et al., 2000).

More formally, a CSP consists of a triplet

(V,D,C). V is the set of variables, V = {v

,...,v

Each variable V

is deﬁned on a domain D

,...,dm} (D

∈ D). C is the set of constraints, C =

,...,c

}, restricting the values that variables can

take (Ruttkay, 1998). A solution to a CSP is a com-

plete assignment of values to all variables such that all

constraints are satisﬁed. CSPs are NP-complete, and

https://orcid.org/0000-0001-7381-1064

many systematic and stochastic methods have been

developed to tackle this challenge in practice. Sys-

tematic search methods guarantee to ﬁnd a solution,

if any, or detect the inconsistency of the CSP. They

do, however, suffer from their exponential time cost.

In order to overcome this difﬁculty in practice, back-

tracking methods improved through constraint propa-

gation and variable ordering heuristics have been pro-

posed (Dechter et al., 2003). Despite these improve-

ments, backtracking does have limitations, especially

for some hard and large CSP instances. In this regard,

nature-inspired and local search techniques have been

proposed to trade the quality of the solution returned

for time efﬁciency (Minton et al., 1992a; Galinier

and Hao, 1997; Blum and Roli, 2003; Glover and

Kochenberger, 2006; Talbi, 2009; Shil et al., 2013;

Korani and Mouhoub, 2021). More precisely, these

stochastic search methods can ﬁnd the solution faster,

thanks to their polynomial running time, but this is

not always guaranteed (Kumar, 1992). Moreover,

stochastic search methods cannot prove the inconsis-

tency of the CSP. Note that recent works combining

234

Korani, W. and Mouhoub, M.

Discrete Mother Tree Optimization and Swarm Intelligence for Constraint Satisfaction Problems.

DOI: 10.5220/0010803100003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 3, pages 234-241

ISBN: 978-989-758-547-0; ISSN: 2184-433X

both systematic and local search methods have been

proposed in order to take advantage of each tech-

nique (Zhang and Zhang, 1996; Jussien and Lhomme,

2002; Mouhoub and Jafari, 2011; Blum and Roli,

2003; Talbi, 2009). Nature-inspired algorithms have

been used to solve CSPs. These techniques include

Genetic Algorithms (GAs), Ant Colony Optimiza-

tion (ACO), Particle Swarm Optimization (PSO), and

Honey Bee Algorithm (HBA). In (Tsang et al., 1999),

Tsang et al. introduced a Guided Genetic Algorithm

(GGA) that combines GA and Guided Local Search

to solve CSPs. The results show that GGA is more

efﬁcient than GAs (Mitchell, 1996). In (Mouhoub

and Jafari, 2011), we introduced the ACO along with

Hill Climbing (HC) to come up with good variable or-

dering heuristics for solving CSPs. The results show

that the proposed method achieves better results, es-

pecially in the case of random hard problem instances.

In (Othman and Bouamama, 2019), the authors in-

troduced a method based on Honey Bee algorithm

to solve Max-CSPs. The results show that the pro-

posed method outperforms other Honey Bee-based al-

gorithms.

In (Korani et al., 2019), we proposed the Mother

Tree Optimization (MTO) algorithm to solve continu-

ous optimization problems based on a ﬁxed-offspring

topology. The results of several comparative exper-

iments show that MTO outperforms different Parti-

cle Swarm Optimization (PSO) variants. In (Korani

and Mouhoub, 2020), we developed a discrete version

of MTO, which we called Discrete MTO (DMTO),

to solve the Traveling Salesman Problem (TSP). The

results of the experiments we conducted on TSP in-

stances demonstrate the efﬁciency of DMTO com-

pared to variants of PSO. DMTO is based on a swap

operator that is well suited for TSPs.

In this paper, we propose a variant of DMTO

adapted to CSPs. The new technique, which we call

DMTO-CSP, relies on gathering constraint violations

(Minton et al., 1992b; Mouhoub and Jafari, 2011;

Mouhoub, 2004; Yong and Mouhoub, 2018) for each

variable and recording this information in a data struc-

ture that we call Recommendation Pool (RP). In ad-

dition, we propose a variant of a PSO algorithm that

we developed for solving dynamic CSPs (Bidar and

Mouhoub, 2019a). This variant, which we call Muta-

tion PSO (MPSO), is also based on RP. In both meth-

ods (DMTO-CSP and MPSO), the main role of RP is

to update candidate solutions, respectively following

the MTO topology, in the case of DMTO-CSP, and the

position and velocity equations in the case of MPSO.

The rest of the paper is organized as follows. Sec-

tion 2 presents an overview of constraint problems

and the related nature-inspired solving techniques. In

section 3, the basic concept of MTO algorithm and

its adaptation, DMTO-CSP, is discussed. In section 4,

we present MPSO. In section 5, we report on the ex-

periments for evaluating the performance of DMTO-

CSP and MPSO. Finally, section 6 lists concluding

remarks and ideas for future works.

2 RELATED WORK

In (Goradia, 2013), Goradia introduced Limited-

Memory Ant-Solver to solve CSPs. In the Ant-Solver,

ants have limited memory, where variables’ value re-

call partial assignments from their previous iteration.

The results show that the proposed method has the

same performance as Ant-Solver with respect to sev-

eral performance criteria. The authors combine their

proposed method along with a local search technique.

The results show that the proposed method along with

local search outperforms Ant-solver, along with local

search, especially for solving large CSPs. In (Liang

et al., 2017), Liang et al. introduced a method that

is built on the Artiﬁcial Bee Colony (ABC) algo-

rithm, called improved ABC (I-ABC) algorithm to

solve constraints optimization problems. In I-ABC

algorithm, the authors proposed a new selection strat-

egy based on rank selection and a search mechanism

using the information of the best so far solution to

balance exploration and exploitation processes(Blum

and Roli, 2003; Glover and Kochenberger, 2006;

Talbi, 2009; Korani and Mouhoub, 2021). In ad-

dition, the authors used the periodic boundary han-

dling model to repair invalid solutions. The authors

conducted extensive experiments to demonstrate the

efﬁciency of their proposed algorithm. In (Zouita

et al., 2019), Zouita et al. introduced a new CSP

solving technique based on arc consistency and ge-

netic algorithms (GAs). Here, a candidate solution

is represented as a chromosome where variables cor-

respond to genes and values represent alleles. Con-

straint propagation, through arc consistency, is used

to remove some inconsistent values, which will make

the remaining search task easier for the GA method.

In (Bidar and Mouhoub, 2019a), we introduced a dis-

crete variant of PSO to solve Dynamic CSPs (DC-

SPs). A DCSP is a dynamic variant of a CSP, where

constraints are added dynamically. In this regard, the

main goal of the proposed PSO is to solve the CSP

in an incremental way anytime new constraints are

added. In addition, the new solution obtained should

be as close possible to the old one. To evaluate the

performance of our proposed PSO, we conducted sev-

eral experiments on CSP instances randomly gener-

ated using the model RB. The results show that our

Discrete Mother Tree Optimization and Swarm Intelligence for Constraint Satisfaction Problems

235

PSO outperforms other exact and stochastic search

algorithms. In (Mouhoub and Jafari, 2011), we pro-

posed two new variable and value ordering heuristics

respectively based on Hill Climbing (HC) and Ant

Colony Optimization (ACO). The goal of these two

heuristics is to provide a good variable and value or-

dering to a backtrack search algorithm. Experimen-

tal evaluation demonstrates the good performance of

backtracking when using our ordering heuristics.

3 DMTO-CSP

The MTO algorithm is based on a ﬁxed-offspring

topology (Korani et al., 2019), where agents (repre-

senting potential solutions) update their positions in

the search space according to the group to which they

belong. MTO is inspired by the symbiotic relation-

ship between Douglas ﬁr trees and mycorrhizal fungi

networks. The population is a set of Active Food

Sources (AFSs) whose size is denoted as N

. Follow-

ing the ﬁxed-offspring topology, the MTO population

is divided into three groups: the TMT (the agent re-

ceiving nutrients from a random source), the Partially

Connected Trees (PCTs) group that has N

PCTs

agents,

and the Fully Connected Trees (FCTs) group that has

FCTs

agents. In addition, the PCTs group is divided

into the First Partially Connected Trees (FPCTs) sub-

group that has N

FPCTs

agents and the Last Partially

Connected Trees (LPCTs) sub-group that has N

LPCTs

agents. The FPCTs group has

− 2 agents in range

[ 2

− 1]. The LPCTs group has

− 2 agents

in range [

+ 3 : N

] and ends at the last agent in

the population. Figure 1 shows the different groups

of candidates, following the ﬁxed-offspring topology.

Here, agents are arranged (top down) in descending

order of their ﬁtness value.

Figure 1: MTO Topology.

In (Korani and Mouhoub, 2020), we proposed the

DMTO algorithm to solve the Traveling Salesman

Problem (TSP). DMTO is based on a swap opera-

tor that is well suited for TSPs. In order to adapt

DMTO to CSPs, we propose a new technique that we

call the recommendation pool (RP). RP main goal is

to help the search converge quickly towards the solu-

tion. Moreover, we deﬁne a recheck operator (r) for

selecting the best candidate from RP. Our proposed

technique is inspired by the hill climbing heuristic

(Minton et al., 1992b; Mouhoub, 2004). Basically, at

each iteration of the DMTO-CSP algorithm, we im-

prove candidate solutions in each of the three groups

(TMT, PCT, and FCT) as done in hill climbing. More

precisely, for each potential solution, we select the

variable involved in most conﬂicts and replace its

value with the one that minimizes the number of con-

ﬂicts. In order to prevent the algorithm from being

trapped in a local optimum, we balance this exploita-

tion strategy with exploration. For this latter, we se-

lect the value randomly for a chosen variable. In the

following, we deﬁne the details of the DMTO-CSP

components.

3.1 Solution Representation, Fitness

Function and Recommendation Pool

(RP)

Following on our past work, (Bidar and Mouhoub,

2019a), each candidate solution (or agent) in the pop-

ulation corresponds to a vector of size n, where n is

the total number of CSP variables. Each vector entry

corresponds to a variable value. The ﬁtness function

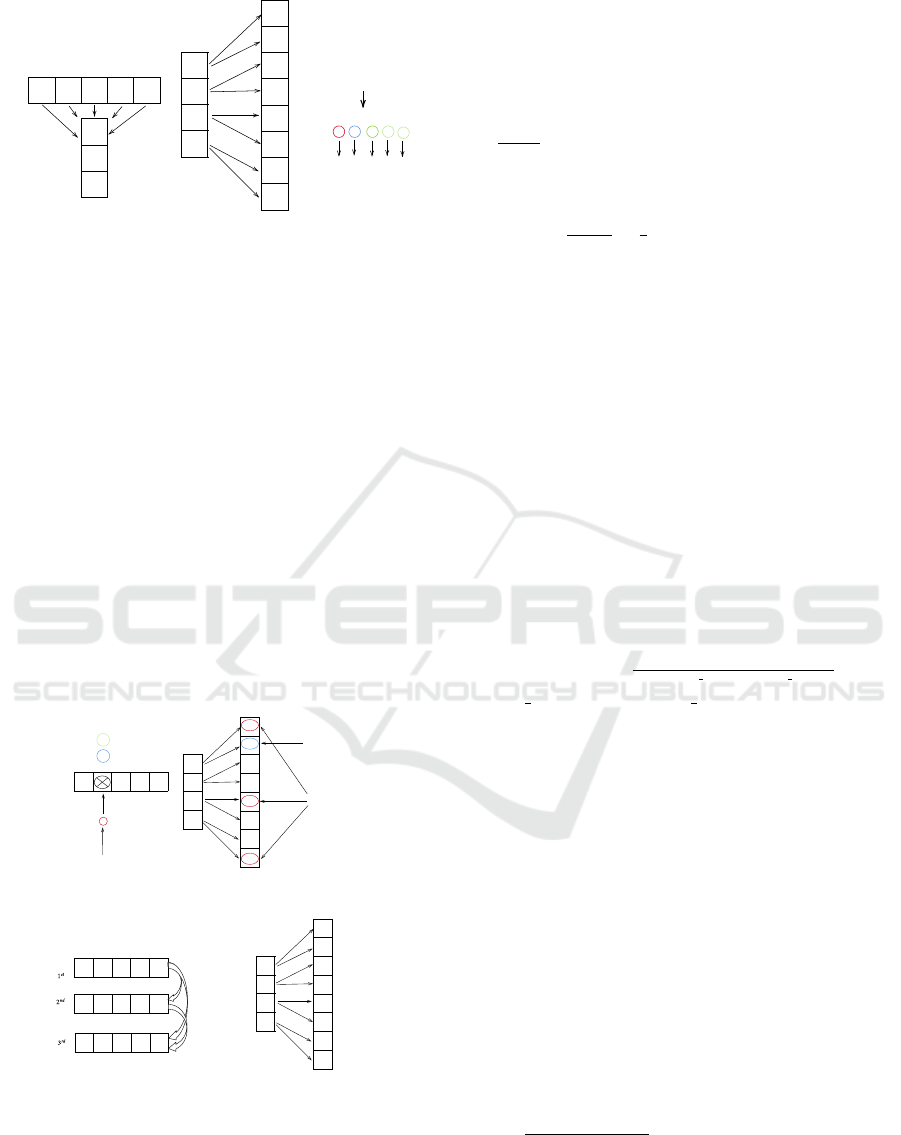
is deﬁned as the number of violated constraints. Fig-

ure 2 shows a candidate solution corresponding to a

CSP with ﬁve variables, each deﬁned on a domain

with three values, {a, b, c}. The candidate solution

listed has a ﬁtness value of 4 (corresponding to four

constraint violations). RP is a list containing all the

CSP variables ranked in descending order of the con-

straint violations they are involved in. RP is produced

from, another list that we call the Violation Pool (VP).

VP contains all variables occurring in each constraint

violation. Figure 2 shows both lists. Variable Var

is involved in most conﬂicts (3), followed by variable

Var

(2 conﬂicts),..., Etc.

3.2 Updating the Top Mother Tree

(TMT) and Other Candidate

Solutions

At each iteration of the DMTO-CSP algorithm, can-

didate solutions are rearranged in descending order

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

236

Solution

Domain

Constrains

Incompatible tuples

bcb

(1, 0)

(4, 3)

(4, 1)

(1, 2)

Var 1 Var 2

Var 3 Var 4Var 0

(c, b)

(b, b)

(a, a)

(a, b)

(a, c)

(c, b)

(a, c)

(c, b)

{ 1, 0, 4, 3, 4, 1, 1, 2}

Violation Pool

{

Recommendation Pool

Number of variables occurance

3, }

Figure 2: A CSP with ﬁve variables and domain of three

values. There are 4 constrains and a total of 8 incompatible

tuples.

of their ﬁtness value. TMT (ranked 1

) is the best

candidate solution (candidate with the lowest ﬁtness

value). The RP of TMT is called Super Recommen-

dation Pool (SRP). Inspired by the root signal level

and mycorrhizal fungi network (MFN) level (Korani

et al., 2019), TMT balances exploitation and explo-

ration as follows. Exploitation is conducted as shown

in Figure 3. First, we select the ﬁrst variable in SRP

(Var

, the variable involved in the largest number of

conﬂicts). Then, we select the value that minimizes

the number of conﬂicts (value a, which reduces the

number of conﬂicts for Var

to 0). If there is no better

value, the algorithm switches to exploration by choos-

ing a random value for the second or the third variable

in SRP. This process will ensure diversiﬁcation as the

algorithm will explore more promising areas.

Constrains

Incompatible tuples

(1, 0)

(4, 3)

(4, 1)

(1, 2)

Var 1 Var 2

Var 3

Var 4

Var 0

(c, b)

(b, b)

(a, a)

(a, b)

(a, c)

(c, b)

(a, c)

(c, b)

{

SRP

1, 0,

}

TMT

Violations var 1 = c

Violations var 1 = b

Violations var 1 = a

winner value

first variable in the super

recommendation pool

Var 1 Var 2 Var 3

Var 4

Var 0

Var 1

Var 2

Var 3 Var 4

Var 0

TMT

Assume we have 6 agents and Nos = 2

feeder

feedee

Constrains

Incompatible tuples

(1, 0)

(4, 3)

(4, 1)

(1, 2)

(c, b)

(b, b)

(a, a)

(a, b)

(a, c)

(c, b)

(a, c)

(c, b)

{

FRP12

var1 = a,

var3 = a

}

when var 1 = a

CVs = 0

when var3 = a

CVs = 2

CVs = 1

Var 1 Var 2 Var 3

Var 4

Var 0

Figure 3: Updating the TMT (left) and the second agent in

the population (right).

Unlike TMT which is updated through exploita-

tion and exploration following a hill climbing heuris-

tic, candidate solutions in PCT and FCT groups are

updated according to the inﬂuence (feeding process)

their parents have on them. This process is guided

by a ﬁxed-offspring topology. More precisely, par-

ticles are inﬂuenced and updated according to their

parents in the topology, with a given probability. This

probability (also called weight of the parent) is equal

n−i+1

where n is the position of the agent, and i

is the position of its parent. The right illustration of

3 illustrates this procedure for the second best agent.

This latter is inﬂuenced by its parent (the TMT), with

probability

2−1+1

, and is updated as follows. The

RP of this second agent, called Feeder Recommended

Pool (FRP), is ﬁlled with all the variable assignments

of the feeder (TMT) that are different from those of

the receiver (the second agent). In our example, this

will result in the following FRP for the second agent

that is inﬂuenced by the ﬁrst one: FRP12 = {Var

= a, Var

= a}. Then, the assignment that mini-

mizes the ﬁtness function of the receiver is selected.

If such assignment does not exist, then the algorithm

switches to exploration and random values will be as-

signed to the variables in FRP. In our case, assign-

ing a to Var

will reduce the ﬁtness function of the

second agent to 0 (as shown in Figure 3). This is a

particular case where the algorithm will ﬁnd and re-

turn a complete solution (given that the ﬁtness value

is equal to 0). In case random assignments are per-

formed, the algorithm will compute the following sig-

moid function value in order to decide if the agent will

be updated: Sig =

(1−e

f itness updated− f itness current

)

. Here,

ﬁtness updated and ﬁtness current represent the ﬁt-

ness of the updated and initial agent, respectively. If

the sigmoid value is greater than the weight of the

parent agent then the agent will not be updated. Fig-

ure 3 shows that agent ranked second receives nu-

trients from only the TMT, and the FRP12 = {Var

= a, Var

= a}. All recommended variables’ value

in the FRP12 are evaluated on the current receiver

and the best variable value that achieve lowest num-

ber of violations is selected, and then updated the re-

ceiver solution. Figure 3 shows that when the value

of Var

of the second solution is changed to a as

recommended in the FRP12 the number of CVs de-

creases to zero violation, which is the global solu-

tion. If no variable value could achieve better solu-

tion, then the 1

and 2

variables’ value in the FRP12

update their values in a random way. Then, the sig-

moid value of the difference between the updated ﬁt-

ness and the current ﬁtness is calculated as follows:

Sig =

(1−e

updated−current

)

. Each feeder has an associated

weight according to our offspring topology (Korani

et al., 2019). If the returned sigmoid value is greater

than the weight of this feeder, then the updating of

this feeder is taken place and the current solution is

Discrete Mother Tree Optimization and Swarm Intelligence for Constraint Satisfaction Problems

237

updated. This feeding process (depicted in Figure 1)

is repeated for all the agents in each group.

3.3 DMTO-CSP Climate Change

The climate change is a diversiﬁcation operation that

helps DMTO-CSP to explore more promising areas

in the hope of ﬁnding the solution to the CSP. The

number of climate change events is denoted by Cl

and each climate change happens once every cycle (a

given number maxCl of iterations). More precisely,

the climate change operation works as follows. The

best updated solution is recorded in a queue called a

Best Solution Pool (BSP) that has a length equal to

the population size. At each climate change event, we

apply a distortion process on all solutions in BSP. The

distortion process consists of randomly changing the

values for rv randomly selected variables. Prelimi-

nary experiments that we conducted show that 10 and

2 are the best values for maxCl and rv, respectively.

4 MPSO

PSO is a very popular nature inspired algorithm that

has been used to tackle challenging continuous and

discrete optimization problems (Kennedy and Eber-

hart, 1995; Fornarelli, 2012). PSO is a population-

based nature inspired algorithm, where candidate so-

lutions (called particles) search for a given solution,

following velocity and position equations. In (Bidar

and Mouhoub, 2019a), we have introduced a variant

of PSO that we call Discrete PSO (DPSO) for solving

dynamic CSPs. In this regard, we have deﬁned the

following equations for position and velocity, in the

case of CSPs.

t+1

= X

t+1

(1)

t+1

= ω ⊗V

| {z }

exploration

⊗ [X

 X

] + c

⊗ [X

 X

]

| {z }

exploitation

(2)

In the above equations, V

and X

are respectively

the velocity and position of particle i (a given candi-

date solution), at time t. ω is the inertia coefﬁcient, c

and c

are acceleration coefﬁcients in range [0,1], and

and r

are random values in range [0,1]. Equation 2

balances exploration and exploitation as follows. Ex-

ploration is expressed by the ﬁrst part (ω ⊗V

) where

the particle moves at random, depending on the in-

ertial coefﬁcient ω. Exploitation is guided by the

rest of the equation, where the particle respectively

moves towards its local best (X

), and to the global

best (X

), according to the acceleration coefﬁcients

and random values. The operator  corresponds to

changing some of the particle (X

) variables values so

it moves closer to its local or global best, respectively.

This is done by having both particles sharing more

identical values. The operator ⊗ decides on how close

should the particle be to its local and global best re-

spectively (according to to the initial coefﬁcients and

random parameters). Similarly, in the case of explo-

ration, ⊗ decides on the level on randomness to apply,

according to the parameter ω.

Our proposed MPSO follows the same individual

representation and ﬁtness function of DPSO, as de-

scribed in Section 3.1. MPSO also follows the same

equations 1 and 2. The difference resides in the way

the operators ⊗ and  are implemented. Like in

DMTO-CSP, we use recommendation pools to per-

form exploration and exploitation, through these two

operators. Similarly to the Feeder Recommended

Pool (FRP), we deﬁned in Section 3.2, we use a Local

RP (LRP) and (respectively a Global RP (GRP)), that

contains all the variables assignments of the local best

(respectively the global best) that are different from

the current particle. Then, we select the assignments

that minimize the number of conﬂicts. The number

of the selected assignments depend on the inertia co-

efﬁcients (respectively the random values). The cor-

responding variables in the current particle will then

be mutated accordingly. Exploration is performed by

randomly mutating a fraction (corresponding to ω) of

the particle variables.

5 EXPERIMENTATION

In order to evaluate the performance of our DMTO-

CSP and MPSO, we conducted several comparative

experiments that we report in this section. The exper-

iments are performed on random as well as real-world

instances. Random instances are generated using the

model RB (Xu and Li, 2000). This model is an vari-

ant of the standard Model B, and is capable of pro-

ducing hard to solve instances (those that are close

to the phase transition). Instances are randomly gen-

erated based on four parameters: the number of vari-

ables (n), the constraint tightness (0 < p < 1), and two

positive constants, α and r, (0 < α,r < 1). The con-

straint tightness is deﬁned as the number of incompat-

ible tuples over the Cartesian product of the variables

domain. Given these four parameters, RB instances

are generated as follows.

1. Select rn ln n distinct random constraints. Each

random constraint is formed by selecting 2 of n

variables.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

238

2. For each constraint, we uniformly select pd

dis-

tinct incompatible pairs of values, where d = n

is the domain size of each variable.

3. All the variables have the same domain corre-

sponding to the ﬁrst d natural numbers (0 ...d −

1).

In the above, the number of constraints, and the

number of incompatible tuples should be rounded to

the nearest integer. According to (Xu and Li, 2000),

the phase transition pt is calculated as follows: pt =

1 − e

−α/r

. Solvable problems are therefore generated

with p < pt.

For real-world problems, we use the Driverlog, the

Quasi Completion Problem (QCP) and the balanced

Quasigroup with holes (BQWH) problems (Rous-

sel and Lecoutre, 2009). The Driverlog is a logis-

tic planning problem with four parameters: drivers,

trucks, packages, and locations. Drivers drive trucks

that carry packages to speciﬁc locations. The main

goal here is to ﬁnd a solution for transporting a subset

of packages, by drivers and trucks, to certain loca-

tions. The number of CSP variables is ranging in [71

: 650], and the number of constraints is ranging in

[217 : 17447]. The Quasi-group Completion Prob-

lem (QCP) consists of completing a partially ﬁlled

Latin square. A Quasi-group can be seen as a mul-

tiplication table, with n rows and n columns, deﬁn-

ing a Latin square. Each row and column of the ta-

ble must be ﬁlled with a unique integer value. QCP

instances are used to bridge the gap between ran-

dom instances (such as those represented by the RB

model) and structured problems (Rossi et al., 2006).

These problems have many relevant real-world ap-

plications including resource allocation, timetabling,

statistical design and error correction codes. Quasi-

group with Holes (QWH) are generated by starting

with a complete Latin square (corresponding to a

complete Quasi-group). Some entries are then re-

moved. BQWH are generated such that the distri-

bution of the holes is balanced. In this regard, the

number of unassigned cells is approximately the same

across the different rows and columns.

Tables 1 and 2 list comparative results, in terms

of Number of Constraint Check (NCC), for CSP in-

stances with 100 and 200 variables, respectively. Our

algorithms are compared to our previous implemen-

tations of DPSO (Bidar and Mouhoub, 2019a) and

the discrete Fireﬂy algorithm (DFA) for CSPs (Bidar

and Mouhoub, 2019b). The results for Table 1 show

that MPSO is outperforming all the other methods for

tightness values ranging from 0.25 to 0.4, excluding

p = 0.35 where DMTO-CSP is the winner. For tight-

ness ranging from 0.45 to 0.6 (corresponding to the

hardest problems to solve) DPSO is the best method.

However, for 200 variables, MPSO is the best method

for all the tightness values, as demonstrated in Table

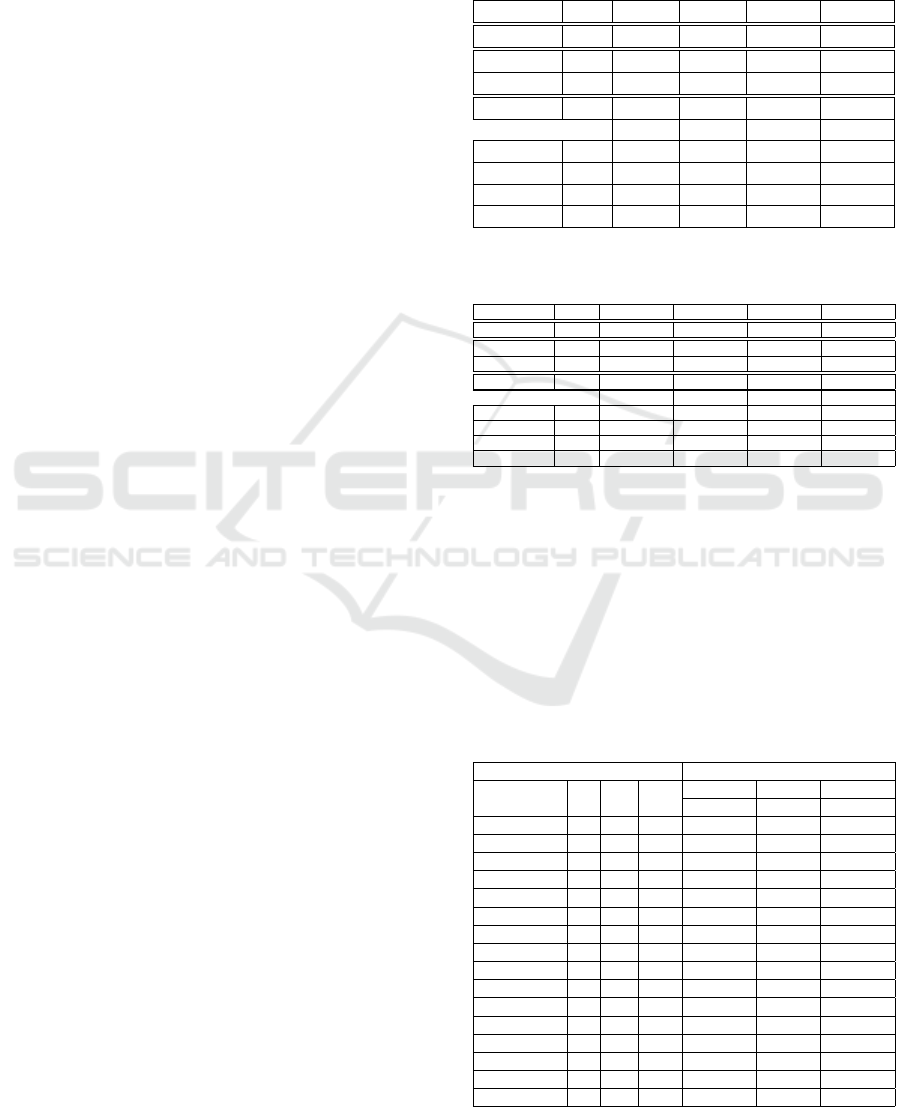
Table 1: Experimentation results on CSPs with 100 vari-

ables with different tightness.

Algorithm factor p=0.25 p=0.3 p=0.35 p=0.4

DMTO-CSP NCC 2209297 1477767 2127931 5445792

FA NCC 4016487 4939168 4940176 5567451

DPSO NCC 1815428 1915214 2216247 3230127

MPSO NCC 929979 1196615 2146649 2432194

p=0.45 p=0.5 p=0.55 p=0.6

DMTO-CSP NCC 8879399 9076893 11499728 10577580

FA NCC 5671379 5973192 6881238 7120192

DPSO NCC 3846671 5171136 5383012 5928431

MPSO NCC 4311061 5369965 6002175 7085718

Table 2: Comparative results for CSP instances with 200

variables.

Algorithm factor p=0.25 p=0.3 p=0.35 p=0.4

DMTO-CSP NCC 40475600 61233920 74535560 89581360

FA NCC 31217848 63102648 89742144 66245760

DPSO NCC 26114584 56745192 57585984 59538080

MPSO NCC 13807200 22245960 33345400 43709160

p=0.45 p=0.5 p=0.55 p=0.6

DMTO-CSP NCC 86075000 119251440 109129680 141961160

FA NCC 132845190 148474200 13975843 217817280

DPSO NCC 71021584 122029320 135748912 131999680

MPSO NCC 56173480 63899000 72359320 88160600

In order to assess the quality of the solutions re-

turned when solving the Driverlog instances (Rous-

sel and Lecoutre, 2009), we conducted experiments

comparing our two methods to the backtrack search

algorithm with dom/wdeg* variable ordering heuris-

tic (Yong and Mouhoub, 2018). This latter heuristic

consists of ordering variables starting with the most

constraining one. More precisely, variables are or-

dered according to the ratio dom/wdeg, where dom

Table 3: Comparative results for the Driverlog, BQWH and

QCP instances.

Instance Algorihtms

No. V R C

DMTO-CSP MPSO dom/wdeg*

# cck # cck # cck

01c 71 14 217 1.05M 1.2M 0.026M

08c 408 648 9321 1003.5M 2862.56M 67.233M

08cc 408 649 9321 1046.26M 3408.71M 75.787M

09 650 1639 17447 3955.9M 4392.02M Not reported

bqwh-15-106-0 106 155 644 .862M 0.069M 5.355M

bqwh-15-106-5 106 135 644 1.335M 0.245M 0.347M

bqwh-15-106-9 106 149 644 2.73M 0.49M 2.870M

bqwh-18-141-0 141 236 966 2.075M 0.104M 26.935M

bqwh-18-141-06 141 229 966 25.27M 0.245M 12.357M

bqwh-18-141-22 141 263 966 3.75M 0.057M 1.941M

qcp-10-67-0 100 12 900 3.1M 1.65M 0.133M

qcp-10-67-7 100 11 900 3.8M 1.31M 1.452M

qcp-10-67-14 100 12 900 6.6M 9.2M 0.089M

qcp-15-120-0 225 17 3150 28.35M 4.6M 12.835M

qcp-10-67-8 225 17 3150 77.68M 24.48M 38.085M

qcp-10-67-14 225 17 3150 28.64M 1.09M 1.565M

Discrete Mother Tree Optimization and Swarm Intelligence for Constraint Satisfaction Problems

239

is the domain size of the variable while wdeg is the

weighted degree of the corresponding node. This

weight is equal to the sum of the weights of the con-

straints associated the variable. The weight of a con-

straint is computed based on the conﬂict and sup-

port counts gathered by a look-ahead method during

search. Given that dom/wdeg* returns a complete so-

lution, we had to let our two methods run for 1000

iterations and only report those results where com-

plete solutions are returned. Table 3 (ﬁrst 4 rows),

lists the results of this experimentation. As we can

notice, dom/wdeg* outperforms our methods for the

ﬁrst three problem instances. For the last and hardest

instance however (No 9), dom/wdeg* was not able to

return the solution while our methods where success-

ful. This is a promising result that will motivate us to

conduct further improvements for both DMTO-CSP

and MPSO.

Table 3 (from the 5th row) lists the number of con-

straint checks when solving BQWH and QCP prob-

lem instances. Here again, DMTP-CSP and MPSO

are compared to the backtrack search algorithm with

dom/wdeg* variable ordering heuristic. As we can

notice from the results, MPSO is the winner in most

of the problem instances. The dom/wdeg* method

was the best in only two problem instances. More-

over, some instances show that DMTO-CSP is also

better than dom/wdeg*. These results favoring our

two methods might be due to the fact that QCP and

BQWH inherit properties from both the random and

the structured problems.

6 CONCLUSION AND FUTURE

WORK

We propose an adaptation of DMTO (Korani and

Mouhoub, 2020) and DPSO (Bidar and Mouhoub,

2019a) for solving CSPs. Our variants are respec-

tively called DMTO-CSP and MPSO and are guided

by a hill climbing heuristic. Indeed, both meth-

ods gather the information regarding those variables

in conﬂict (Mouhoub and Jafari, 2011; Yong and

Mouhoub, 2018), and use it to update their popula-

tion through the MTO topology and PSO position and

velocity equations, respectively. To assess the practi-

cal performance of our proposed techniques, we con-

ducted several comparative tests on randomly gen-

erated as well as real-world instances. Random in-

stances are generated using the known RB model

(Xu and Li, 2000) which can generate hard-to-solve

instances. Real-world instances are taken from the

XCSP library (Roussel and Lecoutre, 2009) and cor-

respond to the Driverlog, the balanced Quasigroup

with holes (BQWH) and the Quasi Completion Prob-

lem (QCP) instances. Our methods were compared

to other nature-inspired techniques (DPSO (Bidar and

Mouhoub, 2019a) and DFA (Bidar and Mouhoub,

2019b)) and backtrack search using variable ordering

heuristics, dom/wdeg* (Yong and Mouhoub, 2018).

Overall, the results are promising and show the su-

periority of our techniques for both random, BQWH,

and QCP instances. For the Driverlog problems, al-

though dom/wdeg* is the winner for most of the in-

stances, our two methods were the only ones capa-

ble of solving the hardest instance. These results

motivated us to conduct further research on improv-

ing both techniques by considering other information

gathering heuristics and a good balance between ex-

ploration and exploitation. We also plan to general-

ize the idea of learning the hardness of constraints

during the search to other nature-inspired techniques

we developed in the past for solving CSPs (Abbasian

and Mouhoub, 2016; Bidar et al., 2018; Bidar and

Mouhoub, 2019c). We will also tackle the case of

variants of CSPs, including dynamic CSPs (Bidar

and Mouhoub, 2019a) and weighted CSPs (Bidar and

Mouhoub, 2019c).

REFERENCES

Abbasian, R. and Mouhoub, M. (2016). A new paral-

lel ga-based method for constraint satisfaction prob-

lems. Int. J. Comput. Intell. Appl., 15(3):1650017:1–

1650017:22.

Apt, K. (2003). Principles of constraint programming.

Cambridge university press.

Bidar, M., Kanan, H. R., Mouhoub, M., and Sadaoui, S.

(2018). Mushroom reproduction optimization (MRO):

A novel nature-inspired evolutionary algorithm. In

2018 IEEE Congress on Evolutionary Computation,

CEC 2018, Rio de Janeiro, Brazil, July 8-13, 2018,

pages 1–10. IEEE.

Bidar, M. and Mouhoub, M. (2019a). Discrete particle

swarm optimization algorithm for dynamic constraint

satisfaction with minimal perturbation. In 2019 IEEE

International Conference on Systems, Man and Cy-

bernetics (SMC), pages 4353–4360. IEEE.

Bidar, M. and Mouhoub, M. (2019b). Self-adaptive discrete

ﬁreﬂy algorithm for minimal perturbation in dynamic

constraint satisfaction problems. In IEEE Congress

on Evolutionary Computation, CEC 2019, Wellington,

New Zealand, June 10-13, 2019, pages 2620–2627.

IEEE.

Bidar, M. and Mouhoub, M. (2019c). Solving weighted

constraint satisfaction problems using a new self-

adaptive discrete ﬁreﬂy algorithm. In 2019 IEEE In-

ternational Conference on Systems, Man and Cyber-

netics, SMC 2019, Bari, Italy, October 6-9, 2019,

pages 2198–2205. IEEE.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

240

Blum, C. and Roli, A. (2003). Metaheuristics in combi-

natorial optimization: Overview and conceptual com-

parison. ACM computing surveys (CSUR), 35(3):268–

308.

Carbonnel, C. and Cooper, M. C. (2016). Tractability

in constraint satisfaction problems: a survey. Con-

straints, 21(2):115–144.

Dechter, R., Cohen, D., et al. (2003). Constraint processing.

Morgan Kaufmann.

Do, M. B. and Kambhampati, S. (2001). Planning as

constraint satisfaction: Solving the planning graph

by compiling it into csp. Artiﬁcial Intelligence,

132(2):151–182.

Fornarelli, G. (2012). Swarm intelligence for electric and

electronic engineering. IGI Global.

Galinier, P. and Hao, J. (1997). Tabu search for maximal

constraint satisfaction problems. In Smolka, G., ed-

itor, Principles and Practice of Constraint Program-

ming - CP97, Third International Conference, Linz,

Austria, October 29 - November 1, 1997, Proceedings,

volume 1330 of Lecture Notes in Computer Science,

pages 196–208. Springer.

Glover, F. W. and Kochenberger, G. A. (2006). Handbook of

metaheuristics, volume 57. Springer Science & Busi-

ness Media.

Goradia, H. J. (2013). Ants with limited memory for solv-

ing constraint satisfaction problems. In 2013 IEEE

Congress on Evolutionary Computation, pages 1884–

1891. IEEE.

Gutin, G. and Yeo, A. (2012). Constraint satisfaction prob-

lems parameterized above or below tight bounds: A

survey. In The Multivariate Algorithmic Revolution

and Beyond, pages 257–286. Springer.

Hmer, A. and Mouhoub, M. (2016). A multi-phase hybrid

metaheuristics approach for the exam timetabling.

Int. J. Comput. Intell. Appl., 15(4):1650023:1–

1650023:22.

Jussien, N. and Lhomme, O. (2002). Local search with con-

straint propagation and conﬂict-based heuristics. Ar-

tiﬁcial Intelligence, 139(1):21–45.

Kennedy, J. and Eberhart, R. (1995). Particle swarm opti-

mization. In Proc. IEEE Intl. Con on Neural Networks

(Perth, Australia), pages 1942–1948. IEEE.

Korani, W. and Mouhoub, M. (2020). Discrete mother tree

optimization for the traveling salesman problem. In

International Conference on Neural Information Pro-

cessing, pages 25–37. Springer.

Korani, W. and Mouhoub, M. (2021). Review on Nature-

Inspired Algorithms. SN Operations Research Forum,

2(3):1–26.

Korani, W., Mouhoub, M., and Spiteri, R. J. (2019). Mother

tree optimization. In 2019 IEEE International Confer-

ence on Systems, Man and Cybernetics (SMC), pages

2206–2213. IEEE.

Kumar, V. (1992). Algorithms for constraint-satisfaction

problems: A survey. AI magazine, 13(1):32–32.

Liang, Y., Wan, Z., and Fang, D. (2017). An improved ar-

tiﬁcial bee colony algorithm for solving constrained

optimization problems. International Journal of Ma-

chine Learning and Cybernetics, 8(3):739–754.

Minton, S., Johnston, M. D., Philips, A. B., and Laird,

P. (1992a). Minimizing conﬂicts: a heuristic re-

pair method for constraint satisfaction and scheduling

problems. Artiﬁcial intelligence, 58(1-3):161–205.

Minton, S., Johnston, M. D., Philips, A. B., and Laird,

P. (1992b). Minimizing conﬂicts: a heuristic re-

pair method for constraint satisfaction and scheduling

problems. Artiﬁcial Intelligence, 58(1):161–205.

Mitchell, M. (1996). An introduction to genetic algorithms

mit press. Cambridge, Massachusetts. London, Eng-

land, 1996.

Mouhoub, M. (2004). Systematic versus non systematic

techniques for solving temporal constraints in a dy-

namic environment. AI Commun., 17(4):201–211.

Mouhoub, M. and Jafari, B. (2011). Heuristic techniques for

variable and value ordering in csps. In Proceedings of

the 13th annual conference on Genetic and evolution-

ary computation, pages 457–464.

Othman, H. B. and Bouamama, S. (2019). A new template

concept guided honey bee optimization for max-csps.

Procedia Computer Science, 159:2154–2161.

Roos, N., Ran, Y., and Van Den Herik, J. (2000). Com-

bining local search and constraint propagation to ﬁnd

a minimal change solution for a dynamic csp. In

International Conference on Artiﬁcial Intelligence:

Methodology, Systems, and Applications, pages 272–

282. Springer.

Rossi, F., van Beek, P., and Walsh, T., editors (2006). Hand-

book of Constraint Programming. Elsevier.

Roussel, O. and Lecoutre, C. (2009). Xml representation of

constraint networks: Format xcsp 2.1. arXiv preprint

arXiv:0902.2362.

Ruttkay, Z. (1998). Constraint satisfaction-a survey. CWI

Quarterly, 11(2&3):123–162.

Shil, S. K., Mouhoub, M., and Sadaoui, S. (2013). Win-

ner determination in combinatorial reverse auctions.

In Contemporary challenges and solutions in applied

artiﬁcial intelligence, pages 35–40. Springer.

Talbi, E.-G. (2009). Metaheuristics: from design to imple-

mentation, volume 74. John Wiley & Sons.

Tsang, E. P., Wang, C. J., Davenport, A., Voudouris, C., and

Lau, T. L. (1999). A family of stochastic methods for

constraint satisfaction and optimization. In The First

International Conference on the Practical Application

of Constraint Technologies and Logic Programming

(PACLP), London, pages 359–383.

Xu, K. and Li, W. (2000). Exact phase transitions in random

constraint satisfaction problems. Journal of Artiﬁcial

Intelligence Research, 12:93–103.

Yong, K. W. and Mouhoub, M. (2018). Using conﬂict and

support counts for variable and value ordering in csps.

Appl. Intell., 48(8):2487–2500.

Zhang, J. and Zhang, H. (1996). Combining local search

and backtracking techniques for constraint satisfac-

tion. In AAAI/IAAI, Vol. 1, pages 369–374.

Zouita, M., Bouamama, S., and Barkaoui, K. (2019). Im-

proving genetic algorithm using arc consistency tech-

nic. Procedia Computer Science, 159:1387–1396.

Discrete Mother Tree Optimization and Swarm Intelligence for Constraint Satisfaction Problems

241