Falsiﬁcation-aware Semantics for CTL and Its Inconsistency-tolerant

Subsystem: Towards Falsiﬁcation-aware Model Checking

Norihiro Kamide and Seidai Kanbe

Teikyo University, Faculty of Science and Engineering, Department of Information and Electronic Engineering,

Toyosatodai 1-1, Utsunomiya-shi, Tochigi 320-8551, Japan

Keywords:

Computation Tree Logic, Inconsistency-tolerant Computation Tree Logic, Falsiﬁcation-aware Kripke-style

Semantics, Falsiﬁcation-aware Model Checking.

Abstract:

This study introduces two falsiﬁcation-aware Kripke-style semantics for computation tree logic (CTL). The

equivalences among the proposed falsiﬁcation-aware Kripke-style semantics and the standard Kripke-style

semantics for CTL are proven. Furthermore, a new logic, inconsistency-tolerant CTL (ICTL) is semantically

deﬁned and obtained from the proposed falsiﬁcation-aware Kripke-style semantics for CTL by deleting a char-

acteristic condition on the labeling function of the semantics. Because ICTL is regarded as an inconsistency-

tolerant and many-valued logic, the proposed semantic framework for CTL and ICTL is regarded as a uniﬁed

framework for combining and generalizing the standard, inconsistency-tolerant, and many-valued semantic

frameworks. This uniﬁed semantic framework is useful for generalized model checking, referred to here as

falsiﬁcation-aware model checking.

1 INTRODUCTION

Computation tree logic (CTL) (Clarke and Emer-

son, 1981) is known to be one of the most use-

ful temporal logics for model checking (Clarke and

Emerson, 1981; Clarke et al., 2018), which is a

computer-assisted method used to verify concurrent

systems that can be modeled by state-transition sys-

tems. Some inconsistency-tolerant variants of CTL,

referred to as inconsistency-tolerant CTLs, paracon-

sistent CTLs, and many-valued CTLs, have been

developed as a theoretical basis for inconsistency-

tolerant (paraconsistent and many-valued) model

checking (Easterbrook and Chechik, 2001; Chen and

Wu, 2006). Some inconsistency-tolerant CTLs have

falsiﬁcation-aware Kripke-style semantics, which are

capable of representing the explicit falsiﬁcation of a

given negated formula and are appropriate for speci-

fying and verifying inconsistency-tolerant reasoning.

For more information on inconsistency-tolerant tem-

poral logics and their model checking applications,

see (Easterbrook and Chechik, 2001; Chen and Wu,

2006; Kamide, 2006; Kamide and Wansing, 2011;

Kamide and Kaneiwa, 2010; Kaneiwa and Kamide,

2011; Kamide, 2015; Kamide and Koizumi, 2016;

Kamide and Endo, 2018).

In this study, we ﬁrst introduce two new

falsiﬁcation-aware Kripke-style semantics for CTL:

falsiﬁcation-aware normal Kripke-style semantics

and falsiﬁcation-aware dual Kripke-style semantics.

We then prove the equivalences among the proposed

falsiﬁcation-aware Kripke-style semantics and the

standard Kripke-style semantics for CTL. Second, we

also semantically deﬁne a new logic, inconsistency-

tolerant CTL (ICTL), which is obtained from the

proposed falsiﬁcation-aware normal and dual Kripke-

style semantics for CTL by deleting a characteris-

tic condition on the labeling function of the seman-

tics. Because ICTL is regarded as an inconsistency-

tolerant and many-valued logic, the proposed seman-

tic framework for CTL and ICTL is regarded as a uni-

ﬁed framework for combining and generalizing the

standard, inconsistency-tolerant, and many-valued se-

mantic frameworks. This uniﬁed semantic framework

is useful for combined and generalized model check-

ing, referred to here as falsiﬁcation-aware model

checking.

Next, we explain the motivation for develop-

ing falsiﬁcation-aware Kripke-style semantics for

CTL and ICTL. An adequate representation of

falsiﬁcation-aware reasoning is considered a major

concern in philosophical logic (Horn and Wansing,

2017). It was suggested in (Kamide, 2021) that se-

242

Kamide, N. and Kanbe, S.

Falsiﬁcation-aware Semantics for CTL and Its Inconsistency-tolerant Subsystem: Towards Falsiﬁcation-aware Model Checking.

DOI: 10.5220/0010803700003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 3, pages 242-252

ISBN: 978-989-758-547-0; ISSN: 2184-433X

mantics and/or proof systems for a logic can be con-

sidered falsiﬁcation-aware if they are capable of pro-

viding (or representing) the direct (or explicit) fal-

siﬁcations or refutations of given negated formulas

(except for negated atomic formulas). Furthermore,

falsiﬁcation-aware Kripke-style semantics are suit-

able for the theoretical basis of model checking be-

cause falsiﬁcation plays a critical role in obtaining

counterexample traces for the underlying object spec-

iﬁcations in model checking. In fact, a falsiﬁcation-

aware technique for explicitly dividing falsiﬁcation

(or refutation) and veriﬁcation (or justiﬁcation) is of-

ten used for model checking (Gurﬁnkel et al., 2006).

A counterexample-guided abstraction and reﬁnement

technique (Clarke et al., 2003) for model check-

ing, which is based on falsiﬁcation-aware Kripke-

style semantics in temporal logics, is also an exam-

ple of a useful technique in model checking. How-

ever, the standard Kripke-style semantics for CTL is

not falsiﬁcation-aware. Thus, we intend to develop

falsiﬁcation-aware Kripke-style semantics for CTL to

obtain a concrete logical foundation of falsiﬁcation-

aware model checking, which is deﬁned as model

checking based on falsiﬁcation-aware semantics.

The proposed falsiﬁcation-aware normal and dual

Kripke-style semantics for CTL are constructed on

the basis of the idea of falsiﬁcation-aware settings for

Nelson’s inconsistency-tolerant (or paraconsistent)

four-valued logic N4 (Almukdad and Nelson, 1984;

Nelson, 1949). Moreover, they are regarded as gen-

eralizations of the previously proposed falsiﬁcation-

aware Kripke-style semantics for some inconsistency-

tolerant CTLs. The proposed falsiﬁcation-aware

Kripke-style semantics for CTL have no standard con-

dition “|= ¬α iff 6|= α” with respect to the satisfaction

relation |= and the classical negation connective ¬.

This standard condition represents the transformation

of a negated formula to a non-negated formula (i.e.,

it is not falsiﬁcation-aware). Instead of this condi-

tion, the falsiﬁcation-aware dual Kripke-style seman-

tics for CTL has two clearly divided satisfaction re-

lations |=

and |=

−

, which explicitly represent ver-

iﬁcation (or justiﬁcation) and falsiﬁcation (or refuta-

tion), respectively. Thus, we can obtain the appropri-

ate falsiﬁcation-aware reasoning with |=

−

. The pro-

posed falsiﬁcation-aware Kripke-style semantics have

the merit of simply deﬁning a natural inconsistency-

tolerant CTL as a subsystem of CTL. In fact, the

inconsistency-tolerant temporal logic ICTL proposed

here can be deﬁned in a modular way from the

falsiﬁcation-aware Kripke-style semantics for CTL

by deleting only one mapping condition for the label-

ing function of the semantics. This type of simple def-

inition cannot be obtained using the standard Kripke-

style semantics for CTL. Thus, we can generalize

the framework and concept of previously proposed

inconsistency-tolerant (or paraconsistent) temporal

logics and inconsistency-tolerant (paraconsistent or

many-valued) model checking by using the proposed

falsiﬁcation-aware Kripke-style semantics and the

new concept of falsiﬁcation-aware model checking.

In what follows, we discuss existing inconsistency-

tolerant temporal logics and inconsistency-tolerant

model checking.

Compared to other non-classical logics,

inconsistency-tolerant (or paraconsistent) logics

including inconsistency-tolerant temporal logics have

no axiom of explosion, (α∧¬α)→β. Hence, they

can be appropriately used in inconsistency-tolerant

reasoning (Priest and Tanaka, 2009; da Costa et al.,

1995; Wansing, 1993). For example, the following

undesirable scenario is considered. The formula

(s(x)∧¬s(x))→d(x), which is an instance of the

axiom of explosion, is valid for any symptom s and

disease d, where ¬s(x) represents “a person x does

not have a symptom s” and d(x) represents “a person

x suffers from a disease d.” The inconsistent scenario

written as clinical-depression(Maria)∧¬clinical-

depression(Maria) will inevitably arise from

the uncertain deﬁnition of clinical depression (or

melancholia). The statement “Maria has clinical de-

pression” can be judged as true or false on the basis of

the perception of different pathologists. In this case,

the formula (clinical-depression(Maria)∧¬clinical-

depression(Maria))→cancer(Maria) is valid in

classical logic and standard temporal logics (as an

inconsistency that has an undesirable consequence)

but invalid in inconsistency-tolerant logics (as these

logics are inconsistency-tolerant). ICTL is also

regarded as an inconsistency-tolerant logic, although

CTL is not.

Several inconsistency-tolerant temporal logics

have been developed. For example, multi-valued

computation tree logic, referred to as χCTL, was de-

veloped by Easterbrook and Chechik (Easterbrook

and Chechik, 2001) to realize multi-valued model

checking, which is regarded as the ﬁrst considera-

tion for inconsistency-tolerant model checking. Qua-

siclassical temporal logic, referred to as QCTL,

was developed by Chen and Wu (Chen and Wu,

2006) to handle inconsistent concurrent systems us-

ing inconsistency-tolerant model checking. Para-

consistent full computation tree logic, referred to as

4CTL

∗

, was proposed by Kamide (Kamide, 2006)

for an expressive base logic for inconsistency-tolerant

model checking. A paraconsistent linear-time tempo-

ral logic, referred to as PLTL, based on a Gentzen-

style sequent calculus was developed by Kamide

Falsiﬁcation-aware Semantics for CTL and Its Inconsistency-tolerant Subsystem: Towards Falsiﬁcation-aware Model Checking

243

and Wansing (Kamide and Wansing, 2011) to ana-

lyze philosophical issues. A paraconsistent compu-

tation tree logic, referred to as PCTL, was devel-

oped by Kamide and Kaneiwa (Kamide and Kaneiwa,

2010; Kaneiwa and Kamide, 2011) to realize ef-

ﬁcient inconsistency-tolerant CTL-model checking.

Another paraconsistent CTL, referred to as pCTL, and

paraconsistent linear-time temporal logic, referred

to as pLTL, were developed by Kamide and Endo

(Kamide and Endo, 2018; Kamide and Endo, 2019)

to realize simple and efﬁcient inconsistency-tolerant

model checking. We remark that the name pCTL

for paraconsistent CTL is rather confusing because

the same name has also been used for probabilistic

CTL (Aziz et al., 1995; Bianco and de Alfaro, 1995),

and this probabilistic temporal logic pCTL has been

used for probabilistic model checking. Probabilistic

temporal logic was developed by Aziz et al. (Aziz

et al., 1995) and Bianco and de Alfaro (Bianco and

de Alfaro, 1995) to verify probabilistic concurrent

systems. In the present study, ICTL is regarded as or

closely related to the classical negation-free subsys-

tems of PCTL and the inconsistency-tolerant tempo-

ral logic pCTL. Namely, ICTL is regarded as a purely

inconsistency-tolerant subsystem of PCTL and pCTL.

Several extensions of inconsistency-tolerant tem-

poral logics have been developed. For example,

a sequence-indexed paraconsistent computation tree

logic, referred to as SPCTL, was developed by

Kamide (Kamide, 2015) by extending CTL with the

addition of both a paraconsistent negation connective

and a sequence modal operator. SPCTL was used to

verify clinical reasoning with inconsistent and hier-

archical information. An inconsistency-tolerant (or

paraconsistent) probabilistic computation tree logic,

referred to as PpCTL, was developed by Kamide

and Koizumi (Kamide and Koizumi, 2015; Kamide

and Koizumi, 2016) to verify stochastic or ran-

domized inconsistent concurrent systems. A loca-

tive inconsistency-tolerant hierarchical probabilistic

computation tree logic, referred to as LIHpCTL, was

developed by Kamide and Bernal (Kamide and Bernal

J.P.A., 2019) as an extension of PpCTL and the hi-

erarchical (or sequential) computation tree logic, re-

ferred to as sCTL, developed in (Kamide and Yano,

2017; Kamide, 2018). An inconsistency-tolerant (or

paraconsistent) hierarchical probabilistic computa-

tion tree logic, referred to as IHpCTL, was devel-

oped by Kamide and Yamamoto (Kamide and Ya-

mamoto, 2021) as a modiﬁed version of the location-

operator-free subsystem of LIHpCTL. For more in-

formation on (extended) inconsistency-tolerant tem-

poral logics and their model checking applications,

see (Easterbrook and Chechik, 2001; Chen and Wu,

2006; Kamide, 2006; Kamide and Wansing, 2011;

Kamide and Kaneiwa, 2010; Kaneiwa and Kamide,

2011; Kamide, 2015; Kamide and Koizumi, 2016;

Kamide and Endo, 2018).

The remainder of this paper is organized as fol-

lows. In Section 2, as the preliminaries of this study,

we deﬁne the standard syntax and Kripke-style se-

mantics for CTL. In Section 3, we introduce the

falsiﬁcation-aware normal Kripke-style semantics for

CTL and prove the equivalence between the standard

Kripke-style semantics and the proposed falsiﬁcation-

aware normal Kripke-style semantics. In Section 4,

we introduce the falsiﬁcation-aware dual Kripke-style

semantics for CTL and prove the equivalence between

the standard Kripke-style semantics and the proposed

falsiﬁcation-aware dual Kripke-style semantics. Fur-

ther, we obtain the equivalences among the standard

and two proposed falsiﬁcation-aware Kripke-style se-

mantics for CTL. In Section 5, we ﬁrst semantically

deﬁne ICTL by deleting a characteristic mapping con-

dition from the falsiﬁcation-aware normal and dual

Kripke-style semantics for CTL. We then prove the

equivalence between the falsiﬁcation-aware normal

and dual Kripke-style semantics for ICTL. In Section

6, we conclude this paper and address some remarks

on falsiﬁcation-aware model checking based on the

proposed and extended falsiﬁcation-aware Kripke-

style semantics.

2 NORMAL KRIPKE-STYLE

SEMANTICS FOR CTL

Formulas of CTL are constructed from countably

many propositional variables by the logical connec-

tives: → (implication), ∧ (conjunction), ∨ (disjunc-

tion), and ¬ (negation); the temporal operators: X

(next-time), G (globally or any-time in the future), F

(eventually or some-time in the future), U (until), and

R (release); and the path quantiﬁers: A (all computa-

tion paths) and E (some computation path). We use

an expression α ↔ β to denote (α→β)∧(β→α). We

use lower-case letters p,q,... to denote propositional

variables, Greek lower-case letters α, β, ... to denote

formulas, and lower-case letters i, j and k to denote

any natural numbers. We use the symbol ω to repre-

sent the set of natural numbers, the symbol ≥ or ≤

to denote the linear order on ω, and the symbol ≡ to

denote the equality of symbols.

Deﬁnition 2.1. Formulas of CTL are deﬁned by the

following Backus-Naur form, assuming p represents

propositional variables:

α ::= p | α ∧ α | α ∨ α | α→α | ¬α

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

244

| AXα | EXα | AGα | EGα | AFα | EFα

| A(αUα) | E(αUα) | A(αRα) | E(αRα).

Deﬁnition 2.2 (Normal Kripke-style semantics for

CTL). A structure (S,S

,R,L) is called a CTL-model if

1. S is the set of states,

2. S

is a set of initial states and S

⊆ S,

3. R is a binary relation on S such that ∀s ∈ S ∃s

∈

S [(s,s

) ∈ R],

4. L is a mapping from S to the power set of a

nonempty set Φ of propositional variables.

A path in a CTL-model is an inﬁnite sequence π =

,... of states such that ∀i ≥ 0 [(s

i+1

) ∈ R].

A CTL-satisfaction relation (M,s) |= α for any

formula α, where M is a CTL-model (S,S

,R,L) and

s is a state in S, is deﬁned inductively by the following

clauses:

1. for any p ∈ Φ, (M, s) |= p iff p ∈ L(s),

2. (M,s) |= α∧β iff (M,s) |= α and (M, s) |= β,

3. (M,s) |= α∨β iff (M,s) |= α or (M, s) |= β,

4. (M,s) |= α→β iff (M,s) 6|= α or (M, s) |= β,

5. (M,s) |= ¬α iff (M,s) 6|= α,

6. (M,s) |= AXα iff ∀s

∈ S [(s,s

) 6∈ R or (M, s

) |= α],

7. (M,s) |= EXα iff ∃s

∈ S [(s,s

) ∈ R and (M,s

) |= α],

8. (M,s) |= AGα iff for any paths π ≡ s

,... with

s ≡ s

, and any states s

along π, we have (M,s

) |= α,

9. (M,s) |= EGα iff there exists a path π ≡ s

,...

with s ≡ s

, and for any states s

along π, we have

(M,s

) |= α,

10. (M,s) |= AFα iff for any paths π ≡ s

,... with s ≡

, there exists a state s

along π such that (M,s

) |= α,

11. (M,s) |= EFα iff there exists a path π ≡ s

,...

with s ≡ s

, and for some state s

along π, we have

(M,s

) |= α,

12. (M,s) |= A(αUβ) iff for any paths π ≡ s

,... with

s ≡ s

, there exists a state s

along π such that (M,s

) |=

β and ∀0 ≤ k < j (M,s

) |= α,

13. (M,s) |= E(αUβ) iff there exists a path π ≡ s

,...

with s ≡ s

, and for some state s

along π, we have

(M,s

) |= β and ∀0 ≤ k < j (M, s

) |= α,

14. (M,s) |= A(αRβ) iff for any paths π ≡ s

,... with

s ≡ s

, and any states s

along π, we have (M,s

) |= β

or ∃0 ≤ k < j (M, s

) |= α,

15. (M,s) |= E(αRβ) iff there exists a path π ≡ s

,...

with s ≡ s

, and for any states s

along π, we have

(M,s

) |= β or ∃0 ≤ k < j (M, s

) |= α.

A formula α is called valid in CTL if (M,s) |= α

holds for any CTL-model M := (S,S

,R,L), any s ∈ S,

and any CTL-satisfaction relation |= on M.

3 FALSIFICATION-AWARE

NORMAL KRIPKE-STYLE

SEMANTICS FOR CTL

A falsiﬁcation-aware normal Kripke-style semantics

for CTL is deﬁned as follows.

Deﬁnition 3.1 (Falsiﬁcation-aware normal Krip-

ke-style semantics for CTL). Let Φ be a non-empty

set of propositional variables and Φ

be the set

{¬p | p ∈ Φ} of negated propositional variables.

A structure (S,S

,R,L

) is called a falsiﬁcation-

aware normal CTL-model if

1. S is the set of states,

2. S

is a set of initial states and S

⊆ S,

3. R is a binary relation on S such that ∀s ∈ S ∃s

∈

S [(s,s

) ∈ R],

4. L

is a mapping from S to the power set of Φ∪ Φ

such that for any p ∈ Φ and any s ∈ S, p ∈ L

(s)

iff ¬p 6∈ L

(s).

A path in a falsiﬁcation-aware normal CTL-model

is deﬁned in the same way as that for CTL-model.

A falsiﬁcation-aware normal CTL-satisfaction re-

lation (M,s) |=

α for any formula α, where M is

a falsiﬁcation-aware normal CTL-model (S,S

,R,L

)

and s is a state in S, is deﬁned inductively by the fol-

lowing clauses:

1. for any p ∈ Φ, (M, s) |=

p iff p ∈ L

(s),

2. (M,s) |=

α∧β iff (M,s) |=

α and (M,s) |=

β,

3. (M,s) |=

α∨β iff (M,s) |=

α or (M,s) |=

β,

4. (M,s) |=

α→β iff (M,s) 6|=

α or (M,s) |=

β,

5. (M,s) |=

AXα iff ∀s

∈ S [(s,s

) 6∈ R or (M,s

) |=

α],

6. (M,s) |=

EXα iff ∃s

∈ S [(s, s

) ∈ R and (M,s

) |=

α],

7. (M,s) |=

AGα iff for any paths π ≡ s

,... with

s ≡ s

, and any states s

along π, we have (M,s

) |=

α,

8. (M,s) |=

EGα iff there exists a path π ≡ s

,...

with s ≡ s

, and for any states s

along π, we have

(M,s

) |=

α,

9. (M,s) |=

AFα iff for any paths π ≡ s

,...

with s ≡ s

, there exists a state s

along π such that

(M,s

) |=

α,

10. (M,s) |=

EFα iff there exists a path π ≡ s

,...

with s ≡ s

, and for some state s

along π, we have

(M,s

) |=

α,

11. (M,s) |=

A(αUβ) iff for any paths π ≡ s

,...

with s ≡ s

, there exists a state s

along π such that

(M,s

) |=

β and ∀0 ≤ k < j (M,s

) |=

α,

12. (M,s) |=

E(αUβ) iff there exists a path π ≡

,... with s ≡ s

, and for some state s

along π,

we have (M,s

) |=

β and ∀0 ≤ k < j (M,s

) |=

α,

13. (M,s) |=

A(αRβ) iff for any paths π ≡ s

,...

with s ≡ s

, and any states s

along π, we have

(M,s

) |=

β or ∃0 ≤ k < j (M,s

) |=

α,

Falsiﬁcation-aware Semantics for CTL and Its Inconsistency-tolerant Subsystem: Towards Falsiﬁcation-aware Model Checking

245

14. (M,s) |=

E(αRβ) iff there exists a path π ≡

,... with s ≡ s

, and for any states s

along π,

we have (M,s

) |=

β or ∃0 ≤ k < j (M,s

) |=

α,

15. for any ¬p ∈ Φ

, (M,s) |=

¬p iff ¬p ∈ L

(s),

16. (M,s) |=

¬¬α iff (M,s) |=

α,

17. (M,s) |=

¬(α∧β) iff (M,s) |=

¬α or (M,s) |=

¬β,

18. (M,s) |=

¬(α∨β) iff (M,s) |=

¬α and (M, s) |=

¬β,

19. (M,s) |=

¬(α→β) iff (M,s) |=

α and (M,s) |=

¬β,

20. (M,s) |=

¬AXα iff ∃s

∈ S [(s,s

) ∈ R and (M, s

) |=

¬α],

21. (M,s) |=

¬EXα iff ∀s

∈ S [(s,s

) 6∈ R or (M, s

) |=

¬α],

22. (M,s) |=

¬AGα iff there exists a path π ≡ s

,...

with s ≡ s

, and for some state s

along π, we have

(M,s

) |=

¬α,

23. (M,s) |=

¬EGα iff for any paths π ≡ s

,...

with s ≡ s

, there exists a state s

along π such that

(M,s

) |=

¬α,

24. (M,s) |=

¬AFα iff there exists a path π ≡ s

,...

with s ≡ s

, and for any states s

along π, we have

(M,s

) |=

¬α,

25. (M,s) |=

¬EFα iff for any paths π ≡ s

,... with

s ≡ s

, and any states s

along π, we have (M, s

) |=

¬α,

26. (M,s) |=

¬A(αUβ) iff there exists a path π ≡

,... with s ≡ s

, and for any states s

along π,

we have (M,s

) |=

¬β or ∃0 ≤ k < j (M, s

) |=

¬α,

27. (M,s) |=

¬E(αUβ) iff for any paths π ≡ s

,...

with s ≡ s

, and any states s

along π, we have

(M,s

) |=

¬β or ∃0 ≤ k < j (M, s

) |=

¬α,

28. (M,s) |=

¬A(αRβ) iff there exists a path π ≡

,... with s ≡ s

, and for some state s

along π,

we have (M, s

) |=

¬β and ∀0 ≤ k < j (M,s

) |=

¬α,

29. (M,s) |=

¬E(αRβ) iff for any paths π ≡ s

,...

with s ≡ s

, there exists a state s

along π such that

(M,s

) |=

¬β and ∀0 ≤ k < j (M, s

) |=

¬α.

A formula α is called n-valid in CTL if (M, s) |=

α holds for any falsiﬁcation-aware normal CTL-

model M := (S,S

,R,L

), any s ∈ S, and any

falsiﬁcation-aware normal CTL-satisfaction relation

on M.

Theorem 3.2. For any falsiﬁcation-aware normal

CTL-model M := (S, S

,R,L

), any falsiﬁcation-

aware normal CTL-satisfaction relation |=

on M,

any formula α, and any s ∈ S, we have: (M,s) |=

iff (M, s) 6|=

¬α.

Proof. By induction on α. We show some cases.

1. Case α ≡ p ∈ Φ: We obtain: (M,s) |=

p iff p ∈

(s) iff ¬p 6∈ L

(s) iff (M,s) 6|=

¬p.

2. Case α ≡ β→γ: We obtain: (M,s) |=

β→γ

iff (M,s) 6|=

β or (M,s) |=

γ iff (M,s) 6|=

or (M,s) 6|=

¬γ (by induction hypothesis) iff

(M,s) 6|=

¬(β→γ).

3. Case α ≡ ¬β: We obtain: (M,s) |=

¬β iff

(M,s) 6|=

β (by induction hypothesis with contra-

position) iff (M, s) 6|=

¬¬β.

4. Case α ≡ AXβ: We obtain: (M, s) |=

AXβ

iff ∀s

∈ S [(s, s

) 6∈ R or (M,s

) |=

β] iff

∀s

∈ S [(s, s

) 6∈ R or (M,s

) 6|=

¬β] (by in-

duction hypothesis) iff not-[∃s

∈ S [(s, s

) ∈ R

and (M,s

) |=

¬β]] iff not-[(M, s) |=

¬AXβ] iff

(M,s) 6|=

¬AXβ.

5. Case α ≡ AGβ: We obtain: (M,s) |=

AGβ iff

for any paths π ≡ s

,... with s ≡ s

, and

any states s

along π, we have (M,s

) |=

β iff

for any paths π ≡ s

,... with s ≡ s

, and

any states s

along π, we have (M, s

) 6|=

¬β (by

induction hypothesis) iff not-[there exists a path

π ≡ s

,... with s ≡ s

, and for some state s

along π, we have (M,s

) |=

¬β] iff not-[(M,s) |=

¬AGβ] iff (M, s) 6|=

¬AGβ.

6. Case α ≡ A(βUγ): We obtain: (M,s) |=

A(βUγ)

iff for any paths π ≡ s

,... with s ≡ s

, there

exists a state s

along π such that (M, s

) |=

and ∀0 ≤ k < j (M,s

) |=

β iff for any paths π ≡

,... with s ≡ s

, there exists a state s

along

π such that (M,s

) |=

γ and ∀0 ≤ k < j (M, s

) 6|=

¬β iff not-[there exists a path π ≡ s

,... with

s ≡ s

, and for any states s

along π, we have

(M,s

) |=

¬γ or ∃0 ≤ k < j (M, s

) |=

¬β] iff

not-[(M,s) |=

¬A(βUγ)] iff (M,s) 6|=

¬A(βUγ).

Remark 3.3. We make the following remarks.

1. Theorem 3.2 shows that the mapping condition

“for any p ∈ Φ and any s ∈ S, p ∈ L

(s) iff ¬p 6∈

(s)” in Deﬁnition 3.1 can be extended to the

falsiﬁcation-aware normal CTL-satisfaction rela-

tion for any formula α.

2. By the contraposition of the statement of Theorem

3.2, we can obtain the following standard Boolean

negation condition for falsiﬁcation-aware nor-

mal CTL-satisfaction relation: (M,s) |=

¬α iff

(M,s) 6|=

α.

3. We use Theorem 3.2 (with the fact discussed just

above) for proving the equivalence between the

falsiﬁcation-aware normal and normal semantics

for CTL. Indeed, Theorem 3.2 will be used for

proving the case α ≡ ¬β in Lemma 3.4.

Prior to prove the equivalence between the

falsiﬁcation-aware normal and normal Kripke-style

semantics for CTL (i.e., the equivalence between the

n-validity and the validity), we need to show the fol-

lowing two lemmas.

Lemma 3.4. For any CTL-model M := (S,S

,R,L)

and any CTL-satisfaction relation |= on M, we can

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

246

construct a falsiﬁcation-aware normal CTL-model

N := (S, S

,R,L

) and a falsiﬁcation-aware normal

CTL-satisfaction relation |=

on N such that for any

formula α and any s ∈ S, (M,s) |= α iff (N,s) |=

α.

Proof. Let M be a CTL-model (S, S

,R,L) and |=

be a CTL-satisfaction relation on M. Then, we de-

ﬁne a falsiﬁcation-aware normal CTL-model N :=

(S,S

,R,L

) such that for any s ∈ S and any p ∈ Φ,

1. p ∈ L

(s) iff p ∈ L(s),

2. ¬p ∈ L

(s) iff p 6∈ L(s).

Then, we can obtain the mapping condition “p ∈

(s) iff ¬p 6∈ L

(s),” because we have: p ∈ L

(s)

iff p ∈ L(s) iff ¬p 6∈ L

(s).

We now prove this lemma by induction on α. We

show some cases.

1. Case α ≡ p ∈ Φ: We obtain: (M,s) |= p iff p ∈

L(s) iff p ∈ L

(s) iff (N,s) |=

2. Case α ≡ β→γ: We obtain: (M, s) |= β→γ

iff (M, s) 6|= β or (M,s) |= γ iff (N,s) 6|=

β or

(N,s) |=

γ (by induction hypothesis) iff (N,s) |=

β→γ.

3. Case α ≡ ¬β: We obtain: (M,s) |= ¬β iff

(M,s) 6|= β iff (N,s) 6|=

β (by induction hypoth-

esis) iff (N,s) |=

¬β (by Theorem 3.2).

4. Case α ≡ AXβ: We obtain: (M,s) |= AXβ iff

∀s

∈ S [(s,s

) 6∈ R or (M,s

) |= β] iff ∀s

∈

S [(s,s

) 6∈ R or (N,s

) |=

β (by induction hy-

pothesis) iff (N,s) |=

AXβ.

5. Case α ≡ AGβ: We obtain: (M, s) |= AGβ iff for

any paths π ≡ s

,... with s ≡ s

, and any

states s

along π, we have (M,s

) |= β iff for any

paths π ≡ s

,... with s ≡ s

, and any states

along π, we have (N,s

) |=

β (by induction hy-

pothesis) iff (N,s) |=

AGβ.

6. Case α ≡ A(βUγ): We obtain: (M,s) |= A(βUγ)

iff for any paths π ≡ s

,... with s ≡ s

, there

exists a state s

along π such that (M, s

) |= γ

and ∀0 ≤ k < j (M,s

) |= β iff for any paths π ≡

,... with s ≡ s

, there exists a state s

along

π such that (N,s

) |=

γ and ∀0 ≤ k < j (N,s

) |=

β (by induction hypothesis) iff (N, s) |=

A(βUγ).

Lemma 3.5. For any falsiﬁcation-aware normal

CTL-model M := (S,S

,R,L

) and any falsiﬁcation-

aware normal CTL-satisfaction relation |=

on M, we

can construct a CTL-model N := (S,S

,R,L) and a

CTL-satisfaction relation |= on N such that for any

formula α and any s ∈ S, (M,s) |=

α iff (N,s) |= α.

Proof. Similar to the proof of Lemma 3.4.

Theorem 3.6 (Equivalence between n-validity and

validity in CTL). For any formula α, we have: α is

n-valid in CTL iff α is valid in CTL.

Proof. By Lemmas 3.4 and 3.5.

4 FALSIFICATION-AWARE DUAL

KRIPKE-STYLE SEMANTICS

FOR CTL

A falsiﬁcation-aware dual Kripke-style semantics for

CTL is deﬁned as follows.

Deﬁnition 4.1 (Falsiﬁcation-aware dual Kripke-style

semantics for CTL). Let Φ be a non-empty set of

propositional variables and Φ

be the set {¬p | p ∈

Φ} of negated propositional variables.

A structure (S,S

,R,L

−

) is called a

falsiﬁcation-aware dual CTL-model if

1. S is the set of states,

2. S

is a set of initial states and S

⊆ S,

3. R is a binary relation on S such that ∀s ∈ S ∃s

∈

S [(s,s

) ∈ R],

4. L

and L

−

are mappings from S to the power set

of Φ such that for any p ∈ Φ and any s ∈ S, p ∈

(s) iff p 6∈ L

−

(s).

A path in a falsiﬁcation-aware dual CTL-model is

an inﬁnite sequence of states, π = s

,... such

that ∀i ≥ 0 [(s

i+1

) ∈ R].

Falsiﬁcation-aware dual CTL-satisfaction rela-

tions (M, s) |=

α and (M,s) |=

−

α for any formula

α, where M is a falsiﬁcation-aware dual CTL-model

(S,S

,R,L

−

) and s is a state in S, are deﬁned in-

ductively by the following clauses:

1. for any p ∈ Φ, (M, s) |=

p iff p ∈ L

(s),

2. (M,s) |=

α∧β iff (M,s) |=

α and (M,s) |=

β,

3. (M,s) |=

α∨β iff (M,s) |=

α or (M,s) |=

β,

4. (M,s) |=

α→β iff (M,s) 6|=

α or (M,s) |=

β,

5. (M,s) |=

¬α iff (M,s) |=

−

α,

6. (M,s) |=

AXα iff ∀s

∈ S [(s,s

) 6∈ R or (M, s

) |=

α],

7. (M,s) |=

EXα iff ∃s

∈ S [(s,s

) ∈ R and (M,s

) |=

α],

8. (M,s) |=

AGα iff for any paths π ≡ s

,... with

s ≡ s

, and any states s

along π, we have (M, s

) |=

α,

9. (M,s) |=

EGα iff there exists a path π ≡ s

,...

with s ≡ s

, and for any states s

along π, we have

(M,s

) |=

α,

10. (M,s) |=

AFα iff for any paths π ≡ s

,...

with s ≡ s

, there exists a state s

along π such that

(M,s

) |=

α,

11. (M,s) |=

EFα iff there exists a path π ≡ s

,...

with s ≡ s

, and for some state s

along π, we have

(M,s

) |=

α,

Falsiﬁcation-aware Semantics for CTL and Its Inconsistency-tolerant Subsystem: Towards Falsiﬁcation-aware Model Checking

247

12. (M,s) |=

A(αUβ) iff for any paths π ≡ s

,...

with s ≡ s

, there exists a state s

along π such that

(M,s

) |=

β and ∀0 ≤ k < j (M,s

) |=

α,

13. (M,s) |=

E(αUβ) iff there exists a path π ≡

,... with s ≡ s

, and for some state s

along π,

we have (M,s

) |=

β and ∀0 ≤ k < j (M,s

) |=

α,

14. (M,s) |=

A(αRβ) iff for any paths π ≡ s

,...

with s ≡ s

, and any states s

along π, we have

(M,s

) |=

β or ∃0 ≤ k < j (M,s

) |=

α,

15. (M,s) |=

E(αRβ) iff there exists a path π ≡

,... with s ≡ s

, and for any states s

along π,

we have (M,s

) |=

β or ∃0 ≤ k < j (M,s

) |=

α,

16. for any p ∈ Φ, (M, s) |=

−

p iff p ∈ L

−

(s),

17. (M,s) |=

−

α∧β iff (M,s) |=

−

α or (M,s) |=

−

β,

18. (M,s) |=

−

α∨β iff (M,s) |=

−

α and (M,s) |=

−

β,

19. (M,s) |=

−

α→β iff (M,s) |=

α and (M,s) |=

−

β,

20. (M,s) |=

−

¬α iff (M,s) |=

α,

21. (M,s) |=

−

AXα iff ∃s

∈ S [(s,s

) ∈ R and (M,s

) |=

−

α],

22. (M,s) |=

−

EXα iff ∀s

∈ S [(s, s

) 6∈ R or (M,s

) |=

−

α],

23. (M,s) |=

−

AGα iff there exists a path π ≡ s

,...

with s ≡ s

, and for some state s

along π, we have

(M,s

) |=

−

α,

24. (M,s) |=

−

EGα iff for any paths π ≡ s

,...

with s ≡ s

, there exists a state s

along π such that

(M,s

) |=

−

α,

25. (M,s) |=

−

AFα iff there exists a path π ≡ s

,...

with s ≡ s

, and for any states s

along π, we have

(M,s

) |=

−

α,

26. (M,s) |=

−

EFα iff for any paths π ≡ s

,... with

s ≡ s

, and any states s

along π, we have (M, s

) |=

−

α,

27. (M,s) |=

−

A(αUβ) iff there exists a path π ≡

,... with s ≡ s

, and for any states s

along π,

we have (M,s

) |=

−

β or ∃0 ≤ k < j (M,s

) |=

−

α,

28. (M,s) |=

−

E(αUβ) iff for any paths π ≡ s

,...

with s ≡ s

, and any states s

along π, we have

(M,s

) |=

−

β or ∃0 ≤ k < j (M,s

) |=

−

α,

29. (M,s) |=

−

A(αRβ) iff there exists a path π ≡

,... with s ≡ s

, and for some state s

along π,

we have (M,s

) |=

−

β and ∀0 ≤ k < j (M,s

) |=

−

α,

30. (M,s) |=

−

E(αRβ) iff for any paths π ≡ s

,...

with s ≡ s

, there exists a state s

along π such that

(M,s

) |=

−

β and ∀0 ≤ k < j (M,s

) |=

−

α.

A formula α is called d-valid in CTL if (M,s) |=

α holds for any falsiﬁcation-aware dual CTL-

model M := (S,S

,R,L

−

), any s ∈ S, and any

falsiﬁcation-aware dual CTL-satisfaction relations

and |=

−

on M.

Lemma 4.2. For any CTL-model M := (S,S

,R,L)

and any CTL-satisfaction relation |= on M, we can

construct a falsiﬁcation-aware dual CTL-model N :=

(S,S

,R,L

−

) and falsiﬁcation-aware dual CTL-

satisfaction relations |=

and |=

−

on N such that for

any formula α and any s ∈ S,

1. (M,s) |= α iff (N,s) |=

α,

2. (M,s) |= ¬α iff (N,s) |=

−

α.

Proof. Let M be a CTL-model (S, S

,R,L) and |=

be an CTL-satisfaction relation on M. Then, we

deﬁne a falsiﬁcation-aware dual CTL-model N :=

(S,S

,R,L

−

) such that for any s ∈ S and any

p ∈ Φ,

1. p ∈ L

(s) iff p ∈ L(s),

2. p ∈ L

−

(s) iff p 6∈ L(s).

Then, we can obtain the mapping condition “p ∈

(s) iff p 6∈ L

−

(s).”

We now prove this lemma by simultaneous induc-

tion on α. We show some cases.

1. Case α ≡ p ∈ Φ: For 1, we obtain: (M,s) |= p iff

p ∈ L(s) iff p ∈ L

(s) iff (N,s) |=

p. For 2, we

obtain: (M,s) |= ¬p iff (M,s) 6|= p iff p 6∈ L(s) iff

p ∈ L

−

(s) iff (N,s) |=

−

2. Case α ≡ β→γ: For 1, we obtain: (M,s) |= β→γ

iff (M,s) 6|= β or (M,s) |= γ iff (N,s) 6|=

β or

(N,s) |=

γ (by induction hypothesis for 1) iff

(N,s) |=

β→γ. For 2, we obtain: (M, s) |=

¬(β→γ) iff (M,s) 6|= β→γ iff (M, s) |= β and

(M,s) 6|= γ iff (M, s) |= β and (M,s) |= ¬γ iff

(N,s) |=

β and (N,s) |=

−

γ (by induction hy-

potheses for 1 and 2) iff (N,s) |=

−

β→γ.

3. Case α ≡ ¬β: For 1, we obtain: (M,s) |= ¬β iff

(N,s) |=

−

β (by induction hypothesis for 2) iff

(N,s) |=

¬β. For 2, we obtain: (M, s) |= ¬¬β

iff (M,s) |= β iff (N, s) |=

β (by induction hy-

pothesis for 1) iff (N,s) |=

−

¬β.

4. Case α ≡ AXβ: For 1, we obtain: (M,s) |= AXβ

iff ∀s

∈ S [(s, s

) 6∈ R or (M,s

) |= β] iff ∀s

∈

S [(s,s

) 6∈ R or (N,s

) |=

β (by induction hy-

pothesis for 1) iff (N,s) |=

AXβ. For 2, we ob-

tain: (M, s) |= ¬AXβ iff (M, s) 6|= AXβ iff not-

[(M,s) |= AXβ] iff not-[∀s

∈ S [(s, s

) 6∈ R or

(M,s

) |= β],] iff ∃s

∈ S [(s, s

) ∈ R and (M,s

) 6|=

β] iff ∃s

∈ S [(s,s

) ∈ R and (M,s

) |= ¬β] iff

∃s

∈ S [(s, s

) ∈ R and (N,s

) |=

−

β] (by induc-

tion hypothesis for 2) iff (N,s) |=

−

AXβ.

5. Case α ≡ AGβ: For 1, we obtain: (M,s) |= AGβ

iff for any paths π ≡ s

,... with s ≡ s

, and

any states s

along π, we have (M,s

) |= β iff for

any paths π ≡ s

,... with s ≡ s

, and any

states s

along π, we have (N,s

) |=

β (by induc-

tion hypothesis for 1) iff (N,s) |=

AGβ. For 2,

we obtain: (M, s) |= ¬AGβ iff (M, s) 6|= AGβ iff

there exists a path π ≡ s

,... with s ≡ s

, and

for some state s

along π, we have (M,s

) 6|= β iff

there exists a path π ≡ s

,... with s ≡ s

, and

for some state s

along π, we have (M, s

) |= ¬β iff

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

248

there exists a path π ≡ s

,... with s ≡ s

, and

for some state s

along π, we have (N,s

) |=

−

β (by

induction hypothesis for 2) iff (N,s) |=

−

AGβ.

6. Case α ≡ A(βUγ): For 1, we obtain: (M,s) |=

A(βUγ) iff for any paths π ≡ s

,... with

s ≡ s

, there exists a state s

along π such that

(M,s

) |= γ and ∀0 ≤ k < j (M,s

) |= β iff for

any paths π ≡ s

,... with s ≡ s

, there ex-

ists a state s

along π such that (N,s

) |=

γ and

∀0 ≤ k < j (N,s

) |=

β (by induction hypoth-

esis) iff (N,s) |=

A(βUγ). For 2, we obtain:

(M,s) |= ¬A(βUγ) iff (M,s) 6|= A(βUγ) iff there

exists a path π ≡ s

,... with s ≡ s

, and

for any states s

along π, we have (M,s

) 6|= γ

or ∃0 ≤ k < j (M,s

) 6|= β iff there exists a path

π ≡ s

,... with s ≡ s

, and for any states

along π, we have (M,s

) |= ¬γ or ∃0 ≤ k < j

(M,s

) |= ¬β iff there exists a path π ≡ s

,...

with s ≡ s

, and for any states s

along π, we have

(N,s

) |=

−

γ or ∃0 ≤ k < j (N, s

) |=

−

β (by in-

duction hypothesis for 2) iff (N,s) |=

−

A(βUγ).

Lemma 4.3. For any falsiﬁcation-aware dual CTL-

model M := (S,S

,R,L

−

) and any falsiﬁcation-

aware dual CTL-satisfaction relations |=

and |=

−

M, we can construct a CTL-model N := (S,S

,R,L)

and a CTL-satisfaction relation |= on N such that for

any formula α and any s ∈ S,

1. (M,s) |=

α iff (N,s) |= α,

2. (M,s) |=

−

α iff (N,s) |= ¬α.

Proof. Similar to the proof of Lemma 4.2.

Theorem 4.4 (Equivalence between d-validity and

validity in CTL). For any formula α, we have: α is

d-valid in CTL iff α is valid in CTL.

Proof. By Lemmas 4.2 and 4.3.

Remark 4.5. We can obtain the following fact by

Theorems 3.6 and 4.4. The following conditions are

equivalent: For any formula α,

1. α is valid in CTL,

2. α is n-valid in CTL,

3. α is d-valid in CTL.

5 FALSIFICATION-AWARE

KRIPKE-STYLE SEMANTICS

FOR ICTL

We now semantically deﬁne ICTL as a subsystem of

CTL. Formulas of ICTL are deﬁned in the same way

as those for CTL.

Deﬁnition 5.1 (Falsiﬁcation-aware normal Krip-

ke-style semantics for ICTL). The falsiﬁcation-aware

normal Kripke-style semantics for ICTL is obtained

from that for CTL by deleting the mapping condi-

tion “for any p ∈ Φ and any s ∈ S, p ∈ L

(s) iff

¬p 6∈ L

(s)” in Deﬁnition 3.1. The notions and nota-

tions concerning this semantics for ICTL can be de-

ﬁned in a similar way as those for CTL.

Remark 5.2. We make the following remarks.

1. We cannot semantically deﬁne ICTL using the

standard non-falsiﬁcation-aware Kripke-style se-

mantics as presented in Deﬁnition 2.2.

2. ICTL is regarded as or closely related to the clas-

sical negation-free subsystems of PCTL (Kamide

and Kaneiwa, 2010; Kaneiwa and Kamide, 2011)

and pCTL (Kamide and Endo, 2018; Kamide and

Endo, 2019). Namely, ICTL is regarded as the

purely inconsistency-tolerant subsystem of PCTL

and pCTL.

3. As will be discussed in the following item 5, ICTL

is a proper subsystem of CTL, because the for-

mula of the form (p∧¬p)→q, where p and q are

distinct propositional variables, is n-valid in CTL,

but not n-valid in ICTL.

4. The same theorem as Theorem 3.2 does not hold

for ICTL (i.e., the negation connective ¬ in ICTL

is not the classical negation connective).

5. In general, a satisfaction relation |= for a logic

is called paraconsistent with respect to a nega-

tion connective ¬ if the condition “∃α,β (M,s) 6|=

(α∧¬α)→β” holds. This condition reﬂects that

(α∧¬α)→β is not valid in the underlying logic.

Based on this deﬁnition of paraconsistency, ICTL

is shown to be paraconsistent with respect to

¬, although CTL is not paraconsistent with re-

spect to ¬. The paraconsistency of ICTL with

respect to ¬ can be shown as follows. Assume

a falsiﬁcation-aware normal ICTL-model M =

(S,S

,R,L

) such that p ∈ L

(s), ¬p ∈ L

(s)

and q /∈ L

(s) for a pair of distinct propositional

variables p and q. Then, we have (M, s) 6|=

(p∧¬p)→q.

6. ICTL is regarded as a four-valued logic. This fact

is shown as follows. For each s ∈ S and each

formula α, we can take one of the following four

cases:

(a) α is veriﬁed at s, i.e., (M, s) |=

α,

(b) α is falsiﬁed at s, i.e., (M, s) |=

¬α,

(d) α is neither veriﬁed nor falsiﬁed at s.

Falsiﬁcation-aware Semantics for CTL and Its Inconsistency-tolerant Subsystem: Towards Falsiﬁcation-aware Model Checking

249

7. We can show the fact that ICTL is embeddable

into the positive (i.e., ¬-less) fragment of CTL.

This fact can be proved in the same way as pre-

sented in (Kamide and Endo, 2018; Kamide and

Endo, 2019). Thus, the paraconsistent negation

connective in ICTL can be handled in the positive

fragment of CTL.

Next, we introduce a falsiﬁcation-aware dual

Kripke-style semantics for ICTL.

Deﬁnition 5.3 (Falsiﬁcation-aware dual Kripke-style

semantics for ICTL). By deleting the mapping con-

dition “for any p ∈ Φ and any s ∈ S, p ∈ L

(s)

iff p 6∈ L

−

(s)” in Deﬁnition 4.1, we can obtain a

falsiﬁcation-aware dual Kripke-style semantics for

ICTL.

Then, we can obtain the following theorem.

Theorem 5.4 (Equivalence between n-validity and d–

validity in ICTL). For any formula α, we have: α is

n-valid in ICTL iff α is d-valid in ICTL.

Proof. We can prove this theorem in a similar way as

the proof of Theorem 3.6. We have to prove the lem-

mas that are similar to Lemmas 4.2 and 4.3. But, to

prove these lemmas, we do not need to use Theorem

3.2 because ICTL has no classical negation.

6 CONCLUDING REMARKS

In this paper, we ﬁrst introduced new falsiﬁcation-

aware normal and dual Kripke-style semantics for

CTL. We then proved the equivalences among

the proposed falsiﬁcation-aware Kripke-style seman-

tics and the standard Kripke-style semantics for

CTL. By using the proposed falsiﬁcation-aware

Kripke-style semantics, we semantically deﬁned the

new inconsistency-tolerant and many-valued tempo-

ral logic ICTL, which is obtained from the pro-

posed falsiﬁcation-aware Kripke-style semantics for

CTL by deleting only one characteristic condition

on the labeling function of the semantics. Thus,

the proposed falsiﬁcation-aware semantic framework

for CTL and ICTL is considered to be a uniﬁed

framework for combining and generalizing the stan-

dard, inconsistency-tolerant, and many-valued se-

mantic frameworks. The proposed framework can be

used for falsiﬁcation-aware model checking, which

is roughly deﬁned as that of combined and gener-

alized model checking based on falsiﬁcation-aware

Kripke-style semantics. The notion of falsiﬁcation-

aware model checking and an illustrative example for

falsiﬁcation-aware model checking will be explained

and addressed in the last part of this section.

We remark that the proposed falsiﬁcation-aware

semantic framework can be extended to other tem-

poral logics. For example, we can obtain the

falsiﬁcation-aware normal and dual Kripke-style se-

mantics for linear-time temporal logic (LTL) (Pnueli,

1977) and its inconsistency-tolerant subsystem ILTL

in a similar manner as those for CTL and ICTL.

Then, we can prove the equivalences among the

falsiﬁcation-aware Kripke-style semantics and the

standard Kripke-style semantics for LTL as well as

those between the falsiﬁcation-aware normal and dual

Kripke-style semantics for ILTL. We can also obtain

the falsiﬁcation-aware normal and dual Kripke-style

semantics for full computation tree logic, referred

to as CTL

∗

(Emerson and Halpern, 1986; Emer-

son and Sistla, 1984), and its inconsistency-tolerant

subsystem ICTL

∗

. We can also prove the equiv-

alences among the falsiﬁcation-aware Kripke-style

semantics and the standard Kripke-style semantics

for CTL

∗

as well as those between the falsiﬁcation-

aware normal and dual Kripke-style semantics for

ICTL

∗

. Thus, we can obtain a falsiﬁcation-aware

model checking framework based on these standard

and inconsistency-tolerant temporal logics.

Furthermore, we can also obtain the falsiﬁcation-

aware normal and dual Kripke-style semantics for

probabilistic CTL, referred to as pCTL, probabilis-

tic CTL

∗

, referred to as pCTL

∗

(Aziz et al., 1995;

Bianco and de Alfaro, 1995), and their inconsistency-

tolerant subsystems IpCTL and IpCTL

∗

. We can also

prove the equivalences among the falsiﬁcation-aware

Kripke-style semantics and the standard Kripke-style

semantics for pCTL and pCTL

∗

, respectively, as well

as those between the falsiﬁcation-aware normal and

dual Kripke-style semantics for IpCTL and IpCTL

∗

respectively. In addition to these results, we can

also obtain the falsiﬁcation-aware normal and dual

Kripke-style semantics for hierarchical (or sequential)

CTL, referred to as sCTL, hierarchical (or sequential)

LTL, referred to as sLTL (Kamide and Yano, 2017;

Kamide, 2018), and their inconsistency-tolerant sub-

systems IsCTL and IsLTL, respectively. Then, we can

prove the equivalences among the falsiﬁcation-aware

Kripke-style semantics and the standard Kripke-style

semantics for sCTL and sLTL, respectively, as well as

those between the falsiﬁcation-aware normal and dual

Kripke-style semantics for IsCTL and IsLTL, respec-

tively. Thus, we can also obtain a falsiﬁcation-aware

model checking framework based on these extended

temporal logics.

Finally, we illustrate a small veriﬁcation exam-

ple based on falsiﬁcation-aware model checking. We

consider the disease diagnosis model shown in Figure

1 for familial adenomatous polyposis (FAP) (Wehbi,

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

250

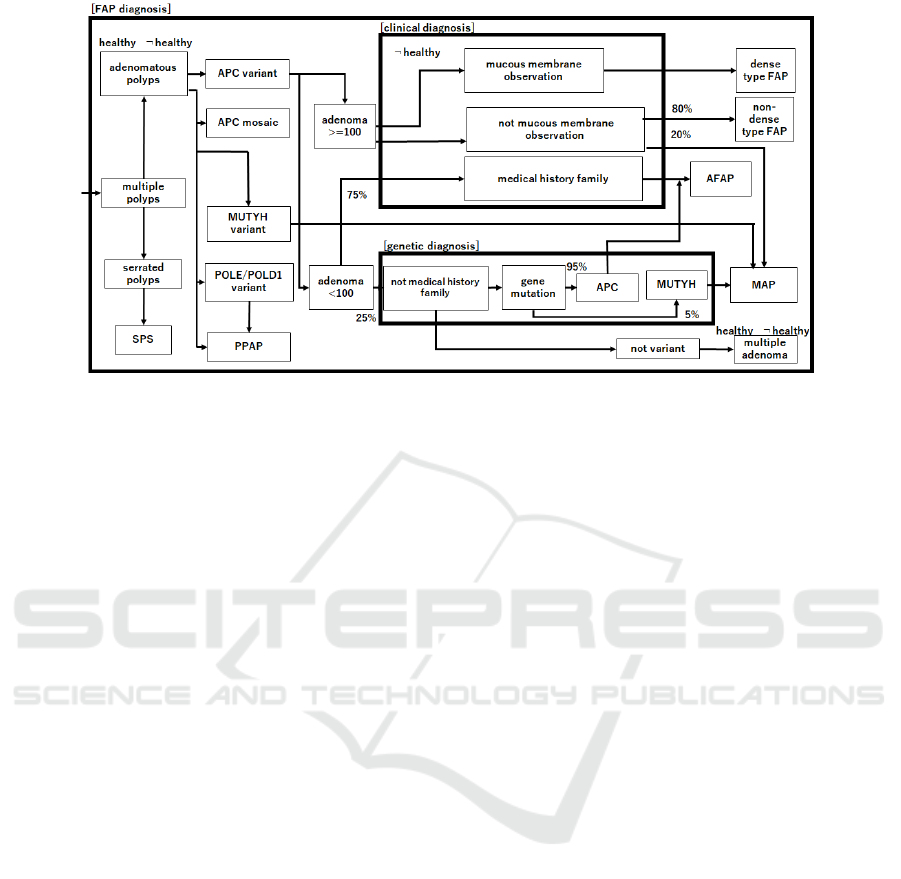
Figure 1: A diagnosis model for familial adenomatous polyposis.

2019). FAP is an inherited disorder characterized by

an autosomal dominant inherited condition in which

numerous adenomatous polyps form mainly in the ep-

ithelium of the large intestine. Although these polyps

start out benign, malignant transformation into colon

cancer occurs when they are left untreated. Three

variants are known to exist: FAP, attenuated FAP

(AFAP), and MUTYH-associated polyposis (MAP).

Furthermore, the ﬁrst variant of FAP is classiﬁed as

dense- or non-dense-type FAP. For these variants, the

resulting colonic polyps and cancers were initially

conﬁned to the colon wall. Detection and removal be-

fore metastasis outside the colon can greatly reduce

and eliminate the spread of cancer in many cases.

For the model presented in Figure 1, we can verify

the following statements:

1. “Is there a state in which a person is both healthy

and unhealthy (i.e., not yet ill), has less than 100

adenomas, and had a medical examination with

genetic diagnosis?”

2. “Is there a state in which a person has a family

medical history, more than 100 adenomas, had a

medical examination with clinical diagnosis, and

has MAP?”

Although the ﬁrst statement is true because there is a

case in which the person has multiple benign adeno-

mas, the second statement is false because this case

does not imply MAP but implies AFAP. These state-

ments are formally expressed as follows:

1. EF(healthy∧¬healthy∧(adenoma<100)

∧geneticDiagnosis)

2. EF(hasMedicalHistoryFamily∧(adenoma>100)

∧clinicalDiagnosis∧MAP)

where the negation connective ¬ in the ﬁrst formula is

regarded as the inconsistency-tolerant negation con-

nective in ICTL. In this example, we can simulta-

neously verify and falsify these formulas using the

falsiﬁcation-aware dual CTL- or ICTL-satisfaction

relations |=

and |=

−

in the falsiﬁcation-aware dual

Kripke-style semantics. Furthermore, we can for-

mally consider a falsiﬁcation-aware model checking

problem as follows. Suppose that M is a falsiﬁcation-

aware dual CTL- or ICTL-model (S,S

,R,L

−

)

and that |=

and |=

−

are falsiﬁcation-aware dual

CTL- or ICTL-satisfaction relations on M. Then, the

falsiﬁcation-aware model checking problem for CTL

or ICTL is deﬁned as follows. For any formula α,

ﬁnd the veriﬁcation set {s ∈ S | M, s |=

α} and fal-

siﬁcation set {s ∈ S | M,s |=

−

α}. These sets can

be simultaneously found. Finally, we remark that

extended falsiﬁcation-aware pCTL-, IpCTL-, sCTL-

, and IsCTL-model checking frameworks, which are

based on the aforementioned extended CTLs, are

more suitable for the veriﬁcation of the model pre-

sented in Figure 1 because probabilistic and hierar-

chical speciﬁcations are also required to verify this

model.

ACKNOWLEDGEMENTS

This research was supported by JSPS KAKENHI

Grant Numbers JP18K11171 and JP16KK0007.

REFERENCES

Almukdad, A. and Nelson, D. (1984). Constructible falsity

and inexact predicates. Journal of Symbolic Logic,

49:231–233.

Falsiﬁcation-aware Semantics for CTL and Its Inconsistency-tolerant Subsystem: Towards Falsiﬁcation-aware Model Checking

251

Aziz, A., Singhal, V., and Balarin, F. (1995). It usually

works: The temporal logic of stochastic systems. In

Proceedings of the 7th Int. Conf. on Computer Aided

Veriﬁcation (CAV 1995), Lecture Notes in Computer

Science 939, pages 155–165.

Bianco, A. and de Alfaro, L. (1995). Model checking of

probabilistic and nondeterministic systems. In Pro-

ceedings of the 15th Conf. on Foundations of Soft-

ware Technology and Theoretical Computer Science

(FSTTCS 1995), Lecture Notes in Computer Science

1026, pages 499–513.

Chen, D. and Wu, J. (2006). Reasoning about inconsistent

concurrent systems: A non-classical temporal logic.

In Lecture Notes in Computer Science, volume 3831,

pages 207–217.

Clarke, E. and Emerson, E. (1981). Design and synthesis of

synchronization skeletons using branching time tem-

poral logic. In Lecture Notes in Computer Science,

volume 131, pages 52–71.

Clarke, E., Grumberg, O., Jha, S., Lu, Y., and Veith, H.

(2003). Counterexample-guided abstraction reﬁne-

ment for symbolic model checking. Journal of the

ACM, 50 (5):752–794.

Clarke, E., Henzinger, T., Veith, H., and Bloem, R. (2018).

Handbook of Model Checking. Springer.

da Costa, N., Beziau, J., and Bueno, O. (1995). Aspects of

paraconsistent logic. Bulletin of the IGPL, 3 (4):597–

614.

Easterbrook, S. and Chechik, M. (2001). A framework for

multi-valued reasoning over inconsistent viewpoints.

In Proceedings of the 23rd International Conference

on Software Engineering (ICSE 2001), pages 411–

420.

Emerson, E. and Halpern, J. (1986). ‘sometimes’ and ‘not

never’ revisited: on branching versus linear time tem-

poral logic. Journal of the ACM, 33 (1):151–178.

Emerson, E. and Sistla, A. (1984). Deciding full branching

time logic. Information and Control, 61:175–201.

Gurﬁnkel, A., Wei, O., and Chechik, M. (2006). Yasm:

A software model-checker for veriﬁcation and refuta-

tion. In Proceedings of the 18th International Con-

ference on Computer Aided Veriﬁcation (CAV 2006),

Lecture Notes in Computer Science, volume 4144,

pages 170–174.

Horn, L. and Wansing, H. (2017). Negation. The Stan-

ford Encyclopedia of Philosophy (Spring 2017 Edi-

tion), Edward N. Zalta (editor), Last modiﬁed on Jan-

uary 2017.

Kamide, N. (2006). Extended full computation-tree logics

for paraconsistent model checking. Logic and Logical

Philosophy, 15 (3):251–276.

Kamide, N. (2015). Inconsistency-tolerant temporal rea-

soning with hierarchical information. Information Sci-

ences, 320:140–155.

Kamide, N. (2018). Logical foundations of hierarchical

model checking. Data Technologies and Applications,

52 (4):539–563.

Kamide, N. (2021). Falsiﬁcation-aware semantics and se-

quent calculi for classical logic. Journal of Philosoph-

ical Logic, Online ﬁrst article.

Kamide, N. and Bernal J.P.A. (2019). Towards loca-

tive inconsistency-tolerant hierarchical probabilistic

ctl model checking: Survey and future work. In

Proceedings of the 11th International Conference on

Agents and Artiﬁcial Intelligence (ICAART 2019),

volume 2, pages 869–878.

Kamide, N. and Endo, K. (2018). Logics and transla-

tions for inconsistency-tolerant model checking. In

Proceedings of the 10th International Conference on

Agents and Artiﬁcial Intelligence (ICAART 2018),

volume 2, pages 191–200.

Kamide, N. and Endo, K. (2019). Foundations of

inconsistency-tolerant model checking: Logics, trans-

lations, and examples. In Agents and Artiﬁcial In-

telligence, the 10th International Conference ICAART

2018 Revised Selected Papers, Lecture Notes in Arti-

ﬁcial Intelligence, volume 11352, pages 1–31.

Kamide, N. and Kaneiwa, K. (2010). Paraconsistent nega-

tion and classical negation in computation tree logic.

In Proceedings of the 2nd International Conference

on Agents and Artiﬁcial Intelligence (ICAART 2010),

volume 1, pages 464–469.

Kamide, N. and Koizumi, D. (2015). Combining paracon-

sistency and probability in ctl. Proceedings of the 7th

International Conference on Agents and Artiﬁcial In-

telligence (ICAART 2015), 2:285–293.

Kamide, N. and Koizumi, D. (2016). Method for combin-

ing paraconsistency and probability in temporal rea-

soning. Journal of Advanced Computational Intelli-

gence and Intelligent Informatics, 20:813–827.

Kamide, N. and Wansing, H. (2011). A paraconsistent

linear-time temporal logic. Fundamenta Informaticae,

106 (1):1–23.

Kamide, N. and Yamamoto, Y. (2021). Inconsistency-

tolerant hierarchical probabilistic computation tree

logic and its application to model checking. Proceed-

ings of the 13th International Conference on Agents

and Artiﬁcial Intelligence (ICAART 2021), 2:490–

499.

Kamide, N. and Yano, R. (2017). Logics and translations

for hierarchical model checking. Proceedings of the

21st International Conference on Knowledge-Based

and Intelligent Information and Engineering Systems

(KES2017), Procedia Computer Science, 112:31–40.

Kaneiwa, K. and Kamide, N. (2011). Paraconsistent com-

putation tree logic. New Generation Computing, 29

(4):391–408.

Nelson, D. (1949). Constructible falsity. Journal of Sym-

bolic Logic, 14:16–26.

Pnueli, A. (1977). The temporal logic of programs. In Pro-

ceedings of the 18th IEEE Symposium on Foundations

of Computer Science, pages 46–57.

Priest, G. and Tanaka, K. (2009). Paraconsistent logic. Web

site of the Stanford encyclopedia of philosophy (2009

Edition), Edward N. Zalta (editor).

Wansing, H. (1993). The logic of information structures.

In Lecture Notes in Computer Science, volume 681,

pages 1–163.

Wehbi, M. (2019). Familial adenomatous polyposis. Web

site of eMedicine Gastroenterology.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

252