Evolving Evaluation Functions for Collectible Card Game AI

Radosław Miernik and Jakub Kowalski

University of Wrocław, Faculty of Mathematics and Computer Science, Poland

Keywords:

Evolutionary Algorithms, Evaluation Functions, Collectible Card Games, Genetic Programming, Strategy

Card Game AI Competition, Legends of Code and Magic.

Abstract:

In this work, we presented a study regarding two important aspects of evolving feature-based game evaluation

functions: the choice of genome representation and the choice of opponent used to test the model. We com-

pared three representations. One simple and limited, based on a vector of weights, and two more complex,

based on binary and n-ary trees. On top of this test, we also investigated the inﬂuence of ﬁtness deﬁned as

a simulation-based function that: plays against a ﬁxed weak opponent, a ﬁxed strong opponent, and the best

individual from the previous population. We encoded our experiments in a programming game, Legends of

Code and Magic, used in Strategy Card Game AI Competition. However, as the problems stated are of general

nature we are convinced that our observations are applicable in the other domains as well.

1 INTRODUCTION

The vast majority of game playing algorithms require

some form of game state evaluation – usually in the

form of a heuristic function that estimates the value

or goodness of a position in a game tree. This applies

not only to classic min-max based methods, as used

for early Chess champions (Campbell et al., 2002),

but also in modern approaches, based on deep neural

networks combined with reinforcement learning (Sil-

ver et al., 2018). The idea of estimating the quality

of a game state using a linear combination of human-

deﬁned features was proven effective a long time ago

(Samuel, 1959), and is still popular, even when ap-

plied to modern video games (García-Sánchez et al.,

2020; Justesen et al., 2016).

One of the recently popular game-related AI

testbeds are Collectible Card Games (e.g., Hearth-

stone (Blizzard Entertainment, 2004), The Elder

Scrolls: Legends (Dire Wolf Digital and Sparkypants

Studios, 2017)). Because they combine imperfect in-

formation, randomness, long-term planning, and mas-

sive action space, they impose many interesting chal-

lenges (Hoover et al., 2019). Also, the speciﬁc form

of game state (combining global board features with

features of individual cards) makes such games partic-

ularly suited for various forms of feature-based state

evaluation utilizing human player knowledge.

The motivation for our research was to compare

two models for evolving game state evaluation func-

tions: a simpler and more limited, based on a vector of

weights that are used in a linear combination of prede-

ﬁned game features; a more complex and non-linear,

based on a tree representation with feature values in

leaves and mathematical operations in nodes.

As a testbed, we have chosen a domain of dig-

ital collectible card games. We encoded our mod-

els in a programming game, Legends of Code and

Magic, used in various competitions played on the

CodinGame.com platform and IEEE CEC and IEEE

COG conferences.

During the initial experiments, we observed some

interesting behaviors of both representations regard-

ing “forgetting” previously learned knowledge. As

these observations were related to the chosen goal of

evolution, we performed additional tests comparing

three ﬁtness functions: playing against a ﬁxed weak

opponent, a ﬁxed strong opponent, and the best indi-

vidual from the previous population.

This paper is structured as follows. In the next sec-

tion, we present the related work describing usages of

evolution for game state evaluation and the domain of

AI for collectible card games. In Section 3, we pro-

vide the details of our model describing the represen-

tations and ﬁtness functions. The following two sec-

tions present our experiments and discuss the results

in the above-mentioned topics: comparing vector ver-

sus tree representations, and a ﬁxed opponent versus

progressive ﬁtness calculation. In the last section, we

conclude our research and give perspectives for future

work.

Miernik, R. and Kowalski, J.

Evolving Evaluation Functions for Collectible Card Game AI.

DOI: 10.5220/0010806900003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 3, pages 253-260

ISBN: 978-989-758-547-0; ISSN: 2184-433X

253

2 BACKGROUND

2.1 Evolving Evaluation Functions

Evolutionary algorithms are used for game playing

mainly in two contexts. One, based on the Rolling

Horizon algorithm (RHEA) (Perez et al., 2013), uti-

lizes evolution as an open-loop game tree search al-

gorithm. The other, more classic approach, employs

evolution ofﬂine, to learn parameters of some model,

usually a game state evaluation function. Such a func-

tion can be further used as a heuristic in alpha-beta,

RHEA, some variants of MCTS (Browne et al., 2012),

or other algorithms; its quality translates directly to

the agent’s power.

The common approach is to deﬁne a list of

game state features and evolve a vector of associated

weights, so that they closely approximate the proba-

bility of winning the game from the given state. This

type of parameter-learning evolution has been applied

to numerous games, like Chess (David et al., 2013),

Checkers (Kusiak et al., 2007), TORCS (Salem et al.,

2018), and Hearthstone (Santos et al., 2017).

Although treating parameters as vectors and

evolving their values using genetic algorithms is more

straightforward, some research uses tree structures

and genetic programming instead for this purpose.

The majority of genetic programming applications

in games are an evolution of standalone agents. It

was successfully applied in various board games, e.g.,

Chess (Groß et al., 2002; Hauptman and Sipper, 2005)

and Reversi (Benbassat and Sipper, 2012).

It is also possible to combine genetic program-

ming with other algorithms and techniques. One ex-

ample is to combine it with neural networks to evolve

Checkers agents (Khan et al., 2008). Another is to

evolve the evaluation function alone and combine it

with an existing algorithm, e.g., MCTS, instead of

evolving fully-featured agents. Such an evolution was

successfully applied in games of varying complex-

ity, e.g., Checkers (Benbassat and Sipper, 2011) and

Chess (Ferrer and Martin, 1995).

Another aspect is measuring the quality of an

evaluation function. Because it has to compare the

strength of the agents, usually a simulation-based ap-

proach is used, utilizing a large number of repetitions

to ensure the stability of obtained results. Thus, such

an evolution scheme is computationally expensive.

2.2 AI for Collectible Card Games

Collectible Card Game (CCG) is a broad genre of

both board and digital games. Although the mechan-

ics differ between games, basic rules are usually sim-

ilar. First, two players with their decks draw an initial

set of cards into their hands.

Then, the main game starts in a turn-based man-

ner. A single turn consists of a few actions, like play-

ing a card from the hand or using an onboard card.

The game ends as soon as one of the players wins,

most often by getting his opponent’s health to zero.

Recently the domain has become popular as an

AI testbed, resulting in a number of competitions

(Dockhorn and Mostaghim, 2018; Janusz et al., 2017;

Kowalski and Miernik, 2018), and publications focus-

ing on agent development and deckbuilding.

Usually, agents are based on the Monte Carlo Tree

Search algorithm (Browne et al., 2012) (as it is known

to perform well in noisy environments with imperfect

information), combined with some form of state eval-

uation either based on expert knowledge and heuris-

tics (Santos et al., 2017), or neural networks (Zhang

and Buro, 2017). An interesting approach combining

MCTS with supervised learning of neural networks

to learn the game state representation based on the

word embeddings (Mikolov et al., 2013) of the actual

card descriptions is described in (

Swiechowski et al.,

2018).

The deckbuilding task for the constructed game

mode (in which players can prepare their decks of-

ﬂine, selecting cards from a wide range of possibil-

ities) has been tackled in several works. The most

common approach is to use evolution (e.g., (Bjørke

and Fludal, 2017) for Magic: The Gathering, (García-

Sánchez et al., 2016; Bhatt et al., 2018) for Hearth-

stone), combined with testing against a small number

of predeﬁned human-made opponent decks. Alterna-

tively, a neural network-based approach for Hearth-

stone has been presented in (Chen et al., 2018).

2.3 Legends of Code and Magic

Legends of Code and Magic (LoCM) (Kowalski and

Miernik, 2018) is a small CCG, designed especially to

perform AI research, as it is much simpler to handle

by the agents, and thus allows testing more sophis-

ticated algorithms and quickly implement theoretical

ideas.

The game contains 160 cards, and all cards’ ef-

fects are deterministic, thus the nondeterminism is

introduced only via the ordering of cards and un-

known opponent’s deck. The game is played in the

fair arena mode, i.e., before every game, both play-

ers create their 30-card decks decks secretly from the

symmetrical yet limited card choices (so-called draft

phase). After the draft phase, the main part of the

game (called the battle phase) begins, in which the

cards are played according to the rules, and the goal is

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

254

to defeat the opponent. LoCM is also used in Strategy

Card Game AI Competition co-organized with CEC

and COG conferences since 2019.

As for today, there is not much research for

the arena game mode. The problem of deckbuild-

ing has been approached in (Kowalski and Miernik,

2020) using an active genes evolutionary algorithm

that in each generation learns only a speciﬁc part of

its genome. An approach using deep reinforcement

learning is presented in (Vieira et al., 2020). Usually,

the deckbuilding phase is solved via predeﬁned card

ordering or some heuristic evaluation of the card’s

strength. The winner of the 2020 COG competition

has been described in (Witkowski et al., 2020). The

authors used static card weights computed using har-

mony search for the draft phase and MCTS with var-

ious enhancements, including an opponent prediction

for the battle game phase. The authors of (Mon-

toliu et al., 2020) perform study on application of On-

line Evolution Planning (Justesen et al., 2016) using

heuristic tuned via N-Tuple Bandit Evolutionary algo-

rithm (Lucas et al., 2018). Other playing approaches

include minimax, best-ﬁrst-search, MCTS, and rule-

based decision making.

3 EVALUATING CARD GAMES

3.1 Representation

We have developed three distinct representations:

Linear, BinaryTree, and Tree. Each one imple-

ments two operations: evalCard (used for the draft

phase and as a part of the state evaluation) and

evalState (used for the battle phase).

To limit the vast space of possible evaluation func-

tions, the ﬁnal state evaluation is a sum of evalState

(based on features related with the global board state)

and evalCard (depending on card-related features)

for each own card on the board, minus evalCard for

each opponent card. It is a common simpliﬁcation,

used in e.g., (Santos et al., 2017).

Note that the expressiveness of the tree-based rep-

resentations is greater, thus it is possible to map indi-

viduals encoded as vectors to trees, but not vice versa.

• Linear, is a constant-size vector of doubles. Each

gene (from 1 to 20) encodes a weight of the cor-

responding feature. The ﬁrst 12 are game state

features (used for evalState), 6 for each of two

players: current mana, deck size, health, max

mana, number of cards to draw next turn, and

next rune (an indicator for an additional draw as

in (Dire Wolf Digital and Sparkypants Studios,

2017)). The other 8 are card features (used for

evalCard): attack, defense, and a ﬂag for each

of the keywords, encoded as 1.0 when set and 0.0

when not. The ﬁnal value is a sum of features

multiplied by their corresponding weights.

• BinaryTree, is a pair of binary trees, encoding

state and card evaluation respectively. The leaf

nodes are either constants (singular double) or

features, same as in Linear. Both trees have

the same set of binary operators (nodes): addition

(l + r, where l and r are the values of left and right

subtree respectively), multiplication (l ∗ r), sub-

traction (l − r), maximum (max(l, r)), and mini-

mum (min(l, r)). The ﬁnal value is calculated re-

cursively accumulating the tree.

• Tree, is a pair of n-ary trees, encoding state and

card evaluation respectively. The leaf nodes are

identical to the ones in BinaryTree. Operators

are now n-ary, storing a vector of subtrees each.

Available operators are addition (

∑

), multiplica-

tion (

∏

), maximum (max), and minimum (min).

Additionally, to ensure that every operation stays

well deﬁned, all subtree vectors are guaranteed to

be nonempty. To make subtraction possible, there

is one additional, unary operator: negation (−x,

where x is the value of its subtree). The ﬁnal value

is calculated recursively accumulating the tree.

3.2 Opponent Estimation

Every evolution scheme evaluates individuals either

by comparing how well they deal with a speciﬁed

task, without a normalized score, or by using an exter-

nal, predeﬁned goal. Both approaches have natural in-

terpretations for CCGs – a win rate against each other

and a win rate against a ﬁxed opponent respectively.

As the course of evolution using a predeﬁned op-

ponent will be heavily impacted by the opponent it-

self, two nontrivial questions arise. What is the differ-

ence between using only the in-population evaluation

from the one using a predeﬁned opponent? And what

is the difference between using a weak and a strong

opponent? We have conducted two experiments to an-

swer both of these questions in terms of the evolution

process and resulting player’s strength.

As both experiments required different evolution

schemes, in total, three groups of individuals were

evolved. First one, called progressive, using the

in-population evaluation (see Sec. 4.1). Second,

called weak-op, using the existing Baseline2 agent

(WeakOp), one of the baseline LoCM agents. Dur-

ing the draft phase, the agent chooses the creature

card with the highest attack (if this is not possible it

Evolving Evaluation Functions for Collectible Card Game AI

255

chooses the leftmost one). During battle, it attacks ev-

erything on board starting with the cards with highest

attack, aiming for the opponent ﬁrst, and then oppo-

nent guard creatures starting from the highest health

ones. And third, called strong-op, using one of the

pre-evolved Tree-from-Linear agents (StrongOp).

weak-op

strong-op

progressive

Linear BinaryTree Tree

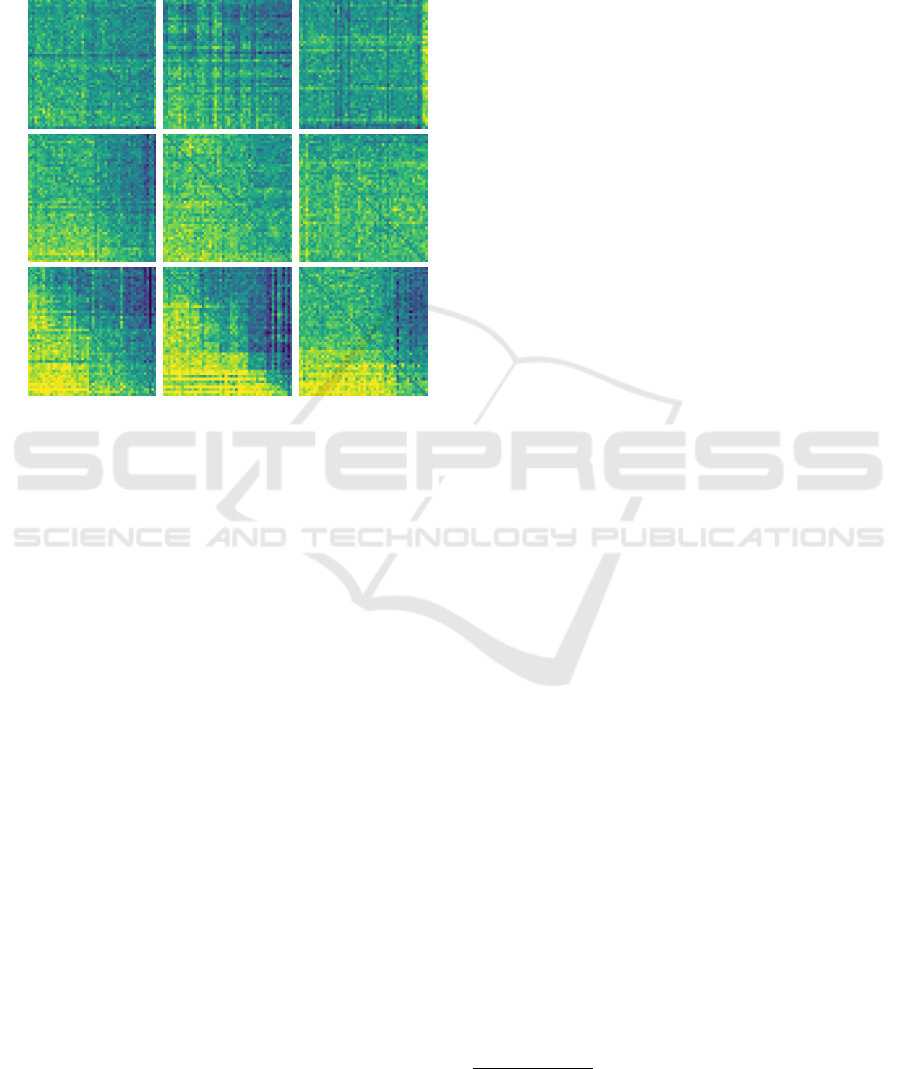
Figure 1: Example self-play win rate heatmaps (other runs

show similar properties). Each cell represents how well the

best individual of generation on the y-axis plays against the

best individual of generation on the x-axis. Visible diago-

nals present self-score (50%). A light section on the bottom

left, present in all three progressive agents, proves that

as the evolution progresses, so all individuals are increas-

ingly better at self-play. Other heatmaps seem to be more

random, indicating no clear progression in self-play.

4 REPRESENTATION STUDY:

TREES VERSUS VECTORS

To measure the impact of different representations on

the evolution, we ran the same experiment multiple

times, each time substituting the underlying genome

structure to one of described in Sec. 3.1. The metrics

we ﬁnd crucial are how well the agent performs in a

real-life scenario, that is, in a proper tournament with

other agents, and whether it progresses, i.e., plays bet-

ter against own previous generations.

4.1 Experiment Setup

We have evolved twelve copies of the progressive

agents, four for each representation. Every run used

the same parameters, that is 50 generations with a

population of size 50 (N parameter), elitism of 5 in-

dividuals, and the mutation rate of 5%. During the

evaluation each two individuals played rounds times

on each of drafts drafts on each side, which makes

2 × (N − 1) × drafts × rounds games in total. In our

experiments, drafts = 10, and rounds = 10.

In order to compare the agents in a standardized

real-life scenario, we ran a tournament. In addition to

our evolved agents, we used two LoCM baselines and

four contestants of 2020 IEEE COG LoCM contest

4.2 Learning Comparison

As visible at the bottom row of Fig. 1, all representa-

tions successfully converged into a light section at the

bottom left. Such shape means that the following gen-

erations were not only preserving the already gained

knowledge but also improving on each step.

Therefore, every representation can be evolved,

playing against own previous generations. Moreover,

the progress of the Linear representation seems to be

more stable, almost constant, while tree-based repre-

sentations tend to improve by making sporadic leaps.

This is not the case for the top and middle rows,

representing evolution with a predeﬁned opponent.

While the Linear representation manages to preserve

hardly visible progress, both tree representations are

more random, indicating no clear improvements in

self-play. Furthermore, the top row contains a few

dark stripes, indicating an exceptionally weak agent.

It is possible, as the evolution goal does not take self-

play into consideration at all.

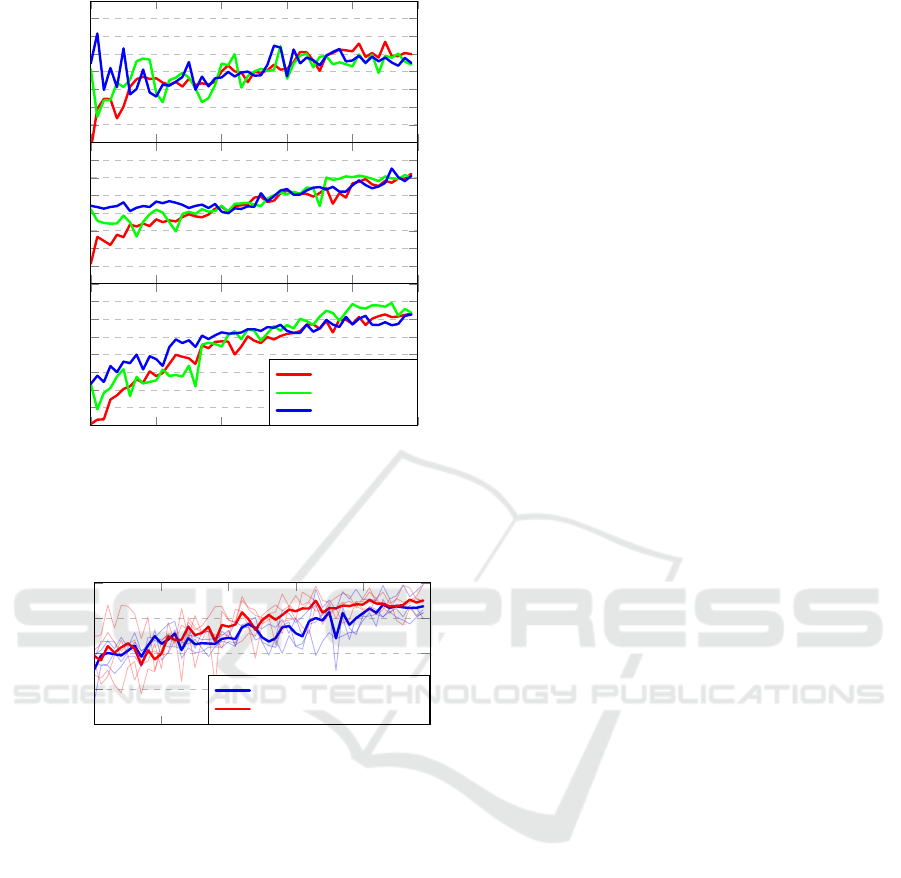
To measure how signiﬁcant the learning progress

is, we compare the win rate of the best individual of

the ﬁrst and the last generation against the best indi-

viduals of all generations.

With such a metric in mind, the Linear repre-

sentation stands out again. As presented in Fig. 2,

both BinaryTree and Tree result in a smaller differ-

ence of about 20% whereas the Linear representation

achieves over 31% difference on average, across all

the evolution schemes.

4.3 Tournament Comparison

When evolved using a ﬁxed, weak opponent

(weak-op), the difference between the representations

is signiﬁcant. There is a huge, almost 10% wide,

gap between Linear (42.9% average win rate) and

BinaryTree (33.8%). The Tree representation is in

between, performing slightly better than its binary

counterpart and achieving 36.2%.

Results are similar when evolved using self-

play evaluation and a randomly initialized population

https://legendsofcodeandmagic.com/COG20/

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

256

weak-op

strong-op

0 10 20 30 40

Generation

progressive

Linear

BinaryTree

Tree

Win rate (%)

Figure 2: Evolution progress of all the agents. Best indi-

viduals from a generation (x-axis) fought against the top

individuals of all own generations, yielding an average win

rate (y-axis).

Linear-from-Linear

Tree-from-Linear

Win rate (%)

Figure 3: Evolution progress of the from-Linear agents.

Best individuals from a generation (x-axis) fought against

the top individuals of all own generations, yielding an aver-

age win rate (y-axis). Each of the four Linear agents was

used as a base for the initial population twice. The two bold

lines average the thin, semi-transparent lines that are the av-

eraged results of agents with the same base.

(progressive). The Linear representation again

yields strictly better results in the tournament (54.8%)

than both BinaryTree and Tree (45.6% and 45.7%).

However, using a better opponent (strong-op)

yields completely different results. In this sce-

nario, the differences between agents’ performance

are less signiﬁcant, around 4%. To be precise,

Linear achieved almost 49%, BinaryTree slightly

over 45%, and Tree nearly 45% average win rate.

This matches the results of playing against own

previous generations, described in the previous sub-

section. We conclude that it is an implication of the

capacity of the representation.

While a more limited Linear representation ﬁnds

a decent solution sooner and gradually improves

it, more capable tree-based representations regularly

leap towards the goal. More detailed tournament re-

sults are presented in Tables 1, 2, and 3.

4.4 Tuning Good Solutions

Knowing that the tree-based model is more general

but also harder to learn, the natural question is if we

can use it to improve the solutions, instead of start-

ing from scratch. The ideal scenario will be to reach

a limit of optimization based on the linear represen-

tation, encode obtained solutions into the tree format,

and continue evolution using this stronger model.

To verify this hypothesis, we have evolved

two more agents: Linear-from-Linear and

Tree-from-Linear. Each of the four previously

evolved Linear-progressive agents was used as a

base for a second evolution process. Here, instead of

randomly, the population was initialized with copies

of the base agent, each one mutated n = 5 times;

hence the from-Linear sufﬁx in their name.

However, translation of a Linear representation

into a Tree representation is ambiguous. We have

used what we believe is the most straightforward one

– an Add operator in the root with a list of Mul +

Literal + Feature subtrees, one for each of the

available features.

As expected, the tournament results for such pre-

evolved agents are entirely different. For the ﬁrst

time, the Linear representation is not the top one.

The Tree agent performs better, ending up with an

average win rate of over 60%, whereas the Linear

agent ﬁnished with 58%. This is a relatively minor

but consistent improvement that may further improve

with a longer evolution. A similar difference is visi-

ble in the process of evolution. Both representations

perform similarly, but Tree is on average above the

Linear almost constantly. Comparison of the best in-

dividuals across the generations is presented in Fig. 3.

Our conclusion is that both results are implica-

tions of the representation. While the more restricted

Linear is not able to progress after a certain point,

more expressive Tree beneﬁts from the bootstrap and

keeps improving. Once again, more detailed results

are presented in Table 3.

5 OPPONENT ESTIMATION

STUDY: PROGRESSIVE

VERSUS FIXED

On the one hand, a decent agent – better than a fully

random one – usually emerges from the task deﬁnition

Evolving Evaluation Functions for Collectible Card Game AI

257

itself. It is often heuristic, ﬁlled with expert knowl-

edge about the problem. On the other, a standard in-

population evaluation is proved to yield a good solu-

tion, e.g., using a linear combination of some expert-

based features and a basic evolution scheme. Our

question is whether one of these approaches is supe-

rior to the other in terms of real-world evaluation.

Additionally, we are interested in what the differ-

ence is between using a weak and a strong opponent

as a measure. This is an interesting dilemma, as both

approaches may be potentially vulnerable to fast stag-

nation. A weak opponent may be too easy to beat, so

the win rate quickly approaches large values, while

against a strong opponent, we may struggle to achieve

any victories thus, there may be no progress at all.

5.1 Experiment Setup

To properly compare the two evolution schemes, one

needs to compare not only their outcomes but also the

costs. In our case, the overhead of a given scheme

is negligible in comparison to the cost of simulations.

Thus, we use the number of simulated games as a met-

ric of evolution cost.

In progressive scenario, each two individuals

played rounds games on each of drafts drafts. In

weak-op and strong-op scenarios, every individual

played N × rounds games on each of drafts drafts for

each side. Overall, all three evaluation schemes use

the same number of games for each individual. In our

experiments, drafts = 10, N = 50, and rounds = 10.

5.2 Learning Comparison

To verify whether the evolution progresses, we com-

pare the best individuals of all generations after the

evolution ﬁnishes. Such progress, visualized in Fig. 1,

is deﬁnite in all of the progressive individuals and

less signiﬁcant for the opponent-based ones. It is clear

that the progressive scheme is better at this task.

The elitism in combination with the in-population

evaluation directly implies it.

Additionally, all three heatmaps of weak-op

agents have some bold dark stripes. Every dark stripe

represents a few consecutive agents that were signiﬁ-

cantly weaker than the local average. The same hap-

pens in other evolution schemes, but it is rather excep-

tional. It is understandable, as only the progressive

evolution takes in-population evaluation into account.

But also, it shows that learning against the stronger

opponent is more resilient to the forgetting issue.

5.3 Tournament Comparison

The lack of progress visible in heatmaps does not im-

ply a lack of general improvement. As seen in Ta-

Table 1: Subset of the tournament results, presenting all weak-op agents and their evolution target, WeakOp, itself. Every

score is an average win rate (along with its standard deviation) of the agent on the left against the agent on top. Given average

win rate is calculated based on the full tournament results.

Linear BinaryTree Tree WeakOp Global avg.

Linear – 56.9±10.2% 47.5±12.6% 65.9±10.0% 42.9±15.7%

BinaryTree 43.0±10.2% – 49.2±12.0% 82.9±2.67% 33.8±14.2%

Tree 52.4±12.6% 50.7±12.0% – 56.0±8.25% 36.2±15.7%

WeakOp 34.0±10.0% 17.0±2.67% 43.9±8.25% – 42.8±17.3%

Table 2: Subset of the tournament results, presenting all strong-op agents and their evolution target, StrongOp, itself. Every

score is an average win rate (along with its standard deviation) of the agent on the left against the agent on top. Given average

win rate is calculated based on the full tournament results.

Linear BinaryTree Tree StrongOp Global avg.

Linear – 52.1±13.3% 52.9±9.15% 38.8±11.5% 48.9±16.6%

BinaryTree 47.8±13.3% – 49.9±11.7% 34.1±9.90% 45.1±16.9%

Tree 47.1±9.15% 50.0±11.7% – 36.7±9.51% 44.8±15.7%

StrongOp 61.1±11.5% 65.8±9.90% 63.2±9.51% – 62.8±14.6%

Table 3: Subset of the tournament results, presenting all progressive and from-Linear agents. Every score is an average

win rate (along with its standard deviation) of the agent on the left against the agent on top. Given average win rate is

calculated based on the full tournament results.

Linear BinaryTree Tree Linear-from-Linear Tree-from-Linear Global avg.

Linear – 59.7±14.2% 61.2±14.1% 43.5±8.40% 41.0±13.7% 54.8±18.0%

BinaryTree 40.2±14.2% – 50.1±13.1% 40.0±11.5% 37.6±10.3% 45.5±16.8%

Tree 38.7±14.1% 49.8±13.1% – 39.5±15.7% 35.2±13.5% 45.6±18.7%

Linear-from-Linear 56.4±8.40% 60.0±11.5% 60.4±15.7% – 44.3±11.1% 58.0±17.1%

Tree-from-Linear 58.9±13.7% 62.3±10.3% 64.7±13.5% 55.6±11.1% – 60.2±17.4%

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

258

Round

Win rate (%)

Linear-weak-op

BinaryTree-weak-op

Tree-weak-op

Linear-strong-op

BinaryTree-strong-op

Tree-strong-op

Linear-progressive

BinaryTree-progressive

Tree-progressive

Linear-from-Linear

Tree-from-Linear

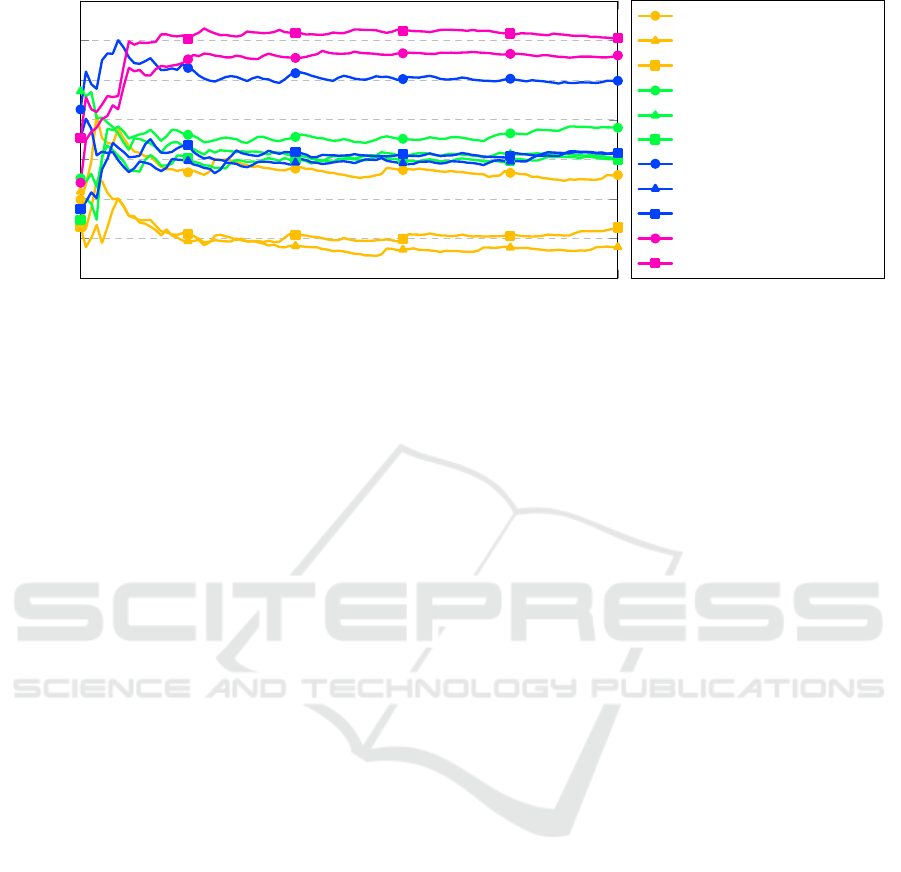
Figure 4: A subset of the tournament results. All scores (y-axis) stabilize as the number of rounds (x-axis) increases.

ble 2 and Table 3, the two tree-based representations

achieve comparable results for both progressive

and strong-op – around 45%.

However, this does not hold for the most straight-

forward Linear representation. The differences be-

tween weak-op, strong-op, and progressive are

large, around 6% each.

When we compare how well both ﬁxed-opponent

agents play against their evolution goals, we see that

their scores do not correlate with the representa-

tion. The BinaryTree representation performs best

in the weak-op variant and achieved 82.9% wins

against the WeakOp, while the other representations

were much weaker – 65.9% and 56% for Linear and

Tree respectively. At the same time, BinaryTree is

the worst in the strong-op variant, achieving only

34.1% wins against StrongOp, whereas Linear and

Tree achieved 38.8% and 36.7% wins respectively.

As presented in Fig. 4, all weak-op agents are

strictly worse than the strong-op since almost the

beginning of the tournament. It is not the case for the

progressive and strong-op – every representation

except Linear is stronger in the former variant.

To summarize, evolution via self-play yields bet-

ter agents than evolution towards a ﬁxed oppo-

nent. However, it is not true if the representation

is not ﬁxed, e.g., Tree-progressive is inferior to

Linear-strong-op.

Additionally, evolution using a ﬁxed opponent has

a slightly different cost characteristic. While evolu-

tion using self-play simulates longer games gradu-

ally, using a ﬁxed opponent starts with much shorter

ones but ends with longer ones – already trained agent

quickly deals with initial, almost random agents and

holds better against the evolved ones. As expected,

the weak-op evolution is faster than the strong-op.

6 CONCLUSION

In this work, we presented a study regarding two im-

portant aspects of evolving feature-based game evalu-

ation functions: the choice of genome representation

(implying the algorithm used) and the choice of op-

ponent used to test the model.

Although our research was focused on the domain

of collectible card games, the problems stated are of

general nature, and we are convinced that our obser-

vations are applicable in the other domains as well.

The key takeaway is that having limited computa-

tional resources, it is probably better to stick with a

simpler linear genome representation. Based on our

research they are more reliable to produce good solu-

tions fast. However, with a large computational bud-

get, we recommend applying a two-step approach of

bootstrapping a stronger model with a limited one.

Another important observation is that self-

improvement is potentially a better strategy than a

predeﬁned opponent when used as a goal of evolution.

Deﬁnitely, there is no point in learning against a weak

opponent. Learning against a strong opponent may be

proﬁtable but does not guarantee good performance in

a broader context like a tournament. And while pro-

gressive learning may also stagnate into some niche

meta, it still seems to be more ﬂexible in this aspect.

For future work, we plan to investigate a gener-

alized bootstrapping-like scheme, that would switch

between the representations automatically, as soon as

the evolution rate drops below a certain threshold.

Separately, we would like to apply our approach to

other tasks as well as evaluate different models, e.g.,

additional expert-knowledge features or trees with

more operators. When it comes to the different evo-

lution schemes, some kind of ensemblement of both

in-population evaluation and an external goal would

Evolving Evaluation Functions for Collectible Card Game AI

259

be interesting. Also, we can consider the extension of

using a portfolio of agents as the opponents, with dy-

namic additions and removals based on the win rates.

REFERENCES

Benbassat, A. and Sipper, M. (2011). Evolving board-game

players with genetic programming. pages 739–742.

Benbassat, A. and Sipper, M. (2012). Evolving both search

and strategy for reversi players using genetic program-

ming. pages 47–54.

Bhatt, A., Lee, S., de Mesentier Silva, F., Watson, C. W.,

Togelius, J., and Hoover, A. K. (2018). Exploring the

Hearthstone deck space. In PFDG, pages 1–10.

Bjørke, S. J. and Fludal, K. A. (2017). Deckbuilding in

magic: The gathering using a genetic algorithm. Mas-

ter’s thesis, NTNU.

Blizzard Entertainment (2004). Hearthstone. Blizzard En-

tertainment.

Browne, C. B., Powley, E., Whitehouse, D., Lucas, S. M.,

Cowling, P. I., Rohlfshagen, P., Tavener, S., Perez, D.,

Samothrakis, S., and Colton, S. (2012). A Survey of

Monte Carlo Tree Search Methods. IEEE TCIAIG,

4(1):1–43.

Campbell, M., Hoane, A. J., and Hsu, F. (2002). Deep Blue.

Artiﬁcial intelligence, 134(1):57–83.

Chen, Z., Amato, C., Nguyen, T.-H. D., Cooper, S., Sun,

Y., and El-Nasr, M. S. (2018). Q-deckrec: A fast deck

recommendation system for collectible card games. In

IEEE CIG, pages 1–8. IEEE.

David, O. E., van den Herik, H. J., Koppel, M., and Ne-

tanyahu, N. S. (2013). Genetic algorithms for evolv-

ing computer chess programs. IEEE transactions on

evolutionary computation, 18(5):779–789.

Dire Wolf Digital and Sparkypants Studios (2017). The El-

der Scrolls: Legends. Bethesda Softworks.

Dockhorn, A. and Mostaghim, S. (2018). Hearthstone AI

Competition. https://dockhorn.antares.uberspace.de/

wordpress/.

Ferrer, G. and Martin, W. (1995). Using genetic program-

ming to evolve board evaluation functions.

García-Sánchez, P., Tonda, A., Fernández-Leiva, A. J., and

Cotta, C. (2020). Optimizing hearthstone agents us-

ing an evolutionary algorithm. Knowledge-Based Sys-

tems, 188:105032.

García-Sánchez, P., Tonda, A., Squillero, G., Mora, A., and

Merelo, J. J. (2016). Evolutionary deckbuilding in

Hearthstone. In IEEE CIG, pages 1–8.

Groß, R., Albrecht, K., Kantschik, W., and Banzhaf, W.

(2002). Evolving chess playing programs.

Hauptman, A. and Sipper, M. (2005). Gp-endchess: Using

genetic programming to evolve chess endgame play-

ers. volume 3447, pages 120–131.

Hoover, A. K., Togelius, J., Lee, S., and de Mesentier Silva,

F. (2019). The Many AI Challenges of Hearthstone.

KI-Künstliche Intelligenz, pages 1–11.

Janusz, A., Tajmajer, T., and

Swiechowski, M. (2017).

Helping AI to Play Hearthstone: AAIA’17 Data Min-

ing Challenge. In FedCSIS, pages 121–125. IEEE.

Justesen, N., Mahlmann, T., and Togelius, J. (2016). On-

line evolution for multi-action adversarial games. In

EvoCOP, pages 590–603. Springer.

Khan, G. M., Miller, J., and Halliday, D. (2008). Develop-

ing neural structure of two agents that play checkers

using cartesian genetic programming. pages 2169–

2174.

Kowalski, J. and Miernik, R. (2018). Legends of Code and

Magic. http://legendsofcodeandmagic.com.

Kowalski, J. and Miernik, R. (2020). Evolutionary Ap-

proach to Collectible Card Game Arena Deckbuilding

using Active Genes. In IEEE Congress on Evolution-

ary Computation.

Kusiak, M., Wal˛edzik, K., and Ma

ndziuk, J. (2007). Evolu-

tionary approach to the game of checkers. In Interna-

tional Conference on Adaptive and Natural Comput-

ing Algorithms, pages 432–440. Springer.

Lucas, S. M., Liu, J., and Perez-Liebana, D. (2018). The

n-tuple bandit evolutionary algorithm for game agent

optimisation. In 2018 IEEE CEC, pages 1–9. IEEE.

Mikolov, T., Sutskever, I., Chen, K., Corrado, G. S., and

Dean, J. (2013). Distributed representations of words

and phrases and their compositionality. In Advances in

neural information processing systems, pages 3111–

3119.

Montoliu, R., Gaina, R. D., Pérez-Liebana, D., Delgado,

D., and Lucas, S. (2020). Efﬁcient heuristic policy

optimisation for a challenging strategic card game. In

EvoAPPS, pages 403–418.

Perez, D., Samothrakis, S., Lucas, S., and Rohlfshagen, P.

(2013). Rolling horizon evolution versus tree search

for navigation in single-player real-time games. In

GECCO, pages 351–358.

Salem, M., Mora, A. M., Merelo, J. J., and García-Sánchez,

P. (2018). Evolving a torcs modular fuzzy driver using

genetic algorithms. In EvoAPPS, pages 342–357.

Samuel, A. L. (1959). Some studies in machine learning

using the game of checkers. IBM Journal of research

and development, 3(3):210–229.

Santos, A., Santos, P. A., and Melo, F. S. (2017). Monte

carlo tree search experiments in hearthstone. In IEEE

CIG, pages 272–279. IEEE.

Silver, D., Hubert, T., Schrittwieser, J., Antonoglou, I., Lai,

M., Guez, A., Lanctot, M., Sifre, L., Kumaran, D.,

Graepel, T., et al. (2018). A general reinforcement

learning algorithm that masters chess, shogi, and Go

through self-play. Science, 362(6419):1140–1144.

Swiechowski, M., Tajmajer, T., and Janusz, A. (2018). Im-

proving Hearthstone AI by Combining MCTS and Su-

pervised Learning Algorithms. In IEEE CIG, pages

1–8. IEEE.

Vieira, R., Tavares, A. R., and Chaimowicz, L. (2020).

Drafting in collectible card games via reinforcement

learning. In IEEE SBGames, pages 54–61. IEEE.

Witkowski, M., Klasi

nski, Ł., and Meller, W. (2020). Imple-

mentation of collectible card Game AI with opponent

prediction. Engineer’s thesis, University of Wrocław.

Zhang, S. and Buro, M. (2017). Improving hearthstone ai

by learning high-level rollout policies and bucketing

chance node events. In IEEE CIG, pages 309–316.

IEEE.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

260