Recommendation System for Student Academic Progress

Horea Grebl

1 a

, C

alin V. Rusu

1,2 b

, Adrian Sterca

1 c

, Darius Bufnea

1 d

and Virginia Niculescu

1 e

Department of Computer-Science, Babes¸-Bolyai University, Romania

Institute for German Studies, Babes¸-Bolyai University, Romania

Keywords:

Recommendation Systems, Machine Learning, Neural Networks, Academic Assessment.

Abstract:

The purpose of this work is to study the possible approaches to build a recommendation system that could help

students in organizing their work and improving their results. More speciﬁcally, we intend to predict grades of

a student for future exams, based on his/her previous results and the past grades received by all students from

the same series/group. We have tried several machine learning methods for predicting future student grades,

and ﬁnally we obtained good results, namely a mean absolute prediction error smaller than 1. The best variant

proved to be the one based on neural networks that leads to a mean absolute prediction error smaller than 0.5.

These results show the practical applicability of our proposed methodology, and consequently, we built, based

on these, a practical recommendation system available to students as a web application.

1 INTRODUCTION

Recommendation systems have grown in popularity

over the past twenty years at the same time with the

development of the Internet and of the online com-

merce. Their grown in popularity is linked in gen-

eral with a ﬁnancial purpose that is pursuit mostly by

companies that operate in the commercial sector (i.e.

businesses). The main scope of such a system is to

increase the sales of products and services or to in-

crease the time spent by clients visiting, watching,

listening, or simply ”consuming” different types of

online content (especially, but not necessarily, mul-

timedia content). The monetization based on recom-

mendation systems is performed either through direct

sales of additional products or services, advertising

revenue or relying on afﬁliate marketing schemes for

obtaining a commission. However, there are speciﬁc

scenarios where the implementation of a recommen-

dation system is not directly ﬁnancial driven, rather

such a system adds more value to the services that a

company offers.

The use of recommendation systems in education

https://orcid.org/0000-0002-8529-5797

https://orcid.org/0000-0002-2056-8440

https://orcid.org/0000-0002-5911-0269

https://orcid.org/0000-0003-0935-3243

https://orcid.org/0000-0002-9981-0139

has been recently proposed, using such tools being ex-

tremely important from a modern academic manage-

ment perspective. Beneﬁts of integrating these sys-

tems in education could imply for example personal-

ization of the learning process, course content adap-

tation based on previous student grades and feedback

or correct decision taking in different other contexts.

The beneﬁts of using recommendation systems can be

obtained either at a course level - for example for con-

tent or assignment adaptation to a speciﬁc student or

group of students - or at a more general level (i.e. in-

stitutional level), for example for determining and op-

timizing the best study paths when building a curric-

ula. Another approach is to integrate recommendation

modules directly into learning management platforms

and course management systems.

The study presented in this paper proposes a rec-

ommendation system suitable for monitoring a stu-

dent progress throughout his or her undergraduate

studies with focus on predicting a student’s grade for

a speciﬁc discipline from the curricula. We inves-

tigated the application of several machine learning

techniques to ﬁnd potential relationships between dis-

ciplines, relying on algorithms such as clustering, re-

gression, decision trees, and neural networks. As for

training and test data, we used anonymised data from

our university records, these records containing stu-

dents’ grades for the last twenty years (since the uni-

versity’s records were digitalized).

Grebl

a, H., Rusu, C., Sterca, A., Bufnea, D. and Niculescu, V.

Recommendation System for Student Academic Progress.

DOI: 10.5220/0010816300003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 3, pages 285-292

ISBN: 978-989-758-547-0; ISSN: 2184-433X

285

A recommendation system featuring such capabil-

ities could be used for:

• helping students to better evaluate their possible

future performance and allowing them to focus

more on the subjects where lower results are es-

timated;

• early tutoring students with predisposition in ob-

taining a lower grade at certain courses;

• analyzing differences in academic performance

between different lines of studies (considering

that our university courses are delivered in four

different languages, two of them being interna-

tional languages) ;

• analyzing the impact of changes in the academic

curricula or the impact or changing a titular pro-

fessor of a speciﬁc course;

• comparison between the academic performance of

different generations of students.

We think that there is a need for a tailor made so-

lution for each university as the structure of the curric-

ula is different along universities and specializations

they propose.

The rest of this paper is structured as follows: Sec-

tion 2 presents the related work, most relevant re-

search in the ﬁeld of recommendation systems applied

in education being reviewed. Section 3 presents our

data collecting methodology and the main logic that

stands behind our recommendation system. In Sec-

tion 4 we analyse the obtained results with several dif-

ferent classiﬁers such as Linear Regressor, Random

Forest Regressor and Neural Network. The proposed

tool is brieﬂy presented in section 5. The paper ends

with conclusions in Section 6, also revealing some fu-

ture work outlines.

2 RELATED WORK

In recent years Technology-Enhanced Learning ben-

eﬁted from a plethora of recommender systems that

support educational stakeholders by personalising the

learning process and help the learners in taking the

correct decisions. Such systems usually have differ-

ent characteristics and use different prediction tech-

niques. A generic template of recommender systems

can be broken down into three phases:(i) the infor-

mation collection phase; (ii) the learning phase and

ﬁnally (iii) the prediction or recommendation phase

(Isinkaye et al., 2015). Filtering is very important

for recommender systems and this could be based

on collaborative ﬁltering, content-based ﬁltering or

hybrid ﬁltering, the most used one being collabo-

rative ﬁltering. Next, the building process can be

done using machine learning (Portugal et al., 2018) or

data mining techniques (Amatriain and Pujol, 2015).

These techniques can quickly recommend a set of

items for the fact that they use pre-computed model

and they have proved to produce recommendation re-

sults that are similar to neighborhood-based recom-

mender techniques. The study presented in (Drachsle

et al., 2015) investigated and categorised a number of

82 recommender systems from 35 different countries.

The reviewed systems have been classiﬁed into seven

clusters according to their characteristics and anal-

ysed for their contribution to the research ﬁeld. An-

other recommender systems review that examined the

context in which recommenders are used, the manners

in which they are evaluated and the results of those

evaluations is available in (Deschenes, 2020).

Since online courses are more and more popular in

developing new skills, choosing them correctly is an

important issue. Several studies have thus focused on

developing recommender systems in the area. A sys-

tem that provides a personalized environment of study

is developed and described in (Mondal et al., 2020).

The system ﬁrst classiﬁes a new learner based on its

past performance using the k-means clustering algo-

rithm. After that, Collaborative ﬁltering is applied in

the cluster to recommend a few suitable courses. In

(Bakhshinategh. et al., 2017) a course recommen-

dation system for students based on the assessment

of their graduate attributes is reported. Graduate at-

tributes are the qualities, skills and understandings

that some university communities agree that their stu-

dents should develop during their time inside the insti-

tution. Students rate the improvement in their gradu-

ating attributes after a course is ﬁnished and a collabo-

rative ﬁltering algorithm is utilized in order to suggest

courses that were taken by fellow students and rated

in a similar way. The ratings are weighted based on

their report time, most recent being considered more

important.

At the same time, other studies have focused on

developing systems that are able to predict student

performance. An approach that takes into consider-

ation only the previous student grades to predict stu-

dent performance in particular courses is reported in

(Byd

zovsk

a, 2015). Collaborative ﬁltering methods

were used, and these proved to be similarly effec-

tive as the commonly used machine learning meth-

ods like Support Vector Machines. The thesis (Kotha,

2013) uses an incremental approach for predicting

student grades at the end of the semester. First, a

simple model using linear function in single variable

and minimized mean square error for predicting stu-

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

286

dent grades, and then the complexity of model is in-

creased by taking the linear function using multiple

variables. After that, classiﬁcation algorithms as de-

cision trees, nearest neighbour, support vector ma-

chines, linear discriminant analysis, and also combi-

nations of classiﬁers were used to predict student ﬁ-

nal grade. A system to predict students’ grades for

the courses they will enroll in during the next enroll-

ment term by learning patterns from historical data

but also using additional information about students,

courses and the professors that teach them is pro-

posed in (Sweeney et al., 2016). Several models were

used: Factorization Machines (FM), Random Forests

(RF), and the Personalized Multi-Linear Regression,

and the best result was obtained using a hybrid FM-

RF method that proved to accurately predict grades

for both new and returning students taking both new

and existing courses; the study of the feature selec-

tion study emphasizes strong connections between in-

structor characteristics and student performance.

3 METHODOLOGY

Our goal is to build a recommendation system for stu-

dent progress; we try to apply several Machine Learn-

ing (ML) techniques to ﬁnd correlation relationships

between disciplines and to be able to predict a future

student’s grade for a discipline based on the previous

grades obtained by all students and see which of these

ML techniques best suites our use case. From the var-

ious Machine Learning classes of algorithms we in-

vestigated an unsupervised learning method, namely

clustering, and three supervised learning techniques,

i.e. linear regression, random forest regression and

neural networks. Our ﬁrst approach considers cluster-

ing techniques to group similar disciplines based on

the grades received by students. First approach was to

use clustering. There are many clustering algorithms

that have emerged over time, some of them being in-

cluded in the stable releases of various data science

libraries due to their maturity and performance they

provide. It is known that there is no ”one algorithm

matches all problems”, but, as the study conducted in

(Saxena et al., 2017) concluded, the well suited clus-

tering algorithm for a vast majority of the problems is

K-Means from the ”Partition” family (Table 1). In Ta-

ble 1 we summarize the main characteristics of a list

of clustering algorithms we have considered. We list

for each considered algorithm, the family of cluster-

ing algorithms to which a speciﬁc algorithm belongs,

its time complexity, scalability, suitability for large

data sets and sensitivity to noise in the data.

Our dataset consists of grades obtained by the stu-

dents of an entire Bachelor’s degree series, across

their entire academic route (spanning over 3 years of

BSc studies). The curricula for such a series contains

both compulsory and optional courses. If, for com-

pulsory courses we have enrolled all students, the op-

tional ones can have enrolled only a fraction of them.

We used only grades obtained by students for the

compulsory courses, such that we have approximately

the same number of grades for each course (there may

be a small number of students that did not attend the

exam for some courses). This would ease our prepro-

cessing of the data and would make our dataset more

balanced. The dataset was exported from the database

in csv format, each row containing the grades for a

speciﬁc student and the header row consists of the stu-

dent id and the 27 compulsory courses. Our aim was

to group courses that have some similarity (similar-

ity is based on the obtained students’ grades) between

them in the same cluster, so, we needed to have each

course on a separate row, the header containing the

student ids and each cell on the table to have the grade

the student from that column obtained for the course

on that row. To obtain this, we ”transposed” the orig-

inal dataset. To be easy for us to run the steps needed

in the clustering process we decided to use Python and

its data science libraries: numpy, pandas, sklearn; the

steps performed were as follows:

• loading dataset in a Pandas

dataframe

• checking that there are no missing values

• dropping the course column and remain only with

numerical data (the grades themselves)

• applying Elbow method to detect the most suit-

able number of clusters as we applied a partition-

ing algorithm (Figure 1)

• run the K-Means clustering algorithm on the

dataset using the above obtained number of clus-

ters

• add the cluster label to each instance from our

original dataset (there we have the course name)

• obtain the Silhouette score for our clustering

scheme (Figure 2)

By running these steps we obtained 8 clusters, but

the Silhouette score was quite low and we decided it

is not good enough for our solution.

An alternative method we considered was to take

into consideration the direct correlation factor be-

tween each 2 different courses that are thought in dif-

ferent semesters, this, in our opinion being relevant

for students trajectory. In order to obtain this correla-

tion factors we had to implement some database side

https://pandas.pydata.org

Recommendation System for Student Academic Progress

287

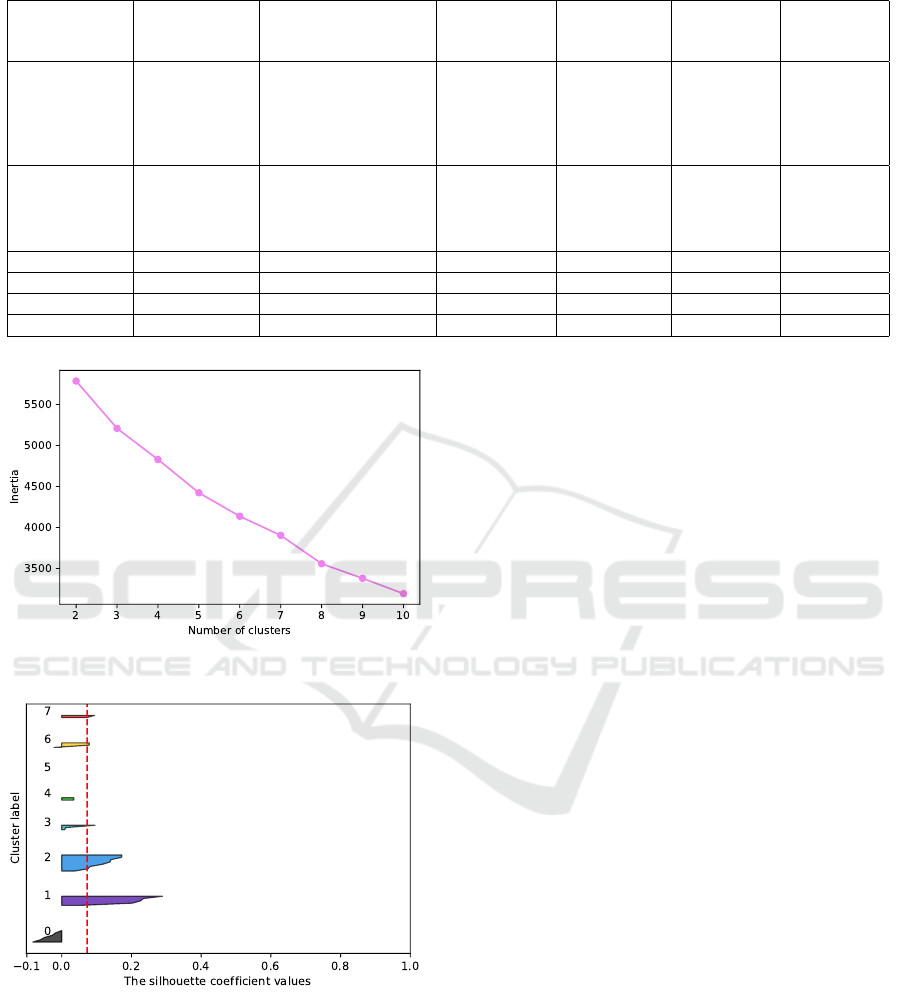
Table 1: Comparison of different clustering algorithms.

Category of

clustering

Alg. name Time complexity Scalability Suitable for

large scale

data

Suitable for

high dim.

data

Sensitive of

noise/outlier

Partition

k-means Low O(knt) Middle Yes No High

PAM High O(k(n −k)

) Low No No Little

CLARA Middle

O(ks

+ k(n −k))

High Yes No Little

CLARANS High O(n

) Middle Yes No Little

Hierarchy

BIRCH Low O(n) High Yes No Little

CURE Low O(s

log(s)) High Yes Yes Little

ROCK High O(n

log(n)) Middle No Yes Little

Chameleon High O(n

) High No No Little

Fuzzy based FCM Low O(n) Middle No No High

Density based DBSCAN Middle O(nlog(n)) Middle Yes No Little

Graph theory CLICK Low O(k ∗ f (v, e)) High Yes No High

Grid based CLIQUE Low O(n + k

) High No Yes Moderate

Figure 1: Elbow method graph.

Figure 2: Silhouette score.

logic as the database management system (DBMS)

had no implementation for computing the correla-

tion factor. The formula used is the classical statis-

tical Pearson correlation coefﬁcient formula and the

threshold for a good correlation was set to 0.65.

After establishing correlations between courses

(see Figure 3), we have tried to predict the future

grade of a student for a course based on the grades

received by this student at courses that had a high

correlation coefﬁcient with this current course. But

the results we have obtained were unsatisfactory (i.e.

the prediction error was high). In Figure 3 the course

names are abbreviated and these abbreviations are

listed in the Appendix of the paper.

In a consequent approach, we used supervised ma-

chine learning techniques to predict a student’s grade

from all the grades received by all students in the

past (for all compulsory courses available). Hence,

we took all grades for all students from all the past

courses and we tried to predict the future grade of a

student for a course based on past grades received by

this student and all other students at past courses (i.e.

in the evaluation section, we tried to predict the fu-

ture grades of students at courses from the 3rd aca-

demic year based on grades received by the same set

of students at courses from the 1st and 2nd academic

years).

We have tried three supervised learning prediction

methods (Marsland, 2015): a Linear Regression, a

Random Forest Regressor, a Neural Network.

The ﬁrst model, the Linear Regression model is

just a basic linear regressor based on least squares

minimization. The second model we used is a Ran-

dom Forest Regressor. In order to check the method’s

applicability to our use case, we decided to use a ba-

sic conﬁguration. This regressor uses 100 decision

trees and ﬁts them on sub-samples of the initial grades

dataset. The results of the classifying decision trees

are averaged at the end. We performed a random

search on the hyper parameters of the decision trees

with 100 iterations and used 3-fold cross validation.

Finally, the Neural Network model is a neural network

with 3 dense layers. The layers use ReLU activation

functions, Adam optimizer and MSE loss function.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

288

Figure 3: Correlations between all courses in the dataset.

The hidden layers have 100, 50 and 20 neurons, re-

spectively. We trained the NN for 1000 epochs, be-

cause we did not see any improvement in the predic-

tion after these 1000 epochs.

After we dropped incomplete student records from

our dataset (i.e. students who did not have grades

for all courses in the dataset), we were left with the

academic records (i.e. grades) of 184 students. We

then split the dataset for training (75%) and valida-

tion (25%). For each of the six courses from the 3rd

year whose grades we are trying to predict, we trained

each of the 3 classiﬁers (i.e. Linear Regressor, Ran-

dom Forest Regressor and Neural Network). Then for

each 3rd year course, we predicted using each of the

three pre-trained classiﬁers, the grade of each student

(out of the total of 184 students). The results we ob-

tained are discussed in the next section.

4 RESULTS ANALYSIS

In this section we present the prediction results of the

three supervised learning classiﬁers (i.e. Linear Re-

gressor, Random Forest Regressor and Neural Net-

work) we considered. We predicted the student grades

received for all mandatory 3rd year courses: PC, PPD,

PM, LFTC, CN, VVSS (the actual course names for

these abbreviations are listed in the Appendix). We

used these 3rd year courses such that we have enough

classiﬁed data for training (i.e. the grades received for

the 1st and 2nd academic year courses).

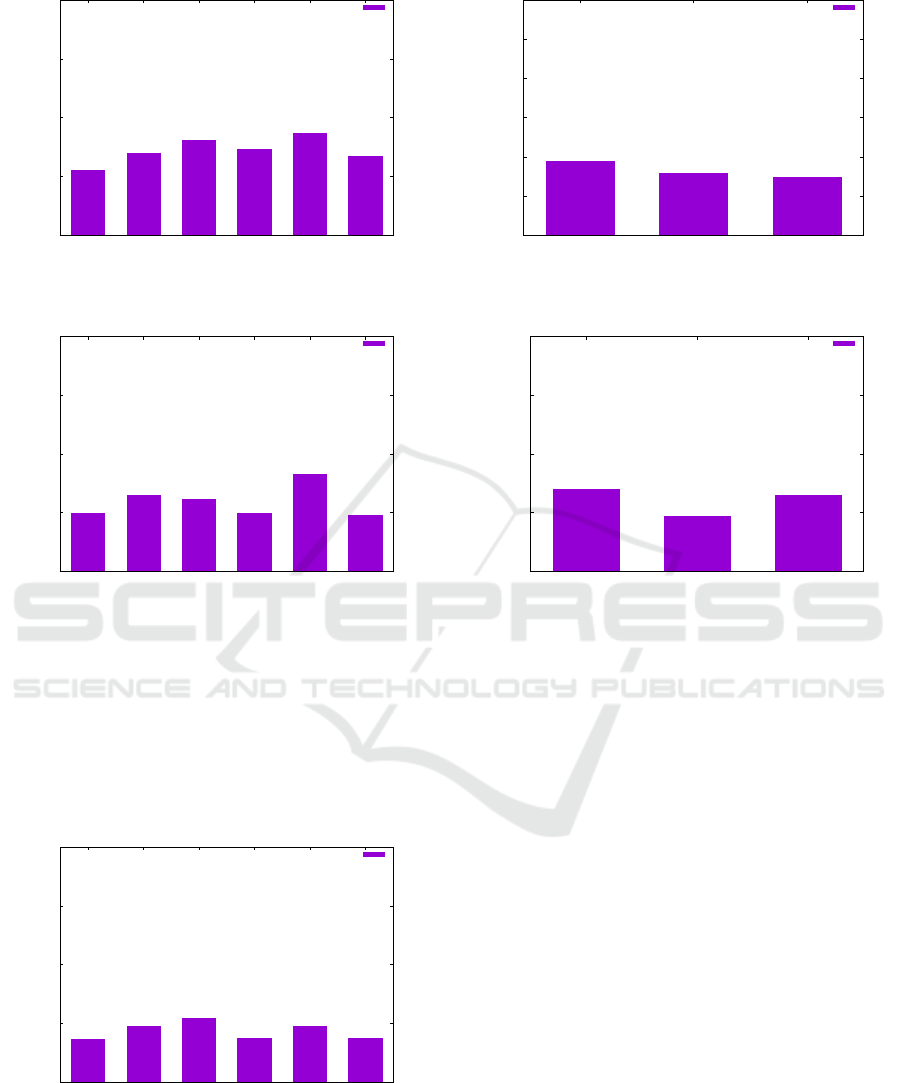
We can see the mean absolute prediction errors

obtained by each of the three employed prediction

methods in Figures 4, 5 and 6. The absolute predic-

tion error is the absolute value of the difference be-

tween the real value and the predicted one. For each

prediction method, we show in the corresponding ﬁg-

ure the mean absolute error obtained for each of the

six 3rd year courses predictions. We can see in these

ﬁgures that the prediction error varies across courses,

but all methods obtain good results (i.e. mean abso-

lute prediction error under 1 point). The neural net-

work obtained the best results, i.e. mean absolute

prediction errors under 0.5. This means, that on av-

erage, the difference between the predicted grade and

the actual grade is below 0.5 (the grades have values

on a scale from 1 to 10). Following the neural network

results, the next best results are the ones obtained by

the random forest regression. The worst results are

the ones obtained by the simple linear regressor, but

still these are acceptable since for most courses the

mean prediction error in close to 0.5.

The standard deviation of the prediction error ob-

tained by the three prediction methods is depicted in

Figure 7. We can see that it is smaller than 1 for all

three models, the neural network obtaining slightly

better results than the other two models.

We can see all three models compared for such a

typical course, for example the PPD course in Figure

8. This ﬁgure displays the mean absolute prediction

error for the single course PPD. We can see that again,

the neural network obtains the best result.

Recommendation System for Student Academic Progress

289

0.5

1.5

PC PPD PM LFTC CN VVSS

Prediction Error

Course

Grade Mean Prediction Error

Figure 4: The mean absolute prediction error obtained by

the Linear Regression method.

0.5

1.5

PC PPD PM LFTC CN VVSS

Prediction Error

Course

Grade Mean Prediction Error

Figure 5: The mean absolute prediction error obtained by

the Random Forest Regression method.

A detailed picture with the individual prediction

error obtained for each (Student;Course) pair by the

neural network is depicted in Figure 9. Here we

ploted the grades for all the 184 students and for all

6 courses, not just mean values as in the previous ﬁg-

ures. We can see here that the number of outliers is

rather small.

0.5

1.5

PC PPD PM LFTC CN VVSS

Prediction Error

Course

Grade Mean Prediction Error

Figure 6: The mean absolute prediction error obtained by

the Neural Network method.

0.5

1.5

2.5

Linear-Regression Random-Forest-Regression Neural-Network

Prediction method

Standard Deviation Error

Figure 7: The standard deviation of the prediction error ob-

tained by the three prediction methods.

0.5

1.5

Linear-Regression Neural-Network Random-Forest-Regression

Prediction Error

Prediction method

Grade Mean Prediction Error

Figure 8: All three methods compared for one course

(PPD). The mean absolute prediction error is shown for

each method.

5 WEB-BASED PREDICTION

TOOL

In order to explore the practical beneﬁts of our

methodology, we developed a web based tool that al-

lows students to perform queries related to their future

exams’ results, trying to stimulate students to early

take action by studying more if needed (i.e. if the pre-

dicted results of future exams are not satisfactory).

This web tools authenticates students based on

their internal credentials offered by the university, and

using a student internal ID and a given future disci-

pline from the curricula, it outputs the prediction of

the grade to the student.

Considering that our previously presented Ma-

chine Learning techniques were implemented in

Python, our web tool contains a backend component

written in Python, too. This backend component di-

rectly calls the A.I. implemented methods and exports

through some endpoints a REST API to the client

component (i.e. frontend) of our tool.

The fronted component is written in JavaScript /

jQuery. But considering the architecture of our tool

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

290

Figure 9: The absolute prediction error obtained by the Neural Network, depicted for each of the 6 courses and each student.

(presented in Figure 10) and the abstraction of the

backend, desktop/stand alone or mobile client appli-

cations can be easily deployed, apart from the web

version.

Students were given access to this tool, but we still

have to manage their feedback in using it.

6 CONCLUSIONS

In this paper we have investigated the prediction of

the future student grades from the past grades. This

would help students to predict their potential grades

for the future exams and would instruct them to study

much more if he/she wants a grade better than the pre-

dicted one.

We tried to build a tailored solution to our fac-

ulty. We considered several approaches, the ﬁrst be-

ing clustering the courses based on grades, and using

the correlation matrix of the courses. The clustering

approach proved to not be efﬁcient for our use case.

Ultimately, we have tried three methods for predicting

future student grades from past ones: a Linear Regres-

sion model based on least squares, a Random Forest

Regressor with 100 decision trees, and an Artiﬁcial

Neural Network with 4 dense layers and ReLU acti-

vation functions. We performed a series of evaluation

tests on a dataset containing all grades received for

mandatory faculty courses by all the students from

a Bachelor’s degree series (i.e. approximately 200

students) throughout their three academic years. All

three methods scored good results obtaining a mean

absolute prediction error smaller than 1 point. The

best results were obtained by the neural network with

a mean absolute prediction error smaller than 0.5.

For a concrete practical usage, we incorporate

these three methods in a web application that would

be of practical use to students. Additionally, we want

to use these methods to evaluate the impact of vari-

ous changes in the curriculum on the students’ per-

formance. Because we have made no assumptions on

the characteristics of the disciplines for which we pre-

dicted the grades, theoretically our solution can be ap-

plied to disciplines from other sciences besides com-

puter science. Our aim is to further develop this sys-

tem to detect if the same course, thought by differ-

ent instructors leads to sensibly different results and

thus future grade predictions; also, based on received

grades for a set of courses, to try to identify possible

masters degree specialization match for each student.

ACKNOWLEDGEMENTS

This research was supported by the following grant:

“Upgrade of the Cloud Infrastructure of the Babes¸-

Bolyai University Cluj-Napoca in Order to Develop

an Academic Management and Decision Support In-

tegrated System Based on Big&Smart Data - Smart-

CloudDSS” - POC/398/1/1/124155 - a Project Co-

ﬁnanced by the European Regional Development

Fund (ERDF) through the Competitiveness Opera-

tional Programme 2014-2020.

REFERENCES

Amatriain, X. and Pujol, J. M. (2015). Data mining methods

for recommender systems. In L., R. F. R. and B.R., S.,

editors, Recommender Systems Handbook. Springer,

Boston, MA.

Bakhshinategh., B., Spanakis., G., Zaiane., O., and ElAtia.,

S. (2017). A course recommender system based on

graduating attributes. In Proceedings of the 9th Inter-

national Conference on Computer Supported Educa-

tion - Volume 1: CSEDU,, pages 347–354. INSTICC,

SciTePress.

Recommendation System for Student Academic Progress

291

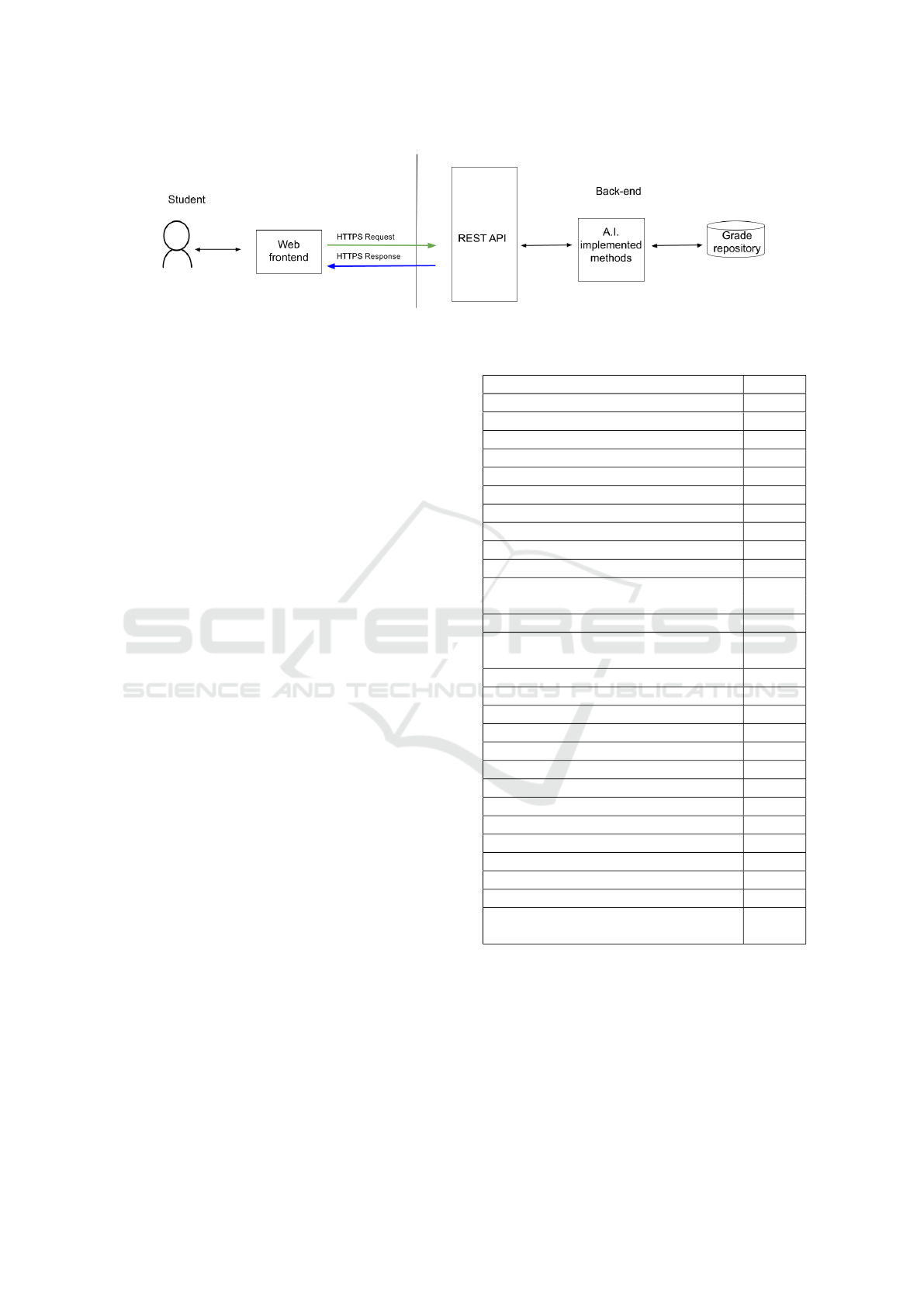
Figure 10: Web-based Prediction Tool Architecture.

Byd

zovsk

a, H. (2015). Are collaborative ﬁltering methods

suitable for student performance prediction? In F., P.,

P., M., and A., C. E. C., editors, Progress in Artiﬁcial

Intelligence. EPIA 2015. Lecture Notes in Computer

Science. Springer.

Deschenes, M. (2020). Recommender systems to support

learners’ agency in a learning context: a systematic

review. Int J Educ Technol High Educ, 17(50).

Drachsle, H., Verbert, K., Santos, O., and Manouselis, N.

(2015). Panorama of recommender systems to sup-

port learning. In Ricci F., Rokach L., S. B., editor,

Recommender Systems Handbook. Springer, Boston.

Isinkaye, F., Folajimi, Y., and Ojokoh, B. (2015). Recom-

mendation systems: Principles, methods and evalua-

tion. Egyptian Informatics Journal, 16(3):261–273.

Kotha, P. (2013). Personalized recommendation system for

students by grade prediction. Master’s thesis, Indian

Institute of Technology Bombay Mumbai.

Marsland, S. (2015). Machine learning: an algorithmic

perspective. CRC press.

Mondal, B., Patra, O., Mishra, S., and Patra, P. (2020). A

course recommendation system based on grades. In

2020 International Conference on Computer Science,

Engineering and Applications (ICCSEA), pages 1–5.

Portugal, I., Alencar, P., and Cowan, D. (2018). The use

of machine learning algorithms in recommender sys-

tems: A systematic review. Expert Systems with Ap-

plications, 97:205–227.

Saxena, A., Prasad, M., Gupta, A., Bharill, N., Patel, O. P.,

Tiwari, A., Er, M. J., Ding, W., and Lin, C.-T. (2017).

A review of clustering techniques and developments.

Neurocomputing, 267:664–681.

Sweeney, M., Lester, J., Rangwala, H., and Johri, A. (2016).

Next-term student performance prediction: A recom-

mender systems approach. In EDM’2016 - Educa-

tional Data Mining.

APPENDIX

The abbreviations for all courses in the dataset are

shown in Table 2.

Table 2: Abbreviations for all courses.

Name Abbrev.

Algebra ALG

Graph Algorithms AG

Mathematical Analysis AM

Computer Systems Architecture ASC

Databases BD

Numerical Calculus CN

Fundamentals of Programming FP

Geometry G

Software engineering ISS

Artiﬁcial Intelligence IA

Formal Languages and Compiler LFTC

Design

Computational Logic LC

Systems for Design and MPP

Implementation

Advanced Programming Methods MAP

Probability Theory and Statistics PS

Functional and Logic Programming PLF

Object Oriented Programming POO

Parallel and Distributed Programming PPD

Mobile Application Programming PM

Web Programming PW

Team Project PC

Computer Networks RC

Database Management Systems SGBD

Operating Systems SO

Dynamical Systems SD

Data Structures and Algorithms SDA

Software Systems Veriﬁcation and VVSS

Validation

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

292