Optimizing Route Planning for Minimising the Non-added-Value

Tasks Times: A Simultaneous Pickup-and-Delivery Problem

Bárbara Romeira

and Ana Moura

1,2 b

Department of Economics, Management, Industrial Engineering and Tourism, University of Aveiro, Aveiro, Portugal

GOVCOPP – Systems for Decision Support Research Group, University of Aveiro, Portugal

Keywords: Vehicle Routing Problem, Simultaneous Delivery and Pickup, Time Windows, Automotive Industry,

Mathematical Integer Linear Programming Model.

Abstract: The quick-change industrial environment pushes organisations to find new ways to improve efficiency,

flexibility, and responsiveness. To do so, companies must not solely focus on improving the main value chain,

but also the support services that provide for it. To this end, this paper focuses on a route optimization study,

inspired by a real-case problem of the Manufacturing Tool Repair Service, from an automotive company. The

problem consists of a vehicle routing problem with simultaneous delivery and pickup and time windows,

subjected to specific service constraints. To solve it, we propose a Mathematical-Integer Linear Programming

model, which is triggered by real-time data from the shopfloor. The approach was tested, and the results show

an average of 30% improvement compared with the current situation. Additionally, the model was tested

using modified benchmark instances and a time windows sensitivity analysis was performed. Considering the

results obtained, future work regarding the application of a hybrid algorithm is proposed

1 INTRODUCTION

The ever-rising market competitiveness pushes

organisations to find new ways to continuously

improve. As a result, it is not effective for

organisations to simply improve production process.

Rather, they must also improve other services that

support the value chain. In this perspective, the

current work intents to improve the manufacturing

tool pickup and delivery (P&D) service of an

automotive company. This problem is a practical

application of a vehicle routing problem (VRP) with

simultaneous delivery and pickup, and time windows

(VRPSDPTW). When applying time windows (TW)

and simultaneous P&D constraints to the VRP, we

obtained the problem addressed in this paper. Here,

each customer can be, simultaneously, a pickup and a

delivery customer, and the P&D must be done within

pre-defined TW. As it will be presented ahead, the

workers of the Manufacturing Tool Repair (MTR)

service are responsible for picking the used tools from

the production lines, repair them, and, after repair,

deliver them. The absence of real-time information on

https://orcid.org/0000-0001-6076-6612

https://orcid.org/0000-0003-4687-2747

the number of tools available, forces MTR workers to

constantly leave their workplace, to check the tools’

availability onsite. As a result, time lost travelling

around the shopfloor is significant and the tool repair

activity is constantly delayed. Thus, the present work

intents to optimize this process, eliminating

unnecessary dislocations and minimising the total

travel times, using a Mathematical-Integer Linear

Programming (MILP) model. To do so, it is

considered that: (i) The MTR service uses 2 different

vehicles with distinct capacities; (ii) A production

line is more critical than another, if the time until the

line stops, due to a lack of tools, is smaller. To the

extent of our knowledge, despite the amount of

literature about P&D, the VRPSDPTW is not

commonly considered, although being usual in real-

world situations. Thus, this paper presents the

following contributions:

 Application of the VRPSDPTW in a real-

world situation, which considers the demand

and minimal stock requirements at the

customer;

Romeira, B. and Moura, A.

Optimizing Route Planning for Minimising the Non-added-Value Tasks Times: A Simultaneous Pickup-and-Delivery Problem.

DOI: 10.5220/0010821000003117

In Proceedings of the 11th International Conference on Operations Research and Enterprise Systems (ICORES 2022), pages 153-160

ISBN: 978-989-758-548-7; ISSN: 2184-4372

153

 Real-time route trigger, definition, and

optimization, by connecting the MILP and the

company’s e-Kanban (presented in Romeira et

al. (2021)), which is continuously monitoring

the number of tools to P&D.

This paper is organized as follows: In section 2, a

brief review of other works, related to the

VRPSDPTW is presented. The current problem, the

optimization approach and the data pre-processing

process are described in detail in section 3. In section

4, the MILP model used is shown and the

computational results of our approach are presented

in section 5. Also, additional test results obtained with

benchmark instances and a sensitivity analysis are

presented. A summary and future works are presented

in section 6.

2 RELATED WORKS

In this section a collection of works related to the

VRPSPDTW is offered. Table 1 introduces a

summary of the constraints used in these works, and

Table 2 summarizes the related objective function(s).

In Shahabi-Shahmiri et al. (2021) an hybrid

approach was used to solve the heterogeneous

VRPSPDTW (HVRPSPDTW) with cross-docking

networks, split delivery and perishable products The

authors achieved a 10% reduction in the travel time and

a 29% reduction in the travel costs, when compared to

a previous approach. Zhang et al. (2020) applied two

different approaches to solve the same problem: an

exact and a metaheuristic approach. These were tested

in 15 instances obtained from company data. Their

conclusions show that for larger instances the exact

approach cannot reach the solution in a reasonable

computational time (CPU). Then, the metaheuristic

approach is used to solve those instances and compared

to several state-of-the-art algorithms, showing that it

converges quicker and has a better performance. L. Li

et al. (2019) also solved this problem using a

metaheuristic approach, which, for real-world

instances, obtained solutions within a low CPU time

(81 seconds). In the work of Madankumar and

Rajendran (2019), an exact approach was used and

tested with 24 modified instances given by Solomon

(1987). The results show that it obtained optimal

solutions with better CPU times than the model of

Wang and Chen (2012). Using 8 to 10 of the same

benchmark instances, Gupta et al. (2017) compared

their metaheuristic approach to the best-known results.

For instances C1 and C2, their approach matched the

best-known results, and for R and RC, it obtained

lower travel distances with a small trade-off in the

number of vehicles. Moreover, in real-world instances

it increased flexibility within the company when

compared to the current situation. Besides the

previously referred works, several others may be of

interest. Liu et al. (2021), Zhou et al. (2020), H. Li et

al. (2018) implemented metaheuristic approaches to

solve the VRPSDPTW. Liu et al. (2021) solved the

problem using metaheuristics aiming to minimise the

transportation costs. The approach was tested with

benchmarks instances generated by Wang and Chen

(2012) and the results proved its effectiveness. Having

a multi-objective VRPSDPTW, both Zhou et al. (2020)

and H. Li et al. (2018) applied a metaheuristic

approach. Both approaches outperformed algorithms

proposed by J. Wang et al. (2016) in terms of

convergence and diversity properties. In contrast, Ji

(2019) applied an exact model to minimise the travel

distance. By testing 2 instances of the Solomon (1987)

benchmarks, the author proved that the method is not

suitable for large-size instances. Tang et al. (2021)

proposed a hybrid approach, which found a good

solution in 66% of the benchmark instances (H. F.

Wang & Chen, 2012) and 10 new best-known

solutions. Lastly, Hof and Schneider (2019), using a

hybrid approach, focused on minimising the number of

vehicles, travel distance and TW’s penalties. This

approach, for medium-size instances, reduced the

number of vehicles and the travel distance in 31

instances. For large instances, the best solution had a

16.93% GAP, and used less CPU time than the

approach proposed by Wang et al. (2015).

Table 1: A summary of the VRPSPDTW constraints found in the literature.

Shahabi-Shahmiri

et al. (2021)

Zhang et

al. (2020)

L. Li et al.

(2019)

Madankumar &

Rajendran (2019)

Gupta et al.

(2017)

Our

Work

Vehicles' capacity x x x x x x

Vehicles' type x

Fleet's size x x x

Each customer is visited by only one vehicle x x x x

Time windows (Customers, Workers, etc) x x x x x x

Each customer must be visited exactly once x x x x

Each customer must be assigned to a route x x x x x

Other constraints x x x x x x

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

154

Table 2: A summary of the VRPSPDTW objectives found in the literature.

Shahabi-Shahmiri

et al. (2021)

Zhang et al.

(2020)

L. Li et al.

(2019)

Madankumar &

Rajendran (2019)

Gupta et al.

(2017)

Our

Work

Minimise travel time x x

Minimise travel distance x x

Minimise number of vehicles x

Minimise transportation costs x x x

Minimise waiting times x

Minimise time windows’ penalties x x

Minimise emissions

To finish, Table 3 summarizes the approaches

referred throughout this section.

Table 3: A summary of the VRPSPDTW approaches found

in the literature.

Paper Exact

Meta-

heuristic

Hybrid

Liu et al.(2021) x

Shahabi-Shahmiri et al.

(2021)

Tang et al. (2021) x

Zhang et al. (2020) x x

Zhou et al. (2020) x

Hof & Schneider (2019) x

Ji (2019) x

L. Li et al. (2019) x

Madankumar & Rajendran

(2019)

H. Li et al. (2018) x

Gupta et al. (2017) x

Our Work x

3 CASE STUDY

3.1 Current MTR Service Description

The MTR support service is responsible for the repair

and calibration of the tools used in the company’s

machines. As these tools have limited lifespans,

which are related to the number of parts produced, the

MTR workers pick the used tools from the production

lines, and deliver, new or repaired ones. Currently,

the MTR service team performs the following tasks:

(i) Repair and calibration of tools (Value-added

activity); (ii) Pick used tools from the production

lines; (iii) Deliver repaired, or new, tools to the

production lines. Since no production line must ever

stop for lack of tools, and there is no real-time

information on their availability to be collected, the

MTR workers are forced to go onsite and check the

stocks. This is a waste of time and productivity. Thus,

the P&D activities must be minimised. Currently, to

go to production, the workers follow 3 different

standardized routes (A, B and C – Figure 1). This

process takes an average of 18, 15 and 8 minutes,

respectively. Presently, each route is done at least 2

times per shift. However, sometimes there is an

average of 6 additional trips per shift. The P&D is

performed using one of 2 different vehicles: an

automatic and a manual vehicle. The first has a higher

average speed and a capacity of 150 tools, while the

other a capacity of 90 tools.

3.2 Optimization of the MTR Service

The company’s e-Kanban system, developed in

Romeira et al. (2021), gathers real-time data along the

company’s internal value chain. To this system, it was

added a Manufacturing Tool Stock menu that allows

us to know, in real-time, which tools are available in

each P&D point (the production lines, and from now

on called customers), and how many are available in

the MTR service to be delivered. During, a

production shift, these data is continuously processed,

and a route is triggered when: (i) There are enough

tools available to create a P&D route; (ii) The tools’

stock is below the defined minimum stock values.

This pre-processing gives us the customers to be

visited and the tools to be picked and delivered. Then,

this information, together with all the considerations

related to the vehicles (average speeds and capacities)

and the priority levels of each customer, are used to

compute the routes. The VRPSDPTW is solved using

a MILP model, where the main objective is to

minimise the total travel time for each vehicle,

considering the following general constraints:

 Each customer is visited exactly once per route;

 MTR service and customers’ TW (these

indicate the priority level);

 Vehicles’ capacities.

Figure 2, sums up the process to obtain the inputs

for the MILP model and shows the given outputs. As

can be seen, the e-Kanban is continuously analysing

Optimizing Route Planning for Minimising the Non-added-Value Tasks Times: A Simultaneous Pickup-and-Delivery Problem

155

the tools onsite, and the tools available for delivery in

the MTR service. Also, it is considered that:

 All tools have similar dimensions;

 The automatic vehicle only serves Route B,

while the manual serves Route A and C;

 The vehicles have different average speeds and

service times (the automatic vehicle has a

higher service time);

 There are no circulation restrictions;

 When a customer has a higher priority (defined

by the stock level), it must be served first;

 Every time a route alert is triggered, the MILP

is called to compute a new route.

Data Pre-processing Process. The data pre-

processing process is performed according to the

flowchart in Figure 2, using the data retrieved by the

e-Kanban regarding the tools’ availability in the

customers and in the MTR service. A new route is

created when the stock in a customer is below the

minimal stock level or, when the number of tools

available for P&D is sufficient to make a distribution.

For the first, whenever the minimal stock level is

reached a trip alert is created, because the related

customer is now considered a priority customer.

Then, the decision process is performed according to

the Figure 2 flowchart. Note that, before the MILP is

called, the Availability of tools for P&D procedure

must be performed. This verifies the existence of non-

priority tools to be delivered and picked from these

priority customers, with the aim of using the vehicle’s

full capacity. So, if the vehicle’s capacity is not

achieved with the priority tools, then for the same

priority customers, the algorithm tries to load the

vehicle with tools with the lowest stock level, re-

stocking the customer and/or tools to pick. For the

second option, when there are no tools below the

minimal stock, another procedure is called: Tools for

P&D. Here, it is verified if there are customers with

pickup stock above a pre-determined level, and for

those, the availability of tools to deliver is checked.

4 MILP MODEL

The VRPSDPTW is defined on a direct graph

𝐺𝐶,𝐴) , where the depot and customers are

represented by a set of nodes and with different

geographical location. The set of nodes and the set of

edges in G are represented as 𝐶1,…,𝑐 and 𝐴

𝑖,𝑗):𝑖,𝑗 ∈ 𝐶,𝑖  𝑗 , respectively. The length of

each arc is given by 𝑡



, which is the time needed to

travel from customer 𝑖 to 𝑗. Also, each customer has

a P&D demand, represented by 𝑝



and 𝑑



respectively. To deliver the required demand, a set of

vehicles 𝑉0,…,𝑣 is available. Two vehicles are

available, each with capacity 𝑄



,k ∈V. Each

customer

𝑖∈𝐶 must be visited within a predefined

time window 𝑎



,𝑏



], and has a predefined service

time 𝑠𝑡





. Furthermore, the depot node (MTR service)

also has a time window, 𝑎



,𝑏



], which defines the

total time available to execute the P&D requirements

in each shift. To meet the TW, the decision variable

𝑠



defines the arrival time of vehicle k ∈ V to

customer 𝑖 and to the depot. Another decision

variable used is 𝑥





that takes value 1 if arc 𝑖,𝑗) is

traversed by vehicle 𝑘∈𝑉, and zero otherwise.

Considering the nature of the problem, the following

integer variables are also considered:

Figure 1: Route creation process and its outputs.

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

156

 𝑙





, gives the total amount of load after vehicle

𝑘 visits customer 𝑖;

 𝑙𝑑





, gives the amount of load that remains to

be delivered, by vehicle 𝑘, to customer 𝑖 and to

all the following customers.

 𝑙𝑝





, gives the amount of load that must be

picked-up after vehicle 𝑘 visits customer 𝑖.

Taking into consideration the above data and decision

variables, a MILP vehicle-flow model was

developed:

Min t



x





















)

The objective (equation 1) is to minimise the total

travel time and is subjected to the following

constraints:

x

i=1, i≠j

=1, ∀ j≠1∈C

k=1

(2)

x

j=1, i≠j

=1, ∀ i≠1∈C

k=1

(3)

 x

i=1, i≠h

-  x

j=1,j≠h

=0, ∀ k∈V, ∀ h∈C

(4)

x

j=1

≤1, ∀ k∈V

(5)

x

i=1

≤1, ∀ k∈V

(6)

+st



-M

1-x

≤s

, ∀ k∈V, ∀ i≠j∈C

(7)

≤ s

≤ b

, ∀k∈V, ∀ i∈C

(8)

≥ ld

-M

(1-x

), ∀ k∈V, ∀i,j≠1∈C

(9)

≥ ld

, ∀ k∈V, ∀j≠1∈C

(10)

≥ l



 p

-M

(1-x

), ∀ k∈V, ∀i≠1,j≠1∈C

(11)

≤ ld

≤ Q

, ∀k∈V, ∀ i∈C

(12

)

≤ l

≤ Q

, ∀k∈V, ∀ i≠1∈C

(13

)

≥ lp

-M

(1-x

), ∀ k∈V, ∀j,i≠1∈C

(14

)

≤ lp

≤ Q

, ∀k∈V, ∀ i∈C

(15

)

= lp

+ ld

-d

, ∀k∈V, ∀ i≠1∈C

(16

)

∈



0,1



0;l

,ld

 0 and integer

(17

)

Constraints (2) and (3) ensure that each customer

is visited exactly once and by only one vehicle.

Constraint (4) guarantees the flow conservation,

which means that if vehicle k arrives at customer i, it

must also leave customer i. Both (5) and (6) ensure

that each vehicle starts and ends its route in the depot.

Inequalities (7) and (8) are related to the TW

constraints. The first specifies the vehicle arrival time

to a customer and the second guarantees that the

vehicle arrives within the related TW. With constraint

(9), the delivery quantity to be loaded at the depot is

specified. Additionally (7) and (9) force an order for

the vehicles visiting the routes, which ensures that no

sub-tours without the depot are generated.

Inequalities (10) and (11) indicate the amount of load

in the vehicles after visiting the first customer and the

other customers in the route, respectively. Constraints

(12) and (13) guarantee that the vehicle capacity is not

exceeded. For more information on the pickup

loadings, 3 more constraints were added. With

inequality (14) the pickup quantity that must be

unloaded in the depot is determined. Constraint (15)

guarantees that the vehicles capacity is not violated,

and constraint (16) correlates the load variables to

each other. Constraint (17) defines the variable’s

domains. Constraints (7), (9), (11) and (14) are

disjunctive constraints that are linearized by using

large multipliers (‘‘big-M values’’). To create valid

inequalities, one set 𝑀𝑇  𝑠





and 𝑀1  𝑀2 

𝑀3  𝑚𝑎𝑥𝑄



Figure 2: Data pre-processing process.

Optimizing Route Planning for Minimising the Non-added-Value Tasks Times: A Simultaneous Pickup-and-Delivery Problem

157

5 COMPUTATIONAL RESULTS

The model was tested with 10 types of instances from

normal demand requirements and 3 types of instances

with high demand quantities for each type of vehicle

(the worst-case scenario). Thus, in total we analysed

26 instances, 13 for the manual vehicle and other 13

for the automatic vehicle. Each problem instance is

defined by the quantity to P&D to each customer. The

vehicles capacity is given in number of tools, and for

the manual vehicle is equal to 90 and equal 150 for

the automatic. Also, the customer’s location was

obtained from the company’s layout (presented in

Figure 1) and the travel arcs times were calculated

according to each vehicles’ average speed. For each

customer the service times (𝑠𝑡



) and time windows

([𝑎



𝑏



]) are defined according to real data. Note that,

the TW are dynamic, based upon the customers’

priority in the route creation moment. Based on this,

the customer with highest priority has earlier and

tighter TW than the others.

Results. The model presented was implemented

using the CPLEX Studio IDE 20.1.0, and the

experiments were run on an Intel (R) CORE(TM) i7-

10750H CPU 2,60GHz with 16Gb of memory.

Table 4 shows the results obtained for the manual

vehicle and Table 5 for the automatic vehicle. In the

tables’ second column, the number of routes that the

vehicle must make (Trips) is presented. This means,

the number of times that the vehicle must leave and

return to the depot to fulfil the demand requirements.

The other columns of the table present the objective

function value (OF) – time needed to perform the

route in minutes, and the CPU time in seconds.

The last column presents the GAP (in %), given

by CPLEX, that is the tolerance on the GAP between

the best integer solution and the best node remaining

(best bound). For the manual vehicle, the results show

that the optimal solution is achieved for 8 of the 13

instances. For the remaining instances the obtained

GAP is in average 5%, except for test instance 8,

where the GAP is 23%. The solutions were obtained

within a low CPU time (average 0.21 seconds). Also,

the number of trips needed to fulfil the customers’

Table 4: MILP results for the manual vehicle.

Instance Trips OF (min) CPU (s) GAP (%)

1 2 9.22 0.17 0

2 2 9.22 0.17 0

3 2 9.22 0.22 5.83

4 2 9.22 0.17 5.04

5 2 9.22 0.09 0

6 2 9.22 0.82 5.1

7 2 9.22 0.13 0

8 2 9.22 0.17 23.03

9 2 9.22 0.16 0

10 2 9.22 0.09 0

11 4 17.77 0.13 0

12 4 15 0.23 4.82

13 4 17.77 0.14 0

demand is 2, except for the last 3 instances (worst-

case scenario instances). These are the ones which

have a high number of P&D demands, which, in some

customers equals the vehicles’ capacity. For the

instances with higher demand values, 2 optimal

solutions were obtained within, approximately, 0.14

seconds. For the automatic vehicle, the model only

reaches the optimum to 3 solutions out of 13.

Although the results obtained have an average GAP

of 9.6%, they were obtained within good CPU time

(17.8 seconds). When it comes to the high demand

instances, the CPU time required is much higher than

the average for other instances, especially for the 11

instance. Figure 3 presents a diagram with the 1

instance solution representation for the manual

vehicle. The yellow circles represent the customers,

and the blue square the depot. In green, we can see

the number of tools delivered to each customer and in

grey, the pickup quantities. Below the diagram, a

table with the following information is presented:

 Vehicle’s arrival time at customer;

 Vehicle’s departure time from customer;

 Picked load after leaving the customer (𝑙𝑝





);

 Load to be delivered to the customer and the

following customers (𝑙𝑑





);

 Total load after the vehicle leaves the customer

( 𝑙





Figure 3: Solution of the 1

instance for the manual vehicle.

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

158

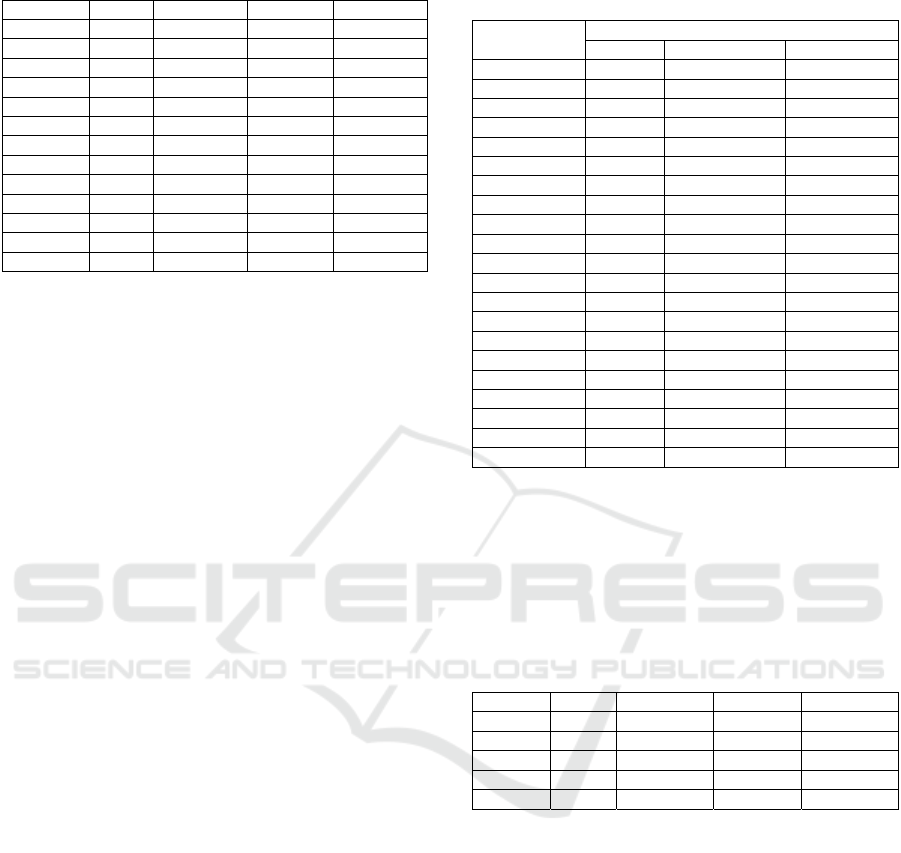
Table 5: MILP results for the automatic vehicle.

Instance Trips OF (min) CPU (s) GAP (%)

1 2 6.96 2.97 10.69

2 2 6.4 2.08 20.19

3 1 5.62 0.72 6.05

4 1 5.62 0.28 0

5 1 5.62 0.61 3.91

6 2 6.96 8.36 12.5

7 1 5.62 0.34 0

8 1 5.62 0.39 0

9 1 5.62 0.42 6.41

10 1 5.62 0.53 4

11 5 12.09 169.58 0.91

12 4 9.93 12.42 18.17

13 4 9.93 20.3 13.59

The total travel time, which includes the arcs

travel times, the service time and possible waiting

times, for this route is 13.19 minutes, and the MTR

worker needs to go 2 times to the depot, due to the

lack of vehicle’s capacity. With the current service

organisation, the workers need 26 minutes to do the

same service. This means that we reduced the time

consumed by 49%. It is important to note that, even

for the worst-case instances, the approach obtains a

smaller travel time than the company’s current one

for normal demand values. For the automatic vehicle,

we have in average a 14% reduction compared to the

current time for the same demand.

Vehicle-flow model efficiency test and time

windows sensitivity analysis. To test the model’s

efficiency in more challenging problem instances, the

adapted benchmarks from Li and Lim (2001) were

used. These problems’ objective is to minimise the

number of vehicles or routes. Due to the size of those

instances, only the first 20 customers of each instance

(IC2, IR2 and IRC2) were considered and adapted to

a VRPSDPTW. The results are presented in Table 6.

If the optimal solution is not reached within a pre-

defined time limit (10 minutes), the costs’ column

shows the best integer solution, and the CPU displays

a “-”. Like in the real problems (section 5.1), the

results in terms of solution GAP are not so good.

According to the problems’ characteristics, the CPU

time is relatively low. For the IRC problems, the

optimal solution was not achieved for the last 2

instances, within the time limit.

A time windows sensitivity analysis using the

automatic vehicle data was also performed. The tests

were made by reducing the time windows range. The

size of the time windows decreases from Case 1 to

Case 5. The results (Table 7) show that for tighter

time windows, the GAP becomes smaller. However,

this only happens until a certain point. This is,

because of the reduced time windows, one single

Table 6: Model results for the adapted benchmark problem

instances.

Instances

Vehicle-Flow Model

Costs CPU (sec) GAP (%)

IC201 252 0.01 0

IC202 202 1.69 11.88

IC203 194 8.69 2.36

IC204 186 4.01 0.96

IC205 251 0.75 1.40

IC206 230 1.64 3.28

IC207 218 1.89 1.87

IC208 205 3.74 3.78

IR202 399 46.84 0.87

IR203 354 91.19 0.71

IR204 289 42.68 0.81

IR205 350 1.86 1.19

IR206 318 11.4 2.83

IR207 318 61.82 0.69

IR208 260 2.53 1.08

IR209 312 3.87 2.26

IR210 353 79.06 0.69

IR211 293 253.83 0.46

IRC202 341 156.23 3.16

IRC203 309 - 20.95

IRC204 268 - 17.91

vehicle is no longer sufficient to make the route, not

because of capacity, but because the depot TW (Case

5). Also, when the TW are small (Case 4 and 5), the

OF values increase by 11% and 32%, respectively.

This can be related to the need to meet the TW, which

results in a visiting order that is not as efficient in

terms of travel distance.

Table 7: Time Windows Sensitivity analysis.

Case Trips OF (min) CPU (s) GAP (%)

Case 1 1 5.02 1.13 21.71

Case 2 1 5.02 1.22 18.63

Case 3 1 5.02 0.58 14.69

Case 4 1 5.62 1.42 10.50

Case 5 2 7.33 1.45 21.25

6 CONCLUSION AND FUTURE

WORK

A real-world problem of a Manufacturing Tool

Repair Support Service of an automotive company is

presented. One of the most time-consuming activities

performed by this service consists in the P&D of the

company’s manufacturing tools. Therefore, to

minimize this time and to increase service efficiency,

we modelled problem as a VRPSDPTW and solved

it. The stock levels in the production lines, together

with the number of repaired tools, are constantly

monitored and processed. Hence, when needed, the

MILP model generates routes with the sequence of

customers to visit and the related tools to P&D. Also,

Optimizing Route Planning for Minimising the Non-added-Value Tasks Times: A Simultaneous Pickup-and-Delivery Problem

159

compared to the current situation, the presented work

shows that, by using this approach, we can reduce up

to 49% the total travel time for one vehicle and 14%

for the other. Even in a worst-case scenario, the model

best results than the current ones for both vehicles. To

further improvements a 3-dimentional packing

problem integrated with the P&D problem is under

study.

REFERENCES

Gupta, A., Heng, C. K., Ong, Y. S., Tan, P. S., & Zhang, A.

N. (2017). A generic framework for multi-criteria

decision support in eco-friendly urban logistics systems.

Expert Systems with Applications, 71, 288–300.

Hof, J., & Schneider, M. (2019). An adaptive large

neighborhood search with path relinking for a class of

vehicle-routing problems with simultaneous pickup and

delivery. Networks, 74(3), 207–250.

Ji, Y. (2019). Optimal Scheduling in Home Health Care. In

ACM International Conference Proceeding Series (pp.

1–6).

Kumar, S. N., & Panneerselvam, R. (2012). A Survey on

the Vehicle Routing Problem and Its Variants,

2012(03), 66–74.

Lagos, C., Guerrero, G., Cabrera, E., Moltedo, A., Johnson,

F., & Paredes, F. (2018). An improved Particle Swarm

Optimization Algorithm for the VRP with

Simultaneous Pickup and Delivery and Time Windows,

16(6), 1732–1740.

Li, Haibing, & Lim, A. (2001). A metaheuristic for the

pickup and delivery problem with time windows.

Proceedings of the International Conference on Tools

with Artificial Intelligence, 160–167.

Li, Hongye, Wang, L., Hei, X., Li, W., & Jiang, Q. (2018).

A decomposition-based chemical reaction optimization

for multi-objective vehicle routing problem for

simultaneous delivery and pickup with time windows.

Memetic Computing, 10(1), 103–120.

Li, L., Li, T., Wang, K., Gao, S., Chen, Z., & Wang, L.

(2019). Heterogeneous fleet electric vehicle routing

optimization for logistic distribution with time windows

and simultaneous pick-up and delivery service. In 2019

16th International Conference on Service Systems and

Service Management, ICSSSM 2019. Institute of

Electrical and Electronics Engineers Inc.

Liu, S., Tang, K., & Yao, X. (2021). Memetic search for

vehicle routing with simultaneous pickup-delivery and

time windows. Swarm and Evolutionary Computation,

66(April), 100927.

Madankumar, S., & Rajendran, C. (2019). A mixed integer

linear programming model for the vehicle routing

problem with simultaneous delivery and pickup by

heterogeneous vehicles, and constrained by time

windows. Sadhana - Academy Proceedings in

Engineering Sciences, 44(2), 1–14.

Romeira, B., Cunha, F., & Moura, A. (2021). Development

and Application of an e-Kanban System in the

Automotive Industry. In IEOM Monterrey 2021

Conference. Monterrey.

Shahabi-Shahmiri, R., Asian, S., Tavakkoli-Moghaddam,

R., Mousavi, S. M., & Rajabzadeh, M. (2021). A

routing and scheduling problem for cross-docking

networks with perishable products, heterogeneous

vehicles and split delivery. Computers and Industrial

Engineering, 157(February), 107299.

Solomon, M. M. (1987). Algorithms for the Vehicle

Routing and Scheduling Problems with Time Window

Constraints.

Tang, K., Liu, S., Yang, P., & Yao, X. (2021). Few-Shots

Parallel Algorithm Portfolio Construction via Co-

Evolution. IEEE Transactions on Evolutionary

Computation, 25

(3), 595–607.

Wang, C., Mu, D., Zhao, F., & Sutherland, J. W. (2015). A

parallel simulated annealing method for the vehicle

routing problem with simultaneous pickup-delivery and

time windows. Computers and Industrial Engineering,

83, 111–122.

Wang, H. F., & Chen, Y. Y. (2012). A genetic algorithm for

the simultaneous delivery and pickup problems with

time window. Computers and Industrial Engineering,

62(1), 84–95.

Wang, J., Zhou, Y., Wang, Y., Zhang, J., Chen, C. L. P., &

Zheng, Z. (2016). Multiobjective Vehicle Routing

Problems with Simultaneous Delivery and Pickup and

Time Windows: Formulation, Instances, and

Algorithms. IEEE Transactions on Cybernetics, 46(3),

582–594.

Zhang, M., Pratap, S., Zhao, Z., Prajapati, D., & Huang, G.

Q. (2020). Forward and reverse logistics vehicle routing

problems with time horizons in B2C e-commerce

logistics. International Journal of Production

Research, 0(0), 1–20.

Zhou, Y., Kong, L., Cai, Y., Wu, Z., Liu, S., Hong, J., & Wu,

K. (2020). A Decomposition-Based Local Search for

Large-Scale Many-Objective Vehicle Routing Problems

with Simultaneous Delivery and Pickup and Time

Windows. IEEE Systems Journal, 14(4), 5253–5264.

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

160