Training Machine Learning Models to Detect Group Differences in

Neurophysiological Data using Recurrence Quantification Analysis

based Features

Gianluca Guglielmo

, Travis J. Wiltshire

and Max Louwerse

Department of Cognitive Science and Artificial Intelligence, Tilburg University, Warandelaan 2, Tilburg, The Netherlands

Keywords: Mathematical Skills, Cognitive Task, Machine Learning, Complex Systems, Recurrence Quantification

Analysis.

Abstract: Physiological data have shown to be useful in tracking and differentiating cognitive processes in a variety of

experimental tasks, such as numerical skills and arithmetic tasks. Numerical skills are critical because they

are strong predictors of levels of ability in cognitive domains such as literacy, attention, and understanding

contexts of risk and uncertainty. In this work, we examined frontal and parietal electroencephalogram signals

recorded from 36 healthy participants performing a mental arithmetic task. From each signal, six RQA-based

features (Recurrence Rate, Determinism, Laminarity, Entropy, Maximum Diagonal Line Length and, Average

Diagonal Line Length) were extracted and used for classification purposes to discriminate between

participants performing proficiently and participants performing poorly. The results showed that the three

classifiers implemented provided an accuracy above 0.85 on 5-fold cross-validation, suggesting that such

features are effective in detecting performance independently from the specific classifiers used. Compared to

other successful methods, RQA-based features have the potential to provide insights into the nature of the

physiological dynamics and the patterns that differentiate levels of proficiency in cognitive tasks.

1 INTRODUCTION

Numerical skills have shown to be strong predictors

of attention, literacy, and decision-making (Merkley

& Ansari, 2016), as well as of socioeconomic status

and planning skills (Fernandez & Liu, 2019).

Therefore, for being able to identify an individual’s

performance on numerical skills – and consequently

other cognitive skills and abilities – it is important to

reliably track processes connected to the development

of numerical skills and their related performance.

Tracking such processes might allow us to detect

when an intervention is needed, helping individuals

who have difficulties in tackling numerical problems,

as well as improving socio-economic status,

unemployment, and other skills connected to

numeracy (Fernandez & Liu, 2019).

Past research has shown that performance in

several skill domains can be effectively tracked using

physiological signals such as electrocardiograms,

https://orcid.org/0000-0002-3581-1319

https://orcid.org/0000-0001-7630-2695

https://orcid.org/0000-0003-0328-7070

galvanic skin response, and electroencephalograms

(Sharma et al., 2020). Processes involved in

mathematical tasks can be effectively monitored

using electroencephalograms (EEG; Río et al., 2019).

EEG tracks the electrical activity of specific

electrodes placed on the subject's scalp, the signal is

used to extract features using linear methods such as

the time-frequency distribution, the fast Fourier

transform, and the autoregressive method (Al-

Fahoum & Al-Fraihat, 2014). Furthermore, EEG

signals have been used for classification tasks using

deep learning models such as long short-term

memory neural networks (Ganguly et al., 2020). Deep

learning models overall yield high accuracy but tend

to not provide insights into the nature of the signal

and the patterns differentiating groups.

In the current study recurrence quantification

analysis (RQA) was used to extract features from the

EEG signal of participants who either performed well

or poorly on a mental arithmetic task. RQA is robust

428

Guglielmo, G., Wiltshire, T. and Louwerse, M.

Training Machine Learning Models to Detect Group Differences in Neurophysiological Data using Recurrence Quantiﬁcation Analysis based Features.

DOI: 10.5220/0010832200003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 3, pages 428-435

ISBN: 978-989-758-547-0; ISSN: 2184-433X

to noise and has the added advantage that it is based

on recurrences and self-similarity. Consequently, it

does not require data transformations or mathematical

assumptions (Zbilut, Thomasson, & Webber 2002).

Using RQA, instead of the time-frequency

distribution, fast Fourier transform, autoregressive

method, or long short-term memory neural networks,

might not only result in extracting effective features

for machine learning purposes but also in obtaining

insights about the nature of the signal itself and the

patterns it contains.

RQA-based features have shown to be effective

for hypothesis testing purposes and for training

machine learning models (Hou et al., 2019; Lyby et

al., 2019). For example, RQA-based features,

combined with machine learning models, have been

used successfully to detect drowsiness and epileptic

seizures (Gruszczyńska et al., 2019; Shabani, Mikaili,

& Noori, 2016). Taken together, the evidence

supports the idea that RQA might effectively capture

the complexity of biological processes, which are

often not linear (Zbilut & Weber 2008). Nevertheless,

RQA-based features, combined with machine

learning, have so far not been used yet to detect

differences in performance on a cognitive task.

The current work aims to explore the possibility

of using RQA-based features to track performance in

cognitive skills within the domain of numeracy. The

hypothesis is that the recurrent structures in the EEG

signals, reflected by the RQA-based features, will

differ between participants performing proficiently

and participants performing poorly in the task. We

will make use of the RQA-based features extracted to

perform a binary classification task to discriminate

proficient and non-proficient participants.

2 BACKGROUND AND THEORY

2.1 Neurophysiology and Numeracy

Mathematical skills are rooted in human capabilities

to deal with space, numbers, and time. These skills

are argued to stem from a non-linguistic ability that

appeared during the late Palaeolithic and underwent

development throughout human history (Amalric, &

Dehaene, 2016; Wildgen, 2020).

Evidence from cognitive neuroscience shows that

brain regions involved in mathematical problems

such as the bilateral intraparietal and prefrontal areas

are present not only in humans but also in non-human

animals, such as monkeys (Cantlon & Brannon,

2007). Similar brain areas seem to be activated by

mathematical tasks belonging to different domains

such as topology, analysis, algebra, and geometry.

These brain areas include the bilateral inferior

temporal regions, bilateral intraparietal sulci,

cerebellum, and several regions of the prefrontal

cortex (dorsolateral, bilateral, superior, and mesial)

(Amalric, & Dehaene, 2016). Different mathematical

tasks involve high activity in the prefrontal and

parietal areas during their execution. Therefore, EEG

signals obtained from these areas are likely to be of

interest when investigating the levels of mathematical

abilities.

2.2 Recurrence Quantification Analysis

2.2.1 RQA and Its Specifications

Performing RQA requires a phase space

reconstruction (PSR) that is used to unfold the

dynamics of the signal. PSR is based on the setting of

a few parameters, such as the delay and the number

of embedding dimensions.

2.2.2 Phase Space Reconstruction

Phase space reconstruction is needed to define the

temporal evolution and behavior of the signals before

one can proceed with the use of RQA on continuous

data. One method to reconstruct the time-series

behavior in a multidimensional phase-space form is

to use the time-delay embedding (Takens, 1981) that

is based on four main parameters: the delay (τ), the

number of embedding dimensions (D), the radius (r),

and the rescaling norm (Wallot & Leonardi, 2018).

The delay specifies the number of time lags to

shift the copies of the signal, while the number of

embedding dimensions refers to the number of

dimensions (i.e., time-delayed copies) needed to

unfold the higher-dimensional dynamics that

characterize the time-series (Wallot, 2017). The

radius and the rescaling norm refer respectively to the

interval that defines two points as recurrent and to the

phase-space rescaling of the distance matrix. The

choice of the aforementioned parameters depends on

the time-series typology, its characteristics, and the

use of specific methods to obtain the optimal values

when considering the embedding dimensions and the

delay parameters.

The optimal delay value is calculated using the

average mutual information function, which provides

the lag representing the first local minima after which

the average mutual information remains generally

quite constant (Wallot, 2019). The number of

embedding dimensions is defined using the false

nearest-neighbor function, which computes the

Training Machine Learning Models to Detect Group Differences in Neurophysiological Data using Recurrence Quantiﬁcation Analysis

based Features

429

optimal number of dimensions considering the

number of delays selected. Conversely, the radius and

the norm are chosen according to the level of noise in

the data and the magnitude of the values composing

the time series. Generally, the radius is set between

0.01 and 0.05 while the norm has three possible

options: Euclidian, Supremum, and Manhattan

(Marwan et al., 2007). Most important in setting the

norm, however, is keeping the norm constant when

comparing different time-series (Wallot & Leonardi,

2018).

2.2.3 Recurrence Plot and Features

The parameters listed in the previous sections are

used as input to create the Recurrence Plot (RP;

Figure 2 and 3). The RP provides a visual

presentation of the patterns, repetitions, and dynamics

contained in the time-series under analysis.

The RQA-based features are directly extracted

from the patterns present in the RP. For the current

study we extracted those features also used in

previous studies (Gruszczyńska et al., 2019; Shabani,

Mikaili, & Noori, 2016; Turianikova et al., 2015):

 Recurrence Rate (RR): The likelihood of

recurrence of a specific state in the signal.

The recurrence rate is obtained by dividing

the number of recurrent elements,

represented by the points in the plot, by the

RP size.

 Determinism (%DET): The percentage of

diagonal recurrent points lying adjacently.

 Laminarity (%LAM): The percentage of the

number of recurrent elements arranged

vertically on the RP.

 Average Diagonal Line (ADL): The mean

length across all the diagonal lines present in

the RP.

 Maximum Diagonal Line (MDL): The length

of the longest diagonal line present in the

RP.

 Entropy (ENT): A feature based on the

frequency distribution of the diagonal lines.

The value obtained in this feature is directly

proportional to the complexity of the signal

analyzed. For example, uncorrelated noise

has a low value of ENT.

Since RQA considers self-similarity within a

single time-series, these features concern the points

on one side of the line of identity (the diagonal line

dividing the RP in two). The features extractable from

the RP are not limited to the ones listed above. For

example, other features include, but are not limited to,

trapping time and trend. Webber & Marwan (2015)

provide further information about additional features

and detailed explanations of the RQA equations.

3 METHODS

3.1 Dataset

For our study, we used the publicly available dataset

on Physionet, the “Electroencephalograms during

Mental Arithmetic Task” dataset (Zyma et al., 2019).

This dataset contains 36 healthy participants that

performed a mental arithmetic task for 4 minutes.

According to their performance, Zyma et al.

(2019) assigned the participants to two different

groups: participants who performed well were

assigned to group “G” (standing for good) and those

who performed poorly were assigned to group “B”

(standing for bad). According to the dataset on

Physionet, 10 participants were assigned to group “B”

calculations

= 7 per minute, SD = 3.6) while group “G”

had 26 participants (M

calculations

= 22 per minute, SD =

7.3).

The data were recorded using a 23 EEG channel

system where the recording sites were defined

according to the international 10/20 scheme; each

channel had a 500 Hz sample rate. The signal was

filtered with a low pass filter (45 Hz) and a power

notch filter (50 Hz). The data are artifact-free and

ready for analysis purposes. More information about

the sample and the task can be found in the original

work by Zyma et al. (2019).

3.2 Workflow

The workflow followed in this work is comparable to

the one used in other works that extracted RQA-based

features from physiological signals, and specifically

from EEG signals (Shabani, Mikaili, & Noori, 2016).

In order to proceed with the RQA-based features

extraction, we focused on four electrodes for our

analyses purposes: the F7, Pz, P4, and Fp1. These

electrodes were adopted in a previous study using the

same dataset to train a long short-term memory neural

network and provided the highest accuracy on a

classification task to detect the signal specific to the

arithmetic task (Ganguly et al., 2020). Furthermore,

the use of pre-selected electrodes, instead of all the

ones present on the EEG cap, was successfully

adopted in other studies using RQA-based features

combined with machine learning techniques

(Gruszczyńska et al., 2019).

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

430

After having selected the electrodes of interest,

the RQA-based features were extracted to train a

Support Vector Machine (SVM), a Random Forest

(RF), and a Gradient Boosting Classifier (GBC).

Before training the classifiers, we selected the five

most relevant features, using the Extra Trees method

(Sharma, Giri, Granmo, & Goodwin, 2019), and

resolved the class imbalance present in the dataset

using the Synthetic Minority Oversampling

Technique (SMOTE) (Chawla et al., 2002). These

processes were implemented to reduce the likelihood

of overfitting (Ying, 2019).

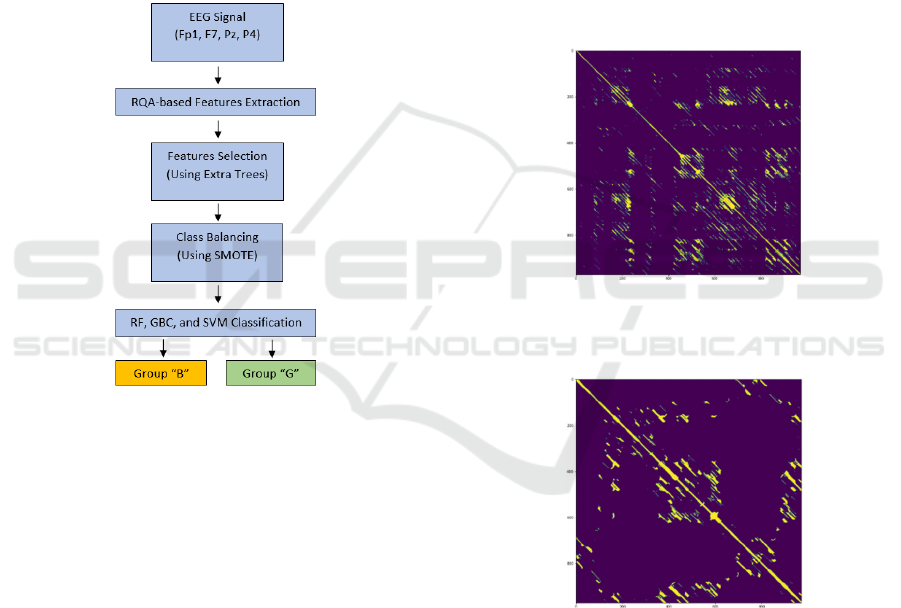
Figure 1 gives the overview of the workflow

followed in this study, which is similar to the one

adopted by Borowska et al. (2018).

Figure 1: An overview of the workflow adopted for this

study.

3.3 RQA-based Features Extraction

Before extracting the RQA-based features, the mutual

average information function and the false nearest-

neighbor function were used to define the optimal

number of dimensional embedding and delays. The

functions were run in R using the Tserieschaos

package (Di Narzo, 2019) and the nonlinearTseries

package (Garcia, 2021). Such functions were applied

to a few subjects across the two groups and to

different electrodes to verify if there was an

approximate constant optimal value across electrodes

and subjects. The signals analyzed had a number of

values for delay generally ranging between 4 and 5,

while the embedding dimensions had a value between

6 and 8. Therefore, the delay value was set to 5 and

the number of embedding dimensions to 7 when

performing RQA on all the data.

These parameters were used to create the RP

together with a radius of 0.05, which is generally used

for physiological data (Wallot, 2017), and Supremum

as norm, which is the default parameter in the

Pyunicorn library (Donges et al., 2015). The

Pyunicorn library, in Python, was used to extract the

RQA-based features and to visualize the RPs. To

slightly reduce the computational power required by

RQA, we used the initial 30,000 data points out of

31,000 composing the original dataset (Zyma et al.,

2019); 30,000 data points correspond approximately

to 3.87 minutes of recording out of a total of 4

minutes.

As conveyed in Figure 2 and Figure 3, the RP

offers preliminary visual information of the

differences between participants belonging to the two

groups.

Figure 2: RP illustrating the F7 electrode signal for a

participant of group “G” (1,000 data points). The x and y

axes represent the data points composing the signal.

Figure 3: RP illustrating the F7 electrode signal for a

participant of group “B” (1,000 data points). The x and y

axes represent the data points composing the signal.

Upon visual inspection, participants who performed

well on the task have an RP characterized by a higher

degree of complexity, compared to those performing

poorly. This visual information might provide early

insights into the differences between groups and how

their physiological signals may affect RP’s outlook.

Training Machine Learning Models to Detect Group Differences in Neurophysiological Data using Recurrence Quantiﬁcation Analysis

based Features

431

3.4 Features Selection

Each electrode selected for this work (F7, Pz, Fp1,

and Pz) was used to extract the six RQA-based

features (RR, %DET, %LAM, MDL, ADL, ENT).

The final dataset contained 24 features obtained by

multiplying the six RQA-based features times the

four electrodes. To avoid overfitting and to select the

most important features, the Extra Trees method

(Sharma, Giri, Granmo, & Goodwin, 2019) was

implemented for features selection. The Extra Trees

method was also used to obtain more insights into

which electrodes and features are likely to be the most

important to track cognitive performance and

differences between groups. After having performed

the Extra Trees method on the data, we selected the

top 5 features out of the 24 initial ones that were

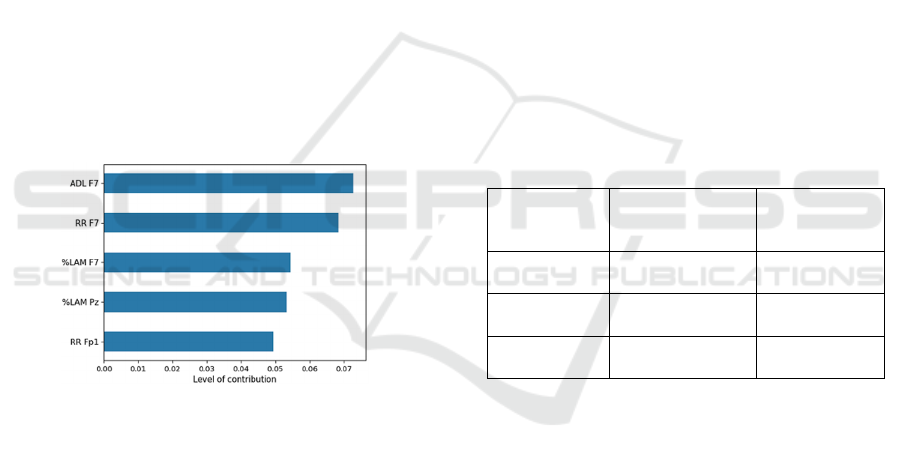
extracted. More specifically, as shown in figure 4, the

features used as input for the classifiers were ADL for

electrode F7, RR for electrode F7, %LAM for

electrode F7, %LAM for electrode Pz, and RR for

electrode Fp1. The features selection process was

performed to reduce potential overfitting especially

considering the limited size of the dataset used for this

work.

Figure 4: The features selected according to their level of

contribution.

After having selected the most relevant features,

the class imbalance present in the dataset (10 subjects

labeled as “B” and 26 labeled as “G”), was solved

using the SMOTE function. Eventually, the final

dataset fed to the classifiers was composed of 5

features and 52 instances of which 36 were original

and 16 synthetically created.

3.5 Classifiers Specifications

Multiple classifiers were used to confirm the

effectiveness of using RQA-based features to detect

cognitive performance. For this reason, an SVM, an

RF and, a GBC were used for classification purposes.

The targets of the classification were group “G” and

group “B”, respectively encoded as 1 and 0.

The hyperparameters selection was performed

using a randomized search on the 3 classifiers. The

hyperparameters adopted after having performed the

randomized search can be found in the following link:

https://osf.io/wtxpv/?view_only=ab98b469151a48a1

a91d221dc6596429.

4 RESULTS

The results obtained using the 3 classifiers show a

performance above 0.85 accuracy using 5-fold-cross

validation. In order to verify that the performance was

not due to the presence of synthetic data, the

classification task was also performed on the

imbalanced dataset containing 36 instances. The

results suggest that, even in the case of an imbalanced

dataset, the classifiers managed to perform

reasonably well on this specific task. A more detailed

overview of the performance obtained by each single

classifier using both the imbalance and balance

datasets can be visualized in Table 1.

Table 1: The accuracy scores obtained using the original

imbalanced dataset and the balanced dataset after resolving

the class imbalance.

Imbalanced

dataset accuracy

Balanced

dataset

accurac

RF 0.77

(

SD = 0.07

)

0.89

(

SD = 0.09

)

SVM 0.75

(SD = 0.13)

0.90

(SD = 0.06)

GBC 0.85

(

SD = 0.12

)

0.87

(

SD = 0.04

)

The use of the classifiers on the imbalanced

dataset seemed to confirm that the three classifiers

adopted in this study still performed above chance

given the information provided by the RQA-based

features.

5 DISCUSSION

This work aimed to investigate whether RQA-based

features could be used to successfully detect group

differences in a mental arithmetic task. We

hypothesized that the dynamics of the EEG signals

can differentiate participants with different levels of

numerical proficiency. The obtained results confirm

the hypothesis that the RQA-based features extracted

from the signal could discriminate effectively

between the two groups in a machine learning binary

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

432

classification task. These results are in line with other

studies that combined machine learning and RQA-

based features to detect epilepsy, drowsiness, and

preterm birth (Borowska et al., 2018; Gruszczyńska

et al., 2019; Shabani, Mikaili, & Noori, 2016). Given

the results of our study, it is reasonable to think that

RQA has the potential to detect or differentiate

performance in other cognitive domains. For

example, RQA-based features might be adopted in

the context of training and when comparing experts

and novices on a domain-specific task. To this extent,

there may be features showing convergence between

novices and experts after a period of training. Future

studies might investigate if our findings can be

extended to skills belonging to other cognitive

domains.

The main contribution of this study consists in

providing insights into the nature of the signal

characterizing the two groups. Using RQA-based

features, instead of other methods such as neural

networks, provide information about how the signal

differs in the two groups. Tracking changes in the

extracted signal, and being able to quantify them,

might be useful when considering the effect of

training or to evaluate if a needed intervention to

improve proficiency had a beneficial outcome. The

results of our study show that %LAM and RR are

present two times among the features selected. The

difference in RR between the two groups seems to be

intuitively visualized where participants belonging to

group “B” seem to have a much more deterministic

structure in the RP compared to participants in group

“G” (see Figure 2 and Figure 3). Interestingly,

according to Zbilut and Webber (2008), %LAM

seems a crucial feature of biological signals, and more

specifically physiological signals given that it

represents transitions such as those occurring

between chaotic and periodic phases. High values of

%LAM, in the context of a physiological signal, were

associated with low flexibility, high stability, and

more time needed for state transitions (Curtin et al.

2017). For example, experts showed lower %LAM

than novices in an experiment involving eye-tracking

when inspecting dermatological images

(Vaidyanathan et al., 2014). ADL, the most important

feature in our selection, might follow a similar pattern

to %LAM where higher values might represent a

more deterministic system. In the context of cognitive

skills, a higher %LAM and a longer ADL might

represent a more deterministic and less complex

signal, which might affect the time needed to switch

from a task to another resulting in poor performance.

The current study also offers insights relevant for

EEG and electrode selection, as it answers the

question of which electrode signals are most relevant

when extracting features using RQA. This study

indicates that F7 alone might be relevant for

classification purposes in this specific task. In fact,

the three top features out of five were extracted from

this electrode. Similarly, Mikaili and Noori (2016)

found that F8 alone was effective in detecting

subjects suffering from drowsiness.

The RQA-based features extracted to detect

cognitive performance related to numeracy seem to

provide high performance, especially once the class

imbalance is resolved, independently of the classifier

used. Ghosh and Saha (2021) employed a recurrent

neural network and features extracted using power

spectral density and correntropy spectral density,

obtaining an accuracy of 0.89 in detecting proficiency

in the same task used for this study. These results,

comparable to the ones obtained in the current study,

seem to provide further evidence about the

effectiveness of using RQA-based features to detect

performance in this domain. Future work might

implement models combining RQA-based features

with features extracted with other methods (e.g.,

spectral content) to verify if this approach might lead

to higher accuracy in classifying tasks in the

numerical domain.

More generally, RQA-based features have

previously been shown to be effective in several

domains to analyze numerous physiological signals

ranging from the electrocardiogram (Zbilut &

Webber, 2008) to the electrohysterogram (Borowska

et al., 2018). RQA is generally noise-resistant and it

does not require any linear transformation before

performing the analysis (Zbilut, Thomasson, &

Webber 2002). Furthermore, the extracted features

offer interpretability giving insights into the nature of

the signal. Such characteristics might encourage

researchers to use this method in other contexts and

domains exploring its potentiality combined with

machine learning and deep learning models.

However, despite the advantages offered by this

method, it is important to put our findings in context.

The dataset used had a relatively small sample, which

may have affected the results. This issue characterizes

most of the recent studies involving physiological

measurements, machine learning, and RQA-based

features where the number of participants often tends

to be small. Consequently, this issue posits limitations

when applying machine learning models.

Another limitation affecting this study is the

limited number of RQA-based features selected.

RQA can be computationally expensive and it might

require a lot of time, or computational power, to

extract its features in case of long time-series and

Training Machine Learning Models to Detect Group Differences in Neurophysiological Data using Recurrence Quantiﬁcation Analysis

based Features

433

phase space reconstructions with several dimensions

and high delay values. Therefore, the current study

was limited to the extraction of 6 RQA-based features

from just 4 electrodes. As a consequence, this work

was not able to provide a wider overview of the

relevance of other features and electrodes, and their

effect on the machine learning models’ performance.

Furthermore, the results obtained in our work do

not provide a thorough comparison between the

features extracted using linear methods on EEG data

and those obtained using RQA. Future studies should

apply RQA to larger datasets and accurately compare

RQA-based features with features extracted using

linear methods. Such efforts might provide more

information about the effectiveness of using this non-

linear method to extract features for machine learning

purposes.

6 CONCLUSIONS

The RQA-based features extracted from EEG signals

seem to provide adequate information to track

cognitive performance. Such an approach might be

implemented as an alternative to the classic linear

methods used to analyze EEG data. Future research

might provide insights into the effect of each single

RQA-based feature on performance and compare the

effectiveness of such features with the ones extracted

using different methods.

ACKNOWLEDGMENTS

The research reported in this study is funded by the

MasterMinds project, part of the RegionDeal Mid-

and West-Brabant, and is co-funded by the Ministry

of Economic Affairs, Region Hart van Brabant,

REWIN, Region West-Brabant, Midpoint Brabant,

Municipality of Breda, and Municipality of Tilburg

awarded to MML.

REFERENCES

Al-Fahoum, A. S., & Al-Fraihat, A. A. (2014). Methods of

EEG signal features extraction using linear analysis in

frequency and time-frequency domains. International

Scholarly Research Notices, 2014.

Amalric, M., & Dehaene, S. (2016). Origins of the brain

networks for advanced mathematics in expert

mathematicians. Proceedings of the National Academy

of Sciences, 113(18), 4909-4917.

Anderson, J. R., Betts, S., Ferris, J. L., & Fincham, J. M.

(2011). Cognitive and metacognitive activity in

mathematical problem solving: prefrontal and parietal

patterns. Cognitive, Affective, & Behavioral

Neuroscience, 11(1), 52-67.

Borowska, M., Brzozowska, E., Kuć, P., Oczeretko, E.,

Mosdorf, R., & Laudański, P. (2018). Identification of

preterm birth based on RQA analysis of

electrohysterograms. Computer Methods and

Programs in Biomedicine, 153, 227-236.

Cantlon, J. F., & Brannon, E. M. (2007). Basic math in

monkeys and college students. PLoS Biology, 5(12),

e328.

Chawla, N. V., Bowyer, K. W., Hall, L. O., & Kegelmeyer,

W. P. (2002). SMOTE: synthetic minority over-

sampling technique. Journal of Artificial Intelligence

Research, 16, 321-357.

Curtin, P., Curtin, A., Austin, C., Gennings, C.,

Tammimies, K., Bölte, S., & Arora, M. (2017).

Recurrence quantification analysis to characterize

cyclical components of environmental elemental

exposures during fetal and postnatal development.

PLoS One, 12(11), e0187049.

Del Río, J. M., Guevara, M. A., González, M. H., Aguirre,

R. M. H., & Aguilar, M. A. C. (2019). EEG correlation

during the solving of simple and complex logical–

mathematical problems. Cognitive, Affective, &

Behavioral Neuroscience, 19(4), 1036-1046.

Di Narzo, F. A. (2019). TseriesChaos: Analysis of

Nonlinear Time Series. R package version 0.1-

13.1.https://cran.rproject.org/web/packages/tseriesCha

os/index.html

Donges, J. F., Heitzig, J., Beronov, B., Wiedermann, M.,

Runge, J., Feng, Q. Y., Tupikina, L., Stolbova, V.,

Donner, R. V., Marwan, R., Dijstra, H. A., & Kurths, J.

(2015). Unified functional network and nonlinear time

series analysis for complex systems science: The

pyunicorn package. Chaos: An Interdisciplinary

Journal of Nonlinear Science, 25(11), 113101.

Fernandez, F., & Liu, H. (2019). Examining relationships

between soft skills and occupational outcomes among

US adults with—and without—university degrees.

Journal of Education and Work, 32(8), 650-664.

Ganguly, B., Chatterjee, A., Mehdi, W., Sharma, S., &

Garai, S. (2020, July). EEG based mental arithmetic

task classification using a stacked long short term

memory network for brain-computer interfacing. In

2020 IEEE VLSI Device Circuit and System (VLSI

DCS) (pp. 89-94). IEEE.

Garcia, C. A (2021). nonlinearTseries: Nonlinear Time

Series Analysis. R package version

0.2.11.https://CRAN.Rproject.org/package=nonlinear

Tseries

Ghosh, A., & Saha, S. (2021). Recurrent neural network

based cognitive ability analysis in mental arithmetic

task using electroencephalogram. In 2021 8th

International Conference on Signal Processing and

Integrated Networks (SPIN) (pp. 1165-1170). IEEE.

Gruszczyńska, I., Mosdorf, R., Sobaniec, P., Żochowska-

Sobaniec, M., & Borowska, M. (2019). Epilepsy

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

434

identification based on EEG signal using RQA method.

Advances in Medical Sciences, 64(1), 58-64.

Hou, Y., Aldrich, C., Lepkova, K., Machuca, L. L., &

Kinsella, B. (2017). Analysis of electrochemical noise

data by use of recurrence quantification analysis and

Lyby, M. S., Mehlsen, M., Jensen, A. B., Bovbjerg, D. H.,

Philipsen, J. S., & Wallot, S. (2019). Use of recurrence

quantification analysis to examine associations between

changes in text structure across an expressive writing

intervention and reductions in distress symptoms in

women with breast cancer. Frontiers in Applied

Mathematics and Statistics, 5, 37. machine learning

methods. Electrochimica Acta, 256, 337-347.

Marwan, N., Romano, M. C., Thiel, M., & Kurths, J.

(2007). Recurrence plots for the analysis of complex

systems. Physics Reports, 438(5-6), 237-329.

Mengarelli, A., Tigrini, A., Fioretti, S., & Verdini, F. (2021,

July). Recurrence quantification analysis of gait rhythm

in patients affected by Parkinson’s Disease. In 2021

IEEE EMBS International Conference on Biomedical

and Health Informatics (BHI) (pp. 1-4). IEEE.

Merkley, R., & Ansari, D. (2016). Why numerical symbols

count in the development of mathematical skills:

Evidence from brain and behavior. Current Opinion in

Behavioral Sciences, 10, 14-20.

Núñez, P., Poza, J., Gómez, C., Barroso-García, V.,

Maturana-Candelas, A., Tola-Arribas, M. A., Cano, M.,

& Hornero, R. (2020). Characterization of the dynamic

behavior of neural activity in Alzheimer’s disease:

Exploring the non-stationarity and recurrence structure

of EEG resting-state activity. Journal of Neural

Engineering, 17(1), 016071.

Shabani, H., Mikaili, M., & Noori, S. M. R. (2016).

Assessment of recurrence quantification analysis

(RQA) of EEG for development of a novel drowsiness

detection system. Biomedical Engineering Letters,

6(3), 196-204.

Sharma, J., Giri, C., Granmo, O. C., & Goodwin, M. (2019).

Multi-layer intrusion detection system with ExtraTrees

feature selection, extreme learning machine ensemble,

and softmax aggregation. EURASIP Journal on

Information Security, 2019(1), 1-16.

Sharma, K., Niforatos, E., Giannakos, M., & Kostakos, V.

(2020). Assessing cognitive performance using

physiological and facial features: Generalizing across

contexts. Proceedings of the ACM on Interactive,

Mobile, Wearable and Ubiquitous Technologies, 4(3),

1-41.

Takens, F. (1981). Detecting strange attractors in

turbulence. In Dynamical systems and turbulence,

Warwick 1980 (pp. 366-381). Springer, Berlin,

Heidelberg.

Timothy, L. T., Krishna, B. M., & Nair, U. (2015,

December). Combined recurrence and cross recurrence

quantification of MCI EEG. In 2015 International

Conference on Power, Instrumentation, Control and

Computing (PICC) (pp. 1-5). IEEE.

Turianikova, Z., Tonhajzerova, I., Czippelova, B., Javorka,

K., Lazarova, Z., & Javorka, M. (2014, September).

Recurrence Quantification Analysis of heart rate and

blood pressure variability in obese children and

adolescents. In Computing in Cardiology 2014 (pp.

445-448). IEEE.

Vaidyanathan, P., Pelz, J., Alm, C., Shi, P., & Haake, A.

(2014). Recurrence quantification analysis reveals eye-

movement behavior differences between experts and

novices. In Proceedings of the symposium on eye

tracking research and applications (pp. 303-306).

Wallot, S. (2017). Recurrence quantification analysis of

processes and products of discourse: A tutorial in R.

Discourse Processes, 54(5-6), 382-405.

Wallot, S., & Leonardi, G. (2018). Analyzing multivariate

dynamics using cross-recurrence quantification

analysis (crqa), diagonal-cross-recurrence profiles

(dcrp), and multidimensional recurrence quantification

analysis (mdrqa) a tutorial in R. Frontiers in

Psychology, 9, 2232.

Wallot, S. (2019). Multidimensional Cross-Recurrence

Quantification Analysis (MdCRQA) a method for

quantifying correlation between multivariate time-

series. Multivariate Behavioural Research, 54(2), 173-

191.

Webber, C. L., & Marwan, N. (2015). Recurrence

quantification analysis. Theory and Best Practices.

Wildgen, W. (2020). Structures, Archetypes, and Symbolic

Forms. Applied Mathematics in Linguistics and

Semiotics. In Structures Mères: Semantics,

Mathematics, and Cognitive Science (pp. 165-185).

Springer, Cham.

Ying, X. (2019, February). An overview of overfitting and

its solutions. In Journal of Physics: Conference Series

(Vol. 1168, No. 2, p. 022022). IOP Publishing.

Zbilut, J. P., Thomasson, N., & Webber, C. L. (2002).

Recurrence quantification analysis as a tool for

nonlinear exploration of nonstationary cardiac signals.

Medical Engineering & Physics, 24(1), 53-60.

Zbilut, J. P., & Webber, C. L. (2008). Laminar recurrences,

maxline, unstable singularities and biological

dynamics. The European Physical Journal Special

Topics, 164(1), 55-65.

Zyma, I., Tukaev, S., Seleznov, I., Kiyono, K., Popov, A.,

Chernykh, M., & Shpenkov, O. (2019).

Electroencephalograms during mental arithmetic task

performance. Data, 4(1), 14.

Training Machine Learning Models to Detect Group Differences in Neurophysiological Data using Recurrence Quantiﬁcation Analysis

based Features

435