
Reinforcement Learning-based Real-time Fair Online Resource
Matching
Pankaj Mishra
1,2
and Ahmed Moustafa
1
1
Department of International Collaborative Informatics, Nagoya Institute of Technology, Gokiso, Naogya, Japan
2
School of Computing and Information Technology, University of Wollongong, Wollongong, Australia
Keywords:
Resource Matching, Reinforcement Learning, Fairness, Online Markets, Contest Success Function.
Abstract:
Designing a resource matching policy in an open market paradigm is a challenging and complex problem. The
complexity is mainly due to the conflicting objectives of the independent resource providers and dynamically
arriving online buyers. In specific, providers aim to maximise their revenue, whereas buyers aim to minimise
their resource costs. Therefore, to address this complex problem, there is an immense need for a fair matching
platform. In specific, the platform must optimise the pricing rule on behalf of resource providers to maximise
their revenue at one end. Then, on the other hand, the broker must fairly match the resource request on behalf
of buyers. Owing to this we propose a two-step unbiased broker based resource matching mechanism in
the auction paradigm. In the first step, the broker computes optimal trade prices on behalf of the providers
using a novel reinforcement learning algorithm. Then, in the second step appropriate provider is matched
with the buyer’s request based on a novel multi-criteria winner determination strategy. Towards the end, we
compare our online resource matching approach with two existing state-of-the-art algorithms. Then, from the
experimental results, we show that the novel matching algorithm outperforms the other two baselines.
1 INTRODUCTION
Resource matching in online settings with multiple
data providers and dynamically arriving buyers is a
widely studied problem. Specifically, in such market
settings, two types of competition co-exist, i.e., com-
petition among the providers and competition among
the buyers. In specific, providers compete amongst
each other to maximise their total revenue by offering
their available resources. On the other end, dynami-
cally arriving buyers compete to fulfil their resource
demands at the minimum possible price. Also, with
the highest possible quality preferences. Usually, auc-
tion paradigms (Krishna, 2009) are widely adopted
(Samimi et al., 2016; Zaman and Grosu, 2013) for
various market setting. These auction paradigms are
owned by an auctioneer, which intermediates each re-
source matching. Specifically, it is the auctioneer’s
responsibility to design optimal allocation and pric-
ing rules (Myerson, 1981) in the market. In addi-
tion, these rules should be fair and maintain stabil-
ity in the market to create a trustworthy environment
(Krishna, 2009) for strategic participants. Besides, a
model should address and effectively handle the con-
flicting objectives of the participants.
Therefore, there is a need for a fair and truth-
ful auctioneer based matching platform to address all
the above constraints. Briefly, designing an optimal
matching platform, i.e., auctioneer, requires the over-
coming of three major challenges, as follows: (1)
designing an optimal pricing rule for the resource
providers, (2) designing an efficient allocation rule
for the online buyers, and (3) maintaining equilib-
rium in the auction paradigm. However, in the litera-
ture, these three challenges are addressed as indepen-
dent problems. For instance, there are optimal pric-
ing rules for static markets (Samimi et al., 2016; Za-
man and Grosu, 2013) as well as gradually changing
market (Kong et al., 2015; Li et al., 2016). However,
these rules fail to adapt to the dynamically changing
and time-sensitive resource requests.
Further, to adapt to the dynamics of such mar-
kets, learning-based approaches are more appropriate.
In this context, many learning-based approaches have
been proposed (Lee et al., 2013; Prasad et al., 2016;
Kumar et al., 2019). In specific, considering such
uncertain open markets, where multiple providers at-
tempting to negotiate with multiple buyers in an on-
line setting, a learning-based dynamic pricing algo-
rithm becomes immensely needed. Because fixed
34
Mishra, P. and Moustafa, A.
Reinforcement Learning-based Real-time Fair Online Resource Matching.
DOI: 10.5220/0010834600003116
In Proceedings of the 14th International Conference on Agents and Artificial Intelligence (ICAART 2022) - Volume 1, pages 34-41
ISBN: 978-989-758-547-0; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

pricing policies (Samimi et al., 2016; Zaman and
Grosu, 2013) or statistical model-based dynamic pric-
ing policies (Kong et al., 2015; Li et al., 2016) fail
to perform in such real-time scenarios. Also, con-
sidering the real-time setting and uncertain change in
supply or demand with a rare repeating pattern, su-
pervised learning is not suitable which learns from
a pattern. Therefore, reinforcement learning (Sut-
ton et al., 1998) becomes the most appropriate choice
for real-time pricing in the considered uncertain and
time-critical open markets. In the literature, recent
advancements in reinforcement-learning (RL) (Char-
pentier et al., 2021) for computational economics pro-
motes its applicability in such real-time market sce-
narios. For instance, the remarkable performance
of actor-critic RL-techniques in real-time bid optimi-
sation for online display advertisements (Cai et al.,
2017; Yuan et al., 2013).
However, these approaches fail to introduce a
comprehensive mechanism that handles the conflict-
ing criteria of each buyer when selecting suitable
providers. Besides, addressing equilibrium in open
cloud markets requires promoting three main char-
acteristics, which are competitiveness (Toosi et al.,
2016), truthfulness (Myerson, 1981) and fairness
(Murillo et al., 2008). In specific, the optimal pric-
ing rules need to maintain competitiveness by dynam-
ically modelling the resource selling prices based on
supply/demand in the market. Meanwhile, the allo-
cation rule needs to observe fairness and truthfulness
and gives equal winning opportunities to all the po-
tential providers in the market. However, to the best
of our knowledge, none of the existing resource al-
locations approaches (Myerson, 1981; Samimi et al.,
2016; Cai et al., 2017) focuses on addressing these
three challenges simultaneously.
To summarise, existing resource matching ap-
proaches are either provider-oriented or buyer-
oriented, but not both. Owing to this, in this work, we
propose a fair broker based online resource matching
mechanism in a double auction paradigm. In this re-
gard, the contributions of this research are as follows:
• First, a novel reinforcement learning-based online
pricing rule, which optimises the selling price as
per the supply and demand in the market.
• Second, a multi-preference provider matching
rule (allocation rule) is proposed, to maximise the
utility of the online buyers.
The rest of this paper is organised as follows:
Section 2 models the resource matching problem as
Markov decision process. Then, Section 3 introduces
a novel online pricing algorithm. In Section 4 presents
the provider matching mechanism. Then, in Section
5, the experimental results are presented for evaluat-
ing the proposed approach. Finally, the paper con-
cludes in Section 6.
2 THE MODEL
In this section, we model the online market setting
and define all the participants. As mentioned before,
we aim to design an optimal broker to carry out a
stable resource matching process in online markets.
In this context, we consider a set P of n providers
and set B
t
of m buyers at time-step t. Further, each
provider i ∈ P has a set of l types of resources de-
notes as, A
i,t
≡ {a
i,t
1
,a
i,t
2
,...,a
i,t
l
}, where a
i,t
j
repre-
sents the quantity of resource type j ∈ [1,l] available
with i ∈ P at time-step t. Similarly, the m arriving
buyers at time-step t report their profile θ
j
, denoted
as θ
j
≡ (R
j
,s
j
,w
j
,bid
j
), where, R
j
≡ {r
j
1
,r
j
2
,...,r
j
l
}
is the bundle of requested k types of resources, s
j
de-
notes the size of request in each time-step, w
j
rep-
resents the maximum waiting time and bid
j
denotes
the maximum budget of the buyer. Also let θ
θ
θ
t
set
of all the profile reported at time step t, i.e., θ
θ
θ
t
≡
{θ
1
,θ
2
,...,θ
m
}.
In the above setting, resource requests from a set
of buyers B
t
are matched dynamically to an appropri-
ate provider from a set of available providers. Figure
1 represents the architecture of the proposed auction-
eer. Also, α
1
,α
2
,...,α
m
, denotes the agents, bidding
on behalf of the providers.
From the figure, auctioneer comprises two mod-
ules: (1) online price optimisation module and (2)
provider matching module. In this regard, we call the
whole novel resource matching mechanism as real-
time resource matching (RTRM), which employs a
double-auction paradigm to match the resources in an
open market setting. Firstly, upon receiving the set of
resource requests from m online buyers at time-step t,
the RTRM platform optimises the offering price for all
the potential providers through autonomous agents.
These agents optimise the offered price for their re-
spective providers using the price optimisation mod-
ule. Finally, based on the provider matching module,
the appropriate provider is matched with buyers at an
optimal price.
Further, to adopt reinforcement-learning (Sutton
et al., 1998) in resource matching problem, we for-
mulate this matching problem as Stochastic Game,
i.e., Markov Decision Process (MDP) (Fink, 1964).
In this context, n autonomous agents bid the offered
price on behalf of n potential providers. In this re-
gard, the MDP has as a set of states S, which denotes
the possible status of all the agents. Then, there is a
Reinforcement Learning-based Real-time Fair Online Resource Matching
35
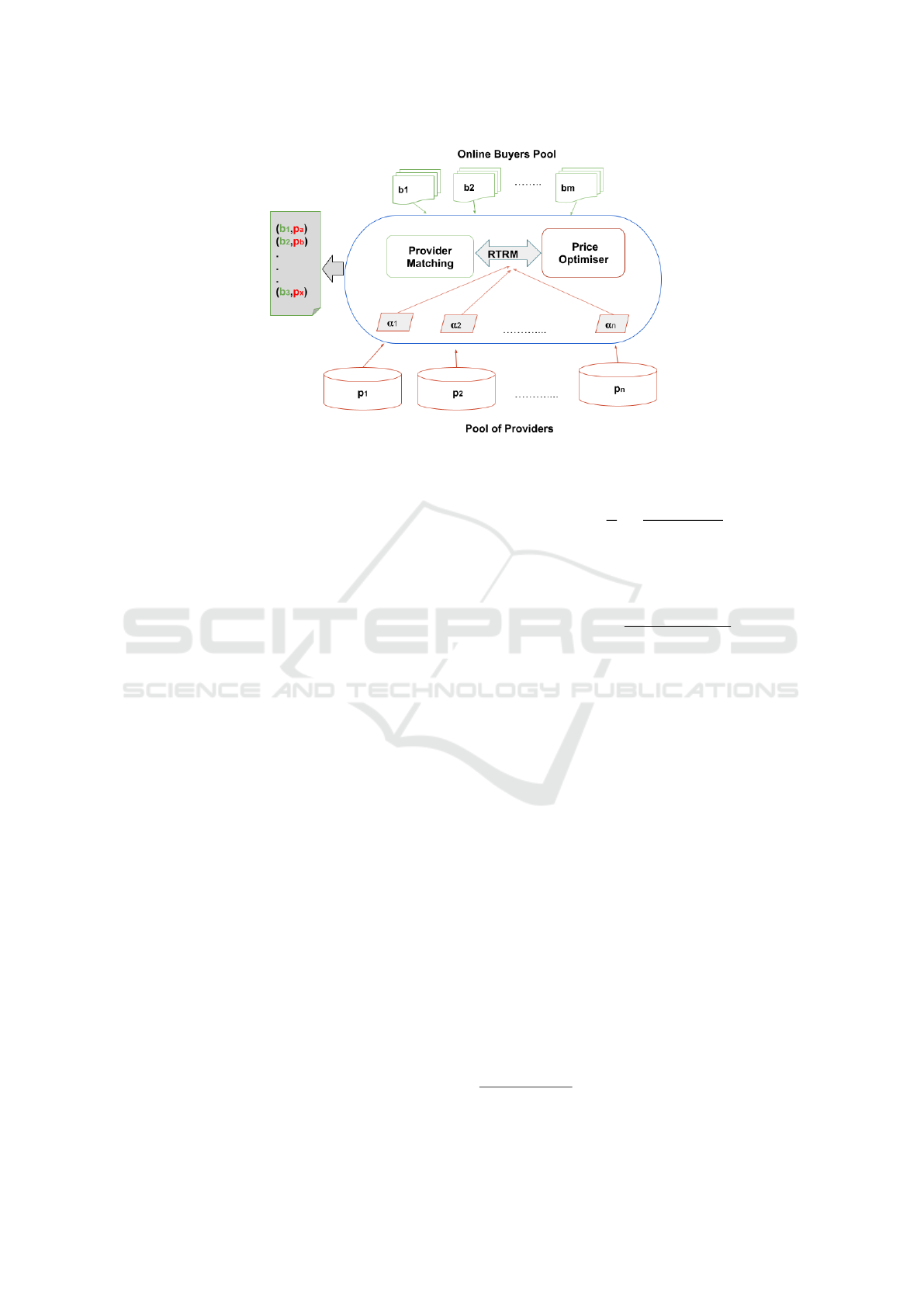
Figure 1: The proposed architecture auctioneer RTRM.
set of actions A, which represents the action space of
the agents. Finally, there is a set of rewards, which
the agent receives on acting. Therefore, we need to
define these three entities to formulate the resources
matching problem as MDP. Since this particular set-
ting involves multiple agents, it is called as Multi-
Agent MDP (MMDP).
In the proposed MMDP-based model, the joint
state-space S
t
represents the status of all the agents
bidding on behalf of providers at time-step t. In this
research, we formulate this joint state-space S
t
by
concatenating the status of all the agents for each re-
source request from buyers at time-step t. The state
of all the agents is updated every time-step t. And it
is reset at the end of the episode at t
max
. However, the
agents are not re-initialised from scratch at the end of
each episode. Also, the base prices (minimum sell-
ing price) of the resources are fixed by the providers.
The base price is denoted as bp
r
i
, ∀i ∈ P,r ∈ [1,l].
Also, these values are disclosed in a seal-bid fashion,
so the other providers are not aware of these values.
Then, upon receiving the reported base price bp
r
i
, the
agents optimise the base prices based on exclusive ad-
justment multipliers for each resource request. These
adjustment multipliers are the action values that are
computed using a proposed RL-based algorithm. In
specific, at time-step t for online buyer j ∈ B
t
, ad-
justment multiplier act
t
i, j
is computed ∀i ∈ P. Finally,
these adjustment multipliers are utilised to compute
the optimal offered price denoted as op
r
i, j
, in Equa-
tion (1):
op
r
i, j
= bp
r
i
×(1 + act
t
i, j
) ×Γ
i, j
) (1)
where Γ
i, j
represents the utilisation of the provider for
next T time-step based on the current requested pro-
file θ
θ
θ
t
and all the past allocated requests, computed
using Equation (2):
Γ
i, j
=
1
T
T
∑
a∈1
η( j,θ
θ
θ
t
) ∗A
i,t
B
b
(2)
where, A
i,t
represents availability of the resources at
time-step t, whereas, η(.) is the contest success func-
tion (Skaperdas, 1996) computed using Equation (3):
η( j,θ
θ
θ
t
) =
bid
j
/w
j
σ
∑
b∈θ
θ
θ
t
\j
bid
b
/w
b
σ
(3)
where, 0 < σ ≤ 1 represents the noise in the contest
in an auction paradigm, s.t. it captures the probability
of winning with increase in the budget values (Shen
et al., 2019). Intuitively, contest success function de-
notes the probability of a particular buyer getting al-
located based on their bid values as compared to other
buyers at time-step t. In this regard, the action space
for n agents are represented as Act ≡ {Act
1
,...Act
n
},
where Act
i
represents the action space for agent i,
where i ∈ P. Further, based on agent i’s pricing pol-
icy π
i
: s
t
i
7→ Act
i
, the action value act
t
i, j
∈ Act
i
is de-
termined. Then, after executing the set of chosen ac-
tions for all the agents (i.e allocating the requested re-
sources), the proposed MMDP model transfers to the
next state S
t+1
. This state change occurs based on the
transition function τ ∗S
t
×Act
1
×···×Act
n
7→ Ω(S
S
S),
where Ω(S
S
S) represents the set of probability distribu-
tions.
Toward this end, on behalf of providers, agents
are competing amongst each other to maximise their
revenue. In this context, the revenue of a certain
agent is maximised by winning the highest possible
number of auctions with higher values while simul-
taneously minimising its loss
1
and non-participation
1
Not able to participate because of unavailability of re-
sources
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
36

rates. Therefore, the reward function represents the
social welfare of the providers at the end of each al-
location. In this context, the episodic reward Rwd is
computed based on the allocation rule and then the
individual rewards rwd
i
are computed based on their
corresponding action values. In specific, at the end
of each episode, all the bidding agents receive re-
wards based on their chosen actions, such that; rwd
i
:
s
t
i
×Act
i
×···×Act
n
7→ Rwd. Furthermore, to reduce
the complexity by not updating the reward values af-
ter each auction; on the contrary, these reward values
are updated only at the end of each episode.
3 ONLINE PRICE
OPTIMISATION
The online price optimisation is performed by the
RTRM auctioneer on behalf of the potential providers.
In this regard, agents collect base-price from the po-
tential providers. Then on behalf of the providers,
communicate with the online pricing optimisation
module. Further, using the online pricing optimi-
sation module, RTRM optimises the base prices of
all the potential providers, aiming to maximise their
revenue. In this way, agents in RTRM platform dy-
namically updates the offered price of the requested
resources considering the limited volume of avail-
able resources. In this setting, the agent’s job is
to optimise the resource prices within the allocation
deadline. Therefore, the proposed online price opti-
misation algorithm adopts a reinforcement learning
scheme (Konda and Tsitsiklis, 2000) to handle the
presumed real-time scenario. The primary objective
of the proposed real-time pricing algorithm is to opti-
mise the offered base price.
In this context, the initial joint state S
0
of all the
agents represents the initial available resources. Each
agent aims to select a certain adjustment multiplier
(action) and leverage it to maximise its total expected
future revenues. These future revenues are discounted
by the factor γ each time step. In this regard, the future
reward at time-step t for agent i is denoted as Rwd
i
=
∑
t
max
t=0
γ
t
rwd
t
i
, where t
max
is the time-step at which the
bidding process ends, i.e., episode length. Then, the Q
function (Sutton et al., 1998) for agent i is computed
using Equation (4):
Q
π
i
(S,a
a
ac
c
ct
t
t) = E
π,τ
[
t
max
∑
t=0
γ
t
rwd
t
i
|S
0
= S,a
a
ac
c
ct
t
t] (4)
where, π = {π
1
,...,π
n
} is the set of joint-policies
of all the agents, and a
a
ac
c
ct
t
t = {act
(i, j)
,...,act
(i, j)
} de-
notes the list of bid multipliers (actions) for all the
agents. Further, the next state S
0
and the next action
a
a
ac
c
ct
t
t
0
are computed using Bellman equation as shown
in Equation (5):
Q
π
i
(S,a
a
ac
c
ct
t
t) = E
rwd,s
0
[rwd(S,act)+ γE
a
a
ac
c
ct
t
t
0
∼π
[Q
π
i
(S
0
,a
a
ac
c
ct
t
t
0
)]
(5)
On the other hand, the mapping function µ
i
maps
the shared state S ≡[A,θ
θ
θ
t
] of each agent i to a selected
action act
(i, j)
, based on Equation (6). This mapping
function µ represents the actor in the adopted actor-
critic architecture (Konda and Tsitsiklis, 2000). Fur-
ther, we derive Equation (7) from Equations (5) and
(6) as follows:
act
(i, j)
= µ(S) = µ
i
([A,θ
θ
θ
t
]) (6)
Q
µ
i
(S,act
(1, j)
,...,act
(n, j)
) = E
rwd,S
0
[rwd(S,act
(1, j)
,...,
act
(n, j)
) + γQ
µ
i
(S
0
,µ
1
(S
0
,...,µ
n
(S
0
))]
(7)
As shown in Equation (7), µ = {µ
1
,...,µ
n
} is the
set of the joint deterministic policies for all the agents.
In this regard, the goal of the proposed algorithm be-
comes to learn an optimal policy for each agent to
attain Nash equilibrium (Hu et al., 1998). In addition,
in such stochastic environments, each agent learns to
behave optimally by learning an optimal policy µ
i
,
which also depends on the optimal policies of the
other co-existing providers. Further, in the proposed
algorithm, the equilibrium of provider is achieved by
gradually reducing the Loss function Loss(ϑ
Q
i
) of the
critic Q
µ
i
with the parameter ϑ
Q
i
as denoted in Equa-
tions (8) and (9). In specific, in Equations (8) and (9),
µ
0
= {µ
0
1
(S
0
),...,µ
0
n
(S
0
)} represents the set of learning
policies of the target actors; each of these actors has a
delayed parameter ϑ
µ
0
i
.
Loss(ϑ
Q
i
) = (y −γQ
i
(S,act
(1, j)
,...,act
(n, j)
))
2
(8)
y = rwd
i
+ γQ
µ
i
(S
0
,µ
1
(S
0
),...,µ
n
(S
0
)) (9)
In this context, Q
µ
0
i
represents the learning pol-
icy of the target critic, which also has a correspond-
ing set of delayed parameters ϑ
Q
0
i
for each actor, and
(S,act
(1, j)
,...,act
(n, j)
,rwd
i
,S
0
) represents a transition
tuple that is pushed into a replay memory ∆. Further,
Reinforcement Learning-based Real-time Fair Online Resource Matching
37

each agent’s policy µ
i
, with parameters ϑ
µ
i
, is learned
based on Equation (10).
∇
ϑ
µ
i
J
≈
∑
j
∇
ϑ
µ
i
µ
i
([A, j])∇
act
q
(i, j)
Q
i
(S,act
(1, j)
,...,act
(n, j)
). (10)
Algorithm 1 depicts the novel online price optimi-
sation algorithm. The proposed algorithm takes three
inputs, which are (i) the buyers’ profile θ
θ
θ
t
, (ii) the
concatenated resource state for agents A
i
, ∀i ∈ D, and
(iii) the cumulative rewards from all the providers.
Then, the proposed algorithm provides adjustment
multipliers for each pair of agent i and buyer j ∈ θ
θ
θ
0
0
0
as output.
Algorithm 1: Online Price Optimisation.
1: Input: A, θ
θ
θ
t
,R
2: Output: a
a
ac
c
ct
t
t bid multipliers
3: Initialise: Q
i
(S,act
(1,b
j
)
,...,act
(n,b
j
)
|ϑ
Q
i
), replay
memory ∆
4: Initialise: actor µ
i
, target actor µ
0
i
5: Initialise: target network Q
0
with θ
Q
0
i
← θ
Q
i
,
6: ϑ
µ
0
i
← ϑ
µ
i
∀i ∈ n.
7: for episode = 1 to E do
8: Initialise: S
0
9: for t = 1 to T
max
do
10: for arriving θ
θ
θ
t
within T
max
, j ∈ θ
θ
θ
t
do
11: Get act
(i,b
j
)
using Equation (6)
12: Calculate Γ using Equation (2)
13: Get rwd
t
i
, where i ∈ n and A
i
: ∀i ∈ D
14: end for
15: rwd
i
=
∑
n
i=1
∑
T
t=1
rwd
t
i
rewards within
T
max
16: Push (S,act
(i,b
j
)
,rwd
i
,S
0
) into ∆ S’
denotes the next state
17: S
0
← S
18: for agent i = 1 to n do
19: Sample mini batch (S, act
(1,b
j
)
, . . . ,
act
(1,b
j
)
, rwd
i
, S
0
) from ∆
20: Update critic using Equation (8)
21: Update actor using Equation (10)
22: Update target network: θ
0
←τθ+(1−
τ)θ
23: end for
24: end for
25: end for
In this regard, these trained agents submit the of-
fered price for every resource requests on behalf of
their corresponding provider. Then, based on the ob-
tained optimal offered bids, provider matching ap-
proach matches the requested resources to an appro-
priate provider, as discussed in the following section.
4 PROVIDER MATCHING
In this subsection, we present the proposed fairness
based provider matching mechanism. In this mecha-
nism, the auctioneer matches each buyer’s request to
a suitable provider from a pool of available providers.
In this context, firstly upon receiving buyers profile
θ
θ
θ
t
at time-step t, based on the bid bid
b
∀b ∈ θ
θ
θ
t
,
the appropriate preference of the buyer is estimated
based on a novel multi preference factor. Specifically,
the multi-preference factor considers different quality
preferences for the buyers while matching their re-
quests with an appropriate provider. In this context,
the set of q quality preference parameters of provider
p ∈ P is denoted as K
p
≡ (k
p
1
,k
p
2
,...k
p
q
), for example:
k
p,utilisation
represents the value of the quality prefer-
ence parameter utilisation. Further, based on these
values, we compute preference factor υ(p, b) ∀p ∈ P
and ∀b ∈ θ
θ
θ
t
using Equation (11).
υ(p,b) =
1
|K|
∑
q∈K
N(k
p
q
)
√
bid
b
(11)
where, |K| denotes the total number of quality prefer-
ence parameters and N(k
p
q
) is the normalised value of
the quality parameter q, which is computed using sim-
ple additive weighting mechanism (Zeng et al., 2003)
as follows:
N(p,q) =
(k
re f
q
−k
p
q
)×ψ
k
max
q
−k
min
q
, if k
max
q
−k
min
q
6= 0;
1, if k
max
q
−k
min
q
= 0.
(12)
wherein, ψ = 1, if the higher value of the quality pa-
rameter is favourable for matching or else ψ = −1.
For example, ψ = 1 for utilisation of the provider,
whereas ψ = −1 for offered selling price. In this re-
gard, we compute the preference factor for each buyer
at time-step t for all the available providers. Then,
computes the preference factor for each pair of buy-
ers and providers. Finally, the resource request from
buyer b is matched with a provider if the highest pref-
erence factor is within the buyer’s budget. In specific,
the winning provider w
b
for buyer b ∈ θ
θ
θ
t
is computed
using Equation (13).
w
b
≡ argmax
p∈P
υ(p,b) ∗1(p,b) (13)
where, 1(.) is the indicator function, s.t., 1(p, b) = 1
if b’s budget is within the offered price of the winning
provider, i.e.,
∑
i∈[1,l]
k
b
i
∗p
i
p,b
≤bid
b
. Finally, in order
to observe truthfulness (Myerson, 1981), we adopt the
general second price (Krishna, 2009). Therefore, in
this context, the payment is computed using Equation
(14):
pay(w
b
,b) ≡
∑
i∈[1,l]
r
b
i
∗op
i
p
0
,b
(14)
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
38

Table 1: Types of providers.
# Type Processing(MIPS) Memory (MBs) Storage(MBs) Bandwidth
d
1
6950 12032 26000 8000
d
2
3450 6144 84000 2650
d
3
4700 7168 48000 1750
d
4
7500 3840 30000 4000
d
5
6100 10752 60000 4700
d
6
4900 8704 47000 3600
d
7
3700 6144 36000 3200
where p
0
≡ argmax
p∈P\w
b
υ(p,b) ∗1(p,b). In this re-
gard, all the online buyers’ requests in θ
θ
θ
t
are matched
with the appropriate available providers. In the next
section, we present the results of the extensive exper-
iments that were conducted to evaluate the proposed
online resource matching approach for open markets.
5 EXPERIMENTAL SETUP AND
RESULTS
This section presents the experimental results and
evaluations performed using Google cluster trace data
(Chen et al., 2010; Buchbinder et al., 2007) to inves-
tigate the performance of the novel online resource
matching approach. In the experiments setting, we
set the hyper-parameters as: (discount factor) λ = 0.9;
learning-rate= 3e
−4
; σ = 0.5 as these values gave
comparatively better results. Finally, we compare
the novel RTRM algorithm with the following bench-
marks:
• Simple Allocation: the combinatorial double
auction resource allocation approach (CDARA)
(Samimi et al., 2016). This approach implements
a fixed pricing strategy, wherein the provider with
the lowest bid is the winner.
• Dynamic Allocation: the combinatorial auction-
based approach based on (ICAA) (Kong et al.,
2015). This approach implements a demand-
based dynamic pricing strategy. Also, the
provider with the lowest bid is the winner.
5.1 Experimental Setup
In this experimental setting, we target building an on-
line resource allocation among the pool of seven in-
dependent providers. Configurations of all the seven
providers are listed in Table 1. In this context, we
sample the resource requests for all the online buy-
ers as extracted from the task events tables of Google
Cluster Trace (Wilkes, 2011). Further, the buyers’
bid values corresponding to their resource requests
are sampled from the uniform distribution [150,500].
Similarly, we preset the base prices of each of the
resources by uniformly sampling from a predefined
uniform distribution. In specific, we choose the base
prices for per unit of Processing, Memory Usage
and Storage Usage from [120, 150]$, [10,70]$, and
[40,100]$, respectively. Further, the time step t at
which buyer’s job is sampled from the dataset is
buyer’s arrival-time, whereas its execution-length and
deadline are set using two random generators which
take values [1,24] time-steps and [1,12] time-steps,
respectively. Towards this end, with such an exper-
imental setting, we initially train the RTRM approach
for 12000 episodes, each of length t
max
= 2000 time-
steps. All the approaches are implemented in Python
3 and the experiments are performed on Intel Xeon
3.6GHz 6 core processor with 32 GB RAM. Also, we
consider three quality preference parameters, namely
price, resource utilisation and average waiting time.
We also set the maximum number of online buyers at
each time step, i.e., m = 24.
There are two primary objectives of this research:
(1) to evaluate the performance of the providers and
buyers in the market, and (2) to evaluate the bidder
drop in the market. In this context, the performance of
the providers and buyers, measured in terms of their
utilities. Computed using Equation (15) and Equation
(16), as follows:
U(p) =
∑
∀b∈B
t
pay(p,b) −
∑
∀r
bp
r
p
(15)
U(b) = bid
b
−pay(.,b) (16)
Further, in order to evaluate the bidder (buyer)
drop in the market, similar to (Hassanzadeh et al.,
2016), we also compute buyer’s drop based on the
number of times a particular buyer looses in each
episode. Specifically, we define that, a particular
buyer drops from the market, if it looses five times
in consecutive auction episodes.
Reinforcement Learning-based Real-time Fair Online Resource Matching
39
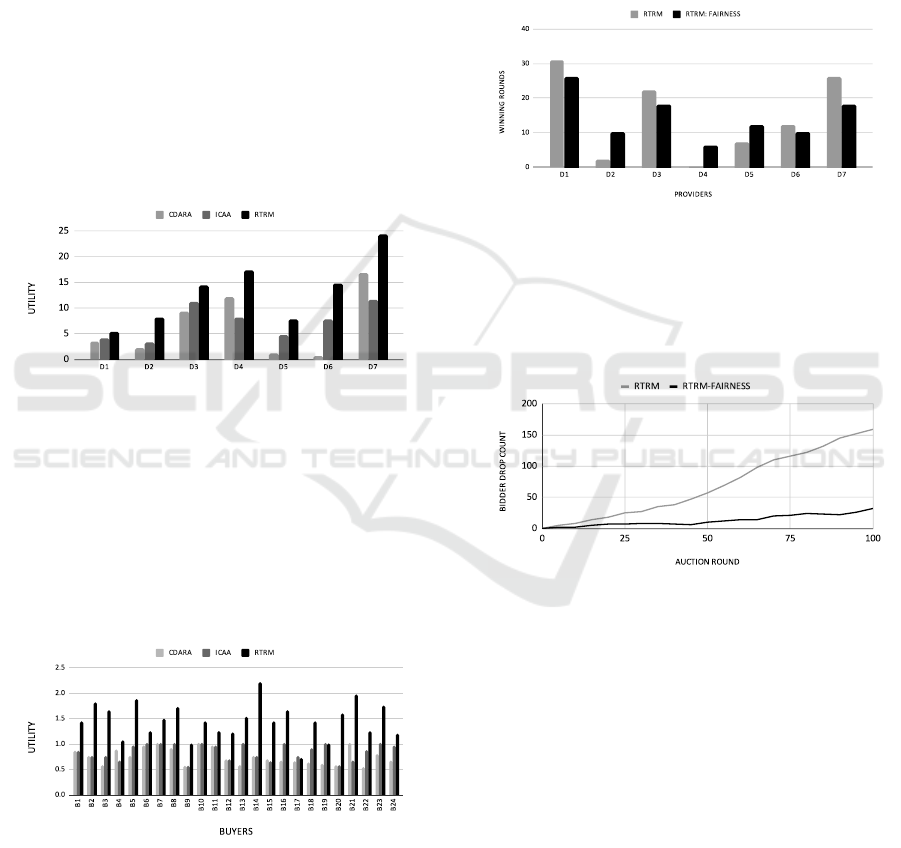
5.2 Evaluation
In this section, we would evaluate and discuss the
performance of the novel RTRM mechanism based
on different characteristics. To begin with, Figure
2, depicts the average episodic utility of the seven
providers for 12000 episodes. From Figure 2, it can
be established that the novel RTRM maximises the
utility of all the providers in the open market. One
of the interesting observations here is that certain
providers with negligible utilities in the benchmarks
have higher utilities in the novel RTRM algorithm.
For instance, provider d5 and provider d6, have the
least utility in CDARA mechanism, however it almost
tripled in RTRM. This shows that introduced fairness
mechanisms help the lowest-performing providers to
enhance their utilities. Overall, for all the providers,
the utilities increased in RTRM as compared to the
other two benchmarks.
PROVIDERS
Figure 2: The utilities of the providers.
Further, Figure 3 depicts the average episodic util-
ity of the 24 buyers who arrived at each time step.
From Figure 3, it is evident the buyers in the proposed
RTRM approach pay marginally less prices, i.e., their
utility is higher as compared to other benchmarks.
Specifically, the utilities of the buyers in RTRM mech-
anism is increased by at least 40% as compared to the
other two mechanisms.
Figure 3: The utilities of the buyers.
Furthermore, to exclusively evaluate the impact
of fairness mechanism on winning of the providers
in the market in RTRM mechanism, we evaluate the
RTRM mechanism with and without fairness mecha-
nism. Figure 4 depicts the episodic average cumula-
tive sum of number of allocations in 2000 episodes
each of length (rounds) t
max
= 100. From the fig-
ure, it is evident unlike RTRM, providers in RTRM-
Fairness wins at least once in the episode. In specific,
provider D4 has zero wins in RTRM. This shows that
the fairness mechanism ensures the fairness amount
the provider’s winning. Some providers have compar-
atively fewer wins in RTRM-Fairness. However, this
ensures social welfare in the market by giving chance
to non-performing lesser competitive providers.
Figure 4: Impact of fairness on providers win.
Towards the end, we evaluate the bidder drop in
the market, by comparing the total number of buyers
dropped in RTRM and RTRM-Fairness. Figure 5 il-
lustrates the average cumulative sum of the number
of buyers drops.
Figure 5: The utilities of the buyers.
Overall, from Figure 5, we can conclude that num-
ber of drops gradually increases with the number of
episodes. However, drop-in RTRM is exponential
more as compared to RTRM-Fairness. This means the
fairness mechanism improves resource utilisation in
the market. Briefly, from the above results and discus-
sions, the proposed approach outperforms the bench-
marks. Such that, the proposed algorithm maximises
the utility of the participants. Also, minimises the bid-
der drop problem in the market based on a novel fair-
ness mechanism.
6 CONCLUSION
In this paper, we introduce a real-time resource
matching mechanism for online open markets. In
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
40

such an open market setting, the proposed RTRM
matches the resource requests from the buyers to
providers using a double-auction paradigm. Specif-
ically, RTRM implements a multi-agent environment
that optimises the offered selling prices for all the in-
dependent providers based on the online pricing algo-
rithm. On the other hand, RTRM implements a fair
matching algorithm to dynamically match the buy-
ers’ resource demands in the open market. In this re-
gard, the proposed approach enables both participants
to maximise their utilities and the participation rate.
Besides, the proposed mechanism enhances resource
utilisation to minimise the bidder drop problem based
on the novel fairness mechanism. The experimental
results evaluate the efficiency of the RTRM by com-
paring the utilities of both the participants. In the fu-
ture, we aim to develop a mechanism that encourages
cooperative behaviour in such a competitive market
by designing a resource sharing mechanism among
the different providers to fulfil resource requests.
REFERENCES
Buchbinder, N., Jain, K., and Naor, J. S. (2007). Online
primal-dual algorithms for maximizing ad-auctions
revenue. In European Symposium on Algorithms,
pages 253–264. Springer.
Cai, H., Ren, K., Zhang, W., Malialis, K., Wang, J., Yu, Y.,
and Guo, D. (2017). Real-time bidding by reinforce-
ment learning in display advertising. In Proceedings
of the Tenth ACM International Conference on Web
Search and Data Mining, pages 661–670. ACM.
Charpentier, A., Elie, R., and Remlinger, C. (2021). Rein-
forcement learning in economics and finance. Com-
putational Economics, pages 1–38.
Chen, Y., Ganapathi, A. S., Griffith, R., and Katz, R. H.
(2010). Analysis and lessons from a publicly available
google cluster trace. EECS Department, University of
California, Berkeley, Tech. Rep. UCB/EECS-2010-95,
94.
Fink, A. M. (1964). Equilibrium in a stochastic n-person
game. Journal of science of the hiroshima university,
series ai (mathematics), 28(1):89–93.
Hassanzadeh, R., Movaghar, A., and Hassanzadeh, H. R.
(2016). A multi-dimensional fairness combinatorial
double-sided auction model in cloud environment. In
2016 8th International Symposium on Telecommuni-
cations (IST), pages 672–677. IEEE.
Hu, J., Wellman, M. P., et al. (1998). Multiagent rein-
forcement learning: theoretical framework and an al-
gorithm. In ICML, volume 98, pages 242–250. Cite-
seer.
Konda, V. R. and Tsitsiklis, J. N. (2000). Actor-critic algo-
rithms. In Advances in neural information processing
systems, pages 1008–1014.
Kong, Y., Zhang, M., and Ye, D. (2015). An auction-based
approach for group task allocation in an open network
environment. The Computer Journal, 59(3):403–422.
Krishna, V. (2009). Auction theory. Academic press.
Kumar, D., Baranwal, G., Raza, Z., and Vidyarthi, D. P.
(2019). Fair mechanisms for combinatorial reverse
auction-based cloud market. In Information and Com-
munication Technology for Intelligent Systems, pages
267–277. Springer.
Lee, C., Wang, P., and Niyato, D. (2013). A real-time group
auction system for efficient allocation of cloud inter-
net applications. IEEE Transactions on Services Com-
puting, 8(2):251–268.
Li, X., Ding, R., Liu, X., Liu, X., Zhu, E., and Zhong, Y.
(2016). A dynamic pricing reverse auction-based re-
source allocation mechanism in cloud workflow sys-
tems. Scientific Programming, 2016:17.
Murillo, J., Mu
˜
noz, V., L
´
opez, B., and Busquets, D. (2008).
A fair mechanism for recurrent multi-unit auctions. In
German Conference on Multiagent System Technolo-
gies, pages 147–158. Springer.
Myerson, R. B. (1981). Optimal auction design. Mathemat-
ics of operations research, 6(1):58–73.
Prasad, G. V., Prasad, A. S., and Rao, S. (2016). A combi-
natorial auction mechanism for multiple resource pro-
curement in cloud computing. IEEE Transactions on
Cloud Computing, 6(4):904–914.
Samimi, P., Teimouri, Y., and Mukhtar, M. (2016). A com-
binatorial double auction resource allocation model
in cloud computing. Information Sciences, 357:201–
216.
Shen, W., Feng, Y., and Lopes, C. V. (2019). Multi-winner
contests for strategic diffusion in social networks. In
Proceedings of the AAAI Conference on Artificial In-
telligence, volume 33, pages 6154–6162.
Skaperdas, S. (1996). Contest success functions. Economic
theory, 7(2):283–290.
Sutton, R. S., Barto, A. G., et al. (1998). Introduction to
reinforcement learning, volume 2. MIT press Cam-
bridge.
Toosi, A. N., Vanmechelen, K., Khodadadi, F., and Buyya,
R. (2016). An auction mechanism for cloud spot mar-
kets. ACM Transactions on Autonomous and Adaptive
Systems (TAAS), 11(1):2.
Wilkes, J. (2011). More Google cluster data. Google re-
search blog. Posted at http://googleresearch.blogspot.
com/2011/11/more-google-cluster-data.html.
Yuan, S., Wang, J., and Zhao, X. (2013). Real-time bidding
for online advertising: measurement and analysis. In
Proceedings of the Seventh International Workshop on
Data Mining for Online Advertising, page 3. ACM.
Zaman, S. and Grosu, D. (2013). Combinatorial auction-
based allocation of virtual machine instances in
clouds. Journal of Parallel and Distributed Comput-
ing, 73(4):495–508.
Zeng, L., Benatallah, B., Dumas, M., Kalagnanam, J., and
Sheng, Q. Z. (2003). Quality driven web services
composition. In Proceedings of the 12th interna-
tional conference on World Wide Web, pages 411–421.
ACM.
Reinforcement Learning-based Real-time Fair Online Resource Matching
41
