
Upper Confident Bound Fuzzy Q-learning and
Its Application to a Video Game
Takahiro Morita
1
and Hiroshi Hosobe
2
1
Graduate School of Computer and Information Sciences, Hosei University, Tokyo, Japan
2
Faculty of Computer and Information Sciences, Hosei University, Tokyo, Japan
Keywords: Machine Learning, Fuzzy Q-learning, UCB Algorithm, Video Game.
Abstract: This paper proposes upper confident bound (UCB) fuzzy Q-learning by combining fuzzy Q-learning and the
UCBQ algorithm and applies it to a video game. The UCBQ algorithm improved the action selection method
called the UCB algorithm by applying it to Q-learning. The UCB algorithm selects the action with the highest
UCB value instead of a value estimate. Since the UCB algorithm is based on the premise that any unselected
actions are selected and value estimates are obtained, the number of unselected actions becomes small, and it
is able to prevent local optimal solutions. The proposed method aims to promote the efficiency of learning by
reducing unselected actions and preventing the Q value from becoming a local optimal solution in fuzzy Q-
learning. This paper applies the proposed method to a video game called Ms. PacMan and presents the result
of an experiment on finding optimum values in the method. Its evaluation is conducted by comparing the
game scores with the scores obtained by a previous fuzzy Q-learning method. The result shows that the
proposed method significantly reduced unselected actions.
1 INTRODUCTION
Recently, there has been a great deal of interest in
artificial intelligence (AI) due to the increase in data
volume and the development of computing and
storage technologies. Research on machine learning,
especially image processing and voice processing
using deep learning, has been increasing, and the
technology is used in familiar places such as early
detection of cancers, automatic driving of
automobiles, and automatic translation of texts.
Research on game AI by machine learning is also
being actively conducted. In 2017, Ponanza, AI of
Shogi (Japanese chess), won a professional player. In
the same year, AlphaGo (Silver, et al., 2016), AI of
another board game Go, also won professional
players. In addition, incomplete board games such as
The Werewolves of Millers Hollow (Katagami, et al.,
2018) and video games such as Tetris and Space
Invaders have been widely studied in the field of AI.
For example, general-purpose AI using deep Q-
learning was created (Mnih V. , et al., 2013); it
automatically generated features and evaluation
functions for simple games such as Pong and
Breakout by using only game screens.
Reinforcement learning, a kind of machine
learning, is frequently used for video game agents. It
is a method of learning the most profitable behavior
for each environment by trial and error. Q-learning
(Watkins & Dayan, Q-Learning, 1992) is one of the
mainstream reinforcement learning methods. It gives
value estimates called Q values to a discrete set of
states and actions. Fuzzy Q-learning (Glorennec,
1994) deals with continuous spaces in Q-learning. It
is used for applications such as robot control that
cannot be treated discretely (Gu & Hu, 2004) (Hu, Li,
Xu, & Xu, 2015).
However, there is a problem in Q-learning. It
always selects the action with the largest Q value.
Therefore, it might generate local optimal solutions
by continuously selecting the actions with the largest
Q values, which will make learning not progress. To
solve this problem, action selection algorithms are
generally used. For example, the ε-greedy algorithm
(Watkins, Learning From Delayed Rewards, PhD
Thesis, 1989) and the upper confident bound (UCB)
algorithm (Auer, Cesa-Bianchi, & Fischer, 2002) are
popular action selection algorithms.
In this paper, we propose UCB fuzzy Q-learning
that combines fuzzy Q-learning and the UCBQ
algorithm (Saito, Notsu, & Honda, 2014) and apply it
454
Morita, T. and Hosobe, H.
Upper Confident Bound Fuzzy Q-learning and Its Application to a Video Game.
DOI: 10.5220/0010835700003116
In Proceedings of the 14th International Conference on Agents and Artificial Intelligence (ICAART 2022) - Volume 3, pages 454-461
ISBN: 978-989-758-547-0; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

to a video game. This method aims to promote the
efficiency of learning by reducing unselected actions
and preventing the Q value from becoming a local
optimal solution in fuzzy Q-learning. The UCBQ
algorithm is an improved method that allows the
action selection method called the UCB algorithm
(Auer, Cesa-Bianchi, & Fischer, 2002) to be applied
to Q-learning. The UCB algorithm selects the action
with the highest UCB value instead of a value
estimate. In addition, in the UCB algorithm, an
unselected action is always selected, and the value
estimate is obtained, which largely reduces the
number of unselected actions in any state. In this
paper, we apply the proposed method to a video game
called Ms. PacMan, and show the changes of
optimum numerical values for the parameters used in
the algorithm. We also compare the scores of our
method with those of a previous fuzzy Q-learning
method (DeLooze & Viner, 2009). The result of the
experiment shows that the unselected actions were
significantly reduced by our method.
2 MS. PACMAN
Ms. PacMan is a video game that was produced in the
United States of America, based on PacMan
previously released by NAMCO in Japan in 1980.
The purpose of this game is to control PacMan
(player) to collect pills and power pills on a map and
earn a high score while avoiding enemies called
ghosts (Figure 1). The scores of each pill and each
power pill are 10 and 50 respectively. There are
several power pills placed on the map, and PacMan
can take a power pill to temporarily neutralize and
attack ghosts and earn a higher score. Especially, by
attacking ghosts continuously, the player can get
Figure 1: Screen of Ms. PacMan.
increased scores such as 200, 400, 800, and 1600
points. Therefore, the key to aiming for a high score
is to get the increased scores.
In the original PacMan of NAMCO, when a ghost
finds PacMan, it acts deterministically, which
allowed establishing AI-based strategies. By contrast,
in Ms. PacMan, ghosts act randomly with a certain
probability, which increases the difficulty in
establishing AI-based strategies. Therefore,
international conferences such as IEEE CEC held
competitions using Ms. PacMan.
3 RELATE WORK
Many studies on game AI have been conducted.
Among them, game AI using fuzzy Q-learning has
been proposed. For example, a football agent based
on fuzzy Q-learning was proposed (Nakajima, Udo,
& Ishibuchi, 2003). It treated continuous state and
action spaces as fuzzy sets, and calculated Q values
from given environments using fuzzy inference to
learn to intercept paths in football. It obtained state
and action spaces by using internal information such
as the relative velocity and relative position of a ball
and other objects. Fuzzy Q-learning was applied to a
car racing game (Umano, Tachino, & Ise, 2013). In
this game, the player competes for points while
aiming for targets placed on a two-dimensional plane.
It used three continuous attributes, i.e., the distance to
a target, the angle to a target, and the speed of a car
agent, as the state space, and additional rewards
depending on the direction of the car agent when
passing the target. By giving a direction reward, it
enabled the car agent to pass with a smaller number
of steps. The direction reward is given when the car
agent passes the current target and the next target is
positioned ahead. This allowed the car agent to learn
the route to the goal smoothly.
Research on game AI for playing a video game,
Ms. PacMan, also has been conducted. DeLooze et al.
(DeLooze & Viner, 2009) made it possible to
discretely capture continuous states by using a fuzzy
state space whose attributes are the distances between
PacMan and the closest enemy, pill, and power pill,
and applied it to Q-learning. To obtain the fuzzy state
space, they acquired the position of each object by
screen capture. They also used the Warshall-Floyd
algorithm to find the shortest path to the closest pill
and power pill. Since they did not use the action
selection method, learning with the highest Q value
was always performed, which might cause a situation
where learning did not proceed. Microsoft's AI (van
Senjen, et al., 2017) had achieved the highest score
Upper Confident Bound Fuzzy Q-learning and Its Application to a Video Game
455

for Ms. PacMan. It used an architecture called Hybrid
Reward Architecture, and consisted of more than 150
single-purpose agents and the top agents that made
comprehensive decisions from the information
obtained from the single-purpose agents. It learned to
improve the play skills of Ms. PacMan by linking
these multiple AI agents in parallel. The single-
purpose agents were rewarded according to one
condition, and multiple conditions were distributed to
the top agents. In the case of Ms. PacMan, some
agents were rewarded for eating a pill, and other
agents are rewarded for being able to keep a distance
from a ghost. The top agents received feedback from
these rewards and the single-purpose agents and made
decisions using weighted averages.
4 PRELIMINARIES
4.1 Q-learning
Q-learning was proposed as a machine learning
method (Watkins & Dayan, Q-Learning, 1992). This
method learns by updating the value estimation
function 𝑄(𝑠,𝑎), which is an index of what kind of
action 𝑎 the agent should take under a certain state 𝑠.
The agent receives a reward according to the result of
the action, and updates 𝑄(𝑠,𝑎) using the reward. The
update equation is as follows:
𝑄
(
𝑠,𝑎
)
(
1−𝛼
)
𝑄(𝑠,𝑎) + 𝛼𝑅(𝑠,𝑎,𝑠
)
+ 𝛾 max 𝑄(𝑠
,𝑎
)
where 𝛼 is a learning rate and 𝛾 is a discount rate. The
term 1−𝛼 represents the current Q value, and the
term 𝛼 represents the value used in learning. This
equation causes a higher reward to make a higher
updated Q value. In addition, the action with the
highest Q value in the current state is selected.
Therefore, if the Q value of one action becomes
higher than the other Q values in a certain state, the
same action will continue to be selected unless the Q
value is lowered by a penalty. Even if there is another
optimal action, it cannot be learned, and the learning
will be delayed.
4.2 Fuzzy Q-learning
Fuzzy Q-learning was proposed (Glorennec, 1994).
The state and action spaces of Q-learning are treated
as fuzzy sets and expressed by the membership
functions. The membership value obtained from the
membership function is used to calculate the Q value
to be able to handle continuous state and action spaces
in Q-learning. In the state space, the label with the
highest membership value is obtained as the attribute
of the state. As an example, the distance between two
objects is divided into three, “near”, “middle”, and
“far”, and is expressed by the membership function of
the fuzzy set in Figure 2.
Figure 2: Fuzzy set.
For example, if the distance between two objects
is 150, the “middle” with the highest membership
value is obtained as an attribute. This attribute is
obtained from multiple fuzzy sets, and the state is
determined by the combination of the attributes.
Multiple Q values are updated based on the degree of
agreement 𝜇 of the state together with the reward
obtained by the action. The Q value is updated by the
following equation:
𝑄
(
𝑠,𝑎
)
(
1−𝜇
𝛼
)
𝑄(𝑠,𝑎) + 𝜇
𝛼𝑅(𝑠,𝑎,𝑠
)
+ 𝛾 max 𝑄(𝑠
,𝑎
)
Fuzzy Q-learning was applied to Ms. PacMan
(DeLooze & Viner, 2009). Since the action space is
discrete, only the state space was treated as a fuzzy set.
As a result, it was able to perform learning with fuzzy
sets, but it could not sufficiently learn with this method
because there were many combinations of states and
actions that did not occur during the learning. The
reason why the learning was hindered was probably
that the actions with the highest Q values were pursued
due to the characteristics of Q-learning.
4.3 UCB Algorithm
The UCB algorithm (Auer, Cesa-Bianchi, & Fischer,
2002) uses UCB values instead of estimated Q values
in Q-learning and selects the action with the highest
UCB value. Another feature is that if there is an
unselected action in a certain state, it is always
selected, and a value estimate is obtained. The UCB
value is expressed by the following formula:
𝑈𝐶𝐵(𝑠,𝑎)𝑄(𝑠,𝑎) + 𝐶
ln
(
𝑛
)
𝑁
(
𝑠,𝑎
)
where 𝑛 is total number of selections in state 𝑠 ,
𝑁(𝑠,𝑎) is the number of selections of action 𝑎 in
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
456

state 𝑠 , and 𝐶 is a constant that determines the
tendency of the search. A larger value of 𝐶 makes the
search more aggressive. By contrast, a smaller value
of 𝐶 makes it more important to utilize the learning.
4.4 ε -Greedy Algorithm
The ε-greedy algorithm (Watkins, Learning From
Delayed Rewards, PhD Thesis, 1989) in Q-learning
basically selects the action with the highest Q value,
but randomly selects the action with a search rate of
𝜀 (0 ≤ 𝜀 ≤ 1). The advantage of the ε-greedy
algorithm is that it improves the efficiency of Q-
learning by alleviating the limitation that it does not
select any action once evaluated as a low value. The
drawback of the ε-greedy algorithm is that, when
making an action selection with a probability of 𝜀, it
behaves randomly regardless of the action value. This
causes the problem that the probability of selecting
the action that seems to be the worst in the action
selection and the probability of selecting the action
that seems to be the most suitable at present are the
same with a probability of 𝜀.
4.5 UCBQ Algorithm
The UCBQ algorithm applies the UCB algorithm to
Q-learning (Saito, Notsu, & Honda, 2014). Problems
arise if the UCB algorithm is simply incorporated into
Q-learning; since the UCB algorithm always selects
an unselected action, there is a possibility that it will
continue to select an action that cannot progress to the
next state. On the other hand, Saito et al. used the ε-
greedy algorithm to randomly select actions with a
constant probability, which solved the problem and
allowed the UCB algorithm to be applied to Q-
learning. They showed that the learning efficiency
was significantly improved by performing an active
search from the early stage of learning, as compared
with the ε-greedy algorithm shown in Subsection 4.4.
5 PROPOSED METHOD
In this paper, we propose UCB fuzzy Q-learning by
combining the UCB Q-learning and fuzzy Q-learning.
This method significantly reduces unselected actions,
and makes learning proceed efficiently. We adopt
UCB fuzzy Q-learning for the following two reasons.
First, since there were few studies that applied fuzzy
Q-learning to the AI of video games, we think that it
has potential for improvement. Second, since the deep
Q-network (DQN) (Mnih V. , et al., 2015) is currently
widely used for the AI of video games, we think that
focusing on another method enables us to make a
contribution to the field.
UCB fuzzy Q-learning is performed by repeating
the following steps:
1. Obtain a fuzzy state from the distances between
PacMan (player) and a ghost (enemy), a pill, and
a power pill;
2. With a probability of 𝜀, select and execute the
action with the highest UCB value in the fuzzy
state, and otherwise randomly select an action;
3. Update the Q value from the numerical value of
the distance and the reward for the result of the
action.
procedure UCB fuzzy Q-learning
1 begin
2
initialize 𝑄,𝑈𝐶𝐵,𝑁
,∀𝑠∈𝑆,∀𝑎∈𝐴
3
for cycle ← 1 to numEpisode
4
initializeState
(
𝑠
)
5 while not done do
6
if rand()>𝜀
7
𝑎←argmax UCB
(
𝑠,∶
)
8 else
9
𝑎←selectRandomly
10 end
11
𝑠′←fuzzyState(pacman, ghost,
pill, powerpill
)
12
𝑅←GetReward(𝑠,𝑎)
13
for cycle ← 0 to len(Q)
14
𝜇
←(membership(pacman, ghost)
+membership(pacman, pill)
+membership(pacman,
powerpill))/3
15
𝑄
(
𝑠,𝑎
)
←
(
1−𝜇
𝛼
)
𝑄
(
𝑠,𝑎
)
+𝜇
𝛼𝑅+𝛾 max
∈
(
)
𝑄
(
𝑠
,𝑎
)
16 end
17
𝑁
←𝑁
+1
18
𝑈𝐶𝐵
(
𝑠,𝑎
)
←𝑄
(
𝑠,𝑎
)
+𝐶
ln∑𝑁
(
𝑠,:
)
𝑁
(
𝑠,𝑎
)
19
𝑠←𝑠′
20 end
21 end
22 end
Figure 3: UCB fuzzy Q-learning.
Figure 3 shows the proposed method in pseudo
code. The 4th to 20th lines indicate the UCB fuzzy Q-
learning algorithm for learning one episode. An
episode in Ms. PacMan means the period from the start
to the end of a game. The 5th to 20th lines repeat
learning until the Boolean variable “done”, which
indicates whether the game is over, becomes true.
From the 6th to the 10th line, the action that has the
maximum value of UCB is selected with a probability
of 𝜀 , and an action is randomly selected with a
probability of 1−𝜀. This is the important feature of
the UCBQ algorithm that prevents continuous
Upper Confident Bound Fuzzy Q-learning and Its Application to a Video Game
457

selection of non-proceeding actions. At the 11th line,
after the action is executed, the next state 𝑠′ is
obtained; it is the combination of the attributes with the
highest membership value in the fuzzy set of the
distances between PacMan and ghosts, pills, and power
pills. From the 13th to the 16th line, it is possible to
treat a fuzzy state space (which is continuous) as a
discrete state space by updating multiple Q values
using the membership value. At the 14th line, the
membership value is obtained from the fuzzy set
according to the attribute of the corresponding state 𝑠′,
and the average is computed to obtain the value 𝜇
. At
the 15th line, the Q value for action 𝑎 in the
corresponding state is updated by 𝜇
, and reward 𝑅 is
obtained by the action. When the degree of coincidence
𝜇
is 0, the Q value does not change. At the 17th line,
the value of 𝑁
corresponding to action 𝑎, which is
selected in state 𝑠, is updated. This records how many
times that action 𝑎 is selected in state 𝑠. At the 18th
line, the UCB value is updated using 𝑁
value and the
updated Q value. Then the next state 𝑠′ is changed to
the current state 𝑠, the loop returns to the beginning,
and the learning is continued.
6 IMPLEMENTATION
6.1 Ms. PacMan
To implement Ms. PacMan, we used OpenAI Gym
(Brockman, et al., 2016). OpenAI Gym is a platform
for the development and evaluation of enhanced
algorithms provided by OpenAI. It provides various
reinforcement learning environments such as inverted
pendulum and video games including Ms. PacMan. In
OpenAI Gym, it is possible to return the contents of
the environment after the action to a variable by using
the function env.step(action). For example, in
Ms. PacMan, the RGB value of each pixel can be
obtained as an array of numbers such as (210, 160, 3).
When a score is obtained, its value can be returned as
a variable, and whether the game is over can be
returned as a Boolean variable. In addition, actions
that can be selected are defined by numbers. These
functions make it easy to develop algorithms for
reinforcement learning.
6.2 Position Coordinates of Objects
OpenCV was used to grasp the positions of PacMan,
ghosts, pills, and power pills on the map. OpenCV is
a library for image processing, image analysis, and
machine learning functions. Since Ms. PacMan of
OpenAI Gym has clear colors, the screen image can
be processed easily. In the implemented program, the
position coordinates of an object were grasped as
follows:
1. Convert the RGB values of the screen to the
HSV values;
2. Extract the HSV values of the object whose
position coordinates are needed;
3. Extract the outline of the object from the screen
where the colors are binarized;
4. Find the center of gravity of the object and
return its coordinates.
Color binarization converts the colors white or
black to clarify the contour and perform contour
extraction easily. In the case of multiple objects such
as pills, the program returns a list of coordinates.
Since in OpenAI Gym the colors of pills, power pills,
and the wall of the map are the same, their sizes are
used in order not to detect other objects.
6.3 Finding the Shortest Distance
We used depth-first search (Tarjan, 1971) to find the
shortest distance. Depth-first search is a graph search
algorithm based on the strategy of visiting adjacent
vertices as much as possible. This algorithm is one of
the methods often used in maze search, and the search
continues from the original start point until all
reachable vertices are found. The search is performed
recursively by selecting one of the unreached vertices
and continuing the search as a new starting point. Our
program finds the closest pill or power pill first by
using the shortest distance from PacMan to the pill or
the power pill. We used the depth-first search instead
of the Warshall-Floyd algorithm, which was used in
the previous study. Since the number of pills is large,
finding the shortest distance for all of them increases
the execution time. The position coordinates of all
pills or power pills are received from the program that
returns the position of the object as an array, and finds
the closest one from the position of PacMan.
6.4 Setting Rewards
The reward is the score obtained by the action. As
mentioned in Section 2, PacMan obtains 10 points
when taking pills, and 50 points when taking power
pills. The first attacked ghost is worth 200 points, and
the second, the thrird, and the fourth are worth 400,
600, and 800 points respectively. This added value is
used as a reward. However, if nothing is done, the
value as a reward is high, and the dependence on one
success becomes high. Therefore, the problem is
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
458
avoided by reducing the reward value by multiplying
the added score value by a constant. The optimum
value of the constant used to reduce the reward value
is obtained by experimenting with different values.
The reward is used to update the Q value. If only the
score is used as the reward, avoiding the ghost cannot
be learned. Therefore, the score of 500 points is used
when PacMan is caught by a ghost. Since this is a
value set according to the value of the score, the value
of the penalty is also multiplied by a constant and
used to update the Q value.
7 EXPERIMENT
We prepared multiple machines (instances of AI) that
adjust the reward for the action of PacMan (player)
and the constant 𝐶 used for updating UCB. We
verified what kind of reward is given for efficient
learning. The experiment is verified and confirmed by
comparing the final scores after learning 200 times.
Scores can be obtained by taking pills and power pills
and attacking neutralized ghosts. State 𝑠 used in
learning consists of a total of 27 combinations of
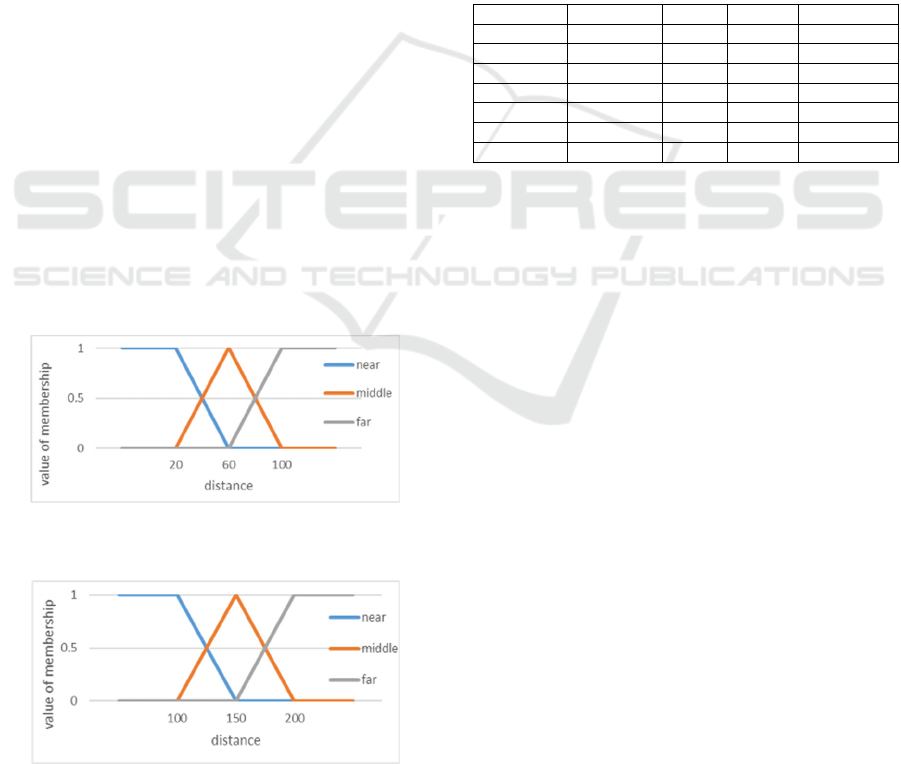
fuzzy sets defined in Figure 4 and Figure 5. Action 𝑎
is selected from three types: “go toward the closest
pill”, “go toward the closest power pill”, and “escape
from the ghost”. The elements of the value estimation
function 𝑄(𝑠,𝑎) are 27 × 3 = 81 in total, and their
values are all 50 before learning. The learning rate 𝛼
used to update the Q value is defined as 𝛼 = 0.9, and
the discount rate 𝛾 is defined as 𝛾 = 0.3.
Figure 4: Fuzzy set of distances between PacMan and a
ghost.
Figure 5: Fuzzy set of distances between PacMan and a
(power) pill.
Table 1 shows the parameters of the experiment
and final scores. Machine 0 is not combined with the
UCBQ algorithm by setting 𝐶 = 0 and 𝜀 = 0 and
applies only fuzzy Q learning as in the previous study.
We used the same 𝜀 and different rewards 𝑅 and
constants 𝐶 for the machines other than machine 0.
Machines 1 and 3 apply the ε-greedy algorithm to
fuzzy Q-learning as an action selection method and
differ only in how to give rewards. The reason for
preparing these machines was to verify whether the
proposed method would be more suitable than the
method incorporating the ε-greedy method when
training Ms. PacMan. Machines 2, 4, 5, and 6 apply
UCB fuzzy Q-learning of the proposed method.
Machines 2 and 4 have different rewards 𝑅, and
machines 2, 5, and 6 have different 𝐶 values.
Table 1: Parameters and final scores of machines.
Machine Reward
𝐶 𝜀
Score
00.03
R
0 0 3360
1
0.03𝑅
0 0.2 3480
2
0.03𝑅
0.01 0.2 3560
3
0.05𝑅
0 0.2 3120
4
0.05𝑅
0.01 0.2 3300
5
0.03𝑅
0.1 0.2 3280
6
0.03𝑅
3.0 0.2 2460
We first compare the scores obtained by the
proposed method. Comparing machines 2 and 4
indicates that machine 2 (which used the reward of
0.03𝑅 ) obtained the higher score. Comparing
machines 2, 5, and 6 indicates that the scores are
higher in the order of machine 6, 5, and 2, which
suggests that a smaller 𝐶 is suitable for a higher score.
Comparing machines 1 and 3 (which incorporated the
ε-greedy algorithm) indicates that machine 1 (which
used the reward of 0.03𝑅) obtained the higher score
again.
Next, we compare the proposed method with the
method of the previous study and the method
incorporating the ε-greedy algorithm. Although the
scores increased in the order of machines 0, 1, and 2,
there were no large differences among these three
machines. Concerning the Q values for the final
scores, machine 0 had more elements with a Q value
of 50 (which was the initial value) than the other
machines. In machines 1, 2, 3, 4, 5, and 6, the Q
values were updated from the initial value of 50 to
different values for most combinations of states and
actions. There were no large differences in the degree
of the updates of the Q values among these four
machines using the proposed method.
Upper Confident Bound Fuzzy Q-learning and Its Application to a Video Game
459
8 DISCUSSION
We compared machines 2, 5, and 6, in which only the
values of the constant 𝐶 (which represents the degree
of search) were changed. As described in Subsection
4.3, a larger value of 𝐶 performs more aggressive
search, and a smaller value of 𝐶 places more
emphasis on the utilization of the learning. The result
of the experiment indicated a larger value of 𝐶
yielded a lower score. If the value of 𝐶 is made too
large, it is difficult to increase the score; this is
because the actions that have already been learned are
selected many times even if they are inappropriate.
Therefore, it is considered that machine 6 with a
particularly large value of 𝐶 has a poor balance
between search and utilization because of focusing on
search. For this reason, it is considered that machine
2 with the 𝐶 value of 0.01 (which had the highest
score among the machines operated in the
experiment) was the one that was the most efficiently
utilized during the learning.
We compared machines 1 and 3 (which
incorporated the ε-greedy algorithm into fuzzy Q-
learning) and machines 2 and 4 (which used the
proposed method). Machines 1 and 2 used 0.03𝑅 as
the reward, and machines 3 and 4 used 0.05𝑅 as the
reward to update the Q values. The results of the
scores indicate that the machines gave higher scores
when the reward of 0.03𝑅 was used. Therefore, it is
considered that the value of the reward suitable for
applying fuzzy Q-learning to Ms. PacMan in this
experiment is 0.03𝑅. Also, the reason why the score
slightly dropped by the reward of 0.05𝑅 was that
taking pills and power pills was prioritized over
escaping from ghosts because of the increased
rewards. As a result, many risky actions were selected.
We compared machine 0 that used only fuzzy Q-
learning, machine 1 that had the highest score among
the machines that used the ε-greedy method, and
machine 2 that had the highest score among the
machines that used the proposed method. Comparing
the Q values, the Q values of machines 1 and 2 had
many updated elements compared to the Q values of
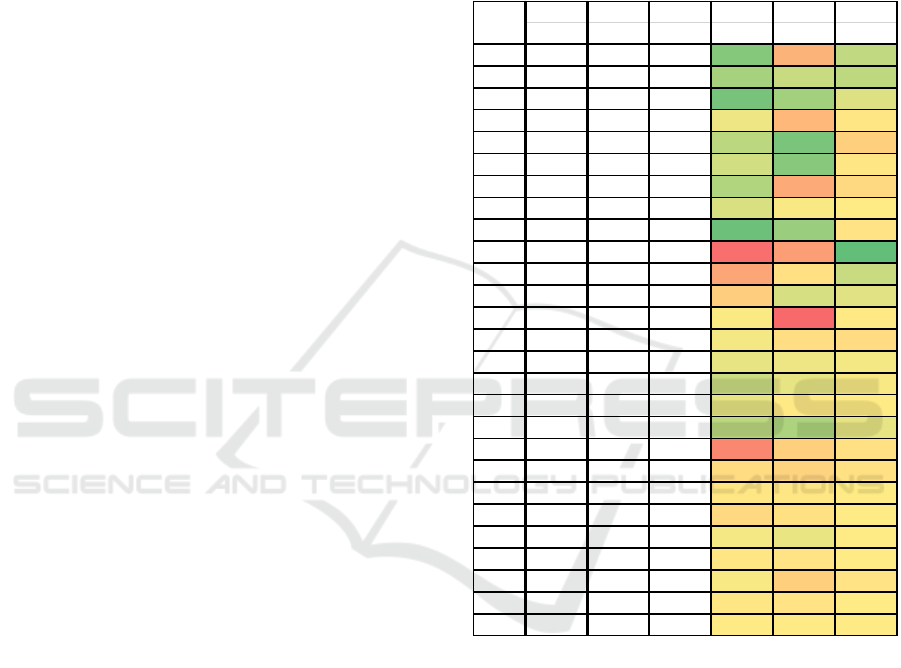
machines 0 (see Figure 6 and Figure 7Figure 7).
Therefore, it is considered that machines 1 and 2
could perform sufficient search and learn efficiently.
However, no large difference in the degree of search
between machines 1 and 2 could be seen. Also,
regarding the score comparison, although machine 1
gave a score that exceeded machine 0 about 100
points, there were no large differences between the
three machines. It is considered that the obtained
points were limited because the program was applied
only to the maps up to stage 2 as in the previous study.
Therefore, it is necessary to reconfirm the usefulness
of the proposed method by applying it to maps on
stages 3 and later. Moreover, to verify the learning
efficiency, it is necessary to obtain not only the final
score and the final Q value but also the score in the
learning process as data on a regular basis. If the Q
value is updated at an early stage and a high score is
obtained, it can be judged that efficient learning is
being performed.
Figure 6: Q values of machine 0.
In our program, we set actions “go toward the
closest pill”, “go toward the closest power pill”, and
“escape from the ghost”. It is considered that the
score did not increase because the action of actively
attacking a neutralized ghost was missing. As a
solution, increasing new actions such as “go to the
ghost” is considered. In addition, by increasing
actions, the number of combinations of states and
actions increases. Therefore, it is possible to learn
more detailed actions, and it is expected that a higher
score can be obtained. Furthermore, since the effect
of action selection increases with the number of
actions, it is considered that the learning efficiency
between the proposed method and previous studies
will appear more prominently.
Closest Closest Closest GoTo GoTo Avoid
Ghost Pill PPill Pill PPill Ghost
1
near near near
14 71 32
2
near near middle
24 34 31
3
near near far
10 23 40
4
near middle near
45 69 52
5
near middle middle
30 11 60
6
near middle far
37 15 52
7
near far near
27 74 57
8
near far middle
39 48 50
9
near far far
72053
10
middle near near
96 79 4
11
middle near middle
76 54 34
12
middle near far
61 38 41
13
middle middle near
49 98 51
14
middle middle middle
47 55 56
15
middle middle far
43 45 47
16
middle far near
35 43 48
17
middle far middle
43 51 50
18
middle far far
30 26 43
19
far near near
87 60 54
20
far near middle
56 59 54
21
far near far
52 52 50
22
far middle near
57 54 50
23
far middle middle
47 44 50
24
far middle far
52 53 50
25
far far near
48 60 53
26
far far middle
52 53 50
27
far far far
50 50 50
St at e
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
460
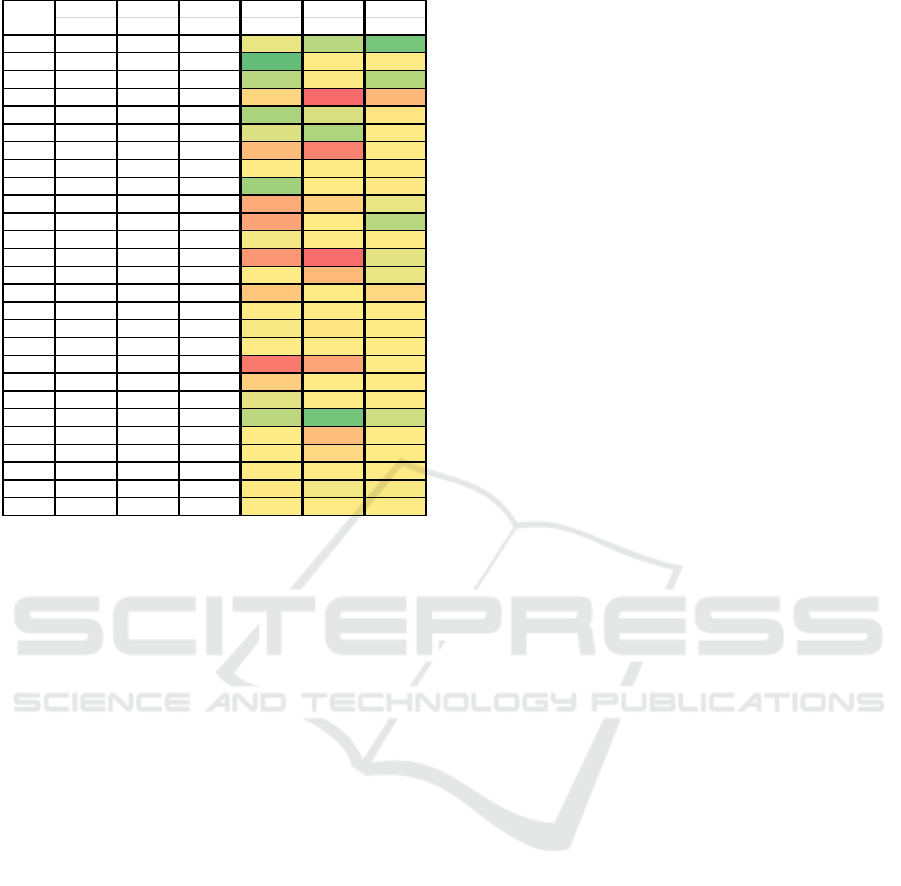
Figure 7: Q values of machine 2.
9 CONCLUSIONS AND FUTURE
WORK
In this paper, we tackled the low learning efficiency
in applying fuzzy Q-learning to Ms. PacMan in the
previous method. To increase the learning efficiency,
we proposed UCB fuzzy Q-learning by combining
fuzzy Q-learning and the UCBQ algorithm that can
learn search and utilization in a well-balanced manner
by reflecting the number of times an action is selected
to eliminate local optimal solutions. In the experiment,
the proposed method was applied to Ms. PacMan. As
a result, the score of the proposed method exceeded
the score of the previous method about 100 points. It
was also shown that a lower constant used in the
proposed method resulted in a higher score.
Our future work is to clarify difference in scores
between our method and the previous method by
making the program cope with maps on stages 3 and
later of Ms. PacMan. In addition, since it is
considered that the influence of an action selection in
UCB fuzzy Q-learning increases with the number of
actions, it is necessary to verify whether the score
increases by further dividing actions. Also, to confirm
the learning efficiency, it is necessary to obtain scores
for many executions of the learning of each machine
and compare the transitions. To confirm its usefulness,
it is necessary to compare it also with DQN.
REFERENCES
Auer, P., Cesa-Bianchi, N., & Fischer, P. (2002). Finite-
time Analysis of the Multiarmed Bandit Problem.
Machine Learning, 47, 235-256.
Brockman, G., Cheung, V., Pettersson, L., Schneider, J.,
Schulman, J., & Tang, J. Z. (2016). OpenAI Gym.
arXiv, 1606.01540.
DeLooze, L. L., & Viner, W. R. (2009). Fuzzy Q-Learning
in a Nondeterministic Environment: Developing an
Intelligent Ms. Pac-Man Agent. Proc. IEEE Symposium
on Computational Intelligence and Games, 162-169.
Glorennec, P. Y. (1994). Fuzzy Q-Learning and Dynamical
Fuzzy. Proc. IEEE International Fuzzy Systems
Conference, 26-29.
Gu, D., & Hu, H. (2004). Accuracy based fuzzy Q-learning
for robot behaviours. Proc. IEEE International Fuzzy
Systems Conference, 25-29.
Hu, Y., Li, W., Xu, H., & Xu, G. (2015). An Online
Learning Control Strategy for Hybrid Electric Vehicle
Based on Fuzzy Q-Learning. Energies, 8(10), 11167-
11186.
Katagami, D., Toriumi, H., Osawa, H., Kano, Y., Inaba, M.,
& Otsuki, T. (2018). Introduction to Research on
Artificial Intelligence Based Werewolf. Journal of
Japan Society for Fuzzy Theory and Intelligent
Informatics in Japanese, 30(5), 236-244.
Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A.,
Antonoglou, I., Wierstra, D., & Riedmiller, M. (2013).
Playing Atari with Deep Reinforcement Learning.
arXiv, 1312.5602.
Mnih, V., Kavukcuoglu, K., Silver, D., Ruse, A. A.,
Veness, J., Bellemare, M. G., & Graves, A. (2015).
Human-Level Control through Deep Reinforcement
Learning. Nature, 518, 529-533.
Nakajima, T., Udo, A., & Ishibuchi, H. (2003). Acquisition
of Soccer Agent Behavior through Fuzzy Q-Learning.
Journal of Japan Society for Fuzzy Theory and
Intelligent Informatics in Japanese, 15(6), 702-707.
Saito, K., Notsu, A., & Honda, K. (2014). The Effect of
UCB Algorithm in Reinforcement Learning. Proc.
Fuzzy System Symposium, 174-179.
Silver, D., Aja, H., Maddison, C. J., Guez, A., Sifre, L.,
Driessche, G. v., & Schrittwieser, J. (2016). Mastering
the Game of Go with Deep Neural Networks and Tree
Search. Nature, 529, 484-489.
Tarjan, R. (1971). Depth-First Search and Linear Graph
Algorithms. SIAM Journal on Computing, 1(2), 146-
160.
Umano, M., Tachino, H., & Ise, A. (2013). Application of
Fuzzy Q-learning to Car Racing Game. Proc. Fuzzy
System Symposium, 1006-1011.
van Senjen, H., Fateme, M., Romoff, J., Laroche, R.,
Barnes, T., & Tsang, J. (2017). Hybrid Reward
Architecture for Reinforcement Learning. arXiv,
1706.04208.
Watkins, C. J. (1989). Learning From Delayed Rewards,
PhD Thesis. University of Cambridge.
Watkins, C. J., & Dayan, P. (1992). Q-Learning. Machine
Learning, 8, 279-292.
Closest Closest Closest GoTo GoTo Avoid
Ghost Pill PPill Pill PPill Ghost
1
near near near
44 30 11
2
near near middle
55050
3
near near far
30 49 29
4
near middle near
60 110 74
5
near middle middle
26 39 53
6
near middle far
40 27 50
7
near far near
72 99 50
8
near far middle
50 50 50
9
near far far
23 50 51
10
middle near near
80 63 44
11
middle near middle
83 50 30
12
middle near far
47 50 50
13
middle middle near
89 108 42
14
middle middle middle
50 73 44
15
middle middle far
67 50 59
16
middle far near
50 50 50
17
middle far middle
48 53 50
18
middle far far
50 50 50
19
far near near
103 82 50
20
far near middle
64 50 50
21
far near far
42 50 50
22
far middle near
31 10 36
23
far middle middle
50 71 50
24
far middle far
50 59 50
25
far far near
50 50 50
26
far far middle
51 46 48
27
far far far
50 50 50
St at e
Upper Confident Bound Fuzzy Q-learning and Its Application to a Video Game
461
