Image-set based Classification using Multiple Pseudo-whitened Mutual
Subspace Method
Osamu Yamaguchi
1,2
and Kazuhiro Fukui
1
1
Department of Computer Science, Graduate School of Systems and Information Engineering, University of Tsukuba, Japan
2
Corporate Research and Development Center, Toshiba Corporation, Japan
Keywords:
Image-set based Classification, Whitening Transformation, Multiple Pseudo-Whitened Mutual Subspace
Method, Ensemble Method, CNN Features.
Abstract:
This paper proposes a new image-set-based classification method, called Multiple Pseudo-Whitened Mutual
Subspace Method (MPWMSM), constructed under multiple pseudo-whitening. Further, it proposes to com-
bine this method with Convolutional Neural Network (CNN) features to perform higher discriminative per-
formance. MPWMSM is a type of subspace representation-based method like the mutual subspace method
(MSM). In these methods, an image set is compactly represented by a subspace in high dimensional vector
space, and the similarity between two image sets is calculated by using the canonical angles between two cor-
responding class subspaces. The key idea of MPWMSM is twofold. The first is to conduct multiple different
whitening transformations of class subspaces in parallel as a natural extension of the whitened mutual subspace
method (WMSM). The second is to discard a part of a sum space of class subspaces in forming the whiten-
ing transformation to increase the classification ability and the robustness against noise. We demonstrate the
effectiveness of our method on tasks of 3D object classification using multi-view images and hand-gesture
recognition and further verify the validity of the combination with CNN features through the Youtube Face
dataset (YTF) recognition experiment.
1 INTRODUCTION
For the past few decades, many image set-based
techniques have been proposed (Zhao et al., 2019).
These techniques have been applied to face recog-
nition (Taskiran et al., 2020), 3D object recognition
(Wang et al., 2018a), and gesture recognition (Wang
et al., 2018b), and are an essential technology in com-
puter vision.
In this paper, we propose a new image-set-based
classification, called Multiple Pseudo-Whitened Mu-
tual Subspace Method (MPWMSM), which is con-
structed under multiple pseudo-whitening trans-
formations. MPWMSM is a type of subspace
representation-based method like the mutual subspace
method (MSM) (Maeda and Watanabe, 1985; Ya-
maguchi et al., 1998) . In subspace-based meth-
ods, image set is compactly represented as a sub-
space, features are extracted by projection from the
subspace representation to a discriminative space,
and classification is performed using the angle be-
tween the subspaces as a similarity. In order to
improve the discriminative performance, the Con-
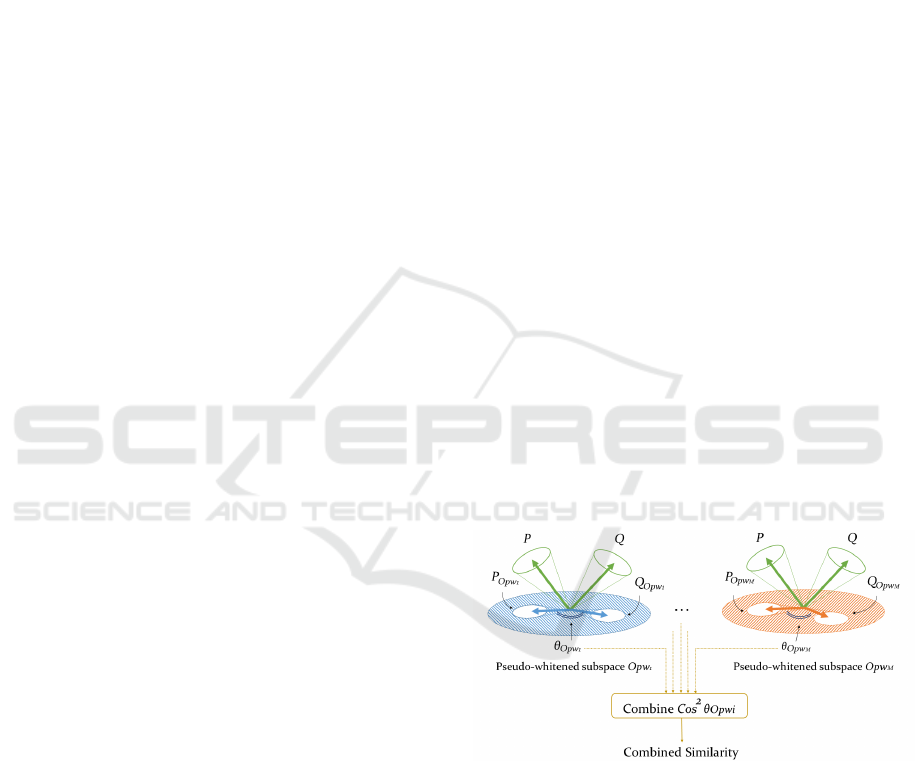
Figure 1: Overview of proposed Multiple Pseudo-Whitened
Mutual Subspace Method.
strained Mutual Subspace Method (CMSM) (Fukui
and Yamaguchi, 2003), the Multiple Constraint Mu-
tual Subspace Method (MCMSM) (Nishiyama et al.,
2005), and the Whitened Mutual Subspace Method
(WMSM) (Kawahara et al., 2007) have been proposed
as methods to perform feature extraction before the
mutual subspace method.
Fig. 1 shows the overview of the proposed MP-
WMSM. As the discriminant space in the proposed
method, we adapt the whitening transformation with
296
Yamaguchi, O. and Fukui, K.
Image-set based Classification using Multiple Pseudo-whitened Mutual Subspace Method.
DOI: 10.5220/0010836500003122
In Proceedings of the 11th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2022), pages 296-306
ISBN: 978-989-758-549-4; ISSN: 2184-4313
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

a modified eigenvalue weighting, which is called the
pseudo-whitening transformation (O
pw
i
in Fig. 1).
The components of whitening transformation with
larger index are heavily weighted by the scaling fac-
tors that are highly sensitive to noise in the training
data. In practice, disturbances due to noise can be ob-
served and the classification using these components
causes performance degradation. Discarding a part of
a sum space of class subspaces in forming the whiten-
ing transformation increases the classification ability
and the robustness against noise. Next, the two sub-
spaces, P and Q, to be compared are transformed by
multiple projection calculation using O
pw
i
indepen-
dently as shown in Fig. 1. Each projection O
pw
i
can
be used with a transformation consisting of a subset
of the training data. Lastly, the similarity between the
transformed subspaces is calculated respectively, and
the final similarity is obtained by integrating multiple
similarities. The combination of multiple feature ex-
tractions can achieve even higher accuracy due to the
effect of ensemble learning with reducing overtrain-
ing and small variances.
Furthermore, in recent years, Convolutional Neu-
ral Network (CNN) features have shown high ef-
fectiveness in discriminative performance in various
fields (Razavian et al., 2014; Azizpour et al., 2016).
Several works have been already published showing
the performance improvement by combining the mu-
tual subspace method with CNN features (Sogi et al.,
2018; Sakai et al., 2019). In our study, we use off-the-
shelf CNN features without retraining Deep Convolu-
tional Neural Networks (DCNNs) to reduce the train-
ing cost for the target domain. While we could take
advantage of the training data to improve the CNN
features with further fine-tuning, it is necessary to first
ensure that the subspace-based feature extraction for
image set works well.
The contributions of this paper include the follow-
ing:
• To improve the noise tolerance to the whitening
transformation, we classified the discriminative
subspace into three categories based on the anal-
ysis of the eigenspectrum and studied the pseudo-
whitening transformation.
• The MPWMSM method, which combines multi-
ple feature extraction based on ensemble learn-
ing, is used to improve performance using sub-
space representations of off-the-shelf CNN fea-
tures without retraining DCNNs.
• We applied the proposed method to several ap-
plications and confirmed its effectiveness. As a
result, we achieved the state-of-the-arts accuracy
for YouTube Faces dataset (YTF) using the latest
deep learning features.
The paper is organized as follows. First, we out-
line the conventional algorithms of MSM, CMSM,
and WMSM in section 2. In order to propose a new
discriminant space, we review each method in terms
of how it introduces the discriminant space. Sec-
tion 3 describes an extension of Whitening transfor-
mation by modification of eigenvalue weighting and
an integrated similarity calculation of multiple fea-
ture extraction methods similar to ensemble learning.
In section 4, we compare the performance on 3D ob-
ject recognition, gesture recognition, and video-based
face recognition using a dataset for image-set based
recognition. Finally we conclude our paper by sum-
marizing the paper.
2 RELATED WORK ON
SUBSPACE-BASED METHODS
In this section, we describe the subspace-based
matching algorithms (Yamaguchi et al., 1998) and
constrained mutual subspace method (Fukui and Ya-
maguchi, 2003) and the whitened mutual subspace
method (Kawahara et al., 2007). Finally, we describe
the problem of WMSM and analyze it from the view
of eigenspectrum. Then, we make a comparison of
the transformation in CMSM and WMSM.
2.1 Mutual Subspace Method
Mutual Subspace Method (MSM) (Maeda and Watan-
abe, 1985) is a method that approximates the entire
pattern variation by a subspace and measures the sim-
ilarity by the angle between the subspaces. This is an
extension of the Subspace Method (Oja, 1983), which
performs identification based on the minimum angle
θ
1
between two subspaces, the input subspace and the
reference subspace.
The identification based on this minimum angle
uses the concept of a canonical angle and is gener-
alized by multiple canonical angles. Between the m-
dimensional subspace P and the n-dimensional sub-
space Q, n canonical angles (n < m) can be defined,
and the first canonical angle θ
1
is the minimum angle
between the two subspaces.
The second canonical angle θ
2
is the minimum an-
gle measured in the direction orthogonal to the mini-
mum canonical angle θ
1
. Similarly, the following n
canonical angles θ
i
(i = 1 ... n) can be obtained se-
quentially. The minimum canonical angle is deter-
mined by the angle between the two subspaces, θ
1
, in
the equation (1). Similarity S between patterns is then
used for classification (Yamaguchi et al., 1998).
Image-set based Classification using Multiple Pseudo-whitened Mutual Subspace Method
297
S = cos
2
θ
1
(1)
The cos
2
θ
1
is the maximum eigenvalue λ
max
of the
following matrix X.
Xa = λa (2)
X = (x
mn
) (m,n = 1 .. .N
d
) (3)
x
mn
=
N
∑
l=1
(ψ
m
,φ
l
)(φ
l
,ψ
n
) (4)
where ψ
m
,φ
l
are the m, lth orthonormal basis vectors
in the subspaces P and Q, where (ψ
m
,φ
l
) is the inner
product of ψ
m
and φ
l
, and N
d
is the number of basis
vectors in the subspace.
The canonical angles between the two subspaces
can be obtained plurals as described. In practice, we
consider the value of the mean of the canonical an-
gles,
S[t] =
1
t
t
∑
i=1
cos
2
θ
i
, (5)
as the similarity between two subspaces. The value
S[t] reflects the structural similarity between two sub-
spaces.
2.2 Constrained Mutual Subspace
Method and Generalized
Differential Subspace
In the previous section, we explained how MSM clas-
sifies a set of feature vectors in the original vector
space. However, the original space is not exactly fa-
vorable for discriminating the subspaces, and it is de-
sirable to embed each subspace in a more discrimina-
tive space.
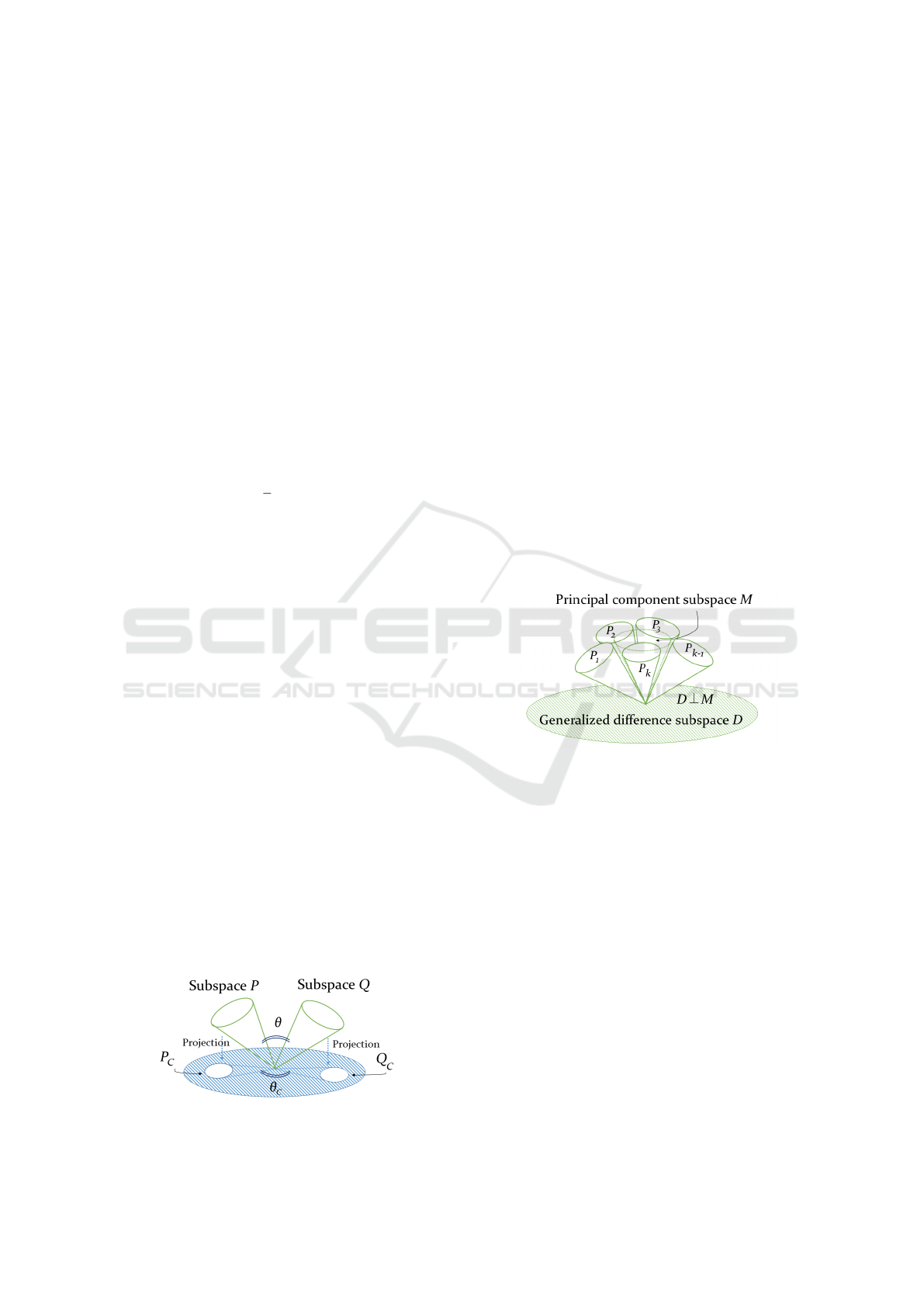
To improve the discrimination performance, the
input subspace P and the reference subspace Q are
projected onto the constrained subspace C consisting
of the components effective for discrimination, and
the canonical angles are measured for the projections
P
c
and Q
c
, as shown in Figure 2. This method adds
the projection onto the constrained subspace to the
mutual subspace method and is called Constrained
Mutual Subspace Method (CMSM) (Fukui and Yam-
aguchi, 2003).
Figure 2: Concept of CMSM.
Futhermore, there is also a method that uses the
generalized differential subspace (Fukui and Maki,
2015). The generalized difference subspace D is
obtained by first calculating the sum matrix G =
∑
k
i=1
P
i
, where P
i
are the projection matrices of R n-
dimensional reference subspaces. The basis vectors
are then obtained by performing the following eigen-
value decomposition:
Gd = λd (6)
where the eigenvectors d
i
correspond to the i-th eigen-
value λ
i
in descending order. Finally, only the N
B
eigenvectors with smallest eigenvalue are kept as the
basis vectors for D. Such dimension is set experimen-
tally.
As shown in Fig. 3, the generalized difference
subspace D is obtained by removing the principal
component space M, which doesn’t contain useful in-
formation for discrimination, from the sum space of
all class subspaces. Geometrically, by removing the
space M, the angle between each class subspace pro-
jected to the generalized difference subspace is ex-
panded.
Figure 3: Concept of generalized difference subspace.
2.3 Whitened Mutual Subspace Method
This section describes the whitening transformation
of a set of subspaces as a process to emphasize the
differences between the subspaces representing each
class. The whitening transformation for a set of sub-
spaces is formulated as an approximate solution to
the minimum value problem of the objective function,
which becomes smaller as the angle between the sub-
spaces increases. Let the set of d-dimensional sub-
spaces of each class be V
1
,. ..,V
R
and the d canonical
angles of V
i
and V
j
be θ
(1)
i j
,. ..,θ
(d)
i j
. Then, the follow-
ing equation holds for the sum of the squares of the
cosines of the canonical angles.
∑
1≤<i≤R
d
∑
k=1
cos
2
θ
(k)
i j
= C
1
σ
2
+C
2
, (7)
ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods
298
where C
1
,C
2
are positive constants and σ
2
is the vari-
ance of the eigenvalues of the autocorrelation matrix
G of the set of subspaces defined below:
G =
1
R
R
∑
i=1
P
i
. (8)
P
i
is a projection matrix (1 ≤i ≤ R) defined in the
basis ψ
i1
,. ..,ψ
iN
p
of V
i
as following equation,
P
i
=
N
p
∑
k=1
ψ
ik
ψ
T
ik
. (9)
From this equation, we can see that the smaller the
variance of the eigenvalues of the matrix G, the wider
is the angle between the subspaces that generated G.
Therefore, the variance of the eigenvalues of the au-
tocorrelation matrix G is minimized by the whitening
transformation W , which sets all eigenvalues to 1, as
defined below.
G = BΛB
T
. (10)
W = Λ
−1/2
B
T
, (11)
where Λ is the diagonal matrix of the eigenvalues of
the autocorrelation matrix G, and B is the matrix of its
eigenvectors arranged vertically.
Figure 4 shows how the whitening transforma-
tion expands the angles between the subspaces. Since
the whitening transformation spreads the angles uni-
formly, the pairs of subspaces with smaller angles be-
tween them will expand more. Therefore, when the
whitening transformation is applied to the subspace
of a certain class, the angle expands in the subspace
of similar classes, emphasizing the difference.
Figure 4: The ellipse and the circle in the center of the figure
represent the distribution of subspaces. Whitening makes
the distribution uniform.
2.4 The Problems of Previous Methods
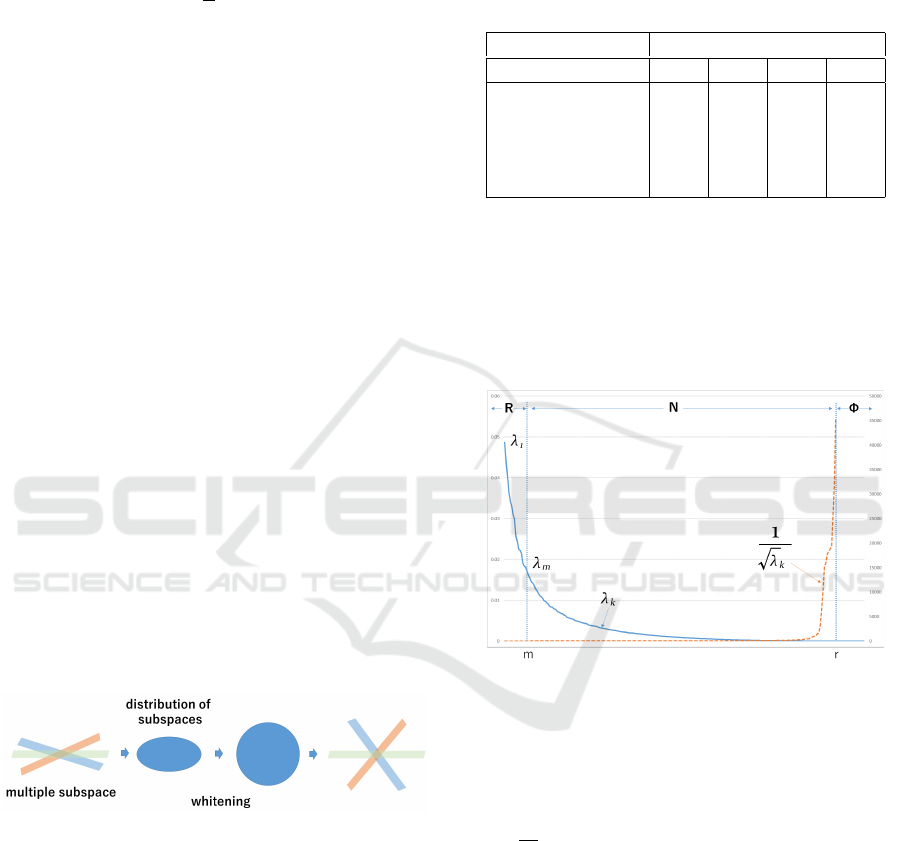
2.4.1 Analysis in View of the Eigenspectrum
In order to prevent the reference subspaces of each
class from being similar to each other, the whitened
mutual subspace method linearly transforms the refer-
ence subspaces into a feature space where the angles
between the reference subspaces are apart, thereby
improving the discrimination accuracy.
However, we have observed in the literature
(Fukui and Yamaguchi, 2006) an interesting result for
the ETH-80 dataset (Leibe and Schiele, 2003).
Table 1: Results for 3D object recognition in (Fukui and
Yamaguchi, 2006).
Accuracy (%)
S[1] S[2] S[3] S[4]
MSM 72.7 73.7 76.3 74.3
CMSM-215 75.7 81.3 76.3 73.7
CMSM-200 73.3 81.0 79.3 77.7
CMSM-190 71.0 73.0 73.0 75.7
WMSM(OMSM) 51.3 54.0 56.0 54.0
As we can see in Table. 1, despite the whitening
transformation, WMSM perform worse than MSM.
This means that feature extraction has lost its meaning
despite the use of discriminant transformations with
the subspace. To improve this performance degra-
dation, we revise the feature extraction by whitening
transformation.
Figure 5: A real distribution of eigenvalues in descending
order (solid line) and the weights of whitening transforma-
tion (dashed line). m denotes split point between Reliable
subspace (R) and Noise subspace (N). r denotes split point
between Noise subspace and Null subspace(Φ).
Fig. 5 shows the distribution of eigenvalues of
G (Eq. (6) ) in descending order and the weights
(1/
p
λ
k
) of whitening transformation. The compo-
nents of whitening transformation of larger index are
heavily weighted by the scaling factors.
The discussion of the eigenspectrum has been dis-
cussed in (Jiang et al., 2008). This paper points
out that noise turbulence and poor estimates of small
eigenvalues due to the finite number of training sam-
ples are the culprits. Due to the limited number of
training samples, the eigenvalues for a dimension can
be so small that they do not represent the true vari-
ance of that dimension well. This may result in se-
vere problems if their inverses are used as the weight
for the whitening transformation.
Image-set based Classification using Multiple Pseudo-whitened Mutual Subspace Method
299

We estimate the eigenspectrum using the equation
in (Jiang et al., 2008). The two parameters α and β,
and the estimating equation are defined by Eq. (12).
(13) and (14).
α =
λ
1
λ
m
(m −1)
λ
1
−λ
m
, (12)
β =
mλ
m
−λ
1
λ
1
−λ
m
, (13)
ˆ
λ
k
=
α
k + β
, (14)
where λ
1
is the maximum eigenvalue, λ
m
is the eigen-
value of the split points m, and
ˆ
λ
k
is the estimated
eigenvalue. The subspaces are divided into three cat-
egories, i.e., Reliable subspace (R), Noise subspace
(N), and Null subspace (φ) (Jiang et al., 2008). The
split point indicates the index m that separates the re-
liable subspace (R) from the noise subspace (N), as
shown in Fig. 5.
We introduce the eigenvalue ratios to observe how
much they differ from the estimated variance,
ˆ
λ
k+1
ˆ
λ
k
=
α
k + 1 + β
×
k + β
α
=
k + β
k + 1 + β
. (15)
Eq. (15) is a monotonically decreasing function
and it calculates the ratio between
ˆ
λ
k
and
ˆ
λ
k+1
.
Figure 6: The comparison of the real eigenvalue ratio (solid
line) and estimated eigenvalue ratio (dashed line) . The os-
cillations arises in the components with large index.
Figure 6 plots the real and estimated eigenvalue
ratio values. It is desirable that the eigenvalue ratios
always decay, even in the high-dimensional part of
the whitening transformation. However, in the large
index eigenvalue part, many of them deviate from the
estimated values. This disturbance leads to large os-
cillations in the inverse eigenspectrum. The compo-
nents with large index k are strongly sensitive to noise
due to training data, leading to poor recognition per-
formance on test data.
In the next section, the discussion will focus on
controlling the magnitude of the eigenvalues of the
autocorrelation matrix of the basis vectors used to
compute the feature extraction.
2.4.2 Comparison between Projection to
Constrained Subspaces and Whitening
Transformation
The constrained mutual subspace method (CMSM)
and the whitened mutual subspace method (WMSM)
are both methods to obtain the transformation matrix
based on the autocorrelation matrix G of the projec-
tion matrix generated from the reference subspace.
The projection matrix P
i
is defined by Eq. (16), where
ψ
i j
is the j-th orthonormal basis vector of the refer-
ence subspace of the i-th category and N
p
is the num-
ber of basis vectors of the reference subspace.
In the CMSM, the constrained subspace O
CMSM
is
defined using the projection matrix of each category
by Eq. (18).
P
i
=
N
p
∑
j=1
ψ
i j
ψ
T
i j
, (16)
G =
1
R
(P
1
+ P
2
+ ···+ P
R
), (17)
O
CMSM
=
N
B
∑
k=1
φ
k
φ
T
k
, (18)
where R is the number of reference subspaces, φ
k
is
the kth eigenvector selected from the smaller eigen-
values of the matrix G, and N
B
is the number of eigen-
vectors of the matrix G.
On the other hand, in the whitening mutual sub-
space method, the transformation matrix for whiten-
ing the reference subspaces O
W MSM
is defined by the
Eq. (19).
O
W MSM
= Λ
−
1
2
B
T
. (19)
As before, B is the matrix of eigenvectors of G, and
Λ represents the diagonal matrix of the eigenvalues of
G. O
CMSM
is represented using the following C
p
.
O
CMSM
= C
p
B
T
, (20)
C
p
= diag(0,0,0,.. .,0, 1, 1,1,1). (21)
In this case, C
p
is the diagonal matrix of rank N
B
.
This weight distribution is shown in Figure 7. The
graph shows the weights of the eigenvectors in each
method. In CMSM, only the vectors after a particu-
lar dimension are used, and the weight is 1.0 in each
case. In the WMSM, on the other hand, the weights
ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods
300
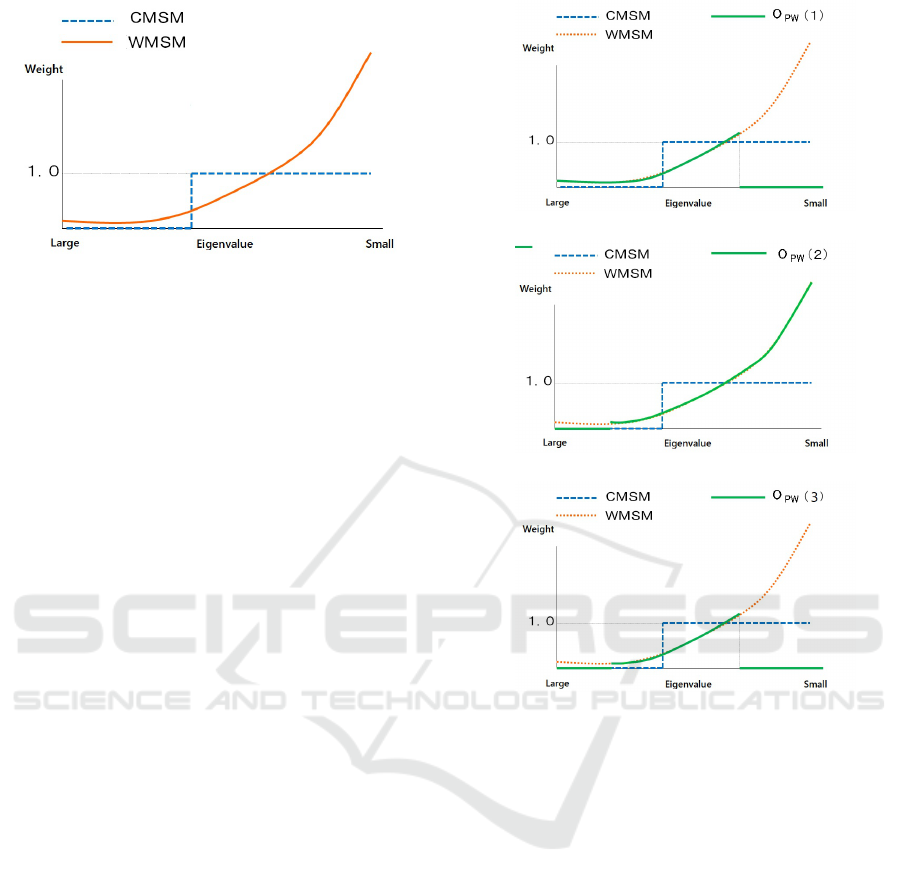
Figure 7: Weighting of Constraint subspace and Whitening
transformation.
are the square root of the reciprocals of the eigenval-
ues, and thus the weights become larger for higher
dimensions. This figure also shows that eigenvectors
of lower dimensions, which are discarded in CMSM,
are given small values in WMSM, while eigenvec-
tors of higher dimensions are given large weights. In
the WMSM, the components extracted by the high-
dimensional eigenvectors are given more importance,
which may cause cases of high similarity between
classes and may lead to a decrease in performance.
This does not occur in the CMSM due to introducing
constant weights.
3 PROPOSED METHOD
In this section, we describe our method, MPWMSM.
We introduce the pseudo-whitening transformation.
After that, we describe the proposed method which
combines multiple feature extraction.
3.1 Introduction of Pseudo-whitening
Transformation
As in the case of the CMSM, we propose to select
the features to be extracted by setting the weights of
some basis vector components to zero, which is like a
combination of WMSM and CMSM.
Figure 8 shows the weighting of the whitening
transformation with different parts set to zero. In Fig.
8(a), the high-dimensional part is set to 0, and in Fig.
8(b), the low-dimensional part is set to 0. Further-
more, in Fig. 8(c), both parts are set to 0 simultane-
ously.
Such weighting has been already discussed
in terms of eigenspectrum regularization models
(ERMs) (Jiang et al., 2008; Tan et al., 2018). These
methods focus on weighting using the full rank. The
CMSM is considered to be divided into two sub-
(a) Eliminate high-dimensional parts
(b) Eliminate low-dimensional parts
(c) Eliminate both parts of high and low-dimension
Figure 8: Variation of changing weights of whitening trans-
formations.
spaces, principal component subspace and general-
ized difference subspace as shown in Figure 3, and the
split points are defined for the binary weights shown
in Figure 7. In our method, we divide the subspace
into three categorized subspaces: principal compo-
nent subspace, reliable difference subspace, and noise
subspace, as shown in Figure 9. The discriminative
space is defined by their combination.
To achieve this, we filter some of the diagonal
components of the matrix Λ, such as some of the
small eigenvalues or some of the large eigenvalues,
setting them to 0, and make changes to it as a pseudo-
whitening matrix O
PW
.
Then, by replacing the whitening matrix O
W MSM
of the whitening mutual subspace method with the
pseudo-whitening matrix O
PW
, it is expected to im-
prove the results for the cases where the WMSM does
not outperform MSM.
The pseudo-whitening matrix O
PW
is defined by
Image-set based Classification using Multiple Pseudo-whitened Mutual Subspace Method
301
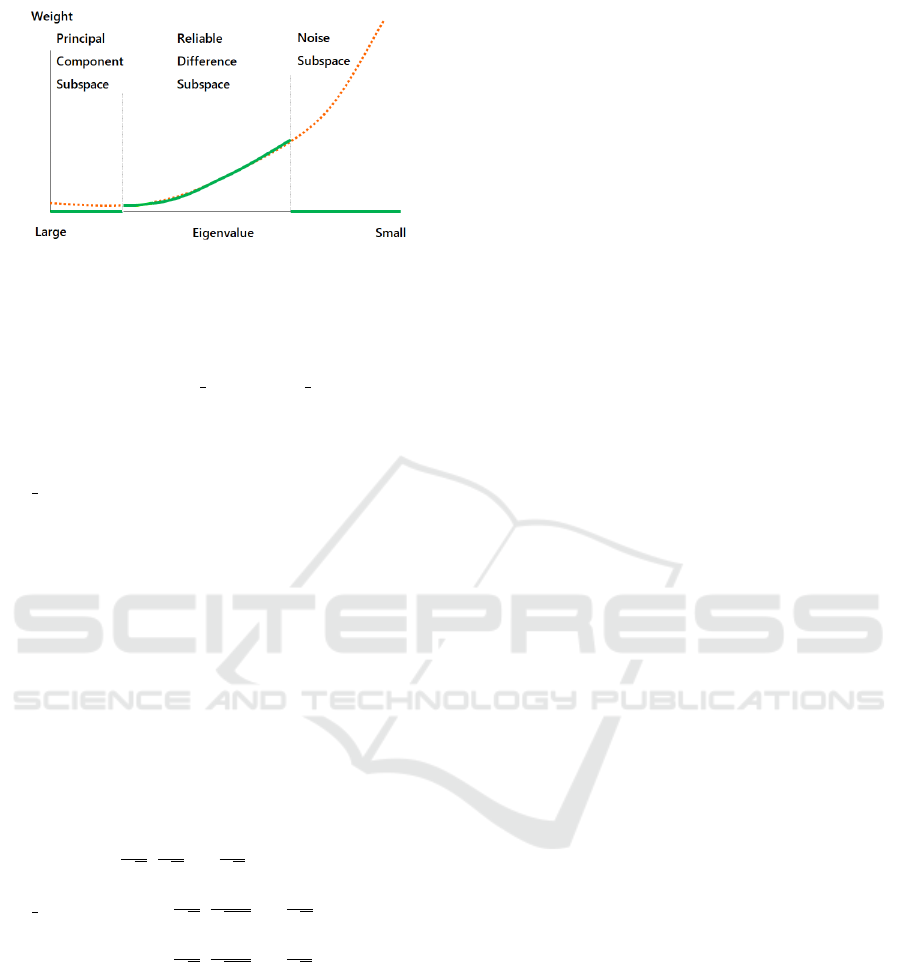
Figure 9: Subspaces divided into three categorized parts in
our method. As for the weights of Principal Component
Subspace and Noise Subspace, we control them by setting
them to zero.
the Equation (22).
O
PW
= C
s
Λ
−
1
2
B
P
T
= Λ
s
−
1
2
B
T
. (22)
Here, B is a matrix of eigenvectors, Λ is a diag-
onal matrix of eigenvalues, and C
s
is a diagonal ma-
trix with 0 and 1 elements given by the equation (23).
Λ
−
1
2
s
is given by the equation (24), where j and k de-
note the dimensions that define the range to be set to
0. Several of the eigenvalues of Λ are replaced by ze-
ros. We can replace some eigenvalues with 0 using
various C
s
.
C
s
=
diag(1,.. . ,1,. ..,1, 0,.. . ,0) .. . (a)
k
diag(0,.. . ,0,1, ..., 1,.. . ,1) .. . (b)
j
diag(0,.. . ,0,1, ..., 1,0,. . .,0) . .. (c)
j k
(23)
Λ
−
1
2
s
=
diag(
1
√
λ
1
,
1
√
λ
2
,...,
1
√
λ
k
,0,...,0) . . . (a)
diag(0,...,0,
1
√
λ
j
,
1
√
λ
j
+1
,...,
1
√
λ
d
) . . . (b)
diag(0,...,0,
1
√
λ
j
,
1
√
λ
j
+1
,...,
1
√
λ
k
,0,...,0) . . . (c)
(24)
Therefore, the Mutual Subspace Method using
the pseudo-whitening transformation O
PW
is denoted
as the Pseudo-Whitened Mutual Subspace Method
(PWMSM).
3.2 Multiple Pseudo-whitened Mutual
Subspace Method
This section presents the Multiple Whitened Mu-
tual Subspace Method (MWMSM) and the Multi-
ple Pseudo-Whitened Mutual Subspace Method (MP-
WMSM) in which we applied ensemble learning to
the Whitened Mutual Subspace Method. This ap-
proach follows (Nishiyama et al., 2005)
To extract effective features for set-based image
recognition, we transform the input subspace and the
reference subspace into multiple feature transforma-
tion. In the experiment we obtained high performance
compared with projecting onto a single transforma-
tion. To generate multiple transformations, we apply
the framework provided by ensemble learning.
Figure 1 in Section 1 shows process diagram of
Multiple Pseudo-Whitened Mutual Subspace Method
(MPWMSM). The multiple pseudo-whitening trans-
formations are represented by the projection matrix
in Eq. (22).
To generate multiple feature extractor in this pa-
per, we use the concept of Bagging (Breiman, 1996),
which is based on an ensemble learning algorithm.
Multiple classifiers are constructed using random
sampling in Bagging. To apply this framework to gen-
erating feature extractor, we randomly select L
0
(< L)
subspaces from L class subspaces. Each projection
subspace is generated independently using selected
training subspaces.
In summary, we generate M constraint subspaces
by the following steps:
1. Select L
0
class subspaces randomly without re-
placement.
2. Generate a projection subspace using selected L
0
class subspaces in Eq. (22).
3. Until M projection subspaces are generated, go to
step 1.
To combine similarities obtained on each projec-
tion subspace, we define the combined similarity S
T
as follows:
S
T
=
M
∑
i=1
α
i
S
O
pw
i
, (25)
where M is the number of the pseudo-whitening trans-
formations; α
i
is the i-th coefficient of O
pw
i
; S
O
pw
i
is
the similarity between P
O
pw
i
and Q
O
pw
i
projected onto
O
pw
i
.
4 EXPERIMENTS
In this section, we will present the experimental eval-
uation of our proposed method. We performed mainly
three experiments, to be explained in the following
subsections.
ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods
302
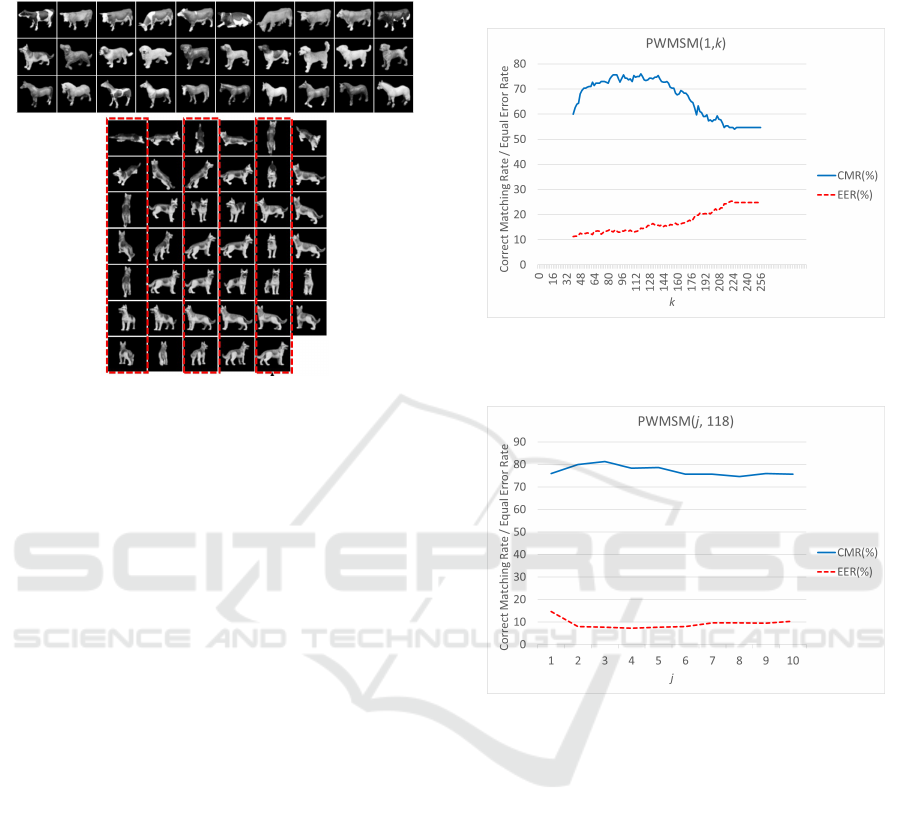
4.1 3D Object Recognition (ETH-80)
Figure 10: Object Recognition experiment using ETH-80.
Top: Selected 30 classes for similar shape classification
test. Bottom: All patterns of dog1 (the dotted columns are
the training images).
We carried out our experiments using the ETH-
80 dataset, which consists of 3D models taken from
multiple viewpoints, as shown in Fig. 10. From this
database, 30 models with similar shapes are extracted.
The experimental conditions for these models are in
accordance with the literature (Fukui and Yamaguchi,
2007). Therefore, CNN features are not used in this
experiment for comparison with conventional proto-
cols.
For each model, a set of images is taken from 41
viewpoints for each object, as shown in Figure 10.
The viewpoints are the same for all models. Of these,
the odd-numbered images (21) are used as the class
subspace, while the even-numbered images (20) are
used as the evaluation data. In other words, the learn-
ing perspective is different from the evaluation per-
spective. For the evaluation data, we took 10 images
from i to i + 9 out of the 20 images to make one
data set, and prepared a total of 10 evaluation sets by
changing the starting frame i from 1 to 10. Therefore,
the total number of trials is 300 (=10×30).
The original image was converted to a
monochrome image of 16 × 16 pixels for the
evaluation. Thus, the dimensionality of the data
is 256. The dimensionality of the input subspace
and the reference subspace of each class was set to
7, and the dimensionality of the subspace used for
training (N
p
) was set to 20. For direct comparison
with WMSM, no multiplication is applied, and the
evaluation is performed as M = 1 and α
1
= 1.0 in Eq.
(25).
Here, PWMSM ( j, k) represents the case where
the j-th to k-th elements in Eq. (23) are set to 1.
Therefore, PWMSM(1, 256) is the same as WMSM.
Figure 11: The correct matching rate and the equal error
rate of PWMSM(1, k) for different dimension of k. O
PW
is
eliminated part of higher dimension.
Figure 12: The correct matching rate and the equal error
rate of PWMSM( j, 118) for different dimension of j. O
PW
is eliminated both part of higher and lower dimension.
Figure 11 shows the correct matching rate and the
equal error rate of PWMSM(1, k) for different dimen-
sion of k. The results were obtained by varying from
the 40th dimension to the 256th dimension sequen-
tially. This refers to classification accuracy improved
to 76.0% compared to 54.6% for the original whiten-
ing transformation.
The result of fixing the 118th dimension at the
maximum value and changing the elements of C
s
of
Eq. (23) from the low-dimensional part to 0, i.e.
PWMSM( j, 118) is shown in Fig. 12. In this case, the
results further improved to 81.4%. When compared to
S[1] in Table 2, it is found to exceed the performance
of other linear feature extraction schemes.
Our best performance of PWMSM was achieved
when using 3 - 100 dimensions, resulting in 83.3% in
classification accuracy. This is the best performance
among the subspace-based methods we compared.
Image-set based Classification using Multiple Pseudo-whitened Mutual Subspace Method
303

Table 2: Results for 3D object recognition.
Acc. (%) by S[1]
MSM 72.7
CMSM-215 75.7
WMSM 54.6
PWMSM (1, 118) 76.0
PWMSM (3, 118) 81.4
PWMSM (3, 100) 83.3
MWMSM 11.0
MPWMSM (3, 104) 84.0
Table 2 summarizes the results and compares the
proposed method with the results from a conventional
linear feature extraction system.
In addition, feature selection performed by the
PWMSM can embed the data in a smaller dimension
than the original data dimension. We believe this is
of great practical significance, as it improves the stor-
age efficiency of the reference subspace and reduces
computational cost.
Furthermore, to perform the multiple version of
proposed methods, the MWMSM and MPWMSM,
the training data is divided into three parts, and the
discriminant transformation is created from 10 sam-
ples of each part. We confirmed that the performance
could be further improved by the multiple pseudo-
whitening transformations, while it gets worse by the
multiple whitening transformations.
4.1.1 Hand Gesture Recognition (IPN Hand)
Hand gesture recognition (HGR) is an essential func-
tion of human-computer interaction, which has a wide
range of applications. IPN Hand (Benitez-Garcia
et al., 2021) is a video dataset for real-time hand ges-
ture recognition. The gestures in this dataset focused
on interaction with touchless screens, including 13
categories. In the 50 subjects, there are 16 females
and 34 males. The dataset was collected from about
30 diverse scenes, with real-world variation in back-
ground and illumination.
We tried the Isolated HGR task, which is eval-
uated as the conventional classification metric. The
data split the data by subject into training (74%) and
testing (26%) sets, resulting in 148 training and 52
testing videos. The numbers of gesture instances in
training and testing splits are 3,117 and 1,101, respec-
tively. In this experiment, we use the RGB-seg used
in literature (Benitez-Garcia et al., 2021). Semantic
segmentation masks were provided as annotated data
and we segmented the RGB images using the masks.
The images are processed by the public pre-trained
ResNet-100 model by ImageNet train, and 2048 di-
Figure 13: Frame Features for HGR. Type (i) is a 2048 di-
mensional feature extracted from DCNNs for each frame;
Type (ii) uses features reduced to 512 dimensions from the
original DCNNs features by PCA and add a time index ele-
ment to represent the time transition.
mensional features are extracted from the C5 layer.
Note that the training data was not used to train the
DCNNs. We use the training data only for subspace-
based feature extraction.
Each gesture instance’s start and end frame index
in the video was manually labeled, providing enough
information to train for forming the subspace. The
video sequences are segmented into isolated gesture
samples based on the beginning and ending frames
manually annotated. We use classification accuracy to
evaluate our method, which is the percent of correctly
labeled examples.
Table 3 shows the results for IPN Hand classifi-
cation. We tried two types of features as shown in
Fig. 13. Type (i) is a 2048 dimensional feature ex-
tracted from DCNNs for each frame; Type (ii) uses
features reduced to 512 dimensions from the origi-
nal DCNNs features by PCA. Moreover, we add a 30-
dimensional time index element to represent the time
transition. For the time index, we let the normal distri-
bution move along the time axis as shown in Fig. 13.
They are equally divided according to the time length
of each gesture and assigned to different locations of
the peaks of the 30-dimensional indices.
Table 3: Results for IPN Hand. (i) 2048 dim. DCNNs Fea-
ture, (ii) Reduced 512 dim. DCNNs Feature with Time In-
dex elements.
Acc.
(%)
(i) MSM (S[1]) 38.23
MSM (S[5]) 43.96
WMSM (S[5]) 50.40
PWMSM(S[5],(j, k)=(1, 388)) 55.40
MPWMSM(S[5],(j, k)=(5, 388)) 57.00
(ii) MSM (S[10]) 35.51
WMSM (S[10]) 47.32
PWMSM (S[10],(j, k)=(20, 320)) 58.94
MWMSM(S[10]) 59.21
MPWMSM (S[10],(j, k)=(20, 400)) 60.13
3D versions of ResNet-50 75.11
(Benitez-Garcia et al., 2021)
ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods
304

The proposed method, MPWMSM, was found to
be superior to these methods with other feature ex-
traction. Although the performance is not as good as
the 3D version of ResNet-50 tested in (Benitez-Garcia
et al., 2021), it was confirmed that the subspace-based
feature extraction is more effective for the original
DCNN features.
4.1.2 Video-based Face Recognition (YTF)
Next, we experiment with recognition using video
face image data. The YouTube Face dataset (YTF) is
the most widely used benchmark for face recognition
on video. It consists of 3,425 videos of 1,595 identi-
ties. In the YTF evaluation protocol, 5,000 video pairs
are matched in 10 folds, and the average accuracy is
required. Each fold consists of 500 video pairs, which
are guaranteed to have mutually exclusive properties
for the subject.
The current top accuracy for the YTF benchmark
is SeqFace (Hu et al., 2018), which uses ResNet-64
based features to compute the final score by applying
the simple average features of all faces in the video.
In ArcFace (Deng et al., 2019), which uses ResNet-
100 based feature trained by MS1Mv2 dataset (Deng
et al., 2019). The simple average features are also ap-
plied to evaluate the results. Therefore, we apply the
proposed method using state-of-the-art CNN features
by deep learning.
As CNN features, we use the ResNet-100 model
using ArcFace loss and trained on Glint360k dataset
(An et al., 2021). We downloaded the public trained
model published by InsightFace (InsightFace, 2021).
The dimensionality of the feature vector is 512. For
the YTF video data, five facial feature points are ob-
tained using MTCNN (Zhang et al., 2016), and the
face image is cropped to a size of 112x112 pixels.
Note that fine-tuning using YTF data was not per-
formed for DCNNs in this experiment.
Table 4: Results for YTF.
Acc. (%)
Simple average features 98.22 ± 0.61
MSM (S[4]) 98.28 ± 0.69
MWMSM (S[2]) 98.30 ± 0.80
MPWMSM (S[2],(j, k)=(3, 277)) 98.38 ± 0.60
SeqFace (Hu et al., 2018) 98.12
ArcFace (Deng et al., 2019) 98.02
We tried different parameters for the number of
canonical angles (Eq. (5)), the number of dimen-
sions of the reference subspace N
p
(Eq. (16)), and
the choice of weights (Eq. (23)). Table 4 shows eval-
uation results for YTF.
When comparing the results with those of Arcface
(Deng et al., 2019), we can see that the accuracy is im-
proved by using simple average features due to the in-
creased training data (MS1Mv2 dataset to Glint360k
dataset). Furthermore, the accuracy is improved by
using MSM with the subspace representation of each
video. S[4] shows that the best performance was ob-
tained when the number of canonical angles of simi-
larity was 4.
Since there are ten folds in YTF when testing a
particular fold, we used one for testing and the re-
maining 9 folds to train the whitening transformation
for MWMSM. Multiplication is then performed ac-
cording to section 3.2.
In high-performance discriminative features, mul-
tiplication using WMSM was confirmed to be bet-
ter than MSM. Note that random selection in bag-
ging is not performed this time. Since there is no
overlap of individual IDs in each fold, the whiten-
ing transformation/pseudo-whitening transformation
is calculated using each fold’s subspace. The dimen-
sionality of the subspace used for training (N
p
) was
set to 20.
Finally, we can see that our proposed pseudo
whitening transformation achieved the best results,
with identification accuracy of 98.38%. The MP-
WMSM showed the same improvement over the
MWMSM as confirmed by 4.1.1 and 4.1.2. We con-
firm that the proposed pseudo-whitening transforma-
tion is more effective than the whitening transforma-
tion.
5 CONCLUSION
This paper proposed the Multiple Pseudo-Whitened
Mutual Subspace Method (MPWMSM), which per-
forms multiple feature extraction by projecting the
input and reference subspaces into multiple discrim-
inative subspaces and then calculating and integrat-
ing multiple similarities. By selecting the weighting
of the basis vectors of the whitening transformation,
we confirmed the improvement of the accuracy by the
pseudo-whitening transformation.
We demonstrated the effectiveness of our method
on tasks of 3D object classification using multi-view
images and hand-gesture recognition. We also ver-
ified the validity of the combination with CNN fea-
tures through the YTF face recognition experiment.
The experiment results show that our method can im-
prove the performance in face recognition by extract-
ing the features of the video without fine-tuning the
DCNNs itself.
Future work includes automatic dimensionality
Image-set based Classification using Multiple Pseudo-whitened Mutual Subspace Method
305

setting of the pseudo-whitening space according to
the data set.
REFERENCES
An, X., Zhu, X., Gao, Y., Xiao, Y., Zhao, Y., Feng, Z., Wu,
L., Qin, B., Zhang, M., Zhang, D., and Fu, Y. (2021).
Partial fc: Training 10 million identities on a single
machine. In Proceedings of the IEEE/CVF Interna-
tional Conference on Computer Vision (ICCV) Work-
shops, pages 1445–1449.
Azizpour, H., Razavian, A. S., Sullivan, J., Maki, A.,
and Carlsson, S. (2016). Factors of transferability
for a generic convnet representation. IEEE Transac-
tions on Pattern Analysis and Machine Intelligence,
38(9):1790–1802.
Benitez-Garcia, G., Olivares Mercado, J., Sanchez-Perez,
G., and Yanai, K. (2021). Ipn hand: A video dataset
and benchmark for real-time continuous hand gesture
recognition. Proc. of IAPR International Conference
on Pattern Recognition (ICPR), pages 4340–4347.
Breiman, L. (1996). Bagging predictors. Machine Learn-
ing, 24(2):123–140.
Deng, J., Guo, J., Xue, N., and Zafeiriou, S. (2019). Ar-
cface: Additive angular margin loss for deep face
recognition. In IEEE/CVF Conference on Computer
Vision and Pattern Recognition (CVPR), pages 4690–
4699.
Fukui, K. and Maki, A. (2015). Difference subspace and
its generalization for subspace-based methods. IEEE
Transactions on Pattern Analysis and Machine Intel-
ligence, 37(11):2164–2177.
Fukui, K. and Yamaguchi, O. (2003). Face recognition us-
ing multi-viewpoint patterns for robot vision. 11th In-
ternational Symposium of Robotics Research (ISRR),
pages 192–201.
Fukui, K. and Yamaguchi, O. (2006). Comparison between
constrained mutual subspace method and orthogonal
mutual subspace method. Proc. of Subspace 2006,
pages 63–71. (In Japanese).
Fukui, K. and Yamaguchi, O. (2007). The kernel orthogo-
nal mutual subspace method and its application to 3d
object recognition. Proc. of ACCV07, pages 467–476.
Hu, W., Huang, Y., Zhang, F., Li, R., Li, W., and Yuan, G.
(2018). Seqface: Make full use of sequence informa-
tion for face recognition. CoRR, abs/1803.06524.
InsightFace (2021). Insightface model zoo. GitHub reposi-
tory.
Jiang, X., Mandal, B., and Kot, A. (2008). Eigenfeature reg-
ularization and extraction in face recognition. IEEE
Transactions on Pattern Analysis and Machine Intel-
ligence, 30(3):383–394.
Kawahara, T., Nishiyama, M., Kozakaya, T., and Yam-
aguchi, O. (2007). Face recognition based on whiten-
ing transformation of distribution of subspaces. In
ACCV’07 Workshop Subspace 2007.
Leibe, B. and Schiele, B. (2003). Analyzing appearance
and contour based methods for object categorization.
Proc. of IEEE Conference on Computer Vision and
Pattern Recognition, pages 409–415.
Maeda, K. and Watanabe, S. (1985). A pattern matching
mathod with local structure. Trans. IEICE(D), J68-
D(3):345–352. (In Japanese).
Nishiyama, M., Yamaguchi, O., and Fukui, K. (2005). Face
recognition with the multiple constrained mutual sub-
space method. In AVBPA.
Oja, E. (1983). Subspace Methods of Pattern Recognition.
Research Studies Press, England.
Razavian, A. S., Azizpour, H., Sullivan, J., and Carlsson,
S. (2014). Cnn features off-the-shelf: an astound-
ing baseline for recognition. In IEEE Conference on
Computer Vision and Pattern Recognition workshops,
pages 806–813.
Sakai, A., Sogi, N., and Fukui, K. (2019). Gait recognition
based on constrained mutual subspace method with
cnn features. In 2019 16th International Conference
on Machine Vision Applications (MVA), pages 1–6.
Sogi, N., Nakayama, T., and Fukui, K. (2018). A method
based on convex cone model for image-set classifica-
tion with cnn features. International Joint Conference
on Neural Networks (IJCNN), pages 1–8.
Tan, H., Gao, Y., and Ma, Z. (2018). Regularized constraint
subspace based method for image set classification.
Pattern Recognition, 76:434–448.
Taskiran, M., Kahraman, N., and Erdem, C. E. (2020). Face
recognition: Past, present and future (a review). Digi-
tal Signal Processing, 106:102809.
Wang, D., Wang, B., Zhao, S., Yao, H., and Liu, H. (2018a).
Off-the-shelf cnn features for 3d object retrieval. Mul-
timedia Tools Appl., 77(15):1983319849.
Wang, T., Li, Y., Hu, J., Khan, A., Liu, L., Li, C.,
Hashmi, A., and Ran, M. (2018b). A Survey on
Vision-Based Hand Gesture Recognition: First Inter-
national Conference, ICSM 2018, Toulon, France, Au-
gust 2426, 2018, Revised Selected Papers, pages 219–
231. Springer.
Yamaguchi, O., Fukui, K., and Maeda, K. (1998). Face
recognition using temporal image sequence. In Pro-
ceedings of the 3rd. International Conference on Face
and Gesture Recognition.
Zhang, K., Zhang, Z., Li, Z., and Qiao, Y. (2016). Joint
face detection and alignment using multitask cascaded
convolutional networks. IEEE Signal Processing Let-
ters, 23(10):1499–1503.
Zhao, Z.-Q., Xu, S.-T., Liu, D., Tian, W.-D., and Jiang, Z.-
D. (2019). A review of image set classification. Neu-
rocomputing, 335:251–260.
ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods
306
