Outpatient Diversion using Real-time Length-of-Stay Predictions

Najiya Fatma

and Varun Ramamohan

Department of Mechanical Engineering, Indian Institute of Technology Delhi, Delhi, India

Keywords:

Length-of-stay, Patient Diversion, Delay Prediction, Primary Health Centers.

Abstract:

In this work, we show how real-time length-of-stay (LOS) predictions can be used to divert outpatients from

their assigned facility to other facilities with lesser congestion. We illustrate the implementation of this diver-

sion mechanism for two primary health centers (PHCs), wherein we divert patients from their assigned PHC to

the other PHC based on their predicted LOSs in both facilities. We develop a discrete-event simulation model

of patient ﬂow operations at these two PHCs in an Indian district and observe signiﬁcantly longer LOSs at one

of the PHCs due to disparities in the patient loads across both PHCs. We ﬁrst determine the expected LOS of

the patient at the point in time at which they are expected to arrive at a PHC using system state information

recorded at the current time at the PHC in question. The real-time LOS predictions are generated by estimat-

ing patient wait times on a real-time basis at the queueing subsystems within the PHC. We then divert the

patient to the appropriate PHC on the basis of the predicted LOS estimates at both PHCs, and show through

simulation that the proposed framework leads to more equitable utilization of resources involved in provision

of outpatient care.

1 INTRODUCTION

Patient length-of-stay (LOS) is an important indi-

cator of the efﬁciency of hospital management sys-

tems (Ayyoubzadeh et al., 2020). Long LOSs and

overcrowding are important operational issues fac-

ing healthcare facilities around the world (Wachtel

and Elalouf, 2020), including in India (Sharma et al.,

2021). This in turn leads to both operational and clini-

cal issues, such as denial of hospital admissions, can-

cellation of surgeries, and higher likelihoods of de-

veloping healthcare acquired infections (Zhou et al.,

2019; Areﬁan et al., 2019).

Congestion and longer LOSs at speciﬁc facilities

within a healthcare facility network, which in turn

lead to inequitable utilization of facilities across the

network, may occur due to patient perceptions of

better quality of care at certain facilities within the

network (Liu et al., 2018). Healthcare administrators

may adopt different strategies to relieve congestion

such as capacity replanning (Whiteside et al., 2020),

patient diversion (Marquinez et al., 2021), and early

discharges for medically stable patients. However,

increasing resource capacity is often difﬁcult due

to the capital investment required and the attendant

https://orcid.org/0000-0001-7790-3679

https://orcid.org/0000-0001-6517-9142

Table 1: Key acronyms and notation.

Acronyms /

Notation

Corresponding constituent words

LOS Length-of-stay

PHC Primary health center

DES Discrete event simulation

Travel time to reach PHC x

ρ Resource utilization

∆

Change in resource utilization

w Wait time in a queue

∆

Change in queue wait time

G(.) Queueing system service time cd f

medical training required when personnel numbers

are increased. Hence, patient diversion is often the

preferred alternative to mitigate overcrowding. In

this study, we describe an approach towards using

real-time LOS predictions to facilitate diversion

of outpatients across primary healthcare facilities.

While we demonstrate our approach via the diversion

of outpatients across two primary healthcare centers

(PHCs) in the Indian context, our approach can be

used in any setting where patient diversion is being

considered due to high LOSs, or more generally,

where signiﬁcant disparities in resource utilization in

a healthcare network is observed.

Fatma, N. and Ramamohan, V.

Outpatient Diversion using Real-time Length-of-Stay Predictions.

DOI: 10.5220/0010837400003117

In Proceedings of the 11th International Conference on Operations Research and Enterprise Systems (ICORES 2022), pages 56-66

ISBN: 978-989-758-548-7; ISSN: 2184-4372

In India, PHCs are the ﬁrst point of contact for

the patients with a formally trained doctor and pro-

vide outpatient care, and limited emergency and in-

patient care (Shoaib and Ramamohan, 2021). The

Indian government has recently undertaken an initia-

tive to expand and upgrade existing PHCs (Blanchard

et al., 2021), and hence it is reasonable to assume

an increase in the patient load at these PHCs given

the established link between increased quality of care,

improved infrastructure and higher demand (Rao and

Sheffel, 2018). Based on previous work regarding

modeling PHC operations (Fatma et al., 2020; Shoaib

and Ramamohan, 2021), we developed a discrete-

event simulation (DES) of medical care operations

of two PHCs in an Indian district. Under conditions

of high outpatient demand, the DES outcomes indi-

cated signifcant disparity in outpatient LOSs across

both facilities, and this would likely extend to the en-

tire public health network in the district. Further, we

also noted that under these high demand conditions,

patient wait times to receive service from the doctor

did not increase signiﬁcantly due to the very high ser-

vice rates of the doctor. Instead, the impact of high

demand was reﬂected in wait times at supporting sub-

systems in the PHC such as the pharmacy and the

laboratory, which in turn yielded high LOSs in the

PHCs as a whole. For example, average LOSs were

approximately 60 minutes, in comparison to average

total service times of less than 10 minutes across all

services that a patient may avail of in a typical PHC

visit. Thus, implementing diversion on the basis of

wait times in this context did not appear appropriate;

hence, we considered diversion based on patient LOS

as a whole in the facility.

The diversion mechanism that we propose utilizes

real-time LOS predictions to inform the diversion de-

cision. Diversion mechanisms based on real-time wait

time or ‘delay’ predictions for emergency patients

have been discussed in previous work (Fatma and Ra-

mamohan, 2021a); however, in this work, we use real-

time delay estimates to calculate real-time LOS pre-

dictions that in turn determine the diversion decision.

The real-time delay estimates, and in turn the real-

time LOS predictions, are generated at the point when

the patient decides to visit the facility in question (as

opposed to when the patient arrives at the facility),

implying that an information technology (IT) system,

including a web/smartphone application, to convey

this information to this patient would be required. Ex-

amples of such IT systems can be found in the United

Kingdom’s National Health Service (Mustafee and

Powell, 2020). In this paper, we develop a mech-

anism for patient diversion based on such real-time

LOS predictions (including a discussion of how such

LOS predictions can be generated) and demonstrate

via DES its impact on the operational outcomes of a

healthcare facility network. Our study provides the

operational basis that an IT system such as that de-

scribed in Mustafee and Powell (2020) can leverage

to implement real-time LOS-based diversion.

We now discuss the literature relevant to this

study, and describe our research contributions with re-

spect to the literature.

2 LITERATURE REVIEW

In this section, we focus on the literature associated

with real-time LOS prediction and patient diversion.

As part of the literature review, we also discuss stud-

ies that highlight the importance of information shar-

ing across facilities in the network wherein diversion

is implemented. We describe the research contribu-

tions of this work at the end of each subsection.

2.1 Length-of-Stay Prediction

The importance of LOS prediction at healthcare fa-

cilities and their subunits such as the emergency de-

partment is reﬂected in the considerable body of lit-

erature devoted to this topic (Song et al., 2015; Als-

inglawi et al., 2020; Shi et al., 2021; El-Bouri et al.,

2021). From the perspective of the methods used for

LOS prediction, it appears that data mining and sta-

tistical learning methods have been most widely used

(Verburg et al., 2014; Barnes et al., 2016; Turgeman

et al., 2017; Guti

errez et al., 2021; Shaaban et al.,

2021). A review conducted by El-Bouri et al. (2021)

found that multiple machine learning techniques such

as deep neural networks, random forest trees, regres-

sion techniques and decision trees among others have

been used to predict the patients LOS. The authors

then conclude that the LOS predictions were found

to be useful in planning patient admission schedules

and, as required, the preparation of post-discharge

care.

LOS prediction studies in the literature have pri-

marily focused on inpatients and emergency patients

using statistical learning techniques. The typical

methodology for LOS prediction for these patient

types involved the following steps: (a) recording clin-

ical information of patients such as medication history

at the time of admission, patient age, and the number

of comorbidities, (b) identifying the set of predictor

variables among the data available for LOS predic-

tion, (c) training and validating the statistical learn-

ing methods on the dataset constructed via mining the

available data (Baek et al., 2018; Aghajani and Kar-

Outpatient Diversion using Real-time Length-of-Stay Predictions

gari, 2016; Hijry and Olawoyin, 2020). The majority

of authors concluded that factors such as severity of

the disease, recency of diagnosis and type of surgery,

patient age, number of comorbidities, surgery type,

number of days of hospitalisation before surgery, etc.,

were signiﬁcantly correlated with patient LOS. These

studies did not determine the effect of operational

variables such as the number of patients in the queue

for system resources, the elapsed service time of pa-

tients currently receiving care, etc., on patient LOS.

In this context, we generate LOS predictions via a

methodology grounded in queueing theory and real-

time delay prediction that estimates patient LOSs in

the PHC as a function of operational ‘system state’

variables such as the number of patients in the queue

at each queueing system within the PHC (e.g., the

queueing system represented by the doctor and the

laboratory), the elapsed service times of patients cur-

rently receiving service at each queueing subsystem,

arrival and service rates of patients in the PHC, and

the average travel time of patients to the PHC from

their point of origin. If the patient decides to leave for

the PHC at time t, then the LOS prediction is gener-

ated for the time of arrival of the patient in the system

- i.e., at time t + δ, where δ is the travel time to the

PHC from the patient’s location.

We note here that because we use real-time de-

lay predictions to generate the LOS predictions, our

approach can be extended to multi-class multi-server

systems for which real-time delay predictors have

previously been developed, including certain sys-

tems with non-stationary arrival and service processes

(Ibrahim, 2018). Further, in general, our approach is

likely to require fewer variables to be recorded for

generating the real-time delay estimates in compari-

son to statistical learning predictors, and its develop-

ment and deployment will not require construction of

a training and validation dataset. We also note that the

majority of previous work focuses on generating LOS

predictions for patients at a single unit of a health-

care facility, such as the emergency department, and

do not generate predictions for patients that receive

service from multiple units within a given facility. In

comparison, our approach generates LOS predictions

at multiple units within the same facility; that is, total

predicted LOS is the summation of time spent at each

PHC subsystem.

2.2 Patient Diversion

There are multiple studies considering patient diver-

sion as a means to reduce congestion at healthcare

facilities. In a review by Li et al. (2019), the au-

thors ﬁnd that patient diversion was initiated based

on multiple measures of congestion, such as the av-

erage wait time of patients before receiving care, the

number of patients waiting to receive care, the num-

ber of occupied beds in a ward, etc. From a method-

ological standpoint, the approaches used to optimize

various aspects of the diversion process include a

Markov decision process formulation to maximize the

cost-effectiveness of diversion policies for ICU pa-

tients in a public-private hospital network (Marquinez

et al., 2021), a simulation optimization approach to

minimize the time to receive care (including wait

times and travel times between facilities) (Ramirez-

Nafarrate et al., 2011), and a mixed integer program-

ming approach to minimize the number of patients

waiting for care across the network (Nezamoddini and

Khasawneh, 2016). Fatma and Ramamohan (2021a)

evaluated via DES the effectiveness of patient diver-

sion strategies on multiple operational outcomes such

as resource utilizations, wait times, and the propor-

tion of patients whose wait time before receiving care

exceeds a threshold duration. The proportion of pa-

tients leaving without receiving care has also been an

operational outcomes of interest in multiple studies

(Morley et al., 2018).

An important consideration in implementing a di-

version mechanism within a healthcare facility net-

work is information sharing across the network re-

garding operational variables at each facility that are

used to determine diversion decisions. In this re-

gard, there is considerable support in the literature re-

garding implementing centralized diversion policies

across healthcare facilities, because diverting patients

without considering the operational information at

other facilities can yield worse operational outcomes

for both patients and the healthcare facilities across

the network, such as increased wait times for the di-

verted patient, and increased crowding at healthcare

facilities in the network (Deo and Gurvich, 2011; Li

et al., 2019; Shi et al., 2021). This has been fur-

ther emphasized in the recently published literature,

wherein Shi et al. (2021) ﬁnd that communication and

coordination among healthcare facilities are crucial to

relieve congestion across all facilities in a healthcare

network, and diversion decisions must be made us-

ing infomation available from electronic management

systems networked across all facilities under consid-

eration (Adjerid et al., 2018; Dong et al., 2019; Pier-

marini and Roma, 2021). In this context, our study

also proposes a diversion mechanism for outpatients

that implicitly assumes the presence of a centralized

IT system that maintains information regarding the

operational status - in terms of system state variables

such as the number of patients waiting and elapsed

service times in various queues within the facility -

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

that is available to all facilities within the network.

We note here that most studies we surveyed, as is

natural, considered diversion of emergency patients.

Only Nezamoddini and Khasawneh (2016) brieﬂy

discuss the effect of diverting non-emergency patients

to other healthcare facilities in a multi-hospital set-

ting. To the best of our knowledge, we did not identify

other studies that considered diversion of outpatients,

and in particular, we did not identify other studies that

utilized real-time LOS estimates for this purpose.

As discussed above, our approach - in relation

with the extant literature - also considers a central-

ized diversion mechanism involving information shar-

ing. In this regard, our work is similar to the work

by Fatma and Ramamohan (2021a); however, where

they use real-time delay estimates to divert emer-

gency (childbirth) patients arriving at facilities within

a healthcare network seeking care, we utilize real-

time delay estimates in generating LOS predictions

- at the point in time when they may access the IT

system associated with the healthcare network - to as-

sign patients to a facility within the network. While

this may seem like a facility assignment exercise in-

stead of patient diversion, we consider this a diversion

issue because patients are typically already assigned

as belonging to the catchment area of their nearest

PHC, and hence our framework determines whether

they must be ‘diverted’ to visit a facility located far-

ther from them on the basis of real-time LOS predic-

tions. However, where such facility assignment is not

a priori performed, our approach can be used for real-

time facility assignment as well.

3 PRIMARY HEALTH CENTERS

In India, PHCs serve as the ﬁrst point of contact be-

tween the population and the healthcare provider with

the objective of making healthcare services accessible

in both the rural and urban areas. PHCs are estab-

lished to cover a population of 30,000 in rural areas

and 20,000 in hilly, tribal, and desert areas, providing

a range of essential outpatient care, and limited inpa-

tients and childbirth care (IPHS-Guidelines, 2012).

PHCs provide six hours of outpatient care ser-

vices and 24×7 emergency services including in-

patient and childbirth care to the patients. PHCs

have one to two doctors, a non-communicable disease

(NCD) nurse for conducting lifestyle disease checks,

one staff nurse per shift, a pharmacist, and a labo-

ratory technician. Routine blood and urine investi-

gations, and sputum tests for suspected tuberculosis

cases are offered by the in-house laboratory within the

PHCs. PHCs also have one labor bed for normal and

assisted deliveries for childbirth patients and four to

six indoor beds for admitting emergency patients to

ensure easy access to public health facilities. We re-

fer readers to Shoaib and Ramamohan (2021) for a

detailed understanding of medical care operations at

PHCs.

We now brieﬂy describe the patient ﬂow within

PHCs. Outpatients aged greater than 30 years ﬁrst

consult the NCD nurse before consulting the doctor.

The NCD nurse checks blood pressure and blood glu-

cose levels, body temperature, and also provides diet-

related consultation to patients, as required. Other

outpatients directly consult the doctor or wait in the

outpatient queue if the doctor is busy with other pa-

tients. Once the outpatients complete their consulta-

tion with the doctor, approximately half the patients

are sent to the in-house laboratory for routine inves-

tigations. All patients exit from PHC via the phar-

macy regardless of whether they require medication,

because the pharmacy also performs the administra-

tive task of registering patient visits before their exit

from the PHC. Outpatient ﬂow through the PHC is

depicted in Figure 1.

During outpatient department (OPD) hours, inpa-

tients and childbirth patients are attended to by the

doctor ﬁrst and if the doctor is unavailable, they are

attended to by the staff nurse. Once their consultation

with the doctor is complete, inpatients are admitted to

the inpatient department (IPD) where the staff nurse

monitors their condition and treats accordingly. In-

patient LOSs in the IPD range from four to six hours,

because patients are typically admitted for minor con-

ditions that require monitoring and treatment for brief

periods. Childbirth patients are taken to the labour

room for delivery under the supervision of the doctor

and the staff nurse. After delivery, childbirth patients

are shifted to the IPD ward. Note that for more com-

plex inpatient and childbirth cases requiring more in-

tensive and specialized care, patients are referred to

higher level facilities. Outside OPD hours, patients

are attended to by the staff nurse alone with doctors

being summoned on very rare occasions.

As documented in Shoaib and Ramamohan

(2021), input parameters such as the average num-

ber of arrivals of each type of patient per day (ar-

rival distributions were assumed to be Poisson), and

the service time distribution parameters of the doc-

tor, nurses, laboratory technicians, and the pharma-

cist were estimated based on data collection from

in person visits to multiple PHCs. For example,

the best-ﬁt distribution for the NCD nurse service

time was found to be the uniform distribution with

parameters U(2, 5). Truncated Gaussian distribu-

tions were found to ﬁt the service times of other

Outpatient Diversion using Real-time Length-of-Stay Predictions

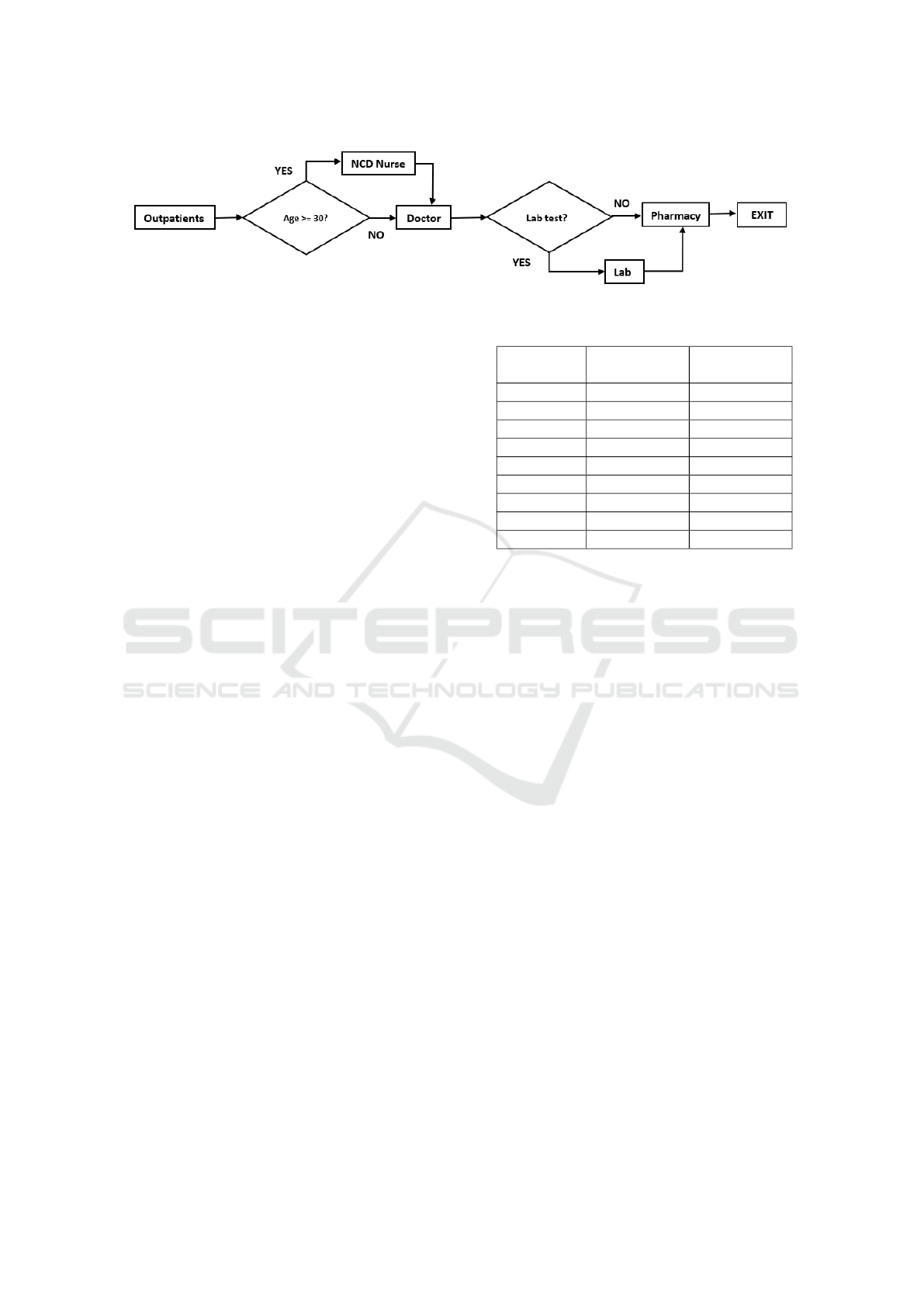
Figure 1: Outpatient ﬂow at the PHC. Lab = laboratory.

resources - the doctor, laboratory technician, and

pharmacist - best, with parameters N(0.87, 0.21

N(3.451, 0.873

), and N(2.084, 0.723

) minutes, re-

spectively. We refer readers to Shoaib and Ramamo-

han (2021) for a complete description of the param-

eter estimation process for other patient types served

by PHCs.

The focus of this analysis is outpatient ﬂow in

the PHCs given that we consider outpatient diver-

sion based on LOS estimates for the PHCs. We ap-

proximate the outpatient ﬂow through the PHC op-

erations as the ﬂow of an entity through one more

M/G/1 queueing systems in series. This approxima-

tion is possible due to the very large disparity in the

arrival rates between outpatients and patients requir-

ing admission (i.e., inpatients and childbirth patients).

This is discussed in further detail in Shoaib and Ra-

mamohan (2021).

Based on the outpatient ﬂow described in Figure 1

and input parameter estimates, we develop a discrete-

event based simulation model of the patient care op-

erations at two PHCs. The programming was done in

Python using the Salabim package on an Intel i7 64-

bit Microsoft Windows operating system with 16 gi-

gabytes of memory. Salabim is a discrete event simu-

lation package in python developed by (van der Ham,

2018). The package provides animation, queues,

states, monitors for data collection and presentation,

and simulation event tracing functionality. A single

replication of the simulation involved a run-time hori-

zon of 365 days with a warm-up period of 180 days.

Each replication required approximately 4 minutes

of computational run-time. We collect data from 40

replications and report the means and standard devi-

ations of key performance measures at both PHCs in

Table 2.

From Table 2, we observe that the average pa-

tient LOS at PHC

is signiﬁcantly higher than that

of PHC

. We also note a similar trend in other per-

formance measures such as resource utilizations and

average wait time for all the staffs involved in pro-

viding medical care to outpatients at both PHCs. We

also see that the individual wait times at each queue-

ing subsystem within PHC

do not appear to be pro-

hibitively long in themselves; however, as the over-

Table 2: PHC simulation outcomes.

Outcomes* PHC

PHC

(9/1/1/1/1) (2/1/1/1/1)

doc

0.392 (0.003) 0.935 (0.003)

NCD

0.512 (0.006) 1.475 (0.019)

phar

0.383 (0.003) 1.705 (0.007)

lab

0.317 (0.005) 1.417 (0.019)

opd

0.036 (0.001) 0.235 (0.002)

phar

0.243 (0.005) 27.93 (0.618)

lab

0.593 (0.012) 17.47 (0.419)

NCD

0.629 (0.023) 30.12 (0.830)

LOS 7.180 (0.033) 57.31 (1.154)

Outpatient interarrival time (in minutes)/number of

doctors/number of NCD nurse/number of laboratory tech-

nicians/number of pharmacists.

∗

Resource utilizations

(ρ) are dimensionless fractions, wait times (w), and average

lengths of stay (LOS) are in minutes.

∗

doc

: doctor’s utilization, ρ

NCD

: NCD nurse’s utilization,

phar

: pharmacist’s utilization, ρ

lab

: laboratory technician’s

utilization, w

opd

: OPD queue wait time, w

phar

: pharmacy

queue wait time, w

lab

: laboratory queue wait time, w

NCD

NCD nurse queue wait time.

all LOS in the facility is considerable given the sig-

niﬁcantly lower service times (for example, the av-

erage consultation time with the doctor is less than

one minute) at these individual subsystems within the

PHC. These observations motivated the development

of a diversion mechanism for outpatients based on

LOS predictions, which we now describe.

4 OUTPATIENT DIVERSION

MECHANISM

The diversion mechanism for outpatients that we de-

velop is depicted in Algorithm 1. We describe this

mechanism using the case of a speciﬁc patient whose

assigned PHC is PHC

. We consider one other PHC,

which we call as PHC

(located farther from the pa-

tient than PHC

), as a potential destination for diver-

sion; however, our approach can be extended to any

number of facilities in a healthcare network. As dis-

cussed in Section 1, we assume that the patient can

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

access an IT system - either a web-based or smart-

phone application - that communicates the LOS pre-

dictions at PHC

and PHC

, and assigns the appro-

priate PHC to the patient based on these predictions.

We assume that the patient accesses the application

at time t, implying that the LOS prediction must be

generated at time t; however, the LOS at each PHC

must be estimated at the time the patient is likely to

arrive at the facility in question. Thus, while the pre-

diction is made at time t, the LOS must be estimated

at time t + δ

or t + δ

, where δ

and δ

are the travel

times of the patient to PHC

and PHC

. If we denote

these LOS estimates as LOS

t+δ

and L OS

t+δ

, then

the patient is assigned the facility with the smaller of

LOS

t+δ

and LOS

t+δ

Algorithm 1: Outpatient diversion mechanism.

1: At time t, estimate LOS

t+δ

at PHC

2: At time t, estimate LOS

t+δ

at PHC

3: Visit PHC with LOS = min{L

t+δ

, L

t+δ

}

We note here that for the purposes of this study,

we assume that the patient is required to visit the as-

signed PHC, and incurs some penalty if they visit any

other facility in the network; however, this mecha-

nism, if adopted, is realistically more likely to pro-

vide a choice to the patient. In such situations the

probability of compliance with the diversion or facil-

ity assignment suggestion must be considered in the

analysis. We do not explore this in our study, and

leave it as an immediate avenue of future research.

Another consideration here is that the diversion

decision can be based on whether the sum of travel

time to the PHC under consideration plus predicted

LOS at the PHC is less than the corresponding quan-

tity at the other PHCs in the network. We do not con-

sider this case in our current version of the LOS-based

diversion mechanism; this is because we wish to in-

troduce this real-time LOS prediction based diversion

mechanism in its simplest form (i.e., based only on

predicted LOS at each facility). However, the diver-

sion mechanism in Algorithm 1 can easily be mod-

iﬁed to take such additional considerations into ac-

count, and we intend to explore this speciﬁc consid-

eration in future work. Note also that the estimates of

travel times used in the above algorithm can be con-

sidered to be average values; however, the actual val-

ues used in the diversion algorithm can be real-time

estimates obtained from applications such as Google

Maps depending upon the application process inter-

face links that can be integrated into the IT system

used for deployment of the diversion mechanism.

It is evident that the key steps within the diversion

mechanism in Algorithm 1 are the estimation of the

LOSs L

t+δ

and L

t+δ

. We now describe how these

LOS predictions are generated.

4.1 Real-time LOS Prediction

As discussed in Section 3, we approximate the outpa-

tient care process at the PHC as receiving care from

one or more M/G/1 systems in series. The four pos-

sible M/G/1 system pathways for an outpatient in the

PHC have also been depicted in Figure 1. We estimate

the LOS in the PHC as the sum of the LOSs in each

of the M/G/1 subsystems where the patient is likely to

receive service.

LOS

phc

= LOS

doc

+ LOS

NCD

+ LOS

lab

+ LOS

pharmacy

(1)

The terms in equation 1 are self-explanatory. We

note here that for LOS

phc

to be as accurate as pos-

sible, the LOSs associated with the laboratory and

NCD nurse queueing systems must be weighted with

the probabilities that the patient avails of service from

these subsystems. However, we do not do this be-

cause of precendence in the literature regarding pro-

viding quantiles higher than the 50

quantile of the

distribution of the predicted delay - or in this case, the

predicted LOS - to increase customer satisfaction in

queues (Whitt, 1999; Ibrahim, 2018). Note that this

implies that we overestimate the LOS; however, given

that each of the terms in equation 1 scales in the same

manner with patient load, and does so to the same ex-

tent for all facilities considered, the diversion decision

itself is not affected by this overestimation. Each LOS

term in the right-hand side of equation 1 is estimated

as the sum of the prediction of the delay experienced

by the patient at the M/G/1 system under question and

the average service time at the system. This is given

in equation 2 below.

LOS

= d

+ E[s], ∀ s ∈ S (2)

In equation 2, s is a subscript indicating an

M/G/1 queueing subsystem in the PHC, and s ∈ S =

{doc, NCD, lab, pharmacy}. d

represents the esti-

mated delay for the patient at a given M/G/1 subsys-

tem, and E[s] represents the expected value of the ser-

vice time. The estimated delay d

is in turn estimated

as a function of the number of patients ahead of the

patient under consideration in the queue, and the ex-

pected remaining service time for the patient currently

receiving service at the queueing system. This is ex-

pressed below.

= L

q(s)

E[s] + r

, ∀ s ∈ S (3)

In equation 3, L

q(s)

represents the number of pa-

tients ahead of the patient under consideration in the

queue at subsystem s, and r

represents the prediction

Outpatient Diversion using Real-time Length-of-Stay Predictions

of the remaining service time given that the elapsed

service time for the patient receiving service is x. We

now discuss how r

is generated. For M/G/1 systems,

the estimation of r

is traditionally done as in equa-

tion 4. In equation 4, T is the random variable repre-

senting the service time (t is thus its realization), G is

the cd f of the service time.

P(T ≤ t|x) =

P(x ≤ T ≤ t + x)

P(T ≥ x)

=⇒ G(t|x) =

G(t + x) − G(x)

1 − G(x)

(4)

is then estimated as the expected value of the

remaining service time by calculating the pd f g(t|X)

from equation 4. However, performing this calcu-

lation can prove tedious depending upon the nature

of the distribution G(t|x) (Fatma and Ramamohan,

2021b). For example, computing r

via equation 4

for the triangular distribution requires working with a

piecewise continuous cd f , and for the Gaussian dis-

tribution requires numerical computation of the inte-

grals involved in computation of r

(which involve

the Gaussian error function). Therefore, we propose

an alternate delay predictor for such systems, which

can potentially also be extended to multi-class multi-

server queueing systems, that is considerably easier to

compute and implement. This delay predictor is given

below.











−1

(0.5) − x , 0 ≤ x < G

−1

(0.5)

−1

(0.75) − x , G

−1

(0.5) ≤ x < G

−1

(0.75)

(b−x)

, G

−1

(0.75) ≤ x ≤ b

(5)

Here, r

is estimated depending upon the range in

which the elapsed service time x of the patient cur-

rently in service lies with respect to the service time

distribution. G

−1

(0.5), and G

−1

(0.75) are the 50

and 75

quantiles of the service time distribution, re-

spectively, and b is the extreme quantile (e.g., equal to

−1

(0.99)) or the upper limit of the service time cd f

(e.g., where the cd f has bounded support).

as estimated from equation 5 can then be used

in conjunction with equations 3 and 2 to estimate the

LOS at the subsystem under consdieration. This com-

putation would sufﬁce if the LOS prediction is re-

quired to be made at time t; however, we require LOS

predictions at time t + δ, where δ is the time required

for the patient to arrive at the PHC. LOS predictions

at time t + δ are generated as follows.

In order to calculate the LOS prediction at time

t + δ, we must ﬁrst estimate the effective average

queue length at t + δ, L

q(t+δ)

, as a function of the

queue length at time t, given by L

q(t)

. This can be ac-

complished using the average post-diversion patient

arrival and service rates, λ

and E[s], respectively.

This is given below.

q(t+δ)

= L

+ (λ

− 1) −



max



δ − r

e(t)

E[s]

, 0



(6)

In equation 6, we substract 1 from λ

to account

for the patient under consideration for diversion, and

the third term on the right hand side represents the av-

erage number of patients that can be served in δ time

units after taking into account the remaining service

time r

e(t)

of the patient in service at time t. The av-

erage elapsed service time at time t + δ, denoted by

t+δ

, is thus estimated as the remainder of

δ−r

e(t )

E[s]

, and

the average remaining service time at t + δ, denoted

by w

e(t+δ)

, is estimated by inputting x

t+δ

into equa-

tion 5. The expected delay at time t + δ for a patient

arriving to subsystem s, d

s(t+δ)

, can thus be estimated

by inputting L

q,s(t+δ)

and r

e,s(t+δ)

into equation 3, and

the LOS at time t + δ can in turn be generated using

the value of d

s(t+δ)

in equation 2. This is summarized

in equation 7 below.

LOS

s(t+δ)

= d

s(t+δ)

+ E[s]

where d

s(t+δ)

= L

q,s(t+δ)

E[s] + r

e,s(t+δ)

(7)

The LOS at subsystem s estimated from equa-

tion 7 can be used to calculate the LOS at each of

the subsystems in S, and then summed per equation 1

to yield the total LOS at the PHC. Note that the LOS

prediction at each subsystem must be calculated at the

point at which the predicted LOS at the previous sub-

system ends. This process of successively calculating

the LOSs is summarized in Algorithm 2.

Algorithm 2: Calculation of the total LOS at a PHC.

1: Initialize with the ordered tuple S

ord

(NCD, doc, lab, pharmacy), δ = travel time

to the PHC, current time t, LOS

tot

= 0.

2: for s ∈ S

ord

3: Estimate LOS at s at time t + δ as LOS

s(t+δ)

4: LOS

tot

= LOS

tot

+ LOS

s(t+δ)

5: δ = δ + LOS

s(t+δ)

We must mention here that in the implementation

of the above algorithm, the arrival rate at each sub-

system is assumed to be the same - that is, λ

. This is

possible only because we assume that patients visit all

subsystems in series (Hopp and Spearman, 2011), and

we consider relaxing this assumption as an immediate

avenue of future work. We describe the outcomes of

implementing the diversion mechanism in the follow-

ing section.

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

We also note here that the deployment and gen-

eration of these LOS predictions is unlikely to incur

signiﬁcant computational expense, regardless of the

size of the facility network. This is because the gen-

eration of the LOS predictions at a facility involves

just a single function evaluation, and this will remain

the same regardless of the type of LOS predictor in-

volved - for example, a queueing theory based predic-

tor or a statistical learning based predictor. However,

the speciﬁc LOS predictor to be employed must be se-

lected taking into account the number of system state

variables that are required for LOS prediction. For ex-

ample, if a particular LOS predictor requires a large

number of system state variables to be recorded and

updated at high frequency, then the complexity of the

IT system required for this purpose will also increase.

On the other hand, if another LOS predictor is avail-

able that requires signiﬁcantly fewer variables to be

recorded at a small loss of predictor accuracy, then it

might be prudent to choose this latter LOS predictor

from the standpoint of ease of deployment.

Now, based on the real-time LOS estimates gener-

ated using Algorithm 2, we can implement the diver-

sion mechanism in Algorithm 1.

5 SIMULATION EXPERIMENTS

In this section, we present results from implementing

the diversion mechanism described in Algorithm 1.

We compare the operational outcomes at both PHCs

for three cases: (a) without diversion, (b) diversion

implemented using actual real-time LOS estimates

(which are available to the simulation modeler), and

methodology described in Section 4.1. Before we

present the operational outcomes, we discuss the ac-

curacy of the real-time LOS predictor.

We characterize the accuracy of the LOS predic-

tor using the mean absolute percentage error (MAPE)

score, which is given by the formula MAPE =

∑

i=1



LOS

a,i

−LOS

p,i

LOS

a,i



. Here LOS

a,i

is the actual LOS

estimate of the i

patient and LOS

p,i

is the predicted

LOS estimate of the i

patient and N is the number

of patients in the sample. When LOS predictions are

generated for the two PHCs that we consider (PHC

and PHC

) in the ﬁrst set of computational experi-

ments that we describe in the following paragraphs,

we ﬁnd that the MAPE scores are 13.00% and 18.14%

at PHC

and PHC

, respectively. While this appears

to indicate reasonable performance of the LOS pre-

dictor, several avenues of improvement of the predic-

tor remain, which we discuss in the following section.

In Table 3, we report results from the implementa-

tion of the diversion mechanism for PHC

and PHC

with operational parameters corresponding to those

described in Table 2. Given that diversion is likely

to make the utilization of resources more equitable

across a network of facilities, and due to space lim-

itations, we report the mean and standard deviation

of the percentage difference between operational out-

comes such as resource utilizations, wait time, and

average LOSs across both healthcare facilities in Ta-

ble 3. We also report the percentage of patients who

are diverted - that is, those who visit a PHC than their

assigned PHC. We report these outcomes for the three

cases discussed in the above paragraphs.

Table 3: Outpatient diversion: operational outcomes across

both PHCs.

Outc-

omes

No diver-

sion

With actual

LOS

With pre-

dicted LOS

∆

doc

58.09 (0.36) 5.91 (0.03) 15.60 (0.01)

∆

ncd

65.26 (0.58) 7.82 (0.02) 13.50 (0.02)

∆

phar

77.52 (0.18) 16.33 (0.02) 22.20 (0.04)

∆

lab

77.59 (0.45) 10.30 (0.03) 18.02 (0.06)

∆

opd

84.53 (0.38) 4.07 (0.02) 46.77 (0.03)

∆

phar

99.12 (0.02) 51.55 (0.08) 74.28 (0.03)

∆

lab

96.60 (0.09) 37.95 (0.05) 79.03 (0.04)

∆

ncd

97.91 (0.10) 14.12 (0.10) 86.16 (0.02)

∆

LOS

87.46 (0.26) 10.21 (0.04) 63.41 (0.08)

∗

0.00 (0.00) 30.95 (2.98) 45.25 (1.48)

∆

doc

= difference in doctor’s utilization, ∆

NCD

= difference in NCD nurse utilization,

∆

phar

= difference in pharmacist’s utilization, ∆

l ab

= difference in laboratory techni-

cian’s utilization, ∆

opd

= difference in OPD queue wait time, ∆

phar

= difference in

pharmacy queue wait time, ∆

l ab

= difference in laboratory queue wait time, ∆

NCD

difference in NCD nurse queue wait time, β

∗

= proportion (%) of outpatients who are

diverted.

It is evident from Table 3 that implementing di-

version leads to signiﬁcantly more equitable opera-

tional outcomes across both PHCs. Without diver-

sion, as seen from Table 2, the LOS at PHC

was

57.31 minutes in comparison to an LOS of 7.18 min-

utes at PHC

. When diversion is implemented using

the actual real-time LOS estimates, we see that the

LOS at PHC

reduces to 15.33 minutes whereas the

LOS at PHC

increases to 13.75 minutes. With diver-

sion implemented using the real-time LOS predictor,

we see LOSs of 25.92 minutes at PHC

and 9.50 min-

utes at PHC

. Thus it is clear that diversion, even

using the real-time LOS predictor, yields a reduction

in LOS at the more heavily utilized system.

From Table 3, we see similar trends in the other

outcomes as well when diversion is implemented us-

ing the real-time LOS predictor. Overall, we see a

signiﬁcant decrease in the congestion in PHC

. A key

observation is that the extent to which operational out-

Outpatient Diversion using Real-time Length-of-Stay Predictions

comes become equitable across both PHCs depend on

the accuracy of the delay predictor employed - that is,

the relative difference in a resource’s utilization or the

wait time at a subsystem increases with a decrease in

the accuracy of the delay predictor used. Another im-

portant observation is that the proportion of patients

diverted also increase with decrease in delay predic-

tor accuracy. However, this is likely due to the sig-

niﬁcant difference in the outpatient loads between the

two PHCs prior to implementing diversion - that is, an

average interarrival time of 9 minutes at PHC

com-

pared to an average interarrival time of 2 minutes at

PHC

In order to check how the operational outcomes

change with diversion when the difference in outpa-

tient loads across both PHCs is not as high as in the

previous case, we conducted a sensitivity analysis by

changing the average interarrival times of outpatients

to 2 minutes at PHC

and 4 minutes at PHC

. We

present the results from this sensitivity analysis re-

sults in Table 4 and observe similar trends in the oper-

ational outcomes across both PHCs as observed in Ta-

ble 3. We note that the MAPE scores of the real-time

LOS predictor that we propose at PHC

and PHC

were found to be 13.82% and 18.33% respectively,

respectively.

Table 4: Sensitivity analysis: operational outcomes across

both PHCs.

Outc-

omes

No diver-

sion

With actual

LOS

With pre-

dicted LOS

∆

doc

37.28 (0.41) 18.82 (0.05) 24.91 (0.01)

∆

ncd

41.92 (0.85) 19.84 (0.04) 26.68 (0.02)

∆

phar

49.92 (0.85) 22.96 (0.04) 34.08 (0.01)

∆

lab

50.02 (1.07) 24.28 (0.04) 33.29 (0.02)

∆

opd

60.01 (0.84) 11.52 (0.05) 17.13 (0.07)

∆

phar

96.19 (0.08) 46.19 (0.07) 64.84 (0.03)

∆

lab

87.59 (0.52) 44.81 (0.09) 71.24 (0.03)

∆

ncd

92.52 (0.23) 29.18 (0.07) 71.24 (0.03)

∆

LOS

83.15 (0.29) 31.48 (0.07) 78.96 (0.01)

∗

0.00 (0.00) 45.37 (0.78) 36.69 (0.10)

∆

doc

= difference in doctor’s utilization, ∆

NCD

= difference in NCD nurse utilization,

∆

phar

= difference in pharmacist’s utilization, ∆

l ab

= difference in laboratory techni-

cian’s utilization, ∆

opd

= difference in OPD queue wait time, ∆

phar

= difference in

pharmacy queue wait time, ∆

l ab

= difference in laboratory queue wait time, ∆

NCD

difference in NCD nurse queue wait time, β

∗

= proportion (%) of outpatients who are

diverted.

Once again, as expected, we notice that the ex-

tent to which operational outcomes become equitable

across both PHCs decreases with a decrease in the

accuracy of the LOS predictor employed. However,

when compared to the corresponding outcome in Ta-

ble 3, we notice the proportion of patients diverted

actually decreases with a decrease in the accuracy of

the LOS predictor. That is, in this case, the proportion

diverted decreases with the less accurate LOS predic-

tor. Thus, our results indicate that the proportion of

patients diverted across a healthcare facility network,

when diverted on the basis of real-time LOS predic-

tions, depend on both the accuracy of LOS predictor

employed as well as the differences in patient loads

across the facilities within the network.

Overall, it is evident that outpatient diversion us-

ing real-time LOS predictions appears to improve op-

erational performance of a healthcare facility network

from both the provider as well as patient standpoints.

We now conclude our work with a discussion of

the contributions of our work and avenues for further

research.

6 DISCUSSION & CONCLUSIONS

In this work, we present preliminary results from the

simulated implementation of a framework for outpa-

tient diversion using real-time LOS predictions. We

emphasize here that the real-time LOS predictions

and the diversion decision are made at the point of

origin of the patient, as opposed to when the patient

arrives at a healthcare facility. We empirically show

via DES that patient diversion results in more equi-

table utilization of resources across the healthcare fa-

cilities that we consider when compared to the case

without diversion. The diversion framework that we

propose can also be repurposed for real-time facility

assignment in health systems where patients are not a

priori assigned their ﬁrst point of contact for medical

care.

To the best of our knowledge, our study is the

ﬁrst of its kind that considers real-time LOS predic-

tions in initiating diversion across healthcare facili-

ties. Previous studies initiated diversion using fac-

tors such as average wait time, number of beds occu-

pied, number of patients in waiting queue. Further, we

demonstrate how LOS can become a criterion for di-

version especially when diversion of non-emergency

patients, and in particular outpatients, is considered.

Once again, we did not come across a previously pub-

lished study that considered outpatient diversion. Fi-

nally, to our knowledge, our study is also the ﬁrst to

develop a methodology for the real-time estimation

of LOSs in the near future. This in turn utilizes a

novel approximation of the real-time delay predictor

for M/G/1 queueing systems. In comparison to most

studies in the literature that utilize LOS predictors

based on statistical learning methods, our analytical

approach grounded in queueing theory may be easier

to program and deploy in practice. Further, our ap-

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

proach also opens up avenues for leveraging the sub-

stantial body of work regarding real-time delay pre-

diction for real-time LOS-based diversion for more

complex queueing systems than that encountered in

this study.

A key avenue of future research involves improv-

ing the accuracy of the real-time LOS predictor that

we develop in this study. While the accuracy of

our real-time LOS predictor appears reasonable, with

MAPEs not exceeding 20%, relaxing our assump-

tion that all patients avail service from all subsystems

within the PHC is likely to improve the accuracy of

the predictor. A related direction for future work in-

volves benchmarking our work against statistical ma-

chine learning based predictors of LOS, and assessing

how the operational outcomes compare with respect

to the outcomes associated with our queueing theory

based predictor. Similarly, our LOS based diversion

mechanism can also be compared to other diversion

mechanisms, such as wait-time based mechanisms.

A key question that arises here is how the imple-

mentation of the diversion mechanism in Algorithm 1

would scale in terms of computational and operational

overheads when the size of the network increases.

One of the questions that must be answered prior to

deploying this approach in a larger network would in-

volve determining, for each facility in the network,

the set of facilities at which real-time LOS predictions

must be generated in order to determine the diversion

decision. For example, in a network with 1,000 fa-

cilities, in order to determine the diversion decision

for a patient, real-time LOS predictions need not be

generated at each of the 1,000 PHCs (as many would

be located at a signiﬁcant distance from the patient’s

assigned PHC). Thus determining the optimal set of

facilities that need to be considered as diversion des-

tinations for a given facility in a large network be-

comes an important avenue of future research when

considering the scaling of this approach to larger fa-

cility networks. As part of this, an immediate avenue

of research we are pursuing includes expanding this

diversion framework to the entire network of 9 PHCs

in the Indian district that we consider, and we plan to

answer the above question for this network.

Finally, another avenue of future research is ex-

tending our work to more complex queueing systems,

including multi-class multi-server systems, which

may be applicable in the case of diversion of inpa-

tients or emergency patients. These more complex

queueing systems can include queueing systems with

non-stationary arrival and service processes. Real-

time delay predictors have been developed for certain

queueing systems with non-stationary arrival, service

or abandonment processes (Ibrahim, 2018); and LOSs

for such systems may correspondingly be calculated

in a manner similar to that which we have described

in this paper. However, in case the non-stationarity is

not complex - for example, increased arrival rates may

be observed during the weekends, and arrival rates re-

main the same during all weekdays - then the method-

ology described for LOS prediction in this paper can

directly be applied by just changing the arrival rates

in the LOS predictor expressions depending upon the

day of the week.

REFERENCES

Adjerid, I., Adler-Milstein, J., and Angst, C. (2018). Reduc-

ing medicare spending through electronic health infor-

mation exchange: the role of incentives and exchange

maturity. Information Systems Research, 29(2):341–

361.

Aghajani, S. and Kargari, M. (2016). Determining factors

inﬂuencing length of stay and predicting length of stay

using data mining in the general surgery department.

Hospital Practices and Research, 1(2):53–58.

Alsinglawi, B., Alnajjar, F., Mubin, O., Novoa, M., Alor-

jani, M., Karajeh, O., and Darwish, O. (2020). Pre-

dicting length of stay for cardiovascular hospitaliza-

tions in the intensive care unit: Machine learning ap-

proach. In 2020 42nd Annual International Confer-

ence of the IEEE Engineering in Medicine & Biology

Society (EMBC), pages 5442–5445. IEEE.

Areﬁan, H., Hagel, S., Fischer, D., Scherag, A., Brunkhorst,

F. M., Maschmann, J., and Hartmann, M. (2019).

Estimating extra length of stay due to healthcare-

associated infections before and after implementation

of a hospital-wide infection control program. PloS

One, 14(5):e0217159.

Ayyoubzadeh, S. M., Ghazisaeedi, M., Kalhori, S. R. N.,

Hassaniazad, M., Baniasadi, T., Maghooli, K., and

Kahnouji, K. (2020). A study of factors related to pa-

tients’ length of stay using data mining techniques in a

general hospital in southern iran. Health Information

Science and Systems, 8(1):1–11.

Baek, H., Cho, M., Kim, S., Hwang, H., Song, M., and

Yoo, S. (2018). Analysis of length of hospital stay

using electronic health records: A statistical and data

mining approach. PloS One, 13(4):e0195901.

Barnes, S., Hamrock, E., Toerper, M., Siddiqui, S., and

Levin, S. (2016). Real-time prediction of inpatient

length of stay for discharge prioritization. Jour-

nal of the American Medical Informatics Association,

23(e1):e2–e10.

Blanchard, J., Washington, R., Becker, M., Vasanthakumar,

N., Gopal, K. M., and Sarwal, R. (2021). Vision 2035

public health surveillance in india.

Deo, S. and Gurvich, I. (2011). Centralized vs. decen-

tralized ambulance diversion: A network perspective.

Management Science, 57(7):1300–1319.

Dong, J., Yom-Tov, E., and Yom-Tov, G. B. (2019). The

impact of delay announcements on hospital network

Outpatient Diversion using Real-time Length-of-Stay Predictions

coordination and waiting times. Management Science,

65(5):1969–1994.

El-Bouri, R., Taylor, T., Youssef, A., Zhu, T., and Clifton,

D. A. (2021). Machine learning in patient ﬂow: a re-

view. Progress in Biomedical Engineering.

Fatma, N., Mohd, S., Ramamohan, V., and Mustafee, N.

(2020). Primary healthcare delivery network simu-

lation using stochastic metamodels. In 2020 Winter

Simulation Conference (WSC), pages 818–829. IEEE.

Fatma, N. and Ramamohan, V. (2021a). Patient diversion

across primary health centers using real time delay

predictors. In 2021 Institute of Industrial and Systems

Engineers (IISE) Annual Conference & Expo.

Fatma, N. and Ramamohan, V. (2021b). Patient diversion

using real-time delay prediction across healthcare fa-

cility networks. http://web.iitd.ac.in/

∼

mez188287/NF.

pdf, accessed 29

November 2021.

Guti

errez, J. M. P., Sicilia, M.-

A., Sanchez-Alonso, S.,

and Garc

ıa-Barriocanal, E. (2021). Predicting length

of stay across hospital departments. IEEE Access,

9:44671–44680.

Hijry, H. and Olawoyin, R. (2020). Application of ma-

chine learning algorithms for patient length of stay

prediction in emergency department during hajj. In

2020 IEEE International Conference on Prognostics

and Health Management (ICPHM), pages 1–8. IEEE.

Hopp, W. J. and Spearman, M. L. (2011). Factory physics.

Waveland Press.

Ibrahim, R. (2018). Sharing delay information in ser-

vice systems: a literature survey. Queueing Systems,

89(1):49–79.

IPHS-Guidelines (2012). Guidelines for Primary Health

Centres. Directorate General of Health Services, New

Delhi, India.

Li, M., Vanberkel, P., and Carter, A. J. (2019). A review

on ambulance ofﬂoad delay literature. Health Care

Management Science, 22(4):658–675.

Liu, Y., Zhong, L., Yuan, S., and van de Klundert, J. (2018).

Why patients prefer high-level healthcare facilities: a

qualitative study using focus groups in rural and urban

china. BMJ Global Health, 3(5):e000854.

Marquinez, J. T., Saur

e, A., Cataldo, A., and Ferrer, J.-C.

(2021). Identifying proactive icu patient admission,

transfer and diversion policies in a public-private hos-

pital network. European Journal of Operational Re-

search.

Morley, C., Unwin, M., Peterson, G. M., Stankovich, J., and

Kinsman, L. (2018). Emergency department crowd-

ing: a systematic review of causes, consequences and

solutions. PloS One, 13(8):e0203316.

Mustafee, N. and Powell, J. (2020). Providing real-time

information for urgent care. Impact, 2021(1):25–29.

Nezamoddini, N. and Khasawneh, M. T. (2016). Model-

ing and optimization of resources in multi-emergency

department settings with patient transfer. Operations

Research for Health Care, 10:23–34.

Piermarini, C. and Roma, M. (2021). A simulation-based

optimization approach for analyzing the ambulance

diversion phenomenon in an emergency department

network. arXiv preprint arXiv:2108.04162.

Ramirez-Nafarrate, A., Fowler, J. W., and Wu, T. (2011).

Design of centralized ambulance diversion policies

using simulation-optimization. In Proceedings of

the 2011 Winter Simulation Conference (WSC), pages

1251–1262. IEEE.

Rao, K. D. and Sheffel, A. (2018). Quality of clinical care

and bypassing of primary health centers in india. So-

cial Science & Medicine, 207:80–88.

Shaaban, A. N., Peleteiro, B., and Martins, M. R. O. (2021).

Statistical models for analyzing count data: predictors

of length of stay among hiv patients in portugal using

a multilevel model. BMC Health Services Research,

21(1):1–17.

Sharma, R., Prakash, A., Chauhan, R., and Dhibar, D. P.

(2021). Overcrowding an encumbrance for an emer-

gency health-care system: A perspective of health-

care providers from tertiary care center in northern in-

dia. Journal of Education and Health Promotion, 10.

Shi, P., Helm, J. E., Deglise-Hawkinson, J., and Pan, J.

(2021). Timing it right: Balancing inpatient conges-

tion vs. readmission risk at discharge. Operations Re-

search.

Shoaib, M. and Ramamohan, V. (2021). Simulation mod-

elling and analysis of primary health centre opera-

tions. arXiv preprint arXiv:2104.12492.

Song, H., Tucker, A. L., and Murrell, K. L. (2015). The

diseconomies of queue pooling: An empirical investi-

gation of emergency department length of stay. Man-

agement Science, 61(12):3032–3053.

Turgeman, L., May, J. H., and Sciulli, R. (2017). Insights

from a machine learning model for predicting the hos-

pital length of stay (los) at the time of admission. Ex-

pert Systems with Applications, 78:376–385.

van der Ham, R. (2018). salabim: discrete event simula-

tion and animation in python. Journal of Open Source

Software, 3(27):767.

Verburg, I. W., de Keizer, N. F., de Jonge, E., and Peek,

N. (2014). Comparison of regression methods for

modeling intensive care length of stay. PloS One,

9(10):e109684.

Wachtel, G. and Elalouf, A. (2020). Addressing overcrowd-

ing in an emergency department: an approach for

identifying and treating inﬂuential factors and a real-

life application. Israel Journal of Health Policy Re-

search, 9(1):1–12.

Whiteside, T., Kane, E., Aljohani, B., Alsamman, M., and

Pourmand, A. (2020). Redesigning emergency depart-

ment operations amidst a viral pandemic. The Amer-

ican Journal of Emergency Medicine, 38(7):1448–

1453.

Whitt, W. (1999). Predicting queueing delays. Management

Science, 45(6):870–888.

Zhou, Q., Fan, L., Lai, X., Tan, L., and Zhang, X. (2019).

Estimating extra length of stay and risk factors of mor-

tality attributable to healthcare-associated infection at

a chinese university hospital: a multi-state model.

BMC Infectious Diseases, 19(1):1–7.

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems