
A Hierarchical Probabilistic Divergent Search
Applied to a Binary Classification
Senthil Murugan
1 a
, Enrique Naredo
1 b
, Douglas Mota Dias
1,2 c
, Conor Ryan
1 d
,
Flaviano Godinez
3 e
and James Vincent Patten
1 f
1
University of Limerick, Limerick, Ireland
2
Rio de Janeiro State University, Rio de Janeiro, Brazil
3
Universidad Aut
´
onoma de Guerrero, Mexico
Keywords:
Genetic Programming, Novelty Search, Classification.
Abstract:
The trend in recent years of the scientific community on solving a wide range of problems through Artificial
Intelligence has highlighted the benefits of open-ended search algorithms. In this paper we apply a probabilis-
tic version for a divergent search algorithm in combination of a strategy to reduce the number of evaluations
and computational effort by gathering the population from a Genetic Programming algorithm into groups and
pruning the worst groups each certain number of generations. The combination proposed has shown encour-
aging results against a standard GP implementation on three binary classification problems, where the time
taken to run an experiment is significantly reduced to only 5% of the total time from the standard approach
while still maintaining, and indeed exceeding in the experimental results.
1 INTRODUCTION
Nowadays, the increasing interest of the scientific
community in the Artificial Intelligence and address-
ing a wide range of real-world problems has led to
increased interest in usage of open-ended search algo-
rithms as a means of finding novel solutions. One ex-
ample of an open-ended algorithm is Novelty Search
(NS) (Lehman and Stanley, 2008). According to (Pat-
tee and Sayama, 2019), there are many examples
throughout the history of evolution on Earth showing
that open-endedness is in fact a consequence of evo-
lution. An open-ended approach has the goal to learn
a repertoire of actions covering the whole space (Kim
et al., 2021).
The original version of NS utilises the k-NN al-
gorithm to explore the search space looking for novel
behaviors and requires an archive to save previous be-
haviors in order to avoid backtracking. Defining the
right parameter k and managing the archive could rep-
a
https://orcid.org/0000-0003-0799-3079
b
https://orcid.org/0000-0001-9818-911X
c
https://orcid.org/0000-0002-1783-6352
d
https://orcid.org/0000-0002-7002-5815
e
https://orcid.org/0000-0001-5531-8989
f
https://orcid.org/0000-0002-1937-2774
resent a problem to efficiently implementing NS. One
approach to tackle these drawbacks is the Probabilis-
tic NS (Naredo et al., 2016), which is the method we
use in the work presented in this paper.
NS has been used successfully to address prob-
lems from different domains, such as the computa-
tional generation of video game content (Skjærseth
et al., 2021), on one of the most impactful tasks in
software development, namely bug repair (Trujillo
et al., 2021), and a multi-objective brain storm opti-
mization based on novelty search (MOBSO-NS) (XU
et al., 2021) as well as many others.
More recently a new family of algorithms called
quality-diversity algorithms (Pugh et al., 2016),
which combine behavior space exploration with a
global or local quality metric. An extensive study of
these related algorithms is however beyond the scope
of the research detailed in this paper.
The contributions of this paper are as follows: (i)
the introduction of an implementation of the prob-
abilistic version of novelty search (PNS) (Naredo
et al., 2016) using DEAP (Fortin et al., 2012) a is
a well known evolutionary computation framework,
and more specifically details of an implementation
that uses a Bernoulli distribution, (ii) the implemen-
tation of Pyramid Search (Ciesielski and Li, 2003) in
Murugan, S., Naredo, E., Dias, D., Ryan, C., Godinez, F. and Patten, J.
A Hierarchical Probabilistic Divergent Search Applied to a Binary Classification.
DOI: 10.5220/0010841900003116
In Proceedings of the 14th International Conference on Agents and Artificial Intelligence (ICAART 2022) - Volume 2, pages 345-353
ISBN: 978-989-758-547-0; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
345

combination with OS and PNS, (iii) details of a case
study conducted on the performance of the implemen-
tation on three binary classification problems, ranging
from easy to hard.
The remainder of this paper is organized as fol-
lows: In Section 2 a review of the main background
concepts. Next, Section 3 presents the experimental
set-up, outlining all of the considered variants and
performance measures. Section 4 presents and dis-
cusses the main experimental results of the described
research problem. Finally, Section 5 presents the con-
clusions and future work derived from this research.
2 BACKGROUND
2.1 Genetic Programming
Genetic Programming (GP) (Koza, 1992) is an evo-
lutionary algorithm which synthesize computer pro-
grams. The evolution process initiates with a popu-
lation of programs randomly created and assigning a
fitness score according to the quality performance to
solve the problem.
This score is then used to select individual pro-
grams following the Darwinian principle of natural
selection to which genetic operators such as mutation
and crossover are later applied, which drives the evo-
lution of new programs in the hope that they are better
than their parents.
Traditionally, evolutionary algorithms such as GP
guide the search by rewarding individuals close to the
predefined optimal fitness score target, which we re-
fer to in this work as Objective-based search or for
short OS. For instance, a predefined score target for
a binary classification problem is is to get 100% of
classification rate.
In this work, we use binary classification problems
and apply the Static Range Selection (SRS) described
by Zhang and Smart (Zhang and Smart, 2006). A de-
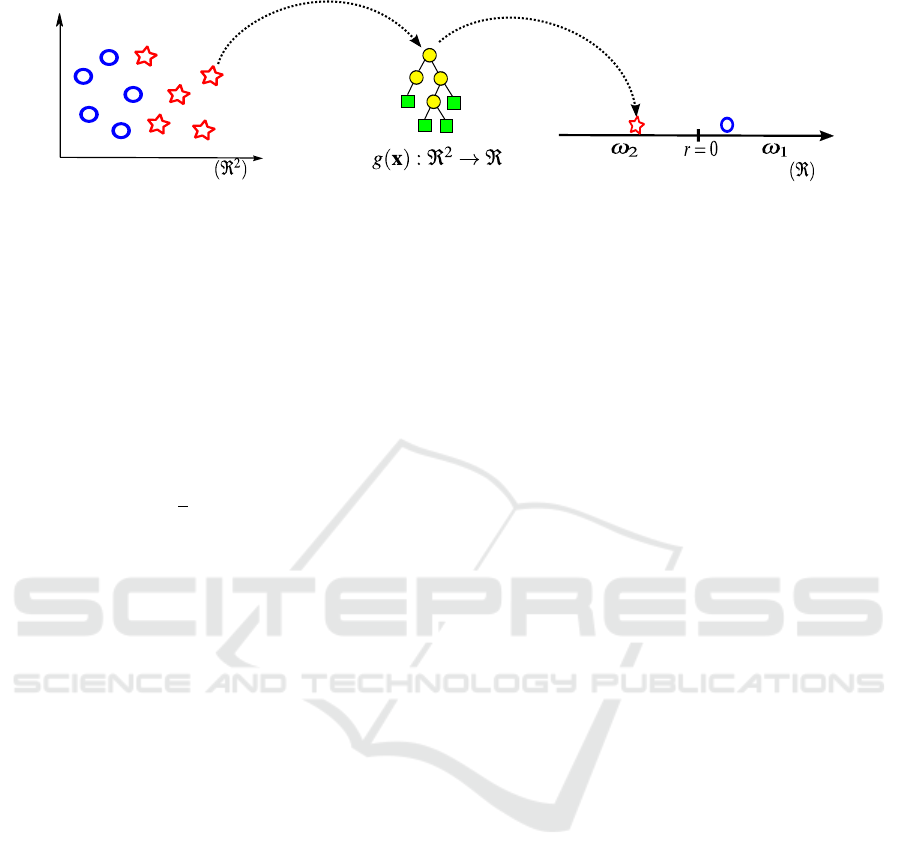
piction of the SRS based classification can be found
in figure 1. In this method, the goal is to evolve a
function g : ℜ
n
→ ℜ represented in the figure as a
tree, which can map the vector of samples x from the
hyper-dimensional feature space into a 1-dimensional
space. In the figure for visualizing purposes we use
a 2D feature space (d
1
,d
2
), meaning that each x
i
=
(d
1
,d
2
), and the general case is x
i
= (d
1
,d
2
,...,d
m
).
For a binary classification problem a typical
threshold to use is zero to split in a natural way the
one-dimensional space into two regions, where we
have at the right the region ω
1
with positive num-
bers and at the left the region ω
2
with negative num-
bers. Predictions from the GP-classifiers are in these
regions, where
b
y are the predictions to the true class
y ∈ {0,1}. More specifically, for the binary case, we
have as predictions a vector of 0s and 1s;
b
y = [
b
y
1
=
0,
b
y
2
= 1,...,
b
y
m
= 0], for short
b
y = [0,1,...,0].
The performance of a GP-classifier is measured
comparing the predictions
b
y against the true class
y assigning 1 when the sample classification is cor-
rect and 0 otherwise, resulting in a vector b =
[b
1
,b
2
,...,b
m
], where the 1s are successes or hits, then
the accuracy of a GP-classifier is computed as follows
Accuracy =
hits
number of samples
=
∑
b = 1
|b|
, (1)
where accuracy gives us an aggregated information of
each GP-classifier through a single score value.
2.2 Novelty Search
Novelty search (NS) (Lehman and Stanley, 2008) is a
diversity mechanism with a high search efficiency that
helps the search to escape from local optima avoiding
premature convergence.
NS is an alternative to OS, in which the objec-
tive function is replaced by a measurement of novelty
and uniqueness (Lehman and Stanley, 2010). On one
hand, we have OS rewarding individuals close to the
target and on the other hand we have NS rewarding
the most novel individuals. NS uses a behavior de-
scriptor, which must capture the actions taken by the
individual to make progress in the solution space. For
a binary classification problem one feasible behavior
descriptor is b described in the previous section 2.1,
whereas OS uses a score value, described in the Equa-
tion 1, where the higher score the better. Therefore,
gradients in OS are towards objective, whereas the NS
is towards behaviour.
The original measure of novelty (Lehman and
Stanley, 2008) uses the k-nearest neighbors algorithm
(k-NN), but instead of concern as to the compactness
of the cluster where the individual is located, NS mea-
sures the sparseness S around each behavior b
i
. In
other words, NS measures how different is the behav-
ior from one individual against the behavior of its k-
neighbors from b
k
, by computing the following equa-
tion:
S(b
i
) =
1
k
k
∑
l=1
dist(b
i
,b
l
) , (2)
where b
l
is the lth-nearest from k-neighbours re-
spect to the average metric dist, which is a domain-
dependent measure of the behavioural descriptor. A
general interpretation of this measure is that a behav-
ior b is novel when located in a sparse region, but not
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
346
h
d
1
d
2
Feature space
1-dimensional space
Figure 1: Graphical depiction of SRS-GPC.
novel when located in a dense region. This NS version
is easy to implement, but requires the definition of k
and this is computationally intensive for large training
sets.
In order to avoid backtracking, the revisiting of
regions that were previously explored in the search
space, NS needs to save behaviors to an archive from
the current generation. The behaviors from the cur-
rent generation and from the archive can form a bigger
seta of behaviors to compute sparseness S as follows:
S(b) =
1
k
k
∑
l=1
dist(b
i
,a
l
) , (3)
where a
l
is the lth-nearest from k-neighbours behav-
iors from both the actual generation t and the archive
with behaviors from the previous generation t-1. For
this version, when dealing with easy problems the
amount of behaviors is usually manageable, but with
more complicated problems a more considered man-
agement strategy is required. A well known method
to manage the behaviors as a queue is the first-in first-
out (FIFO). In this paper, we are not using the original
version of NS.
2.3 Probabilistic Novelty Search
The original version of NS requires the tuning the pa-
rameter k, to decide what behaviors to store in the
archive and to manage the archive. Probabilistic Nov-
elty Search (PNS) (Naredo et al., 2016) aims to tackle
these drawbacks, eliminating the parameter k, not us-
ing any archive, and as a consequence considerably
reducing the computational effort without compro-
mising the quality performance.
PNS is a probabilistic approach towards comput-
ing novelty using the same behavioral descriptor b for
NS. PNS assumes that a behaviour b
i
from an individ-
ual is independent of the behavior from any other in-
dividual, modeling the behaviors as random vectors.
During the evolutionary search process, performed by
GP, we have a population of B behaviors correspond-
ing to the GP-classifiers,
B
t
= [b]
t
j
=
h
[b]
t
1
,[b]
t
2
,...,[b]
t
n
i
, (4)
where j is the index for each individual in the popu-
lation, and t is the actual generation. Expanding the
mathematical notation we have a matrix of behaviors
each generation, as follows
B
t
=
b
t
1,1
··· ··· b
t
1,n
.
.
.
.
.
.
.
.
.
b
t
i, j
.
.
.
.
.
.
.
.
.
b
t
m,1
··· ··· b
t
m,n
. (5)
Since we are using the hits, the matrix contains 0s
and 1s. If we consider each outcome from the behav-
ior descriptor as a random variable R, we can model
the behaviors using a Bernoulli distribution, where
the random variable R takes the success value 1 with
probability p, and the failure value 0 with probability
q = 1 − p. Then, the probability of success is given
by P(R = 1) = p, and the probability of failure by
P(R = 0) = q = 1 − p, where p and q depends on the
number of samples and it is a well known fact that the
estimator of p is the sample mean.
Taking the successful case where the random vari-
able R = 1, we consider the hit from each behavior
descriptor b
t
i, j
= 1, in order to reduce the complexity
of the mathematical notation and get a more readable
notation, we simplify it by removing t, assuming that
each behavior from the population is from the actual
generation t.
As an illustrative example, say we had 7 samples
from the dataset (rows) and 6 individuals (columns)
in the population, then the order of the matrix B
∗
is
7 × 6. As can be seen in the matrix B shown in the
Equation 6, in the first row it has all 0s, and in the
last row has all 1s, meaning that the first is difficult
to classify, whereas the last one is an easy sample to
classify.
A Hierarchical Probabilistic Divergent Search Applied to a Binary Classification
347

B =
0 0 0 0 0 0
0 0 0 1 0 0
0 1 1 0 0 1
1 0 1 1 1 0
0 1 1 0 0 0
1 0 0 1 1 1
1 1 1 1 1 1
, p =
0
/6
1
/6
3
/6
4
/6
2
/6
4
/6
6
/6
. (6)
The probability p for each sample shown in B to be
correctly classified is given by the rate of number of
successes R = 1 over the number of observations and
shown in the vector p. For instance, the first sample
has a probability of
0
/6 = 0, while the last one has
6
/6 = 1 with 100% of successes.
We consider the product of the hit matrix, B with
its probability of hits, p. To make the product pos-
sible, the vector is converted to a diagonal matrix
D = diag(p), where each diagonal component is p
i
.
This way the product is P
1
= DB, where it only con-
siders the hits cases, as follows:
P
1
=
0 0 0 0 0 0
0 0 0
1
/6 0 0
0
3
/6
3
/6 0 0
3
/6
4
/6 0
4
/6
4
/6
4
/6 0
0
2
/6
2
/6 0 0 0
4
/6 0 0
4
/6
4
/6
4
/6
6
/6
6
/6
6
/6
6
/6
6
/6
6
/6
, (7)
for the first individual we have [0,0,0,
4
/6,0,
4
/6,
6
/6]
T
and summing up these probabilities we have
14
/6 =
2.33. Doing similar computation for the rest of
the individuals results in a vector of accumulated
expected values [2.33,1.83,2.50,2.50,2.33,2.17] re-
lated to each individual.
The case where all the individuals successfully
classify each sample 6/6 = 1 and having 7 samples in
this example, then the maximum accumulated prob-
ability is 7, normalizing the previous vector we have
[0.33,0.26,0.35,0.35,0.33,0.31]. Finally, we have an
aggregated probability information where PNS cap-
tures the probability differences among the individu-
als’ behaviors.
PNS(b)
t
j
=
n
∑
i=1
1
P
i
(b
t
i, j
) + ε
, (8)
where ε is the total error of the probabilistic model
against the true model. The novelty of each individ-
ual behavior is inversely proportional to the probabil-
ity of predicting correctly (hit) each sample. Instead
of managing an archive, we can save the parameters
from the probability density function (PDF) for each
sample and update them by using for example a con-
volution strategy between the previous and the actual
PDFs.
2.4 Pyramid Search
There is a wide range of approaches in the literature
to address evolutionary algorithms in a hierarchical
way. For instance, a recent approach to address Deep
Learning is proposed in (Houreh. et al., 2021), where
the authors addresses the problem of evolving a neu-
ral network in a hierarchical way using GA as the
search engine to automatically find the best architec-
ture combination from a set of U-net architectures to
solve the Retinal Blood Vessel Segmentation.
A novel hierarchical approach named Pyramid is
proposed by (Ryan et al., 2020), where the main idea
is to decompose a complex problem into subsets of
simpler versions from the original and while scaling
up to finally address the entire problem the popula-
tion size is reduced keeping only the top individuals
in each step.
Another hierarchical approach which shares part
of the name with the previous approach is the Pyra-
mid Search proposed by (Ciesielski and Li, 2003).
In this approach the strategy is to split the popula-
tion into groups and prune them a certain number of
generations to reduce the number of evaluations and
keeping competitive results. In this work, we use the
latter approach applying it to solve a set of classifica-
tion problems.
According to (Ciesielski and Li, 2003), Pyramid
Search evolve optimal solutions using a reduced num-
ber of generations and individuals in the population
by removing the worst performing groups. The Algo-
rithm 1 gives the guidelines for the implementation of
this method.
Algorithm 1: Pyramid Search.
Input: The given problem and the solution representation.
Output: Best solution (with less groups of individuals).
1 Pop size = No. of individuals in a group
2 Groups = No. of groups
3 Pruning ratio = No. of least fit groups to be removed
4 Gens to prone = No. of generation to be pruned
5 Initialize groups = Individuals(Pop size)
6 while problem not solved or single group remains: do
7 Do evolution process
8 Prune Groups(pruning ratio * groups)
9 if problem not solved then
10 Continue iterations until single population exists
11 else
12 Problem solved or max generations is reached
13
In this approach the evolutionary process starts in
the traditional manner by randomly creating an initial
population, but in the next step, Pyramid Search splits
the population into groups of fixed size. Each group
is ranked based on its top individual, in other words,
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
348
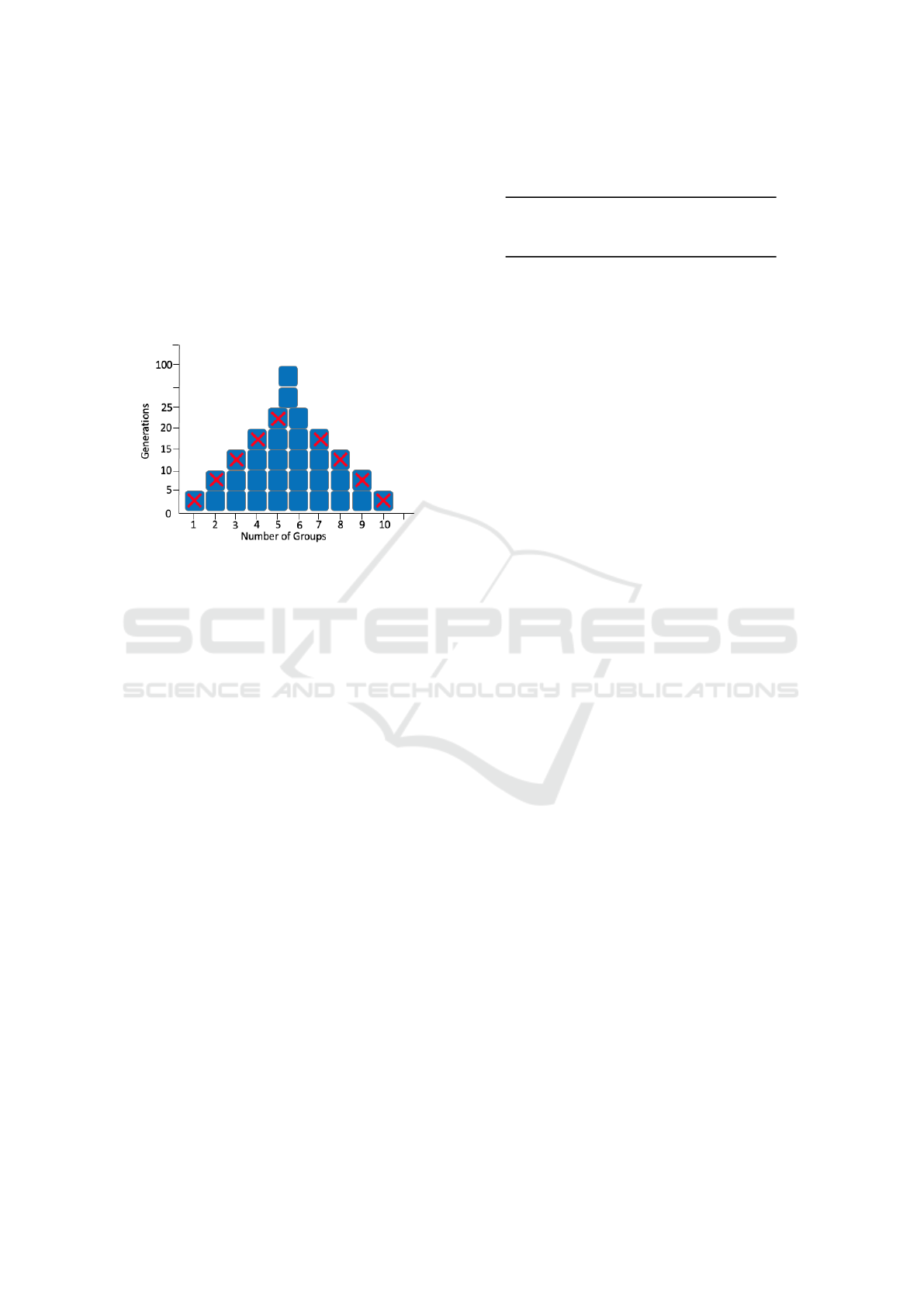
the best individual from each group gives the repre-
sentative fitness score to rank the group. The prun-
ing process is based on the pruning ratio parameter,
where the groups showing the lowest fitness value will
be discarded, in other words, the groups bring their
champions and the worst of them are executed with
the whole group (all of them). The rest of the cham-
pions go to the next level with their entire group, this
pruning process continue until the problem is solved
or the maximum number of generations are reached.
Figure 2: Graphical depiction of Pyramid Search.
In the figure 2, we can see a visual representa-
tion of the pruning process in the Pyramid Search. In
the example every five generations a group competi-
tion takes place and the worst two groups are removed
(represented by a red cross), an alternate way of look-
ing at this is that the groups are sorted in such a way
that the worst are placed at the ends. At the generation
20, only one group is removed and it remains until the
evolutionary process stop.
3 EXPERIMENTAL SETUP
We designed a set of experiments based on binary
classification problems to test both methods OS and
PNS, and their combination with Pyramid, namely
Py-OS and Py-PNS, particularly for the PNS meth-
ods we neither use an archive nor updated the PDF
with previous distributions parameters.
3.1 Datasets
Three datasets were selected: Cervical Cancer, Heart
Disease, and Genetic Variation, sorted, from easy to
hard.
Dataset 1: Cervical Cancer. The dataset (Repos-
itory, a) contains features such as age sex, smoke
Table 1: Binary Classification Datasets.
Datasets Class Vars Samples
Cervical Cancer
§
2 33 857
Heart Disease
†
2 31 303
Genetic Variation
§
2 57 3373
habits, STDs & other hormonal reading & the depen-
dent variable represents the predictions of indicators
or diagnosis of cervical cancer (Classes 0 or 1).
Dataset 2: Heart Disease. The dataset (Repository,
b) has 13 independent variables which represents at-
tributes such as age, sex, serum cholesterol, chest pain
types, heart rate etc. The dependent variable refers
to the presence of heart disease in the patient. Class
0 represents no/less chance of heart attack, and the
Class 1 represents more chance of heart attack.
Dataset 3: Genetic Variation Classification. This
is a public dataset containing annotations about hu-
man genetic variants (Clinvar, ). These variants are
manually classified by clinical laboratories on a cat-
egorical spectrum ranging from benign, likely be-
nign, uncertain significance, likely pathogenic, and
pathogenic. Variants that have conflicting classifi-
cations can cause confusion when clinicians or re-
searchers try to interpret whether the variant has an
impact on the disease of a given patient. The objec-
tive is to predict whether a Clinical Var variant will
have conflicting classifications. This is presented here
as a binary classification problem, where each record
in the dataset is a genetic variant.
3.2 GP Parameters
Table 2 shows the parameters for GP in the top section
and for the Pyramid Search at the bottom. The fitness
function is the accuracy as shown in the Equation 1.
Finally, all experiments were conducted using DEAP
(Fortin et al., 2012).
4 EXPERIMENTAL RESULTS
The table 3 summarizes the experimental results, con-
ducted over 30 experimental runs. The first column
shows the datasets: Cervial Cancer, Heart Disease,
and Genetic Variation, where the first is the easiest
and the last the hardest. Second column shows the
methods used: OS, PNS, Py-OS, Py-PNS, where OS
stands for the Objective-based search and it is the tra-
ditional approach to rewards solutions closer to the
target. The second method is PNS, which stands for
A Hierarchical Probabilistic Divergent Search Applied to a Binary Classification
349

Table 2: GP and Pyramid Search parameters.
Parameter Value
Runs 30
Population 200
Replacement Tournament
Crossover 0.7
Function Set I +, -, *, /, cos, sin
Function Set II log, and, or ,not, if
Pyramid Search
Pruning Ratio 0.2
Prune After Generations 5
No.of.Groups 10
Group Size 20
Probabilistic Novelty Search, which is a probabilis-
tic approach to implement a divergent search. The
rest are combinations of the first two methods with
the Pyramid Search.
The experimental results start with the column
’Train’, which stands for the average results in all runs
using the training dataset, and ’Test’ for the he aver-
age results on test dataset. The column with ’Time;
give us the information of the time spent by each run
in average. Finally, the ’AvgSize’ stands for the av-
erage size of the solutions considering the number of
nodes in the GP-tree.
4.1 Results in Training
Results shown in table 3, specifically for the Cervical
Cancer dataset in training favors OS but does not have
a statistical significant difference from PNS, even the
standard deviation are similar among them. On the
other hand, the combination using Pyramid Search
shows results which are inferior to OS and PNS, but
still in the same order, so both combinations show
very good results. The results show PNS performs
better in training for the Heart Disease with a signifi-
cant difference against OS. The results in training for
the Genetic Variation dataset, again place PNS as the
champion, but followed closely by OS and the Pyra-
mid combination are not that far.
figure 3 shows the convergence plot for the three
datasets using OS and PNS, where it can be noted
that the degree of difficulty for the methods to evolve
good solutions for each of the datasets, the results
clearly show that in training the easiest dataset is Cer-
vical Cancer while the hardest is the Genetic Varia-
tion dataset. Figure 4 shows the convergence from the
combination with Pyramid. Cervical Cancer dataset
OS shows a better convergence can be seen and PNS
struggles to continue evolving solutions. In the rest of
the datasets while Py-OS demonstrates a tendency to
evolve good solutions, they are not as good as those
evolved by OS and PNS, with Py-PSN getting trapped
at a local optima in both datasets. A summarised per-
formance in training is shown in the Figure 5, where
Py-OS is worst than OS and PNS, and Py-PNS can-
not find good solutions in training as the rest of the
methods.
4.2 Results in Test
Results in test shown for Cervical Cancer in table 3
interestingly favor Py-PNS, which shows the worst
performance in training. Morover, Py-PNS is the
champion in test on all the datasets, this confirm the
hypothesis that PNS can find novel solutions and in
combination with Pyramid Search keeps best solu-
tions with a reduced number of individuals from the
original population.
The figure 6 shows the boxplots of the perfor-
mance of each method in test, it can be observed in
these that the median of Py-PSN is always above than
the rest of the methods tested.
4.3 Time Consumption
The experimental results shown in the table 3 regard-
ing the time taken in average to run a single experi-
ment from each method place Py-OS in the first place
in all the datasets followed close by Py-PNS, inter-
estingly PNS goes third in Cervical Cancer, but got
the last position on the remaining datasets. This same
trend is graphically observed in the Figure 7, where
clearly both combinations using Pyramid in average
take 5% of the time used by OS or PNS.
4.4 Average Size
The experimental results shown in the table 3 re-
garding the average size from each method place Py-
PNS in the first place followed by Py-OS, interest-
ingly PNS ranks third in Cervical Cancer, but got the
last place on the remaining datasets. The figure 8
shows the size grow for OS and PNS. For Cervical
Cancer OS shows higher size in average than PNS,
even though around the generation 85 both method
show similar size average. For Heart Disease and
Genetic Variation, OS shows a more flat grow rate,
whereas PNS evolves more complex solutions on av-
erage. PNS does not get better performance than OS,
but observing the boxplots from figure 6 can be ob-
served that PNS gets a more diverse set of solutions
than OS. The trend observed in the figure 9 regarding
the average size of the solutions evolved by the meth-
ods in combination with Pyramid shows that Py-PNS
evolve smaller solutions than Py-OS.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
350
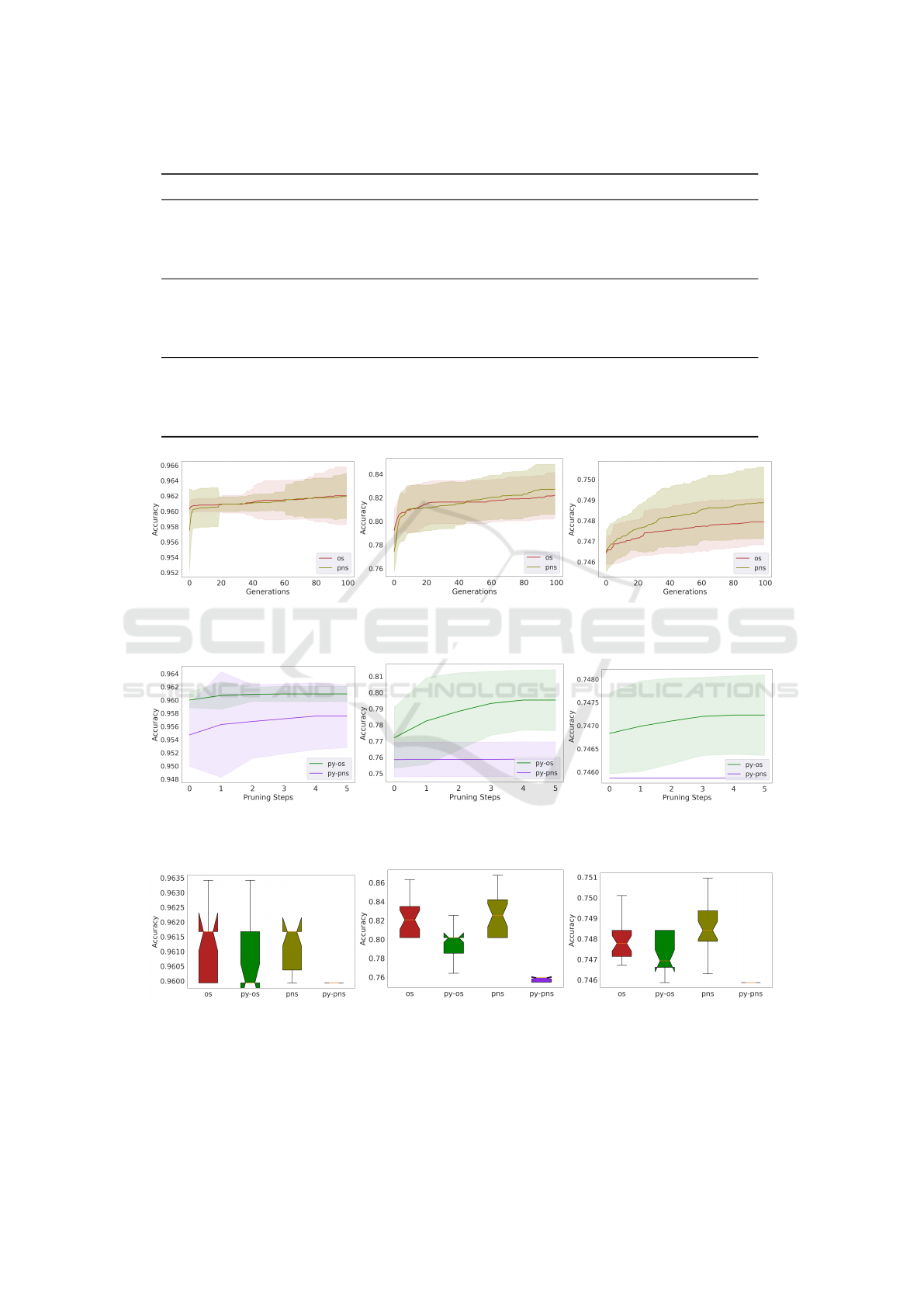
Table 3: Experimental results averaged over 30 runs, best results are bold.
Dataset Method Train Test Time Avg Size
Cervical Cancer OS 0.9620 ±0.003 0.9580 ±0.002 98.92 ±0.00 5.00 ±8.68
Py-OS 0.9609 ±0.001 0.9582 ±0.002 5.82 ±0.00 4.71 ±0.51
PNS 0.9619 ±0.003 0.9583 ±0.003 125.56 ±0.00 4.25 ±3.86
Py-PNS 0.9575 ±0.004 0.9621 ±0.006 6.52 ±0.00 3.44 ±0.37
Heart Disease OS 0.8221 ±0.019 0.7289 ±0.059 29.65 ±0.00 5.69 ±3.44
Py-OS 0.7952 ±0.020 0.7194 ±0.046 1.86 ±0.00 6.13 ±1.93
PNS 0.8272 ±0.021 0.7322 ±0.053 38.31 ±0.00 7.48 ±5.31
Py-PNS 0.7588 ±0.010 0.7362 ±0.044 2.25 ±0.00 3.13 ±0.29
Genetic Variation OS 0.7479 ±0.001 0.7222 ±0.001 411.30 ±0.00 9.17 ±6.22
Py-OS 0.7472 ±0.000 0.7222 ±0.002 25.36 ±0.00 6.80 ±2.41
PNS 0.7488 ±0.001 0.7224 ±0.002 533.92 ±0.00 13.01 ±14.34
Py-PNS 0.7458 ±0.000 0.7243 ±0.000 25.60 ±0.00 2.82 ±0.30
(a) Cervical Cancer (b) Heart Disease (c) Genetic Variation
Figure 3: Convergence of training accuracy on datasets.
(a) Cervical Cancer (b) Heart Disease (c) Genetic Variation
Figure 4: Pyramid Search - Convergence of training accuracy on datasets.
(a) Cervical Cancer (b) Heart Disease (c) Genetic Variation
Figure 5: Accuracy on training data, box plot of all runs.
A Hierarchical Probabilistic Divergent Search Applied to a Binary Classification
351
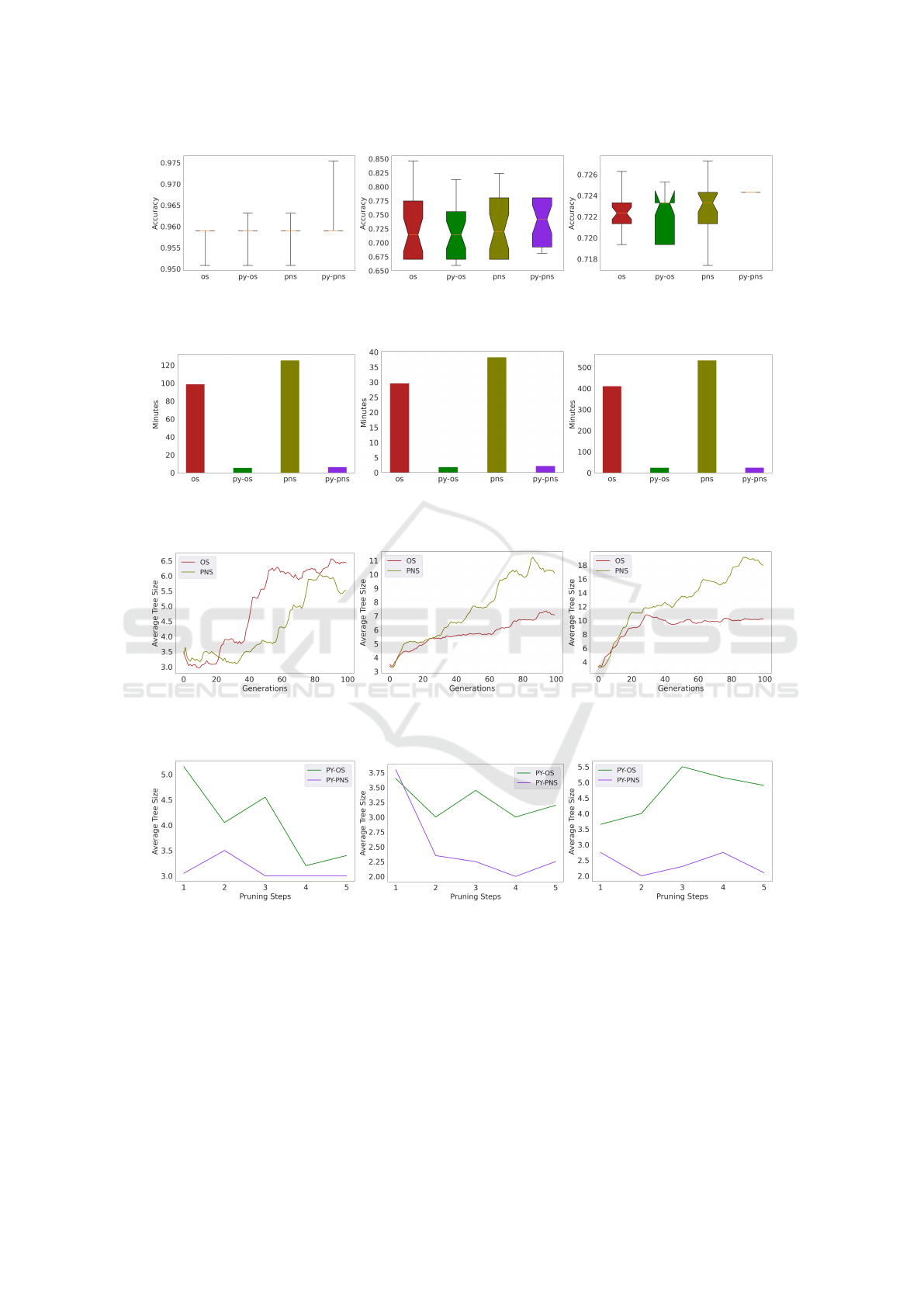
(a) Cervical Cancer (b) Heart Disease (c) Genetic Variation
Figure 6: Accuracy on test data, box plot of all runs.
(a) Cervical Cancer (b) Heart Disease (c) Genetic Variation
Figure 7: Time taken to run 30 runs on Datasets.
(a) Cervical Cancer (b) Heart Disease (c) Genetic Variation
Figure 8: Average tree size of all 30 runs.
(a) Cervical Cancer (b) Heart Disease (c) Genetic Variation
Figure 9: Pyramid Search - Average tree size of all 30 runs.
5 CONCLUSIONS
This paper introduced the implementation of the prob-
abilistic version of novelty search, PNS for short, us-
ing a Bernoulli distribution, using the probabilities
to successfully classify correctly the samples in the
training set. Furthermore, the authors implemented
a combination of Pyramid Search with the traditional
approach to guide the search named as Py-OS and the
combination with PNS named as Py-PNS. As study
case, three binary classification problems were used
and the experimental results from 30 runs have shown
that the combination with Pyramid gives good results
and particularly Py-PNS is an interesting combination
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
352

to evolve diverse and optimal solutions reducing the
average time for each experiment to 5% from the stan-
dard approach and getting even better results on some
experiments.
In future work, the authors plan to compute nov-
elty using PNS by (i) taking the probabilities for fail-
ure to classify the samples, (ii) considering both the
success and failure. For future work we are consider-
ing Pyramid Search to automatically select the num-
ber of groups taking the population size and the num-
ber of generations as arguments.
ACKNOWLEDGEMENTS
The authors are supported by Research Grants
13/RC/2094 and 16/IA/4605 from the Science Foun-
dation Ireland and by Lero, the Irish Software
Engineering Research Centre (www.lero.ie). The
third is partially financed by the Coordenac¸
˜
ao de
Aperfeic¸oamento de Pessoal de N
´
ıvel Superior -
Brasil (CAPES) - Finance Code 001.
REFERENCES
Ciesielski, V. and Li, X. (2003). Pyramid search: finding
solutions for deceptive problems quickly in genetic
programming. In The 2003 Congress on Evolution-
ary Computation, 2003. CEC ’03., volume 2, pages
936–943 Vol.2.
Clinvar, N. Genetic variant classification dataset.
ftp://ftp.ncbi.nlm.nih.gov/pub/clinvar/vcf\ GRCh37/
clinvar.vcf.gz. Online; accessed 28-September-2021.
Fortin, F.-A., De Rainville, F.-M., Gardner, M.-A., Parizeau,
M., and Gagn
´
e, C. (2012). DEAP: Evolutionary algo-
rithms made easy. Journal of Machine Learning Re-
search, 13:2171–2175.
Houreh., Y., Mahdinejad., M., Naredo., E., Dias., D., and
Ryan., C. (2021). Hnas: Hyper neural architecture
search for image segmentation. In Proceedings of the
13th International Conference on Agents and Artifi-
cial Intelligence - Volume 2: ICAART,, pages 246–
256. INSTICC, SciTePress.
Kim, S., Coninx, A., and Doncieux, S. (2021). From explo-
ration to control: Learning object manipulation skills
through novelty search and local adaptation. Robotics
and Autonomous Systems, 136:103710.
Koza, J. R. (1992). Genetic Programming - On the pro-
gramming of Computers by Means of Natural Selec-
tion. Complex adaptive systems. MIT Press.
Lehman, J. and Stanley, K. (2008). Exploiting open-
endedness to solve problems through the search for
novelty. In Bullock, S., Noble, J., Watson, R., and Be-
dau, M. A., editors, Artificial Life XI: Proceedings of
the Eleventh International Conference on the Simula-
tion and Synthesis of Living Systems, pages 329–336.
MIT Press, Cambridge, MA.
Lehman, J. and Stanley, K. O. (2010). Efficiently evolving
programs through the search for novelty. In Pelikan,
M. and Branke, J., editors, GECCO, pages 837–844.
ACM.
Naredo, E., Trujillo, L., Legrand, P., Silva, S., and Mu
˜
noz,
L. (2016). Evolving genetic programming classifiers
with novelty search. Information Sciences, 369:347 –
367.
Pattee, H. H. and Sayama, H. (2019). Evolved Open-
Endedness, Not Open-Ended Evolution. Artificial
Life, 25(1):4–8.
Pugh, J. K., Soros, L. B., and Stanley, K. O. (2016). An
extended study of quality diversity algorithms. In
Proceedings of the 2016 on Genetic and Evolution-
ary Computation Conference Companion, GECCO
’16 Companion, page 19–20, New York, NY, USA.
Association for Computing Machinery.
Repository, U. M. L. Cervical cancer dataset.
https://archive.ics.uci.edu/ml/datasets/Cervical+
cancer+\%28Risk+Factors\%29. Online; accessed
28-September-2021.
Repository, U. M. L. Heart disease dataset. https://
archive.ics.uci.edu/ml/datasets/heart+disease. Online;
accessed 28-September-2021.
Ryan, C., Rafiq, A., and Naredo, E. (2020). Pyramid: A
hierarchical approach to scaling down population size
in genetic algorithms. pages 1–8.
Skjærseth, E. H., Vinje, H., and Mengshoel, O. J. (2021).
Novelty search for evolving interesting character me-
chanics for a two-player video game. In Proceedings
of the Genetic and Evolutionary Computation Confer-
ence Companion, GECCO ’21, page 321–322, New
York, NY, USA. Association for Computing Machin-
ery.
Trujillo, L., Villanueva, O. M., and Hernandez, D. E.
(2021). A novel approach for search-based program
repair. IEEE Software, 38(4):36–42.
XU, Q., Pan, X., Wang, J., Wei, M., and Li, H. (2021).
Multiobjective brain storm optimization community
detection method based on novelty search. Hindawi,
Mathematical Problems in Engineering, 2021:14. Ar-
ticle ID 5535881.
Zhang, M. and Smart, W. (2006). Using gaussian distri-
bution to construct fitness functions in genetic pro-
gramming for multiclass object classification. Pattern
Recogn. Lett., 27(11):1266–1274.
A Hierarchical Probabilistic Divergent Search Applied to a Binary Classification
353
