
A Novel Key Exchange Protocol using Logic Algebra for the
Factorization Problem
Junhui Xiao, Ashish Neupane, Hiba F. Fayoumi and Weiqing Sun
University of Toledo, Toledo, Ohio, U.S.A.
Keywords: Logic Algebra, Key Exchange, Factorization Problem, OpenSSL, Cryptography.
Abstract: Our current key exchange protocols are at risk of failing to keep private data secret due to advancements in
technology. Therefore, there is a need to develop an efficient and secure key exchange protocol which can
function in the new computing era to come. In this paper, we propose and develop a novel key exchange
protocol based on logic algebra for the factorization problem. Both the security analysis and experimentation
evaluation demonstrate promising results of our proposed approach.
1 INTRODUCTION
In 1976, the Diffie-Hellman public key exchange
algorithm (Diffie and Hellman, 1976), which is
known as the first asymmetric encryption algorithm,
was proposed. A Key Exchange Protocol is a protocol
in which a key is established by exchanging
information between two parties. The scheme to
accomplish this is as follows:
(1) Each party holds a private key and a public key.
(2) The encrypted message and public key are sent to
the other party.
(3) The two parties use a series of mathematical
methods to calculate the private key and public
key in their hands and the other party’s public key
obtained from the communication to generate a
common key that can encrypt or decrypt a
message (Diffie and Hellman, 1976; Li, 2010).
The advantage of the public key cryptosystem is that
the communicating parties do not need to have a
shared secret key before communicating. The private
keys held by the communicating parties are generated
randomly by themselves, and the communicating
parties cannot calculate the others’ private key from
the private key they each hold. While this method can
prevent network data snooping to a certain extent, it
cannot prevent the tampering of network data, which
is known as the man-in-the-middle attack (MITM)
(Kader and Hadhoud, 2009).
In order to address this problem, many
suggestions have been made over the years. Most of
them are based on the optimization of Diffie-Hellman
key exchange protocol. Each includes a key exchange
system that combine the Diffie-Hellman algorithm
with various digital certificate algorithms such as
RSA and DSA, which rely on signature algorithms for
identity verification (Chen and Wang, 2019; Pal and
Alam, 2017; Yusfrizal et al., 2018; Thayananthan and
Albeshri, 2015; Bhavani and Krishna, 2021). Each
also includes some algorithms that optimize the key
generation based on the DH algorithm. For instance,
the ECDH algorithm, which solves the “Discrete
Logarithm Problem” in the DH protocol is replaced
with solving the “Elliptic Curve Discrete Logarithm
Problem”. Another example includes an algorithm
which changes the prime number in the DH algorithm
to a group or a matrix (Vidhya and Rathipriya, 2020;
Megrelishvili, 2018; Rudy and Monico, 2021;
Bharathi et al., 2017). Gentile and Migliorato (2002)
proposed cryptosystems that use hypergroupoids as
keys for encryption on the issue of key structure. In
(Shpilrain, 2008; Grigoriev and Shpilrain, 2014,
2019), Shpilrain proposed tropical algebra as the key
structure based on the study of key exchange protocol
using random natural number with exponential
operations; the key exchange protocol using public
non-commutative rings; and an analysis of a linear
algebra attack. Ezhilmaran and Muthukumaran
(2016) proposed the key exchange protocol using
“The Decomposition Problem” in the near-ring
scheme. These schemes have become the main trend
of the current cryptosystem.
In this paper, we have further optimized the key
construction scheme based on the ideas of using
classical algebra and tropical algebra and chose to use
396
Xiao, J., Neupane, A., Fayoumi, H. and Sun, W.
A Novel Key Exchange Protocol using Logic Algebra for the Factorization Problem.
DOI: 10.5220/0010843300003120
In Proceedings of the 8th International Conference on Information Systems Security and Privacy (ICISSP 2022), pages 396-403
ISBN: 978-989-758-553-1; ISSN: 2184-4356
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

logic algebra as the basis for key construction. The
groupoid factorization proposed by Fayoumi
(Fayoumi, 2020), splits a given groupoid into
different factors according to the characteristics of
logic algebra. A different operation, diamond
(Fayoumi, 2020), is used instead of the usual
mathematical operations. By optimizing key
generation, we can greatly mitigate the man-in-the-
middle attacks. Section 2 discusses the background
and related work. Our proposed key exchange
protocol is described in Section 3, followed by its
security analysis in Section 4. The implementation
and evaluation of the proposed protocol are covered
in Sections 5 and 6. Finally, we conclude and propose
our future work in Section 7.
2 BACKGROUND
2.1 Algebras
In this paper, a groupoid is the main component of the
key. To obtain the required groupoid efficiently and
to make the groupoid strong and diverse, different
types of logic algebras, such as BCK-algebra, BCI-
algebra, BCH-algebra, and d-algebra, will be used.
Several of their properties, which are used as axioms
to define each algebraic structure, are in the following
list (Fayoumi, 2020). Let
𝑋,• ,0
be an algebra, for
any 𝑥,𝑦,𝑧 ∈ 𝑋:
B1: 𝑥 • 𝑥 0,
B2: 𝑥 • 0 𝑥,
BG: 𝑥
𝑥•𝑦
•
0•𝑦
,
BH: 𝑥 • 𝑦 0 𝑎𝑛𝑑 𝑦 • 𝑥 0 ⇒ 𝑥 𝑦,
BF: 0 •
𝑥•𝑦
𝑦•𝑥,
K: 0 • 𝑥 0,
B:
𝑥•𝑦
•𝑧𝑥•𝑧•
0•𝑦
,
BM:
𝑧•𝑥
•
𝑧•𝑦
𝑦•𝑥,
BN:
𝑥•𝑦
•𝑧
0•𝑧
•
𝑦•𝑥
,
BO: 𝑥 •
𝑦•𝑧
𝑥•𝑦
•
0•𝑧
,
BP1: 𝑥 •
𝑥•𝑦
𝑦,
BP2:
𝑥•𝑧
•
𝑦•𝑧
𝑥•𝑦,
Q:
𝑥•𝑦
•𝑧
𝑥•𝑧
•𝑦,
CO:
𝑥•𝑦
•𝑧𝑥•
𝑦•𝑧
,
BZ:
𝑥•𝑧
•
𝑦•𝑧
•
𝑥•𝑦
0,
I:
𝑥•𝑦
•
𝑥•𝑧
•
𝑧•𝑦
0,
BI: 𝑥 •
𝑦•𝑥
𝑥.
By combining two or more of these axioms, we can
get different types of algebras we need to generate the
groupoid (Table 1).
Table 1: Axioms of different types of algebras (Fayoumi,
2020).
For example, if we want to generate a fr-algebra,
based on the axioms in Table 1, we know that the
groupoid should satisfy B1, B2 and K. A groupoid
𝑋,•
satisfies axiom B1 means for any 𝑥 ∈ 𝑋, we
can always get
𝑥•𝑥
0. If
𝑋,•
satisfies B2, then
for any 𝑥∈𝑋,
𝑥•0
𝑥. Finally, if
𝑋,•
satisfies
property K, means for any 𝑥 ∈ 𝑋, t
0•𝑥
0. As
for this, we can first generate an algebra frame as
follows:
•
0 1 2 3 4
0
0 0 0 0 0
1
1 0
x
x
x
2
2
x
0
x
x
3
3
x
x
0
x
4
4
x
x
x
0
And then, we can fill up the groupoid using
random method or brute-force method to get a
complete groupoid with fr-algebra.
2.2 Factorization
Factorization is an important part in our experiment.
As we mentioned in Section 1, we used a different
type of binary operation, the diamond operation (⋄),
to calculate two groupoids. Corresponding to this, we
use factorizations to divide a groupoid into two factor
groupoids (Fayoumi, 2020). In this section, we
present two different types of factorizations.
2.2.1 Similar-Signature Factorization
Similar-Signature Factorization is a unique
factorization of a given groupoid in which two factors
are derived from itself and from the left-zero-
semigroup (Fayoumi, 2020).
Let
𝑋,•
be a groupoid of finite order n. Then d
•
is the diagonal function of
𝑋,•
such that
d
•
: ℕ → 𝑋 𝑤ℎ𝑒𝑟𝑒 d
•
𝑖
𝑥
• 𝑥
,
A Novel Key Exchange Protocol using Logic Algebra for the Factorization Problem
397

𝑖1,2,…,𝑛 𝑓𝑜𝑟 𝑎𝑙𝑙 𝑥
∈𝑋.
2.2.2 Orient-Skew Factorization
Orient-Skew Factorization is another unique
factorization which can be applied to groupoids with
the orientation property OP: 𝑥∗𝑦∈𝑥,𝑦 for all
𝑥,𝑦 ∈ 𝑋 . We can derive the orient-factor of a
groupoid such that all its elements are the same as
those of a left-zero-semigroup except elements
belonging to the anti-diagonal (Fayoumi, 2020).
Similarly, the skew-factor is derived from the
groupoid by letting its anti-diagonal change to its
skew-diagonal, and the other elements are kept the
same as the original groupoid.
2.3 Binary Operations
Given a binary operation “∗” on a non-empty set X,
groupoid
𝑋,∗
is then considered a generalization of
the very well-known structure of a group. Consider
the collection of all groupoids defined on X, call it
𝐵𝑖𝑛
𝑋
. Let
𝑋,∗
and
𝑋,∘
be two random
groupoids in Bin
X
, define a groupoid product
operation “⋄” where
𝑋,⋄
𝑋,∗
⋄
𝑋,∘
such that
𝑥⋄𝑦
𝑥∗𝑦
∘
𝑦∗𝑥
for all x, y ∈ X. This turns
𝐵𝑖𝑛𝑋,⋄ into a semigroup with identity
𝑥∗𝑦𝑥
,
the left-zero-semigroup, and an analog of negative
one in the right-zero-semigroup. One can naturally
observe that we can always get such a product if we
know groupoids
𝑋,∗
and
𝑋,∘
. However, reversing
this action is not so straightforward. There are four
cases we need to note:
Case 1 Distinct Factors:
𝑋,•
𝑋,∗
⋄
𝑋,∘
, such that
𝑋,∗
𝑋,∘
.
Case 2 Uniqueness:
𝑋,•
𝑋,∗
⋄
𝑋,∘
, such that if
𝑋,∙
𝑋,∗
⋄
𝑋,∘
, then
𝑋,∙
𝑋,•
.
Case 3 Relatively prime to
X,•
:
𝑋,•
𝑋,∗
⋄
𝑋,∘
, such that
𝑋,∗
𝑋,•
and
𝑋,∘
𝑋,•
.
Case 4 Commutative:
𝑋,•
𝑋,∗
⋄
𝑋,∘
, such that if
𝑋,•
𝑋,∘
⋄
𝑋,∗
, then
𝑋,∘
⋄
𝑋,∗
𝑋,∗
⋄
𝑋,∘
.
Of course, one can consider the subcases of each
of the above four cases or even the combinations of
two or more of them. We should notice that not all
groupoids can satisfy case 4, in other words, not all
groupoids commute. It is important to be able to find
a collection of groupoids that do commute, and logic
algebras using Similar-Signature Factorization and
Orient-Skew Factorization can more likely generate
commuting groupoids under our special diamond
operation. It means, all groupoids can be factorized
using the Similar-Signature Factorization and the
Orient-Skew Factorization into two factor groupoids,
but not all pairs of factor groupoids commute. In our
experiment, an important step is to obtain groupoids
which can be factorized into two commuting factor
groupoids. Here is an example of using the Similar-
Signature Factorization to generate two commuting
factors.
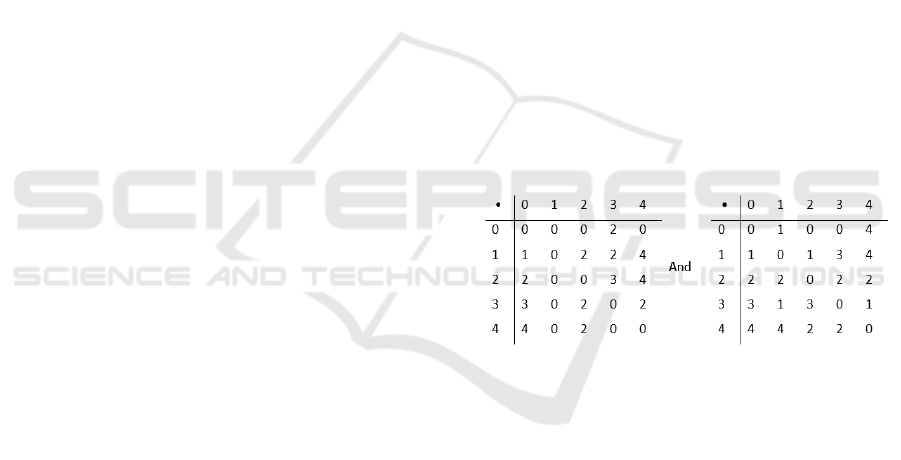
Example. Let
𝑋,•
=
𝑍
,• ,0
be a groupoid with 0,
and binary operation defined by:
•012 3 4
0000 0 0
1101 0 1
2220 3 0
3332 0 3
4441 1 0
Then we can find factors
𝑋,∗
and
𝑋,∘
which
commute, as follows:
and,
2.4 OpenSSL
OpenSSL is an open-source software library written
in the C programming language and has a wide
variety of cryptographic functions to implement
secure features. It is a powerful tool that implements
the popular SSL and TLS protocols (Ruiter, 2016).
Some of the features implemented by the OpenSSL
library include symmetric encryption, asymmetric
encryption, certificate handling and hash functions.
Apart from that, OpenSSL also supports a wide range
of cipher suites.
One of the main reasons for choosing OpenSSL
platform is that OpenSSL has all the features already
built into it to test a new cryptographic protocol.
Researchers trying to test the functionality of a
cryptographic algorithm or a protocol in a full-
fletched application can do so by implementing that
module in the OpenSSL library and using the already
available applications like HTTP to test its
performance. However, to integrate the module into
the OpenSSL, we need to understand the libraries the
ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy
398

two main libraries of OpenSSL – libssl and libcrypto.
Libssl, as the name suggests is a library that
implements SSL and TLS functions like opening and
closing a connection, forming packets, managing
handshakes, creating certificates, and using lib-crypto
library to perform cryptographic operations. The
libcrypto library has a wide variety of symmetric,
asymmetric, and key-exchange protocols, which
provides the low-level implementation of
cryptographic algorithms to the libssl library.
Another reason is that since OpenSSL is an open-
source software, all of its software packages rolled
out in the past is easily accessible. In addition, the
older cipher suits, which have been retired by the
IETF, can be modified in a specific way to add a new
cryptographic algorithm easily. Modifying the older
cipher suites like AECDH-NULL-SHA allows us to
integrate our new key exchange algorithm by
modifying the already present Elliptic Curve Diffie-
Hellman key exchange without having to write a
symmetric algorithm that goes with it, as indicated by
NULL in the middle. Moreover, the “A” in AECDH
means anonymous, i.e., the key exchange algorithm
will not have to use an Ephemeral Key for changing
the keys periodically. However, we should be careful
not to use those cipher suites on their own as these
generally have security vulnerabilities. This
important feature allows us to test the functionality of
our key exchange algorithm in isolation without
having to implement a Pseudo Random Function for
generating symmetric keys as well as making the keys
ephemeral. It is important to note that these two
components are the foundation of modern
cryptography and should not be excluded from any
cryptographic implementation. However, these
components have been left out from our
implementation as it gives us more flexibility to test
the raw performance of our key exchange protocol.
3 PROPOSED PROTOCOL
3.1 Basic Scenario
The basic scenario of our proposed key exchange
protocol is as follows:
1. Picking commuting groupoid pairs
Alice:
Randomly picks two private groupoids 𝐴
𝑋,∗
and 𝐴
𝑋,∘
.
Sends Bob the shared groupoid 𝑢𝐴
⋄𝐴
.
Bob:
Randomly picks two private groupoids 𝐵
𝑋,⊛
and 𝐵
𝑋,⊙
.
Sends Alice the shared groupoid 𝑣𝐵
⋄𝐵
.
2. Generating the decryption key:
Alice computes
𝐾
𝐴
⋄
𝑣
⋄𝐴
𝑋,∘
⋄
𝑋,⊛
⋄
𝑋,⊙
⋄
𝑋,∗
𝑋,∘
⋄
𝑋,⊛
⋄
𝑋,⊙
⋄
𝑋,∗
𝑋,⊛
⋄
𝑋,∘
⋄
𝑋,∗
⋄
𝑋,⊙
Bob computes
𝐾
𝐵
⋄
𝑢
⋄𝐵
𝑋,⊛
⋄
𝑋,∗
⋄
𝑋,∘
⋄
𝑋,⊙
𝑋,⊛
⋄
𝑋,∘
⋄
𝑋,∗
⋄
𝑋,⊙
Figure 1: Proposed key exchange protocol.
Thus, Alice and Bob have a shared secret key
𝐾 𝐾
𝐾
. For this protocol to work, we need
the following pairs of groupoids to commute:
1.
𝑋,∗
and
𝑋,∘
2.
𝑋,⊛
and
𝑋,⊙
3.
𝑋,∘
and
𝑋,⊛
4.
𝑋,⊙
and
𝑋,∗
Additional conditions considering Eve interception:
If she intercepts the key exchange, then she can
either compute:
𝑢⋄𝑣
𝑋,∗
⋄
𝑋,∘
⋄
𝑋,⊛
⋄
𝑋,⊙
𝑋,∗
⋄
𝑋,⊛
⋄
𝑋,∘
⋄
𝑋,⊙
Or she can compute:
𝑢⋄𝑣
𝑋,⊛
⋄
𝑋,⊙
⋄
𝑋,∗
⋄
𝑋,∘
𝑋,⊛
⋄
𝑋,∗
⋄
𝑋,⊙
⋄
𝑋,∘
For this to not recover the shared secret key K, we
would need both of the following pairs of
groupoids to not commute:
5.
𝑋,∗
and
𝑋,⊛
6.
𝑋,∘
and
𝑋,⊙
Hence, by ensuring 1-6 hold, we have our public key
exchange systems.
3.2 Groupoid Generation
Our protocol is based on a series of groupoid
operations. Thus, how to generate a useful groupoid
as the exchange key is important. A useful groupoid
first means that it can use the Similar-Signature
Factorization to derive a pair of commuting factor
groupoids or it can be decomposed into two
commuting factor groupoids using the Orient-Skew
A Novel Key Exchange Protocol using Logic Algebra for the Factorization Problem
399

Factorization. After factorization, we must then
ensure that these factor groupoids meet the four
“commute” conditions and the two “not commute”
conditions.
In this paper, we decided to use two different
groupoids as shared groupoids for both parties. It
means while Alice and Bob communicate with each
other, they send the different shared groupoids.
Step 1: Read the input value of the groupoid length
“
L
” and the type of logic algebra 𝑡
, 𝑡
or 0.
Type “ 𝑡
” will use the Similar-Signature
Factorization.
Type “𝑡
” will use the Orient-Skew Factorization.
Input “0” will choose a random type of logic
algebra.
Step 2: Based on the properties of the “𝑡
” algebra
shown in Table 1, create one groupoid frame (a two-
dimensional array) “𝐺
” with dimensions 𝐿 𝑏𝑦 𝐿. Fill
up the rest of the groupoid table with random integers
greater than or equal to 0 and less than the length of
the groupoid “
L
”.
Step 3: Factor groupoid “𝐺
” using the Similar-
Signature Factorization to get factor groupoids
𝐴
𝑋,• ,0
and 𝑈
𝑋,• ,0
. If they commute, we store
them and continue to the next step. Otherwise, go
back to step 2.
Step 4: Based on the properties of the “𝑡
” algebra
shown in Table 1, create one groupoid frame “𝐺
”
with dimensions 𝐿 𝑏𝑦 𝐿 . Fill up the rest of the
groupoid table with random integers greater than or
equal to 0 and less than the length of the groupoid “L”.
Step 5: Factor groupoid “G
2
” using Orient-Skew
Factorization and we can get factor groupoids
𝑂
𝑋,• ,0
and 𝐽
𝑋,• ,0
. If they commute, we store
them and continue to the next step. Otherwise, go
back to step 4. We can define a count number and a
maximum number of times. If it cannot find the
required groupoid G
2
in the number of times, go back
to step 2 to find a new groupoid G
1
.
Step 6: Use check functions to check if the four factor
groupoids satisfy the four commute conditions and
the two non-commute conditions. If not satisfied, go
back to Step 4 or Step 2 depending on the number of
times.
Step 7: Assign 𝐴
𝑈
𝑋,• ,0
, 𝐴
𝑂
𝑋,• ,0
,
𝐵
𝐽
𝑋,• ,0
, 𝐵
𝐴
𝑋,• ,0
. The private
groupoids of Alice are 𝐴
and 𝐴
; while her shared
groupoid is 𝑢𝐴
⋄𝐴
. Similarly, the private
groupoids of Bob are 𝐵
and 𝐵
; while his shared
groupoid is 𝑣𝐵
⋄𝐵
.
4 SECURITY ANALYSIS
Different from the simple addition and multiplication
operations of matrices, the groupoid of this
encryption algorithm adopts the ⋄ operation of
multiple coordinate values, by taking values of 𝑥, 𝑦
and 𝑦, 𝑥, and then taking the values according to the
value of 𝑥, 𝑦 and 𝑦, 𝑥. This means that the length
of one diamond operation is
O
𝐿
, which is efficient
for generating groupoids of size L. It not only ensures
the complexity of the operation, but also makes the
encryption algorithm simple, operable, and advanced
in operation. However, to ensure the operability of the
encryption key, it is essential to generate an effective
groupoid. In this protocol of the encryption algorithm,
we have analyzed the attacks that our proposed
algorithm may suffer.
Brute Force Attack. It is known that the most
important factor affecting the brute force attack is
the length of the key. In our key exchange protocol,
the key is actually an 𝐿∗𝐿 groupoid. Hence, given a
nonempty set X with |X| = L, we can deduce the
complexity of the groupoids in our protocol (which
are elements in Bin(X)) to be
L
. Therefore, while
we use this protocol, a sufficiently large enough “L”
can ensure that the key exchange protocol will not
be cracked within an effective period of time
through brute force attack.
Man-in-the-Middle Attack. When the man-in-the-
middle or the eavesdropper obtains the shared
groupoids sent by both parties, the closest calculation
method to the encryption key is to perform the
obtained two groupoids ⋄ product operations or factor
them into factor groupoids. However, as
demonstrated in Section 3, after ensuring the
generated private groupoids satisfy the four
“commute” conditions, we can ensure that both
parties can obtain the same key. We added two “non-
commute” conditions to ensure that the man-in-the-
middle cannot get the key by using the obtained two
shared groupoids. Besides it, due to the particularity
of the operation, it is very difficult for the attacker to
generate another pair of groupoids that meet the six
conditions for the groupoids of one or both parties and
equal to the key. We can also make sure that the
groupoids will never be the left-zero-semigroup,
which is the identity in Bin(X), so that man-in-the-
middle cannot use any of the two shared groupoid
directly as the key. Moreover, we assign groupoids U
and O to Alice and groupoids J and A to Bob. The
shared groupoid of each party will not be the same
and will not be factored into any of the four factor
groupoids, in which way we can say that this protocol
is irreversible, that makes our protocol more secure.
ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy
400
5 IMPLEMENTATION OF
PROTOCOL
All the implementations and experiments are
performed on a PC workstation with the following
specifications:
• Operating System: Windows 10 Home
• Processor: Intel i5-9600k
• Processor Speed (Base): 3.70 GHz
• Storage Type: SSD
• System Memory (RAM): 32 GB
5.1 Algorithm Implementation
Our main groupoid generation algorithm and
factorization algorithm are written in JAVA
language. At the beginning, according to the study of
different algebras, we present an array framework
represent the groupoid which basically satisfies the
axioms of selected algebra, and then we use brute
force algorithm and random function to fill up the
array. We have defined checkAU and checkOJ
functions, while the array can be factorized to a pair
of commutative factor groupoids A and U and a pair
of commutative factor groupoids O and J, the factor
groupoids A, U, O and J will be stored. Then we use
commute function to check if the four factor
groupoids meet the four commute and two not
commute conditions. If all the conditions are met, we
store the array as the result and use it in OpenSSL to
see how it performs. Otherwise, we restart the
groupoid generation process.
5.2 OpenSSL Implementation
Key exchange is a vital technique used by the
SSL/TLS protocol to secretly exchange keys between
the communicating parties, to obtain the final session
keys by some form of conversion using Pseudo
Random Function and other methods.
The application layer sits on the top of the protocol
stack and has applications like ciphers and genpkey.
This component is responsible for high-level
implementation of ciphers. Below that component is
TLS component, which is in charge of handling the
connections. It has a state machine, a record layer,
packet, and buffer formation mechanisms and so on.
The crypto component below it implements all the
encryption and key exchange algorithms needed for
TLS in low-level. The engine is a dynamically
loadable module that uses the available hooks to
provide cryptographic algorithm implementations.
OpenSSL operates everything in a state machine.
The full operation of the state machine in SSL/TLS
has been explained in (Ruiter, 2016). Using state
machines makes it easier to get the current state of
operation and makes packet management easier. An
SSL/TLS connection can have states like ClientHello,
ServerHello, ServerKeyExchange and so on. The
next state of the connection depends on the previous
states and the type of packet. Since the world of
Internet is unpredictable, any of these packets could
be dropped on its way. Hence, this way of message-
passing handles the situation by keeping track of
every state and packet to manage them more easily.
6 PROTOCOL EVALUATION
6.1 Evaluation of Groupoid Generation
In this section, we evaluate the performance of the
groupoid generation algorithm. We ran the groupoid
generation program by choosing the size as “5”, and
the algebra t
1
and t
2
as “3”, the BH-algebra. We
changed the variable count, the maximum number of
times of groupoid generation to exit, as 10000000.
Then, we ran the check function and finally got 5173
pair of groupoids as the result with one example:
We can use the Similar-Signature Factorization to
derive the first groupoid and use Orient-Skew
factorization to derive the second groupoid to get four
factor groupoids. Next, by computing, we can get the
same result from 𝐾
and 𝐾
, and we can find that the
assumed man-in-the-middle attacks will not get the
same Key groupoid. This means the groupoid is ready
to be the key composition of our protocol.
6.2 Evaluation based on the OpenSSL
Platform
In this section, we will test the time it takes for each
type of messages to be received. Each of these tests
records the amount of time taken to form a
ClientHello, ServerHello, ServerKeyExchange and
ClientKeyExchange messages. That will essentially
test the message passing time of the sender. We also
need to test the amount of time the receiver takes to
process the message. Finally, the times of the new key
A Novel Key Exchange Protocol using Logic Algebra for the Factorization Problem
401

exchange algorithm will be compared with the ECDH
protocol.
We modified the message passing in ECDH
algorithm’s built-in extension to make it work as a
new key exchange protocol. The Elliptic Curve
Diffie-Hellman sends two extensions in a ClientHello
message. The first extension selects the client’s
preference for the type of EC point format to use like
compressed or uncompressed. The most common
type of EC point format has an extension type 000b
and is called Elliptic curve point formats
uncompressed. The other extension that ECDH uses
is for sending the preference on the EC curves. It has
an extension of 000a and is called Elliptic curves. For
our purpose, we will not need the extension 000b, and
will only use 000a to send the preference on the type
of matrix to use for our algorithm.
Custom extensions are treated differently in the
OpenSSL library. Separate callback function needs to
be written for these extensions and the performance
of the protocol depends largely on the programmer.
The first implementation is the unmodified ECDH
key-exchange in OpenSSL. The second
implementation modifies the built-in ECDH
extension to piggyback our new key exchange data in
OpenSSL. Finally, we used a custom extension using
the private-use extension number provided by IETF.
The packets formed by using our second and third
implementation look very identical, the only
difference is how OpenSSL treats these extensions.
When built-in extension is used, the OpenSSL
designers would have already set the properties of
these extensions like extension number, maximum
allowed data, information to be included in the
certificate, etc. There is no flexibility in choosing the
new functionality required for a new protocol. The
gist is that although modifying built-in extensions for
a new protocol is easy, it is impossible to add new
functionality when it is needed later.
In this paper, we look at two criteria to evaluate
the performance of each implementation. The
construction time is the time taken by the OpenSSL
library to construct a particular message. This
includes the time taken to fill in the header and data
portion of the messages. For a ClientHello message,
a header includes handshake message type, message
version, content length, and client hello protocol
version. Similarly, the data portion includes a random
value, session ID length, cipher suites length, a list of
cipher suites and extension data.
The processing time is the time taken to process
the message at the other end. Precisely, it is the time
taken between receiving a message and deciding what
to do next in the state machine. For a ClientHello
message, that includes parsing the raw ClientHello
message into ClientHello_MSG structure that has
fields and variables to store each component of the
message. Tables 2 and 3 compare the message
construction time and processing time of the three
implementations.
Table 2: Comparison of message construction time.
Construction Time (Microseconds)
Type of Message ECDH Built-in ext. Custom ext.
ClientHello 337 116 582
ServerHello 91 107 304
ServerKeyExchange 1238 834 1540
ClientKeyExchange 1953 1748 1762
Table 3: Comparison of message processing time.
Processing Time (Microseconds)
Type of Message ECDH Built-in ext. Custom ext.
ClientHello 56 44 195
ServerHello 94 267 331
ServerKeyExchange 34 26 37
ClientKeyExchange 943 532 819
As seen in Tables 2 and 3, the proposed key
exchange algorithm implemented using built-in
extension performed well compared to the ECDH
algorithm. The use of built-in extensions for
implementing a new key-exchange algorithm
certainly limits the overall performance of the
protocol because it is designed to work well with a
particular algorithm. With that in mind, we also
implemented the new protocol using custom
extensions, and it showed a good performance.
7 CONCLUSION
In this paper, we proposed a novel key exchange
protocol, which use logical algebra to solve the
factorization problem, in order to greatly alleviate
common attacks and deal with the challenges of
cryptography brought by the rapid development of
technology. We generated commutative groupoids
based on different logical algebras by using two
factorization functions, Similar-Signature
Factorization and Orient-Skew Factorization, and
used the diamond operation to perform operations on
groupoids. We analyzed the brute force attack and
man-in-the-middle attack on the proposed protocol
and proved that it is secure against them. We also
implemented a groupoid generation algorithm using
ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy
402

Java language and evaluated its efficiency. Finally,
we implemented our key exchange protocol on the
open-source OpenSSL platform and evaluated its
runtime performance. Experimental results
demonstrated our proposed protocol has comparable
performance with the built-in ECDH key exchange
algorithm in the OpenSSL platform.
For the future work, we plan to improve the
algorithm of groupoid generation by increasing the
size and optimizing its structure. We also plan to
continue to verify the possibility of generating
groupoids based on different logic algebras.
Moreover, we intend to optimize the code of our
built-in extension and custom extension on the
OpenSSL platform and aim to apply it to real-world
network applications.
REFERENCES
Bharathi, M. B., Manivasagam, M. G., & Kumar, M. A.
(2017). Metrics For Performance Evaluation of
Encryption Algorithms. In International conference on
emerging trends in engineering, science and
management.
Bhavani, Y., & Krishna, B. J. (2021). Security
Enhancement Using Modified AES and Diffie–
Hellman Key Exchange. In Advances in Computational
Intelligence and Communication Technology (pp. 173-
183). Springer, Singapore.
Chen, C. M., Wang, K. H., Yeh, K. H., Xiang, B., & Wu, T.
Y. (2019). Attacks and solutions on a three-party
password-based authenticated key exchange protocol
for wireless communications. Journal of Ambient
Intelligence and Humanized Computing, 10(8), 3133-
3142.
de Ruiter, J. (2016, November). A tale of the OpenSSL state
machine: A large-scale black-box analysis. In Nordic
Conference on Secure IT Systems (pp. 169-184).
Springer, Cham.
Diffie, W., & Hellman, M. (1976). New directions in
cryptography. IEEE transactions on Information
Theory, 22(6), 644-654.
Ezhilmaran, D., & Muthukumaran, V. (2016). Key
exchange protocol using decomposition problem in
near-ring. Gazi University Journal of Science, 29(1),
123-127.
Fayoumi H F. (2020). Groupoid Factorizations in the
Semigroup of Binary Systems. Scientiae Mathematicae
Japonicae Online, e-2020-13 and to appear (2022)
Scientiae Mathematicae Japonicae, Vol.84-3.
Gentile, G., & Migliorato, R. (2002). Hypergroupoids and
cryptosystems. Journal of Discrete Mathematical
Sciences and Cryptography, 5(2), 119-138.
Grigoriev, D., & Shpilrain, V. (2014). Tropical
cryptography. Communications in Algebra, 42(6),
2624-2632.
Grigoriev, D., & Shpilrain, V. (2019). Tropical
cryptography II: extensions by homomorphisms.
Communications in Algebra, 47(10), 4224-4229.
Kader, H. M., & Hadhoud, M. M. (2009). Performance
evaluation of symmetric encryption algorithms.
Performance Evaluation, 58-64.
Li, N. (2010, April). Research on Diffie-Hellman key
exchange protocol. In 2010 2nd International
Conference on Computer Engineering and Technology
(Vol. 4, pp. V4-634). IEEE.
Megrelishvili, R. (2018). New asymmetric algorithm for
fast message transmission and tropical cryptography. In
Proceedings of the eleventh international scientific-
practical conference INTERNET-EDUCATION-
SCIENCE-2018, Vinnytsia, 22-25 May, 2018: 175-178.
ВНТУ.
Pal, O., & Alam, B. (2017). Diffie-Hellman Key Exchange
Protocol with Entities Authentication. International
Journal Of Engineering And Computer Science, 6(4).
Rudy, D., & Monico, C. (2021). Remarks on a tropical key
exchange system. Journal of Mathematical Cryptology,
15(1), 280-283.
Shpilrain, V. (2008, June). Cryptanalysis of Stickel’s key
exchange scheme. In International Computer Science
Symposium in Russia (pp. 283-288). Springer, Berlin,
Heidelberg.
Thayananthan, V., & Albeshri, A. (2015). Big data security
issues based on quantum cryptography and privacy with
authentication for mobile data center. Procedia
Computer Science, 50, 149-156.
Vidhya, E., & Rathipriya, R. (2020). Key Generation for
DNA Cryptography Using Genetic Operators and
Diffie-Hellman Key Exchange Algorithm. Computer
Science, 15(4), 1109-1115.
Yusfrizal, Y., Meizar, A., Kurniawan, H., & Agustin, F.
(2018, August). Key management using combination of
Diffie–Hellman key exchange with AES encryption. In
2018 6th International Conference on Cyber and IT
Service Management (CITSM) (pp. 1-6). IEEE.
A Novel Key Exchange Protocol using Logic Algebra for the Factorization Problem
403
