Community Detection based on Node Relationship Classiﬁcation

Shunjie Yuan, Hefeng Zeng and Chao Wang

School of Cyber Engineering, Xidian University, Xi’an 710126, China

Keywords:

Complex Network, Community Detection, Machine Learning.

Abstract:

Community detection is a salient task in network analysis to understand the intrinsic structure of networks. In

this paper, we propose a novel community detection algorithm based on node relationship classiﬁcation. The

node relationship between two neighboring nodes is deﬁned as whether they afﬁliate to the same community. A

trained binary classiﬁer is deployed to classify the node relationship, which considers both the local inﬂuence

from the two nodes themselves and the global inﬂuence from the whole network. According to the classiﬁed

node relationship, community structure can be detected naturally. The experimental results on both real-

world and synthetic networks demonstrate that our algorithm has a better performance compared to other

representative algorithms.

1 INTRODUCTION

In recent years, complex networks have been ap-

plied in several ﬁelds, such as social networks (Zheng

et al., 2019; Li et al., 2012), genetic biology (Hu

et al., 2018), disease prevention and control (Goltsev

et al., 2012) as well as transportation (Dong et al.,

2016). Community detection is a fundamental task in

complex networks because many further works such

as information propagation and inﬂuence maximiza-

tion depend on community structure. Community

structure is a series of sets of nodes, where nodes

within the same community are tightly connected and

links between the different communities are relatively

sparse. The purpose of community detection is to de-

tect these node sets.

Because of the importance of community de-

tection, many community detection algorithms have

been proposed. And these algorithms have already

been deployed in many real-world applications such

as link prediction (Wang et al., 2016), recommender

systems (Moradi et al., 2015), detection of terror-

ist groups in online social networks (Benigni et al.,

2017). However, the existing community detection

algorithms cannot fully satisfy the need of the current

applications with respect to accuracy because of the

variety of network structures. On the other hand, sev-

eral algorithms detect community structure only from

a single perspective, which may limit the performance

of these methods. For example, GN (Girvan and New-

man, 2002) algorithm detects communities from a

global view by removing edges with large between-

ness. On the contrary, LPA (Raghavan et al., 2007) al-

gorithm detects communities from a local view, where

the community of a node is determined by its neigh-

boring nodes.

Given two neighboring nodes in a network, the

node relationship of whether belonging to the same

community for these two nodes is speciﬁc. If the

node relationship between all nodes and their cor-

responding neighbors can be obtained, the commu-

nity structure can be detected naturally. In this paper,

we propose an algorithm called CDNC (Community

Detection Based on Node Relationship Classiﬁcation)

to detect community structure. A trained classiﬁer is

built to classify the node relationship from both the

global and local perspectives. Then we detect com-

munity structure based on the classiﬁed node relation-

ship. The main contributions of this paper are sum-

marized as follows. First, we propose a new perspec-

tive for community detection—transforming commu-

nity detection to node relationship classiﬁcation. Sec-

ond, we design the method CDNC based on node re-

lationship classiﬁcation. Third, our method does not

require parameter settings and does not rely on prior

knowledge, such as the number of communities. Ex-

perimental results on several real-world and synthetic

networks demonstrate that our algorithm has a bet-

ter performance compared with other competing al-

gorithms in most cases.

The structure of this paper is as follows. In Sec-

tion 2, we introduce the related work on community

596

Yuan, S., Zeng, H. and Wang, C.

Community Detection based on Node Relationship Classiﬁcation.

DOI: 10.5220/0010850600003122

In Proceedings of the 11th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2022), pages 596-601

ISBN: 978-989-758-549-4; ISSN: 2184-4313

detection. In Section 3, we present the CDNC algo-

rithm in detail including the basic principle and the

steps. In Section 4, we present two evaluation metrics

and analyze the performances of CDNC and other al-

gorithms on both real-world and synthetic networks.

At last, we conclude this paper in Section 5.

2 RELATED WORK

Many methods have been proposed for community

detection from different perspectives during the past

decades, such as the divisive hierarchical clustering

methods (Girvan and Newman, 2002), label prop-

agation (Raghavan et al., 2007; Zong-Wen et al.,

2014), methods based on random walk (Pons and

Latapy, 2005; Rosvall and Bergstrom, 2008), meth-

ods based on modularity optimization (Blondel et al.,

2008; Newman, 2004), and methods based on intelli-

gent computing algorithms (Moradi and Parsa, 2019;

Cai et al., 2020; Ding et al., 2018; Hu et al., 2020; Li

et al., 2020).

Girvan Newman (GN) algorithm (Girvan and

Newman, 2002) is a typical divisive hierarchical clus-

tering method, proposed by Newman and Girvan. The

main idea of this algorithm is that the bigger between-

ness an edge has, the more likely this edge is between

different communities. By calculating the between-

ness of each edge and removing the edges with big

betweenness iteratively, the community structure will

appear gradually.

The label propagation algorithm (Raghavan et al.,

2007) was proposed by Raghavan et al. in 2007,

which starts by marking each node with a unique la-

bel and then iterates through all nodes until each node

has the same label as most of its neighbors have. The

striking advantage of this algorithm is its high speed

and simplicity. But the random update orders of the

algorithm cause the instability of the detected com-

munity structure. Liang et al.(Zong-Wen et al., 2014)

introduced consensus weight to the basic label propa-

gation algorithm and proposes a method named the

label propagation algorithm with consensus weight

(LPAcw) which enhances both the stability and the

accuracy of community detection greatly.

The idea of the random walk was proposed by

Pearson (Pearson, 1905). Since then, the random

walk has been used in many different ﬁelds including

community detection where the main principle is that

the random walker tends to become trapped within

communities because of the high connectivity within

communities. Based on the random walk, many al-

gorithms have been put forward, such as WalkTrap

(Pons and Latapy, 2005) and Infomap (Rosvall and

Bergstrom, 2008). The complexity of WalkTrap is

O(mn

), which means WalkTrap is not suitable for

large-scale networks. Infomap is also based on in-

formation theory, which regards community detection

as a coding problem——the optimal partition corre-

sponding to the minimum description length princi-

ple.

The concept of modularity was put forward by

Newman (Newman and Girvan, 2004) ,which is

used as a metric to measure partitions. The ba-

sic idea of modularity optimization algorithms is to

optimize modularity because greater modularity al-

ways corresponds to a better community partition.

However, modularity optimization has been proved

to be an NP-complete problem (Fortunato, 2010).

The modularity optimization algorithms such as Lou-

vain (Multilevel),(Blondel et al., 2008) Fastgreedy

(FG)(Newman, 2004) are devised to approximate the

optimal modularity.

So far researchers have designed many algorithms

based on intelligent computing algorithms such as ge-

netic evolution (Moradi and Parsa, 2019), convolu-

tional neural network (Cai et al., 2020), Hopﬁeld neu-

ral network (Ding et al., 2018), and graph embedding

(Hu et al., 2020). Moradi et al. use genetic evolution

to optimize modularity (Moradi and Parsa, 2019). Cai

et al. elaborately represent edges as images ﬁrstly,

then perform edge classiﬁcation with a convolutional

neural network, ﬁnally detect communities based on

edge classiﬁcation (Cai et al., 2020). Ding et al. pro-

pose a method that detects community structure by

maximizing modularity with a Hopﬁeld neural net-

work (Ding et al., 2018). Hu et al. utilize the graph

representation learning algorithm to represent nodes,

then apply the spectral clustering algorithm to detect-

ing communities with the node embeddings (Hu et al.,

2020).

Figure 1: The overview of the algorithm CDNC proposed

in this paper.

3 THE CDNC ALGORITHM

Given a network G, there are only two types of node

relationship between two neighboring nodes, afﬁliat-

ing to the same community or not. If we can pre-

cisely predict this node relationship for all neighbor-

ing node pairs and then connect the nodes that belong

to the same community, the community structure can

Community Detection based on Node Relationship Classiﬁcation

597

be detected naturally. The overview of the proposed

algorithm CDNC is illustrated in Figure 1.

Selection of features. We believe that whether af-

ﬁliating to the same community for two neighboring

nodes depends on the global inﬂuence from the whole

network and the local inﬂuence from the two nodes

themselves. The betweenness (Wang et al., 2008)

is selected to measure the global inﬂuence, because

the bigger betweenness the edge has, the more un-

likely these two nodes over the edge are in the same

communities. The Jaccard coefﬁcient (Hamers et al.,

1989) of these two nodes and the cosine of vectors

as well as the relative Euclidean distance of vectors

of these two nodes are used to assess the local inﬂu-

ence since a bigger Jaccard coefﬁcient and two similar

vectors indicate that these two nodes are more likely

to be in the same community. In this algorithm, we

use node2vec (Grover and Leskovec, 2016) to vec-

torize nodes. Node2vec is an algorithmic framework

for representational learning on graphs. The experi-

ments demonstrate that these features are useful and

indispensable when considering the complex network

structure.

Binary classiﬁcation. We train a fully connected

neural network with four inputs and one output as a

binary classiﬁer and select the binary cross-entropy

as the loss function, which is widely used in binary

classiﬁcation. Adam is selected as the gradient de-

scent method, and the ReLU and Sigmoid functions

are used as the activation functions in hidden layers

and output layer respectively. The prediction accu-

racy of the trained binary classiﬁer on the test dataset

is higher than 97%, but it still exists misprediction.

Therefore, we introduce modularity as a supplemen-

tary criterion to judge whether two nodes belong to

the same community, which is based on the idea that

the true prediction of node relationship always corre-

sponds to larger modularity.

Community detection. First, we extract the data

from the target network which consists of quadruples

including the relative betweenness, the Jaccard coef-

ﬁcient, the relative Euclidean distance of vectors as

well as the cosine of vectors. Second, we feed the

dataset to the classiﬁer and obtain the prediction of the

node relationship. Then we connect the nodes that af-

ﬁliate to the same community according to the predic-

tion. The detailed algorithm procedure is illustrated in

Algorithm 1. The time complexity of this algorithm is

O(nkc) where k and c are the average degree and the

average community size of the network respectively.

Algorithm 1.

Input:

The target network: G = (V,E)

The Node Relationship classiﬁer: model

Output:

Community information C

1: Extract the data from the target network G for

node relationship classiﬁcation.

2: Use the model to classify the node relationship

and get the classiﬁed result R.

3: for node in V do

4: for neighbor in node’s neighbors do

5: if node and neighbor belong to the same

community according to R then

6: Compute the modularity M1 if they

are not in the same community

7: Compute the modularity M2 if they

are in the same community

8: if M2 >M1 then

9: Node and neighbor belong to the

same community

10: end if

11: end if

12: end for

13: end for

14: return C

4 NUMERICAL EXPERIMENTS

In this section, we evaluate the performance of CDNC

on both the real-world networks and synthetic net-

works and compare it with other representative com-

munity detection algorithms including GN, LPA,

WalkTrap, Infomap, Multilevel, and FG.

4.1 Training Data

Several networks generated by LFR Benchmark (Lan-

cichinetti et al., 2008) are used to extract the training

dataset to train the binary classiﬁer. The parameter of

LFR Benchmark generating networks is illustrated in

Table 1. The total number of nodes varies from 100

to 1000; the average degree varies from 10 to 50; the

maximum degree varies from 40 to 80; the mixing pa-

rameter µ varies from 0.1 to 0.9.

Table 1: The main parameters of LFR Benchmark to gener-

ate training networks.

Parameter N t1 t2 K Maxk µ

100-1000 2 1 10-50 40-80 0.1-0.9

ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods

598

4.2 Evaluation Metrics

To quantify the performance of community detection

algorithms, Normalized Mutual Information (NMI)

(Danon et al., 2005) and Adjusted Rand Index (ARI)

(Rand, 1971) are selected to evaluate the perfor-

mance. NMI is a metric to measure the similarity be-

tween different sets, which measures how close the

predicted communities are to the ground truth, and is

deﬁned as:

NMI(X ,Y ) =

−2

∑

i=1

∑

j=1

i j

log

i j

∑

i=1

log





∑

j=1

log





(1)

where x is the real partition, y is partition found by

the algorithm, c

is the number of communities in x

and c

is the number in y, N is the number of nodes

in the network, N

i j

is the number of nodes shared by

community i in x and community j in y, N

denotes

the sum over row i of matrix N

i j

, and N

denotes the

sum over column j. ARI is also a metrics to com-

pare two partitions, evaluating the outcome of an al-

gorithm, which is deﬁned as:

ARI =

∑

i j



i j



− [

∑





∑









[

∑





∑





] − [

∑





∑









(2)

where n

i j

, a

and b

are values from the contingency

table.

4.3 Simulation on Real-world Networks

In this section, we evaluate our proposed algorithm

CDNC on several real-world networks to demonstrate

its superiority compared to several representative

community detection algorithms. These real-world

networks including Zachary’s karate club (Zachary,

1977), Dolphin (Lusseau et al., 2003), Polbooks,

and American college football (Girvan and Newman,

2002) are widely used to assess the performance of

community detection algorithms. The statistics of

these networks are listed in Table 2. Karate is a

friendship network among 34 members in a karate

club, which is divided into two groups. Dolphins

is a social network of frequent associations among

62 dolphins where nodes represent dolphins, edges

represent the association. Polbooks is a network

of books about US politics where nodes represent

books, edges between books represent frequent co-

purchasing of books. Football is an undirected net-

work from the American football games, where nodes

represent teams, and an edge represents a match be-

tween two teams.

Table 2: Statistics of several real-world networks with

ground-truth partition.

Network Nodes Edges Communities Average degree

Karate 34 78 2 4.5

Dolphins 62 159 2 5.1

Polbooks 105 441 3 8.4

Football 115 613 12 10.6

Table 3: Results of CDNC and other methods in terms of

NMI and ARI on the four real-world networks with ground-

truth partition.

Karate Dolphins Polbooks Football

NMI ARI NMI ARI NMI ARI NMI ARI

CDNC 1.00 1.00 0.77 0.83 0.56 0.69 0.89 0.78

Infomap 0.69 0.70 0.56 0.36 0.49 0.53 0.91 0.89

Multilevel 0.58 0.46 0.51 0.32 0.51 0.55 0.89 0.80

FG 0.69 0.68 0.57 0.45 0.53 0.63 0.69 0.47

GN 0.57 0.46 0.55 0.39 0.55 0.68 0.87 0.77

LPA 0.83 0.88 0.59 0.44 0.50 0.53 0.90 0.82

WalkTrap 0.50 0.33 0.53 0.41 0.54 0.65 0.88 0.81

The experimental result is illustrated in Table 3.

Compared with other algorithms, CDNC achieves the

highest NMI and ARI values in Karate, Dolphins, and

Polbooks, which indicates CDNC can provide a more

robust community structure with better partition qual-

ity. In Football, Infomap performs the best. In a word,

CDNC works better on these real-world networks.

4.4 Simulation on Synthetic Networks

We generate several synthetic networks to evaluate

CDNC and other competing algorithms with LFR

Benchmark, which has some parameters to control

the attributes of the generated networks. The mixing

parameter µ is one of these parameters, which con-

trol the complexity of networks by inter-community

edges. The inter-community edges, also called noise

edges, are added more and more to a synthetic net-

work while increasing the mixing parameter µ. Here

we mainly explore the inﬂuence of the complexity and

size of networks on the performance of these commu-

nity detection methods.

First, we verify the inﬂuence of the size of net-

works on the performance of these algorithms by in-

creasing the number of nodes from 1k to 10k and ﬁx-

ing other parameters. The results of the algorithms

are shown in Figure 2, where Figure 2 shows the re-

sults of NMI, and Figure 3 shows the results of ARI.

We ﬁnd that the performance of our algorithm, LPA,

and WalkTrap is much better than other algorithms

no matter on NMI or ARI, and almost without ﬂuctu-

ation.

Then, we demonstrate the inﬂuence of the com-

plexity of networks on the performance of these algo-

rithms. We ﬁx other parameters to N = 1000, K = 20,

Community Detection based on Node Relationship Classiﬁcation

599

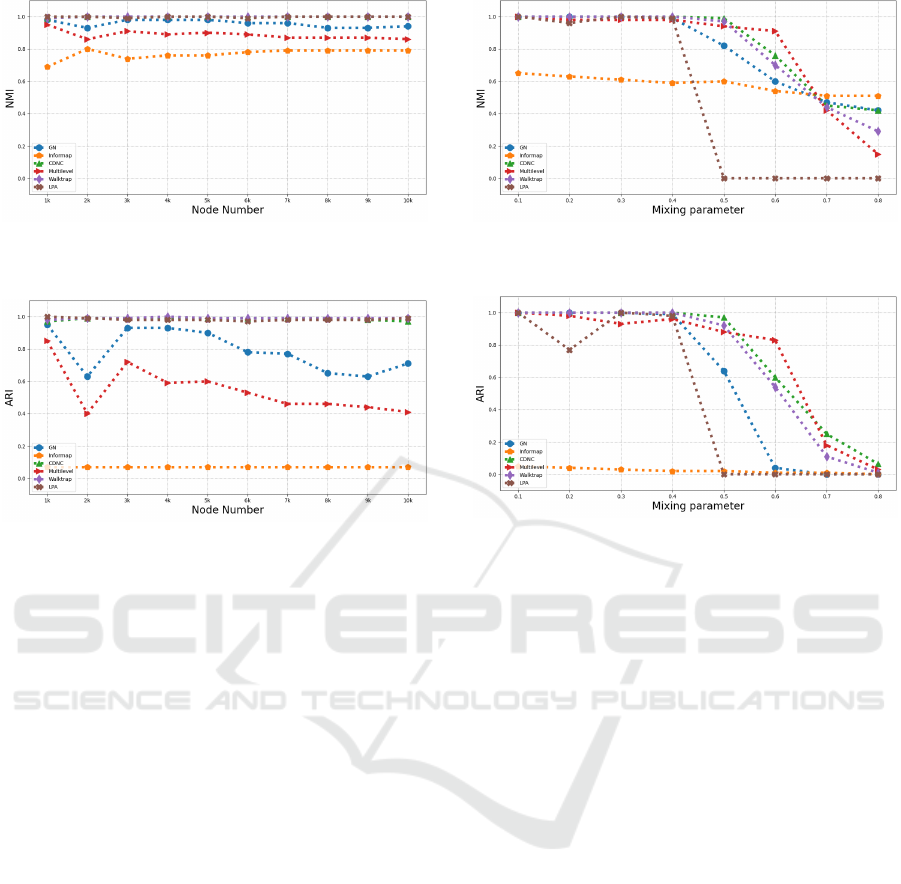
Figure 2: Results of different algorithms in terms of NMI

on synthetic networks with varying numbers of nodes.

Figure 3: Results of different algorithms in terms of ARI on

synthetic networks with varying numbers of nodes.

MaxK = 100 and vary the mixing parameter µ from

0.1 to 0.8 to generate a series of networks with dif-

ferent quantities of noise edges. The results of the

algorithms are shown in Figure 4 and Figure 5, where

Figure 4 shows the results of NMI and Figure 5 shows

the results of ARI. With the increasing of µ, the ef-

fectiveness of all algorithms is attenuated. When µ

is between 0.1 and 0.5, our algorithm always has the

best performance. When µ = 0.6, the result of CDNC

is worse than Multilevel but better than other algo-

rithms both in Figure 4 and 5. When µ is bigger than

0.7, Infomap performs the best, CDNC and GN algo-

rithms perform slightly worse than it but better than

others in Figure 4. In Figure 5, we can see that our

algorithm performs better than other algorithms, only

when µ=0.6, Multilevel algorithm has a higher ARI

value.

5 CONCLUSIONS

In this paper, we transform community detection to

node relationship classiﬁcation and propose an algo-

rithm called CDNC to detect community structure

based on node relationship classiﬁcation. A binary

classiﬁer is trained to classify node relationship which

considers both the global inﬂuence and the local in-

ﬂuence. The experiments demonstrate that our algo-

Figure 4: Results of different algorithms in terms of NMI

on synthetic networks with varying mixing parameter.

Figure 5: Results of different algorithms in terms of ARI on

synthetic networks with varying mixing parameter.

rithm has higher accuracy compared to other repre-

sentative algorithms on both the synthetic and real-

world networks. In the future, we hope to implement

CDNC in parallel and use it for overlapping commu-

nity detection.

ACKNOWLEDGEMENTS

This work was supported in part by the National Key

Research and Development Program of China under

Grant 2016YFB0801100

REFERENCES

Benigni, M. C., Joseph, K., and Carley, K. M. (2017). On-

line extremism and the communities that sustain it:

Detecting the isis supporting community on twitter.

PloS one, 12(12):e0181405.

Blondel, V. D., Guillaume, J.-L., Lambiotte, R., and Lefeb-

vre, E. (2008). Fast unfolding of communities in large

networks. Journal of statistical mechanics: theory

and experiment, 2008(10):P10008.

Cai, B., Wang, Y., Zeng, L., Hu, Y., and Li, H. (2020).

Edge classiﬁcation based on convolutional neural net-

works for community detection in complex network.

Physica A: Statistical Mechanics and its Applications,

556:124826.

ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods

600

Danon, L., Diaz-Guilera, A., Duch, J., and Arenas, A.

(2005). Comparing community structure identiﬁca-

tion. Journal of statistical mechanics: Theory and ex-

periment, 2005(09):P09008.

Ding, J., Sun, Y.-z., Tan, P., and Ning, Y. (2018). Detecting

communities in networks using competitive hopﬁeld

neural network. In 2018 International Joint Confer-

ence on Neural Networks (IJCNN), pages 1–7. IEEE.

Dong, L., Li, R., Zhang, J., and Di, Z. (2016). Population-

weighted efﬁciency in transportation networks. Scien-

tiﬁc reports, 6(1):1–10.

Fortunato, S. (2010). Community detection in graphs.

Physics reports, 486(3-5):75–174.

Girvan, M. and Newman, M. E. (2002). Community struc-

ture in social and biological networks. Proceedings of

the national academy of sciences, 99(12):7821–7826.

Goltsev, A. V., Dorogovtsev, S. N., Oliveira, J. G., and

Mendes, J. F. (2012). Localization and spreading of

diseases in complex networks. Physical review letters,

109(12):128702.

Grover, A. and Leskovec, J. (2016). node2vec: Scal-

able feature learning for networks. In Proceedings

of the 22nd ACM SIGKDD international conference

on Knowledge discovery and data mining, pages 855–

864.

Hamers, L. et al. (1989). Similarity measures in scientomet-

ric research: The jaccard index versus salton’s cosine

formula. Information Processing and Management,

25(3):315–18.

Hu, F., Liu, J., Li, L., and Liang, J. (2020). Community

detection in complex networks using node2vec with

spectral clustering. Physica A: Statistical Mechanics

and its Applications, 545:123633.

Hu, K., Hu, J.-B., Tang, L., Xiang, J., Ma, J.-L., Gao,

Y.-Y., Li, H.-J., and Zhang, Y. (2018). Predicting

disease-related genes by path structure and commu-

nity structure in protein–protein networks. Journal

of Statistical Mechanics: Theory and Experiment,

2018(10):100001.

Lancichinetti, A., Fortunato, S., and Radicchi, F. (2008).

Benchmark graphs for testing community detection

algorithms. Physical review E, 78(4):046110.

Li, H.-J., Wang, L., Zhang, Y., and Perc, M. (2020). Opti-

mization of identiﬁability for efﬁcient community de-

tection. New Journal of Physics, 22(6):063035.

Li, H.-J., Zhang, J., Liu, Z.-P., Chen, L., and Zhang, X.-S.

(2012). Identifying overlapping communities in social

networks using multi-scale local information expan-

sion. The European Physical Journal B, 85(6):1–9.

Lusseau, D., Schneider, K., Boisseau, O. J., Haase, P.,

Slooten, E., and Dawson, S. M. (2003). The bot-

tlenose dolphin community of doubtful sound features

a large proportion of long-lasting associations. Behav-

ioral Ecology and Sociobiology, 54(4):396–405.

Moradi, M. and Parsa, S. (2019). An evolutionary method

for community detection using a novel local search

strategy. Physica A: Statistical Mechanics and its Ap-

plications, 523:457–475.

Moradi, P., Ahmadian, S., and Akhlaghian, F. (2015). An

effective trust-based recommendation method using a

novel graph clustering algorithm. Physica A: Statisti-

cal mechanics and its applications, 436:462–481.

Newman, M. E. (2004). Fast algorithm for detecting com-

munity structure in networks. Physical review E,

69(6):066133.

Newman, M. E. and Girvan, M. (2004). Finding and eval-

uating community structure in networks. Physical re-

view E, 69(2):026113.

Pearson, K. (1905). The problem of the random walk. Na-

ture, 72(1867):342–342.

Pons, P. and Latapy, M. (2005). Computing communities

in large networks using random walks. In Interna-

tional symposium on computer and information sci-

ences, pages 284–293. Springer.

Raghavan, U. N., Albert, R., and Kumara, S. (2007).

Near linear time algorithm to detect community struc-

tures in large-scale networks. Physical review E,

76(3):036106.

Rand, W. M. (1971). Objective criteria for the evaluation of

clustering methods. Journal of the American Statisti-

cal association, 66(336):846–850.

Rosvall, M. and Bergstrom, C. T. (2008). Maps of random

walks on complex networks reveal community struc-

ture. Proceedings of the national academy of sciences,

105(4):1118–1123.

Wang, H., Hernandez, J. M., and Van Mieghem, P. (2008).

Betweenness centrality in a weighted network. Phys-

ical Review E, 77(4):046105.

Wang, Z., Wu, Y., Li, Q., Jin, F., and Xiong, W. (2016). Link

prediction based on hyperbolic mapping with commu-

nity structure for complex networks. Physica A: Sta-

tistical Mechanics and its Applications, 450:609–623.

Zachary, W. W. (1977). An information ﬂow model for con-

ﬂict and ﬁssion in small groups. Journal of anthropo-

logical research, 33(4):452–473.

Zheng, J., Wang, S., Li, D., and Zhang, B. (2019). Per-

sonalized recommendation based on hierarchical in-

terest overlapping community. Information Sciences,

479:55–75.

Zong-Wen, L., Jian-Ping, L., Fan, Y., and Petropulu, A.

(2014). Detecting community structure using label

propagation with consensus weight in complex net-

work. Chinese Physics B, 23(9):098902.

Community Detection based on Node Relationship Classiﬁcation

601