
Optimizing Multi-objective Knapsack Problem using a Hybrid Ant
Colony Approach within Multi Directional Framework
Imen Ben Mansour
1,2
1
ESPRIT School of Engineering, Tunis, Tunisia
2
ENSI-LARIA, University of Manouba, Tunisia
Keywords:
Knapsack Problem, Multi-objective Optimization, Ant Colony Optimization, Local Search Method,
Multi-directional Framework.
Abstract:
Balancing the convergence and diversity simultaneously is very challenging for multi-objective evolutionary
algorithms on solving multi-objective optimization problems (MOPs). The proposed approach MD-HACO
coupled an Ant Colony Optimization (ACO) algorithm with a multi-objective local search procedure, and
evolves it into a multi-directional framework. The idea is to optimize the overall quality of Pareto set approx-
imation by using different configurations of the hybrid approach by means of different directional vectors.
During the optimization process, the artificial ants work in different search directions in the objective space
trying to approximate small parts of the Pareto front. Afterward, a local search procedure is applied to each
sub-region to enhance the search process toward the extreme Pareto-optimal solutions with respect to the
weight vector under consideration. A multi-directional set holding the non-dominated solutions according
to all directional archives is maintained. The proposed approach is tested on widely used multi-objective
multi-dimensional knapsack problem (MOMKP) instances and compared with well-known state-of-the-art al-
gorithms. Experiments highlight that the use of a multi-directional paradigm as well as a hybrid schema can
lead to interesting results on the MOMKP and ensure a good balance between convergence and diversity.
1 INTRODUCTION
Optimizing multi-objective problems is considered as
a hard task since multiple objectives should to be opti-
mized simultaneously while satisfying a several con-
straints. Indeed, the aim is to find the optimal trade-
offs between the different objectives that are usually
conflicting. To this end, researchers have proposed
many metaheuristic algorithms in order to achieve the
set of compromise solutions which is called Pareto
front in a reasonable time.
In this paper, we address the multi-objective
multi-dimensional knapsack problem (MOMKP) that
consists to find a subset of items subject to a set of
resource constraints while maximizing several objec-
tives. Due to its NP-hard nature (Martello, 1990),
and wide-range applicability (Chabane et al., 2017),
(Ehrgott and Ryan, 2002), (Kellerer et al., 2004)
MOMKP has been considered among the most in-
triguing multi-objective optimization problems, and
has attracted considerable attention from the oper-
ations research community. As a result, a signifi-
cant number of works have investigated the MOMKP,
giving rise to various solution methods (Lust and
Teghem, 2012).
Considering multi-objective metaheuristics, the
main purpose behind designing a approximate ap-
proach, is balancing exploration and exploitation. The
population-based methods such as ant colony opti-
mization (ACO) are powerful techniques in the ex-
ploration of the solution space but less efficient in
the exploitation of the search toward promising re-
gions. However, local search approaches have per-
fect plans for intensification, but have a tendency of
getting stuck in local optima due to lack of diversi-
fication. Therefore, to intensify the search and es-
cape from being trapped into local optima, a local en-
hancement will be coupled with an ACO approach.
Within the scope of this paper, a hybrid approach is
proposed as a synergy of the ACO algorithm with
a Tchebycheff-based Local Search (TLS) procedure
coined as a Multi-Directional Hybrid Ant Colony Op-
timization approach (MD-HACO) to handle the knap-
sack problem within the multi-objective framework.
The design of a hybrid approach is motivated by the
need to enhance the convergence of the solutions to-
Ben Mansour, I.
Optimizing Multi-objective Knapsack Problem using a Hybrid Ant Colony Approach within Multi Directional Framework.
DOI: 10.5220/0010865600003116
In Proceedings of the 14th International Conference on Agents and Artificial Intelligence (ICAART 2022) - Volume 2, pages 409-418
ISBN: 978-989-758-547-0; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
409

ward the optimal Pareto front and to promote diversity
of the search space.
The proposed approach uses an improved version
of the Gw-ACO approach (Mansour et al., 2019). In-
deed, this version differs from Gw-ACO mainly in the
used Ant System variant and the solutions construc-
tion phase:
(i) Here, the proposed algorithm follows
M AX − M I N Ant System (St
¨
utzle and Hoos,
2000) scheme. Whereas Gw-ACO is based on an
elitist version of Ant System (Dorigo et al., 1996).
(ii) Gw-ACO uses many heuristic matrices, it as-
signs to each objective a weighted heuristic informa-
tion. In MD-HACO, all ants in the algorithm share
one heuristic matrix in the process of constructing the
solution and this matrix changes configuration during
the optimization phase using weighted pseudo-utility
ratio. The objectives were considered fairly, i.e., no
objective has any precedence over the others and the
evaluation of a candidate solution is rather based on
its position in the objective space. Therefore, the
Pareto optimal set may be found (Iredi et al., 2001).
The rest of this paper is organized as follows.
In section two, we introduce briefly the context of
multi-objective optimization. The studied problem
MOMKP is formulated in section 3. Next, the multi-
objective ACO (MOACO) approach is introduced.
The hybrid approach is presented in section five. The
experiments are detailed on a multi-objective multi-
dimensional knapsack problem in the next section.
The last section is devoted to conclusion and discus-
sion about possible future research directions.
2 MULTI-OBJECTIVE
OPTIMIZATION PROBLEMS
In multi-objective optimization problems, a set of ob-
jective functions must be maximized or minimized,
subjected to a set of constraints. In the following, we
assume that m objective functions F = ( f
1
, · ·· , f
m
)
are to be maximized. Each objective function f
k
is
defined as f
k
: D
1
× · ·· ×D
n
→ R , where the D
i
are the domains of the decision variables. An op-
timization problem is defined by an objective space
Z = {z = (z
1
, · ·· , z
m
)|∀1 ≤ k ≤ m, z
k
∈ R } and a deci-
sion space X = {x = (x
1
, · ·· , x
n
)|∀1 ≤ i ≤ n, x
i
∈ D
i
}.
Each decision vector x ∈ X is associated to an ob-
jective vector z = ( f
1
(x), · · · , f
m
(x)) ∈ Z. In order
to compare solutions in a multi-objective context, the
concept of Pareto dominance is used. The definition
1 formally defines the Pareto dominance relation in a
maximization context without loss of generality.
Definition 2.1. A decision vector x ∈ X is said to
dominate another decision vector x
0
∈ X (written as
x x
0
), if ∀1 ≤ k ≤ m, f
k
(x) ≥ f
k
(x
0
) and ∃1 ≤ j ≤
m, f
j
(x) > f
j
(x
0
).
Accordingly, a decision vector x ∈ X is said to be
Pareto optimal (resp. non-dominated) if and only if it
is not dominated by any other solution of the search
space (resp. within a set of solutions).
3 MULTI-OBJECTIVE
MULTI-DIMENSIONAL
KNAPSACK PROBLEM
The multi-objective multidimensional knapsack prob-
lem could be formulated as follows:
Maximize
n
∑
j=1
p
k
j
x
j
k = 1, ..., m (1)
Sub ject to
n
∑
j=1
w
i
j
x
j
≤ b
i
i = 1, ..., q (2)
x
j
∈ {0, 1} j = 1, ..., n
n denotes the number of items I
j
, x
j
corresponds to
the decision variable for the item I
j
i.e., the item is
taken or not taken since we consider a 0/1 knapsack
problem. Each item I
j
has a profit p
k
j
relatively to the
objective k and a weight w
i
j
relatively to the resource
i and b
i
is the total quantity available for the resource
i.
4 MULTI-OBJECTIVE ANT
COLONY OPTIMIZATION
ACO metaheuristic, initially developed by Dorigo
(Dorigo et al., 1991b), is a cooperative population-
based construction algorithm inspired from the behav-
ior of real ants while searching for a food source. The
colony of ants cooperates to perform some tasks for
the whole group using an indirect form of communi-
cation, called pheromone, deposited by the member
of the colony while building their solutions. From
an initial point, each ant moves on the search space
through a finite sequence of points. Its movements
depend on a stochastic construction policy directed
by two types of information: (i) the ancient ant
movements recorded in his memory (ii) pheromone
traces and heuristic information specific to the prob-
lem being treated. These informations are used by
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
410

ants to help them to converge on the most inter-
esting areas of the search space. The first exam-
ple of such an algorithm was Ant System and intro-
duced by Dorigo, Maniezzo and Colorni in (Dorigo
et al., 1991b),(Dorigo et al., 1991a),(Dorigo et al.,
1996) and Colorni, Dorigo and Maniezzo in (Colorni
et al., 1991) and (Colorni et al., 1992) using Traveling
Salesman Problem (TSP) as a sample application.
Due to the success of ACO for mono-objective
problems (Dorigo and Blum, 2005) many authors
investigated the capabilities of this metaheuristic to
handle multi-objective problems. In (Gambardella
et al., 1999), a multiple ant colony system is proposed
to solve the vehicle routing problems with time win-
dows (MACS-VRPTW). The algorithm is organized
with a hierarchy of ant colonies designed to succes-
sively optimize a multi-objective function: the first
colony minimizes the number of vehicles while the
second optimizes the feasible solutions found by the
first. Each colony uses an independent pheromone
structure for its specific purpose and they collabo-
rate by sharing the best overall solution found. In
(Alaya et al., 2007), a generic multi-objectif ACO
approach named m-ACO, is proposed and instanti-
ated with four variants. This algorithm is parameter-
ized by the number of ant colonies and the number
of the pheromone structures. In (Mansour and Alaya,
2015), an ACO algorithm called IBACO was intro-
duced to slove MOMKP. The IBACO algorithm em-
ploys binary indicators. It uses hypervolume and ep-
silon indicators to guide the artificial ants to find the
best solutions by laying pheromone trails relatively to
the indicator values. (Yagmahan and Yenisey, 2010)
solved the flow shop scheduling problem with a multi-
objective ant colony system algorithm combined to
a local search strategy. proposed a MOACO for
the mixed-model assembly line balancing problem to
minimize the balance delay and the smoothness index
for a given cycle time.
On the above approaches, the objectives were con-
sidered fairly where they foster search in specific di-
rections in the objective space. Iredi, Merkle and
Middendorf proposed using different weight vectors
in order to force ants to search in different regions of
the optimal Pareto set. They introduced the Bicriteri-
onAnt algorithm in (Iredi et al., 2001). Since the suc-
cess of BicriterionAnt, several ant-based approaches
following the multi-directional idea were developed.
(Angus, 2007) solved the multi-objective TSP using
population-based ACO algorithm with an average-
rank-weight method to determine weightings for each
objective. A MOACO approach based on decompo-
sition method called MOEA/D-ACO is introduced in
(Ke et al., 2013). In MOEA/D-ACO, each ant tar-
gets a particular point in the Pareto front by means of
uniformly distributed weight vectors, each group of
ants tries to approximate a particular part of the Pareto
front. Recently, (Mansour et al., 2019) conceived an
ant colony approach based on multiple search direc-
tions to optimize the MOMKP. The algorithm uses
a generation-based weight assignment strategy to en-
hance population diversity.
5 MULTI-DIRECTIONAL
HYBRID ANT COLONY
OPTIMIZATION ALGORITHM
FOR MOMKP
Since ant colony should be able to generate a set of
diverse new solutions when solving large and hard
optimization problems, the use of directional vectors
seems to be an interesting paradigm. A possible op-
tion for multi-directional metaheuristics consists in
using different combinations of weight vector during
the optimization process. The directional model is
used to guide the optimization on exploiting new and
different parts of the objective space.
Our algorithm follows the M AX − M I N Ant
System (St
¨
utzle and Hoos, 2000) scheme. As a first
step, the pheromone traces are initialized to an upper
bound τ
max
. Then, the Multi-directional optimization
process is launched. The idea is to decompose the ob-
jective space into several sub-regions i.e search direc-
tions by means of different Λ vectors. Here, we use
the method that has been proposed in (Mansour et al.,
2018) and (Mansour et al., 2019). This method, called
Gradual weights generation method (Gw), is interest-
ing because it uses not only a different weight vec-
tor at each search step, but also gradually distributed
weights in the objective space (progressively gener-
ated from 0 to 1 or/and from 1 to 0) more details can
be found in (Mansour et al., 2019) (especially con-
cerning the weight assignment process). Each sub-
region has its own directional Pareto set A holding all
non-dominated solutions of the current direction i.e.
small part of the whole Pareto front. At each genera-
tion, the colony focuses in one single sub-region and
constructs solutions according to the search direction
under consideration. Therefore, it can compute a par-
ticular part of the Pareto front. Once the construc-
tion phase is done, all solutions are added to a local
set Sol and the directional Pareto set A is update with
the non-dominated solutions of Sol. Then, the Multi-
directional iterated local search procedure is applied
to each solution S
h
in Sol (see Section 5.3). Once the
directional optimization phase is carried out, a shar-
Optimizing Multi-objective Knapsack Problem using a Hybrid Ant Colony Approach within Multi Directional Framework
411

ing step is performed. First, the pheromone structure
is update as detailed in Section 5.2 and then the multi-
directional Pareto set called P manages the update of
the non-dominated solutions sent by the directional
Pareto sets A. This stage constitutes the general in-
formation sharing between the different sub-regions,
since the multi-directional Pareto set benefits from the
respective potential contribution of each directional
Pareto set.
The proposed Multi-directional Hybrid Ant
Colony Optimization approach is described in algo-
rithm 1. To have a clear understanding of the pro-
cess of MD-HACO, Figure 1 provides an illustration
of flowchart of the proposed approach.
Algorithm 1: Multi-directional Hybrid Ant Colony Opti-
mization Algorithm.
Input: Nbants (number of ants)
g
max
(maximum number of generations)
λ = (λ
1
, ·· · , λ
m
) (weight vector)
Output: P (multi-directional Pareto set P)
Initialize the traces of pheromone to τ
max
Initialize the multi-directional Pareto set P ←
/
0
ForEach direction λ(g), g ∈ {1, ·· · , g
max
} do
Step 0: Initialize A ←
/
0 , Sol ←
/
0
Step 1: Compute λ
k
for each objective f
k
Step 2: Construct solution S
h
, h ∈ {1, ·· · , Nbants}
and Sol ← Sol ∪ S
h
Step 3: A ← Non-dominated solutions of A ∪ Sol
Step 4: Execute the Multi-directional iterated local
search procedure for each S
h
in Sol
EndForEach
Update pheromone structure
P ← Non-dominated solutions of (P
S
A). If g
max
is
reached then stop and return P; else performs another
directional optimization step.
5.1 Solutions Construction
Each ant h constructs one feasible solution by ap-
plying repeatedly a stochastic function named a state
transition rule. This function is used to select the
most appropriate item I
j
to be added to the solution
S
h
among a set of feasible items Feas (candidate ver-
tices). This set is updated by including items not yet
added and that don’t violate any constraint. The tran-
sition rule p
S
h
is directed by the pheromone value τ
S
h
and the heuristic information η
S
h
:
p
S
h
(I
j
) =
[τ
S
h
(I
j
)]
α
.[η
S
h
(I
j
)]
β
∑
I
l
∈Feas
[τ
S
h
(I
l
)]
α
.[η
S
h
(I
l
)]
β
(3)
The heuristic information is used to guide the
search process of artificial ants. In order to orientate
ants to look in different regions of the non-dominated
front, different configurations of the heuristic in-
formation matrix are executed, i.e. using different
weight vectors. For that, η
S
h
for a given ant h, is set
as:
η
S
h
(I
j
) =
∑
m
k=1
λ
k
(g)p
k
j
∑
q
i=1
w
i
j
R
S
h
(i)
(4)
where R
S
h
(i) = b
i
−
∑
t∈S
h
r
it
is the remaining
amount of the resource i when an ant h is currently
building its solution S
h
. p
k
j
and w
i
j
are respectively
the profit and the weight of the candidate item.
5.2 Pheromone Update
The pheromone matrix is defined as an aggregation of
objectives. Once all ants have constructed their solu-
tions and the set Sol is updated with all created solu-
tions, the pheromone update phase will be needed:
τ(I
j
) ← (1 − ρ) ∗ τ(I
j
) + ∆τ(I
j
) (5)
To exploit the most promising parts, ants that are al-
lowed to update the pheromone trails are only those
that have found non-dominated solutions S
ND
during
the actual iteration. Furthermore, to give every gen-
eration of ants the same influence in a particular part
of the Pareto front, ants that are authorized to update,
lay the same amount of pheromone ∆τ(I
j
) equal to the
current archive set size |A|.
5.3 Enhancement by Multi-directional
Iterated Local Search
Local search aims to improve the quality of solu-
tions generated by the Ant Colony algorithm. To that
end, the enhancement procedure follows the direc-
tional model using by the proposed multi-directional
ACO approach. Since our proposed approach uses
a multi-directional framework, the multi-directional
Ant Colony Optimization algorithm explicitly decom-
poses the objective space in sub-regions. Indeed, the
weight vector is necessary here for the computation
of the pseudo-utility ratio (Mansour et al., 2017a) and
(Mansour et al., 2017b), it evaluates the performance
of the potentially efficient solution relatively to the
different objectives. That is, the selection of the so-
lution for a given vector is based on the position of
the solution in the objective space. Where each ant
attempts to find a new solution according to this posi-
tion.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
412
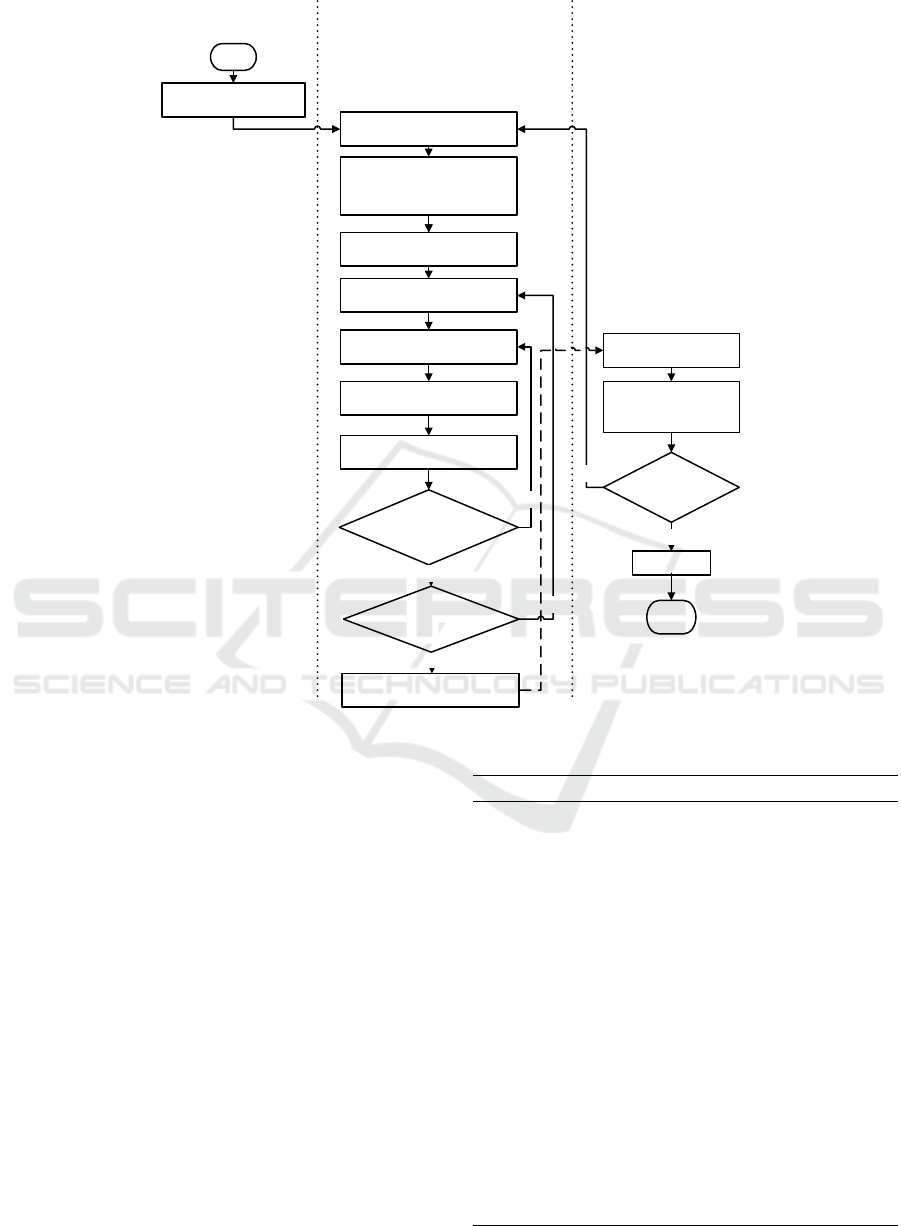
Start
Construct solution S
h
and
Update Sol with S
h
,
1≤h≤Nbants
Is all neighbors are
explored or w ≠ S
h*
Update directional Pareto
set A with A ꓴ Sol
No
Yes
Compute λ
k
(g) for each f
k
1≤k≤m
Update directional Pareto
set A with A ꓴ Sol
Calculate fitness value for
unvisited solution S
h
in Sol
Generate an unexplored
neighbor S
h*
from S
h
Compute fitness value for
S
h*
Remove worst solution w in
Sol
Initialize the traces of
pheromone
Update pheromone
structure
Update muli-
directional Pareto set
P
Is g
max
is reached
?
Return P
Finish
No
Yes
Yes
Is all S
h
in Sol are
visited ?
No
Initialization phase
Muli-directionnel
optimization process
Sharing phase
Figure 1: Flowchart of the proposed Multi-directional Hybrid Ant Colony Optimization Algorithm: MD-HACO.
5.3.1 Algorithm Description
The local search steps are performed on each sub-
region and for each solution found by the colony. Al-
though the method proposed here is inspired from the
one introduced in (Mansour et al., 2018), here only
one local search procedure is executed using multi-
ple search directions. The proposed method operates
as outlined in Algorithm 2: Before performing a lo-
cal search step, the fitness value of each solution in
Sol is calculated. This step involves the exploring of
the neighborhood of each solution S
h
in Sol until we
find a solution S
h∗
that is better than the worst solu-
tion w of Sol regarding the search direction λ under
consideration. Then, S
h∗
is added to Sol and replaces
the solution w. The neighborhood exploration process
stops once the first improving neighbor is found.
To evaluate a solution S
h
against the whole popu-
lation, we use the augmented weighted Tchebycheff
method. This scalarization approach measure the
Algorithm 2: Multi-directional iterated local search.
Input: Sol (Solutions set)
Λ (the weight vectors set)
Output: A (Directional Pareto set)
For Each S
h
∈ Sol
U pdate re f erence point z
∗
Calculate Fit(S
h
|λ, z
∗
)= g
AT
(S
h
|λ, z
∗
)
Repeat
Generate neighbor S
h∗
f rom S
h
Calculate Fit(S
h∗
|λ, z
∗
)
Find w with the worst f itness value Fit(w|λ, z
∗
)
If Fit(S
h∗
|λ, z
∗
) > Fit(w|λ, z
∗
)
Replace w with S
h∗
in Sol
EndIf
Until S
h∗
6= w or all neighbors are explored
End For Each
A ← Non-dominated solutions o f A ∪ Sol
Optimizing Multi-objective Knapsack Problem using a Hybrid Ant Colony Approach within Multi Directional Framework
413

population diversity without sacrificing convergence
with respect to the number of objectives in terms of
computational time(L’opez et al., 2013) and (D
¨
achert
et al., 2012):
g
AT
(S
h
|λ, z
∗
) = max
k=1...m
{λ
k
.|z
∗
k
− f
k
(S
h
)|}
+ ε
m
∑
k=1
|z
∗
k
− f
k
(S
h
)| (6)
where ε ≥ 0 is usually chosen as a small posi-
tive number and where z
∗
is the ideal point and up-
date it during the execution of the algorithm as: z
∗
k
=
max
k=1...m
f
k
(S
h
)
In this paper, we examine the augmented weighted
Tchebycheff to calculate the fitness value of each so-
lution. Therefore, good solutions are emphasized in
each sub-region to maintain a balance between con-
vergence and diversity using the distance between the
solutions and the reference vectors.
5.3.2 Neighborhood Structure
Since the 0/1 multi-objective knapsack problem is a
constrained problem, all individuals should satisfy all
resource constraints. Indeed, we have to define an
efficient neighborhood structure for this problem to
both handle constraints and increases the solutions
quality.
A solution S
h
to the MOMKP can be presented
as a double list I = (I
+
l
, I
−
l
). The first list I
+
l
cor-
responds to the taken item (belonging to the solu-
tion) I
+
l
={I
+
1
,I
+
2
,...,I
+
T
}, where T is the size of the list.
The second list I
−
l
is the list of the remaining items
I
−
l
={I
−
1
,I
−
2
,...,I
−
NT
}, where NT is the number of uns-
elected items. The transition from one solution S
h
to
S
h
0
is referred as a move. Two neighborhood opera-
tors are performed in sequential order in this paper for
the MOMKP:
(1) U(l
+
): The extraction ratio is calculated for
all items in list I
+
l
, which measures the utility value
of each item. The lower this ratio is, the worst the
item is.
(2) U (l): The insertion ratio is calculated for all
unselected items in list I
−
l
, the ratio measures the
quality of the candidate item according to the solu-
tion S
h
where the higher this ratio is, the better the
item is.
6 SIMULATION AND
EVALUATION
We examine the performance of the proposed algo-
rithm, Multi-Directional Hybrid Ant Colony Opti-
mization algorithm MD-HACO, by means of com-
putational experiments in an enlarged sampling size
scheme to solve the MOMKP. An empirical com-
parison to powerful decomposition-based multiobjec-
tive algorithms (Gw-ACO: (Mansour et al., 2019),
MOEA/D: (Zhang and Li, 2007) and MOEA/D-ACO:
(Ke et al., 2013)) and state-of-the-art reference ap-
proaches (2PPLS: (Lust and Teghem, 2012)) is inves-
tigated.
In order to evaluate the efficiency of a proposed
approach we use the following performance met-
rics: The hypervolume difference (Zitzler and Thiele,
1999) and the summary attainment surface (Da Fon-
seca et al., 2001). Moreover, we use the non-
parametric Mann-Whitney statistical test to verify if
the difference between the tested algorithms is statis-
tically significant with a confidence level greater than
95% (p-value ≤ 0.05). Note that we obtain similar
results using other statistical tests.
6.1 Parametrization of the MD-HACO
Metaheuristic algorithms require a crucial decision
about the values of numerous parameters. The so-
lution quality and speed may be affected by the pa-
rameter settings. Indeed, we have been striven to de-
termine an appropriate set of parameter values for the
MD-HACO. The FQ (frequency in the Gw method)
and g
max
are determinate according to the number of
objectives. For instances with 2 objectives, FQ and
g
max
are respectively 800 and 200. For instances with
3 objectives, they are equal to 40 and 100 and for in-
stances with 4 objectives, FQ and g
max
are set to 20
and 125.
The significance weights for pheromone trail α is
set to 1, the significance weights for heuristic infor-
mation β to 10, the pheromone evaporation rate ρ to
0.90, the number of ants set to 10. The lower and
upper bound of pheromone τ
min
and τ
max
are respec-
tively set to 1 and 5 and the epsilon parameter of g
AT
function ε is set to 10
−3
.
6.2 Experimental Results
Table 1 reports the mean CPU (M-CPU) running
time (in second) spent for each instance by Gw-ACO,
2PPLS, MOEA/D, MOEA/D-ACO and MD-HACO.
From this table, it is clear that the proposed algorithm
is faster (bold values) than the other compared ap-
proaches on large instances with 3 and 4 objectives.
Figures 2 plot respectively the median attainment
surfaces obtained by comparing Gw-ACO, 2PPLS,
MOEA/D, MOEA/D-ACO and MD-HACO on bi-
objective instances. The figures illustrate that the
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
414

Table 2: Average and standard deviation values of the hypervolume difference metric.
Instance Gw-ACO 2PPLS MOEA/D
MOEA/
D-ACO MD-HACO
Avg Std Avg Std Avg Std Avg Std Avg Std
2 250 4.33E-01 2.72E-02 1.84E-01 1.27E-01 3.05E-01 8.82E-02 2.91E-01 1.49E-01 1.72E-01 3.74E-02
2 500 4.41E-01 2.85E-02 1.76E-01 1.19E-01 3.26E-01 9.08E-02 1.73E-01 1.59E-01 2.05E-01 1.71E-02
2 750 4.28E-01 3.18E-02 2.19E-01 1.40E-01 3.63E-01 7.03E-02 2.51E-01 1.30E-01 1.57E-01 8.56E-03
3 250 5.35E-01 1.85E-02 4.54E-01 2.91E-02 1.91E-01 1.74E-01 2.07E-01 1.95E-02
3 500 5.47E-01 1.73E-02 4.30E-01 6.72E-02 3.65E-01 1.39E-01 2.04E-01 1.34E-02
3 750 5.63E-01 1.00E-02 4.20E-01 6.79E-02 2.87E-01 1.69E-01 2.09E-01 9.75E-03
4 250 5.38E-01 2.53E-02 4.79E-01 2.39E-02 2.96E-01 8.64E-02 2.53E-01 1.17E-02
4 500 5.25E-01 2.67E-02 4.36E-01 6.69E-02 3.67E-01 9.16E-02 1.84E-01 1.54E-02
4 750 5.58E-01 2.42E-02 4.59E-01 4.66E-02 3.87E-01 5.76E-02 1.70E-01 1.21E-02
Table 3: p-values of the Mann-Whitney statistical test.
Instance 2 250 2 500
Algorithm Gw-ACO 2PPLS MOEA/D MOEA/D-ACO Gw-ACO 2PPLS MOEA/D MOEA/D-ACO
MD-HACO ≤0.05 0.440 ≤0.05 ≤0.05 ≤0.05 0.518 ≤0.05 0.674
Instance 2 750
Algorithm Gw-ACO 2PPLS MOEA/D MOEA/D-ACO
MD-HACO ≤0.05 0.092 ≤0.05 0.075
Instance 3 250 3 500
Algorithm Gw-ACO MOEA/D MOEA/D-ACO Gw-ACO MOEA/D MOEA/D-ACO
MD-HACO ≤0.05 ≤0.05 0.900 ≤0.05 ≤0.05 ≤0.05
Instance 3 750
Algorithm Gw-ACO MOEA/D MOEA/D-ACO
MD-HACO ≤0.05 ≤0.05 ≤0.05
Instance 4 250 4 500
Algorithm Gw-ACO MOEA/D MOEA/D-ACO Gw-ACO MOEA/D MOEA/D-ACO
MD-HACO ≤0.05 ≤0.05 ≤0.05 ≤0.05 ≤0.05 ≤0.05
Instance 4 750
Algorithm Gw-ACO MOEA/D MOEA/D-ACO
MD-HACO ≤0.05 ≤0.05 ≤0.05
Table 1: CPU running time (seconds).
Instance Gw-ACO 2PPLS MOEA/D
MOEA/
D-ACO MD-HACO
2 250 13.2 3.1 4.8 5.1 4.6
2 500 56.6 14.8 14.8 15.2 15.1
2 750 126.1 25.1 28.6 24.7 24.8
3 250 34.1 9.2 8.7 3.5
3 500 135.9 24.5 20.7 12.4
3 750 310.3 48.4 37.9 26.3
4 250 51.0 22.1 11.8 8.7
4 500 206.0 46.6 29.9 20.9
4 750 471.8 130.8 50.5 48.0
differences between the attainment surfaces returned
by MD-HACO, 2PPLS and MOEA/D-ACO are small
and therefore it is difficult to distinguish visually.
Nevertheless, it is evident from figures 2 (b) and 2
(c) that the surfaces obtained by MD-HACO are bet-
ter than those obtained by Gw-ACO and MOEA/D.
Indeed, we can clearly observe that the solutions gen-
erated by these compared algorithms are below those
obtained by the proposed approach.
Table 2 presents the mean and standard deviation
of the hypervolume difference of MD-HACO and the
state-of-the-art reference approaches. Outputs clearly
highlight that the proposed hybrid approach is com-
petitive compared to Gw-ACO, 2PPLS, MOEA/D and
MOEA/D-ACO. By analyzing the results, one can say
that MD-HACO obtains the best performance for 7
out of the 9 instances and MOEA/D-ACO find the
best results for 2 out of the 9 instances. However, Gw-
ACO, 2PPLS and MOEA/D fail to achieve best val-
ues on all tested instances. Moreover, the differences
between values obtained by MD-HACO and those re-
turned by Gw-ACO and MOEA/D are very important
on the 9 instances. These gaps are smaller between
MD-HACO, 2PPLS and MOEA/D-ACO only on the
bi-objective instances which confirm the curves rel-
atively close obtained in figures 2. But these gaps
grow significantly on the instances with 3 and 4 ob-
jectives. Table 3 summarizes the p-values returned
by the Mann-Whitney statistical test when comparing
MD-HACO against Gw-ACO, 2PPLS, MOEA/D and
MOEA/D-ACO. These values are confirmed those of
the previous table. Indeed, we can clearly see that
on the 2 250 instance, MD-HACO statistically out-
performs Gw-ACO, MOEA/D and MOEA/D-ACO.
On the 2 500 and 2 750 instances, the proposed ap-
proach performs statistically better than Gw-ACO and
MOEA/D. When comparing MD-HACO and 2PPLS,
Optimizing Multi-objective Knapsack Problem using a Hybrid Ant Colony Approach within Multi Directional Framework
415
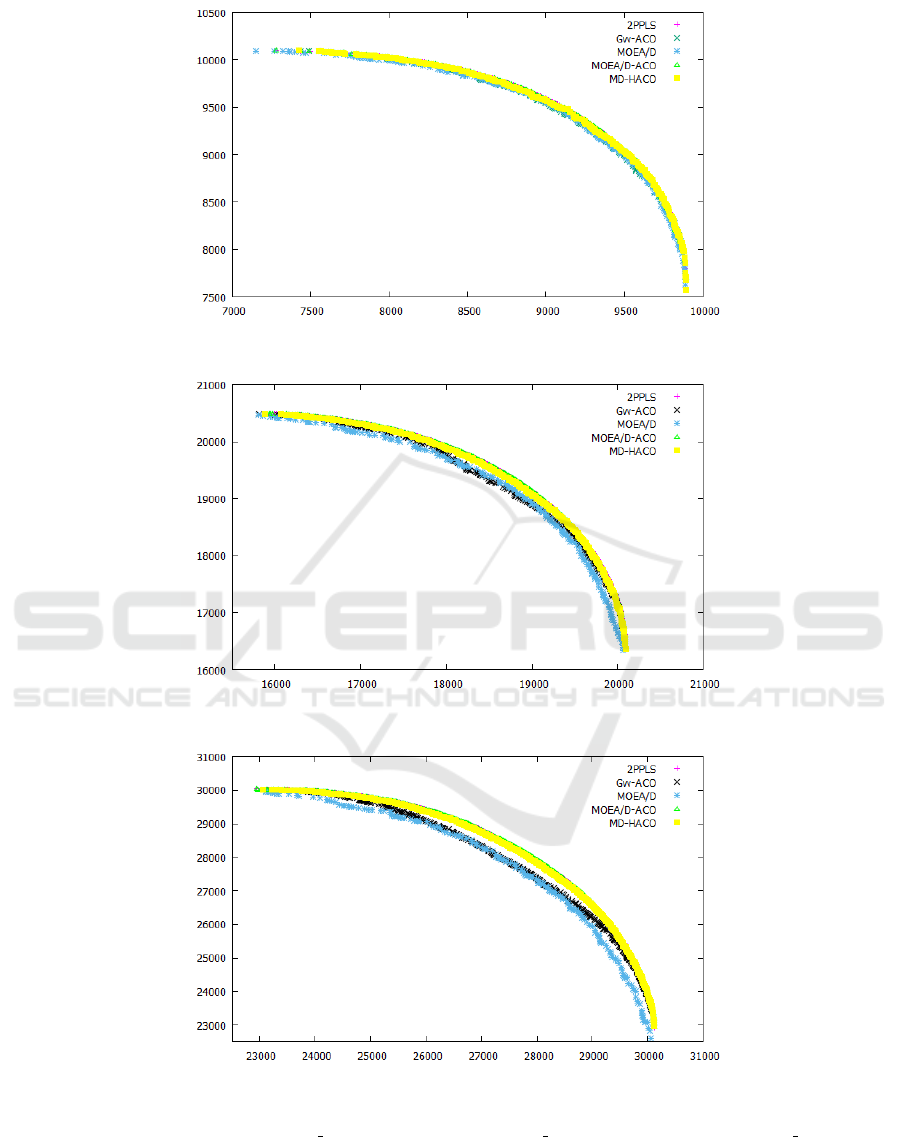
(a)
(b)
(c)
Figure 2: The median attainment surfaces obtained by Gw-ACO, 2PPLS, MOEA/D, MOEA/D-ACO and MD-HACO for
bi-objective instances with (a) representes 2 250 instance, (b) representes 2 500 instance and (c) representes 2 750 instance.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
416

on the bi-objectives instances, the difference is statis-
tically insignificant. On instances with 3 and 4 objec-
tives, the table clearly highlight the performance of
MD-HACO.
7 CONCLUSION
This paper presented a new hybrid method for solv-
ing the MOMKP based on ACO and local search.
The objective space was explored through the use of
a multi-directional ant colony optimization approach
to search for a promising path in the region consid-
ered as well as the contribution of the local search
procedure to drive the search toward the Pareto opti-
mal front. From the viewpoints of both the compu-
tational expenses and solution quality, the proposed
hybrid multi-directional ant colony optimization ap-
proach is efficient for MOMKP and performs consis-
tently well especially for high-dimensional problems
such as those frequently encountered in real-world
applications. An interesting direction of future re-
search would be to investigate a self-adapting version
of MD-HACO. In particular, at the level of the opti-
mization part by ant colony, it will be interesting to
adopt a self-configuration mechanism where the pa-
rameters related to diversification and intensification
are automatically configured during the construction
process and research.
REFERENCES
Alaya, I., Solnon, C., and Ghedira, K. (2007). Ant colony
optimization for multi-objective optimization prob-
lems. In Tools with Artificial Intelligence, 2007. ICTAI
2007. 19th IEEE International Conference on, vol-
ume 1, pages 450–457. IEEE.
Angus, D. (2007). Crowding population-based ant colony
optimisation for the multi-objective travelling sales-
man problem. In Computational Intelligence in Multi-
criteria Decision Making, IEEE Symposium on, pages
333–340. IEEE.
Chabane, B., Basseur, M., and Hao, J.-K. (2017). R2-
ibmols applied to a practical case of the multiobjective
knapsack problem. Expert Systems with Applications,
71:457–468.
Colorni, A., Dorigo, M., and Maniezzo, V. (1991). Dis-
tributed optimization by ant colonies.
Colorni, A., Dorigo, M., Maniezzo, V., et al. (1992). An
investigation of some properties of an” ant algorithm”.
In PPSN, volume 92.
Da Fonseca, V. G., Fonseca, C. M., and Hall, A. O. (2001).
Inferential performance assessment of stochastic op-
timisers and the attainment function. In Interna-
tional Conference on Evolutionary Multi-Criterion
Optimization, pages 213–225. Springer.
D
¨
achert, K., Gorski, J., and Klamroth, K. (2012). An
augmented weighted tchebycheff method with adap-
tively chosen parameters for discrete bicriteria opti-
mization problems. Computers & Operations Re-
search, 39(12):2929–2943.
Dorigo, M. and Blum, C. (2005). Ant colony optimiza-
tion theory: A survey. Theoretical computer science,
344(2-3):243–278.
Dorigo, M., Maniezzo, V., and Colorni, A. (1991a). The ant
system: An autocatalytic optimizing process.
Dorigo, M., Maniezzo, V., and Colorni, A. (1991b). Positive
feedback as a search strategy.
Dorigo, M., Maniezzo, V., Colorni, A., et al. (1996).
Ant system: optimization by a colony of cooperating
agents. IEEE Transactions on Systems, man, and cy-
bernetics, Part B: Cybernetics, 26(1):29–41.
Ehrgott, M. and Ryan, D. M. (2002). Constructing robust
crew schedules with bicriteria optimization. Journal
of Multi-Criteria Decision Analysis, 11(3):139–150.
Gambardella, L. M.,
´
Eric Taillard, and Agazzi, G. (1999).
Macs-vrptw: A multiple colony system for vehicle
routing problems with time windows. In New Ideas
in Optimization, pages 63–76. McGraw-Hill.
Iredi, S., Merkle, D., and Middendorf, M. (2001). Bi-
criterion optimization with multi colony ant algo-
rithms. In Evolutionary Multi-Criterion Optimization,
pages 359–372. Springer.
Ke, L., Zhang, Q., and Battiti, R. (2013). Moea/d-aco: A
multiobjective evolutionary algorithm using decom-
position and antcolony. IEEE transactions on cyber-
netics, 43(6):1845–1859.
Kellerer, H., Pferschy, U., and Pisinger, D. (2004). Multidi-
mensional knapsack problems. pages 235–283.
L’opez, A., Coello, C. A. C., Oyama, A., and Fujii, K.
(2013). An alternative preference relation to deal
with many-objective optimization problems. In Inter-
national Conference on Evolutionary Multi-Criterion
Optimization, pages 291–306. Springer.
Lust, T. and Teghem, J. (2012). The multiobjective multi-
dimensional knapsack problem: a survey and a new
approach. International Transactions in Operational
Research, 19(4):495–520.
Mansour, I. B. and Alaya, I. (2015). Indicator based
ant colony optimization for multi-objective knapsack
problem. Knowledge-Based and Intelligent Informa-
tion & Engineering Systems 19th Annual Conference,
60:448–457.
Mansour, I. B., Alaya, I., and Tagina, M. (2017a). A
min-max tchebycheff based local search approach for
momkp. In ICSOFT, pages 140–150.
Mansour, I. B., Alaya, I., and Tagina, M. (2017b). Solv-
ing multiobjective knapsack problem using scalariz-
ing function based local search. In International Con-
ference on Software Technologies, pages 210–228.
Springer.
Mansour, I. B., Alaya, I., and Tagina, M. (2019). A gradual
weight-based ant colony approach for solving the mul-
Optimizing Multi-objective Knapsack Problem using a Hybrid Ant Colony Approach within Multi Directional Framework
417

tiobjective multidimensional knapsack problem. Evo-
lutionary Intelligence, pages 1–20.
Mansour, I. B., Basseur, M., and Saubion, F. (2018). A
multi-population algorithm for multi-objective knap-
sack problem. Applied Soft Computing, 70:814–825.
Martello, S. (1990). Knapsack problems: algorithms and
computer implementations. Wiley-Interscience series
in discrete mathematics and optimiza tion.
St
¨
utzle, T. and Hoos, H. H. (2000). Max–min ant system.
Future generation computer systems, 16(8):889–914.
Yagmahan, B. and Yenisey, M. M. (2010). A multi-
objective ant colony system algorithm for flow shop
scheduling problem. Expert Systems with Applica-
tions, 37(2):1361–1368.
Zhang, Q. and Li, H. (2007). Moea/d: A multiob-
jective evolutionary algorithm based on decomposi-
tion. IEEE Transactions on evolutionary computation,
11(6):712–731.
Zitzler, E. and Thiele, L. (1999). Multiobjective evolu-
tionary algorithms: A comparative case study and the
strength pareto approach. IEEE transactions on Evo-
lutionary Computation, 3(4):257–271.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
418
