
Enabling Markovian Representations under Imperfect Information
Francesco Belardinelli
1,2 a
, Borja G. Le
´
on
1 b
and Vadim Malvone
3 c
1
Department of Computing, Imperial College London, London, U.K.
2
D
´
epartement d’Informatique, Universit
´
e d’Evry, Evry, France
3
INFRES, T
´
el
´
ecom Paris, Paris, France
Keywords:
Markov Decision Processes, Partial Observability, Extended Partially Observable Decision Process, non-
Markovian Rewards.
Abstract:
Markovian systems are widely used in reinforcement learning (RL), when the successful completion of a task
depends exclusively on the last interaction between an autonomous agent and its environment. Unfortunately,
real-world instructions are typically complex and often better described as non-Markovian. In this paper we
present an extension method that allows solving partially-observable non-Markovian reward decision pro-
cesses (PONMRDPs) by solving equivalent Markovian models. This potentially facilitates Markovian-based
state-of-the-art techniques, including RL, to find optimal behaviours for problems best described as PON-
MRDP. We provide formal optimality guarantees of our extension methods together with a counterexample
illustrating that naive extensions from existing techniques in fully-observable environments cannot provide
such guarantees.
1 INTRODUCTION
One of the major long-term goals of artificial intelli-
gence is to build autonomous agents that execute tem-
porally extended human instructions (Oh et al., 2017;
Lake, 2019; Le
´
on et al., 2021; Hill et al., 2021; Abate
et al., 2021). Markov Decision Processes (MDPs)
are a widely-used mathematical model for sequen-
tial decision-making (Mnih et al., 2015; Bellemare
et al., 2017; Hill et al., 2020). MDPs are particularly
relevant for reinforcement learning (RL) (Sutton and
Barto, 2018), where an agent attempts to maximise a
reward signal given by the environment according to a
predefined goal. RL has proved successful in solving
various challenging real-world scenarios, after vari-
ous breakthroughs (Silver et al., 2017; Vinyals et al.,
2019; Bellemare et al., 2020). However, MDPs – and
consequently RL – rely on the Markovian assumption,
which intuitively says that the effects of an action de-
pend exclusively on the state where it is executed. Un-
fortunately, many real-world instructions are naturally
described as non-Markovian. For instance, we may
ask our autonomous vehicle to drive us home eventu-
a
https://orcid.org/0000-0002-7768-1794
b
https://orcid.org/0000-0002-5990-8684
c
https://orcid.org/0000-0001-6138-4229
ally, without hitting anything in the process, which is
a temporally-extended, non-Markovian specification.
The problem of solving non-Markovian problems
through Markovian techniques was first tackled in
(Bacchus et al., 1996). Therein, the authors solved
an MDP with non-Markovian rewards (NMRDP) by
generating an equivalent MDP so that an optimal
policy in the latter is also optimal for the former.
Building on this, (Brafman et al., 2018; Giacomo
et al., 2019; Le
´
on and Belardinelli, 2020) extended
the scope and applications of this method to solving
temporally-extended goals. Still, this line of works
focuses on fully observable environments, where the
agent has perfect knowledge of the current state of the
system. Assuming complete (state) knowledge of the
environment is often unrealistic or computationally
costly (Badia et al., 2020; Samvelyan et al., 2019),
and while there exists successful empirical works ap-
plying (Bacchus et al., 1996) or similar extensions in
scenarios of imperfect knowledge (Icarte et al., 2019;
Le
´
on et al., 2020), there is no theoretical analysis
on which conditions these extensions should fulfill to
guarantee solving the original non-Markovian model
under imperfect state knowledge (also called partial
observability or imperfect information).
Contribution. In this work we present a novel
method to solve a partially-observable NMRDP
450
Belardinelli, F., G. León, B. and Malvone, V.
Enabling Markovian Representations under Imperfect Information.
DOI: 10.5220/0010882200003116
In Proceedings of the 14th International Conference on Agents and Artificial Intelligence (ICAART 2022) - Volume 2, pages 450-457
ISBN: 978-989-758-547-0; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

(PONMRDP) by building an equivalent partially-
observable MDP (POMDP), while providing formal
guarantees that any policy that is optimal in the latter
has a corresponding policy in the former that is also
optimal. We also prove that naive extensions of exist-
ing methods for fully-observable models can induce
optimal policies that are not applicable in the original
non-Markovian problem.
2 PARTIALLY OBSERVABLE
MODELS
In this section we recall standard notions on partially
observable (p.o.) Markov decision processes and their
non-Markovian version. Furthermore, for both mod-
els we present their belief-state counterparts, poli-
cies, and policy values. Given an element U in an
MDP, U denotes its non-Markovian version, and U
b
denotes its belief version. Given a tuple ~w, we de-
note its length as |~w|, and its i-th element as ~w
i−1
.
Then, last(~w) = v
|~w|−1
is the last element in ~w. For
i ≤ |~w| − 1, let ~w
≥i
be the suffix w
i
,...,w
|w|−1
of ~w
starting at w
i
and ~w
≤i
its prefix w
0
,. ..,w
i
. Moreover,
we denote with ~w ·
~
w
0
the concatenation of tuples ~w
and
~
w
0
. Finally, given a set V , we denote with V
+
the
set of all non-empty sequences on V .
Definition 1 (PONMRDP). A p.o. non-
Markovian reward decision process is a tuple
M =hS,A, T, R,Z,O,γi, where:
• S is a finite set of states.
• A is the finite set of actions.
• T : S × A × S → [0,1] is the transition probabil-
ity function that returns the probability T (s
0
| s,a)
of transitioning to the successor state s
0
, given the
previous state s and action a taken by the agent.
• R is the reward function defined as R : (S · A)
+
·
S → R.
• Z is the set of observations.
• O : S ×A × S → Z is the observation function that
given the current state s and action a, draws an
observation z, based on the successor state s
0
.
• γ ∈ (0,1] is the discount factor.
Note that, we consider a deterministic observation
function for simplicity of presentation. However,the
environment is still stochastic due to the transition
function. We adopt this modelling since it is the stan-
dard approach for RL algorithms working in p.o. sce-
narios (Rashid et al., 2018; Icarte et al., 2019; Vinyals
et al., 2019; Zhao et al., 2021)
A trajectory s
0
,a
1
,. ..,s
n
∈ (S ·A)
+
· S, denoted as
~
s, is a finite (non-empty) sequence of states and ac-
tions, ending in a state, where for each 1 ≤ i ≤ n,
T (s
i
| s
i−1
,a
i
) > 0. By Def. 1, a p.o. Markov decision
process (POMDP) is a PONMRDP where the reward
function only depends on the last transition. That is,
the reward function is a function R : S × A × S → R.
Because the agent cannot directly observe the
state of the environment, she has to make decisions
under uncertainty about its actual state. Then the
agent updates her beliefs by interacting with the en-
vironment and receiving observations. A belief state
b is a probability distribution over the set of states,
that is, b : S → [0,1] such that
∑
s∈S
b(s) = 1.
Definition 2 (Belief update). Given a belief state b,
action a, and observation z, we define an update oper-
ator ρ such that b
0
= ρ(b,a,z) iff for every state s
0
∈ S,
b
0
(s
0
) =
η
∑
s∈S
T (s
0
| s, a)b(s) if O(s,a,s
0
) = z;
0 otherwise.
where b(s) denotes the probability that the en-
vironment is in state s; η = 1/Pr(z | b, a)
is the normalization factor for Pr(z | b,a) =
∑
{s
0
∈S|O(s,a,s
0
)=z}
∑
s∈S
T (s
0
| s, a)b(s).
Now, we have all the ingredients to define a belief
non-Markovian reward decision process.
Definition 3 (BNMRDP). Given a PONMRDP M ,
the corresponding belief NMRDP is a tuple M
b
=
hB,A,T
b
,R
b
,γi where:
• A and γ are defined as in Def. 1.
• B is the set of belief states over the states of M .
• T
b
: B ×A × B → [0,1] is the belief state transition
function defined as:
T
b
(b,a,b
0
) =
∑
z∈Z
Pr(b
0
| b, a,z)Pr(z | b,a)
where Pr(b
0
| b, a,z) =
(
1 if b
0
= ρ(b, a,z);
0 otherwise.
• the reward function R
b
: (B · A)
+
·B→R is defined
as:
R
b
(b
0
,a
1
,...,b
n
)=
∑
s
0
,...,s
n
∈S
b
1
(s
0
)...b
n
(s
n
)R(s
0
,a
1
,...,s
n
)
By Def. 3, given a POMDP M , the correspond-
ing belief MDP is a tuple M
b
= hB,A, T
b
,R
b
,γi, where
The reward function R
b
: B × A × B → R is defined as
R
b
(b,a,b
0
) =
∑
s,s
0
∈S
b(s)b
0
(s
0
)R(s,a,s
0
)
Remark 1. In what follows we assume w.l.o.g. an ini-
tial distribution b
0
. Such belief state b
0
can be gener-
ated by assuming an initial state s
0
and suitable aux-
iliary transitions over the states in b
0
.
Enabling Markovian Representations under Imperfect Information
451

We now define policies, policy values, and opti-
mal policies in a similar fashion to (Sutton and Barto,
2018) for all frameworks described above.
Definition 4 (Non-Markovian Policy). A non-
Markovian policy π : (S·A)
+
·S → A is a function from
trajectories to actions. The value v
π
(
~
s) of a trajectory
~
s following a non-Markovian policy π is defined as:
v
π
(
~
s) =
∑
s
0
∈S
T
s
0
| last(
~
s),π(
~
s)
h
R(
~
s,π(
~
s),s
0
) + γv
π
~
s · s
0
i
An optimal non-Markovian policy π
∗
is one that max-
imizes the expected value for any given trajectory
~
s ∈ (S · A)
+
· S, that is, for all
~
s, v
π
∗
(
~
s)
.
= max
π
v
π
(
~
s).
By Def. 4, a Markovian policy π : S → A is a non-
Markovian policy that only depends on the last visited
state. Then, the value v
π
(s) of a Markovian policy π
at state s is:
v
π
(s) =
∑
s
0
∈S
T
s
0
| s, π(s)
R(s,π(s),s
0
) + γv
π
s
0
Finally, an optimal Markovian policy π
∗
is such
that for all s ∈ S, v
π
∗
(s)
.
= max
π
v
π
(s).
Definition 5 (non-Markovian Belief Policy). A non-
Markovian belief policy π
b
: (B · A)
+
· B → A is a
function from belief trajectories to actions. The value
v
π
b
(
~
b) of a non-Markovian belief policy π
b
for a tra-
jectory
~
b of belief states is defined as:
v
π
b
(
~
b) =
∑
b
0
∈B
T
b
b
0
|last(
~
b),π
b
(
~
b)
h
R
b
(
~
b,π
b
(
~
b),b
0
)+γv
π
b
~
b·b
0
i
An optimal non-Markovian belief policy in a p.o.
model is one that achieves the maximum value for any
trajectory of belief state
~
b ∈ (B · A)
+
· B: v
π
∗
(
~
b)
.
=
max
π
b
v
π
b
(
~
b).
By Def. 5, a Markovian belief policy π
b
: B → A
is a non-Markovian belief policy that only depends
on the last belief state. Then, the value v
π
b
(b) of a
Markovian belief policy π
b
at belief state b is given
as:
v
π
b
(b) =
∑
b
0
∈B
T
b
b
0
| b,π
b
(b)
R
b
(b,π
b
(b),b
0
) + γv
π
b
b
0
Finally, an optimal Markovian belief policy is such
that for all b ∈ B, v
π
∗
b
(b)
.
= max
π
b
v
π
b
(b).
Notice that, in a PONMRDP, i.e., a model where
the rewards depend on trajectories of states and ac-
tions, optimal policies might also be Markovian as in
the case of the counterexample in Sec 4. In following
sections, when not explicitly stated, we will assume
an element to be Markovian, e.g. we will refer to
π as
a non-Markovian policy and π as a policy.
3 EXTENDED POMDPs
In this section, we describe a state-space exten-
sion method to generate a correspondence between
POMDPs and PONMRDPs. In particular, we extend
the method originally proposed in (Bacchus et al.,
1996) to partial observability.
First of all, we show how to generate a belief tra-
jectory from a state trajectory.
Definition 6 (Belief trajectory). Given a model M ,
let s
0
a
1
,p
1
−→ s
1
·· ·s
n−1
a
n
,p
n
−→ s
n
be a trajectory, where
p
i
= T (s
i
| s
i−1
,a
i
), for all 1 ≤ i ≤ n. We define the
corresponding belief trajectory b
0
a
1
,p
0
1
−→ b
1
·· ·b
n−1
a
n
,p
0
n
−→
b
n
, where p
0
i
= T
b
(b
i
| b
i−1
,a
i
) and b
i
= ρ(b
i−1
,a
i
,z
i
)
for all 0 < i ≤ n
1
.
Note that, in Def. 6, we make use of observa-
tions. In particular, the observation z
i
is generated
by the observation function and the trajectory, i.e.
z
i
= O(s
i−1
,a
i
,s
i
), and it is used in the belief update
function to generate the next belief state.
Now, we can define our notion of expansion.
Definition 7 (Expansion). A POMDP M =
hES,A,T
ES
,R,EZ,O
ES
,γi is an expansion of a
PONMRDP M = hS,A,T,R,Z, O,γi, if there exist
functions τ : ES → S, σ : S → ES, τ
0
: EZ → Z, and
σ
0
: Z → EZ such that:
1. For all s ∈ S, τ(σ(s)) = s.
2. For all s
1
,s
2
∈ S and es
1
∈ ES, if T (s
2
| s
1
,a) > 0
and τ(es
1
) = s
1
, then there exists a unique es
2
∈
ES such that τ (es
2
) = s
2
and T
ES
(es
2
| es
1
,a) =
T (s
2
| s
1
,a).
3. For all z ∈ Z, τ
0
(σ
0
(z)) = z.
4. For all z ∈ Z, s, s
0
∈ S, and es, es
0
∈ ES, if
O(s,a,s
0
) = z, τ(es) = s, and τ(es
0
) = s
0
, then
there exist a unique ez ∈ EZ such that τ
0
(ez) = z
and O
ES
(es,a,es
0
) = ez.
5. For any trajectory s
0
,. ..,s
n
in M with corre-
sponding belief trajectory b
0
,. ..,b
n
as per Def. 6,
the trajectory es
0
,. ..,es
n
in M that satisfies
τ(es
i
) = s
i
for each 0 ≤ i ≤ n and σ(s
0
) = es
0
,
generates a belief trajectory eb
0
,. ..,eb
n
such that
R
b
(b
0
,. ..,b
n−1
,a,b
n
) = R
b
(eb
n−1
,a,eb
n
).
Intuitively the extended state es and observation
ez such that τ(es) = s and τ
0
(ez) = z, can be thought
of as labelled by s◦ l and z ◦ l
0
, where s ∈ S is the base
state (i.e. a state of
M ), z ∈ Z is the base observation
1
As detailed in Remark 1, we define an auxiliary initial
state s
0
with suitable auxiliary transitions. Consequently b
0
is assumed to be the distribution assigning 1 to s
0
and 0 to
all other states.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
452
s
3
s
1
s
2
s
3
s
1
s
2
O(s
2
)s
3
O(s
1
)s
3
O(s
3
)s
2
O(s
3
)s
1
a
1
|a
2
a
1
|a
2
a
2
a
1
a
1
|a
2
a
1
|a
2
a
2
a
1
a
2
a
1
a
2
a
1
a
1
|a
2
a
1
|a
2
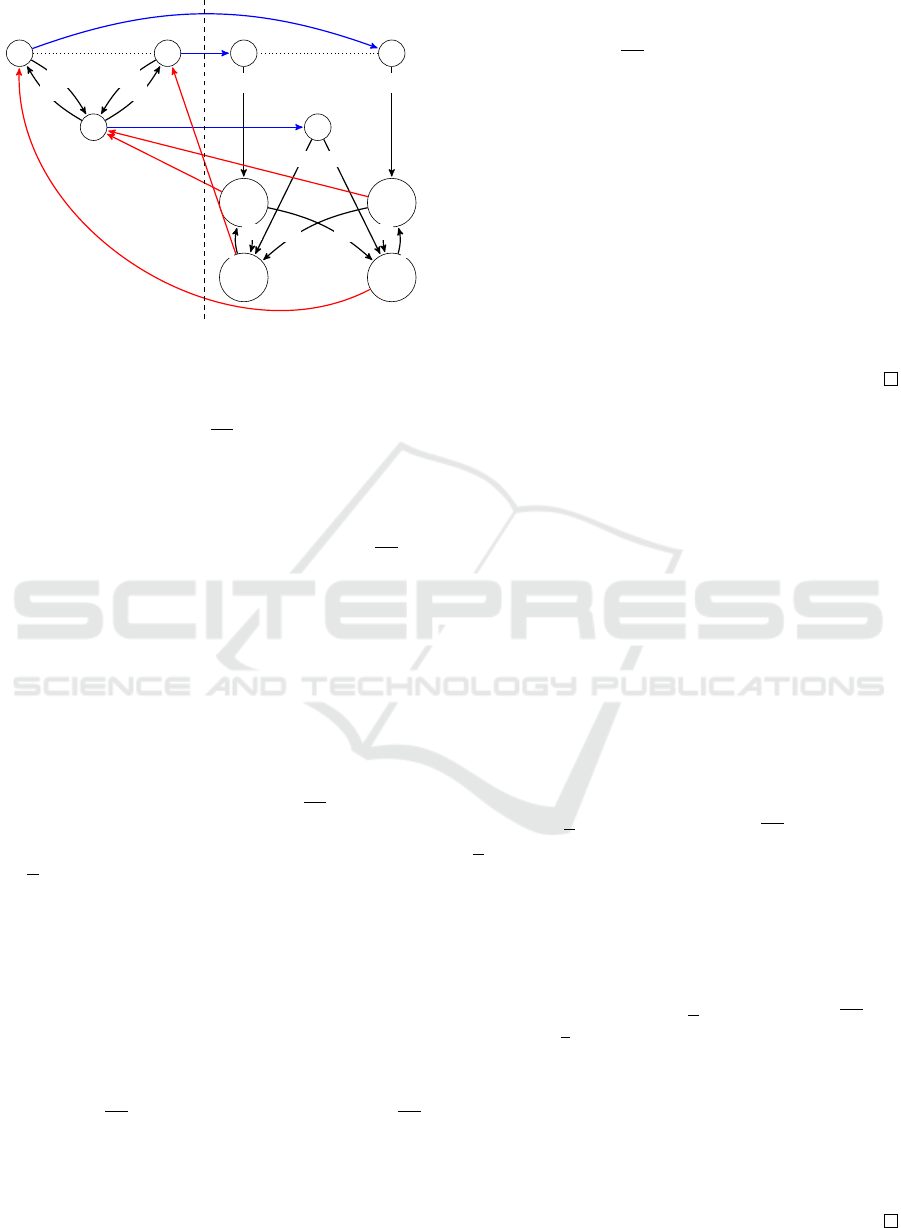
Figure 1: The models for the PONMRDP (left side) and an
extended POMDP (right side) following Def. 7. Red lines
denote some τ(es) transformations while blue lines we il-
lustrate the cases in which σ(s) is only the current state.
(i.e. an observation from M ), and l and l
0
are labels
that distinguish es and ez from other extensions of the
same base elements. Figure 1 illustrates a POMDP
and an extended POMDP that follow Def. 7.
The most important items in Def. 7 are points 2, 4
and 5. Points 2 and 4 ensure that both M and M are
equivalent regarding their respective base elements in
both state and observation dynamics. Point 5 asserts
equivalence in reward structure from the agent’s per-
spective. Note that, differently from the expansions in
fully observable models (Bacchus et al., 1996; Braf-
man et al., 2018), it is not enough that equivalent tra-
jectories have the same rewards. Here, we require that
they induce equivalent beliefs rewards (for details see
Sec. 4).
An optimal agent, i.e., an agent that always fol-
lows an optimal policy, working in M would con-
struct a BNMRDP, where it follows the policy that
maximizes the value of each belief state according
to R
b
. Similarly, an optimal agent working in M
would construct an extended BMDP maximizing the
discounted expectation of R
b
.
Since belief states are generated exclusively from
transition probabilities and observations given states
and actions, clauses 2 and 4 induce a similar behav-
ior between equivalent trajectories of believe states to
what is presented in (Bacchus et al., 1996) for trajec-
tories of states.
Lemma 1. Let the POMDP M be an extension of the
PONMRDP M . Given a belief trajectory
~
b in M :
b
0
a
1
,p
b1
−→ b
1
·· ·b
n−1
a
n
,p
bn
−→ b
n
, there is a trajectory
~
eb in
M defined as: eb
0
a
1
,p
b1
−→ eb
1
·· ·eb
n−1
a
n
,p
bn
−→ eb
n
where
eb
i
(es
i
) = b(τ(es
i
)) for all 0 ≤ i ≤ n.
We say that
~
b and
~
eb are weakly corresponding
belief trajectories.
Proof. From clause 2 immediately follows that for
any trajectory
~
s in M
~
s = s
0
a
1
,p
1
−→ s
1
·· ·s
n
a
n
,p
n
−→ s
n
there is a trajectory
~
es in M of similar structure
~
es = es
0
a
1
,p
e1
−→ s
1
·· ·s
n
a
n
,p
en
−→ s
n
where p
ei
= p
i
and τ(es
i
) = s
i
, for all 0 ≤ i ≤ n.
In this case we say that
~
s and
~
es are weakly corre-
sponding trajectories. Symmetrically, clause 4 as-
sures that these weakly correspondent real states tra-
jectories will generate as well weakly correspondent
observation trajectories. As a consequence, it fol-
lows immediately that these trajectories will generate
weakly correspondent belief trajectories.
Given Lemma 1 we can define strong correspon-
dence.
Definition 8. Let
~
b and
~
eb be weakly corresponding
trajectories with initial belief states b
0
and eb
0
, re-
spectively. We say that
~
b and
~
eb are strongly corre-
spondent when eb
0
is an initial belief state.
This means that when the transformation induced
by σ, i.e., eb
i
(σ(s
0
)) = b
i
is a trajectory contain-
ing only the current belief state, i.e, the first state
of the trajectory in the non-Markovian model is the
first state in the environment, we have strongly cor-
respondent belief trajectories. Note that clause 5 re-
quires that strongly correspondent belief trajectories
have the same rewards.
Now we can introduce corresponding policies.
Definition 9 (Corresponding Policy). Let π
b
be a be-
lief policy for expansion M . The corresponding be-
lief policy π
b
for the PONMRDP M is defined as
π
b
(
~
b) = π
0
b
(last(
~
eb)), where
~
eb is the strongly cor-
responding trajectory for
~
b.
Given the expanded MDP from Def. 7 and corre-
sponding policies as in Def. 9, we can now present the
following result.
Proposition 1. For every policy π
b
in expansion
M , corresponding policy π
b
in PONMRDP M , we
have that v
π
b
(
~
b) = v
π
b
(last(
~
eb)), where
~
eb and
~
b are
strongly corresponding trajectories.
Proof. This is evident since corresponding policies
will generate the same actions for any correspondent
belief trajectory and predict the same expected dis-
counted return given the equivalent transition and ob-
servation dynamics from clauses 1-4 in Def. 7 and that
clause 5 imposes the same belief rewards.
Enabling Markovian Representations under Imperfect Information
453

Consequently we can find optimal policies for the
PONRMDP by working on the POMDP instead.
Corollary 1. Let π
b
an optimal policy for expansion
M . Then the corresponding policy π
b
is optimal for
the PONMRDP M .
Thus, given an optimal policy in the extended
POMDP one can easily obtain an optimal solution
for the original PONMRDP. As in previous fully-
observable approaches, there is no need to generate
π
b
explicitly and, instead, the agent can run with π
b
while assuming that the underlying model is M .
4 A COUNTEREXAMPLE TO A
NAIVE EXTENSION
As anticipated in the introduction, we illustrate now
the relevance of item 5 in Def. 7. In particular, equiva-
lences under perfect knowledge (Bacchus et al., 1996;
Brafman et al., 2018) require only that strongly corre-
spondent trajectories of states have the same rewards.
Here we show that a naive extension of the definition
of expansion in (Bacchus et al., 1996), i.e., one that
requires equivalent dynamics on states and observa-
tions, and enforces equivalence between rewards on
state trajectories only, may induce policies that are un-
feasible in the non-Markovian model. Formally, con-
sider a variant of Def. 7, where item 5 only is replaced
as follows:
5
0
. For every trajectory s
0
,. ..,s
n
in M and
es
0
,. ..,es
n
in M such that τ (es
i
) = s
i
for
each 0 ≤ i ≤ n and σ(s
0
) = es
0
, we have
R(s
0
,. ..,s
n−1
,a
n−1
,s
n
) = R (es
n−1
,a
n−1
,es
n
).
We also introduce the notion of feasible policies:
Definition 10 (Feasible Policy). Given a PONMRDP
M with an extended POMDP M . We say that a policy
π in M is not feasible in M if there exist a pair of
states s in M and es in M , where
~
s is a trajectory in
M ending in s, τ(es) = s and v
π
(es) 6= v
π
(
~
s) for every
policy π in M .
Now, we can prove the following theorem.
Theorem 1. There exist a PONMRDP M with ex-
pansion M given as in Def. 7 with item 5 replaced by
item 5’, where the optimal policy in M is not feasible
in M .
Proof. Consider the PONMRDP M =
hS,A, T, R,Z,O, γi depicted in Fig. 2, such that:
1. S = {s
1
,s
2
,s
3
};
2. A = {a
1
,a
2
};
3. T
a
1
= {[0,0,1],[0,0,1],[1,0,0]} and
T
a
2
= {[0,0,1], [0,0, 1],[0, 1,0]}, where T
a
1
[1] =
T
a
1
(s
1
)[s
1
,s
2
,s
3
], T
a
1
[2] = T
a
1
(s
2
)[s
1
,s
2
,s
3
],...;
4. the reward function R is given as
R(~w) =
1 if ~w = w
0
,w
1
,w
2
and w
0
6= w
2
;
0 otherwise.
5. the observation function O is such that O(s
1
) =
O(s
2
) = z
1
and O(s
3
) = z
2
for Z = {z
1
,z
2
} (we as-
sume that observations are independent from the
action taken);
6. γ = 1.
Finally, we assume an initial distribution b
0
=
[0.3,0.7,0]. Note that, we consider time horizons of 3
time steps only.
Since both initial states s
1
and s
2
are indistinguish-
able (i.e., they return the same observation), but there
is a higher chance of starting in s
2
, an optimal policy
in M is taking action a
1
for every state.
π
∗
(b
i
) = [p(a
1
) = 0, p(a
2
) = 1] for any b
i
(1)
Now consider the expansion M , where states and
observations are extended with a labelling that tells
the agent the previous state visited. Formally, M =
hES,A, T
ES
,R,EZ,O
ES
,γi, where:
• A and γ are the same as in M ;
• ES = {s
1
,s
2
,s
1
s
3
,s
2
s
3
,s
3
s
1
,s
3
s
2
};
• EZ = {ez
1
,ez
2
,ez
3
,ez
4
,ez
5
};
• O
ES
(
/
0,
/
0,s
1
) = O
ES
(
/
0,
/
0,s
2
) = ez
1
and for
all a ∈ A, es ∈ ES, O
ES
(es,a,s
3
s
1
) = ez
2
,
O
ES
(es,a,s
2
s
1
) = ez
3
, O
ES
(es,a,s
3
s
1
) = ez
4
,
O
ES
(es,a,s
3
s
2
) = ez
5
.
• The transition function is as depicted in Fig 2.
• The reward function is defined as:
R(es
i
,a
i
,es
i+1
)=
1 if es
i
=s
1
s
3
,a
i
=a
2
,es
i+1
=s
3
s
2
;
1 if es
i
=s
2
s
3
,a
i
=a
1
,es
i+1
=s
3
s
1
;
0 otherwise.
Now, functions τ : ES → S, σ : S → ES, τ
0
: EZ →
Z, and σ
0
: Z → EZ are intuitively defined as follows:
τ and τ
0
add the information of the previous state vis-
ited to construct the extended state or observation re-
spectively, while σ and σ
0
remove that information.
The POMDP M satisfies the requirements in Def. 7
with condition 5’ to be an expansion of M . Figure 2
illustrates M and M .
We now show that the optimal policies in this
model is not feasible in the original. In the expansion
POMDP M an optimal policy is one that:
π
∗
b
(eb
i
) =
a
2
if ez
i
= ez
2
;
a
1
if ez
i
= ez
3
;
a
1
or a
2
otherwise.
(2)
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
454
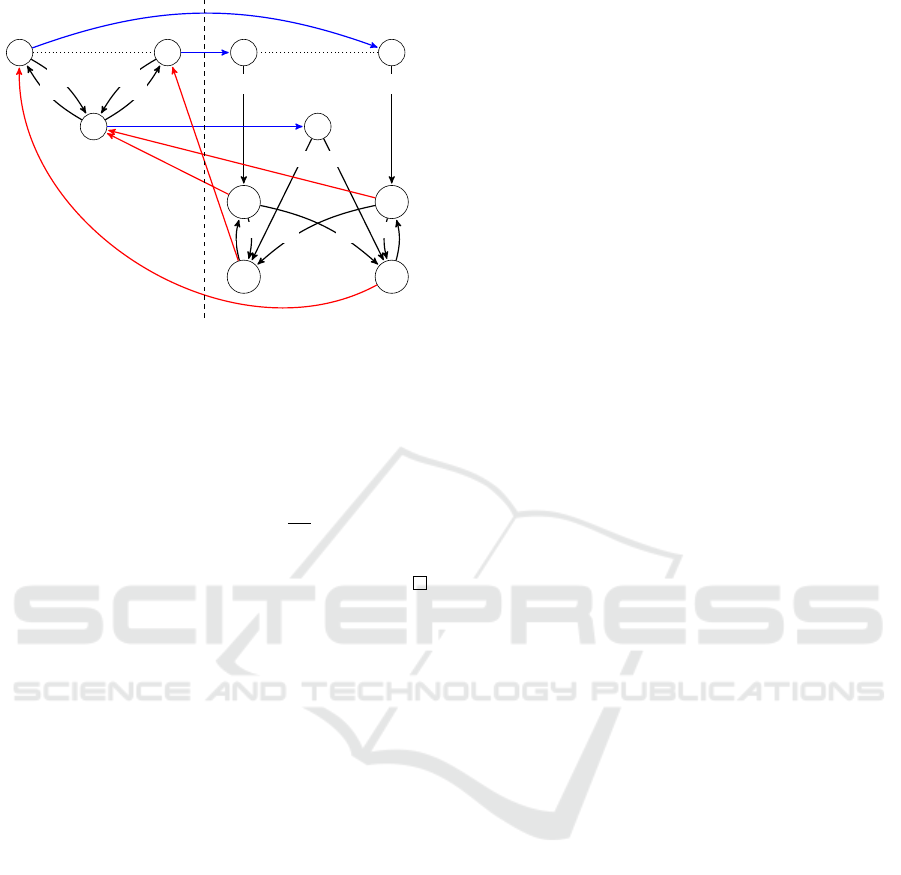
s
3
s
1
s
2
s
3
s
1
s
2
s
2
s
3
s
1
s
3
s
3
s
2
s
3
s
1
a
1
|a
2
a
1
|a
2
a
2
a
1
a
1
|a
2
a
1
|a
2
a
2
a
1
a
2
a
1
a
2
a
1
a
1
|a
2
a
1
|a
2
Figure 2: Counterexample to naive extension. The mod-
els for the PONMRDP (left side) and its extended POMDP
(right side), satisfying item 5’ instead of the proposed item
5 from Def. 7. Red lines denote some τ(es) transformations
while blue lines illustrate the cases in which σ(s) is only the
current state.
where ez
i
is the last observation used to obtain eb
i
.
So, we have that v
eπ
∗
(s
1
s
3
) = v
eπ
∗
(s
1
s
2
) = 1.
However, in the original model M the maximum
value we can obtain for τ(s
1
s
3
) is v
π
∗
(s
3
) = 0.7. Thus
we have that v
eπ
∗
6= v
π
∗
.
Intuitively, an expansion with condition 5’ does
not prevent generating an equivalent model where the
dynamics are the same, but information differ. In
models with knowledge of the state, the expansion
method must ensure that the agent has access to the
same information available in the trajectories of the
original system.
5 RELATED WORK
The intersection between formal methods and rein-
forcement learning has lead to a growing interest
and demand of reinforcement learning agents solv-
ing temporally extended instructions that are naturally
described as non-Markovian. Early work (Bacchus
et al., 1996) focus on facilitating the application of RL
algorithms to non-Markovian problems by introduc-
ing the concept of extended MDP as a minimal equiv-
alent Markovian construction that allows RL agents
to tackle a problem where rewards are naturally con-
ceived as non-Markovian. Later literature (Toro Icarte
et al., 2018; Giacomo et al., 2019; Illanes et al., 2020)
has applied similar constructions with increasingly
complex benchmarks, e.g., the Minecraft-inspired
navigation environment (Andreas et al., 2017) or Min-
iGrid (Chevalier-Boisvert et al., 2018), and expressive
languages such as co-safe linear-time temporal logic
(co-safe LTL) (Kupferman and Vardi, 2001) or lin-
ear dynamic logic over finite traces (LDL
f
) (Brafman
et al., 2018). This combination of temporal logic and
RL has also sparkled interest in multi-agent systems
in a comparable extending-the-non-Markovian-model
fashion with examples such as the extended Markov
games (Le
´
on and Belardinelli, 2020) and the product
Markov games (Hammond et al., 2021). Some of the
latest contributions (Toro Icarte et al., 2019) have em-
pirically applied this kind of extensions to partially
observable environments. However, to the best of
our knowledge, no previous work has provided the-
oretical studies about how a PONMRDP should be
extended to ensure finding an optimal policy that is
guaranteed to be optimal and applicable to the origi-
nal non-Markovian problem at hand.
6 CONCLUSIONS
When tackling real world problems with autonomous
agents it is common to face settings that are natu-
rally described as non-Markovian (i.e. relying on the
past) and partially observable. We presented an ex-
pansion method for extending p.o. non-Markovian
reward decision processes, so as to obtain an equiv-
alent POMDP, where a Markovian agent can find an
optimal policy that is guaranteed to be optimal for
the original non-Markovian model. We also pro-
vided proof that naive expansions from existing meth-
ods for fully observable models might find solutions
that are not applicable in the original problem. Note
that, in this work we considered the setting in which
the observation function is deterministic to simplify
the presentation. Nonetheless, a counterexample for
the naive extension in this setting is a counterexam-
ple for the general case. Our work provides theo-
retical ground for research lines solving complex in-
structions, such as complex temporal logic formulas,
through RL in environments with imperfect knowl-
edge of the state of the system.
REFERENCES
Abate, A., Gutierrez, J., Hammond, L., Harrenstein, P.,
Kwiatkowska, M., Najib, M., Perelli, G., Steeples,
T., and Wooldridge, M. (2021). Rational verifica-
tion: game-theoretic verification of multi-agent sys-
tems. Applied Intelligence, 51(9):6569–6584.
Andreas, J., Klein, D., and Levine, S. (2017). Modular mul-
titask reinforcement learning with policy sketches. In
Proceedings of the 34th International Conference on
Enabling Markovian Representations under Imperfect Information
455

Machine Learning-Volume 70, pages 166–175. JMLR.
org.
Bacchus, F., Boutilier, C., and Grove, A. (1996). Rewarding
behaviors. In Proceedings of the National Conference
on Artificial Intelligence, pages 1160–1167.
Badia, A. P., Piot, B., Kapturowski, S., Sprechmann, P.,
Vitvitskyi, A., Guo, D., and Blundell, C. (2020).
Agent57: Outperforming the atari human benchmark.
arXiv preprint arXiv:2003.13350.
Bellemare, M. G., Candido, S., Castro, P. S., Gong, J.,
Machado, M. C., Moitra, S., Ponda, S. S., and
Wang, Z. (2020). Autonomous navigation of strato-
spheric balloons using reinforcement learning. Na-
ture, 588(7836):77–82.
Bellemare, M. G., Dabney, W., and Munos, R. (2017).
A distributional perspective on reinforcement learn-
ing. In Proceedings of the 34th International Con-
ference on Machine Learning-Volume 70, pages 449–
458. JMLR. org.
Brafman, R., De Giacomo, G., and Patrizi, F. (2018).
Ltlf/ldlf non-markovian rewards. In Proceedings of
the AAAI Conference on Artificial Intelligence, vol-
ume 32.
Chevalier-Boisvert, M., Willems, L., and Pal, S. (2018).
Minimalistic gridworld environment for openai gym.
https://github.com/maximecb/gym-minigrid.
Giacomo, G. D., Iocchi, L., Favorito, M., and Patrizi, F.
(2019). Foundations for restraining bolts: Reinforce-
ment learning with LTLf/LDLf restraining specifica-
tions. In Benton, J., Lipovetzky, N., Onaindia, E.,
Smith, D. E., and Srivastava, S., editors, Proceed-
ings of the Twenty-Ninth International Conference on
Automated Planning and Scheduling, ICAPS 2018,
Berkeley, CA, USA, July 11-15, 2019, pages 128–136.
AAAI Press.
Hammond, L., Abate, A., Gutierrez, J., and Wooldridge,
M. (2021). Multi-agent reinforcement learning with
temporal logic specifications. In Proceedings of the
20th International Conference on Autonomous Agents
and MultiAgent Systems, pages 583–592.
Hill, F., Lampinen, A., Schneider, R., Clark, S., Botvinick,
M., McClelland, J. L., and Santoro, A. (2020). Envi-
ronmental drivers of systematicity and generalization
in a situated agent. In International Conference on
Learning Representations.
Hill, F., Tieleman, O., von Glehn, T., Wong, N., Merzic, H.,
and Clark, S. (2021). Grounded language learning fast
and slow. In International Conference on Learning
Representations.
Icarte, R. T., Waldie, E., Klassen, T., Valenzano, R., Cas-
tro, M., and McIlraith, S. (2019). Learning reward
machines for partially observable reinforcement learn-
ing. In Advances in Neural Information Processing
Systems, pages 15497–15508.
Illanes, L., Yan, X., Icarte, R. T., and McIlraith, S. A.
(2020). Symbolic plans as high-level instructions for
reinforcement learning. In Proceedings of the In-
ternational Conference on Automated Planning and
Scheduling, volume 30, pages 540–550.
Kupferman, O. and Vardi, M. Y. (2001). Formal Methods
in System Design, 19(3):291–314.
Lake, B. M. (2019). Compositional generalization through
meta sequence-to-sequence learning. In Advances in
Neural Information Processing Systems, pages 9788–
9798.
Le
´
on, B. G. and Belardinelli, F. (2020). Extended markov
games to learn multiple tasks in multi-agent reinforce-
ment learning. In Giacomo, G. D., Catal
´
a, A., Dilkina,
B., Milano, M., Barro, S., Bugar
´
ın, A., and Lang, J.,
editors, ECAI 2020 - 24th European Conference on
Artificial Intelligence, 29 August-8 September 2020,
Santiago de Compostela, Spain, August 29 - Septem-
ber 8, 2020 - Including 10th Conference on Pres-
tigious Applications of Artificial Intelligence (PAIS
2020), volume 325 of Frontiers in Artificial Intelli-
gence and Applications, pages 139–146. IOS Press.
Le
´
on, B. G., Shanahan, M., and Belardinelli, F. (2020). Sys-
tematic generalisation through task temporal logic and
deep reinforcement learning. CoRR, abs/2006.08767.
Le
´
on, B. G., Shanahan, M., and Belardinelli, F. (2021).
In a nutshell, the human asked for this: Latent goals
for following temporal specifications. arXiv preprint
arXiv:2110.09461.
Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness,
J., Bellemare, M. G., Graves, A., Riedmiller, M., Fid-
jeland, A. K., Ostrovski, G., et al. (2015). Human-
level control through deep reinforcement learning.
Nature, 518(7540):529.
Oh, J., Singh, S., Lee, H., and Kohli, P. (2017). Zero-
shot task generalization with multi-task deep rein-
forcement learning. In Proceedings of the 34th In-
ternational Conference on Machine Learning-Volume
70, pages 2661–2670. JMLR. org.
Rashid, T., Samvelyan, M., Schroeder, C., Farquhar, G., Fo-
erster, J., and Whiteson, S. (2018). Qmix: Monotonic
value function factorisation for deep multi-agent rein-
forcement learning. In International Conference on
Machine Learning, pages 4295–4304. PMLR.
Samvelyan, M., Rashid, T., Schroeder de Witt, C., Farquhar,
G., Nardelli, N., Rudner, T. G., Hung, C.-M., Torr,
P. H., Foerster, J., and Whiteson, S. (2019). The star-
craft multi-agent challenge. In Proceedings of the 18th
International Conference on Autonomous Agents and
MultiAgent Systems, pages 2186–2188. International
Foundation for Autonomous Agents and Multiagent
Systems.
Silver, D., Hubert, T., Schrittwieser, J., Antonoglou, I., Lai,
M., Guez, A., Lanctot, M., Sifre, L., Kumaran, D.,
Graepel, T., et al. (2017). Mastering chess and shogi
by self-play with a general reinforcement learning al-
gorithm. arXiv preprint arXiv:1712.01815.
Sutton, R. S. and Barto, A. G. (2018). Reinforcement learn-
ing: An introduction. MIT press.
Toro Icarte, R., Klassen, T. Q., Valenzano, R., and McIl-
raith, S. A. (2018). Teaching multiple tasks to an RL
agent using LTL. In Proceedings of the 17th Interna-
tional Conference on Autonomous Agents and Multi-
Agent Systems, pages 452–461.
Toro Icarte, R., Waldie, E., Klassen, T., Valenzano, R., Cas-
tro, M., and McIlraith, S. (2019). Learning reward ma-
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
456

chines for partially observable reinforcement learning.
volume 32, pages 15523–15534.
Vinyals, O., Babuschkin, I., Chung, J., Mathieu, M., Jader-
berg, M., Czarnecki, W. M., Dudzik, A., Huang,
A., Georgiev, P., Powell, R., et al. (2019). Alphas-
tar: Mastering the real-time strategy game starcraft ii.
DeepMind blog, page 2.
Zhao, M., Liu, Z., Luan, S., Zhang, S., Precup, D., and
Bengio, Y. (2021). A consciousness-inspired planning
agent for model-based reinforcement learning. In Ad-
vances in Neural Information Processing Systems.
Enabling Markovian Representations under Imperfect Information
457
