
T-Balance: A Unified Mechanism for Taxi Scheduling in a City-scale
Ride-sharing Service
Jiyao Li and Vicki H. Allan
Department of Computer Science, Utah State University, Logan, Utah, U.S.A.
Keywords:
Ridesharing Service, Task Assignment, Vehicle Repositioning, Q-learning.
Abstract:
In this paper, we propose a unified mechanism known as T-Balance for scheduling taxis across a city. Balanc-
ing the supplies and demands in a city scale is a challenging problem in the field of the ride-sharing service.
To tackle the problem, we design a unified mechanism considering two important processes in ride-sharing
service: ride-matching and vacant taxi repositioning. For rider-matching, the Scoring Ride-matching with
Lottery Selection (SRLS) is proposed. With the help of Lottery Selection (LS) and smoothed popularity score,
the Scoring Ride-matching with Lottery Selection (SRLS) can balance supplies and demands well, both in the
local neighborhood areas and hot places across the city. In terms of vacant taxi repositioning, we propose Q-
learning Idle Movement (QIM) to direct vacant taxis to the most needed places in the city, adapting to dynamic
change environments. The experimental results verify that the unified mechanism is effective and flexible.
1 INTRODUCTION
Thanks to the rapid development of wireless networks
and the prevalence of portable smart devices, ride-
sharing services have become an important part of
our daily life. Ride-sharing services pool passengers
with similar itineraries and time schedules together in
a single taxi. Such services may provide positive im-
pacts on society and the environment by reducing traf-
fic congestion, emission of carbon dioxide, and taxi
fare. A recent global market report found that there
are a rapidly growing number of passengers partici-
pating in ride-sharing services such as Uber, Lyft and
Didichuxing. From the Ride-Sharing Industry Statis-
tics (Stasha, 2021), about one fourth of the U.S. popu-
lation uses ride-sharing services and there are 3.8 mil-
lion drivers worldwide working for Uber. A recent
market report (Curley, 2019) also showed that global
ride-sharing service is valued at $61.3 billion and ex-
pected to reach $218 billion by 2025. To increase fu-
ture market shares, ride-sharing service corporations
are willing to spend large sums of money optimizing
service operations such as reducing travel cost, serv-
ing more riders with fewer taxis, and improving pas-
sengers’ satisfaction.
If the distribution of taxis across the city could be
coordinated for maximum efficiency, then the service
rate of riders and taxi utilization could be improved,
as well as reducing riders’ response time (the time be-
tween requesting a ride and being picked up). There-
fore, organizing taxis to meet demands across a city
is a crucial problem in the ride-sharing service. How-
ever, balancing supply and demand is extremely chal-
lenging when there are a large amount of riders and
taxis. Evaluating demand patterns in a city scale at a
specific period is difficult, since the number of rider
requests might fluctuate dramatically in as little as an
hour. Also, some riders’ destinations are in demand-
sparse areas such that delivery will lead taxis away
from demand-dense areas, leaving many passengers
in busy areas unserved even though corporations em-
ploy a large number of taxis. In addtion, each rider
has a patience period, that is, they will cancel the re-
quest and change to other alternative services after
their patience period has elapsed.
Many research papers that focus on how to sched-
ule taxis in the ride-sharing industry have been pub-
lished. However, most of the previous work has the
following limitations: (i) Most existing studies did
research on forecasting taxi demand patterns across
a city. However, their works focused on predicting
taxi demand patterns at a given timestamp rather than
evaluating long-term demand (Zhang et al., 2017a)
(Xu et al., 2018) (Liu et al., 2019); (ii) Many current
works proposed various solutions of ride-matching in
order to meet the balance between supply and de-
mand, but they only consider balancing taxi distri-
458
Li, J. and Allan, V.
T-Balance: A Unified Mechanism for Taxi Scheduling in a City-scale Ride-sharing Service.
DOI: 10.5220/0010884100003116
In Proceedings of the 14th International Conference on Agents and Artificial Intelligence (ICAART 2022) - Volume 2, pages 458-465
ISBN: 978-989-758-547-0; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

bution in local areas rather than citywide (Banerjee
et al., 2018) (Wang et al., 2018) (Xu et al., 2018)
(Zhang et al., 2017b) (Li and Allan, 2019); (iii)
Most research papers designed different repositioning
strategies to guide vacant taxis to busy areas where
drivers would have greater opportunities for picking
up passengers, but such solutions often omitted bal-
ancing supply and demand in local areas, although
taxis could be scheduled in a wider area (Wen et al.,
2017) (Lin et al., 2018) (Qu et al., 2014) (Jha et al.,
2018); (iv) In addition, several price mechanisms
have been provided as incentives for drivers to move
to needed places. However, experienced drivers typ-
ically are not tempted by such incentives. (Lu et al.,
2018).
To address the challenges and the limitations of
ride-sharing service, we propose a unified mechanism
known as T-Balance. The main contributions of the
current work are described as following:
• The Lottery Selection (LS) selects appropriate
riders to be served such that taxis can be sched-
uled to needed places in the process of ride-
matching.
• Since neighboring zones impact each other, we
calculate a new popularity score to estimate long-
term demand density for each zone of the city.
Equipped with Lottery Selection (LS) and the
new popularity score, a ride-matching mecha-
nism named Scoring Ride-Matching with Lottery
Selection (SRLS) balances supply and demand
across the city.
• In addition, we utilize a Q-learning Idle Move-
ment (QIM) mechanism to reposition vacant taxis
citywide, increasing the taxi service’s ability to
meet demand in the busiest areas of a city.
The remainder of the paper is organized as fol-
lows: we discuss recent related works of ride-sharing
services in section 2; in section 3, the business model
of ride-sharing service is introduced; in section 4,
we propose a novel unified mechanism known as T-
Balance for a city-scale ride-sharing service; in sec-
tion 5, we compare our method to other approaches
with the city-scale real data set; section 6 concludes
our contributions and achievements.
2 RELATED WORK
We organize the previous works in terms of demand
prediction, ride-matching, repositioning, and price
scheme.
Demand forecast plays an important role in cur-
rent smart transportation systems. It can help ride-
sharing platforms be smarter in scheduling taxis
across a city. (Zhang et al., 2017a) proposed a
deep learning-based approach known as Deep Spatio-
Temporal Residual Networks (ST-ResNet) to pre-
dict the demand of a city. (Xu et al., 2018) de-
signed a sequence learning model based on Recur-
rent Neural Networks (RNN) to predict rider requests
in different areas of a city. (Yao et al., 2018) con-
structed a novel Deep Multi-View Spatial-Temporal
Network (DMVST-Net) framework to model both
spatial and temporal relations. Taxi demand can then
be predicted with some semantic information. (Liu
et al., 2019) proposed a novel Contextualized Spatial-
Temporal Network (CSTN) that would effectively
capture the diverse contextual information in order to
learn the demand patterns. Most of these works focus
on predicting future demand at a given timestamp, but
do not consider providing the ride-sharing platform
with a long-term model.
Ride-matching is a core building block in any
ride-sharing platform. (Banerjee et al., 2018) pro-
posed a Scaled MaxWeight (SMW) approach to
schedule vehicles for demands in local areas. This
method utilizes a closed queueing network and dis-
patches taxis from the queue with the most supplies.
SMW has proven effective, but the authors do not
offer a concrete solution for how to estimate de-
mand weight. (Wang et al., 2018) optimizes the ride-
matching policy by deep reinforcement learning. A
Deep Q-network (DQN) with an action search was
proposed. In addition, to speeding up the learning
process, a knowledge transfer method was also used.
While this solution can adapt to changes in the en-
vironment, coordination among vehicle agents is ig-
nored.
(Xu et al., 2018) applied a two-step approach to
solve the order dispatch problem. The offline learning
step summarizes demand and supply patterns through
historical data, then driver-order pairs are created by
a combinatorial optimizing algorithm. (Zhang et al.,
2017b) proposed Stochastic Gradient Descent (SGD)
forecasting the combined probability of each rider and
driver pairs and the Hill Climbing algorithm was used
to maximize the global success rate. The drawback
of both methods is that passengers may be forced
to wait longer for service, although the serving rate
is increased. (Li and Allan, 2019) proposed a po-
lar coordinates based ride-matching method, but this
method failed to improve performance in demand
sparse places.
Repositioning techniques can direct vacant taxis
from low demand areas to busier places. (Wen et al.,
2017) proposed a model-free reinforcement learning
approach for dispatching empty taxis across a city to
T-Balance: A Unified Mechanism for Taxi Scheduling in a City-scale Ride-sharing Service
459

keep balance between supply and demand. The fleet
size can be reduced by 14% with slightly increased
extra taxi travel distance, but this method might lead
to excess taxis in busy areas. (Lin et al., 2018) mod-
eled the movement of vacant taxis as a multi-agent
problem and proposed an approach known as contex-
tual multi-agent actor-critic, which is a novel version
of Multiagent Reinforcement Learning (MARL). (Qu
et al., 2014) aimed to maximize the net profit of taxis.
The authors created a graph representing road net-
works through historical data, then proposed a novel
recursion approach to seek for the optimal route for
vacant taxis. (Jha et al., 2018) tried to guide vacant
taxis by the Driver Guidance System (DGS) depended
on forecast data of road demand . The researchers did
not show the performance of serving rate, although
they argued that drivers’ net profit could be maxi-
mized.
In addition, various price mechanisms have been
proposed for ride-sharing services. A monetary con-
straint function was proposed by (Ma et al., 2014) to
motivate passengers to participate in a ride-sharing
service. (Kleiner et al., 2011) aimed to minimize
the total travel distance of taxis and maximize the
serving rate and the Sealed-Bid Second-Price Auction
(SBSPA) was proposed to distribute taxi resources
among passengers. (Asghari et al., 2016) allocate
requesting customers through Sealed-Bid First-Price
Auction (SBFPA) mechanism such that the profit of
drivers could be maximized. A VCG (Wooldridge,
2009) auction approach was proposed to maximize
the global utility function by (Zheng et al., 2019), and
individual rationality and truthfulness can be ensured.
(Chen, 2016) tried to maintain balance between sup-
ply and demand by utilizing a surge price, but failed
to guarantee the efficiency of dispatching taxis across
a city.
3 BACKGROUND
In the business model of ride-sharing service, a cus-
tomer can send the service provider a request when
they need a taxi. The request contains information
like time, source, and destination. If the customer
cannot get service within a certain period, he or she
can give up the request and turn to an alternative ser-
vice without any penalty.
On the other hand, each taxi sends the provider
status message periodically. The status message con-
tains information like: taxi identification, time, cur-
rent location, and availability. With the information
of customer request and taxis status, the provider can
dispatch appropriate taxis to serve customers (Ride-
matching) and direct the vacant taxis to needed places
(Idle Movement)
4 METHOD
To provide passengers with better service and increase
drivers’ earning, we propose an enhanced version of
the hybrid solution called T-Balance based on (Li and
Allan, 2020): The city consists of different zones.
With the help of the Scoring Ride-Matching with Lot-
tery Selection (SRLS) algorithm, rider groups whose
destinations are located in busy areas will have more
chances to be served, and available taxis from less
popular zones will have more opportunities to be dis-
patched, thus simultaneously balancing supply and
demand in both a local areas. In addition, consid-
ering the impact of the high ride request zones on
other zones, a Q-learning Idle Movement (QIM) ap-
proach is applied to guide vacant taxis to busier zones
such that taxi distribution could be balanced across
the citywide.
4.1 Scoring Ride-matching with Lottery
Selection (SRLS)
Definition 1: Popularity Score. The popularity score
P(t, z) is defined as the summation of predicted rider
demand from the specific time t to the future at a spe-
cific zone z, which is described as Eq.(1), where D is a
demand predictor that could be implemented by (Yao
et al., 2018) and evaluates the scale of demand at spe-
cific time and zone, γ
p
being a decay and γ
p
∈ [0, 1].
P(t, z) = E(
+∞
∑
k=0
γ
k
p
· D(t + k, z)) (1)
The popularity score estimates the degree of de-
mand popularity at a specific zone over time. The im-
pact of the future demand is determined by the scale
of γ
p
. If the value of γ
p
approaches 1, then the future
demand greatly impacts the current popularity score;
the future demand has less impact on the current pop-
ularity score when the γ
p
is approaches 0.
In (Li and Allan, 2020), riders were randomly
selected from the rider list at each zone and then
assigned to the appropriate taxi through Adjacent
Matching. However, the approach failed to dispatch
taxis to most needed places in the process of ride-
matching since riders with different destinations have
the same chance to be served. In other word, taxis
are distributed to various places of the city. There-
fore, riders in busy areas would lose opportunities to
be served even though the quantity of taxis is enough.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
460

In this work, we propose the Lottery Selection (LS)
to select appropriate rider requests for drivers in the
process of ride-matching, such that taxis would have
more chances to be dispatched to the busier zones that
need more supplies than others. The idea of the Lot-
tery Selection is described as following: each rider is
given a certain amount of lottery tickets L
r
according
to the popularity score P of their destination, and a lot-
tery number LOT T ERY NUM is drawn then the ap-
propriate rider to be served is the rider who owns the
LOT T ERY NUM in his tickets. The solution is given
in Algorithm.1, where M is a multiplier factor. Since
Lottery Selection (LS) has stochastic property, taxis
have more chances to be delivered to hot places in
the process of driver-rider matching, and riders whose
destination is less popular can still be served.
Algorithm 1: Lottery Selection (LS).
Input : Rider list l
z
at zone z at timestamp t
Output: The the appropriate rider to be
served
1 for each rider r in l
z
do
2 Get rider r’s destination zone z
d
and
calculate the traveling time T
trip
.
3 L
r
= M ∗ P(t + T
trip
, z
d
)
4 end
5 LOTT ERY NU M = rand range(1, sum(L
r
))
6 sum = 0
7 for each rider r in l
z
do
8 sum = sum + L
r
9 if sum > LOT T ERY NUM then
10 return r
11 end
12 end
Definition 2: Balanced Factor. Given specific times-
tamp t and zone z, the balanced factor B is the propor-
tion between the number of available taxis A(t, z) and
the smoothed popularity score smooth(P(t, z)). It can
be defined by the Eq.(2):
B(t, z) =
A(t, z)
1 + smooth(P(t, z))
(2)
In (Li and Allan, 2020), the popularity score of
each zone was estimated individually in the Supply-
Demand Ratio, ignoring the impact of connectivity
among zones. In this work, we smooth the popular-
ity score smooth(P(t, z)) considering the demand im-
pact from its neighbor zones, the formula is shown in
Eq.(3), where O(z) is a collection of neighbor zones
of z, and β ∈ [0, 1] is the impact factor of neighboring
zones.
smooth(P(t, z)) = P(t, z) + β
∑
i∈O(z)
P(t, i) (3)
Based on the Lottery Selection and Balanced Fac-
tor, a new ride-matching algorithm named Scoring
Ride-matching with Lottery Selection (SRLS) is pro-
posed. The main idea is to dispatch taxis from
the least busy zone (highest Balanced Factor) in the
neighborhood to serve rider requests, while taxis from
the busier zones (lower Balanced Factor) are reserved
for future use. The algorithm can be described as fol-
lows: the appropriate rider r is selected by Lottery
Selection (LS) and the zone where the rider r is lo-
cated can be retrieved by z(r), we iterate the neighbor
zones O(z(r)) to find the zone with highest Balanced
Factor and randomly select taxi v from that zone. As
described by Algorithm 2:
Algorithm 2: Scoring Ride-matching with Lottery
Selection (SRLS).
Input : Rider list l
z
at zone z at timestamp t
Output: The selected taxi v
1 Select the appropriate rider r through Lottery
Selection.
2 MAX BF = B(z(r), t)
3 Z = z(r)
4 for each z in O(z(r)) do
5 Estimate Zone z’s Balanced Factor B(t, z)
at timestamp t.
6 if B(t,z) > MAX BF then
7 MAX BF = B(t,z)
8 Z = z
9 end
10 end
11 Randomly pick taxi v from zone Z.
12 return v
4.2 Q-Learning Idle Movement (QIM)
The Scoring Ride-Matching with Lottery Selection
(SRLS) can send taxis to needed places and effec-
tively balance taxis distribution locally in the process
of ride-matching. However, there are still a certain
number of taxis that will fail to be dispatched dur-
ing ride-matching. Such taxis wander across the city
to seek riders aimlessly, leading to the problem that
rider requests cannot be served on time and drivers’
traveling cost would be increased. In previous work, a
Greedy Idle Movement (GIM) was proposed to tackle
the issue. However, this approach cannot adapt to the
dynamic environment. For this reason, a flexible Idle
Movement Strategy based on Q-learning (Watkins
and Dayan, 1992) named Q-Learning Idle Movement
(QIM) is proposed. Each vacant taxis can learn the
movement strategy by itself according to the current
environment.
T-Balance: A Unified Mechanism for Taxi Scheduling in a City-scale Ride-sharing Service
461

Considering each taxi as an autonomous agent, we
want to let vacant taxis decide where to go. A Q-
learning approach is applied to train taxi agents such
that they are able to make a reasonable decision in idle
mode. The movement of a vacant taxi is model as a
Markov Decision Process (MDP) (Puterman, 2014).
The components of the MDP are defined as follows:
State: The state s of a taxi is defined as a three tu-
ple (t, z, δ), where t ∈ T is a timestamp, z ∈ Z is a
zone index, and δ indicates the maximum Balanced
Factor difference between z and its adjacent zones,
which can be formulated as Eq.(4), where O(z) are
adjacency zones of zone z, and we round up the value
to b decimals.
δ = round(B(t, z) − min
z
0
∈O(z)
B(t, z
0
), b) (4)
We also constrain the value of δ to the range
[δ
min
, δ
max
]. If the value of δ is inside the range, then it
is unchanged. If δ < δ
min
, then δ = δ
min
, and δ = δ
max
if δ > δ
min
Action: A taxi driver may implement two types of
actions. One action is staying at the current zone z; the
other is moving to an adjacent zone with the lowest
updated Balanced Factor argmin
z
0
∈O(Z)
B
0
(t, z
0
).
Reward: At each timestamp t, if taxi agents can serve
rider requests, then they will receive a positive reward
R
c
, where R
c
is a positive constant. If taxi agents
stays at the current zone without receiving rider re-
quests, they will receive a penalty −R
c
. If the taxi
moves to its adjacent zone without receiving rider re-
quests, they will receive a penalty −2R
c
, which con-
siders travel cost.
Discount Factor: The discount factor γ
q
∈ [0, 1].
At each simulated cycle, the Q-learning is applied
to learn the action value Q(s,a) indicating the sum of
reward from now to future that an agent may achieve
given a specific state s and action a. At start, the
values in the Q-table are initialized as 0. At each
timestamp, a taxi selects an action based on Q(s, a),
it would get the reward and transfer to another state
s
0
, then Q(s, a) can be updated. The details are de-
scribed in Algorithm 3, where the α is the learning
rate.
When a taxi is in idle mode, it will select an action
according to argmax
a∈A
q(s, a). If a = 0, it would not
move and stop at the current place, otherwise, it will
move to the adjacency zone with minimized φ
0
(t, z).
Algorithm 3: Q-Learning Idle Movement (QIM).
1 Select action a from current state s using
ε − greedy policy derive from Q.
2 Take action a, then the state is transfer from s
to s
0
.
3 if receive rider request then
4 R = R
c
5 else
6 if Action is move then
7 R = −2
˙
R
c
8 else
9 R = −R
c
10 end
11 end
12 Q(s, a) =
Q(s, a) +α
q
˙
(R + γ
q
˙
max
a
0
Q(s
0
, a
0
) − Q(s, a))
13 s
0
= s
14 return a
5 EXPERIMENT
The experiment is performed using the taxi data
records of the city of Chicago (cit, 2018). Every
record contains the timestamp, the start zone ID, the
end zone ID, and payment. In our setting, the inter-
val of one simulated cycle δ
t
is 3 minutes, the trav-
eling cost of a taxi to adjacent area is 1, while it is
0.5 if it just drives around within its current area, and
the money spent per unit of travel cost is $2.5. The
patience period is 20 minutes (in other words, after
20 minutes waiting in our simulation, customers will
change to another service). To verify the effectiveness
of the T-Balance, 43,764 rider requests during busy
hours (from 11:00 to 23:59) of a weekday is used.
SMW in (Banerjee et al., 2018) and the Hybrid So-
lution in (Li and Allan, 2020) are implemented as a
baseline. We suppose that all the three methods are
equipped with the cluster algorithm in (Li and Allan,
2020). Furthermore, we also study the impact of Lot-
tery Selection on the quantity of unserverd riders and
the average online running time of each algorithm.
Figure 1 and Figure 2 present the performance
evaluation on the service rate and taxi utilization. The
service rate reflects what percentage of passengers are
served by the fleet of taxis, and taxi utilization indi-
cates the percentage of time when taxis are used to
serve passengers rather than wandering to seek pas-
sengers. From the plots, we see that increasing taxi
fleet volume can serve more passengers, but on the
other hand, decreases the utilization of taxis. (in other
words, an individual driver would have less chance to
serve riders and earn less). We also discovered that
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
462
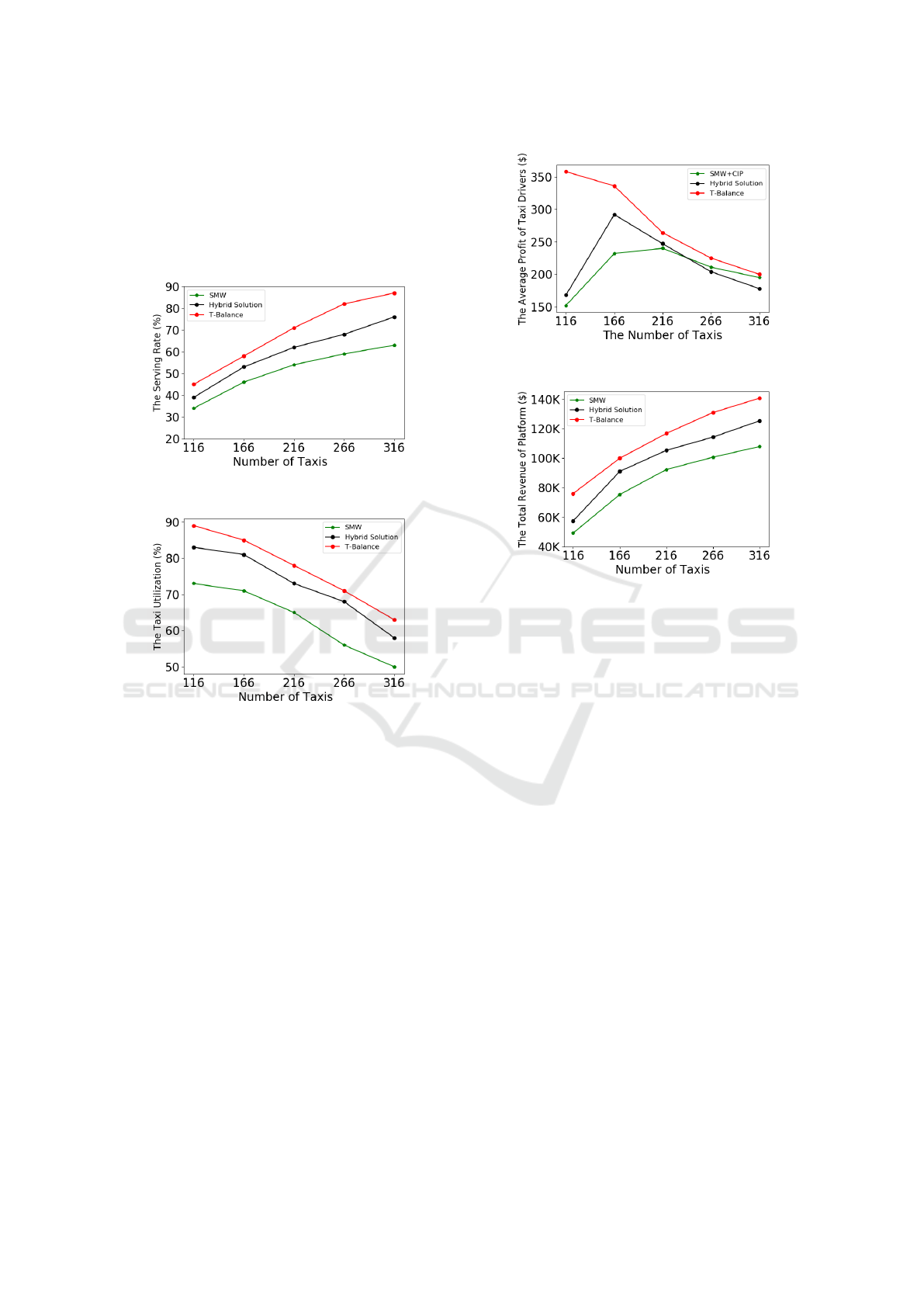
T-Balance is better than the two other methods. The
main reason is that the Lottery Selection (LS) helps
the service rate due to dispatching taxis to busy zones
for future use in ride-matching process, and the Q-
learning Idle Movement (QIM) improves both metrics
by guiding vacant taxis to the most needed places to
serve demands.
Figure 1: The Service Rate.
Figure 2: The Taxi Utilization Rate.
Figure 3 and Figure 4 reflect the economic side of
the ride-sharing service. Figure 3 shows how much
profit a taxi driver can earn on each solution while
Figure 4 plots the total income of the ride-sharing ser-
vice provider. Both Figures assume that all drivers
work continuously for 13 hours of that day. We can
see that a large fleet can help the provider earn more
money, but thin down the profit of each individual
driver. This is mainly because a larger number of taxis
can serve more passengers such that provider’s rev-
enue can be increased, but shrink the taxi utilization,
causing drivers to have more idle hours and have less
chances to earn money from passengers. Also, the
T-Balance work much better than other two methods
when there are fewer taxis, this is because the Lottery
Selection (LS) and Q-learning Idle Movement (QIM)
can deliver taxis to needed places precisely under the
circumstances that the supplied resources are limited.
Figure 5 reflects the expected response time of
each approach along with various number of taxis.
The response time is the time interval between the
Figure 3: The Average Profit of Taxi Drivers.
Figure 4: The Total Revenue of Provider.
timestamp when a rider request is send out and the
timestamp when the customer can be picked up by
a taxi. We may observe that larger number of taxis
can help to shrink the response time in all three ap-
proaches. It seems that all three methods can schedule
taxi across the city well as long as supplied resource
is enough. We also observe that the response time of
T-Balance is the least. This is mainly because the Lot-
tery Selection (LS) and the Q-learning Idle Movement
(QIM) can schedule taxis to places where there would
be large amount of demands in current or future such
that riders can be served in a short time.
We also study how the Lottery Selection (LS) af-
fects the number of unserved riders in several hypo-
thetical taxi services employing a varying number of
cars. As shown in the Figure 6, the efficiency of the
Lottery Selection (LS) seemed significant when deal-
ing with a small fleet of taxis, but as the number of
cars increased, the effort from the LS is not obvious.
The main reason is that the LS can still arrange sup-
plied resources for future use well especially under
the circumstance where resources are limited.
In addition, we estimate the online running time
of the Scoring Ride-matching with Lottery Selection
(SRLS) and Q-learning Idle Movement (QIM), and
compare them to the ARDL and GIM in (Li and Al-
lan, 2020) separately, as shown in Table 1. The online
running time indicates how much time we need to run
T-Balance: A Unified Mechanism for Taxi Scheduling in a City-scale Ride-sharing Service
463
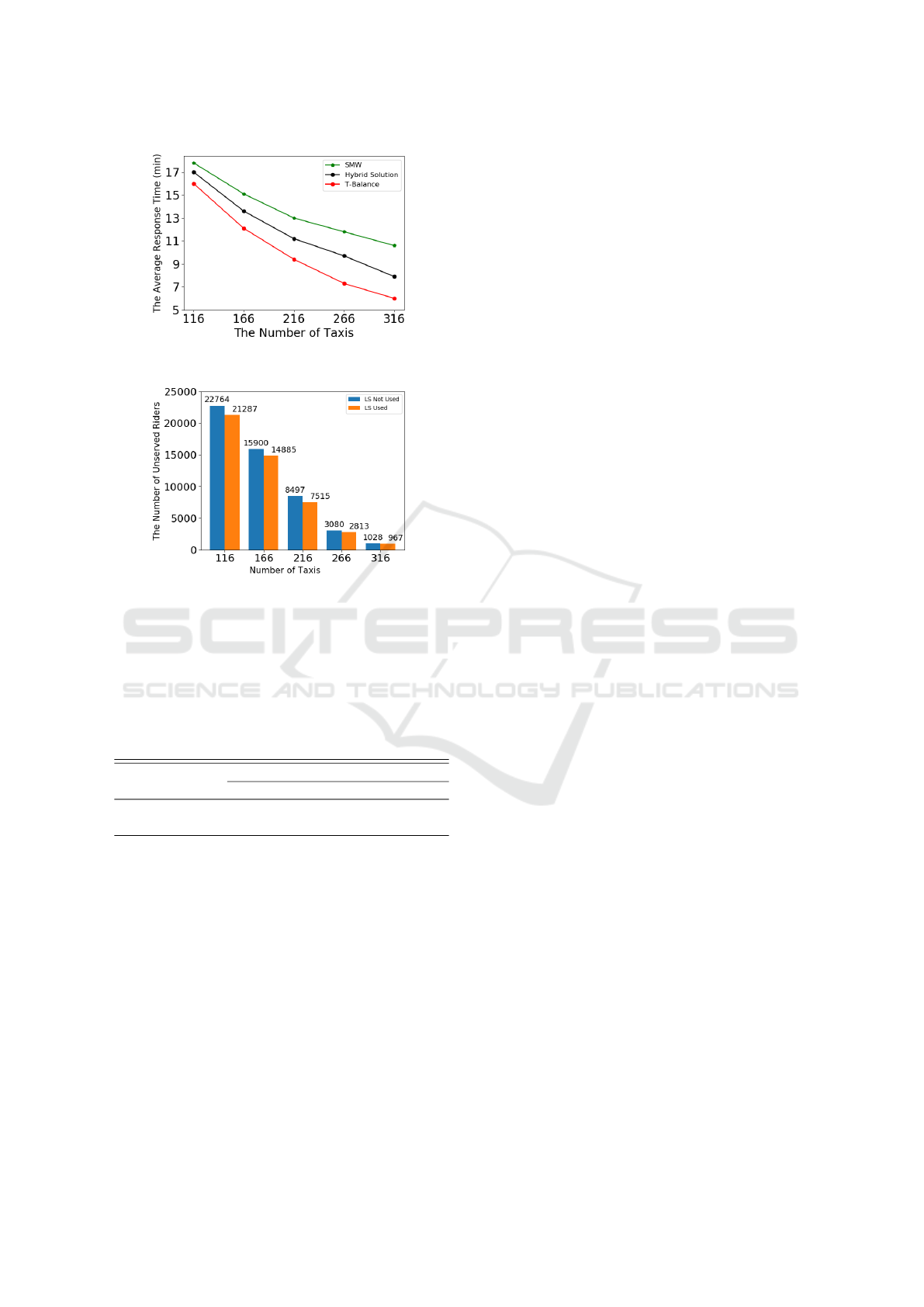
Figure 5: The Average Response Time of Riders.
Figure 6: Unserved Riders with or without Lottery Selec-
tion.
an algorithm once. Although the methods in the T-
Balance cost more several millisecond, they achieve
much better performance on effectiveness as above
shown.
Table 1: The Average Online Running Time of Each Algo-
rithm(sec).
T-Balance Hybrid Solution
Method/Time Method/Time
Ride-Matching SRLS/0.039 ARDL/0.034
Idle Movement QIM/0.065 GIM/0.050
From the above experiments and comparisons, the
T-Balance works better than the two other methods
across various performance metrics. This indicates
that the Scoring Ride-matching with Lottery Selec-
tion (SRLS) can balance the supplies and demands
well. The Q-learning Idle Movement (QIM) is effec-
tive in directing vacant taxis to the most needed places
adapting to the change of the dynamic environment.
Therefore, T-Balance is more flexible and adjustable
in various scenarios such that taxis can be frequently
sent to the most needed places without wasting too
much traveling cost.
6 CONCLUSION
This work has four contributions. First, we design a
Lottery Selection (LS) algorithm which delivers taxis
to areas of high need by selecting high priority rid-
ers, while low priority riders can still have chances to
be served. Second,using Lottery Selection (LS) and
the smoothed popularity score computed from among
neighbor zones, the Scoring Ride-matching with Lot-
tery Selection (SRLS) keeps balance between sup-
plies and demands in each local neighborhood and hot
places. Third, the Q-Learning Idle Movement (QIM)
directs vacant taxis to the most needed places adapt-
ing to the change of the dynamic environment. Four,
comparing our current work to state-of-the-art meth-
ods, the results verify the effectiveness and flexibility
of the T-balance.
REFERENCES
(2018). Chicago data portal: Taxi Trips. City of Chicago.
https://data.cityofchicago.org/Transportation/
Taxi-Trips/wrvz-psew.
Asghari, M., Deng, D., Shahabi, C., Demiryurek, U., and
Li, Y. (2016). Price-aware real-time ride-sharing at
scale: an auction-based approach. In Proceedings of
the 24th ACM SIGSPATIAL international conference
on advances in geographic information systems, pages
1–10.
Banerjee, S., Kanoria, Y., and Qian, P. (2018). State depen-
dent control of closed queueing networks. ACM SIG-
METRICS Performance Evaluation Review, 46(1):2–
4.
Chen, M. K. (2016). Dynamic pricing in a labor market:
Surge pricing and flexible work on the uber platform.
In Proceedings of the 2016 ACM Conference on Eco-
nomics and Computation, pages 455–455.
Curley, R. (2019). Global ride sharing industry valued at
more than $61 billion. Technical report.
Jha, S. S., Cheng, S.-F., Lowalekar, M., Wong, N., Rajen-
dram, R., Tran, T. K., Varakantham, P., Trong, N. T.,
and Rahman, F. B. A. (2018). Upping the game of
taxi driving in the age of uber. In Thirty-Second AAAI
Conference on Artificial Intelligence.
Kleiner, A., Nebel, B., and Ziparo, V. A. (2011). A mech-
anism for dynamic ride sharing based on parallel auc-
tions. In IJCAI, volume 11, pages 266–272.
Li, J. and Allan, V. H. (2019). A ride-matching strategy
for large scale dynamic ridesharing services based on
polar coordinates. In 2019 IEEE International Con-
ference on Smart Computing (SMARTCOMP), pages
449–453. IEEE.
Li, J. and Allan, V. H. (2020). Balancing taxi distribution
in a city-scale dynamic ridesharing service: A hybrid
solution based on demand learning. In 2020 IEEE In-
ternational Smart Cities Conference (ISC2), pages 1–
8.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
464

Lin, K., Zhao, R., Xu, Z., and Zhou, J. (2018). Efficient
large-scale fleet management via multi-agent deep re-
inforcement learning. In Proceedings of the 24th
ACM SIGKDD International Conference on Knowl-
edge Discovery & Data Mining, pages 1774–1783.
Liu, L., Qiu, Z., Li, G., Wang, Q., Ouyang, W., and Lin,
L. (2019). Contextualized spatial–temporal network
for taxi origin-destination demand prediction. IEEE
Transactions on Intelligent Transportation Systems,
20(10):3875–3887.
Lu, A., Frazier, P., and Kislev, O. (2018). Surge pric-
ing moves uber’s driver partners. Available at SSRN
3180246.
Ma, S., Zheng, Y., and Wolfson, O. (2014). Real-time city-
scale taxi ridesharing. IEEE Transactions on Knowl-
edge and Data Engineering, 27(7):1782–1795.
Puterman, M. L. (2014). Markov decision processes: dis-
crete stochastic dynamic programming. John Wiley &
Sons.
Qu, M., Zhu, H., Liu, J., Liu, G., and Xiong, H. (2014). A
cost-effective recommender system for taxi drivers. In
Proceedings of the 20th ACM SIGKDD international
conference on Knowledge discovery and data mining,
pages 45–54.
Stasha, S. (2021). Ride-Sharing Industry Statistics to get
you going in 2021. https://policyadvice.net/insurance/
insights/ride-sharing-industry-statistics/.
Wang, Z., Qin, Z., Tang, X., Ye, J., and Zhu, H. (2018).
Deep reinforcement learning with knowledge transfer
for online rides order dispatching. In 2018 IEEE Inter-
national Conference on Data Mining (ICDM), pages
617–626. IEEE.
Watkins, C. J. and Dayan, P. (1992). Q-learning. Machine
learning, 8(3-4):279–292.
Wen, J., Zhao, J., and Jaillet, P. (2017). Rebalancing shared
mobility-on-demand systems: A reinforcement learn-
ing approach. In 2017 IEEE 20th International Con-
ference on Intelligent Transportation Systems (ITSC),
pages 220–225. IEEE.
Wooldridge, M. (2009). An introduction to multiagent sys-
tems. John Wiley & Sons.
Xu, J., Rahmatizadeh, R., B
¨
ol
¨
oni, L., and Turgut, D. (2018).
Real-time prediction of taxi demand using recurrent
neural networks. IEEE Transactions on Intelligent
Transportation Systems, 19(8):2572–2581.
Xu, Z., Li, Z., Guan, Q., Zhang, D., Li, Q., Nan, J., Liu,
C., Bian, W., and Ye, J. (2018). Large-scale order dis-
patch in on-demand ride-hailing platforms: A learning
and planning approach. In Proceedings of the 24th
ACM SIGKDD International Conference on Knowl-
edge Discovery & Data Mining, pages 905–913.
Yao, H., Wu, F., Ke, J., Tang, X., Jia, Y., Lu, S., Gong, P.,
Ye, J., and Li, Z. (2018). Deep multi-view spatial-
temporal network for taxi demand prediction. In Pro-
ceedings of the AAAI Conference on Artificial Intelli-
gence, volume 32.
Zhang, J., Zheng, Y., and Qi, D. (2017a). Deep spatio-
temporal residual networks for citywide crowd flows
prediction. In Proceedings of the AAAI Conference on
Artificial Intelligence, volume 31.
Zhang, L., Hu, T., Min, Y., Wu, G., Zhang, J., Feng,
P., Gong, P., and Ye, J. (2017b). A taxi order dis-
patch model based on combinatorial optimization. In
Proceedings of the 23rd ACM SIGKDD international
conference on knowledge discovery and data mining,
pages 2151–2159.
Zheng, L., Cheng, P., and Chen, L. (2019). Auction-based
order dispatch and pricing in ridesharing. In 2019
IEEE 35th International Conference on Data Engi-
neering (ICDE), pages 1034–1045. IEEE.
T-Balance: A Unified Mechanism for Taxi Scheduling in a City-scale Ride-sharing Service
465
