Adversarial Examples by Perturbing High-level Features in Intermediate

Decoder Layers

Vojt

ech

Cerm

ak and Luk

s Adam

Faculty of Electrical Engineering, Czech Technical University in Prague, Technick

a 2, Prague, Czech Republic

Keywords:

Adversarial Examples, Robust Machine Learning, Representation Learning, High-level Features,

Intermediate Latent Representation.

Abstract:

We propose a novel method for creating adversarial examples. Instead of perturbing pixels, we use an encoder-

decoder representation of the input image and perturb intermediate layers in the decoder. This changes the

high-level features provided by the generative model. Therefore, our perturbation possesses semantic meaning,

such as a longer beak or green tints. We formulate this task as an optimization problem by minimizing

the Wasserstein distance between the adversarial and initial images under a misclassiﬁcation constraint. We

employ the projected gradient method with a simple inexact projection. Due to the projection, all iterations are

feasible, and our method always generates adversarial images. We perform numerical experiments by fooling

MNIST and ImageNet classiﬁers in both targeted and untargeted settings. We demonstrate that our adversarial

images are much less vulnerable to steganographic defence techniques than pixel-based attacks. Moreover, we

show that our method modiﬁes key features such as edges and that defence techniques based on adversarial

training are vulnerable to our attacks.

1 INTRODUCTION

In the past decade, the widespread application of deep

neural networks raised security concerns as it creates

incentives for attackers to exploit any potential weak-

ness. For example, attackers could create trafﬁc signs

invisible to autonomous cars or make malware ﬁlters

ignore threats. Those security concerns rose since

(Szegedy et al., 2014) showed that deep neural net-

works are vulnerable to small perturbations of inputs

that are designed to cause misclassiﬁcation of a classi-

ﬁer. These adversarial examples are indistinguishable

from natural examples as the perturbation is too small

to be perceived by humans.

We extend the usual approach to constructing

adversarial examples that focuses on norm-bounded

pixel modiﬁcations. Instead of perturbing the pixels

directly, we perturb features learned by an encoder-

decoder model. There are several ways to perturb

the features from the decoder, ranging from high-level

features collected from initial decoder layers to much

ﬁner features collected from decoder layers near the

reconstructed image. When we perturb features in

the initial layers near the latent image representation,

https://orcid.org/0000-0001-8748-4308

even small perturbations may completely change the

image meaning. On the other hand, perturbations on

ﬁne features are very close to pixel perturbations and

carry little semantic information. As a compromise,

we suggest perturbing intermediate decoder layers.

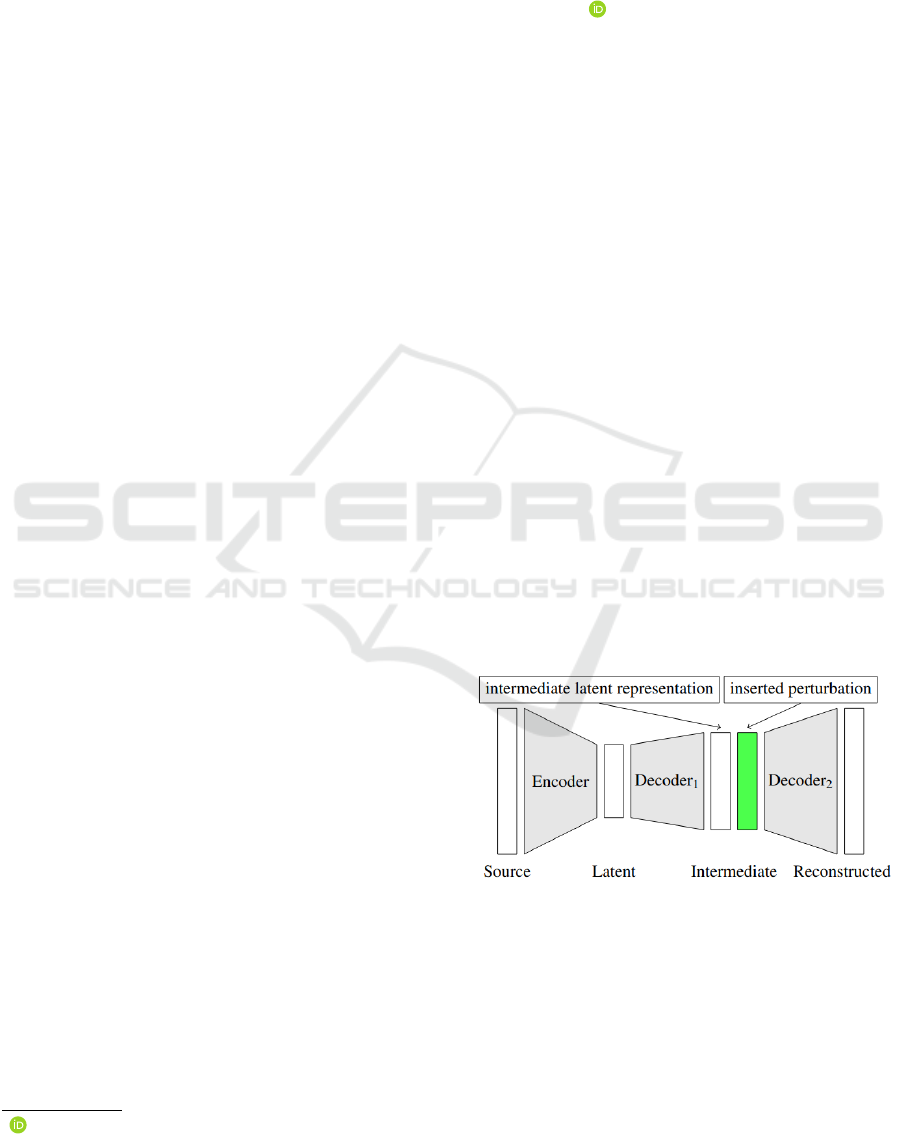
Figure 1.

Our way of generating adversarial images pro-

vides several advantages:

• The perturbations are interpretable. They mod-

ify high-level features such as fur colour or beak

length.

• The perturbations often follow edges. This means

that they are less detectable by steganographic de-

fence techniques (Johnson and Jajodia, 1998).

496

Cermák, V. and Adam, L.

Adversarial Examples by Perturbing High-level Features in Intermediate Decoder Layers.

DOI: 10.5220/0010892800003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 2, pages 496-507

ISBN: 978-989-758-547-0; ISSN: 2184-433X

• The perturbations keep the structure of the unper-

turbed images, including hidden structures unre-

lated to their semantic meaning.

• The decoder ensures that the adversarial images

have the correct pixel values; there is no need to

project to [0,1].

The drawback of our approach is that we cannot per-

turb an arbitrary image but only those representable

by the decoder.

To obtain a formal optimization problem, we min-

imize the distance between the original and adversar-

ial images in the reconstructed space. To successfully

generate an adversarial image, we add a constraint re-

quiring that the perturbed image is misclassiﬁed. To

handle this constraint numerically, we propose to use

the projected gradient method. We approximate the

projection operator by a fast method which always re-

turns a feasible point. This brings additional beneﬁts

to our method:

• The method works with feasible points. Even if it

does not converge, it produces an adversarial im-

age.

• Because we minimize the distance between the

original and adversarial images, we do not need to

specify their maximal possible distance as many

methods do.

Numerical experiments present results on samples

from MNIST and ImageNet in both targeted and un-

targeted settings. They support all advantages men-

tioned above. We use both the l

and Wasserstein dis-

tances and show in which settings each performs bet-

ter. We select a simple steganography defence mech-

anism and show that our attack is much less vulnera-

ble to it than pixel-based perturbations. We examine

the difference between perturbing the latent and in-

termediate layers and show that the intermediate lay-

ers indeed modify the high-level features of the re-

constructed image. Finally, we show how our algo-

rithm gradually incorporates the high-level features

from the initial to the adversarial image. Our codes

are available online to promote reproducibility.

1.1 Related Work

The threat model based on small l

norm-bounded

perturbations has been the main focus of research. It

was originally introduced in (Szegedy et al., 2014),

where they used L-BFGS to minimize the l

distance

between the original and adversarial images. Since

then, many new ways how to both attack and defend

against adversarial examples have been introduced.

https://github.com/VojtechCermak/latent-adv-examples

(Goodfellow et al., 2015) introduced Fast Gradient

Sign Method (FGSM), which is bounded by the l

∞

metric. The authors used FGSM to generate new

adversarial examples and used them to augment the

training set in the adversarial training defence tech-

nique. A natural way to extend the FGSM attack is to

iterate the gradient step as it is done in the Basic Iter-

ative Method of (Kurakin et al., 2016) and Projected

Gradient Descend attack of (Madry et al., 2018). (Pa-

pernot et al., 2016) argued to use the l

distance to

model human perception and proposed a class of at-

tacks optimized under l

distance. (Carlini and Wag-

ner, 2017) designed strong attack algorithms based on

optimizing the l

, l

and l

∞

distances.

(Xiao et al., 2018) used GANs to generate noise

for adversarial perturbation. Other authors used gen-

erative models in defence against adversarial exam-

ples. MagNet of (Meng and Chen, 2017) used recon-

struction error of variational autoencoders to detect

adversarial examples. A similar idea was used in De-

fenceGAN of (Samangouei et al., 2018), where they

cleaned adversarial images by matching them to their

representation in latent space of the GAN trained on

clean data.

We use similar optimization techniques as in

decision-based attacks such as Boundary attack of

(Brendel et al., 2018) and HopSkipJump attack of

(Chen et al., 2020). The optimization techniques al-

ways keep intermediate results in the adversarial re-

gion and always outputs misclassiﬁed examples.

Some works have already investigated adversarial

examples outside of the l

norm. (Wong et al., 2019)

used the Sinkhorn approximation of the Wasserstein

distance to create adversarial images with the same

geometrical structure as the original images. The

Wasserstein distance is based on the cost needed

to move mass between two probability distributions.

Compared to standard distance metrics, such as l

dis-

tance, it includes information about the spatial distri-

bution of pixels. This makes the Wasserstein distance

more suitable for adversarial examples than the stan-

dard l

distance metrics because it can capture differ-

ences in high-level features. We increase this beneﬁt

by additionally modifying the high-level features in-

stead of pixels.

The Unrestricted Adversarial Examples of (Song

et al., 2018), are adversarial examples constructed

from scratch using conditional generative models.

Our paper differs in several aspects. First, we use

the intermediate instead of the latent representation

to perturb high-level features. Second, we use an un-

conditional generator, which allows us to freely move

in the intermediate latent space and perform several

operations such as the projection.

Adversarial Examples by Perturbing High-level Features in Intermediate Decoder Layers

497

2 PROPOSED FORMULATION

Finding an adversarial image amounts to ﬁnding some

image x which is close to a given x

, and the neu-

ral network misclassiﬁes it. For reasons mentioned in

the introduction, we do not work with the original im-

ages but with their latent representations. Therefore,

we need a decoder D which maps the latent repre-

sentation z to the original representation x. Since we

want to insert some perturbation p to the intermedi-

ate layer in the decoder, we split the decoder into two

parts D = D

◦ D

. We call D

(z) the intermediate

latent representation and D

(z)) the reconstructed

image.

The mathematical formulation of ﬁnding an ad-

versarial image close to x

reads:

minimize

distance(x,x

)

subject to x = D

) + p),

= D

)),

g(x) ≤ 0,

x ∈ [0,1]

(1)

Here, z

is the latent representation of the image x

We insert the perturbation p to the intermediate latent

representation D

) and only then reconstruct the

image by applying the second part of the decoder D

When D

is the identity, and D

is the decoder, we

obtain the case when perturbations appear in the la-

tent space. Similarly, when D

is the decoder, and D

is the identity, we recover the standard pixel perturba-

tions. Therefore, our formulation (1) generalizes both

approaches.

2.1 Objective

The objective function measures the distance between

the adversarial x and the original x

image in the re-

constructed space. We will use the l

norm and the

Wasserstein distance. Having the distance in the ob-

jective is advantageous because we do not need to

specify the ε-neighborhood when this distance is in

the constraint.

2.2 Constraints

Formulation (1) has multiple constraints. Constraint

x ∈ [0,1]

says that the pixels need to stay in this

range. Since x is an output of the decoder, this con-

straint is always satisﬁed.

The other constraint g(x) ≤ 0 is a misclassiﬁcation

constraint. We employ the margin function

m(x,k) = max

i,i6=k

(x) −F

(x), (2)

where F = [F

(x),...,F

(x)] is a classiﬁer with m

classes and k is a class index. We deﬁne this con-

straint for both targeted and untargeted attacks:

targeted : g(x) = m(x, k),

untargeted : g(x) = −m(x, argmax

i=1,...,m

(x)).

(3)

For the targeted case, we need to specify the target

class k, while for the untargeted case, the class k is

the classiﬁer prediction. For the latter case, we need

to multiply the margin by −1 as we require the mis-

classiﬁed images to satisfy g(x) ≤ 0.

We will later use that the original image always

satisﬁes g(x

) > 0 because otherwise the original im-

age is already misclassiﬁed, and no perturbation (p =

0) is the optimal solution of (1).

3 PROPOSED SOLUTION

METHOD

We propose to solve (1) by the projected gradient

method (Nocedal and Wright, 2006) with inexact pro-

jection. Our algorithm produces a feasible point at

every iteration. Therefore, it always generates a mis-

classiﬁed image.

3.1 Proposed Algorithm

Since we optimize with respect to p, we deﬁne the

objective and constraint by

f (p) = distance(D

) + p),x

ˆg(p) = g(D

) + p)).

(4)

We describe our procedure in Algorithm 1. First, we

initialize p by some feasible p

init

and then run the

projected gradient method for max

iter

iterations. Step

8 computes the optimization step by minimizing the

objective f and step 9 uses the inexact projection (de-

scribed later) to project the suggested iteration p

back to the feasible set. As we will see later, the

constraint p

6= p implies that p

was not feasi-

ble, and it was projected onto the boundary. In such

a case, steps 4-7 “bounce away” from the boundary.

Since −∇ ˆg(p) points inside the feasible set, step 5

ﬁnds some β > 0 such that p − β∇ ˆg(p) lies in the in-

terior of the feasible set.

3.2 Inexact Projection

Step 9 in Algorithm 1 uses the inexact projection.

We summarize this projection in Algorithm 2. Its

main idea is to ﬁnd a feasible point on the line be-

tween p and p

. This line is parameterized by

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

498

Algorithm 1: For ﬁnding adversarial images by solving (1).

1: p ← p

init

2: for i ∈ {0,...,max

iter

} do

3: if i > 0 and p

6= p then

4: β ← β

5: while ˆg(p − β∇ ˆg(p)) ≥ 0 do

6: β ←

7: p ← p − β∇ ˆg(p)

8: p

← p −α

∇ f (p)

9: p ← PROJECT(p

, p,δ)

10: return p

(1 − c)p + cp

for c ∈ [0,1]. Due to the construc-

tion of Algorithm 1, p is always strictly feasible and

therefore ˆg(p) < 0. If ˆg(p

) < 0, then p

is fea-

sible and we accept it in step 4. In the opposite case,

we have ˆg(p) < 0 and ˆg(p

) ≥ 0 and we can use the

bisection method to ﬁnd some c ∈ (0,1) for which the

constraint is satisﬁed. The standard bisection method

would return a point with ˆg((1 − c)p + cp

) = 0,

however, since the formulation (1) contains the in-

equality constraint, we require the constraint value to

lie only in some interval [−δ,0] instead of being zero.

Algorithm 2: Inexact projection onto the feasible set.

1: procedure PROJECT(p

, p,δ)

2: assert ˆg(p) < 0

3: if ˆg(p

) < 0 then

4: return p

5: a ← 0, b ← 1, c ←

(a +b)

6: while ˆg((1 − c)p +cp

) /∈ [−δ,0] do

7: if ˆg((1 −c)p +cp

) > 0 then

8: b ← c

9: else

10: a ← c

11: c ←

(a +b)

12: return (1 − c)p + cp

Figure 2 depicts the projection in the intermediate

latent space. The light-grey region is feasible, and

the white region is infeasible. The infeasible region

always contains D

), while the feasible region al-

ways contains D

) + p. If D

) + p

lies in

the feasible region, the projection returns p

. In

the opposite case, we look for some point on the line

between D

) + p and D

) + p

. The points

which may be accepted are depicted by the thick solid

line. The length of this line is governed by the thresh-

old δ. The extremal case δ = 0 always returns the

point on the boundary, while δ = ∞ prolongs the line

to D

) + p.

Feasible region

Infeasible region

) + p

)

Accepted

projection

Figure 2: Inexact projection in the intermediate latent space.

The points which may be accepted are depicted by the thick

solid line.

3.3 Analysis of the Algorithm

The preceding text mentioned that Algorithm 1 gen-

erates a strictly feasible point p, thus g(D

) +

p)) < 0. We prove this in the next theorem and add a

speed of convergence.

Theorem 1. Assume that g◦ D

is a continuous func-

tion. Then Algorithm 2 generates a strictly feasible

point in a ﬁnite number of iterations. If g◦D

is more-

over Lipschitz continuous with modulus L, then Algo-

rithm 2 either immediately returns p

or converges

in at most log

Lkp

−pk

min{δ,− ˆg(p)}

iterations.

Proof. If ˆg(p

) < 0, then the algorithm immedi-

ately terminates. Assume thus ˆg(p

) ≥ 0. Denote

the iterations from Algorithm 2 by b

and a

with the

initialization b

= 1 and a

= 0. Since the interval

halves at each iteration, we obtain

− a

k−1

− a

k−1

) =

− a

) =

. (5)

Deﬁne

˜g(c) = ˆg((1 − c)p + cp

Since we have

˜g(b

) = ˜g(1) = ˆg(p

) ≥ 0,

˜g(a

) = ˜g(0) = ˆg(p) < 0.

due to the construction of the algorithm, we have

˜g(b

) ≥ 0 and ˜g(a

) < 0 for all k. Since ˜g is a contin-

uous function due to continuity of D

◦ g, Algorithm

2 converges in a ﬁnite number of iterations.

Assume that g ◦D

is a Lipschitz continuous func-

tion with modulus L, then ˆg is also Lipschitz continu-

Adversarial Examples by Perturbing High-level Features in Intermediate Decoder Layers

499

ous with modulus L. Then

| ˜g(c

) − ˜g(c

= | ˆg((1 − c

)p + c

) − ˆg((1 − c

)p + c

≤ Lk(1 − c

)p + c

− (1 − c

)p − c

= Lk(p

− p)(c

− c

≤ Lkp

− pk|c

− c

Therefore, ˜g is a Lipschitz continuous function with

constant Lkp

− pk. Together with (5) this implies

˜g(b

) − ˜g(a

) ≤ Lkp

− pk(b

− a

)

= Lkp

− pk

(6)

If the algorithm did not ﬁnish within k itera-

tions, there are two possibilities. The ﬁrst possibility

˜g(a

) < −δ implies ˜g(a

) < −δ. The second possi-

bility ˜g(a

) ∈ [−δ,0] implies ˜g(a

) ≤ ˜g(a

) because

otherwise the algorithm would have stopped already.

Both possibilities imply

˜g(b

) − ˜g(a

) ≥ − ˜g(a

) ≥ min{δ, − ˆg(p)}. (7)

The comparison of (6) and (7) implies that the algo-

rithm cannot run for more than the number of itera-

tions speciﬁed in the theorem statement.

The previous theorem implies that all iterations p

produced by Algorithm 1 are strictly feasible. The

theorem also provides another explanation why Algo-

rithm 1 must bounce away from the boundary in steps

4-7. If these steps were not present, ˆg(p) would of-

ten converge to zero and the number of iterations for

Algorithm 2 would increase to inﬁnity.

4 EXPERIMENTAL SETUP

This section describes the experimental setup.

4.1 Used Architectures

As the classiﬁers to be fooled in our MNIST experi-

ments, we train a non-robust classiﬁer with architec-

ture based on VGG blocks (Simonyan and Zisserman,

2015) and use the approach of (Madry et al., 2018)

to train robust networks with respect to l

and l

∞

at-

tacks. We generate new digits using an unconditional

ALI generator (Donahue et al., 2016; Dumoulin et al.,

2016). For ImageNet we use EfﬁcientNet B0 (Tan and

Le, 2019) as a classiﬁer and BigBiGAN (Donahue

and Simonyan, 2019) as an encoder-decoder model.

4.2 Numerical Setting

As an objective we use the standard l

distance and the

Sinkhorn approximation (Cuturi, 2013) to the Wasser-

stein distance. This approximation adds a weighted

Kullback-Leibler divergence to solve

minimize

hC,W i + λhW,logW i

subject to W 1 = x

1 = x,W ≥ 0.

(8)

The optimal value of this problem is the Sinkhorn dis-

tance between images x

and x. The matrix C speci-

ﬁes the distance between pixels. Since x

and x are

required to be probability distributions, we normal-

ize the pixels from decoder output to sum to one.

We do not need to impose the non-negativity con-

straint because the decoder outputs positive pixel in-

tensities. We use the implementation from the Geom-

Loss package (Feydy et al., 2019). Since the number

of elements W from (8) equals the number of pixels

squared, using the Sinkhorn distance was infeasible

for ImageNet, where we use only the l

distance.

For MNIST experiments, we randomly generate

the latent images z

and then use the decoder for re-

constructed images x

. We required that the classi-

ﬁer predicts the digit into the correct class with the

probability of at least 0.99. For ImageNet, this tech-

nique produces images of lower quality, and we fed

the encoder with real images and used their encoded

representation.

We run all experiments for 1000 iterations. Algo-

rithm 1 requires stepsizes α and β, while Algorithm

2 requires the threshold δ. We found that the stepsize

α is not crucial because even if it is large, the projec-

tion will reduce it. We therefore selected α = 1. For

the second stepsize β, we selected a simple anneal-

ing scheme with exponential decay. In both cases, we

used the normed gradient. For the threshold we se-

lected δ = 1. Since the margin function (2) is bounded

by 1, Figure 2 then implies that the acceptable projec-

tion increases all the way to D

)+ p. Since at least

one iteration of the projection is performed, the dis-

tance to the boundary at least halves. We found this

to be a good compromise between speed and approx-

imative quality. Theorem 1 then implies that Algo-

rithm 1 converges in at most log

L iterations.

We run our experiments on an Nvidia GPU with

6GB of VRAM.

4.3 Evaluation Metrics

Besides standard evaluation metrics, we also use

the least signiﬁcant bit metric, which is a standard

steganographic defence technique to capture changes

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

500

in the hidden structure of the data. For pixel intensi-

ties in x ∈ [0,1], it is deﬁned by

lsb(x) = mod(round(255x), 2). (9)

Therefore, it transforms the image x ∈ [0,1] into its 8-

bit representation and takes the last (least signiﬁcant)

bit.

5 EXPERIMENT RESULTS

This section presents numerical experiments to sup-

port our key claims from the introduction. Here, we

only present a short summary of both qualitative and

quantitative results. We postpone thorough descrip-

tions of our results to the next sections.

Qualitative results:

• Figures 4 and 5 show that our algorithm pro-

duces interpretable adversarial examples that fol-

low edges and does not break the structure of the

original dataset.

• Figure 7 shows how the choice of intermediate

layer affects the interpretation of perturbations

created by our algorithm.

• Figure 6 documents how the interpretability of our

perturbations naturally emerges due to the con-

struction of our algorithm.

Quantitative results :

• Table 1 shows that our algorithm often produces

reasonably strong attacks against both standard

and robust networks.

• Table 2 shows that our algorithm keeps the hidden

structure of the original data better than the CW

attack.

We split the discussion for results on the image

datasets MNIST (LeCun et al., 2010) and ImageNet

(Deng et al., 2009).

5.1 Numerical Results for MNIST

For the numerical experiments, we use the notation

of l

and Wasserstein attacks based on the objective

function in the model (1). For MNIST, we would like

to stress that none of the images was manually se-

lected, and all images were generated randomly.

Figure 3 shows targeted l

attacks (left) and tar-

geted Wasserstein attacks (right). Even though both

attacks performed well, the Wasserstein attack shows

fewer grey artefacts around the digits. This is natu-

ral as the Wasserstein distance considers the spatial

distribution of pixels. The is not the case for the l

distance.

Tables 1 and 2 show a numerical comparison be-

tween these two attacks and the CW l

attack (Car-

lini and Wagner, 2017) implemented in the Foolbox

library (Rauber et al., 2020). Besides the targeted at-

tacks, we also implemented untargeted attacks and at-

tacks against robust networks (additional ﬁgures are

in the appendix). The two robust networks were

trained to be robust with respect to l

and l

∞

attacks.

Table 1 shows the l

and Wasserstein distances.

The table shows that if we optimize with respect to

the Wasserstein distance, the Wasserstein distance be-

tween the original and adversarial images (column 8)

is the smallest. The same holds for the l

distance

(column 4). Even though the CW attack generated

smaller values in the l

distance, this happened be-

cause it is not restricted by the decoder. Moreover, as

we will see from the next ﬁgure, the CW attack gener-

ates lower-quality images which do not keep the hid-

den structure of the original images. It is also not sur-

prising that the needed perturbations are smaller for

untargeted attacks and the non-robust network. This

table demonstrates that our attacks are better in met-

rics that capture high-level features (Wasserstein dis-

tance).

Table 2 shows that our attack keeps the hidden

structure intact when compared to standard pixel-

based attacks. The right part shows the average frac-

tion of modiﬁed pixels, while the left side shows the

average fraction of modiﬁed least signiﬁcant bits (9)

between the original and perturbed images. The table

shows that our algorithm is superior in both metrics.

Moreover, compared to standard pixel-based attacks,

our attacks yields consistent results in those metric

even when evaluated on robust models.

Figure 4 shows a visual comparison for untargeted

attacks. It shows the original image (left) and the CW

(middle left), l

(middle right) and Wasserstein (right)

attacks. Each three columns contain the adversarial

image, the least signiﬁcant bit representation (9) and

the difference between the original and adversarial

images. A signiﬁcant difference between our attacks

and the pixel-based CW attack is that our attacks pro-

vide interpretability of perturbations. Figure 4 shows

that there is no clear pattern in the pixel perturba-

tions of the CW attack, neither in the least signiﬁcant

bit nor in the (almost) uniformly distributed perturba-

tions. On the other hand, our method keeps the least

signiﬁcant bit structure. This implies that the least

signiﬁcant bit defence can easily recognize the CW

attack, while our attacks cannot be recognized. At the

same time, our methods concentrate the attack around

the edges of the image. Therefore, our attacks are

compatible with the basic steganographic rule stating

that attacks should be concentrated mainly around key

Adversarial Examples by Perturbing High-level Features in Intermediate Decoder Layers

501

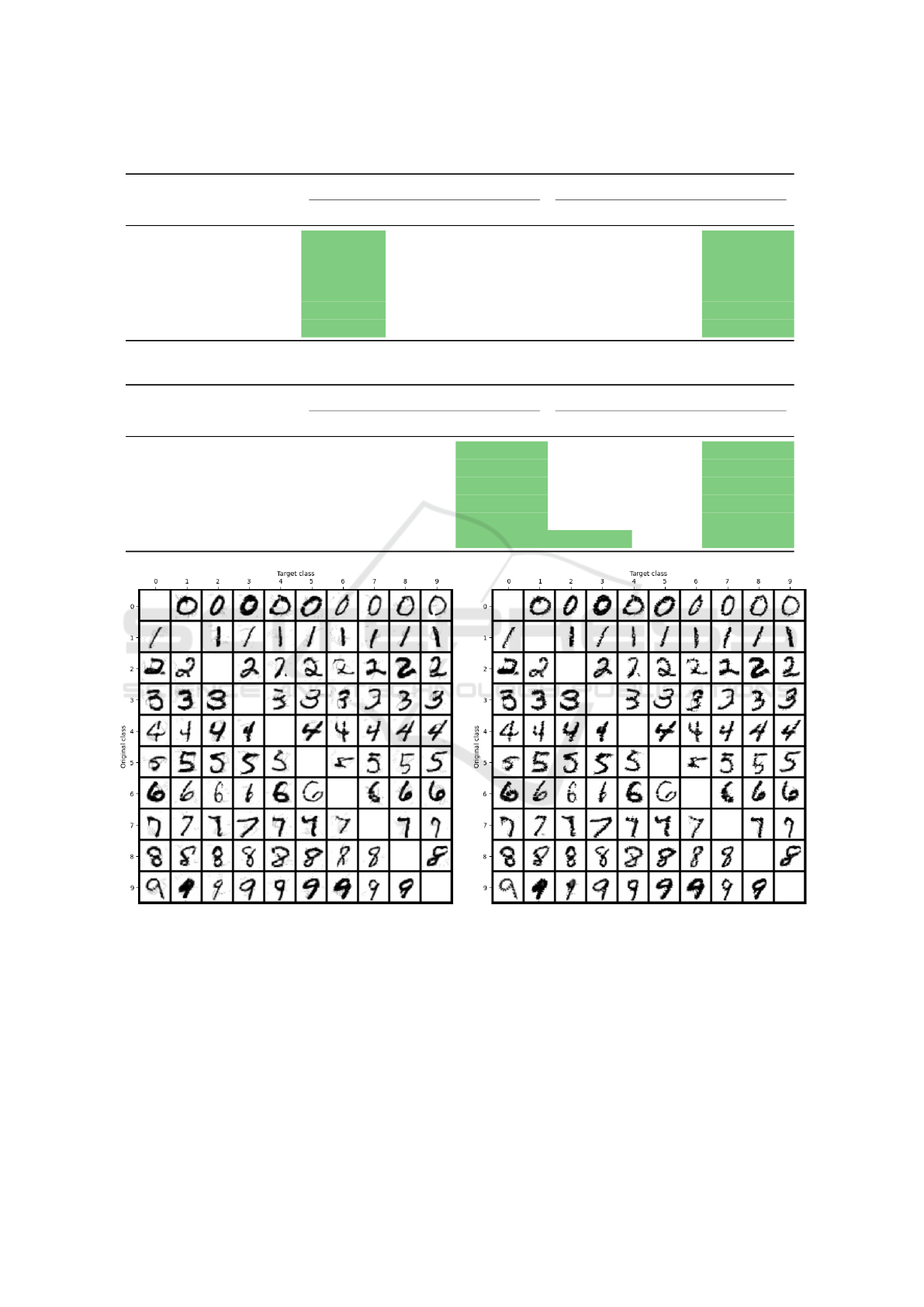
Table 1: Mean l

and Wasserstein distances between original and adversarial images over 90 randomly selected images.

Network Attack l

distance Wasserstein distance

CW attack l

attack Wasserstein CW attack l

attack Wasserstein

Non-robust Targeted 10.07 16.78 24.01 2.76 1.83 0.12

Untargeted 7.85 15.28 20.87 1.77 1.49 0.08

Robust l

Targeted 28.33 33.56 47.88 3.47 5.60 1.08

Untargeted 22.50 29.06 42.34 2.42 4.20 0.80

Robust l

in f

Targeted 23.51 29.56 35.63 1.11 3.84 0.46

Untargeted 19.26 25.44 31.04 0.58 2.53 0.31

Table 2: Metrics of change in structure between original and adversarial images over 90 randomly selected images.

Network Attack Fraction of modiﬁed LSB Fraction of modiﬁed pixels

CW attack l

attack Wasserstein CW attack l

attack Wasserstein

Non-robust Targeted 0.33 0.20 0.15 0.58 0.33 0.25

Untargeted 0.32 0.19 0.14 0.55 0.32 0.24

Robust l

Targeted 0.26 0.18 0.16 0.40 0.30 0.27

Untargeted 0.22 0.18 0.16 0.34 0.29 0.27

Robust l

in f

Targeted 0.17 0.17 0.15 0.28 0.29 0.26

Untargeted 0.16 0.17 0.15 0.25 0.28 0.25

Figure 3: Targeted l

attacks (left) and Wasserstein attacks (right). Rows represent the original while columns the target class.

features such as edges. We show the same ﬁgure for

the robust classiﬁer in the appendix.

5.2 Numerical Results for ImageNet

When fooling the ImageNet classiﬁer, we use only

the targeted version of our algorithm to prevent triv-

ial class changes in the case of the untargeted attack,

such as changing the dog’s breed. We manually select

several pictures of various animals as original images.

As the target class, we chose broccoli due to its dis-

tinct features.

Figure 5 demonstrates the differences between

original and adversarial images. In all experiments,

we perturbed the second intermediate layer of the

BigBiGAN decoder. The ﬁrst row shows the origi-

nal images, while the second row shows the adver-

sarial images misclassiﬁed all as broccoli. The third

row highlights the difference between original and ad-

versarial images by taking the mean square root of

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

502

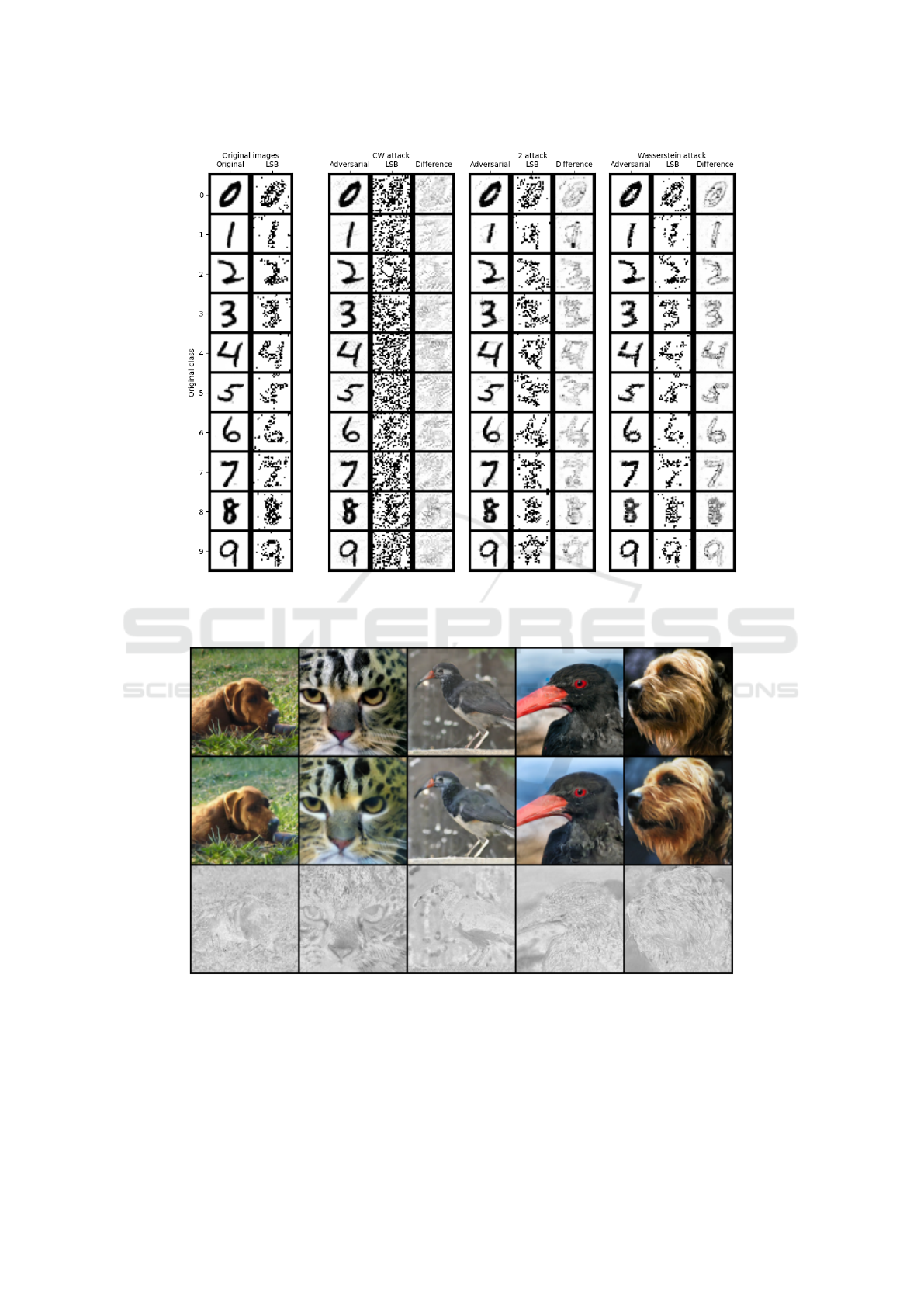
Figure 4: Comparison of CW and our attacks. Least signiﬁcant bit (LSB) is deﬁned in (9), the difference is between the

original and adversarial images. The ﬁgure shows that our attacks keep the hidden structure of the data (LSB) and that the

perturbations are not located randomly but around edges.

Figure 5: Unperturbed image (top), perturbed image (middle) and their difference (bottom). The perturbations happen around

key animal features.

the absolute pixel difference across all channels. This

difference shows interpretable silhouettes, which al-

lows us to assign semantical meaning to many per-

turbations. Most of the differences are concentrated

in key components of the animals, such as changes

of texture, colouring and brightness of their semanti-

cally meaningful components. For example, the dog

fur has a different texture, and the grass has lighter

colour. Another example is the bird’s beak, which is

longer in the third and thicker in the fourth adversar-

Adversarial Examples by Perturbing High-level Features in Intermediate Decoder Layers

503

Figure 6: Development of perturbed images over iterations. Broccoli features get gradually incorporated into the dog.

Figure 7: Effect of the intermediate layer choice. The

columns show the perturbation in the ﬁrst (left), second

(middle) and third (right) intermediate layer.

ial image. The difference plot also shows that signif-

icant perturbations happen around animals edges or

key features such as eyes and nose.

The crucial idea of our paper is to perturb the in-

termediate decoder layers. However, we can place

the perturbation in any intermediate layer, each with

a different effect. The earlier layers generate high-

level features, while later layers generate much ﬁner

features or even perturbations in pixels without any

semantic meaning. Figure 7 shows the impact of the

choice of the intermediate layer. The columns show

the adversarial images when perturbing the ﬁrst (left

column), second (middle column) and third (right col-

umn) intermediate layer. The ﬁgure shows that the

deeper we perturb the decoder, the more the perturba-

tions shift from high-level to ﬁner perturbations. The

ﬁrst layer results in a purely black bird and uniform

background. The silhouettes show that while the ﬁrst

layer perturbs the colour of the chest, the beak or the

background, the silhouette in the third layer disap-

pears, and the perturbations amount almost to pixel

perturbations.

Figure 6 documents a similar effect of high-level

perturbations. While the previous ﬁgure showed the

dependence of high-level features on the intermedi-

ate layer choice, this ﬁgure shows this dependence

on the development of iterations in Algorithm 1. The

left image shows the broccoli image used for the ini-

tialization of our algorithm. The right image shows

the unperturbed dog. The middle ﬁve images visual-

ize how the perturbations modify the broccoli image

as the number of iterations increases. At the begin-

ning of the algorithm run, the perturbations are inter-

pretable: the dog is reconstructed by high-level broc-

coli features. As the algorithm gradually converges,

the perturbed image increasingly resembles the origi-

nal dog as the broccoli features fuse with the dog im-

age. Some of the original broccoli features remain

integrated into the ﬁnal adversarial image. For exam-

ple, the next-to-last picture contains a slightly lighter

green shade than the original dog picture. Similarly,

we can interpret the changes in the dog fur and muzzle

textures as they originate from the broccoli texture.

We point out that all central images are classiﬁed as

broccoli due to the construction of our algorithm.

6 CONCLUSION

This paper presented a novel method for generat-

ing adversarial images. Instead of the standard pixel

perturbation, we use an encoder-decoder model and

perturb high-level features from intermediate decoder

layers. Our method generates high-quality adversarial

images in both targeted and untargeted settings on the

MNIST and ImageNet datasets. Since our adversarial

images perturb high-level features, they are more re-

silient to being recognized as adversarial by standard

defence techniques.

ACKNOWLEDGEMENTS

This material is based upon work supported by, or

in part by, the Army Research Laboratory and the

Army Research Ofﬁce under grant number W911NF-

20-1-0197. The authors acknowledge the sup-

port by the project Research Center for Informatics

(CZ.02.1.01/0.0/0.0/16 019/0000765).

REFERENCES

Brendel, W., Rauber, J., and Bethge, M. (2018). Decision-

based adversarial attacks: Reliable attacks against

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

504

black-box machine learning models. In Inter-

national Conference on Learning Representations

(ICLR) 2018.

Carlini, N. and Wagner, D. (2017). Towards evaluating the

robustness of neural networks. In 2017 IEEE Sympo-

sium on Security and Privacy (SP), pages 39–57.

Chen, J., Jordan, M. I., and Wainwright, M. J. (2020). Hop-

skipjumpattack: A query-efﬁcient decision-based at-

tack. In 2020 IEEE Symposium on Security and Pri-

vacy (SP), pages 1277–1294.

Cuturi, M. (2013). Sinkhorn distances: Lightspeed com-

putation of optimal transport. In Advances in Neural

Information Processing Systems 26, volume 26, pages

2292–2300.

Deng, J., Dong, W., Socher, R., Li, L.-J., Li, K., and Fei-Fei,

L. (2009). Imagenet: A large-scale hierarchical image

database. In 2009 IEEE conference on computer vi-

sion and pattern recognition, pages 248–255.

Donahue, J., Kr

ahenb

uhl, P., and Darrell, T. (2016).

Adversarial feature learning. arXiv preprint

arXiv:1605.09782.

Donahue, J. and Simonyan, K. (2019). Large scale adver-

sarial representation learning. In Advances in Neu-

ral Information Processing Systems, volume 32, pages

10541–10551.

Dumoulin, V., Belghazi, I., Poole, B., Mastropietro, O.,

Lamb, A., Arjovsky, M., and Courville, A. (2016).

Adversarially learned inference. arXiv preprint

arXiv:1606.00704.

Feydy, J., S

ejourn

e, T., Vialard, F.-X., Amari, S.-i., Trouve,

A., and Peyr

e, G. (2019). Interpolating between op-

timal transport and mmd using sinkhorn divergences.

In The 22nd International Conference on Artiﬁcial In-

telligence and Statistics, pages 2681–2690.

Goodfellow, I. J., Shlens, J., and Szegedy, C. (2015). Ex-

plaining and harnessing adversarial examples. In In-

ternational Conference on Learning Representations

(ICLR) 2015.

Johnson, N. F. and Jajodia, S. (1998). Exploring steganog-

raphy: Seeing the unseen. Computer, 31(2):26–34.

Kurakin, A., Goodfellow, I., and Bengio, S. (2016). Ad-

versarial machine learning at scale. arXiv preprint

arXiv:1611.01236.

LeCun, Y., Cortes, C., and Burges, C. (2010). Mnist hand-

written digit database. ATT Labs [Online]. Available:

http://yann.lecun.com/exdb/mnist, 2.

Madry, A., Makelov, A., Schmidt, L., Tsipras, D., and

Vladu, A. (2018). Towards deep learning models re-

sistant to adversarial attacks. In International Confer-

ence on Learning Representations (ICLR) 2018.

Meng, D. and Chen, H. (2017). Magnet: A two-pronged

defense against adversarial examples. In Proceedings

of the 2017 ACM SIGSAC Conference on Computer

and Communications Security, pages 135–147.

Nocedal, J. and Wright, S. (2006). Numerical optimization.

Springer Science & Business Media.

Papernot, N., McDaniel, P., Jha, S., Fredrikson, M., Celik,

Z. B., and Swami, A. (2016). The limitations of deep

learning in adversarial settings. In 2016 IEEE Euro-

pean Symposium on Security and Privacy (EuroS&P),

pages 372–387.

Rauber, J., Zimmermann, R., Bethge, M., and Brendel, W.

(2020). Foolbox Native: Fast adversarial attacks to

benchmark the robustness of machine learning models

in PyTorch, TensorFlow, and JAX. Journal of Open

Source Software, 5(53):2607.

Samangouei, P., Kabkab, M., and Chellappa, R. (2018).

Defense-gan: Protecting classiﬁers against adver-

sarial attacks using generative models. In Inter-

national Conference on Learning Representations

(ICLR) 2018.

Simonyan, K. and Zisserman, A. (2015). Very deep con-

volutional networks for large-scale image recognition.

In International Conference on Learning Representa-

tions (ICLR) 2015.

Song, Y., Shu, R., Kushman, N., and Ermon, S. (2018).

Constructing unrestricted adversarial examples with

generative models. In Advances in Neural Information

Processing Systems, volume 31, pages 8312–8323.

Szegedy, C., Zaremba, W., Sutskever, I., Bruna, J., Erhan,

D., Goodfellow, I., and Fergus, R. (2014). Intriguing

properties of neural networks. In International Con-

ference on Learning Representations (ICLR) 2014.

Tan, M. and Le, Q. V. (2019). Efﬁcientnet: Rethink-

ing model scaling for convolutional neural networks.

In International Conference on Machine Learning,

pages 6105–6114.

Wong, E., Schmidt, F. R., and Kolter, J. Z. (2019). Wasser-

stein adversarial examples via projected sinkhorn it-

erations. In International Conference on Machine

Learning, pages 6808–6817.

Xiao, C., Li, B., yan Zhu, J., He, W., Liu, M., and Song,

D. (2018). Generating adversarial examples with ad-

versarial networks. In Proceedings of the Twenty-

Seventh International Joint Conference on Artiﬁcial

Intelligence, pages 3905–3911.

APPENDIX: ADDITIONAL

RESULTS

This section extends the results from the main

manuscript body. We will always present a ﬁgure and

then compare it with the corresponding ﬁgure from

the manuscript body. The former ﬁgures start with a

letter while the latter ﬁgures with a digit.

Figure 8 shows the untargeted attacks for the non-

robust network. It corresponds to Figure 3 from the

manuscript body. The images are again nice, with the

Wasserstein attack performing better than the l

at-

tack. The small digit in each subﬁgure shows to which

class the digit was misclassiﬁed. As we have already

mentioned, our method always works with feasible

points and, therefore, all digits were successfully mis-

classiﬁed. In other words, these images were gener-

ated randomly without the need for manual selection.

Adversarial Examples by Perturbing High-level Features in Intermediate Decoder Layers

505

Figure 8: Untargeted l

attacks (left) and Wasserstein attacks (right). Rows represent the class. The small number in each

subﬁgure shows to which class the digit was classiﬁed.

Figure 9: Development of perturbed images over iterations. Broccoli features get gradually incorporated into the dog.

Figure 10 shows the attacks on the robust network

of (Madry et al., 2018). It corresponds to Figure 4

from the main manuscript body. The quality of the

CW attack increased. It now preserves the least sig-

niﬁcant bit structure, and the perturbations shifted to-

wards the digit edges. The Wasserstein attack keeps

the superb performance with visually the same results

as in Figure 4. We conclude that our attacks are efﬁ-

cient against adversarially trained networks.

Figure 11 shows the effect of the choices of the in-

termediate layer to perturb and of the initial point for

Algorithm 1. It corresponds to Figure 7 from the main

manuscript body. The ﬁrst column shows the point

which was used to initialize Algorithm 1. The next

three columns present the adversarial images with the

perturbation inserted in different intermediate layers.

The last column shows the original image. The effect

of the initialization is negligible when perturbing the

third intermediate layer (column 4). However, it has

a huge impact when perturbing earlier intermediate

layers. The intermediate latent representation of the

second broccoli (rows 2 and 4) carries a preference

for the white colour, which is visible in the adversar-

ial image for the ﬁrst intermediate layer (column 2).

Figure 9 also shows the effect of the initial point

for Algorithm 1. It corresponds to Figure 6 from the

main manuscript body. We see that the features of the

initial broccoli (column 1) gradually incorporate into

the dog image (columns 2-5). The adversarial image

(column 6) still have some connection to the initial

broccoli, for example, in the background colour. The

adversarial image is close to the original image (col-

umn 7). This ﬁgure shows that our algorithm works

with high-level features and not pixel modiﬁcations.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

506

Figure 10: Comparison of CW and our attacks on the robust network. Least signiﬁcant bit (LSB) is deﬁned in (9), the

difference is between the original and adversarial images.

Figure 11: Effect of the intermediate layer choice. The columns show initial point for Algorithm 1 (column 1), the adversarial

image when perturbations were performed in the ﬁrst (column 2), second (column 3) and third (column 4) intermediate layer

and the original image (column 5).

Adversarial Examples by Perturbing High-level Features in Intermediate Decoder Layers

507