
Stochastic Programming Model for Elective Surgery Planning: An Effect
of Emergency Surgery
Ryota Akiyama, Mari Ito, Ryuta Takashimaand Kinju Hoshino
Department of Industrial Administration Faculty of Science and Technology, Tokyo University of Science,
2641 Yamazaki, Noda, Chiba 278-8510, Japan
Keywords:
Stochastic Programming, Emergency Surgery, Surgery Planning, Operating Room.
Abstract:
This paper introduces a stochastic programming model for a hospital with two surgery types: elective and
emergency surgeries. We propose a model that decides the number of the elective surgeries per day according
to a scheme that makes best use of the operating rooms. Specifically, we model when the demand capacity
for emergency surgery in the operating room of one day is uncertain. We created multiple surgery times, per-
formed random sampling, and conducted numerical experiments. In the results, emergency surgery changed
the allocation of elective surgery. In this paper, we report on the proposed model and numerical results, and
discuss these and the future research prospects.
1 INTRODUCTION
Operating room management is one of the critical fac-
tors in the management of hospitals. It is important
both for achieving high patient treatment quality and
suppressing hospital costs. From the viewpoint of
the treatment quality, a long waiting time for patients
caused by a delay relative to the scheduled end time of
a previous surgery is a serious problem. From an eco-
nomic point of view, about 60% of hospital income
comes from surgery (Jacson et al., 2002). In contrast,
about 40% of expenditure comes from surgery (Mar-
cro et al., 1995). Therefore, hospitals are creating op-
erating room schedules to improve the usage rate of
operating rooms and reduce the cost of surgery.
Surgery can be broadly divided into two types:
elective surgery and emergency surgery. Elective
surgery refers to surgery that is scheduled in advance.
Emergency surgery is not scheduled through discus-
sions between the patient and the doctor. Rather,
emergency surgery becomes necessary suddenly due
to a life-threatening condition in the patient. Emer-
gency surgery treatment must be done on the same
day. Many hospitals use the same operating room
for both elective surgery and emergency surgery. At
Erasmus University Medical Center Rotterdam, the
operating room dedicated to emergency surgery was
closed, so both types of surgery are being performed
in the same operating room (van Veen-Berkx et al.,
2016). The closure was due to a published study that
reported that performing the two different types of
surgery in the same operating room is more efficient.
However, in the case of performing elective surgery
and emergency surgery in the same operating room,
operating room management needs to take into ac-
count the uncertainty of emergency surgery. This is
because not considering the uncertainty of emergency
surgery in operating room management would result
in poor service, such as delays in elective surgery.
Therefore, additional costs may be incurred under this
arrangement, including overtime operating room us-
age, labor costs, and hospitalization costs if carried
forward.
The flow until the schedule is set starts with the
surgeon and patient deciding the date of the elec-
tive surgery by mutual agreement. This surgery date
will also depend on the available reserved capacity
for elective surgery on each day. Since when emer-
gency surgery will occur is uncertain, in order to man-
age elective surgery efficiently, the manager must aim
at the creation of a robust surgery planning schedule
that considers the timing uncertainty associated with
emergency surgery.
In elective surgery planning, costs associated with
overuse of the operating room and costs associated
with performing elective surgery should be mini-
mized. However, few studies have considered the un-
certainty of emergency surgery (Cardoen et al., 2010,
Zhu et al., 2019). If uncertainty is not taken into ac-
count, service degradation such as delayed procedures
can occur, which incurs associated additional costs.
Akiyama, R., Ito, M. and Hoshino, R.
Stochastic Programming Model for Elective Surgery Planning: An Effect of Emergency Surgery.
DOI: 10.5220/0010901800003117
In Proceedings of the 11th International Conference on Operations Research and Enterprise Systems (ICORES 2022), pages 231-235
ISBN: 978-989-758-548-7; ISSN: 2184-4372
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
231

Therefore, surgery planning carries forward overtime
use of the operating room and elective surgery. It
is considered necessary to minimize the costs in-
curred by this. Gerchak et al. (1996) proposed a
dynamic programming model for pre-scheduling pa-
tients with single-period elective surgery. Lamiri et
al. (2006, 2009) suggested considering the uncer-
tainty of emergency surgery demand and proposed
optimization models and algorithms for surgery plan-
ning. Their optimization models use the time of emer-
gency surgery as a random variable generated for each
surgery according to an exponential distribution. We
propose elective surgery plans with multiple planning
periods. However, it is unclear whether the best ap-
proach is to follow Lamiri et al. (2006, 2009) and gen-
erate a probabilistic emergency surgery time and cre-
ate a deterministic schedule. Akiyama et al. (2021)
proposed a probabilistic planning model for schedul-
ing surgery. Comparing the propose model and the
Lamiri model, it can be seen that the proposed model
is superior to the Lamiri model because the amounts
of overtime are shorter.
In this study, we propose a stochastic program-
ming model for elective surgery planning. The ef-
fectiveness of the proposed model was verified by
considering the uncertainty of duration of emergency
surgery, as well as the allocation of elective surgery.
An emergency surgery scenario created using Monte
Carlo sampling was used to analyze how elective
surgery was assigned. Our results were that the
surgery was carried over if the surgical capacity for
a later period was sufficient. The question of whether
the commonly used one-week planning period is cor-
rect was also considered.
The structure of the remainder of the manuscript
is as follows. Section 2 shows the proposed formula-
tion of elective surgery planning. Section 3 describes
the problem setting used for the numerical analysis.
Section 4 presents and discusses the results. Section
5 summarizes the paper and describes future research.
2 THE MODEL
In this section, we introduce proposed formulation of
elective surgery planning under uncertainty in emer-
gency surgery.
2.1 Elective Surgery Planning
The elective surgery planning determines the number
of elective surgeries per day using an uncertain
demand model for emergency surgery. In operating
room scheduling, it is necessary to schedule all
surgeries performed during a given planning period.
In this study, the capacity of all operating rooms
subject to operating room scheduling is available for
surgery. Thus, the total daily capacity of operating
rooms is the same as the time per day that they are
open. The cost carried forward and total capacity are
considered here. We consider overtime, defined as
the amount of time beyond the intended closing time,
of the operating room, but not the penalties for low
operating room usage.
Notation
Index Sets
T : The set of days for scheduling.
I: The set of elective surgery index values.
S: The set of emergency surgery scenarios.
Parameters
p
i
: time needed for performing elective surgery i,
which is assumed to be a given constant.
B
i
: earliest period for performing elective surgery i.
CE
it
: cost ratio of performing elective case i within
day t.
T
t
: total available regular capacity of all ORs on
day t.
CO
t
: cost ratio per unit of overtime on day t.
W
s
t
: capacity needed for emergency surgery on day t.
Variables
O
t
: expected operating room overtime on day t.
Y
it
: probability of allocated elective surgery i on
day t.
X
s
it
: 1 if elective surgery i is to be scheduled in
scenario s on day t; 0 otherwise.
Formulation
Minimize
∑
i∈I
|T |+1
∑
t=B
i
CE
it
Y
it
+
∑
t∈T
CO
t
O
t
(1)
subject to
O
t
= E
s
[(W
s
t
+
∑
i∈I
p
i
X
it
− T
t
)], ∀t ∈ T, (2)
|T |+1
∑
t=1
X
it
= 1, ∀i ∈ I, (3)
X
s
it
= {0, 1}, ∀i ∈ I, ∀t ∈ |T | + 1, ∀s ∈ S, (4)
Y
it
= E
s
[X
s
it
], ∀i ∈ I, ∀t ∈ T, ∀s ∈ S, (5)
Y
it
≥ 0, ∀i ∈ I, ∀t ∈ T. (6)
ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems
232
In the above formulation, the objective function
(1) minimizes carry-forward costs and overtime ac-
ceptance costs. Constraint (2) defines overtime from
the closing time of operating room on day t. Con-
straint (3) guarantees that each elective surgery is al-
located only once. Constraint (4) is a binary con-
straint . Constraint (5) is an equation to find the al-
located distribution of elective surgery. Constraint (6)
represents a non-negativity constraint on Y
it
.
3 ANALYTICAL METHOD
In this study, we conducted numerical experiments
on how elective surgery was assigned for 100 emer-
gency surgery scenarios. The procedure was as fol-
lows. Based on the surgery data of an actual hospital
(Akiyama et al., 2021), we assume five types of elec-
tive surgery and one type of emergency surgery. We
selected the top five types with the largest sample size
from about 9,000 actual surgery data. The time of
each of the five elective surgeries follows a lognormal
distribution, and ten random numbers are generated
for each type of elective surgery to create a total of 50
data. The operation time of emergency surgery is also
lognormal. It is assumed that a normal distribution
is followed, and 10 units are created. In the verifica-
tion of this study, two operating rooms are assumed.
The open time per room is 480 minutes. In addition,
elective surgery is performed every day. It is assumed
that 4 elective surgeries and one emergency surgery
occur every day. The scheduling period is 6 to 8 days.
In the case of 6 days, a total of 24 elective surgeries
will occur and 6 emergency surgeries will occur. For
these 24 elective surgeries, further random sampling
is performed from the created 50 data.
The above data are applied to the proposed model
to determine the optimal number of elective surgery
assignments for each day, considering the uncer-
tainty of emergency surgery. We generate emergency
surgery scenarios by Monte Carlo sampling. The
probability of the occurrence of a scenario follows a
uniform distribution. We assume that a schedule for
emergency surgery will always be accepted. The to-
tal available capacity of the operating rooms here is
about 960 minutes, which is the capacity of the two
operating rooms.
Table 1 shows the expected value and standard
deviation of the surgery duration, and the end time,
Table 1: Duration for elective and emergency surgery [min].
Surgery ID A B C D E Emergency
Expected value 154 177 293 215 235 91
Standard deviation 95 77 78 87 64 79
which is the time when the surgery needs to be com-
pleted.
4 RESULTS AND DISCUSSION
In this study, we performed and analyzed multiple nu-
merical experiments. Here, we mention the analysis
of one of these in detail as an example.
Table 2 shows the elective surgery requests. As
described in Section 3, we assumed in the created
surgical data that randomly occurring elective surgery
was performed. The values in the table are the dura-
tion of each elective surgery in minutes and the letters
in parentheses refer to the surgery ID.
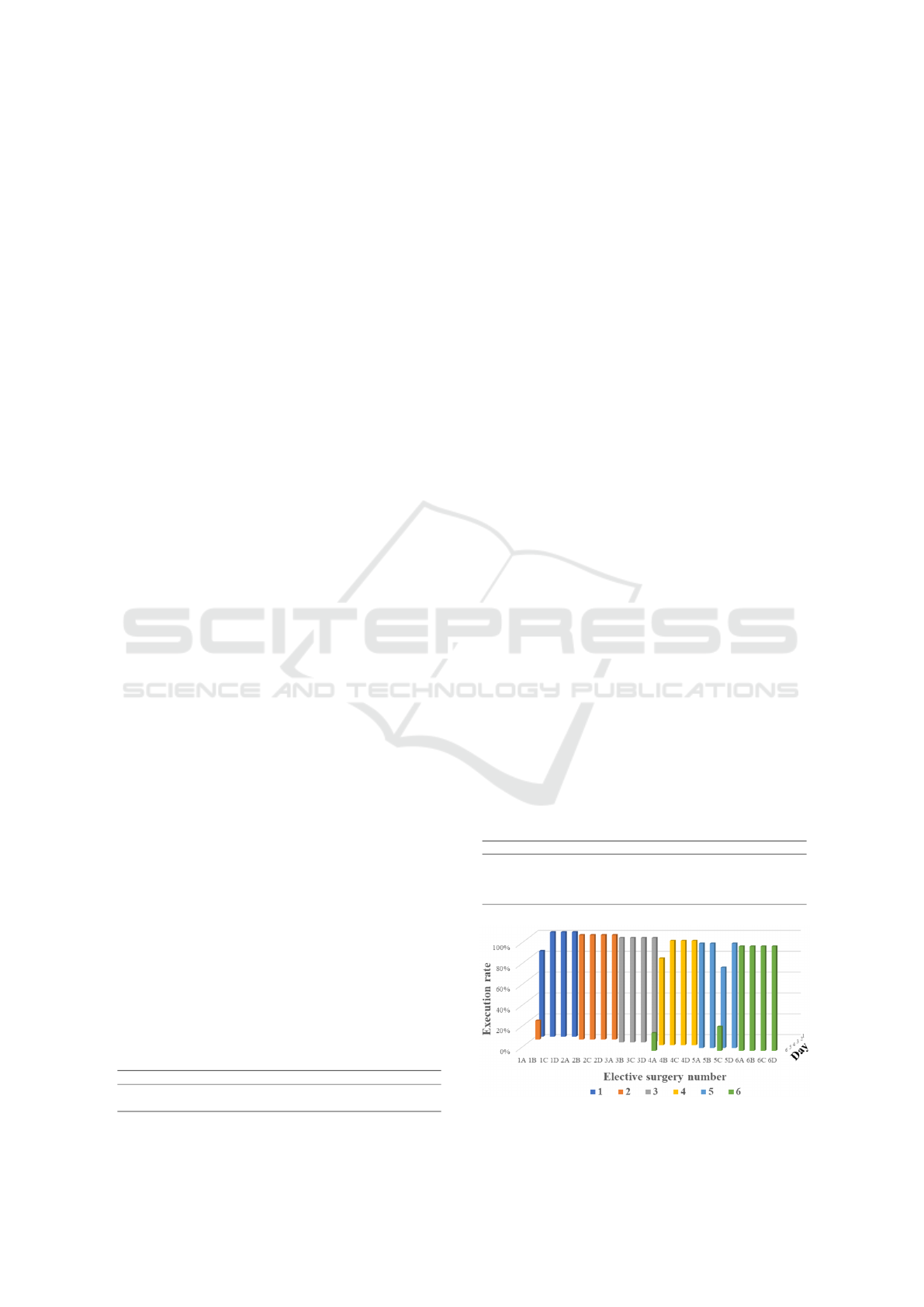
Figures 1–3 show which surgery was carried
over and how frequently among the 100 emergency
surgery scenarios for each day. In the figures 1–3,
the vertical axis gives the execution rate, which is
the ratio of which day the elective surgery was as-
signed among 100 emergency surgery scenarios.The
horizontal axis shows the “elective surgery number”.
The depth axis shows the day. Regarding the surgery
numbers on the horizontal axis, theses represent the
dates, and A to D indicate the four elective surgeries
scheduled for that day. The longer the period, the
more often elective surgery will be carried over. The
results show that this carrying over occurred when
there was unused capacity of the operating room in a
later period. This implies that as a result of extending
the planning period, the number of carry-overs has in-
creased because the number of days with unused sur-
gical capacity has increased. On the other hand, how-
ever, it would be represented that even if the planning
period is extended, overtime will increase if the num-
Table 2: Elective surgery requests: surgery duration
(surgery ID) [min].
Surgery Day 1 Day 2 Day 3 Day 4 Day 5 Day 6
1(Elective) 332(C) 126(B) 383(C) 353(D) 212(B) 33(A)
2(Elective) 309(E) 209(B) 263(B) 212(A) 256(B) 286(B)
3(Elective) 214(C) 269(C) 269(E) 231(B) 277(D) 59(B)
4(Elective) 71(A) 253(E) 253(A) 335(C) 189(A) 404(C)
Figure 1: Execution rate for 6 days.
Stochastic Programming Model for Elective Surgery Planning: An Effect of Emergency Surgery
233

Figure 2: Execution rate for 7 days.
Figure 3: Execution rate for 8 days.
Figure 4: Overtime for 6 days.
ber of days exceeding the surgical capacity increases.
Overtime will also increase if surgical capacity is ex-
ceeded on the last day of the planning period.
Figures 4–6 show overtime as a function of day. In
these figures, the vertical axis shows the time and the
horizontal axis shows the day. In this result, we found
that the length of overtime decreases in proportion to
the length of the period. Operating room capacity for
later days must be available in order to accept elective
surgery.
Most hospitals create operating room schedules
for a period of one week, but the results here indicate
that a longer planning period reduces overtime. This
Figure 5: Overtime for 7 days.
Figure 6: Overtime for 8 days.
raises the question of whether the planning period cur-
rently in use is appropriate. However, although there
is a possibility that overtime can be shortened by ex-
tending the planning period, there is also a overtime
that it will increase. Three cases were carried forward.
We found that the surgery with the longest operation
time was selected among these three cases during the
scheduling period, and that these surgeries could be
significantly delayed if performed on time.
5 CONCLUDING REMARKS
In this study, we developed an elective surgery plan-
ning model for establishing a surgical plan for multi-
period elective surgery considering the uncertainty of
the occurrence of emergency surgery. The proposed
model considers the uncertainty of emergency surgery
by scenario. Considering the uncertainty duration of
emergency surgery for the elective surgery schedul-
ing, the number of elective surgery allocations sched-
uled during the period was determined. In the re-
sults, the elective surgery was assigned to another
day to avoid overtime in the operating room due to
elective surgery during the scheduling period. Cur-
rently, most hospitals create operating room schedules
ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems
234

for one week. However the results here indicate that
a longer planning period reduces overtime. There-
fore, there is room to consider whether one week is
appropriate for the length of the planning period for
scheduling.
As potential future research, the uncertainty in the
number of emergency surgeries should be taken into
consideration. In addition, the operating room capac-
ity of each operating room should be separately con-
sidered, rather than just the total operating room ca-
pacity. Therefore, we would like to extend the pro-
posed model to a model of multiple operating rooms.
We would also like to further examine whether the
appropriate planning period is one week.
ACKNOWLEDGEMENTS
This work was supported by JSPS KAKENHI Grant
Number JP21K14371.
REFERENCES
Akiyama, R., Ito, M., and Takashima, R., Hoshino,
K., Hashimoto, M., Yamamoto, H., Fujii, H. (2021).
Stochastic programming model for elective surgery plan-
ning considering emergency surgery, Informs Healthcare
2021.
Cardoen, B., Demeulemeester, E., Beli
¨
en, J., (2010). Oper-
ating room planning and scheduling: A literature review.
European Journal of Operational Research, 201(3),
921–932.
Gerchak, Y., Gupta, D., and Henig, M. (1996). Reservation
planning for elective surgery under uncertain demand for
emergency surgery. Management Science, 42 (3), 321–
334.
Jackson, R. (2002). The bushiness of surgery. Health Man-
agement Technology, 23(7), 20–22.
Lamiri, M., Xie, X., Dolgui, A., and Grimaud, F. (2006). A
stochastic model for operating room planning with elec-
tive and emergency demand for surgery. European Jour-
nal of Operational Research, 185, 1026–1037.
Lamiri, M., Grimaud F., and Xie, X. (2009). Optimization
methods for a stochastic surgery planning problem. Int.
J. Production Economics, 120, 400–410.
Macario, A., Vitez, T. S., Dunn, B., and McDonald, T.
(1995). Where are the costs in perioperative care?: Anal-
ysis of hospital costs and charges for inpatient surgical
care. Anesthesiology, 83(6), 1138–1144.
van Veen-Berkx, E., Elkhuizen, S.G., Kuijper, B., and
Kazemier, G. (2016). Dedicated operating room for
emergency surgery generates more utilization, less over-
time, and less cancellations. The American Journal of
Surgery, 211(1), 122–128.
Zhu, S., Fan, W., Yang, S., Pei, J., and Pardalos, P.
M. (2019). Operating room planning and surgical case
scheduling: a review of literature. Journal of Combina-
torial Optimization, 37, 757–805.
Stochastic Programming Model for Elective Surgery Planning: An Effect of Emergency Surgery
235
