Towards Model Transformation with Structural Level-spanning Patterns

andor B

acsi

and Gergely Mezei

Department of Automation and Applied Informatics, Budapest University of Technology and Economics,

Muegyetem rkp. 3., Budapest, Hungary

Keywords:

Multi-level Modeling, Multi-layer Modeling, Multi-level Transformation, Model-driven Engineering, MDE,

Deep Instantiation, DMLA, Level-blind.

Abstract:

In MDE, models are meant to be transformed, thus model transformation is one of the basic pillars of MDE.

Besides generating source code, transformation is often used to refactor or optimize the models. While the the-

ory and application of graph transformations are active research ﬁelds for many years now, existing approaches

focus mainly on classic two-level meta-modeling setups. It is a promising research direction however to use

graph pattern-based transformations on multi-level models as well. This position paper proposes a textual

model transformation language — the DMLA Transformation Language (DTL) — which enables the deﬁni-

tion of level-spanning transformation rules in a level-blind multi-layer environment.

1 INTRODUCTION

Model transformations are one of the key pillars of

model-driven engineering (MDE) (Sendall and Koza-

czynski, 2003) and are key to the productivity and

ﬂexibility that make model-driven development so at-

tractive. This is reﬂected in the rapidly growing inter-

est in model transformations in academia and the in-

creasing sophistication of the transformation capabil-

ities offered by leading modeling environments, such

as the Eclipse Modeling Framework (EMF) (Stein-

berg et al., 2009). While the theory and application

of model transformations are active research ﬁelds

for decades, the most contemporary model transfor-

mation technologies suffer from the same fundamen-

tal weakness as the modeling languages are based on

the restriction to a two-level modeling architecture

that accommodates only one pair of classiﬁcation lev-

els, the meta-model (types) and model (instances).

This makes it difﬁcult for models, and transforma-

tion languages building on them, to handle scenarios

when there are more than just two classiﬁcation levels

in a domain of interest without introducing the phe-

nomenon, called accidental complexity (Atkinson and

uhne, 2008) into models and thus transformations.

Over the last few years, a paradigm for model

organization has emerged that supports an arbitrary

number of modeling levels, called multi-level mod-

https://orcid.org/0000-0002-4814-6979

https://orcid.org/0000-0001-9464-7128

eling (Atkinson and K

uhne, 2001). Multi-level

modeling aims to solve the shortcomings of classic

(meta-)modeling approaches such as OMG’s four-

level Meta-Object Facility (MOF) (MOF, 2005).

Multi-level modeling allows for an unlimited

number of instantiation levels as opposed to the four

levels prescribed by OMG. One of the main goals of

multi-level modeling is to reduce accidental complex-

ity, which refers to parts of the solution needed only

to express its multi-level nature, instead of describing

the domain in question (Atkinson and K

uhne, 2008).

A good example of this is the application of the Item

Description (Coad, 1992) pattern to describe multi-

ple domain levels in object-oriented languages. The

main idea behind the pattern is that objects play the

role of classes, and as such, type-related information

can be encoded in them. This means that classiﬁca-

tion is replaced by association, which — in addition

to objects representing class information — leads to

accidental complexity. Compared to classic model-

ing approaches, multi-level models are often reduced

in size, are more compact, and describe the target

domain more accurately. Therefore, many domains

can beneﬁt from multi-level modeling. In recent

years, several research groups have developed proto-

type realizations and applications of multi-level mod-

eling environments, for example Melanee (Atkinson

and Gerbig, 2016), MetaDepth (de Lara and Guerra,

2010), MultEcore (Mac

ıas et al., 2018) or XModeler

(Frank, 2014).

352

Bácsi, S. and Mezei, G.

Towards Model Transformation with Structural Level-spanning Patterns.

DOI: 10.5220/0010918800003119

In Proceedings of the 10th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2022), pages 352-357

ISBN: 978-989-758-550-0; ISSN: 2184-4348

There exist many efﬁcient methodologies to ﬁnd

and replace patterns in classic meta-models, but these

methodologies suppose that all elements of the pattern

are on the same abstraction level. It is a promising

direction to use graph pattern-based transformations

on multi-level models as well. Our research aims at

this goal: creating an approach that supports model

transformation consisting of level-spanning patterns.

These patterns could capture domain concepts across

multiple abstraction levels, where the elements can

refer to each other independently of their abstraction

level. A typical modeling scenario for this is when

we have a domain concept containing several compo-

nents, some of which are concrete, while others are

more abstract, i.e. not yet speciﬁed completely.

In this position paper, we propose a model trans-

formation language — DMLA Transformation Lan-

guage (DTL) — which can capture level-spanning do-

main concepts in a multi-layer context and supports

model-to-model (M2M) transformations in our multi-

layer modeling framework, the Dynamic Multi-Layer

Algebra (DMLA) (Urb

an et al., 2018; Urb

an et al.,

2017). The feasibility of the language is demonstrated

by the manipulation of concrete domain models.

The structure of the paper is as follows. Section 2

is dedicated to discuss the related work showing how

other multi-level approaches support model transfor-

mation, while Section 3 describes the basics of our

multi-layer framework, DMLA. In Section 4 we elab-

orate on our motivation and compare multi-layer and

classic two-level model transformations in general.

Section 5 contains our contribution, where we present

DTL using illustrative examples. Concluding remarks

are outlined in Section 6.

2 RELATED WORK

The theory and practise of graph transformations are

well-studied, and the concept of model transforma-

tions applied to multi-level modeling is not novel.

Earlier works in the area have extended existing

model transformation languages to be able to manip-

ulate multi-level models and model hierarchies.

An important concern when discussing multi-level

approaches is the basis upon how they handle levels

(Atkinson et al., 2014). Approaches that acknowledge

the existence of explicit modeling levels are often re-

ferred to as level-adjuvant. Similar yet highly differ-

ent approaches have also emerged in the form of level-

blind approaches, which do not acknowledge explicit

instantiation levels, although they can still implic-

itly implement the concept of levels. To date, trans-

formations between multi-level models represented

using level-blind frameworks have barely been ex-

plored. Previous works have exclusively focused on

level-adjuvant model transformation methodologies

that enforce “strict metamodeling” principles (Atkin-

son, 1997). In (Atkinson et al., 2013), the authors

adapt ATL (Jouault et al., 2008) to manipulate multi-

level models built with the level-adjuvant Melanee

tool (Atkinson and Gerbig, 2016). In a similar man-

ner, (Lara et al., 2013) proposes the adaptation of ETL

(Kolovos et al., 2008) and other languages from the

Epsilon family for the application of model transfor-

mation rules into multi-level hierarchies created with

MetaDepth (de Lara and Guerra, 2010). A much more

formal approach can be found in (Wolter et al., 2020).

The authors represent multi-level models by multi-

level typed graphs whose manipulation and transfor-

mation are carried out by multi-level typed graph

transformation rules.

As opposed to the aforementioned level-adjuvant

approaches, our multi-layer approach, DMLA can

be considered level-blind since levels are not explic-

itly modeled. To our knowledge, no prior studies

have examined applying model transformation in a

level-blind environment. This position paper pro-

poses a textual model transformation language — the

DMLA Transformation Language (DTL) — which

enables the simple deﬁnition of transformation rules

in a level-blind environment.

3 DMLA

The main goal of Dynamic Multi-Layer Algebra

(DMLA) (Urb

an et al., 2018; Urb

an et al., 2017) is

to offer an environment in which one can model con-

cepts, connect these concepts and then reﬁne them

step-by-step following a top-down method. DMLA

aims to provide a high-level of ﬂexibility, but at the

same time a rigorous validation mechanism during re-

ﬁnement. Typically, one initially only has a vague

conceptualization of the domain concepts and only

gradually obtains a more concrete understanding of

them. Modeling in DMLA aims to follow and aid this

process by providing a multi-layer modeling environ-

ment.

In DMLA, the main relationship between ele-

ments at different levels of abstraction is “reﬁnement”

which is used to gradually constrain concepts. Please

note that reﬁnement in DMLA is special in nature,

its semantics is completely different from the classi-

cal object-oriented “specialization” or “instantiation”

relations. Reﬁnement relates a DMLA entity to its

“meta” and the framework automatically validates if

there is indeed a valid reﬁnement relationship be-

Towards Model Transformation with Structural Level-spanning Patterns

353

tween the two entities. Note that while each en-

tity has a meta-entity, DMLA is a “level-blind” ap-

proach (Atkinson et al., 2014) since levels are not ex-

plicitly modeled. DMLA does not use a global level

organisation that requires reﬁnement relationships to

align with each other in any way. Each modeled entity

can refer to any other entity along the meta-hierarchy,

as long as the validation rules are not violated.

Modeling entities, which have an internal struc-

ture, describe their setup by slots. The slots of an en-

tity set up its structure, for example a Bicycle has a

Wheels slot containing a list of references to Wheels.

At the topmost abstraction level, one does not usually

have much information about the exact structure and

the details of an entity, therefore slots are used merely

as placeholders. Further down one can reﬁne the en-

tity: add new slots, reﬁne slots or omit them. Only

optional slots (slots with cardinality 0..n) can be omit-

ted from an entity. Each of these decisions are vali-

dated against the validation formulae and constraints

describing the reﬁnement rules of the entity.

Validation formulae can be attached to any entity

and since slots themselves are also modeled as enti-

ties, to any slots as well. These formulae may cus-

tomize the reﬁnement rules of the given entity. The

formulae are speciﬁed as DMLA operations using the

built-in operation language. The operation language

is also completely modeled.

A constraint deﬁnes a reusable validation mech-

anism (e.g. type conformance check) attachable to

slots. Reﬁnement of slots is usually driven by adding

new constraints and further down narrowing existing

ones, thus restricting the structure and/or the behav-

ior of the slot. DMLA offers built-in constraints for

re-occuring tasks and allows creating universal, or

domain-speciﬁc constraints in a ﬂexible way. The two

most important built-in constraints kinds are: i) type

constraint restricting the type of the values to be put

in the slot (e.g. when ﬁlling the slot Frame in en-

tity RaceBike, one can only use reﬁnements of Race-

Frame entity there), and the ii) cardinality constraint

prescribing the allowed number of reﬁnements within

a given slot (e.g. Conﬁguration may have zero-to-

many Components).

Although the basic, built-in entities are not de-

tailed in this paper, one of them, ComplexEntity,

should be mentioned since it acts as a base entity for

domain modeling. It has a slot called Fields. The car-

dinality of the slot Fields allows any number of reﬁne-

ments (0..*) of any practically available type. Since

all slots in DMLA must have a meta, it is not possible

to add new features to an entity, unless the meta-entity

has an appropriate meta-slot. The Fields slot allows

one to extend entities with new slots. By omitting the

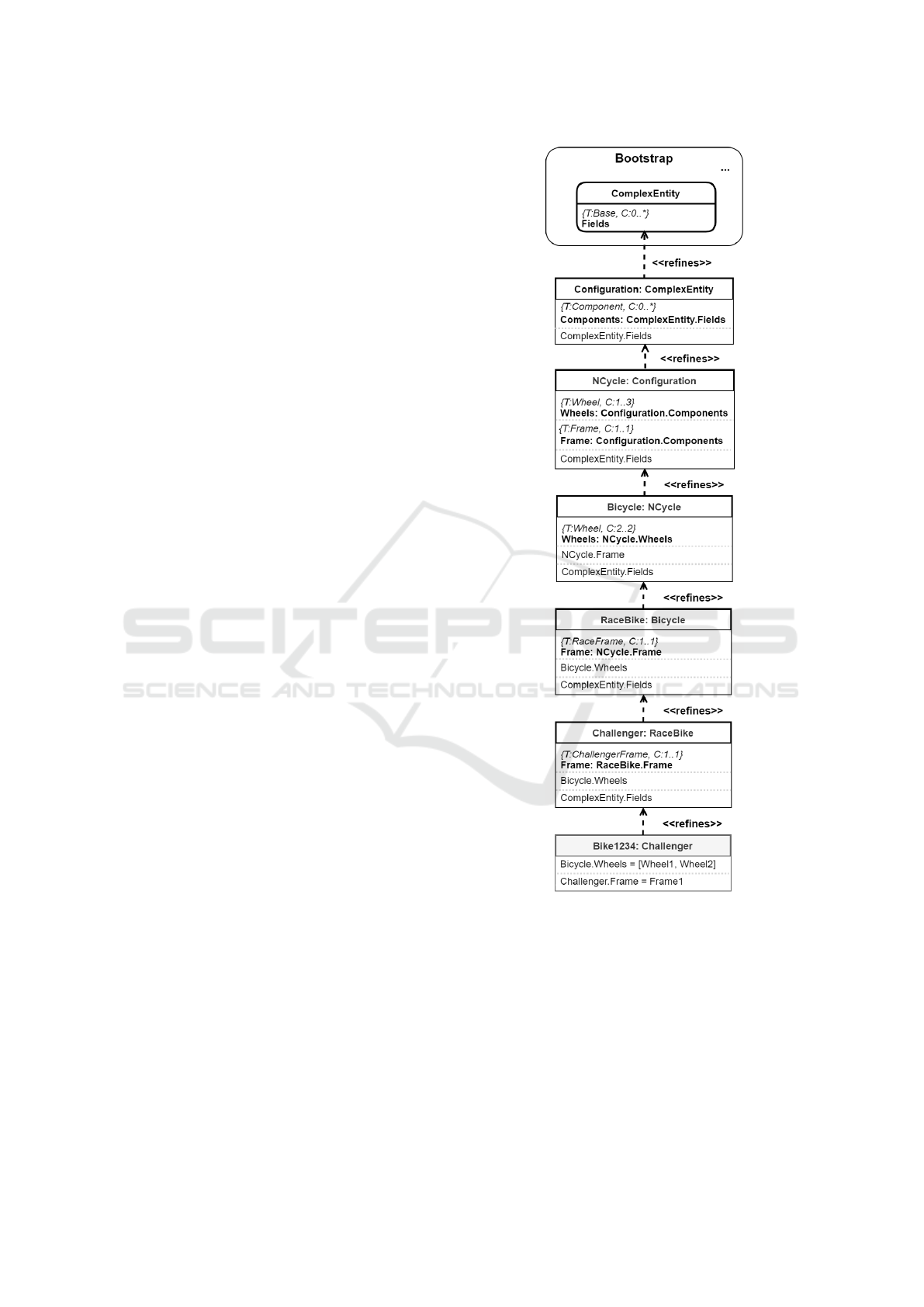
Figure 1: DMLA model fragment.

slot, reﬁnements can deny the ability to introduce any

further slots.

Figure 1 shows a DMLA model fragment (an ex-

ample reﬁnement chain), depicting entities as boxes.

This model fragment is also used in Section 4 and 5

to illustrate our level-spanning model transformation

concepts. ComplexEntity is represented by a rounded

rectangle indicating that it is not part of the domain

model, while concrete objects are differentiated from

more abstract entities by their gray color. The reﬁne-

ment relationship between the entities are denoted by

MODELSWARD 2022 - 10th International Conference on Model-Driven Engineering and Software Development

354

dashed arrows with “reﬁnes” stereotypes. For exam-

ple, RaceBike is a reﬁnement of Bicycle.

The slots are shown embedded into entities simi-

larly to attributes of a class in UML class diagrams.

Attributes pointing to another entity are modeled by

slots and therefore visualized embedded in the box,

not as associations between the entities. Meta-slot

relationships are represented by Slot: MetaSlot la-

bels. In DMLA, slots can be explicitly kept (cloned)

or omitted. Whenever a new slot is introduced, it is

shown in bold (e.g. introducing slot Wheels in NCy-

cle). Constraints of slots are denoted above the cor-

responding slot in curly brackets with T: (type con-

straint) and C: (cardinality constraint).

The entry point of domain deﬁnition is the Com-

plexEntity. ComplexEntity uses a different notation

(rounded rectangle) compared to other entities, as it

is not part of the domain deﬁnition. This reﬁnement

chain in the model exempliﬁes a key feature of the

underlying DMLA: step-wise reﬁnement. One starts

from a highly abstract entity and reﬁnes it step-by-

step until a fully concretized object is eventually ob-

tained. For example, RaceBike references supported

frame type via a slot (Frame). When reﬁning Race-

Bike and creating the Challenger entity, the type con-

straints applied on slot Frame are narrowed so that the

slot can contain only reﬁnements of the Challenger-

Frame entity. Type constraints automatically ensure

that the concretization is always consistent whenever

the validation succeeds, thus there is no need to deﬁne

additional constraints.

4 MOTIVATION

In the scope of mainstream two-level modeling,

Model2Model transformation aims to provide a mean

to specify the way to produce target models from a

number of source models. For this purpose, it should

enable developers to deﬁne the way source model ele-

ments must be matched and navigated in order to ini-

tialize the target model elements. Formally, a simple

model transformation has to deﬁne the way for gener-

ating a model M

, conforming to a meta-model MM

from a model M

conforming to a meta-model MM

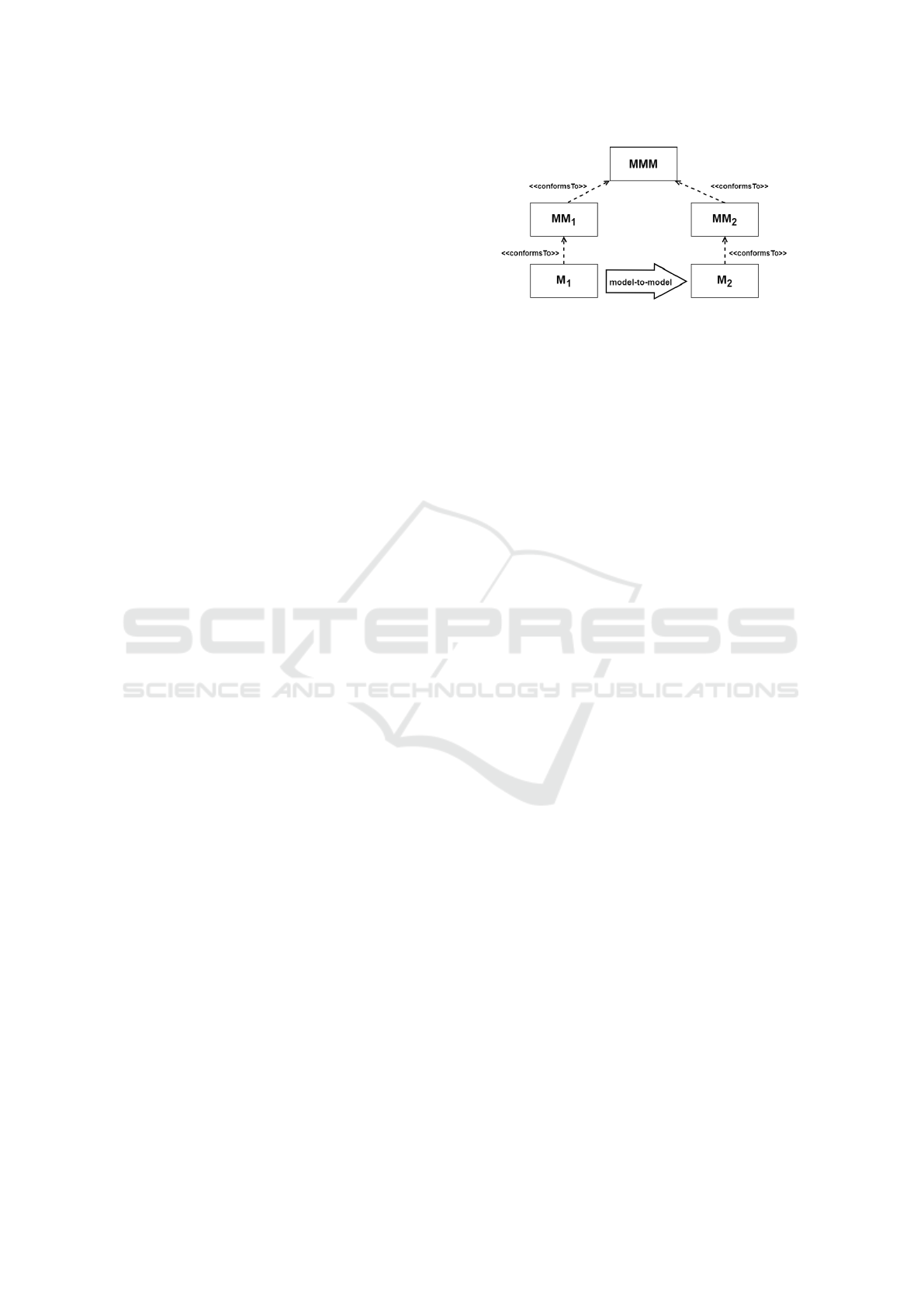
Figure 2 summarizes a typical model transfor-

mation process in a standard modeling scenario. A

model M

, conforming to a meta-model MM

, is

transformed into a model M

that conforms to a meta-

model MM

. The transformation is deﬁned by a

model transformation language (such as ATL (Jouault

et al., 2008) or ETL (Kolovos et al., 2008)) that en-

ables to specify how one (or more) target model can

be produced from a set of source model. The MM

Figure 2: Classic model transformation approach.

and MM

meta-models, has to conform to a meta-

meta-model MMM (such as Ecore).

In the multi-layer setup of DMLA, however, it

cannot be presumed that all elements of the model

transformation pattern are on the same abstraction

level, like the modeling elements of M

and M

, be-

cause there can be more than two meta-levels at a

time and meta-levels can also inﬂuence other levels

beyond the immediate one. For example, in the reﬁne-

ment chain of ﬁgure 1 Conﬁguration is reﬁned ﬁve

times before it reaches its fully concretized state as

Bike1234 and the contained slots gain more and more

concrete information as we getting more and more

concrete along the reﬁnement chain. Moreover, in

early phases of modeling at higher abstraction levels

one may not know the concrete name and the structure

of the modeling elements of lower levels for which

the transformation rule should be formulated. For ex-

ample, if one may want to formulate a transforma-

tion rule at the level of Conﬁguration, extra conditions

need to be added in order to match the desired source

model elements at lower levels.

In the next section, we introduce our work-in-

progress transformation language which can be an

ideal candidate to capture level-spanning model ele-

ments in transformation rules across multiple abstrac-

tion levels.

5 THE TRANSFORMATION

LANGUAGE

By designing DMLA Transformation Language

(DTL), our primary goal is to provide a ﬂexible and

concise way for the model-to-model transformation

of level-blind multi-layer models in DMLA. DTL is

very similar to ATL (Jouault et al., 2008) in that

in both languages transformation code is composed

of rules that deﬁne how source model elements are

matched and navigated to create and initialize the ele-

ments of the target models. Each transformation rule

contains a unique name. It is introduced by the key-

word rule that is followed by the rule’s name. Its logic

Towards Model Transformation with Structural Level-spanning Patterns

355

is surrounded by curly brackets. In the source pattern

(from part), rules declare which element type of the

source model has to be transformed, while in the tar-

get pattern (the to part), rules declare to which ele-

ment(s) of the target model the source pattern has to

be transformed to. The implementation of the target

pattern declares the details of the transformation.

DTL is a hybrid of declarative and imperative

style. The basic style of transformation writing is

declarative, which means mappings and matching

rules can be easily expressed in the source pattern.

However, imperative constructs are provided in the

target pattern so that basic operations like add and

delete can also be expressed.

One of the most important features of DTL is that

it allows to customize the level-spanning model el-

ements to search in the reﬁnement chain. For each

model element (entity, slot, constraint) one can spec-

ify additional conditions to restrict what is included

in the source model. It also possible to specify the

searching strategy for reﬁnements: (i) inclusive tran-

sitive reﬁnements with :| operator, (ii) exclusive tran-

sitive reﬁnements with :ˆ operator and (iii) direct re-

ﬁnement with : operator. The term “inclusive tran-

sitive reﬁnements” covers the matching modeling el-

ement and all of its reﬁnements, while the term “ex-

clusive transitive reﬁnements” excludes the matching

modeling element and only transitive reﬁnements are

included. “Direct reﬁnement” refers to the immediate

reﬁnement of the matching modeling element.

In the following, we explain some of the features

of DTL through practical transformation rules formu-

lated for the domain model of Figure 1. For the sake

of clarity, we have slightly simpliﬁed the model frag-

ment of Figure 1, thus only those parts of the enti-

ties are displayed that are necessary to illustrate the

mechanisms of DTL. We use ﬁctional requirements to

which we formulate transformation rules in order the

modify and refactor the original DMLA model frag-

ment.

REQ1: Each bicycle model has a regular sales

price.

Listing 1 depicts the transformation rule for

adding the Price slot to the inclusive reﬁnements of

Bicycle entity. The slot is originated from Complex-

Entity.Fields, it has a Number type and zero-to-one

cardinality . Price slot is added with an imperative

statement in the target pattern. Note that is also pos-

sible to specify identiﬁers for the matching elements

in the source pattern, e.g. identiﬁer bicycle s refers to

the matching inclusive reﬁnements of Bicycle entity.

rule AddPriceSlot

{

from {

entity bicycle _ s :| B i cycle {}

}

to {

@Type: N umber

@Cardinality: 0..1

new slot P r ice : ComplexEntity .

Fiel d s ;

add P r ice to b i c ycle_s ;

}

Listing 1: Add Price slot to Bicycle.

REQ2: The introduction of new features is no

longer allowed in Bicycle reﬁnements.

According to this requirement, we should deny the

introduction of new features by omitting Complex-

Entity.Fields and its direct slots. By omitting these

slots, reﬁnements deny the ability to introduce any

further slots. Note that we also formulate additional

conditions for the matching slot: only slots that have

Base as their type constraint will be matched. Listing

2 depicts the transformation rule for deleting direct

Fields elements from inclusive transitive Bicycle re-

ﬁnements.

rule D e l e t e D i r e c t F ie l d sE l e me n t s

{

from {

entity bicycle _ s :| B i cycle

{

slot matchingSlot :

ComplexEntity . F ield s {

constraint t1 :| T y p e C o n s t r a i n t

{ slot . Typ e = B ase }

}}}

to { delete b i c y c l e_s . m a t c h i n g S l o t ; }

}

Listing 2: Delete direct Fields elements.

REQ3: Race bike models are no longer sup-

ported. From now on, Challengers can be considered

Bicycle models.

Listing 3 depicts the transformation rule for

changing the meta of Challenger to Bicycle. We

search challenger as the direct reﬁnement of Race-

Bike and bicycle as the direct reﬁnement of Conﬁgu-

ration. Then, meta of challenger is set to bicycle.

rule M o d i f y M e t a O f C h a l l e n g e r

{

from {

entity challeng e r : R a c eBike {}

entity bicy c l e : C o n f iguration {}

}

to { c h allenger .meta = b i c ycle ; }

}

Listing 3: Change meta of Challenger.

MODELSWARD 2022 - 10th International Conference on Model-Driven Engineering and Software Development

356

6 CONCLUSIONS

In this paper, we presented DTL, our work-in-

progress multi-layer transformation language, high-

lighting its features regarding capturing level-

spanning model elements. Although the paper fo-

cused on the level-blind setup provided by DMLA,

we believe that our experiences and conclusions are

worthy of general discussion. Even though the DTL

language is in explanatory phase, we have presented

simpliﬁed transformation rules to illustrate the fore-

seen language mechanisms. Currently, we are de-

veloping an ANTLR-based implementation of DTL

and also working on more complex case studies in

order to demonstrate the feasibility of our level-

spanning transformation approach. From a techno-

logical perspective, the signiﬁcance of our research

lies in the usage of a modeling language which is

based on a reﬁnement relation and not on the classi-

cal object-oriented specialization or instantiation rela-

tions. Thus,DTL can capture domain concepts across

multiple abstraction levels, where the elements can

refer to each other independently of their abstraction

level. We believe that apart from the technological

concepts of DTL, future research should certainly fur-

ther examine whether DMLA models could be for-

mally represented by multi-level typed graphs, whose

manipulation and transformation could be carried out

by multi-level typed graph transformation rules.

ACKNOWLEDGEMENT

The work presented in this paper has been carried

out in the frame of project no. 2019-1.1.1-PIACI-

KFI-2019-00263, which has been implemented with

the support provided from the National Research, De-

velopment and Innovation Fund of Hungary, ﬁnanced

under the 2019-1.1. funding scheme.

REFERENCES

Atkinson, C. (1997). Meta-modeling for distributed object

environments. In Enterprise Distributed Object Com-

puting, pages 90–101. IEEE.

Atkinson, C. and Gerbig, R. (2016). Flexible deep mod-

eling with melanee. In Modellierung 2016 - Work-

shopband : Tagung vom 02. M

arz - 04. M

arz 2016

Karlsruhe, MOD 2016, volume 255, pages 117–121,

Bonn. K

ollen.

Atkinson, C., Gerbig, R., and K

uhne, T. (2014). Comparing

multi-level modeling approaches. In CEUR Workshop

Proceedings, volume 1286.

Atkinson, C., Gerbig, R., and Tunjic, C. (2013). Enhanc-

ing classic transformation languages to support multi-

level modeling. Software and Systems Modeling, 14.

Atkinson, C. and K

uhne, T. (2001). The essence of multi-

level metamodeling. In Proceedings of the 4th Inter-

national Conference on The Uniﬁed Modeling Lan-

guage, Modeling Languages, Concepts, and Tools,

pages 19–33, Berlin, Heidelberg. Springer-Verlag.

Atkinson, C. and K

uhne, T. (2008). Reducing accidental

complexity in domain models. Software & Systems

Modeling, 7(3):345–359.

Coad, P. (1992). Object-oriented patterns. Communications

of the ACM, 35(9):152–159.

de Lara, J. and Guerra, E. (2010). Deep meta-modelling

with metadepth. In Objects, Models, Components,

Patterns, pages 1–20, Berlin, Heidelberg. Springer

Berlin Heidelberg.

Frank, U. (2014). Multilevel modeling: Toward a new

paradigm of conceptual modeling and information

systems design. Business & Information Systems En-

gineering, 6(6):319–337.

Jouault, F., Allilaire, F., B

ezivin, J., and Kurtev, I. (2008).

Atl: A model transformation tool. Science of Com-

puter Programming, 72(1):31–39. Special Issue on

Second issue of experimental software and toolkits

(EST).

Kolovos, D. S., Paige, R. F., and Polack, F. A. C. (2008).

The epsilon transformation language. In Vallecillo,

A., Gray, J., and Pierantonio, A., editors, Theory

and Practice of Model Transformations, pages 46–60,

Berlin, Heidelberg. Springer Berlin Heidelberg.

Lara, J., Guerra, E., and S

anchez Cuadrado, J. (2013).

Model-driven engineering with domain-speciﬁc meta-

modelling languages. Software and Systems Model-

ing, 14.

Mac

ıas, F., Rutle, A., Stolz, V., Rodr

ıguez-Echeverr

ıa, R.,

and Wolter, U. (2018). An approach to ﬂexible mul-

tilevel modelling. Enterprise Modelling and Informa-

tion Systems Architectures, 13:10:1–10:35.

MOF (2005). OMG: MetaObject Facility.

http://www.omg.org/mof/. Accessed:2020-03-10.

Sendall, S. and Kozaczynski, W. (2003). Model transfor-

mation: The heart and soul of model-driven software

development. IEEE Softw., 20:42–45.

Steinberg, D., Budinsky, F., Paternostro, M., and Merks,

E. (2009). EMF: Eclipse Modeling Framework 2.0.

Addison-Wesley Professional, 2nd edition.

Urb

an, D., Mezei, G., and Theisz, Z. (2017). Formalism

for static aspects of dynamic metamodeling. Peri-

odica Polytechnica Electrical Engineering and Com-

puter Science, 61(1):34–47.

Urb

an, D., Theisz, Z., and Mezei, G. (2018). Self-

describing operations for multi-level meta-modeling.

In Proceedings of the 6th International Conference

on Model-Driven Engineering and Software Develop-

ment - Volume 1: MODELSWARD,, pages 519–527.

INSTICC, SciTePress.

Wolter, U., Mac

ıas, F., and Rutle, A. (2020). Multilevel

typed graph transformations. pages 163–182. Springer

International Publishing.

Towards Model Transformation with Structural Level-spanning Patterns

357