Understanding Summaries: Modelling Evaluation in Extractive

Summarisation Techniques

Victor Margallo

PublicSonar, Zuid Hollandlaan 7, The Hague, The Netherlands

Keywords:

NLP, Extractive Summarisation, Evaluation, Summary Quality Modelling.

Abstract:

In the task of providing extracted summaries, the assessment of quality evaluation has been traditionally tack-

led with n-gram, word sequences, and word pairs overlapping metrics with human annotated summaries for

theoretical benchmarking. This approach does not provide an end solution for extractive summarising algo-

rithms as output summaries are not evaluated for new texts. Our solution proposes the expansion of a graph

extraction method together with an understanding layer before delivering the ﬁnal summary. With this tech-

nique we strive to achieve a categorisation of acceptable output summaries. Our understanding layer judges

correct summaries with 91% accuracy and is in line with experts’ labelling providing a strong inter-rater reli-

ability (0.73 Kappa statistic).

1 INTRODUCTION

One of the multiple applications of Natural Language

Processing is summarisation. The goal of such a task

is to extract or generate a shorter version of the origi-

nal text. There are two approaches for summarisation;

the ﬁrst one is extractive and the second one is gener-

ative.

Extractive summarisation makes use of literal sen-

tences or keywords from the original text ranking

them with an importance metric. On the other hand,

generative models rely predominantly on Deep Learn-

ing techniques that decode the original text into a

shorter version, mimicking human summaries shown

in the training phase. Even though the latter strikes

to yield a more human-like synthesis, extractive sum-

marisation is unsupervised and the only technique ap-

plicable when dealing with no training datasets. Due

to the lack of availability in summarisation datasets

for minor languages, extractive methods are still of

great relevance and the main driver for this research

in the Dutch language.

Methods to address evaluation of summarising

output are limited to overlapping metrics based on n-

gram, word sequences, and word pairs ratios. These

metrics described in methods as ROUGE (Lin, 2004)

present drawbacks such as the ambiguity of the

ground truth depending on the annotators and the lack

https://orcid.org/0000-0002-5765-6671

of evaluation on newly summarised text. Even though

evaluation on new text is not a concerning issue in

theoretical research of the model—as it is evaluated

against a predeﬁned ground truth—it becomes criti-

cal in a real world usage of the algorithm since it is

to be executed on new text with no manual annota-

tion for its quality evaluation. More recent research,

as in Wu et al. (2020), includes advanced text embed-

ding comparisons in order to provide a score, also in

new summaries. Yet, it is not deﬁning a line regard-

ing quality acceptability. Hence, a gap between the

research usage and the practical usage of summaris-

ing algorithms exists. As a result of a missing qual-

ity check, extractive algorithms can deliver unsuitable

summaries for human end-readers, drawing the pur-

pose of a summarising technique—this is, shortening

input text into an output text that is concise, readable

and understandable—away.

We propose an integration of a graph model to-

gether with a layer replicating the understanding crite-

ria for a readable and correct summary. This pipeline

provides the summary, ﬁrstly created by the graph

model, as long as the understanding layer conﬁrms

it is readable. We achieve 91% accuracy in this task.

Plus, the results show the algorithm to be in consistent

agreement with the variability of the human assess-

ment concerning summary output quality, measured

with an inter-rater reliability Kappa value of 0.73.

The paper follows with Section 2 introducing re-

lated work in the ﬁeld, focusing on the nature of ex-

Margallo, V.

Understanding Summaries: Modelling Evaluation in Extractive Summarisation Techniques.

DOI: 10.5220/0010954300003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 2, pages 605-611

ISBN: 978-989-758-547-0; ISSN: 2184-433X

605

tractive summarising algorithms and the main model

evaluation method ROUGE; Section 3 describes the

data used in this research together with the criteria

established for the deﬁnition of a good quality sum-

mary, the algorithmic architecture for the solution—

from the graph model to the developed understanding

layer and its optimization—and the construction of in-

put features from source text and output text that feed

the understanding layer; ﬁnally, Section 4 and Sec-

tion 5 show the results of the research and end it with

a conclusion and future work.

2 RELATED WORK

Extractive summarisation sets its foundations on

graph-based ranking algorithms such as PageRank

(Brin and Page, 1998) and HITS (Kleinberg, 1999).

These algorithms were successfully applied to cita-

tion analysis, link-network of webpages and social

networks. The translation of these approaches to nat-

ural language tasks rendered algorithms as TextRank

(Mihalcea and Tarau, 2004) and progressive reﬁne-

ments as in Barrios et al. (2016).

Graph-based methods utilize the holistic knowl-

edge of the text of interest in order to make local rank-

ing of sentences or words. With a structured ranking

of sentences the algorithm selects a reduced version

of the original text containing a presupposed high rel-

evancy.

The TextRank method uses the importance of ver-

tex connections to create a ﬁnal score. To formalize,

given that G = (N, E) is a directed graph with nodes

N and edges E. Edges are connections between nodes

and thus, a NxN subset. For a N

node, TextRank sets

In(N

) as predecessor nodes pointing at the current N

node and Out(N

) as the nodes it points out to. The

score of N

is deﬁned as:

S(N

) = (1 −d) +d ∗

∑

j∈In(N

)



Out(N

)



S(N

) (1)

Where d represents a damping factor to account

for the random surfer model probability Brin and

Page (1998). However, sentence units in natural text

relate to each other with similarity scores. TextRank

reshapes (1) so that a W factor captures it:

W S(N

) = (1−d)+d ∗

∑

∈In(N

)

∑

∈Out(N

)

W S(N

)

(2)

The score of sentences and therefore the weights

of the edges between sentences is given by the overlap

described as:

Similarity(S

) =



∈ S

}



log(

) + log(|S

(3)

Where S

and S

are composed of tokens S

,...,w

that represent processed words. The re-

sulting most signiﬁcant sentences—those with high-

est ranks—form the ﬁnal summary representation.

In the succession of research in this ﬁeld, most ef-

fort was focused on improving a key component of the

algorithm—the similarity score. Barrios et al. (2016)

show how the use of cosine distance with TF-IDF and

BM25 improve the quality of the results. Yet, one

of the drawbacks of TextRank algorithms is their dis-

ability to address the suitability of incoming natural

text. Consequently, it always produces an output re-

gardless of what input text is given. This results into

poor quality and low readability summaries for some

texts as it is illustrated in Figure 1.

Concerning the evaluation of the output, Mihal-

cea and Tarau (2004) appraise their method using the

ROUGE technique. Lin (2004) presents ROUGE as a

solution to the expensive and difﬁcult process of hu-

man judgement on evaluating the different factors of

a resulting summary. ROUGE employs a set of refer-

ence summaries extracted by humans. The algorith-

mic solutions are then compared to the human ones

by means of co-occurrence statistics. The problem

with this approach is that we assume the reference

summary as the ground truth. However, there may

be several combinations which provide a good quality

summary that still do not match the human’s approach

(Mani, 2001). Therefore, even though ROUGE-like

metrics deliver a reliable benchmarking for fair com-

parison, with this paper we expand the evaluation

method by answering the question Can we detect a

human acceptable summary output?

We observe that, when applying these TextRank-

based algorithms, it is uncertain whether results are

summaries of good or bad quality. Given an origi-

nal text being noisy and not formally structured, the

resulted summary will be of the expected same low

quality. Likewise, if the original text does not contain

clear sentences that help summarize the content, the

output will not make sense to the reader. We can think

of an interview article formatted in dialogues. Ex-

tractive algorithms are limited to selecting sentences

and, in scenarios such as a dialogue/interview, there

are no good candidates to form a complete summary.

Another example is ﬁnancial news which touch upon

many topics. Last example refers to sports articles;

we may face a long article describing all the matches

of the day. The output will not be satisfactory on sum-

marising well all the content information. Some ex-

amples of the above mentioned situations are listed in

Figure 1.

Thus, in this paper, we aim at the deﬁnition of

quality and readability for summaries delivered by

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

606

Figure 1: Examples of bad quality summaries.

TextRank methods and hereby propose an under-

standing layer to avoid poor output and solve its non-

discriminant nature.

3 METHOD

Hereinafter, we proceed to describe our modelling

methodology. The following subsections will consist

on the annotated data utilized to model decision mak-

ing on the summary output; the algorithmic architec-

ture of our solution; and the construction of input fea-

tures from both incoming and outcoming text.

3.1 Data

Our dataset is composed of 500 Dutch annotated doc-

uments forming our ground truth. The articles con-

tained in our sample have been randomly selected in

a pool of different news sources with a diverse range

of topics.

A group of experts annotated the sample dataset

following guidelines in pursuit of a harmonious an-

notation result. The annotation guidelines converge

the assessment of the summary quality in the pillars

of readability, information or content, and coherence.

Readability refers to the lack of textual barriers

or noise—for instance, misplacement or presence of

unsought characters or wrong parsing. Information

or content introduce the rules in which a summary is

considered correct when it delivers a general under-

standing of the main topic of the article. Finally, co-

herence covers the complete sense of the text. Hence,

it implies the holistic correctness of the summary—

this includes the absence of unrelated or incongruous

sentences in the summary.

Additionally, we implement an anonymous feed-

back mechanism so that reviewers can vote on the

summary independently. A majority vote decides the

ﬁnal label for the summary. Herewith we hope to al-

leviate annotators’ bias in the assessment of the sum-

mary. One potential bias is, for instance, the familiar-

ity of the annotator with the topic of the text and thus,

his better understanding of a small context compared

to an uninformed annotator. Despite these efforts, it

is safe to assume discrepancies in human judgement

Understanding Summaries: Modelling Evaluation in Extractive Summarisation Techniques

607

towards the quality of the summary and therefore, we

include the Kappa statistic (Cohen, 1960; McHugh,

2012) to consider the inter-rater degree of agreement.

The Kappa statistic calculates the agreement between

two sets of annotations or evaluations considering the

possibility of random agreement.

3.2 Algorithmic Architecture

Our graph extraction pipeline is based on the algo-

rithm of Barrios et al. (2016) and works on the sen-

tence level of the text. We optimize the preprocess-

ing pipeline for the Dutch language, speciﬁcally, the

stopwords list curation, the sentence splitter and the

stemmer. The graph extraction model ranks processed

sentences on their centrality values:

centrality(S

) =

∑

i=1

IDF(q

) ·

f (q

) · 2.2

f (q

) + 1.2 ·



1 − 0.75 + 0.75 ·

avgsl



(4)

Equation 4 shows the calculation of centrality for

and S

which represent a pair of sentences in the

text. The variable q

are the terms of S

. IDF(q

) is the

function computing the Inverse Document Frequency

(Jones, 1972) of the term q

. In order to avoid non-

valid IDF values for terms out of the vocabulary, the

function has a ﬂoor given by 0.25 · avgIDF for those

cases. The function f (q

) is the term frequency of

in S

. The length of S

in words is |S

| and avgsl is

the average sentence length in the original document.

The most central sentences, ordered by appear-

ance on the original article, compose the summary.

The number of sentences will be parametrized as a

preset percentage of the original length. In our re-

search, the ratio of summary sentences to original sen-

tences is set at 0.15.

Our understanding layer forms the second part of

the algorithm. This layer mimics a quality evalua-

tor in order to exclusively pass through readable and

comprehensible text. Three different models deﬁne

the architecture of this layer. An ensemble of Ran-

dom Forest, Support Vector Machine and a Neural

Network. The reason to use an ensemble of models

is to exploit the strengths of each individual compo-

nent. The strategy of bringing different classiﬁers to-

gether provides an improvement on the generalization

performance (G

unes¸ et al., 2017). Plus, the combina-

tions of outputs reduces the probability of choosing

a poor classiﬁer and the average error rate. Namely,

following Wolpert (1992), assuming a constant error

rate ε and the independence of classiﬁers, the error

rate of the ensemble beneﬁts from the diversiﬁcation

effect shown by:

ensemble

∑





(1 − ε)

N−n

(5)

Where N is the number of classiﬁers in the ensem-

ble model and n is the majority voting number. The

term ε is the error rate. One of the requirements in the

selection of the components is the diversity between

them. This diversity in the classiﬁers will reinforce

the independence assumption of the error rate made

beforehand by a lower correlation in the predictions.

Random Forests are excellent stand-alone algo-

rithms as they are composed by an ensemble of de-

cision trees. This method bootstraps random samples

and selects a random number of features. As a result,

Random Forest becomes a robust classiﬁer to outliers

and noise, with a good generalization to new data and

highly parallelizable (Breiman, 2001).

Support Vector Machines, on the other hand, are

suited methods for binary classiﬁcation that work em-

pirically better on sparse data such as text classiﬁca-

tion problems (Hearst et al., 1998). Its nature resides

on the distance of support vectors in order to draw a

decision boundary.

Finally, Neural Networks are connected layers

that tend to outperform Machine Learning models as

the training dataset increases. Additionally, the inclu-

sion of a sequential model allows to capture the text

linearity that Bag of Words techniques in ML mod-

els fail to address (Schuster and Paliwal, 1997; Zhou

et al., 2016).

In this paper we design a weighted voting ensem-

ble model architecture. The three models previously

mentioned are combined with different input features

explained in the next section. The ensemble model is

exposed to a Monte Carlo simulation selecting train-

ing and validation data. The process is performed

thousand times to assure the covering of most train-

ing/validation splits and help minimize the bias of

the estimates following Zhang (1993). The probabil-

ity results of the ensemble model are eventually opti-

mized by:

max(AUC) = max



x=0

TPR

(FPR

−1

(x))dx



(6)

Where TPR is the True Positive Rate and FPR is the

False Positive Rate for every i weight distribution of

the ensemble models. Formally, we deﬁne both rates

as:

TPR

(T) =

∞

)dx, FPR

(T) =

∞

)dx

(7)

Where T is the probability threshold to classify the

prediction X and under the conditions deﬁned by:

) =



| X

> T



, f

) =



| X

< T



(8)

The probability density function is f

(x) for positive

predictions and f

(x) for the negative ones. We deﬁne

as:

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

608

= (w

SVM

+ w

) (9)

Where j is the different data points in the valida-

tion set and (w

SVM

) belong to a set W contain-

ing all combinatory possibilities for the weight distri-

bution of the ensemble model.

The AUC or Area Under the Curve shows the per-

formance by comparing the TPR versus FPR trade-

off. In an intuitive way, the result of AUC is the

probability of a random positive data point ranking

higher than a negative one. Section 4 will visualize

the optimal AUC in the Receiver Operating Charac-

teristic curve or ROC curve (Bradley, 1997). ROC

is the graphical representation of the AUC trade-off,

plotting the TPR against the FPR levels.

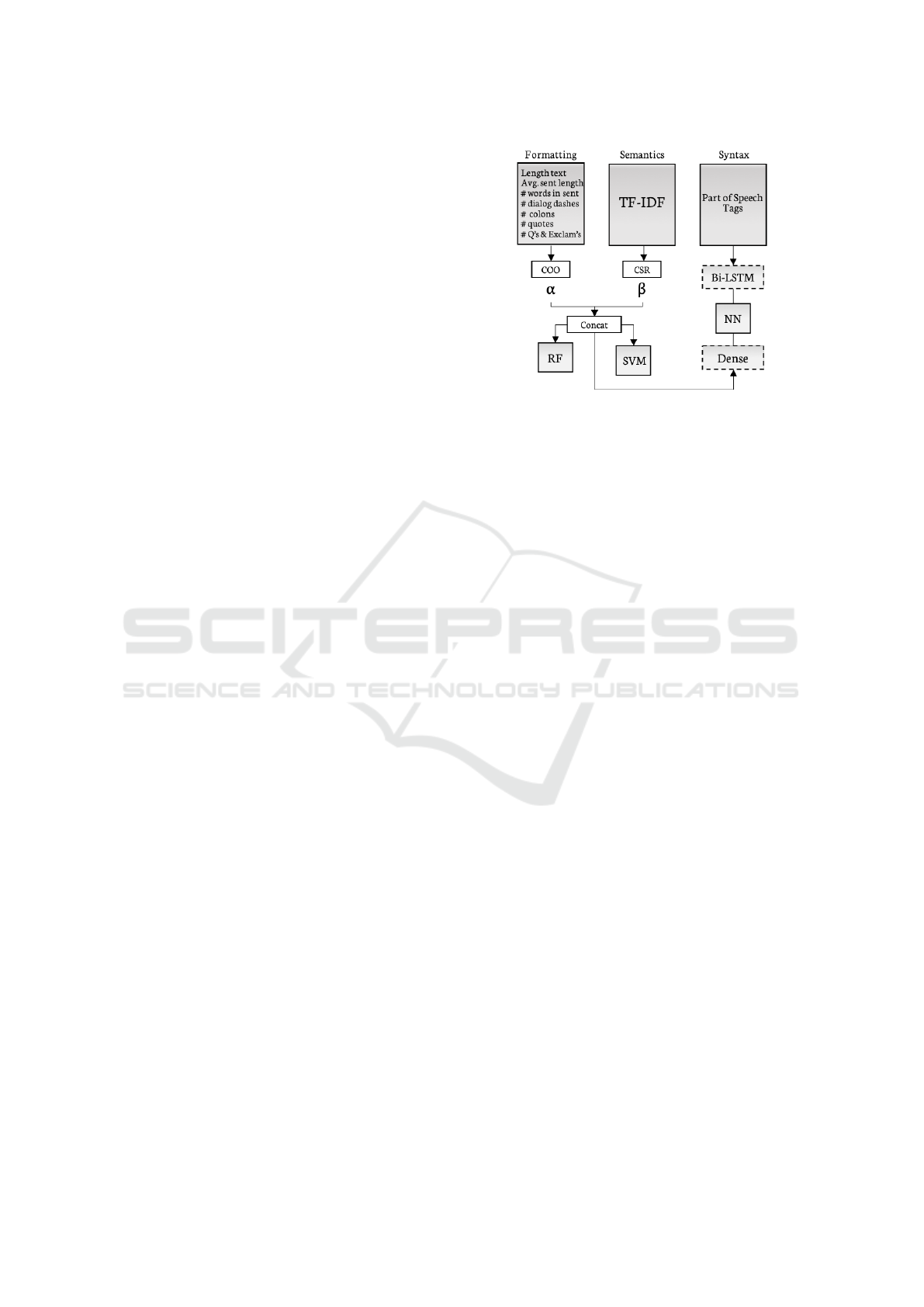
3.3 Input Features

Our input features are built in order to provide the

differentiable aspects of the text so that the ensemble

model can determine the correct class.

There are three pillars—the formatting, the se-

mantics and the syntax. The formatting of the text in-

cludes the length of the text measured on the number

sentences, the average sentence length in characters,

average number of words per sentence, and number

of dialogue dashes, colons, quotes, question and ex-

clamation marks. These features are specially deter-

minant on texts containing complex formats on which

the summarisation algorithm fails and, consequently,

translates to a non-readable summary. The semantic

layer helps deﬁne how likely a text is to be correct

or incorrect given its thematic. For instance, sports

and interview articles are prone to produce unsatis-

factory summaries. The syntax layer considers what

an acceptable concatenation of syntactic units is. This

helps detect when sentences are wrongly extracted—

we may think of two sentences put together due to a

mistake in the sentence splitter in the pre-processing.

As a result of its sequential nature, this input is only

available to the LSTM layers of the Neural Network

model.

Following Figure 2, we store the extracted for-

matting features in a Coordinate list (COO) with (row,

column, value) structure, this will help coordinate the

stacking with the semantic layer extracted through

TF-IDF (Jones, 1972) stored in Compressed sparse

row (CSR). Furthermore, we parameterize the weight

of each array before concatenating. This is deﬁned

by α in the formatting array and β in the semantic ar-

ray. In the background α and β are subdivided into

two more parameters (ε

,θ

) for v = α,β that provide

the weight distribution to arrays from the original text

and arrays from the summarized text. This sparse ar-

ray is fed to the Random Forest and to the Support

Figure 2: Input features.

Vector Machine as well as to the dense layer of the

Neural Network. Syntax is captured by a ﬁxed length

sequence containing the Part of Speech tags from only

the summary text. This feature is read left-to-right

and right-to-left by a Bidirectional LSTM (Bi-LSTM)

(Schuster and Paliwal, 1997).

4 RESULTS

Input weights α and β are ﬁne-tuned on cross-

validation with grid search during warm-up simula-

tions. The ensemble model weight distribution is as-

signed to the predicted probabilities from each of the

models and optimized based on equation (6). Figure 3

shows the result of such optimization, where the best

performing weight distribution is marked with red and

visualises the True Positive Rate trade-off with the

False Positive Rate of the ensemble for the different

threshold T as explained in (7). The blue channel

in Figure 3 represents all other weight combinations

arisen from the simulations. Lastly, the grey area is

the baseline for a random guess.

Table 1 exhibits the evaluation metrics for the op-

timized understanding layer at T = 0.5. Our ensem-

ble model obtains a conclusive 90.84% accuracy on

our validation rounds. The ensemble model seems

to weaken in recalling bad quality summaries, such

lower recall determines consequently the impact on

the precision metric of good quality summaries due

to its binary outcome. This ﬂaw in bad quality sum-

maries recall can be explained by the smaller amount

of such examples in the training phase. Overall, the

results in Table 1 show that it is possible to transmit

quality checks through an engineered formatting layer

together with the syntax and the semantics. These

ﬁndings satisfy our objective to create an algorith-

mic solution that could substitute or emulate expen-

sive manual evaluation.

Understanding Summaries: Modelling Evaluation in Extractive Summarisation Techniques

609

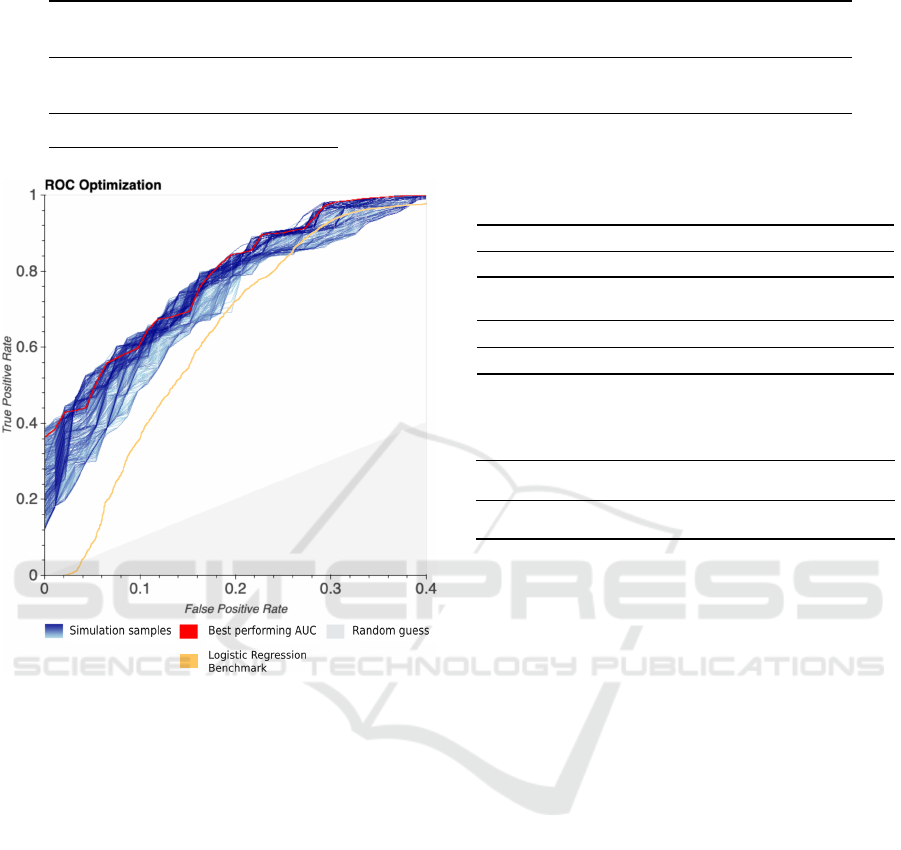
Table 1: Understanding layer: Evaluation metrics.

Label

Precision (Std.)

Recall (Std.)

F1 (Std.)

Samples support

Support pct.

Bad quality 98.65 (2.70) 64.63 (7.60) 78.09 (5.80) 3158 25.26

Good quality 89.29 (2.72) 99.70 (0.64) 94.21 (1.56) 9342 74.73

Accuracy (Std.) % 90.84 (2.33)

Figure 3: Optimization for model distribution.

Nevertheless, and despite the usefulness of the

previous metrics for reference and model ﬁne-tuning,

we face an evaluation with different outcomes based

on the speciﬁc individuals assessing the quality of the

ﬁnal summary. This lack of agreement produces po-

tential mismatches on the same summary outcome.

Thus, it is crucial to quantify the consensus between

the labelling experts and the algorithmic solution to

judge the performance of our understanding layer in

perspective. Therefore, we proceed to evaluate the

variability in the data labeled by the experts.

We introduce Cohen’s Kappa statistic (κ) (Cohen,

1960) to measure the degree of agreement or disagree-

ment happening by chance. It ranges from -1 to 1

where 0 is random chance and 1 represents perfect

agreement.

In our experiment, we merge our experts’ labels

and we include the algorithm as a second rater in or-

der to model the raters’ agreement probabilities. In

Table 2 the results for our model are listed. Table 2

are the agreement probabilities calculated from our

dataset and from the model’s results. The latter proba-

Table 2: Results of Kappa statistic through agreement prob-

abilities.

Agreement probabilities

max

Good

Bad

Values (%) 90.84 91.29 62.37 4.18 66.55

(a) Agreement probabilities from our testing dataset.

Kappa statistics κ κ

max

CI (95%)

Values 0.7262 0.7395 0.0077 [0.7185,0.7339]

(b) Kappa statistics calculated from the agreement proba-

bilities.

Table 3: Kappa agreement levels.

Std. range <0 <0.2 <0.4 <0.6 <0.8 <1

Norm. range <0 <0.15 <0.3 <0.44 <0.59 <0.74

Agreement

magnitude

None Slight Fair Moderate Substantial Almost

perfect

Note: Magnitude assessment following Landis and Koch

(1977).

bilities are the input for the calculus of the Kappa val-

ues in Table 2b. In Table 3 we provide the standard

range for equally distributed categories and the nor-

malised range for our speciﬁc sample. The standard

range is used as a Kappa benchmark established by

Landis and Koch (1977) in order to express the agree-

ment magnitude for different Kappa values. The nor-

malised range takes into account the unbalanced dis-

tribution of our classes and scales the standard range

based on the maximum Kappa value. Our understand-

ing layer achieves a 0.7262 Kappa statistic of a maxi-

mum of 0.7395. By considering chance agreement in

an ambiguous qualitative task such as summary eval-

uation, the ﬁnding of a strong Kappa (0.7262) shows a

behaviour almost completely in line with the expected

behaviour from a human data labeler.

5 CONCLUSION AND FUTURE

WORK

In the lack of quality assessment of extractive sum-

maries, we present an understanding layer in order to

determine the readability of the outcome. We have

shown how we may translate human assessment of

summaries output into a modelling process that suc-

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

610

cessfully performs the task with 91% accuracy. Fur-

thermore, our Kappa statistic (0.73) reinforces a con-

sistent agreement between algorithm’s and expert’s

summary labelling. This solution links the evalua-

tion of co-reference solutions for benchmarking (Lin,

2004) to an applicable solution for real summary un-

derstanding.

Future research will focus on the readability of the

models. This refers to whether we may have a snap-

shot from the ensemble model of the main features

delivering the ﬁnal decision. In other words, we want

to be knowledgeable of the relevance of the format-

ting, semantic and syntactic layers on the result. This

would elucidate the understanding of the potential for

new applications regarding the machine-human cor-

relation on decision making in the task of summary

evaluation.

Lastly, the scope of this study is limited to the

Dutch language. It is to be expected a similar perfor-

mance in close relative languages such as German and

English, yet challenges increase in more distant types.

Therefore, modelling techniques should be ﬁne-tuned

and adapted to each speciﬁc language to validate the

results previously presented.

REFERENCES

Barrios, F., Lopez, F., Argerich, L., and Wachenchauzer,

R. (2016). Variations of the similarity function

of textrank for automated summarization. CoRR,

abs/1602.03606.

Bradley, A. P. (1997). The use of the area under the

roc curve in the evaluation of machine learning algo-

rithms. Pattern recognition, 30(7):1145–1159.

Breiman, L. (2001). Random forests. Machine learning,

45(1):5–32.

Brin, S. and Page, L. (1998). The anatomy of a large-scale

hypertextual web search engine.

Cohen, J. (1960). A coefﬁcient of agreement for nominal

scales. Educational and psychological measurement,

20(1):37–46.

unes¸, F., Wolﬁnger, R., and Tan, P.-Y. (2017). Stacked

ensemble models for improved prediction accuracy. In

Proc. Static Anal. Symp, pages 1–19.

Hearst, M. A., Dumais, S. T., Osuna, E., Platt, J., and

Scholkopf, B. (1998). Support vector machines. IEEE

Intelligent Systems and their Applications, 13(4):18–

28.

Jones, K. S. (1972). A statistical interpretation of term

speciﬁcity and its application in retrieval. Journal of

documentation.

Kleinberg, J. M. (1999). Authoritative sources in a hy-

perlinked environment. Journal of the ACM (JACM),

46(5):604–632.

Landis, J. R. and Koch, G. G. (1977). The measurement of

observer agreement for categorical data. biometrics,

pages 159–174.

Lin, C.-Y. (2004). Rouge: A package for automatic evalua-

tion of summaries. Text summarization branches out,

page 74–81.

Mani, I. (2001). Automatic summarization. J. Benjamins

Pub. Co.

McHugh, M. L. (2012). Interrater reliability: the kappa

statistic. Biochemia Medica, page 276–282.

Mihalcea, R. and Tarau, P. (2004). Textrank: Bringing or-

der into text. Proceedings of the 2004 Conference on

Empirical Methods in Natural Language Processing,

page 404–411.

Schuster, M. and Paliwal, K. K. (1997). Bidirectional re-

current neural networks. IEEE transactions on Signal

Processing, 45(11):2673–2681.

Wolpert, D. H. (1992). Stacked generalization. Neural net-

works, 5(2):241–259.

Wu, H., Ma, T., Wu, L., Manyumwa, T., and Ji, S.

(2020). Unsupervised reference-free summary qual-

ity evaluation via contrastive learning. arXiv preprint

arXiv:2010.01781.

Zhang, P. (1993). Model selection via multifold cross vali-

dation. The Annals of Statistics, 21(1):299–313.

Zhou, P., Qi, Z., Zheng, S., Xu, J., Bao, H., and Xu, B.

(2016). Text classiﬁcation improved by integrating

bidirectional lstm with two-dimensional max pooling.

arXiv preprint arXiv:1611.06639.

APPENDIX

In Table 2 we deﬁne p

as the raters’ accuracy.

The maximum agreement probability is P

max

∑

i=1

min(P

) where P

and P

are the row and

column probabilities from the original raters’ matrix.

Good

and p

Bad

are the probability of random agree-

ment for the different summary categories. p

the random probability for both categories together,

thus, p

= p

Good

+ p

Bad

. Kappa value is deﬁned as

κ =

−p

1−p

. The maximum value for the unequal

distribution of the sample is κ

max

and is calculated

by κ

max

−P

1−P

. The standard error and conﬁ-

dence interval are calculated by SE

(1−p

)

N(1−p

)

and

CI : κ ± Z

1−α/2

respectively.

Understanding Summaries: Modelling Evaluation in Extractive Summarisation Techniques

611