
Code Generation by Example
Kevin Lano
a
and Qiaomu Xue
King’s College London, London, U.K.
Keywords:
Code Generation, MDE, MTBE, CGBE.
Abstract:
Code generation is a key technique for model-driven engineering approaches of software construction. Code
generation enables the synthesis of applications in executable programming languages from high-level speci-
fications in UML or a domain-specific language. Specialised code-generation languages and tools have been
defined, such as Epsilon EGL and Acceleo, however the task of writing a code generator remains a sub-
stantial undertaking, requiring a high degree of expertise in both the source and target languages, and in the
code-generation language. In this paper we show how symbolic machine learning techniques can be used to
reduce the time and effort for developing code generators. We apply the techniques to the development of a
UML-to-Java code generator.
1 INTRODUCTION
Code generation involves the automated synthesis of
executable code, usually in a 3GL such as Java, C,
C++ or Swift, from a software specification defined
as one or more models in a modelling language such
as UML/OCL or a domain-specific language (DSL).
Code generators may directly produce target lan-
guage text (M2T approaches) (Epsilon project, 2021),
or produce a model that represents the target code
(M2M approaches) (Greiner et al., 2016; Lano et al.,
2017). More recently, text-to-text (T2T) code genera-
tors have been defined (Lano et al., 2020).
At present, code generation is often carried out
by utilising template-based M2T languages such as
EGL (Epsilon project, 2021) and Acceleo (Acceleo
project, 2021). In these, templates for target language
elements such as classes and methods are specified,
with the data of instantiated templates being com-
puted using expressions involving source model ele-
ments. Thus, a developer of a template-based code
generator needs to understand the source language
metamodel, the target language syntax, and the tem-
plate language.
A M2M code generation approach separates code
generation into two steps: (i) a model transformation
from the source language metamodel to the target lan-
guage metamodel (Greiner et al., 2016), and (ii) text
production from a target model. In this case, the au-
thor of the code generator must know both the source
a
https://orcid.org/0000-0002-9706-1410
and target language metamodels, the model transfor-
mation language, and the target language syntax.
A T2T approach to code generation specifies the
translation from source to target languages in terms
of the source and target language concrete syntax or
grammars, and does not depend upon metamodels
(abstract syntax) of the languages.
In order to reduce the knowledge and resources
needed to develop code generators, we propose a
symbolic machine learning (ML) approach to auto-
matically create code-generation rules based on trans-
lation examples (Section 3). The rules are represented
in the CS T L T2T code-generation language (Section
2). We provide an evaluation of the approach in Sec-
tion 4, a summary of related work in Section 5, and
conclusions in Section 6.
2 CSTL
C S T L transformations map elements of a source lan-
guage L
1
into the textual form of elements of a target
language L
2
. C S T L rules have the form
LHS |--> RHS <when> condition
where the LHS and RHS are schematic text represen-
tations of corresponding elements of L
1
and L
2
, and
the optional condition can place restrictions on when
the rule is applicable.
Neither the source or target metamodel is referred
to, instead, a rule LHS can be regarded as a pattern for
matching nodes in a parse tree of L
1
elements (such
84
Lano, K. and Xue, Q.
Code Generation by Example.
DOI: 10.5220/0010973600003119
In Proceedings of the 10th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2022), pages 84-92
ISBN: 978-989-758-550-0; ISSN: 2184-4348
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

as types, expressions or statements). When the trans-
formation is applied to a particular parse tree s, rules
are tested to determine if they match s, if so, the first
matching rule is applied to s. Rules are grouped into
rulesets, based on the syntactic categories of L
1
.
For example, some rules for translating OCL
(OMG, 2014) types to Java 7+ could be:
OclType::
Integer |-->BigInteger
Real |-->BigDecimal
OclAny |-->Object
Boolean |-->boolean
String |-->String
Set(_1) |-->HashSet<_1>
Sequence(_1) |-->ArrayList<_1>
Map(_1,_2) |-->HashMap<_1,_2>
Variables 1, ..., 9 represent subnodes of an L
1
syn-
tax tree node s. If s matches an LHS containing vari-
ables, these variables are bound to the corresponding
subnodes of s, and these subnodes are then translated
in turn, in order to construct the subparts of the RHS
denoted by the variable name.
Thus for the above ruleset OclType, applied to
the OCL type Map(Integer, String), the final rule
matches against the type, with 1 bound to Integer
and 2 bound to String. These are translated to
BigInteger and String respectively, and hence the out-
put is HashMap < BigInteger, String >.
The special variable ∗ denotes a list of subnodes.
For example, the rule
Set{_*} |-->Ocl.initialiseSet(_*)
translates OCL set expressions with a list of argu-
ments, into a corresponding call on the static method
initialiseSet of the Java Ocl.java library. Elements of
the list bound to ∗ are translated according to their
own syntax category, and separators are preserved.
Conditions are a conjunction of predicates, sepa-
rated by commas. Individual predicates have the form
_i S
or
_i not S
for a stereotype S, which can constrain the kind of
element bound to i. For example, the type of i can
be tested by using stereotypes Integer, Real, Boolean,
Object, Sequence, etc.
A ruleset r can be explicitly applied to variable
i by the notation i‘r. ∗ ‘r denotes the application
of r to each element of ∗. This facility enables the
use of auxiliary functions within a code generator. In
addition, a separate set of rulesets in a file f .cstl can
be invoked on i by the notation i‘f .
By default, if no rule in a ruleset applied to source
element s matches to s, s is copied unchanged to the
result. Thus the rule String 7−→ String above is not
necessary. Because rules are matched in the order of
their listing in their ruleset, more specific rules should
precede more general rules. A transitive partial order
relation r1 @ r2 can be defined on rules, which is true
iff r1 is strictly more specific than r2. For example,
if the LHS of r2 and r1 are equal but r1 has stronger
conditions than r2.
C S T L is a simpler notation than template-based
code generation formalisms, in the sense that no refer-
ence is made to source or target language metamod-
els, and no interweaving of target language text and
code-generation language text is necessary. The tar-
get language syntax and the structure of the source
language grammar need to be known, in order to write
and modify the rules.
C S T L has been applied to the generation of Swift
5 and Java 8 code, to support mobile app synthe-
sis (Lano et al., 2021a). It has also been applied to
natural language processing and reverse-engineering
tasks. However, a significant effort is still required
to define the C S T L rules and organise the transfor-
mation structure. In the next section we discuss how
this effort can be reduced by automated learning of
a C S T L code generator from pairs of corresponding
source language, target language texts. This removes
the need for C S T L users to understand the details of
the source language grammar.
3 SYNTHESIS OF CODE
GENERATORS FROM
EXAMPLES
The goal of our machine learning procedure is to auto-
matically derive a C S T L code generator g mapping a
software language L
1
to a different language L
2
, based
on a set D of examples of corresponding texts from L
1
and L
2
. The generated g should be correct wrt D, ie.,
it should correctly translate the source part of each
example d ∈ D to the corresponding target part of d.
In addition, g should also be able to correctly
translate the source elements of a validation dataset
V of (L
1
, L
2
) examples, disjoint from D.
We term this process code generation by-example
or CGBE.
Thus, from a dataset
Integer int
Real double
Boolean boolean
Set(Integer) HashSet<int>
Code Generation by Example
85

Set(Boolean) HashSet<boolean>
Sequence(Integer) ArrayList<int>
Sequence(Real) ArrayList<double>
it should be possible to derive a specification equiva-
lent to:
OclType::
Integer |-->int
Real |-->double
Boolean |-->boolean
Set(_1) |-->HashSet<_1>
Sequence(_1) |-->ArrayList<_1>
The datasets D will be organised in the same man-
ner as datasets of paired texts for ML of natural lan-
guage translators
1
: each line of D holds one example
pair, and the source and target texts are separated by
one or more tab characters \t.
Because software languages are generally organ-
ised hierarchically into sublanguages, eg., concerning
types, expressions, statements, operations/functions,
classes, etc., D will typically be divided into parts cor-
responding to the main source language divisions.
3.1 Symbolic versus Non-symbolic
Machine Learning
ML for machine translation of natural languages typ-
ically makes use of a recurrent neural net machine
learning technology such as LSTM. Adaptions of
LSTM and other neural net approaches to learn map-
pings of software languages have been defined (Bur-
gueno et al., 2019; Chen et al., 2018). These ap-
proaches are not suitable for our goal, since the
learned translators are not represented explicitly, but
only implicitly in the internal parameters of the neu-
ral net. Thus it is difficult to formally verify the
translators, or to manually adapt them. In addition,
neural net approaches typically require large training
datasets (eg., over 100MB) and long training times.
This impairs agility and also has resource and envi-
ronmental implications.
Symbolic ML approaches include inductive logic
programming (ILP) (Balogh and Varro, 2008) and the
MTBE approach of (Lano et al., 2021b). These typi-
cally use considerably smaller (ie., KB-scale) training
datasets compared to non-symbolic ML. One disad-
vantage of ILP is that counter-examples of a relation
to be learned need to be provided, in addition to pos-
itive examples. The approach of (Lano et al., 2021b)
uses only positive examples. It is able to learn in-
dividual String-to-String functions and Sequence-to-
Sequence functions from small numbers (usually un-
der 10) of examples of the function. In this paper,
1
www.tensorflow.org/text/tutorials/nmt with attention
we extend this MTBE approach to learn functions of
software language parse trees.
The approach of (Lano et al., 2021b) takes as
input metamodels for the source and target lan-
guages, and an initial mapping of source metaclasses
to target classes. In our adaption of the tool, we
use the language element categories of L
1
and L
2
as the source and target metamodels. The initial
mapping is defined to indicate which L
1
categories
map to L
2
categories. For example, in mapping
UML/OCL to Java, there could be OCL language
categories OclLambdaExpr and OclConditionalExpr
(subcategories of OclExpression), and Java category
JavaExpr, with the outline mappings
OclLambdaExpr 7−→ JavaExpr
OclConditionalExpr 7−→ JavaExpr
The process also takes as input a model m containing
example instances of the source and target languages,
and a mapping relation 7→ defining which source and
target elements correspond. For example:
x1 : OclLambdaExpr
x1.text = "lambda x : String in x+x"
y1 : JavaExpr
y1.text = "x->(x+x)"
x1 |-> y1
In order to infer functional mappings from source
data such as OclLambdaExpr::text to type-compatible
target data such as JavaExpr::text, at least 2 exam-
ples of each SC 7−→ TC language category correspon-
dence must be present in the model. String-to-String
mappings of several forms can be discovered by the
MTBE approach of (Lano et al., 2021b): where the
target data are formed by prefixing, infixing or ap-
pending a constant string to the source data; by re-
versing the source data; by replacing particular char-
acters by a fixed string, etc. Similarly, functions of
other datatypes can be proposed based on relatively
few examples.
3.2 Machine Learning of Parse-tree
Mappings
Different forms of software representation could be
used for CGBE:
• Text, eg.: “sq[i] + k”
• Sequences of tokens, eg.: ‘sq’, ‘[’, ‘i’, ‘]’, ‘+’, ‘k’
• Syntax/parse trees:
(OclBinaryExpression
(OclBasicExpression
MODELSWARD 2022 - 10th International Conference on Model-Driven Engineering and Software Development
86
(OclBasicExpression sq)
[ (OclBasicExpression i) ])
+
(OclBasicExpression k))
Parse trees generally express more detailed informa-
tion about the software element, specifically its in-
ternal structure in terms of the grammar of the lan-
guage. As (Chen et al., 2018) discuss, this represen-
tation therefore provides a more effective basis for
ML of language mappings, compared to token se-
quences or raw text. For example, it is difficult to in-
fer a String-to-String mapping between OCL expres-
sions and Java expressions represented as text, as the
lambda expression example of the preceding section
demonstrates.
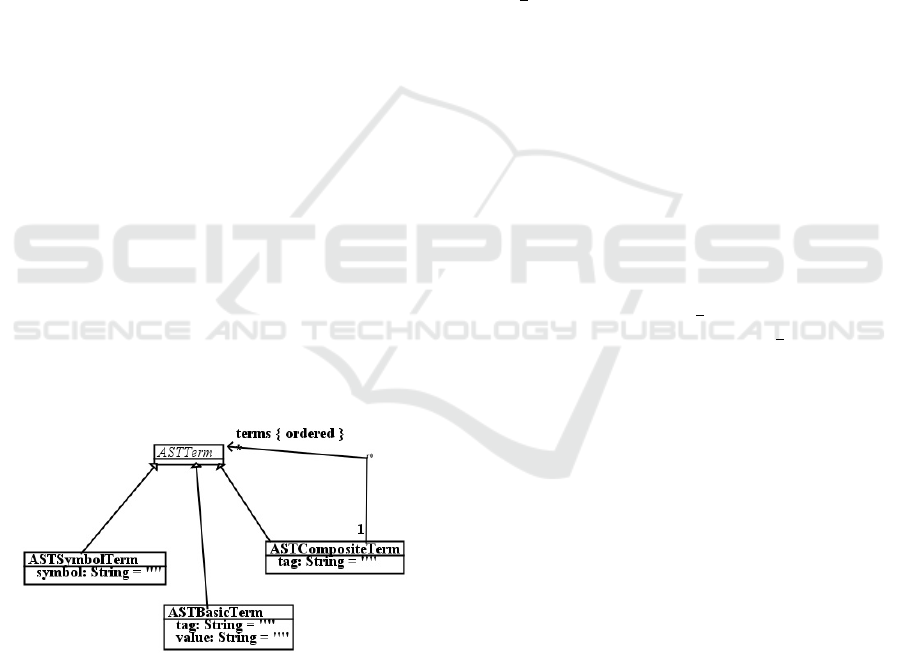
Figure 1 shows the metamodel which we use for
parse trees (ie., AST terms). This metamodel is of
wide applicability, not only for representation and
processing of software language artefacts, but also
for natural language artefacts. ASTSymbolTerm repre-
sents individual symbols such as ‘[’ in the above ex-
ample. ASTBasicTerm represents other terminal parse
tree nodes. For example (OclBasicExpression
sq). ASTCompositeTerm represents non-terminal
nodes, such as the root OclBinaryExpression node of
the example. The tag of a basic or composite term
is the identifier immediately following the initial (, in
the text representation of parse trees. The arity of a
symbol is 0, of a basic term is 1, and of a compos-
ite term is the size of terms (the direct subnodes of
the tree node). The tag is used as the syntactic cate-
gory name of the tree, when the tree is processed by
a C S T L script – ie., rules in the ruleset of this name
are applied to the tree if possible.
Figure 1: Metamodel of parse trees.
Model elements representing software language
elements are given an ast : ASTTerm attribute, whose
value is a parse tree of the software element. For ex-
ample:
x1 : OclLambdaExpr
x1.ast = (OclUnaryExpression
lambda x :
(OclType String) in
(OclBinaryExpression
(OclBasicExpression x) +
(OclBasicExpression x)))
Based on examples of translation between Java
and UML/OCL, we identified a family of relevant
tree-to-tree mappings of parse trees, which our CGBE
process should be able to recognise from examples.
These mappings include structure elaborations (eg.,
more levels of structure are present in the parse trees
of elements in one language, compared to the trees
of corresponding elements in the other language); ad-
dition of new constant elements to tree nodes; re-
ordering the subnodes of tree nodes; functional map-
pings of source symbols to target symbols, etc.
We document tree-to-tree mappings by using vari-
ables i for digit i to represent the parts of source el-
ement trees x.ast for x : SC which vary. i is the index
of the part in the subnode list x.ast.terms.
A typical example of structural elaboration arises
when mapping OCL basic expressions to Java expres-
sions. An OCL parse tree
(OclBasicExpression i)
representing a variable i maps to
(expression (primary i))
as a Java expression parse tree. As a mapping
from the source language category OclIdentifier to
JavaExpr this is denoted
(OclBasicExpression 1) 7−→
(expression (primary 1))
In other words, this translation of source trees to tar-
get trees is assumed to be valid for all OclIdentifier
elements with the same structure, regardless of the
identifier in the first subnode of the source element
parse tree.
New subnodes of the target trees can be introduced
when a simple OCL expression is represented by a
more complex Java expression. For example, an array
access sq[i] in OCL becomes sq[i−1] in Java, because
Java arrays are 0-indexed. As parse trees, this means
that:
(OclBasicExpression
(OclBasicExpression sq) [
(OclBasicExpression i) ])
maps to:
(expression (expression (primary sq)) [
(expression (expression (primary i)) -
(expression (integerLiteral 1)) ) ])
Figure 2 shows the graphical version of the Java
parse tree.
Functional mappings of symbols arise when op-
erators are represented by different symbols in the
Code Generation by Example
87

Figure 2: Java parse tree.
source and target languages. For example, OCL unary
prefix expressions
(OclUnaryExpression op expr)
map to
(expression f(op) expr’)
in Java, where expr maps to expr
0
and f (not) is !, f (−)
is −, f (+) is +.
Schematically this can be represented as
(OclUnaryExpression 1 2) 7−→
(expression f ( 1) 2)
More complex cases involve re-ordering the subn-
odes of a tree; embedding the source tree as a subn-
ode of the target tree, etc. Tree-to-tree mappings can
be constructed and specified recursively.
In order to recognise such mappings, our CGBE
procedure operates successively on each postu-
lated category-to-category mapping between two lan-
guages:
SC 7−→ TC
The ast values of all linked instances x : SC and y : TC
are compared, ie., for all such pairs with x 7→ y, the
values x.ast and y.ast are checked to see if a consistent
relationship holds between the value pairs. At least
2 instances x
1
, x
2
of SC linked to TC elements must
exist for this check to be made.
The basic mappings of trees consisting of single
symbols are:
• Identical source and target symbols: s 7−→ s
• Functional mapping of symbols: s 7−→ f (s)
These are schematically represented as i 7−→ i and
i 7−→ f ( i) where the source symbol s is the ith subn-
ode of its parent node.
Composed tree-to-tree mappings are formed as
follows. Firstly, for target trees of arity 1, if s 7−→ t
has been recognised as a valid tree-to-tree mapping in
dataset D, then the following are also valid mappings:
• s 7−→ (tag t) for any tag
• (tag1 s) 7−→ (tag2 t) for any tag1, tag2.
These are expressed as
1 7−→ (tag 1)
(tag1 1) 7−→ (tag2 1)
If target trees t have the form (tag2 t
1
... t
n
) and
source terms s have the form (tag1 s
1
... s
m
), with the
same arities n and m for all examples under consid-
eration, ie., for each x : SC, y : TC with x 7→ y and
s = x.ast, t = y.ast, then s 7−→ t is recognised as a
valid mapping if each t
i
is either:
• A constant K for all considered y
• A symbol equal to or a function of some s
j
• Mapped from s
j
: s
j
7−→ t
i
• Mapped from the entire source: s 7−→ t
i
As an example, unary arrow operator OCL expres-
sions such as
(OclUnaryExpression expr ->front ( ))
are consistently mapped to
(expression Ocl .
(methodCall front (
(expressionList expr’) ) ) )
where expr 7−→ expr
0
. The Java expression repre-
sents a call Ocl.front(e) of a Java library for the OCL
collection operations. Here the first and second terms
‘Ocl’ and ‘.’ of the target trees are constants, and the
third term has four subterms. The first term is the
method name, eg., ‘front’, and this is a function of the
second term, the operation name such as ‘→front’, of
the source tree; the second is constant ‘(’; the third
is mapped from the first term of the source; and the
fourth ‘)’ is constant.
Generalising over all unary arrow operators, the
schematic form of this mapping is:
(OclUnaryExpression 1 2 ( ) ) 7−→
(expression K .
(methodCall f ( 2)
((expressionList 1) ) ) )
where K is constant. This shows that the mapping
involves embedding of the source node as a subtree of
the target, and re-ordering of nodes, plus a functional
mapping of the operator symbols.
Finally, there can be cases where related source
and target trees have variable numbers of subnodes.
For example, in Java, a parse tree (expressionList
...) representing a comma-separated list of expres-
sions can have any number n ≥ 1 of direct subnodes
t
i
. Such trees should be recognised as being mapped
MODELSWARD 2022 - 10th International Conference on Model-Driven Engineering and Software Development
88

from source (tag ...) trees which also have n di-
rect subterms s
i
, if each t
i
is mapped from s
i
.
Eg: (OclSetExpression Set {
(OclElementList ...) }) will map
to (expression Ocl . (methodCall
initialiseSet ( (expressionList ...)
) ) ) for any number of corresponding sub-
trees within the list nodes (OclElementList ...) and
(expressionList ...), provided that the arities of these
two nodes are equal for all corresponding source
and target elements. Schematically, this mapping is
represented as
(OclSetExpression Set
{(OclElementList ∗)}) 7−→
(expression Ocl .
(methodCall initialiseSet
( (expressionList ∗) )))
There may also be replacement or removal of sep-
arator symbols and other transformations when map-
ping from source lists to target lists. In this case the
mapping has the form
(slistTag ∗) 7−→ (tlistTag f ( ∗))
for a suitable function f .
3.3 Implementation of CGBE
The above MTBE inference of tree-to-tree mappings
is the core step of CGBE, which involves three stages:
1. Pre-processing the text dataset D to generate parse
trees of the UML/OCL and program elements,
and to store these in a model file m of examples for
input to the MTBE step. The AgileUML toolset is
used to parse the UML/OCL examples and gener-
ate parse trees (Eclipse Agile UML project, 2021),
and the Antlr toolset with a Java grammar file is
used to parse the program examples (in the case
of Java code) and generate Java parse trees (Antlr,
2021);
2. Recognition of tree-to-tree mappings between the
parse trees of corresponding examples, using
MTBE;
3. Conversion of the tree-to-tree mappings to C S T L
rules.
Figure 3 shows the steps of this process.
We use the SOIL notation (Buttner and Gogolla,
2014) as a procedural OCL language, ie., as the
OclStatement category of L
1
.
The final step involves producing the C S T L tex-
tual form of the schematic source to target parse tree
rules produced by MTBE. This is carried out by a left
to right preorder traversal of the two trees, discarding
tags and returning the content of symbol and basic
terms. Spaces are inserted where necessary. Appli-
cations f ( v) of functions f to schematic variables are
expressed as v‘f in C S T L notation.
For example, the schematic mapping:
(OclUnaryExpression 1 2 ( ) ) 7−→
(expression K .
(methodCall f ( 2)
((expressionList 1) ) ) )
becomes the C S T L rule:
_1 _2 ( ) |-->Ocl._2‘f(_1)
Rules l 7−→ r are inserted into a ruleset for the syn-
tactic category SC of l. They are inserted in @ order,
so that more specific rules occur prior to more general
rules in the same category. New function symbols
f introduced for functional symbol-to-symbol map-
pings are also represented as rulesets with the same
name as f , and containing the individual functional
mappings v 7−→ f (v) of f as their rules.
4 EVALUATION
We evaluated the approach by constructing a code
generator from OCL and UML to Java, based on text
examples. The example dataset D was separated into
four files: for type examples, expression examples,
statement examples, and declaration examples,
including operation and attribute declarations and
declarations of complete classes. Table 1 shows
the size of these files in terms of number of ex-
amples, the number of generated rules, and the
accuracy of the generated code generator, in terms
of the F-measure of the generator results on valida-
tion datasets typeValidation, expressionValidation,
statementValidation, declarationValidation, com-
pared to the correct reference results given
in these datasets. F =
2∗p∗r
p+r
where precision
p =
correct translations
total translated
and recall r =
correct translations
total correct
.
The large size of the expressions dataset is due to
the need to include an example for each unary and
binary operator of (OMG, 2014).
In order to demonstrate the versatility of our ap-
proach, we also generated a UML to ANSI C code
generator using CGBE (Table 2). The structure of
the C grammar is substantially different to the Java
grammar. In this case we only considered the types,
expressions and statements subparts of the source lan-
guage.
Table 3 compares the person-hours expended in
the CGBE approach with that required for manually-
coded C S T L generators. The effort is significantly
Code Generation by Example
89
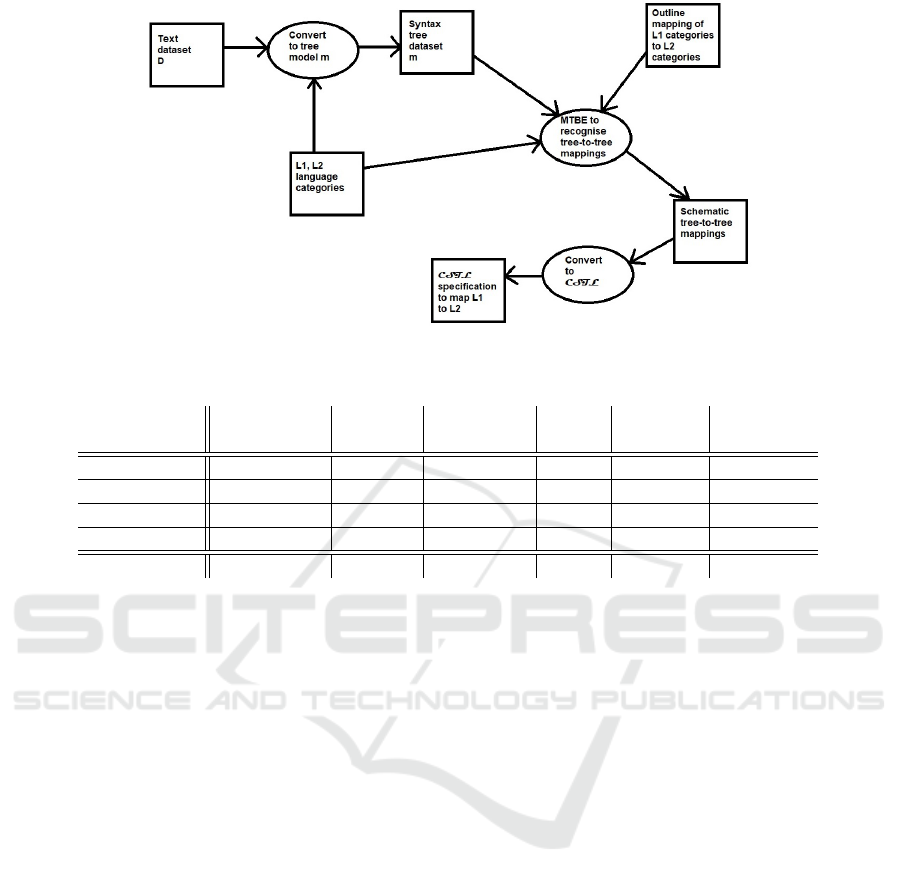
Figure 3: CGBE process steps.
Table 1: Evaluation on UML/OCL to Java code generation.
Sublanguage D size Training Generator Recall Precision F-measure
(#examples) time (s) size (LOC)
Types 21 8.5 23 1.0 1.0 1.0
Expressions 91 56.2 122 1.0 1.0 1.0
Statements 30 11.6 22 0.8 0.9 0.85
Declarations 25 11 44 1.0 1.0 1.0
Averages 42 21.8 52.8 0.95 0.98 0.96
reduced by the use of CGBE, as the creator of the
code generator does not need to design a C S T L spec-
ification. In this respect it is a ‘low code’ approach
requiring no explicit programming.
The creator of the code generator must however
have devised a coherent strategy for the translation
from source to target language, and they need to select
examples which convey accurately and comprehen-
sively the chosen strategy (eg., that OCL sequences
are to be represented by Java array lists, sets by hash
sets, etc). We do not include the time for strategy de-
sign in Table 3, only the time required to encode the
design in CS T L or to express it in suitable examples.
The basic requirement on the training dataset D is
that it provides at least two examples for each source
syntactic category. To learn a context-sensitive map-
ping f of symbols, one example of use of each dif-
ferent source symbol in the context must be provided.
For example, to learn the mapping of unary prefix op-
erators
func ::
‘−
0
7−→ ‘−
0
‘+
0
7−→ ‘+
0
‘not
0
7−→ ‘!
0
an example of each case must be included in D:
-x -x
+1 +1
not p !p
In addition to these numeric constraints on D, the
source and target examples must be syntactically cor-
rect for their languages and category. There should
also be sufficient diversity in the examples so that
rules of sufficient generality to process new examples
are induced. Specifically, not all examples of the same
category should have the same literal value in any one
argument place. Thus
-x -x
+x +x
not x !x
would be an insufficiently diverse example set for pre-
fix unary expressions: the rule
_1 x |-->_1‘func x
would be produced, instead of
_1 _2 |-->_1‘func _2
One current limitation is that training model data
should be organised so that examples of composite
elements only use subelements which have been pre-
viously introduced. Thus an example
if b then 0 else 1 endif
of a conditional expression should use expressions
(here, basic expressions) which are examples in their
own category.
MODELSWARD 2022 - 10th International Conference on Model-Driven Engineering and Software Development
90

Table 2: Evaluation on UML/OCL to C code generation.
Sublanguage D size Training Generator Recall Precision F-measure
(#examples) time (s) size (LOC)
Types 21 1.5 15 1.0 1.0 1.0
Expressions 33 3.5 26 0.78 1.0 0.88
Statements 14 1.3 8 1.0 1.0 1.0
Averages 22.7 2.1 16.3 0.93 1 0.96
Table 3: Effort of manual/CGBE code generators.
Code Approach Effort
generator (person hours)
UML2Java C S T L (CGBE) 16
UML2C C S T L (CGBE) 6
UML2Java8 C S T L (manual) 42
UML2Swift C S T L (manual) 56
Currently the approach is oriented to the produc-
tion of code generators from UML/OCL to 3GLs.
It is particularly designed to work with target lan-
guages supported by Antlr Version 4 parsers, and with
context-free grammars. Antlr parsers are available
for over 200 different software languages, so this is
not a strong restriction
2
. In order to apply CGBE to
target language T, the user needs to supply scripts
parseProgramType.bat, etc, which parse the corre-
sponding program elements of language T. The out-
line mapping of syntactic categories may also need to
be modified.
In principle, the approach could be generalised to
any source language with an available grammar and
parser. In future work, we will investigate the appli-
cation of the approach for the code generation of other
languages, and its application for abstraction (reverse-
engineering) in addition to code generation.
All the datasets and code used in this paper are
available at https://www.zenodo.org/record/5803090.
5 RELATED WORK
Our work is related to model transformation by-
example approaches such as (Balogh and Varro, 2008;
Burgueno et al., 2019), and to program translation
work utilising machine learning (Chen et al., 2018;
Facebook Research, 2021; Lachaux et al., 2020). The
approach of (Balogh and Varro, 2008) uses ILP to
learn model transformation rules. ILP appears to be
appropriate for the task of learning tree-to-tree map-
pings, since trees are naturally representable as Prolog
terms. In contrast to our approach, ILP requires the
user to manually provide counter-examples for invalid
2
https://github.com/antlr/grammars-v4
mappings. Neural network-based ML approaches
have achieved successful results for MTBE (Bur-
gueno et al., 2019) and language translation (Chen
et al., 2018) tasks. In contrast to our approach, these
do not produce explicit transformation or translation
rules, and they also require large training datasets of
corresponding examples. The Transcoder language
translation approach developed by Facebook (Face-
book Research, 2021; Lachaux et al., 2020) uses in-
stead monolingual training datasets. The approach
is based on recognising common aspects of differ-
ent languages, eg., common loop and conditional pro-
gram structures. As with the bilingual neural net ap-
proaches, large datasets are necessary, and only im-
plicit representations of learnt language mappings are
produced. In our view, neural net approaches are suit-
able for situations where precise rules do not exist
or cannot be identified (for example, translation be-
tween natural languages). However for discovering
precise translations, such as code generation map-
pings, a symbolic ML approach seems more appro-
priate.
Our approach utilises the MTBE approach of
(Lano et al., 2021b), by representing collections of
language categories as simple metamodels, and by
mapping paired text examples to instance models of
these metamodels. We extend the MTBE approach
with the capability to recognise tree-to-tree mappings,
and the facility to translate the resulting mappings to
C S T L.
6 CONCLUSIONS
We have described a process for synthesising code
generator transformations from datasets of text exam-
ples. The approach uses symbolic machine learning
in order to produce explicit specifications of the code
generators.
We have shown that this approach can produce
correct and effective code generators, with a signifi-
cant reduction in effort compared to manual construc-
tion of code generators.
Code Generation by Example
91

REFERENCES
Acceleo project (2021). https://www.eclipse.org/acceleo,
accessed 27.11.2021.
Antlr (2021). https://www.antlr.org.
Balogh, Z. and Varro, D. (2008). Model transformation by
example using inductive logic programming. SoSyM.
Burgueno, L., Cabot, J., and Gerard, S. (2019). An LSTM-
based neural network architecture for model transfor-
mations. In MODELS ’19, pages 294–299.
Buttner, F. and Gogolla, M. (2014). On OCL-based imper-
ative languages. Science of Computer Programming,
92:162–178.
Chen, X., Liu, C., and Song, D. (2018). Tree-to-tree neu-
ral networks for program translation. In 32nd Con-
ference on Neural Information Processing Systems
(NIPS 2018).
Eclipse Agile UML project (2021).
projects.eclipse.org/projects/modeling.agileuml,
accessed 27.11.2021.
Epsilon project (2021). https://projects.eclipse.org/projects/
modeling.epsilon. Accessed 27.11.2021.
Facebook Research (2021). TransCoder, github.com/ face-
bookresearch/TransCoder.
Greiner, S., Buchmann, T., and Westfechtel, B. (2016).
Bidirectional transformations with QVT-R: a case
study in round-trip engineering UML class models
and Java source code. In Modelsward 2016.
Lachaux, M.-A., Roziere, B., Chanussot, L., and Lample,
G. (2020). Unsupervised translation of programming
languages. arXiv:2006.03511v3.
Lano, K., Kolahdouz-Rahimi, S., and Alwakeel, L. (2021a).
Synthesis of mobile applications using AgileUML. In
ISEC 2021.
Lano, K., Kolahdouz-Rahimi, S., and Fang, S. (2021b).
Model Transformation Development using Auto-
mated Requirements Analysis, Metamodel Match-
ing and Transformation By-Example. ACM TOSEM,
31(2):1–71.
Lano, K., Xue, Q., and Kolahdouz-Rahimi, S. (2020). Ag-
ile specification of code generators for model-driven
engineering. In ICSEA 2020.
Lano, K., Yassipour-Tehrani, S., Alfraihi, H., and
Kolahdouz-Rahimi, S. (2017). Translating from
UML-RSDS OCL to ANSI C. In OCL 2017, STAF
2017, pages 317–330.
OMG (2014). Object Constraint Language (OCL) 2.4 Spec-
ification.
MODELSWARD 2022 - 10th International Conference on Model-Driven Engineering and Software Development
92
