Development of a New Fundamental Period Formula for Steel

Structures Considering the Soil-structure Interaction with the Use of

Machine Learning Algorithms

Ashley Megan van der Westhuizen

, George Markou

and Nikolaos Bakas

Department of Civil Engineering, University of Pretoria, South Africa

Department of RnD, RDC Informatics, Athens, Greece

Keywords: Seismic Design, Fundamental Period, Steel Structures, Nonlinear Regression, Soil-structure Interaction,

Machine-Learning Algorithms.

Abstract: The fundamental period of buildings is an important parameter when designing seismic resistant structures.

The current formulae proposed in design codes for determining the fundamental period of steel structures

cannot accurately predict the fundamental period of real structures. In addition, most of the current formulae

only consider the height of the structure in their formulation, while soil structure interaction (SSI) and the

orientation of the I-columns that influence the fundamental period are usually neglected. This research focuses

on the use of machine learning algorithms to obtain a new formula that accounts for different geometrical

features of the superstructure, where the SSI effect is also considered. After training and testing a 40-feature

formula, an additional 138 out-of-sample numerical results were used to further test the accuracy of the

proposed formula’s prediction abilities. The validation resulted in a correlation of 99.71%, which suggests

that the proposed formula exhibits high predictive features for the steel structures considered in this study.

1 INTRODUCTION

An important structural feature related to the dynamic

response of a structure is the fundamental period

(Young, 2011). Current building codes use empirical

equations to predict the fundamental period of

structures (Jiang et al., 2020, Taljaard et al., 2021 and

Gravett et al., 2021). For determining the

fundamental period of buildings, current international

codes have oversimplified formulae as they require

only the height of the structure and do not account for

the actual 3D geometry of the building nor account

for the interaction between the superstructure and

substructure.

The following design formulae are currently used

in the estimation of the fundamental period of steel

structures:

EC8:

𝑇



=𝐶





𝐻

)

.

Where:

𝐶



= 0.085 for momen

resistant space steel frames

𝐶



= 0.075 for eccentrically

raced steel frames

(1)

ASCE 7-05:

𝑇



= 0.0724



𝐻

)

.

for steel

moment-resisting frames

𝑇



= 0.0731



𝐻

)

.

for

eccentrically braced steel

frames

(2)

(3)

Another formula proposed by Cinitha (2012) also

takes into account the plan area of the building



𝐿×𝐵

)

and can be seen below:

𝑇



=𝐶





𝐿∙𝐵

)

.∙

(4)

With

𝐶



= 0.0247𝑒

.∙

(5)

𝛼 = 0.4473𝑒

.∙

(6)

Another work was also presented by Nassani,

2014, where a simple model for calculating the

fundamental period of vibration in steel structures

was presented. The proposed formulae in the

aforementioned research works do not consider the

SSI effect, therefore, the development of a formula

that will be able to account this important feature is

required. The phenomenon of SSI involves a

multidisciplinary field of structural mechanics, soil

mechanics and structural dynamics (Jayalekshmi and

Chinmayi, 2013 and Gravett et al., 2021). It has been

952

van der Westhuizen, A., Markou, G. and Bakas, N.

Development of a New Fundamental Period Formula for Steel Structures Considering the Soil-structure Interaction with the Use of Machine Learning Algorithms.

DOI: 10.5220/0010978400003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 3, pages 952-957

ISBN: 978-989-758-547-0; ISSN: 2184-433X

found that the SSI can increase the fundamental

period, thus is an important consideration when

determining the fundamental period of a structure

(Khalil et al., 2007 and Mourlas et al., 2020).

According to the research gap discussed in this

section, the objective of this research work is to

develop a new formula for predicting the fundamental

period of steel structures that considers the SSI effect.

Additionally, the proposed formula considers other

parameters such as the base conditions and

orientation of the I-columns. A total of 576 numerical

models using Reconan FEA (2020) were created to

obtain a dataset containing 1,152 numerical results.

The dataset is used to train a machine learning

algorithm to formulate a 40-feature formula, using a

higher order NLR model, which was then validated

through the use of out-of-sample data. It is important

to note here that the ability of Reconan FEA to predict

the fundamental period of structures was validated

through the use of experimental data found in the

international literature (Mourlas et al., 2019 and

Mourlas et al., 2021).

2 MACHINE LEARNING

There are 18 independent variables used in this

research work to train the machine learning

algorithm. These include the initial parameters such

as soil depth, Young’s Modulus of soil, height, length

and width of the superstructure, and the orientation of

the I-columns. The modified parameters added during

the training procedure to improve the predictability of

the developed closed form solution included



𝑝𝑎𝑟𝑎𝑚𝑒𝑡𝑒𝑟 + 1

)

and





Algorithm 1: Higher Order Regression.

Input: XX

(matrix of Independent Variables), YY (Vector of

Dependent Variable),

nlf (number of nonlinear features to be kept in the model)

Output: Prediction Formulae

1. Create all nonlinear features

(anlf)

2. For i from 1 to nlf do

3. For j from 1 to anlf do

4. Add j

feature to the model

5. Calculate Prediction Error, MAPE

6. End

7. Keep in the model the j

feature which yields the

minimum prediction error

5. End

Return: Prediction Formula

*with all inter-items combinations up to the 3

degree,

**Mean Absolute Percentage Error (MAPE).

The features were created to contain a

combination of the parameters up to the third degree

(Dimopoulos and Bakas, 2019). The algorithm was

set to use 85% of the data to train the algorithm and

15% of the data to test the proposed fundamental

period formula. The algorithm shown below

represents the applied procedure for developing the

proposed formula (Gravett et al., 2021).

3 DEVELOPMENT OF

NUMERICAL MODELS AND

DATASET

The main challenge for proposing a new design

formula is in the development of a sufficient number

of models that have varying soil depths, number of

stories, plan area and orientation of I-columns. In

addition to the test dataset, a validation dataset is

developed that contains the numerically obtained

fundamental period results of models that foresee out-

of-sample parameters as discussed below.

The finite element software Femap is used to

graphically create the models and Reconan FEA

(2020) is used to analyse and obtain the fundamental

periods numerically. The models were created using

a varying number of stories, bays and base conditions.

The development of the models started with an initial

model, which is a single storey, single bay structure

with a height of 3.5 m and a raft foundation assuming

a fixed base (see Figure 1). The geometry of the single

bay has a length of 5 m (in the x-direction) and a

width of 3 m (in the y-direction). The initial model

was used to develop additional building geometries

by altering the number of stories, number of spans,

depth of soil and orientation of I-columns.

Figure 1: Initial model.

Development of a New Fundamental Period Formula for Steel Structures Considering the Soil-structure Interaction with the Use of Machine

Learning Algorithms

953

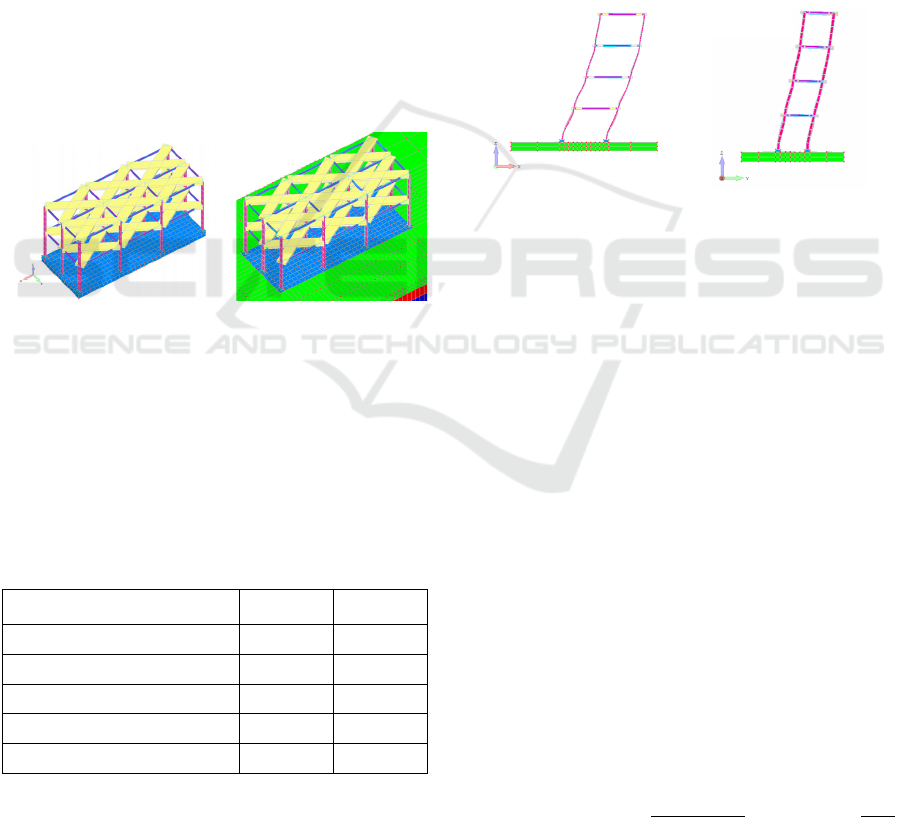
The initial model was modified to develop new

models that foresaw 2, 4, 6, 8 and 10 stories, each

with a 3.5 m height. Each of these models were then

modified to contain single, double, and triple spans

along the x-axis and, single and double spans along

the y-axis. The largest total plan area used to develop

the dataset foresaw a 15x6 m plan view, where the

smallest was 5x3 m.

The models were further modified to include the

SSI effect as seen in Figure 2. The discretization of

the soil domain foresaw depths of 1, 5, 12.5, 22.5 and

37.5 m. It is important to note that the superstructure

was discretized through the use of Natural Beam-

Column Flexibility-Based (NBCFB) finite elements,

where the raft slab and the soil domain were

discretized through 8-noded isoparametric

hexahedral elements. Three soil types were

considered in this research investigation, namely: soft

soil with a Young’s modulus of 65 MPa, soft to

medium soil with a Young’s modulus of 350 MPa and

medium soil with a Young’s modulus of 700 MPa.

(

)

(

)

Figure 2: 2-storey steel building. Triple span in long

direction, double span in short direction (a) fixed base wit

raft foundation (b) flexible base with soil hexahedral mesh.

Table 1 contains the minimum and maximum

values that each parameter had according to the

design of the geometrical features of the buildings

and the soil domains.

Table 1: Minimum and maximum parameter values for

model development.

Parameter Minimum Maximum

Soil Depth [m] 1 37.5

Soil E [kPa] 65 000 700 000

Height [m] 3.5 35

Length (along x-axis) [m] 5 15

Width (along y-axis) [m] 3 6

After the construction of the initial numerical

models that foresaw the use of the positioning of the

steel IPE columns’ section along a specific direction,

the number of models was increased by changing the

orientation of the columns’ section by 90

. The

columns’ strong axis orientation was modified from

being parallel to the global x-axis to being parallel to

the global y-axis direction of the structure, thus

allowing the investigation of this feature on the

fundamental period. It is important to note here that

the IPE200 section was used for all beams and the

IPE300 for constructing all columns.

Additionally, the slabs of the buildings were

assumed to be reinforced concrete (RC) slabs and

were modeled as diaphragms with a mass equal to the

mass of a 150 mm thick slab that foresees a live load

of 2 kN/m

Figure 3 shows the first two modal shapes of a 4-

storey, 1-bay steel building with 1 m soft soil.

(

)

(

)

Figure 3: Modal shape (a) 1 and (b) 2 of a 4-storey, 1-

steel buildin

founded on 1 m dee

soft soil.

4 PROPOSED FUNDAMENTAL

PERIOD FORMULA

The proposed formula for determining the

fundamental period of steel structures was

determined from the numerical results of 1,152 data

points. The formula contains 40-features, which are a

combination of the following parameters:

𝑇 is the fundamental period (s)

𝐷



is the depth of soil (m)

𝐸 is the soils Young’s Modulus (kPa)

𝐻 is the building height (m)

𝐿 is the length of the building parallel to the

oscillating direction (m)

𝐵 is the width of the building perpendicular to

the oscillating direction (m)

𝐶𝑂 is the orientation of the columns (either a 1

or 2)

𝑙𝑃𝑎𝑟𝑎𝑚𝑒𝑡𝑒𝑟 is ln



𝑃𝑎𝑟𝑎𝑚𝑒𝑡𝑒𝑟 + 1

)

i.e., 𝑙𝐷





𝐷



)

𝐼𝑛𝑣𝑃𝑎𝑟𝑎𝑚𝑒𝑡𝑒r is





i.e., 𝐼𝑛𝑣𝐷











The developed formula is given in Equation 7. It

must be noted here that numerous formulae have been

=1.524 s T

=0.518

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

954

investigated that foresaw 5, 10 and 20 features, where

it was found that the 40-feature formula was able to

provide with the highest accuracy in terms of fitting

into the training and test data, but most importantly in

terms of predicting accurately the out-of-sample data

compared to other machine learning generated

formulae.

Figure 4: Relationship between numerically predicted and

formula predicted fundamental periods on test and train

dataset.

𝑇 =0.194630 ∙𝑙𝐻



+0.0580556 ∙ 𝐶𝑂



∙𝐵

−9.39027 ∙𝐼𝑛𝑣𝐶𝑂∙𝐼𝑛𝑣𝐵∙𝑙𝐵

−8.49213 ∙𝐼𝑛𝑣𝐿∙𝐶𝑂∙𝐻

−41.8498 ∙𝐼𝑛𝑣𝐶𝑂∙𝑙𝐿∙𝐻

−8.14564 ∙𝐼𝑛𝑣𝐸∙𝐸∙𝐻−0.800465 ∙𝐶𝑂∙𝐵∙𝐻

+114.808 ∙𝐼𝑛𝑣𝐶𝑂∙𝐼𝑛𝑣𝐵∙𝐻

+46.6778 ∙𝐼𝑛𝑣𝐶𝑂∙𝐼𝑛𝑣𝐵



+0.0631499 ∙ 𝐵



∙𝐻

+4.20803 ∙𝑙𝐵∙𝐶𝑂∙𝐻−0.144945 ∙𝑙𝐿∙𝐻∙𝐿

+0.847694 ∙𝐵∙𝐻∙𝐼𝑛𝑣𝐿+9.37930 ∙𝐼𝑛𝑣𝐿



∙𝐻

−1.08930 ∙𝐼𝑛𝑣𝐶𝑂



∙𝐿+4.04342 ∙𝐼𝑛𝑣𝐿

−0.251627 ∙𝐼𝑛𝑣𝐿∙𝐶𝑂∙𝐵

−0.00783561 ∙𝐼𝑛𝑣𝐵∙𝑙𝐶𝑂∙𝑙𝐸

+0.523388 ∙𝑙𝐿



∙𝐼𝑛𝑣𝐶𝑂

+0.0947335 ∙𝐼𝑛𝑣𝐻∙𝑙𝐻∙𝐿

+46.8309 ∙𝐼𝑛𝑣𝐸∙𝐻∙𝑙𝐷𝑠+0.00764850 ∙𝑙𝐻∗𝐵

+0.000161108 ∙𝑙𝐿∙𝐿∙𝑙𝐸

−20.5554 ∙𝐼𝑛𝑣𝐸∙𝐶𝑂∙𝐷𝑠

−0.00474725 ∙𝐼𝑛𝑣𝐿



∙𝐼𝑛𝑣𝐷𝑠

+2.73101 ∙𝐼𝑛𝑣𝐿∙𝐼𝑛𝑣𝐻∙𝐶𝑂

+0.403996 ∙𝐼𝑛𝑣𝐶𝑂∙𝑙𝐵∙𝐿

−0.0105914 ∙𝑙𝐿∙𝐿∙𝐵

−0.228100 ∙𝑙𝐵



∙𝐶𝑂

+0.00265642 ∙𝐼𝑛𝑣𝐿∙ 𝐻



−2.58386 ∙𝐼𝑛𝑣𝐵∙𝐼𝑛𝑣𝐻∙𝐶𝑂

+5.84142 ∙𝐼𝑛𝑣𝐶𝑂∙𝐻∙𝐿

+29.5168 ∙𝐼𝑛𝑣𝐶𝑂∙𝐻

+0.849560 ∙𝐼𝑛𝑣𝐿∙𝑙𝐻∙𝐶𝑂

−2.14776 ∙𝐼𝑛𝑣𝐵∙𝑙𝐻∗𝑙𝐶𝑂

+1.34222 ∙𝑙𝐵∙𝑙𝐻∙𝐼𝑛𝑣𝐻

−0.00333495 ∙𝑙𝐸∙𝐿∙𝐼𝑛𝑣𝐻

−2.64111 ∙𝐼𝑛𝑣𝐵



∙𝐼𝑛𝑣𝐻

+71.1358 ∙𝐼𝑛𝑣𝐻∙𝐷𝑠∙𝐼𝑛𝑣𝐸

−17.9194 ∙𝐼𝑛𝑣𝐸∙𝑙𝐸∙𝑙𝐿−1.16636

(7)

Figure 4 shows the similarity ratio of the proposed

formula compared to the numerically predicted data

used to train and test the developed relationship. The

correlation ratio was found to be 99.95% as it derives

from the training and testing procedure.

5 FURTHER VALIDATION OF

THE PROPOSED FORMULA

A set of 138 fundamental periods were generated

through the use of additional models that were not

used during the training and testing procedure so as

to investigate the performance of the proposed 40-

feature formula when out-of-sample data are used.

The validation dataset was created using random

parameter values not included in the train and test

datasets. 3, 5, 7 and 9-storey models and models with

Young’s modulus of 10 MPa and 100 MPa were used.

Figure 5 shows two of these models that were

developed for the validation stage that foresaw 5 and

9 storeys. The out-of-sample parameters were

assumed to validate whether the new proposed

formula would be able to accurately predict the

fundamental period of steel structures that had

parameter values that differ from those that were used

to train and test the predictive model.

(

)

(

)

Figure 5: (a) 5-storey, 1-bay, (b) 9-storey, 3-bay 5m soil

models developed for validation stage.

The numerically predicted periods were plotted

against those obtained using the proposed formula as

seen in Figure 6. By evaluating the correlation

between the numerically predicted periods and those

obtained using the proposed formula, it is observed

that a high correlation (𝑅



= 99.71%) was achieved.

This shows that the formula yields a high accuracy

prediction and can be used to predict the fundamental

period of framed steel structures that have

geometrical features within the limits presented in

Table 1.

y = 0,9994x + 0,0008

R² = 0,9995

0,5

1,5

2,5

3,5

4,5

0 0,5 1 1,5 2 2,5 3 3,5 4 4,5

Formula Predicted Period [s]

Numerically Predicted Period [s]

Development of a New Fundamental Period Formula for Steel Structures Considering the Soil-structure Interaction with the Use of Machine

Learning Algorithms

955

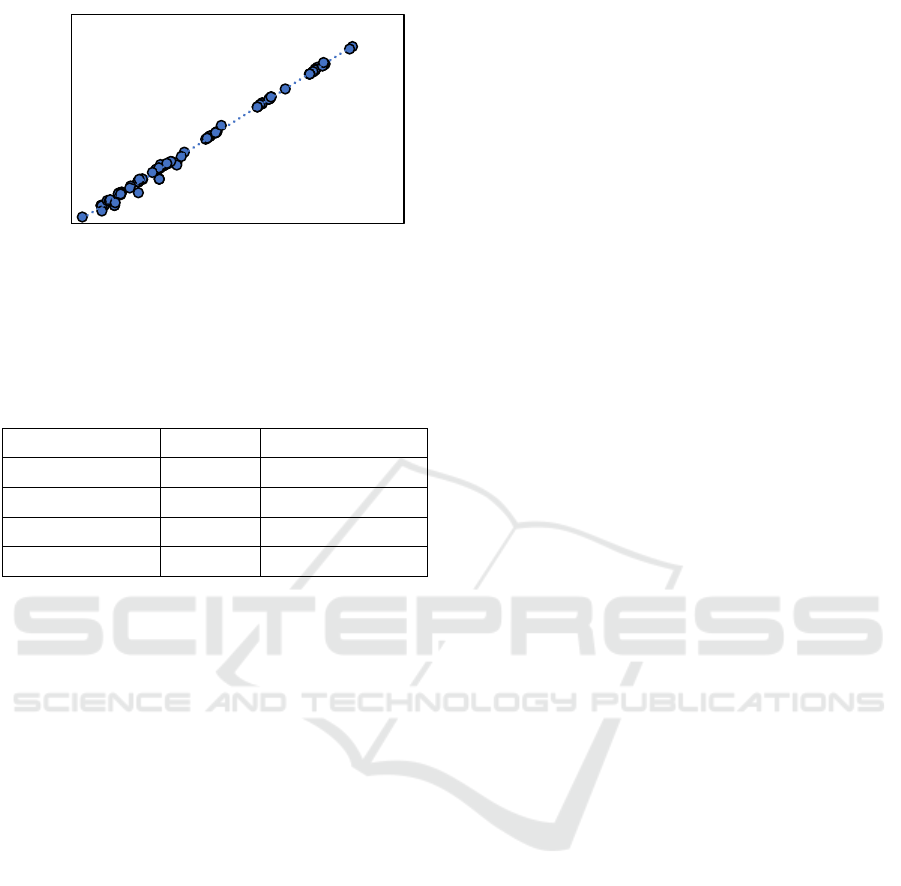
Figure 6: Relationship between numerically predicted and

formula predicted fundamental periods on the out-of-

sample validation dataset.

Table 2: Comparison of fundamental period error

predictions on the validation dataset.

Description Formula Mean absolute error

40-feature formula Equation 7 2.8%

EC8 Equation 1 76%

ASCE Equation 2 76%

Cinitha (2012) Equation 4 92%

Table 2 shows the comparison between the

numerically obtained fundamental periods and those

obtained using the proposed formula as well as the

formulae currently found in design codes and the

international literature. It is evident that the current

design codes estimate the fundamental period with a

high mean absolute error as compared to the new

proposed formula.

6 CONCLUSIONS AND

RECOMMENDATIONS

A newly proposed formula for predicting the

fundamental period of steel structures with the use of

machine-learning algorithms was presented. The

proposed formula considers the depth of soil,

Young’s modulus of soil, height and plan area of the

structure, as well as the orientation of the I-columns.

The 40-feature formula proposed was developed

using an algorithm combining the parameters using a

higher order NLR.

The proposed fundamental period formula was

tested on out-of-sample steel structures, where a

correlation of 99.71% was achieved. This shows that

the proposed formula produces accurate results and

can be further used to predict the fundamental period

of out-of-sample results. Design code formulae for

the calculation of the fundamental period of steel

structures were compared to the proposed formula,

where it was found that the proposed predictive

model derived a 27 times smaller mean absolute error.

In addition to that, the proposed fundamental period

formula was found to be superior to other existing

proposed equations found in the international

literature when used on the under-study datasets.

The study focuses on steel structures with regular

plans. To expand the dataset and further investigate

the dynamic response of steel framed structures,

irregular in plan buildings will be investigated, where

braced and infill frames will be modeled in future

research work. Finally, for each type of steel framing

system, larger models will be created to develop

formulae that will be applicable to a broader spectrum

of frame geometries.

REFERENCES

Cinitha, A 2012. A rational approach for fundamental

period of low and medium rise steel building frames.

International Journal of Modern Engineering Research,

2(5):3340-3346.

Dimopoulos, T and Bakas, N 2019. Sensitivity analysis of

machine learning models for the mass appraisal of real

estate. Case study of residential units in Nicosia,

Cyprus. Remote sensing, 11(24):3047

Gravett, Z D, Mourlas, C, Taljaard V L, Bakas, P N,

Markou, G and Papadrakakis, M 2021. New

Fundamental Period Formulae for Soil-Reinforced

Concrete Structures Interaction Using Machine

Learning Algorithms and ANNs. Soil Dynamics and

Earthquake Engineering, 144: 106656

Jayalekshmi, B and Chinmayi, H 2013. Effect of soil

flexibility on lateral natural period in RC framed

buildings with shear wall. International Journal of

Innovative Research in Science, Engineering and

Technology, 2(6):2067-2076.

Jiang, R, Jiang, L, Hu, Y, Jiang, L and Ye, J 2020. A

simplified method for fundamental period prediction of

steel frames with steel plate shear walls. The structural

design of tall and special buildings, 29(7):1-15.

Khalil, L, Sadek, M and Shahrour, I 2007. Influence of the

soil–structure interaction on the fundamental period of

buildings. Earthquake engineering & structural

dynamics, 36(15):2445-2453.

Mourlas, C, Markou, G and Papadrakakis, M 2019.

Accurate and Computationally Efficient Nonlinear

Static and Dynamic Analysis of Reinforced Concrete

Structures Considering Damage Factors. Engineering

Structures, 178:258–285.

Mourlas, C, Khabele, N, Bark, H A, Karamitros, D, Taddei,

F, Markou, G and Papadrakakis, M 2020. The Effect of

Soil-Structure Interaction on the Nonlinear Dynamic

Response of Reinforced Concrete Structures.

y = 1,0171x - 0,0442

R² = 0,9971

0,5

1,5

2,5

3,5

4,5

00,511,522,533,544,5

Formula Predicted Period [s]

Numerically Predicted Period [s]

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

956

International Journal of Structural Stability and

Dynamics, 20(13): 2041013 doi:10.1142/S02194554

20410138

Mourlas, C. and Markou, G. 2020. ReConAn v2.00 Finite

Element Analysis Software User's Manual.

Nassani, D E 2014. A simple model for calculating the

fundamental period of vibration in steel structures.

APCBEE procedia, 9:339-346.

Reconan FEA v2.00, User’s Manual. 2020.

https://www.researchgate.net/publication/342361609_ReC

onAn_v200_Finite_Element_Analysis_Software_User

's_Manual

Spijkerman, Z, Bakas, N, Markou, G and Papadrakakis, M

2021. Predicting the Shear Capacity of Reinforced

Concrete Slender Beams Without Stirrups by Applying

Artificial Intelligence Algorithms. COMPDYN 2021,

27-30 June 2021, Streamed from Athens, Greece.

Taljaard, V L, Gravett, D Z, Mourlas, C, Bakas, N, Markou,

G and Papadrakakis, M 2021. Development of a New

Fundamental Period Formula by Considering Soil-

Structure Interaction with the Use of Machine Learning

Algorithms, COMPDYN 2021, 27-30 June 2021,

Streamed from Athens, Greece.

Young, K C 2011. An Investigation of the Fundamental

Period of Vibration of Irregular Steel Structures. The

Ohio State University.

Development of a New Fundamental Period Formula for Steel Structures Considering the Soil-structure Interaction with the Use of Machine

Learning Algorithms

957