
A Step Towards the Explainability of Microarray Data for Cancer
Diagnosis with Machine Learning Techniques
Adara S. R. Nogueira
1
, Artur J. Ferreira
1,3 a
and M
´
ario A. T. Figueiredo
2,3 b
1
ISEL, Instituto Superior de Engenharia de Lisboa, Instituto Polit
´
ecnico de Lisboa, Portugal
2
IST, Instituto Superior T
´
ecnico, Universidade de Lisboa, Portugal
3
Instituto de Telecomunicac¸
˜
oes, Lisboa, Portugal
Keywords:
Machine Learning, Feature Selection, Feature Discretization, Microarray Data, Cancer Explainability.
Abstract:
Detecting diseases, such as cancer, from from gene expression data has assumed great importance and is a
very active area of research. Today, many gene expression datasets are publicly available, which consist of
microarray data with information on the activation (or not) of thousands of genes, in sets of patients that have
(or not) a certain disease. These datasets consist of high-dimensional feature vectors (very large numbers of
genes), which raises difficulties for human analysis and interpretation with the goal of identifying the most
relevant genes for detecting the presence of a particular disease. In this paper, we propose to take a step towards
the explainability of these disease detection methods, by applying feature discretization and feature selection
techniques. We accurately classify microarray data, while substantially reducing and identifying subsets of
relevant genes. These small subsets of genes are thus easier to interpret by human experts, thus potentially
providing valuable information about which genes are involved in a given disease.
1 INTRODUCTION
The problem of analysing a patient’s DNA data to
identify the presence/absence of specific genes, in-
dicative of certain diseases, such as cancer, is an
active topic of research where machine learning
tools play an important role. Many gene expres-
sion datasets are publicly available (Alonso-Betanzos
et al., 2019)
1
, which include microarray data with in-
formation on the activation (or not) of thousands of
genes, in sets of patients who have (or not) a certain
disease. Ideally, one would like to use these datasets
to learn to predict the presence of a given disease on
new patients, given their microarray data, and to iden-
tify the most relevant genes for that purpose. How-
ever, these datasets are very high-dimensional, which
raises difficulties for human experts to interpret the
data. It is laborious to identify the most important
genes that explain the presence of a particular disease.
In addition to their high dimensionality, these datasets
have a small number of instances due to the high cost
of acquiring new instances.
Applying classification techniques directly on
a
https://orcid.org/0000-0002-6508-0932
b
https://orcid.org/0000-0002-0970-7745
1
http://csse.szu.edu.cn/staff/zhuzx/Datasets.html
these datasets poses challenges due to the “curse of
dimensionality” issues (Bishop, 1995). The perfor-
mance of the classifiers is sub-optimal and it is often
not possible to determine, in detail, which genes are
relevant to detect a given disease. In this paper, we
apply feature discretization (FD) (Garcia et al., 2013),
feature selection (FS) (Duda et al., 2001; Guyon et al.,
2006), to microarray datasets, to overcome these is-
sues. Moreover, analysing the resulting feature sub-
sets allows identifying the smallest subset of features
that are indicative of a given disease. These subsets
allow human interpretability of the data. Figure 1
depicts the main steps of the approach taken in this
work.
Figure 1: The key steps of the proposed approach.
The remainder of this paper is organized as fol-
362
Nogueira, A., Ferreira, A. and Figueiredo, M.
A Step Towards the Explainability of Microarray Data for Cancer Diagnosis with Machine Learning Techniques.
DOI: 10.5220/0010980100003122
In Proceedings of the 11th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2022), pages 362-369
ISBN: 978-989-758-549-4; ISSN: 2184-4313
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

lows. Section 2 overviews the state-of-the-art on
DNA microarray techniques and reviews some ap-
proaches. The proposed approach as well as the mi-
croarray datasets are presented in Section 3. The ex-
perimental evaluation is reported in Section 4. Fi-
nally, Section 5 ends the paper with concluding re-
marks and directions for future work.
2 DNA MICROARRAYS
In this section, we review the key aspects regarding
the DNA Microarray technique and data generation
(Section 2.1) as well as some approaches to deal with
this type of data (Section 2.2).
2.1 The DNA Microarray Technique
Every biological organism has a set of genes encoded
in its DNA. These may be expressed, i.e., active,
in different cells at different points in time. In the
context of biological/medical research, it’s important
to understand which genes are being expressed (ac-
tive/inactive) in a given cell, at a given point in time.
However, living beings have thousands of genes, e.g.,
humans have approximately 21000 (Forero and Pa-
trinos, 2020; Weinberg, 2014). Each one of these
genes is responsible for encoding a protein, which is
in charge of a specific functionality. Given the com-
plexity and amount of information, it is currently in-
feasible to analyse this data one gene at a time. Even
if it were possible, it would take a very long time and
the efficiency and accuracy of the analysis would be
extremely low.
The DNA microarray technique (Simon et al.,
2003) addresses this issue. A DNA microarray allows
researchers and healthcare professionals to carry out
an investigation on thousands of genes at a time, i.e.,
in one single experiment
2
and determine which genes
are being expressed by a cell. A DNA microarray has
the following characteristics:
• a microarray is a solid surface with thousands of
spots arranged in well-ordered columns and rows;
• each spot on this microarray characterizes only
one gene and contains multiple strands of the
same DNA, i.e. the DNA sequence is unique;
• each spot location and its respective DNA se-
quence is recorded in a database.
DNA microarrays can identify dissimilarities be-
tween cancer cells and healthy cells, more specif-
2
https://learn.genetics.utah.edu/content/labs/
microarray/
ically, which genes in a cancer cell are being ex-
pressed, but not in a healthy cell.
Figure 2: Overview of the DNA Microarray Technique.
Figure 2 presents an overview of the DNA mi-
croarray technique. First, it’s necessary to extract
the ribonucleic acid (RNA) from the samples cells
and then draw out the messenger RNA (mRNA) from
the existing RNA, because only the mRNA devel-
ops gene expression. Then, a DNA copy is made
from the mRNA with the aid of the reverse transcrip-
tase enzyme, which will generate the complementary
DNA (CDNA). In this process, a label is added in the
CDNA representing each cell sample, e.g., a fluores-
cent red for the cancer cell and a fluorescent green
for the healthy cell. This step is necessary because
DNA is a more stable molecule than RNA and the
labelling allows identifying the genes in each sam-
ple later. Both CDNA types previously created are
added to the DNA microarray and because each spot
of it already has many unique CDNA. When mixed
together they will base pair each other due to the
DNA property, designated complementary base pair-
ing. This process is denominated “hybridization”.
Not all CDNA strands will bind to each other, some
may not hybridize therefore they need to be washed
off. Finally, the DNA microarray is analyzed with a
scanner, which can find patterns of hybridization by
detecting the fluorescent colors. As a result, we can
observe the following:
• only a few red CDNA molecules bound to a spot,
which means the gene was being expressed only
in the red (cancer) cell;
• only a few green CDNA molecules bound to an-
other spot, which means the gene was being ex-
pressed only in the green (healthy) cell;
• some of both red and green CDNA molecules
bound to a single spot on the microarray (forming
a yellow spot), which means the gene was being
expressed both in the cancer and the healthy cell;
• several spots of the microarray don’t have a single
red or green CDNA strand bound to it, because
the gene is not being expressed in either cell.
The red color on a spot indicates the higher produc-
tion of mRNA in the cancer cell compared to the
healthy cell. On the other hand, the green color spec-
ifies the higher production of mRNA in the healthy
A Step Towards the Explainability of Microarray Data for Cancer Diagnosis with Machine Learning Techniques
363

cell as compared to the cancer cell. However, a yel-
low spot suggests that the gene is expressed equally
in both cells and therefore, they are not relevant as
the cause of the disease, because when the healthy
cell becomes cancerous its activity does not undergo
a change. Using DNA microarray, we can analyze
a large amount of genes at the same time, find which
genes are being expressed and decide on a better prog-
nosis based on the previous analyzes.
Figure 3 depicts the process of generating a
dataset from the use of the DNA microarray technique
mentioned in Figure 2. The datasets considered in this
work are obtained with this process.
Figure 3: Dataset generation from DNA Microarray.
2.2 Related Approaches
In the last decades, there has been considerable re-
search on microarray data classification for cancer
diagnosis (Alonso-Betanzos et al., 2019; Yip et al.,
2011; Statnikov et al., 2005b). Many unsupervised
and supervised FD and FS techniques have been em-
ployed on this type of data, before classification takes
place. Since microarray datasets are typically la-
belled, supervised techniques are usually preferred to
unsupervised ones. In this section, we briefly review
some of the existing related work using FD, FS, and
classification techniques.
A survey of common classification techniques and
related methods to increase their accuracy for mi-
croarray analysis is presented by Alonso-Betanzos
et al. (2019); Yip et al. (2011). The experimental
evaluation is carried out in publicly available datasets.
Saeys et al. (2007) surveyed FS techniques used for
this type of data, showing their adequacy.
It has been found that unsupervised FD performs
well when combined with several classifiers. For
instance, the equal frequency binning (EFB) tech-
nique with Na
¨
ıve Bayes (NB) classifier produces very
good results (Witten et al., 2016). It has also been
reported that applying equal interval binning (EIB)
and EFB with microarray data, together with support
vector machines (SVM) classifiers, yields good re-
sults (Meyer et al., 2008). The work of Statnikov et al.
(2005a) shows that FS significantly improves the clas-
sification accuracy of multi-class SVM classifiers and
other classification algorithms.
An FS filter for microarray data, with an
information-theoretic criterion named double input
symmetrical relevance (DISR), which measures fea-
ture complementarity, was proposed by Meyer et al.
(2008). The reported experimental results on one syn-
thetic dataset and 11 microarray datasets show that the
DISR criterion is competitive with existing FS filters.
Diaz-Uriarte and Andres (2006) explored FS tech-
niques, such as backwards elimination of features
and classification, both using random forests (RF).
The authors applied the chosen method on one simu-
lated and nine real microarray datasets and found that
RF has better performance than other classification
methods, such as diagonal linear discriminant analy-
sis (DLDA), K-nearest neighbors (KNN), and SVM.
They also showed that the used FS technique led to a
smaller subset of features than alternative techniques,
namely Nearest Shrunken Centroids and a combined
method of filter and nearest neighbor classifier.
The work by Li et al. (2018) introduced the use of
large-scale linear support vector machine (LLSVM)
and recursive feature elimination with variable step
size (RFEVSS) as an enhancement to the traditional
FS technique based on SVM with recursive feature
elimination (SVMRFE), which is considered one of
the best methods in the literature, but exhibits large
computational cost. The improved approach consists
in upgrading the RFE by varying the step size with
the goal of reducing the number of iterations (the step
size is kept higher in the initial stages of this process
where non-relevant features are discarded). In addi-
tion, the standard SVM is upgraded to a large-scale
linear SVM and thus accelerating the method of as-
signing weights. The authors compare their approach
to FS with SVM and RF, and use the SVM, NB, KNN
and logistic regression (LR) classifiers. These tech-
niques are applied on six microarray datasets and the
approach provides better performance with compara-
ble levels of accuracy, showing that SVM and LR out-
perform the other two classifiers.
Recently, in the context of cancer explainability,
Consiglio et al. (2021) considered the problem of
finding a small subset of features capable of discern-
ing among six classes of instances. These classes may
be healthy or cancerous. The goal was to define a
comprehensive set of rules based on the most relevant
features (selected by their technique) that can distin-
guish classes based on their gene expressions. The
proposed method combines a genetic algorithm (GA)
to conduct FS and a fuzzy rule-based system to ex-
ecute classification on a dataset, with 21 instances,
more than 45 thousand features, and 6 classes. Ten
rules were devised, each one of them taking into ac-
count specific features, which make them crucial in
ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods
364

explaining the classification results of ovarian cancer
detection.
3 PROPOSED APPROACH
In this section, we present our proposed approach to
handle DNA microarray datasets with machine learn-
ing techniques. Section 3.1 describes the public do-
main datasets used in the experimental evaluation.
Section 3.2 presents the pipeline of techniques that we
apply on the data and the procedures that we follow.
3.1 Microarray Datasets
Table 1 presents the main characteristics of the 11 mi-
croarray datasets used in this work. In this table, n
denotes the number of instances, d indicates the num-
ber of features, and c the number of classes. We also
show the
d
n
ratio.
These datasets exhibit the common characteristic
of having many more features than instances, thus
n >> d, making the
d
n
ratio quite high for some
datasets, which conveys a challenge in applying ma-
chine learning techniques in these data (Bishop, 1995;
Duda et al., 2001). All datasets have a large number
of features, with d ranging from 2000 to 24481. In ad-
dition, as evidenced by the n column, all datasets have
a small number of instances, with n ranging from 60
to 253.
Table 2 describes the classification task for each
of datasets presented in Table 1. We have binary
classification and multi-class classification problems.
A binary dataset indicates the presence/absence of a
specific tumor/cancer (such as in the CNS, Colon,
and Ovarian datasets), the re-incidence of a dis-
ease (such as in the Breast dataset), or the diag-
nosis between two types of cancer (such as in the
Leukemia dataset). A multi-class dataset distin-
guishes between different types of cells (such as
in the Leukemia 3c, Leukemia 4c and Lymphoma
datasets), and tumors/cancer (such as in the Lung,
Table 1: Microarray Datasets Characteristics.
Name n d c d/n
Breast 97 24481 2 252.38
CNS 60 7129 2 118.81
Colon 62 2000 2 32.25
Leukemia 72 7129 2 99.01
Leukemia
3c 72 7129 3 99.01
Leukemia 4c 72 7129 4 99.01
Lung 203 12600 5 62.06
Lymphoma 66 4026 3 61.00
MLL 72 12582 3 174.75
Ovarian 253 15154 2 59.89
SRBCT 83 2308 4 27.80
Table 2: Microarray Datasets Clinical Tasks.
Name Description
Breast Breast cancer diagnosis
CNS Central Nervous System tumor diagnosis
Colon Colon tumor diagnosis
Leukemia Acute Lymphocytic Leukemia and
Acute Myelogenous Leukemia diagnosis
Leukemia 3c Distinguishes types of blood cells which became cancerous
Leukemia 4c Distinguishes types of blood cells which became cancerous
Lung Lung cancer diagnosis
Lymphoma Distinguishes subtypes of non-Hodgkin lymphoma
MLL Distinguishes types of acute leukemia, including
Mixed Lineage Leukemia
Ovarian Ovarian cancer diagnosis
SRBCT Distinguishes types of of Small Round Blue Cell Tumors
MLL, and SRBCT datasets).
3.2 Machine Learning Pipeline
The connection between our proposal and the related
work is that we consider the microarray datasets re-
ferred in these studies as well as the most often used
classifiers. We also address different data represen-
tation techniques, combining FD and FS techniques,
before classification. Our aim is not solely the correct
classification (regarding the error rate, false negative
rate, and false positive rate), but also to find the sub-
sets of features that are more decisive for the classifi-
cation task. In detail, the steps of our approach are:
• choose which techniques to evaluate, based on the
existing literature;
• build a machine learning pipeline using data rep-
resentation/discretization, dimensionality reduc-
tion and data classification techniques;
• compare the performance of each technique;
• and finally, identify the best suited technique as
well as the best subset of features to the problem
and datasets under consideration.
Figure 4 depicts the machine learning pipeline of
the actions that we apply on the datasets.
Figure 4: The pipeline of the proposed approach.
4 EXPERIMENTAL EVALUATION
This section reports the experimental evaluation of the
proposed approach on the 11 microarray datasets de-
scribed in Table 1 and Table 2. The machine learning
pipeline is depicted in Figure 4. The experimental re-
sults are organized as follows:
A Step Towards the Explainability of Microarray Data for Cancer Diagnosis with Machine Learning Techniques
365

• Section 4.1 describes the baseline classification
results without FD and FS techniques, using the
SVM and decision tree (DT) classifiers (phases
(a), (d), and (e) of the pipeline). We chose
these classifiers since they take rather different ap-
proaches for classification.
• Section 4.2 addresses the use of FD techniques
(phases (a), (b), (d), and (e) from the pipeline)
and also reports the experimental results of FS
techniques (phases (a), (c), (d), and (e) of the
pipeline). Finally, it identifies the best parameter
configuration found for each dataset.
• Section 4.3 presents experimental results toward
the explainability of the classification, by identify-
ing the best subsets of features for some datasets.
4.1 Baseline Classification Results
First, we evaluate the data classification phase of the
pipeline, on each dataset. We check the performance
of the selected classifiers (SVM and DT) to establish
the baseline results. We have chosen the SVM clas-
sifier because it is the classification technique that in
the literature reports the best results. We have also
chosen DT because it is a different classification ap-
proach, which is seldom applied to this type of data.
As the methodology for training and testing the classi-
fiers, we consider the leave-one-out cross-validation
(LOOCV) technique for all the evaluations in this pa-
per. Since the number of instances n is small, we
achieve a better estimate of the generalization error
and the other evaluation metrics, since there is no
standard deviation due to the data sampling procedure
as it happens on standard 10-fold cross-validation.
Table 3 presents the baseline results (no FD nor
FS) with phase (b) of the pipeline being the normal-
ization of all feature values to the range 0 to 1. Ta-
ble 4 shows a similar evaluation for the DT classifier.
In our experiments, we have found that using entropy
as a criterion to build the tree is better than using the
Gini index; we have also found that the initial ran-
dom state parameter set to 42 is the best choice.
These experimental results from Table 3 and Ta-
ble 4 show that DT does not achieve better results
than the SVM classifier (DT only performs better than
SVM on the CNS dataset). Thus, from these experi-
ments and from the existing literature, SVM with lin-
ear kernel seems to be an adequate classifier for this
type of data. It is also preferable to normalize the data
before doing any machine learning tasks.
4.2 Feature Discretization Assessment
In the literature of microarray data and for other types
of data and machine learning problems, the unsuper-
vised EFB method is know to produce adequate re-
sults. Thus, we have carried out some experiments
using this discretization method. Table 5 reports the
results of the SVM classifier on data discretized by
EFB, with different number of bins.
Analyzing these results for all datasets, we con-
clude that EFB discretization yields a small improve-
ment for the SVM classifier (lower standard deviation
in all datasets). Table 6 shows a summary of the re-
sults of the best configurations of EFB discretization
and SVM/DT classifiers. For each dataset, we select
the best configuration found in our experiments.
We now address the use of FS on the normal-
ized features (without discretization). For our experi-
ments, we consider the Laplacian score (LS), Spec-
tral, Fisher Ratio (FiR), and relevance-redundancy
feature selection (RRFS) (Ferreira and Figueiredo,
2012). Table 7 shows the experimental results for the
SVM classifier. RRFS works in unsupervised mode
using the mean-median (MM) relevance metric and
in supervised mode using FiR as metric.
The RRFS method attains the best classification
error results. We also achieve considerable dimen-
sionality reduction. For instance, on the Ovarian
dataset, we get a reduction to 4% of the original di-
mensionality: the number of selected features is about
606, from the original set of 15154 features. A similar
result is obtained for the Lymphoma dataset, in which
we keep 2% of the original features.
We now address the joint effect of all the pipeline
phases depicted in Figure 4. Table 8 presents the best
configurations for each phase and each dataset.
4.3 Explainability of the Data
In this section, we aim to identify the most rele-
vant features for a given dataset, now that we have
acceptable classification results on the previous sec-
tions. Figure 5 (top) shows the feature indices that
are chosen more often on the LOOCV procedure for
the Lymphoma and Ovarian datasets. For a dataset
with n instances, each feature can be chosen up to n
times. The importance of a feature to (accurately clas-
sify) a dataset and to explain the classification results
is proportional to the number of times that feature is
chosen in this procedure. We show the top 100 fea-
tures. In the bottom of this figure, we show a similar
plot for the Leukemia and Leukemia 3c datasets. We
now consider all the features in the dataset, displaying
the number of times each feature is chosen. For both
ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods
366
Table 3: Test error rate (Err) of LOOCV for the SVM classifier. For five datasets that have a class label of “no cancer”, we
also consider the false negative rate (FNR) and false positive rate (FPR). For the other six datasets, we dont report the FNR
and FPR metrics, because the task is to distinguish between cancer types. The best result is in boldface.
Linear kernel Poly kernel RBF kernel Sigmoid kernel
Dataset Err FNR FPR Err FNR FPR Err FNR FPR Err FNR FPR
Breast 0.31 0.30 0.31 0.33 0.28 0.37 0.37 0.46 0.29 0.47 1.00 0.00
CNS 0.33 0.62 0.18 0.37 0.62 0.23 0.35 1.00 0.00 0.35 1.00 0.00
Colon 0.18 0.27 0.12 0.27 0.55 0.12 0.21 0.50 0.05 0.39 0.82 0.15
Leukemia 0.01 – – 0.03 – – 0.15 – – 0.35 – –
Leukemia 3c 0.04 – – 0.06 – – 0.26 – – 0.47 – –
Leukemia 4c 0.07 – – 0.10 – – 0.32 – – 0.47 – –
Lung 0.05 0.01 0.12 0.05 0.01 0.18 0.09 0.01 0.24 0.32 0.00 1.00
Lymphoma 0.00 – – 0.00 – – 0.00 – – 0.30 – –
MLL 0.03 – – 0.06 – – 0.10 – – 0.61 – –
Ovarian 0.00 0.00 0.00 0.004 0.00 0.01 0.02 0.01 0.02 0.36 0.00 1.00
SRBCT 0.00 – – 0.01 – – 0.07 – – 0.65 – –
Average, X 0.09 0.24 0.15 0.12 0.29 0.18 0.18 0.40 0.12 0.43 0.56 0.43
Std. dev.,σ 0.12 0.23 0.10 0.13 0.26 0.12 0.13 0.37 0.12 0.11 0.47 0.47
Table 4: Test error rate (Err), FNR, and FPR of LOOCV for the DT classifier using entropy as criterion and random state set
to 42, with normalized features in the range 0 to 1. Different values for the max depth parameter are evaluated (the learned
tree maximum allowed depth).
Max Depth=2 Max Depth=5 Max Depth=7 Max Depth=10
Dataset Err FNR FPR Err FNR FPR Err FNR FPR Err FNR FPR
Breast 0.40 0.35 0.45 0.33 0.30 0.35 0.33 0.30 0.35 0.33 0.30 0.35
CNS 0.18 0.48 0.03 0.25 0.33 0.21 0.25 0.33 0.21 0.25 0.33 0.21
Colon 0.18 0.36 0.08 0.19 0.23 0.18 0.19 0.23 0.18 0.19 0.23 0.18
Leukemia 0.26 – – 0.26 – – 0.26 – – 0.26 – –
Leukemia 3c 0.15 – – 0.17 – – 0.17 – – 0.17 – –
Leukemia 4c 0.11 – – 0.15 – – 0.15 – – 0.15 – –
Lung 0.13 0.01 0.06 0.07 0.01 0.12 0.07 0.01 0.12 0.07 0.01 0.12
Lymphoma 0.00 – – 0.00 – – 0.00 – – 0.00 – –
MLL 0.08 – – 0.08 – – 0.08 – – 0.08 – –
Ovarian 0.03 0.01 0.07 0.03 0.01 0.07 0.03 0.01 0.07 0.03 0.01 0.07
SRBCT 0.27 – – 0.17 – – 0.17 – – 0.17 – –
Average, X 0.16 0.24 0.14 0.15 0.18 0.19 0.15 0.18 0.19 0.15 0.18 0.19
Std. dev., σ 0.11 0.19 0.16 0.10 0.14 0.10 0.10 0.14 0.10 0.10 0.14 0.10
Table 5: Test error rate (Err), FNR, and FPR of LOOCV for the SVM classifier (C=1 and kernel=linear) with EFB discretiza-
tion. Different values for the n bins parameter were evaluated (the number of discretization bins).
Num. Bins=2 Num. Bins=3 Num. Bins=4 Num. Bins=5 Num. Bins=6 Num. Bins=7
Dataset Err FNR FPR Err FNR FPR Err FNR FPR Err FNR FPR Err FNR FPR Err FNR FPR
Breast 0.32 0.30 0.33 0.33 0.33 0.33 0.32 0.33 0.31 0.32 0.33 0.31 0.30 0.30 0.29 0.31 0.33 0.29
CNS 0.35 0.71 0.15 0.30 0.62 0.13 0.38 0.71 0.21 0.32 0.62 0.15 0.32 0.62 0.15 0.37 0.67 0.21
Colon 0.18 0.27 0.12 0.18 0.27 0.12 0.16 0.27 0.10 0.15 0.23 0.10 0.15 0.23 0.10 0.16 0.27 0.10
Leukemia 0.01 – – 0.01 – – 0.01 – – 0.01 – – 0.01 – – 0.01 – –
Leukemia 3c 0.03 – – 0.03 – – 0.03 – – 0.03 – – 0.04 – – 0.04 – –
Leukemia 4c 0.08 – – 0.07 – – 0.07 – – 0.07 – – 0.07 – – 0.07 – –
Lung 0.05 0.01 0.18 0.05 0.01 0.18 0.05 0.01 0.18 0.04 0.01 0.18 0.04 0.01 0.18 0.04 0.01 0.18
Lymphoma 0.00 – – 0.00 – – 0.00 – – 0.00 – – 0.00 – – 0.00 – –
MLL 0.04 – – 0.03 – – 0.03 – – 0.03 – – 0.03 – – 0.03 – –
Ovarian 0.004 0.00 0.01
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
SRBCT 0.00 – – 0.00 – – 0.00 – – 0.00 – – 0.00 – – 0.00 – –
Average, X 0.10 0.26 0.16 0.09 0.25 0.15 0.10 0.26 0.16 0.09 0.24 0.15 0.09 0.23 0.14 0.09 0.26 0.16
Std. dev., σ 0.12 0.26 0.10 0.12 0.23 0.11 0.13 0.26 0.10 0.12 0.23 0.10 0.11 0.23 0.10 0.12 0.25 0.10
datasets, we can observe that only one single feature is
chosen n times (on the LOOCV folds), thus it is iden-
tified as the most relevant feature (gene) for cancer
detection, to be checked by the clinical staff. After-
ward, we observe a decreasing function that shows the
relative importance of the features to perform classifi-
cation. We observe that only a few features are chosen
n times, being the most relevant in clinical terms.
5 CONCLUSIONS
Cancer detection and classification from high-
dimensional DNA microarray data is an important
problem, with many techniques having been success-
fully applied to these problems. However, more than
just classifying the data, it is also important to iden-
tify the most relevant genes for the classification task,
A Step Towards the Explainability of Microarray Data for Cancer Diagnosis with Machine Learning Techniques
367

Table 6: Summary of the best results and respective configurations, for each dataset with normalized features, obtained during
the data representation phase with the EFB discretizer. The * symbol denotes an improvement over the baseline classification
results of Table 3 and Table 4, without discretization.
Configurations
Dataset Classifier Num. Bins Err FNR FPR
Breast SVM 6 0.30* 0.30 0.29
CNS DT 5 0.18 0.33 0.10
Colon SVM 5, 6 0.15* 0.23 0.10
Leukemia SVM, DT 2, 3, 4, 5, 6, 7 0.01 – –
Leukemia 3c SVM 2, 3, 4, 5 0.03* – –
Leukemia 4c SVM 3, 4, 5, 6, 7 0.07* – –
Lung SVM 5, 6, 7 0.04* 0.01 0.18
Lymphoma SVM 2, 3, 4, 5, 6, 7 0.00 – –
MLL SVM 3, 4, 5, 6, 7 0.03 – –
Ovarian SVM 3, 4, 5, 6, 7 0.00 0.00 0.00
SRBCT SVM 2, 3, 4, 5, 6, 7 0.00 – –
Average, X – – 0.07 0.17 0.13
Std. dev., σ – – 0.09 0.14 0.10
Table 7: Test error rate (Err), FNR, and FPR of LOOCV for the SVM classifier (C=1 and kernel=linear) with LS, SPEC, FiR,
and RRFS (with MM and FiR relevance and maximum similarity m
s
=0.7), with normalized features.
Unsupervised Supervised
LS SPEC RRFS (MM) FiR RRFS (FiR)
Dataset Err FNR FPR Err FNR FPR Err FNR FPR Err FNR FPR Err FNR FPR
Breast 0.33 0.35 0.31 0.32 0.30 0.33 0.31 0.28 0.33 0.31 0.28 0.33 0.31 0.28 0.33
CNS 0.35 0.52 0.26 0.33 0.62 0.18 0.27 0.48 0.15 0.30 0.57 0.15 0.33 0.67 0.15
Colon 0.16 0.27 0.10 0.19 0.32 0.12 0.21 0.36 0.12 0.19 0.32 0.12 0.18 0.27 0.12
Leukemia 0.01 – – 0.01 – – 0.01 – – 0.01 – – 0.01 – –
Leukemia 3c 0.04 – – 0.06 – – 0.04 – – 0.04 – – 0.03 – –
Leukemia 4c 0.08 – – 0.10 – – 0.07 – – 0.07 – – 0.07 – –
Lung 0.05 0.01 0.12 0.05 0.01 0.12 0.05 0.01 0.12 0.04 0.01 0.12 0.05 0.01 0.18
Lymphoma 0.00 – – 0.00 – – 0.03 – – 0.00 – – 0.02 – –
MLL 0.04 – – 0.06 – – 0.03 – – 0.03 – – 0.04 – –
Ovarian 0.00 0.00 0.00 0.00 0.00 0.00 0.004 0.00 0.01 0.00 0.00 0.00 0.00 0.00 0.00
SRBCT 0.02 – – 0.00 – – 0.00 – – 0.00 – – 0.00 – –
Average, X 0.10 0.23 0.16 0.10 0.25 0.15 0.09 0.23 0.15 0.09 0.24 0.14 0.09 0.25 0.16
Std. dev., σ 0.12 0.20 0.11 0.12 0.23 0.11 0.11 0.19 0.10 0.11 0.21 0.11 0.12 0.24 0.11
Table 8: Pipeline’s best configuration found for each dataset.
Pipeline Configuration
Dataset Discretization Selection Classification
Breast EFB (n bins=6) RRFS (with FiR; ms=0.7) SVM (C=1; kernel=linear)
CNS EFB (n bins=5) SPEC DT (criterion=entropy, max depth=6, and random state=42)
Colon MDLP LS DT (criterion=entropy, max depth=None, and random state=5)
Leukemia EFB (n bins=2) LS SVM (C=1; kernel=linear)
Leukemia 3c EFB (n bins=2) RRFS (with FiR; ms=0.7) SVM (C=1; kernel=linear)
Leukemia 4c EFB (n bins=3) RRFS (with FiR; ms=0.7) SVM (C=1; kernel=linear)
Lung EFB (n bins=5) FiR SVM (C=1; kernel=linear)
Lymphoma EFB (n bins=2) LS SVM (C=1; kernel=linear)
MLL EFB (n bins=3) RRFS (with MM; ms=0.7) SVM (C=1; kernel=linear)
Ovarian EFB (n bins=3) RRFS (with FiR; ms=0.7) SVM (C=1; kernel=linear)
SRBCT EFB (n bins=2) SPEC SVM (C=1; kernel=linear)
allowing for the human interpretability of the classifi-
cation results. In this work, we have proposed an ap-
proach using feature selection and feature discretiza-
tion techniques, able to identify small subsets of rele-
vant genes for the subsequent classifier. The proposed
approach is based on standard machine learning pro-
cedures, achieves large degrees of dimensionality re-
duction on several public-domain datasets. By using
the LOOCV procedure, identify the features (genes)
that are often more relevant for the classifier decision.
In future work, we will explore supervised fea-
ture discretization techniques. We will also fine tune
the maximum similarity parameter of the RRFS algo-
rithm to further reduce the size of the subsets, allow-
ing medical experts to focus on fewer features.
REFERENCES
Alonso-Betanzos, A., Bol
´
on-Canedo, V., Mor
´
an-
Fern
´
andez, L., and S
´
anchez-Marono, N. (2019). A
review of microarray datasets: Where to find them and
specific characteristics. Methods in Molecular Biology,
1986(1):65–85.
Bishop, C. (1995). Neural Networks for Pattern Recogni-
tion. Oxford University Press.
ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods
368
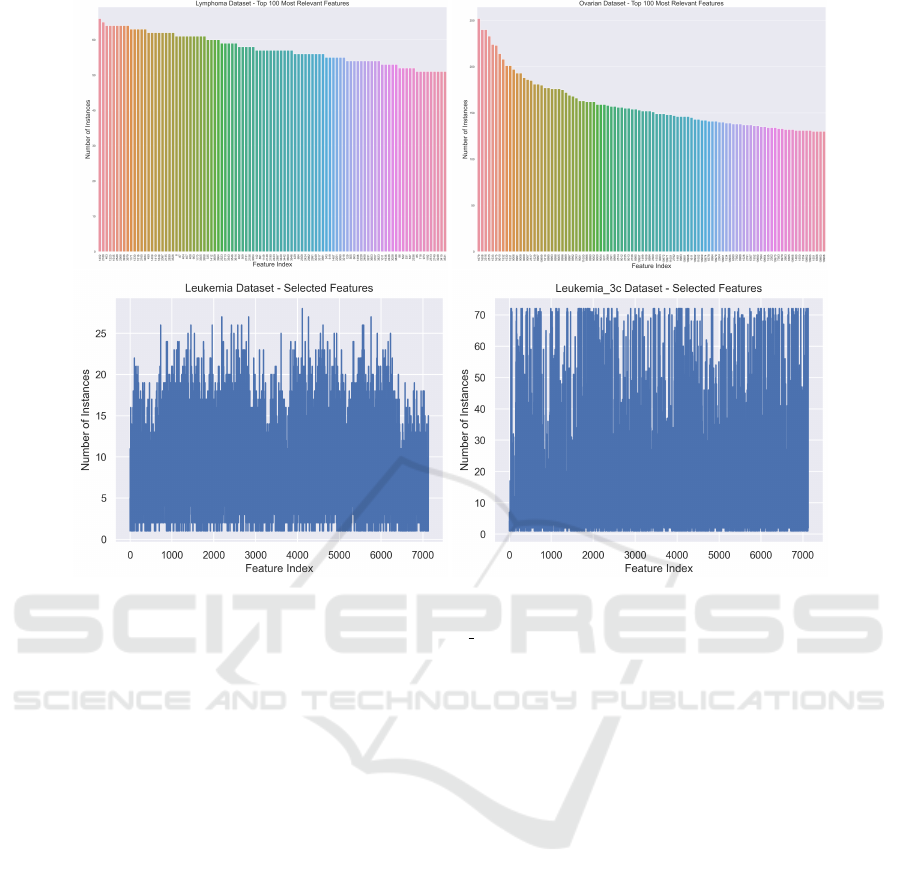
Figure 5: Top: The top-100 of the number of times each feature is chosen/selected on the FS step on the LOOCV procedure
for the Lymphoma (n=66, d=4026) and Ovarian datasets (n=253, d=15154). Bottom: The number of times each feature is
chosen/selected for the Leukemia (n=72, d=7129) and Leukemia 3c datasets (n=72, d=7129).
Consiglio, A., Casalino, G., Castellano, G., Grillo, G., Per-
lino, E., Vessio, G., and Licciulli, F. (2021). Explaining
ovarian cancer gene expression profiles with fuzzy rules
and genetic algorithms. Electronics, 10(4):375.
Diaz-Uriarte, R. and Andres, S. (2006). Gene selection
and classification of microarray data using random for-
est. BMC bioinformatics, 7(1):1–13.
Duda, R., Hart, P., and Stork, D. (2001). Pattern classifica-
tion. John Wiley & Sons, second edition.
Ferreira, A. and Figueiredo, M. (2012). Efficient feature se-
lection filters for high-dimensional data. Pattern Recog-
nition Letters, 33(13):1794 – 1804.
Forero, D. and Patrinos, G. (2020). Genome Plasticity
in Health and Disease. Translational and Applied Ge-
nomics. Elsevier Science.
Garcia, S., Luengo, J., Saez, J., Lopez, V., and Herrera, F.
(2013). A survey of discretization techniques: taxon-
omy and empirical analysis in supervised learning. IEEE
Trans. Knowledge and Data Eng., 25(4):734–750.
Guyon, I., Gunn, S., Nikravesh, M., and Zadeh, L.
(2006). Feature extraction, foundations and applica-
tions. Springer.
Li, Z., Xie, W., and Liu, T. (2018). Efficient feature se-
lection and classification for microarray data. PloS One,
13(8):e0202167.
Meyer, P., Schretter, C., and Bontempi, G. (2008).
Information-theoretic feature selection in microarray
data using variable complementarity. IEEE Journal of
Selected Topics in Signal Processing, 2(3):261–274.
Saeys, Y., Inza, I., and naga, P. L. (2007). A review of
feature selection techniques in bioinformatics. Bioinfor-
matics, 23(19):2507–2517.
Simon, R., Korn, E., McShane, L., Radmacher, M., Wright,
G., and Zhao, Y. (2003). Design and analysis of DNA
microarray investigations. Springer.
Statnikov, A., Aliferis, C., Tsamardinos, I., Hardin, D., and
Levy, S. (2005a). A comprehensive evaluation of multi-
category classification methods for microarray gene ex-
pression cancer diagnosis. Bioinformatics, 21(5):631–
643.
Statnikov, A., Tsamardinos, I., Dosbayev, Y., and Aliferis,
C. (2005b). GEMS: a system for automated cancer di-
agnosis and biomarker discovery from microarray gene
expression data. International Journal of Medical Infor-
matics, 74(7-8):491–503.
Weinberg, R. (2014). The Biology of Cancer. Garland Sci-
ence, second edition.
Witten, I., Frank, E., Hall, M., and Pal, C. (2016). Data min-
ing: practical machine learning tools and techniques.
Morgan Kauffmann, fourth edition.
Yip, W.-K., Amin, S. B., and Li, C. (2011). A Survey of
Classification Techniques for Microarray Data Analysis,
pages 193–223. Springer Berlin Heidelberg.
A Step Towards the Explainability of Microarray Data for Cancer Diagnosis with Machine Learning Techniques
369
