
SecTL: Secure and Verifiable Transfer Learning-based inference
Abbass Madi, Oana Stan, Renaud Sirdey and C
´
edric Gouy-Pailler
Universit
´
e Paris-Saclay, CEA, List, F-91120, Palaiseau, France
Keywords:
Homomorphic Encryption, Verifiable Computing,Transfer Learning.
Abstract:
This paper investigates the possibility of realizing complex machine learning tasks over encrypted inputs with
guaranteed integrity. Our approach combines Fully Homomorphic Encryption (FHE) and Verifiable Comput-
ing (VC) to achieve these properties. To workaround the practical difficulties when using these techniques -
high computational cost for FHE and limited expressivity for VC, we leverage on transfer learning as a mean to
(legitimately) decrease the footprint of encrypted domain calculations without jeopardizing the target security
properties. In that sense, our approach demonstrates that scaling confidential and verifiable encrypted domain
calculations to complex machine learning functions does not necessarily require scaling these techniques to
the evaluation of large models. We furthermore demonstrate the practicality of our approach on an image
classification task.
1 INTRODUCTION
In recent years, a major domain of research con-
cerns the machine learning (ML) methods and the ef-
forts in having high quality predictive models.(Yin
et al., 2006; Kuncheva and Rodriguez, 2007; Bar-
alis et al., 2007). Yet, in practical usage scenario,
it is often necessary to evaluate these models in a
privacy-preserving fashion, for example by evaluat-
ing a model on a server over encrypted data, the in-
puts or the derived predictions are not disclosed to the
server. In this context, this paper studies how complex
machine learning can be performed securely in prac-
tice by combining Fully Homomorphic Encryption
(for computing over encrypted data), Verifiable Com-
puting (for integrity guarantees) as well as Transfer
Learning (as a means for scaling without prohibitively
large volumes of costly encrypted operations). The
common point of the most previous works in the Ma-
chine Learning domain is that the training data and
testing data enjoy precisely the same feature space
and identical data distributions. In contrast, Transfer
Learning (TL) aims to build an effective model that
transfers knowledge in one context to enhance learn-
ing in a different context. Therefore, it predicts even
if the data distribution is not identical with the previ-
ous one, without constructing a new model from the
scratch. This is interesting for various reasons such as
saving efforts, energy, and time.
Classification is one of the most investigated ap-
plications of transfer learning (Tommasi and Caputo,
2009; Tommasi et al., 2010; Wang et al., 2011; Ay-
tar and Zisserman, 2011; Jie et al., 2011; Zhu et al.,
2011; Kuzborskij et al., 2013; Long et al., 2013; Pa-
tricia and Caputo, 2014; Rohrbach et al., 2013; Sri-
vastava and Salakhutdinov, 2013; Wang et al., 2015).
The problem of lacking sufficient labeled or unlabeled
data in a target domain can be solved by the trans-
fer learning, which also leads to more reliable clas-
sification results. Other typical applications exploit-
ing TL have been proposed in recent years, such as
pedestrian detection (Cao et al., 2013), improved im-
age recognition in the medical field (Romera-Paredes
et al., 2013), improving visual tracking (Gao et al.,
2014), and features selection (Kuzborskij et al., 2015;
Kuzborskij et al., 2017). In the machine learning con-
text, one important issue is data confidentiality and
model integrity. Homomorphic Encryption is one of
the methods to ensure the data privacy that allows to
apply an operation over encrypted data without de-
crypting it first. The integrity of computation on en-
crypted data or clear data can be further on verified
using verifiable computing techniques.
In this context, this paper against addresses the
confidentiality threat and the leakage of information
in the transfer learning process. We leverage homo-
morphic encryption and verifiable computing to pro-
vide solutions for the secure evaluation step of the
transfer learning. Our contributions are as follows:
• Propose a secure architecture for privacy-
preserving and verifiable TL by means on Ho-
220
Madi, A., Stan, O., Sirdey, R. and Gouy-Pailler, C.
SecTL: Secure and Verifiable Transfer Learning-based inference.
DOI: 10.5220/0010987700003120
In Proceedings of the 8th International Conference on Information Systems Security and Privacy (ICISSP 2022), pages 220-229
ISBN: 978-989-758-553-1; ISSN: 2184-4356
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

momorphic Encryption and Verifiable Comput-
ing. Beside this architecture, we also give an ex-
ample of a practical medical use case for our se-
cure transfer learning solution.
• Provide an instantiation of our framework using
the VC protocol from (Fiore et al., 2014) with the
BFV (Fan and Vercauteren, 2012) homomorphic
encryption scheme, to classify an encrypted im-
age into two classes (dogs and cats)
1
.
• Propose PEOLE, a method of dimension reduc-
tion of the features space in order to efficiently ap-
ply the homomorphic encryption techniques with-
out a significant accuracy loss.
• Evaluate the practical performances of our archi-
tecture (≈2 min for prediction an encrypted im-
age) by several classification experiments consist-
ing in extracting the featurea from a pre-trained
model VGG16 (Simonyan and Zisserman, 2014)
for image classification and train a MLP (Multi-
Layer Perceptron) classifier on top of it.
2 RELATED WORK
It is worth noting that most of the studies in the pri-
vacy of data to machine learning consisting of ap-
plying homomorphic encryption to machine learning
models concentrates on making the inference on pri-
vate data (e.g. CryptoNets (Gilad-Bachrach et al.,
2016), TAPAS (Sanyal et al., 2018), NED (Hesam-
ifard et al., 2019)) and not so much on the train-
ing phase. Other notable works (Zhu, 2005; Nigam
et al., 2000; Blum and Mitchell, 1998; Joachims et al.,
1999). Zhu and Wu. (Zhu and Wu, 2006) have fine-
studied how to deal with noisy class label problems
in the line of research between supervised and unsu-
pervised learning. In another line of research, Yang et
al. (Yang et al., 2006) have studied the cost of learn-
ing when the additional tests can be made to future
samples.
A particularly interesting application approach us-
ing encryption for performing machine learning for
Deep Neural Network nets (DNNs) has been done in
(Tanaka, 2018) where all the images used for train-
ing are encrypted using a tailored-made cryptosys-
tem called Tanaka. Sirichotedumrong, Kinoshita, and
Kiya (SKK) scheme (Sirichotedumrong et al., 2019)
proposed a privacy-preserving scheme for DNN that
encrypts the images ( pixel-based image encryption
method) under different keys, and allows one to use
data augmentation in the encrypted domain. Glyph
1
Dataset available at https://www.kaggle.com/shivamb/
cnn-architectures-vgg-resnet-inception-tl/data.
(Lou et al., 2019) is another approach, based on ho-
momorphic encryption, allowing to fast and accu-
rately train DNNs on encrypted data by switching be-
tween TFHE (Fast Fully Homomorphic Encryption
over the Torus) and BGV cryptosystems.
The problem of ensuring privacy and verifiability
in a deep learning system is examined in a few works
such as SafetyNets (Ghodsi et al., 2017), and Slalom
(Tramer and Boneh, 2018). However, these schemes
(SafetyNets, Slalom) propose only a small variety of
activation functions or require additional hardware as-
sistance as in (Tramer and Boneh, 2018). An interest-
ing architecture proposed by Madi et al. (Madi et al.,
2020) to achieve both confidentiality and integrity for
the inference step of a neural network is comprised
of three entities: client, server, and operator. Even
if similar to ours, in their case, the server executes
the first layers privately (using FHE and VC) and it is
the operator which is performing on clear the last lay-
ers of the NN. As such, they cannot take advantage
of a public pre-trained model and moreover, they are
obliged to use an adversarial learning model against
the leakage of information after decryption on the op-
erator side.
To the best of our knowledge, this is the first work
to use the application of the verifiable computing and
homomorphic encryption for the transfer learning set-
ting (i.e. verify the integrity of the encrypted predic-
tion results returned by the model).
3 BACKGROUND
3.1 Transfer Learning (TL)
Transfer Learning (TL) is the process of learning to
solve a problem in a ”target” domain using part of the
knowledge acquired on the reference problem to solve
a similar target problem. In this context, we can dis-
tinguish several approaches depending on what, when
and how we want to transfer. The application of this
idea in ML implies reusing all or part of a model
learned on reference data to solve a target problem
by re-learning on the target data. This is attractive
for several purposes, such as learning about sensitive
data, while respecting privacy policies and business
requirements and in different domains like the health
or the autonomous driving field.
In a Transfer Learning setting, some labeled data
D
src
are available in a source domain, while only
unlabeled data D
tar
are available in the target do-
main. We denote the source domain data as D
src
=
{(x
src
1
,y
src
1
),.. .,(x
src
n
1
,y
src
n
1
)}, where x
src
i
∈ R
m
is
the input data and y
src
i
is the corresponding label.
SecTL: Secure and Verifiable Transfer Learning-based inference
221

Furthermore, we indicate the target domain data as
D
tar
= {x
tar
1
,.. .,x
tar
n
2
}, and, without loss the gener-
ality, we suppose the input x
tar
i
in R
m
. Let P (X
src
)
and Q (X
tar
) (denoted by P, and Q in short) being the
marginal distributions of X
src
and X
tar
, respectively.
Generally, they can be different. The task of transfer
learning is then to predict the labels y
tar
i
correspond-
ing to the inputs x
tar
i
∈ D
tar
.
3.2 Homomorphic Encryption (HE)
Fully Homomorphic Encryption (FHE) schemes al-
low to perform arbitrary computations directly over
encrypted data. That is, with a fully homomorphic
encryption scheme E, we can compute E(m
1
+ m
2
)
and E(m
1
× m
2
) from encrypted messages E(m
1
) and
E(m
2
).
In this section we recall the general principles of
the BFV homomorphic cryptosystem (Fan and Ver-
cauteren, 2012), which we use in combination with a
VC scheme. Since we know in advance the function
to be evaluated homomorphically, we can restrain to
the somewhat homomorphic version described below.
The biggest problem of Homomorphic Encryp-
tion, especially in the homomorphic multiplicative is
the size of the ciphertext that is growing exponentially
in the number of operations, which can have a great
influence on the correctness and the capability of de-
cryption. For this reason for some HE scheme, there
exists a relinearisation operation to solve the growth
of error rate. We skip the description of the relineari-
sation step for the BFV since this is not needed for our
usage - we evaluate only multi-variate quadratic poly-
nomials of degree at most 2 (i.e. at most 2 multiplica-
tions and a modular reduction which can be realized
upon decryption).
Let R = Z [x]/Φ
m
(x) denote the polynomial ring
modulo the m-cyclotomic polynomial with n
0
= ϕ(m).
The ciphertexts in the scheme are elements of polyno-
mial ring R
q
, where R
q
is the set of polynomials in R
with coefficients in Z
q
. The plaintexts are polynomi-
als belonging to the ring R
t
= R/tR.
As such, BFV scheme is defined by the following
probabilistic polynomial-time algorithms:
BFV.ParamGen(λ): → (n
0
,q,t,χ
key
,χ
err
,w).
It uses the security parameter λ to fix several other
parameters such as n
0
, the degree of the polynomials,
the ciphertext modulus q, the plaintext modulus t, the
error distributions, etc.
BFV.KeyGen(n
0
,q,t,χ
key
,χ
err
,w):→ (pk,sk, evk).
Taking as input the parameters generated in
BFV.ParamGen, it calculates the private, pub-
lic and evaluation key. Besides the public and the
private keys, an evaluation key is generated to be
used during computation on ciphertexts in order to
reduce the noise.
BFV.Enc
pk
(m):→ c = (c
0
,c
1
,c
2
= 0)
It produces a ciphertext c according to BFV-
cryptosystem for a plaintext m using the public key
pk.
BFV.Dec
sk
(c):→ m
It computes the plaintext m from the ciphertext c, us-
ing private key sk.
BFV.Eval
pk,evk
( f , c
1
,.. . ,c
n
):→ c, with
c =BFV.Enc
pk
( f (m
1
,.. . ,m
n
)), where
c
i
=BFV.Enc
pk
(m
i
), and f has n inputs and has
degree at most two.
It allows the homomorphic evaluation of f , gate-
by-gate over c
i
using the following functions:
BFV.Add(c
1
,c
2
) and BFV.Mul
evk
(c
1
,c
2
).
For further details on this scheme, we refer the
reader to the paper (Fan and Vercauteren, 2012).
Let us just note that a BFV ciphertext c can be
seen as an element in R
q
[y] = Z/qZ[X,Y ]/Φ
m
(x) with
a degree at most 2 (i.e., c = c
0
+ c
1
y + c
2
y
2
).
3.3 Verifiable Computing (VC)
Verifiable computation VC techniques allow to prove
and verify the integrity of computations on authenti-
cated data. A Verifiable Computation scheme is de-
fined as a protocol in which a client (usually weak)
has a function f and some data denoted x and del-
egates to another client (in most cases a server) the
computation of y = f (x). Then the same client or an-
other one can receive the result y plus a short proof
of its correctness. More in details, a user generates
an authentication tag σ
x
associated with his/her data x
with his/her secret key and the server computes an au-
thentication tag σ
f ,y
that certifies the value y = f (x)
as an output of the function f . Now, anyone using
the verification key (public or secret) can verify y to
check that y is indeed the result of f (x).
A VC scheme includes the following algorithms:
1. (PK,SK)←KeyGen( f ,λ): Taking as input the se-
curity parameter λ and a function f , this random-
ized key generation algorithm generates a public
key (that encodes the target function f ) used by
the server to compute f . It also computes a match-
ing secret key, kept private by the client.
2. (σ
x
,τ
x
)←ProbGen
SK
(x): The problem generation
algorithm uses the secret key SK to encode the
input x as a public value σ
x
, given to the server to
compute with, and a secret value τ
x
which is kept
private by the client.
3. σ
y
←Compute
PK
(σ
x
): Using the client’s public
key and the encoded input, the server computes an
encoded version for the function output y = f (x).
ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy
222

4. (acc,y) ←Verify
SK
(τ
x
,σ
y
): Using the secret key
SK and the secret τ
x
, this algorithm converts the
server output into a bit acc and a string y. If acc =
1 we say that the client accepts y = f (x), meaning
that the proof is correct, else (i.e. acc = 0) we say
that the client rejects it.
4 PROPOSED APPROACH
4.1 Our Model
We begin by explaining our proposal for an architec-
ture allowing to deploy the secure transfer learning
model using homomorphic encryption and verifiable
computing. Our architecture is composed of three en-
tities: user, server, and operator. In the following, we
describe a high-level view of our TL design with the
role of each entity as revealed in the Figure 1. Let us
denote by f , the global Machine Learning model de-
ployed by our architecture, consisting of n layers and
taking as input the data x.
1. The user - owner of some data denoted x - starts
the process by applying the first (n-i) layers of the
model, i.e. f
n−i
(x) When the result is calculated,
the user encrypts homomorphically f
n−i
(x) , and
she generates the associated integrity tag. These
encryption data and the associated tag are sent to
the server.
2. The server has the task of evaluating in the homo-
morphic domain, the remaining layers of the neu-
ral network over the private data [ f
n−i
(x)]
HE
. Due
to the restrictions imposed by the Verifiable Com-
puting protocol used in our approach (i.e. abil-
ity to evaluate the correctness of the evaluation of
multi-variate polynomials of degree at most two),
in our case the server will homomorphically eval-
uate only a quadratic function (which is totally
feasible and with really good performances by ex-
isting FHE means). Now, the homomorphic eval-
uation of the private part of the model along with
the associated integrity proof is sent to the opera-
tor.
3. The operator has access to the evaluation of the
server evaluation, and to the result of the TL
model. Therefore, it can check the validity of the
server computation. If it is correct it decrypts the
result, and then employs it as it wants.
We note that the number of layer i evaluated on
the server side depends directly on the limitation of
the VC and FHE methods.
4.2 Security Guarantees and Threats
Unlike other works using homomorphic encryption
for private inference, we set up our study in the case
of a malicious server, which can possible alter the
results of the evaluation (e.g. by not running the
specified algorithm). We argue that it is necessary
to have integrity guarantees against threats coming
from this adversary in addition to the confidential-
ity offered by the homomorphic encryption.The mali-
cious adversaries may conduct arbitrarily (i.e. execute
any computation) for stealing, corrupting, and modi-
fying data, without any specifications, and may com-
pute any function over data instead of the required
computation (function delegated). For this goal, in
our approach, we use verifiable computing technique,
in particular the VC protocol of Fiore et al. (Fiore
et al., 2014), that allows anyone to check efficiently
the calculation evaluated on the server over encrypted
data, in order to check that the server correctly cal-
culates the layers delegated to it. To the best of our
knowledge, this VC is the most practical verifiable
computing protocol to address the validity of com-
putation over encrypted data with the limitation that
it evaluates mutivariate functions of degree at most
2
2
. Therefore, this constraint restrains the number of
layers that can be delegated to the server in our archi-
tecture (i.e. the server can evaluate homomorphically
maximum the last quadratic layers of a model).
In our architecture, unlike other works using ho-
momorphic encryption, especially Glyph (Lou et al.,
2019) and Madi et al. work (Madi et al., 2020),
the server evaluates in the homomorphic domain the
last layers of the model as knowing the encrypted of
f
n−i
(x) to obtain the encryption of f (x). The operator,
after receiving the encryption result decrypts f (x),
which is contrary to the Glyph and Madi approach,
where they compute the first layers of the model and
send this encrypted to the operator that decrypts this
result and obtain f
1
(x) and complete model. There-
fore, at the level of leakage information, it is clear
that our model is the best in the prevention of reduce
the leakage of information. In summary, using our ar-
chitecture we prevent threats coming from the server
executing the last layer and wanting to infer informa-
tion about the learning.
4.3 Medical Use-case
As quickly described in (Mormont et al., 2018), imag-
ine a scenario where a radiologist (user) has just ac-
2
This is due to the need to go beyond bilinear maps
to achieve higher degrees in the underlying cryptographic
primitives involved in both VC and FE.
SecTL: Secure and Verifiable Transfer Learning-based inference
223
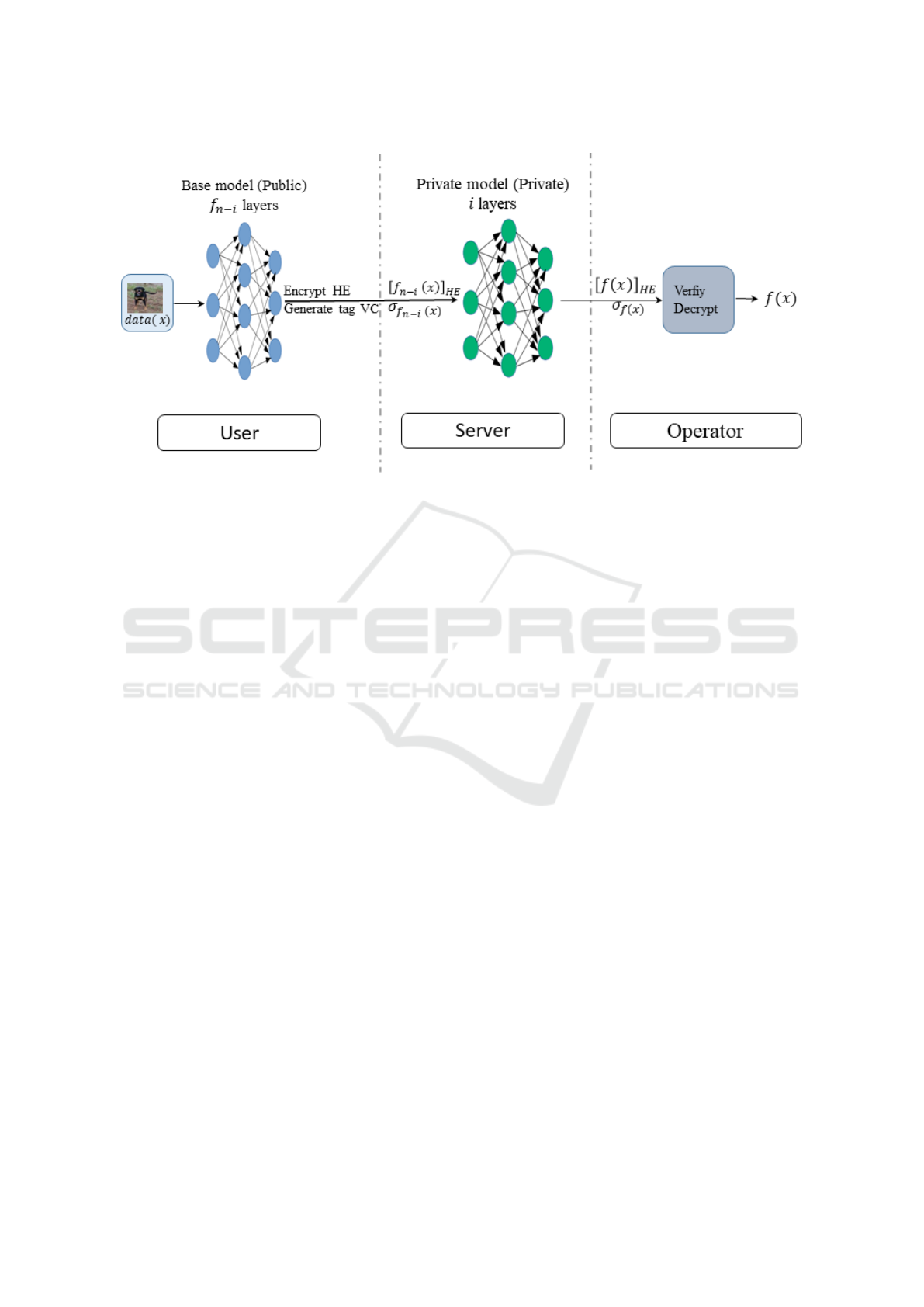
Figure 1: Our architecture for a confidentiality & integrity preserving inference phase of transfer learning.
quired images from the body of one of its patient and
needs to interact with a remote proprietary diagnostic
service (server) to get some insights. The service it-
self is expecting images as input and crunches them
through an advanced deep neural network which out-
puts highly reliable insights in terms of the pathology
the patient is suffering from as well as personalized
treatment approaches. Clearly, as health-related data,
the patient images and data are considered sensitive
and cannot be shared without protecting their confi-
dentiality. On the other hand, the neural network has
been carefully crafted by the service provider using a
lot of precious hard-earned training data and is con-
sidered critical intellectual property. In this scenario,
it is thus acceptable neither that the service provider is
granted access to the patient data (or to a by-product
of these) nor that the radiologist is disclosed the net-
work. Thus without additional means to prevent dis-
closure of these assets, a high value service is pre-
vented to exist.
One way to resolve these conflicting requirements
is by bringing privacy preserving FHE calculations
into the picture. In principle, in the above scenario,
the radiologist may be the owner of a FHE cryptosys-
tem and send its patient’s data encrypted under that
cryptosystem to the service provider. The service
provider then evaluates its neural network directly
over these encrypted data, producing results which are
sealed under the radiologist’s cryptosystem. The final
results are then sent back to the radiologist who is the
only party able to decrypt them. So we are done. The
patient data are not disclosed to the service provider
(since they, and their by-products, are sealed under
a cryptographic layer at all time) and the network is
not disclosed to the radiologist since it stays on the
service provider computing premises. Unfortunately,
this na
¨
ıve view is impractical since, despite the ad-
vances made and yet to be made in FHE operators
efficiency, it is unlikely that they will be sufficient to
enable practical homomorphic evaluation of the large
scale neural nets involved in advanced machine learn-
ing tasks. Fortunately, as we shall now see, scaling
FHE calculations to complex machine learning tasks
does not necessarily mean scaling FHE calculations
to large scale models.
Now let us assume that the service provider has
followed the transfer learning philosophy to build its
neural network. As such, its network can thus be split
in two parts:
• A first preprocessing network (e.g. VGG16)
which is publicly available and has no dependen-
cies on the precious hard-earned training data of
the service provider.
• A second much smaller decisional network
trained on the service provider sensitive data
which turns VGG16 ouputs into the highly reli-
able insights expected by the radiologist.
In light of the above, we can now rework our sce-
nario to make it much more FHE friendly. Indeed, the
publicly available preprocessing network can be dis-
closed to the radiologist’s information system and run
in the clear domain before encryption. So rather than
sending FHE-encrypted images, the radiologist(’s in-
formation system) only sends a FHE-encryption of
the resulting feature vector(s), which is furthermore
of much smaller size than high-resolution images. On
the service provider side, only the smaller decisional
ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy
224

network has to be run in the encrypted domain there-
fore dramatically decreasing the footprint of FHE-
calculations and resulting de facto in much better scal-
ing properties. Since transfer learning techniques are
widely applicable and applied in the neural network
community we can therefore claim that performing
advanced machine learning tasks over encrypted data
does not require scaling encrypted-domain calcula-
tion to large networks, as, as argued above, the fact
of running the preprocessing on the user/radiologist
side does not impact the confidentiality properties of
the setup.
5 DIMENSIONALITY
REDUCTION OF TARGET
DOMAIN
In order to provide a good TL model, that can be used
with our architecture, we propose a dimensionality re-
duction method of the target domain D
tar
.
The proposed TL dimensionality reduction, which
will be called Probability Elimination of Output with
Light Effect (PEOLE) uses a projection map ψ :
R
m
→ R
m
0
that eliminates the features extracted by
the public model of the public model. It consists in
finding the minimal dimension of the feature space
such that there is not a very high of accuracy in the
prediction of the final model (i.e. finding m
0
s.t.
m
0
= ψ(R
m
) ).
We note by X ∈ R
n
2
×m
the matrix representing the
D
tar
where we put the x
tar
i
in the i − th line of X. We
want to find the new matrix X
0
∈ R
n
2
×m
0
respresenting
the D
tar
.
Our method consists in performing of two steps:
First Step. For any column, we calculate the percent-
age of element less than a chosen threshold s(s can be
for example 10
−6
).
Second Step. Eliminate the column that has a per-
centage bigger than a chosen percentage p for exam-
ple for p = 90% , and s = 10
−6
, we eliminate the
column that has more than 90% elements small than
10
−6
).
For a percentage p and a sill s, if we delete all
the columns of X that have a percentage more than p
elements small than s, so we do not lose a remarkable
amount of accuracy
6 EXPERIMENTAL EVALUATION
In our experiments, we want to evaluate our architec-
ture for the case where we extract the features from
a pre-trained model for image classification and train
a classifier on top of it. We note that the ML imple-
mentations in this chapter are done on Google Collab.
We use a dataset consisting in images containing only
2 types of animals (dogs and cats)
3
where the train
folder contains 12500 images for each class. Each im-
age in this folder has the label as part of the filename.
The test dataset contains 12,500 images, named ac-
cording to a numeric id.
As for the public pre-trained model, we used the
VGG16 model (Simonyan and Zisserman, 2014) to
extract the data features, which is a convolutional
neural network model proposed by K. Simonyan and
A. Zisserman (Simonyan and Zisserman, 2014). We
note that this model is trained over the ImageNet
4
,
a dataset of 14 million images belonging to 1000
classes. Our evaluation metric was the accuracy of
prediction for the test sets.
The VGG16 architecture consists of:
1. A total of 16 layers in which weights and bias pa-
rameters are learnt.
2. This network contains a total of 13 convolutional
layers with 3 ∗ 3 kernel size, and increasing num-
bers of filters corresponding to the layers, with
3 dense layers for classification (comprises of
4096,4096, and 1000 nodes each).
3. Each convolutional layers is followed by a ReLu
activation, and a final softmax output layer
(25,088 total parameters).
4. A 2 ∗ 2 max pooling applied at different steps (af-
ter the: 2nd, 4th, 7th, 10th, 13th convolution layer
) to obtain the informative features.
We state that, in our experimentation, we do not
want to add the last layer of VGG16 architecture,
since we add a classifier, essentially a Multilayer per-
ceptron.
On top of the VGG16 model, we build our own
private model, a simple neural network - MLP (Multi-
Layer Perceptron) to classify over our own dataset
(images of dogs and cats). Then, our private model
is a MLP composed of one hidden layer with 55 neu-
rons with an identity activation function that trains us-
ing the pre-trained features by VGG16. We note that
the weight matrix for the first layer is 25, 088×55 and
the hidden layer consists of 55 × 1 weight vector. We
recall that the features extracted from VGG16 are in
the form of a vector of length 25,088. The Figure 2
represents the different steps in our test architecture.
The first step of our experiment is to encrypt the
extracted features using VGG16 and to generate the
3
Dataset available at https://www.kaggle.com/shivamb/
cnn-architectures-vgg-resnet-inception-tl/data.
4
Dataset available at https://www.image-net.org/
SecTL: Secure and Verifiable Transfer Learning-based inference
225

Figure 2: Our test architecture.
corresponding authentication tags. Afterwards, we
evaluate the MLP model over these encrypted data
and their tags (the server private computation part)
and send the encrypted result with the computed re-
sult tag to an operator that can verify (over the result
tag) that the calculation is correct, and decrypt this
result if the verification passed.
We build two distinct sets of experimentation. On
one hand, we aimed at reducing the output of VGG16
of 25088 features to an acceptable size which permits
us to encrypt it using a homomorphic encryption sys-
tem and to improve the speedup of the prediction over
encrypted features. Using our PEOLE method we
tried to find the best set of parameters (s, p)
5
while
preserving the accuracy level. Let us emphasise that
our main focus was on the evaluation of the tech-
niques for privacy and integrity (i.e. homomorphic
encryption and respectively VC) in order to achieve a
secure transfer learning model without degrading its
performance.
6.1 Transfer Learning Parameters
To evaluate the speedup of the prediction process rel-
ative to the TL parameter and to accelerate the com-
putation of the private model over encrypted data, we
start our experiments by describing the variation of
the dimension of the target domain (more precisely
the output of VGG16) corresponding to the elimina-
tion of the column depending on the percentage p of
elements with value less than s = 10
−2
. As expected,
the dimension of the features vector after elimination
is reduced, as seen in Figure 3. For example, we re-
mark that the dimension of the output VGG vector is
decreased by 75% for p=80% meaning that its size
decreases from 25088 to 5638.
To show a complete view of our method and
its importance, we need to describe the accuracy
modification using PEOLE with different values for
the percentage p. Figure 4 describes the evolu-
tion of the accuracy with p ∈ [80,100] and s ∈
5
Notations are those introduced in section 5
Figure 3: Variation of VGG16 output vs percentage using
our idea PEOLE.
{10
−6
,10
−5
,10
−4
,10
−3
,10
−2
}. As we can see in
this figure the accuracy for (s, p) = (10
−2
,80) is
97.5625 for an initial accuracy of 98.3125 (without
PEOLE) and then it is an small decrease of accu-
racy of accuracy(0,75%).We remark that the accuracy
can be the same for multiple choices of s and p, e.g.
p=83,84 and s = 10
−3
,10
−4
where we obtain an ac-
curacy different from the other s and p.
As such, PEOLE method is a relatively easy way
to explore the features space obtained with the initial
public model and to diminish its dimension without
small loss in the accuracy of the final model - i.e. as
seen in the Figure 4, for p = 80% and s = 10
−2
, the
accuracy becomes 97.5625.
Figure 4: Evolution of the model testing accuracy with
respect to the percentage p and different s with PEOLE
method.
As for the homomorphic encryption the plaintext
are polynomials from the ring R
t
= R/tR with inte-
ger coefficients modulo t, where R = Z [x]/Φ
m
(x) de-
note the polynomial ring modulo the m-cyclotomic
polynomial. One has to encode the features and
ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy
226

the parameters of the model before performing ho-
momorphic operations on top of them. As such,
we also conducted experiments to analyze the im-
pact of this quantization on the accuracy of the final
model. In this test we fixed the parameters s and p
to (10
−2
,80%). The accuracy varies depending on the
precision of both features (output of VGG16) and the
weights of each layer. In Table 1, we focus on the per-
formance deterioration due to the approximations on
both w
k
and f
e
by showing the accuracy for the model
with regards to the rounding precision for the weights
and the features.
Table 1 describes the evolution of accuracy de-
pending on the approximation of both: weight and
features with fixed (p,s) = (80%,10
−2
). We draw
your attention that when we refer to a precision of an
element of 10
2
for exemple, then we round it to the
nearest integer element by taking only the two-digit
after the floating point (i.e; for a feature value of 12,
345 the approximated value will be 1234). As you
see in this table the accuracy varies from 97.5625%
to 97.5 %, then with loss = 0.0625 %, with preci-
sion 10
2
of features for any precision of weights, but
it is unremarkable variance. For this reason, and tak-
ing into account all of the results for the previously
mentioned experiments, we work with the following
parameters: s = 10
−2
, p = 80% that produces a fea-
ture vector of length 5638, with a good accuracy 97.5
(loss equal 0.8125 %).
6.2 Performance of Our Architecture
In the beginning, let us specify that all tests pre-
sented in this section were performed on a 2016
DELL PC(Genuine-Intel Core i7 − 6600U, 4 cores at
2.60GHz with 16GB RAM at 2.13GHz), on Ubuntu
(Linux kernel 4.15.0 − 91 − generic, with the archi-
tecture x86 − 64 ) as an operating system. Finally we
used the C++ language to implement the encryption
and verifiable computing part of our architecture.
In our experiments, we encrypt and decrypt homo-
morphically the data with the SEAL (SEAL, 2018) li-
brary and we use the HAL (Zuber and Fiore, 2017)
library for authentication but for BFV encrypted data.
We note that we choose the security parameters in the
way that achieve a 128 bits of security
Table 2 shows the sequential evaluation times for
the different steps of our architecture to predict the
class of one image after applying our PEOLE method
for a percentage p = 80% and a sill s = 10
−2
. Then,
the dimension of the features extracted using VGG16
passes from 25088 to 5638. As presented in this ta-
ble the encryption of this vector of 5638 takes 36.6 s
and the generation of the tag for authentication takes
0.005 s. The last one is the cost of generation for a
single tag since we note that the tags can be generated
in parallel for each encrypted element. The applica-
tion of MLP over this encryption data takes about one
minute and the execution of MLP over the tag takes
about 2 seconds (1.48 s), we also note that the evalua-
tion of the MLP model and the tag can be executed in
parallel. Finally, the verification of authentication the
result is very fast and it takes about 0.027 s.
7 CONCLUSION AND FUTURE
WORK
The architecture proposed in this paper is the first in
the TL domain to address both integrity and confiden-
tiality threats by means of homomorphic and verifi-
able computing techniques. To validate our approach,
we evaluated for the evaluation of the last layer of a
ML model using using unencrypted weights and en-
crypted feature data. In this scenario, we prevent the
threats coming from the server executing the last layer
and wanting information about the learning, poten-
tially interested in infering. We create our architec-
ture using the Keras (Chollet et al., 2015) library to
build the VGG16 trained over the Imagenet, and test
our approach using the MLP with one hidden layer of
55 neurons that show a good accuracy for the private
prediction of the class for one image (∼ 97 % ) in an
acceptable time (∼ 2 min=(2min for HE and in par-
allel 1.512 min for VC) ) with a fast verification of
result.
Our architecture remains generic and can be eas-
ily extended to further deployments where the private
evaluation of the neural network model delegated to
the server is more complex (more layers, other acti-
vation functions, etc). In order to go further, there are
several interesing directions to follow. First, a con-
crete optimization idea consists in the use of the VC
protocols for the homomorphic schemes in batched
mode which can improve the performance and reduce
the memory used for the encryption data. Other idea
is to use newer and more complex verifiable comput-
ing protocols, in order to be able to evaluate more than
quadratic multivariate polynomials. Finally, we hope
that this paper opens the door to further work cov-
ering a more general threat model for the secure AI
applications using homomorphic encryption.
REFERENCES
Aytar, Y. and Zisserman, A. (2011). Tabula rasa: Model
transfer for object category detection. In 2011 inter-
SecTL: Secure and Verifiable Transfer Learning-based inference
227
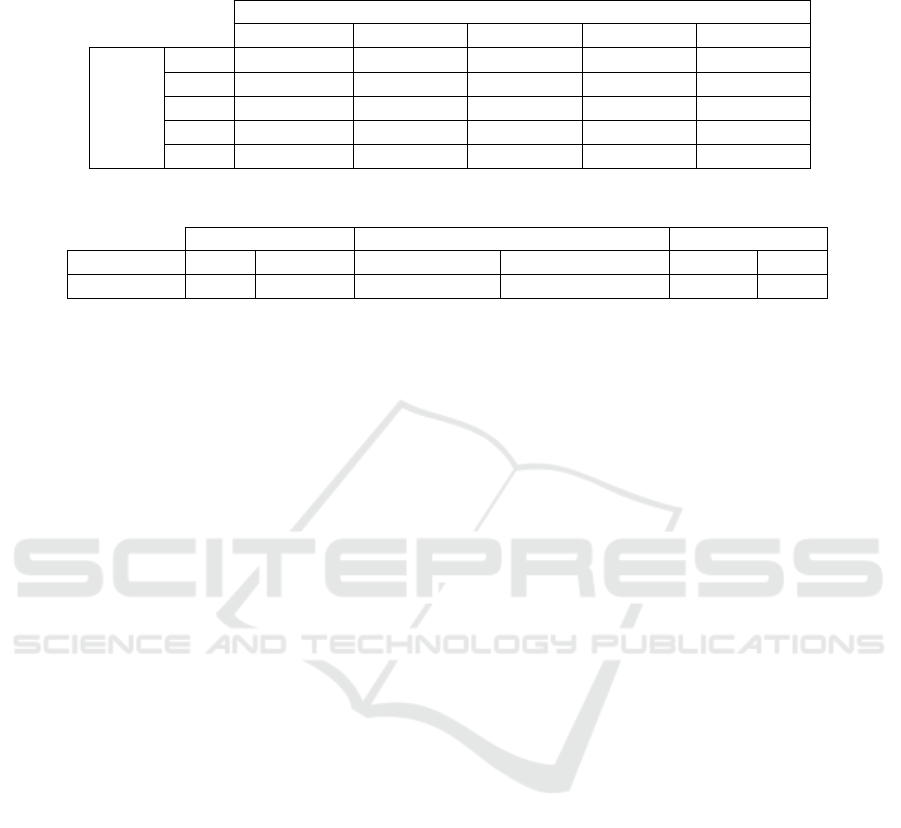
Table 1: Accuracy of model after application of our PEOLE method with (p,s) = (80%, 10
−2
) depending on precision on
both w
i
and f e.
precision on w
i
10
2
10
3
10
4
10
5
10
6
10
2
97.5 % 97.5% 97.5% 97.5% 97.5%
10
3
97.5625 % 97.5625% 97.5625% 97.5625% 97.5625%
10
4
97.5625 % 97.5625% 97.5625% 97.5625% 97.5625%
10
5
97.5625 % 97.5625% 97.5625% 97.5625% 97.5625%
precision
on f e
10
5
97.5625 % 97.5625% 97.5625% 97.5625% 97.5625%
Table 2: Costs (in seconds) for our architecture, where x = (x
1
,... , x
785
).
User-side Server-side Operator-side
Operation Enc GenTag MLP(Enc(x)) MLP(σ
1
,.. . ,σ
n
) Veri f y Dec
times 36.11 0.005 66.3 1.48 0.027 0.002
national conference on computer vision, pages 2252–
2259. IEEE.
Baralis, E., Chiusano, S., and Garza, P. (2007). A
lazy approach to associative classification. IEEE
Transactions on Knowledge and Data Engineering,
20(2):156–171.
Blum, A. and Mitchell, T. (1998). Combining labeled and
unlabeled data with co-training. In Proceedings of the
eleventh annual conference on Computational learn-
ing theory, pages 92–100.
Cao, X., Wang, Z., Yan, P., and Li, X. (2013). Transfer
learning for pedestrian detection. Neurocomputing,
100:51–57.
Chollet, F. et al. (2015). Keras. https://github.com/fchollet/
keras.
Fan, J. and Vercauteren, F. (2012). Somewhat practical fully
homomorphic encryption. IACR Cryptology ePrint
Archive, 2012:144.
Fiore, D., Gennaro, R., and Pastro, V. (2014). Efficiently
verifiable computation on encrypted data. In Proceed-
ings of the 2014 ACM SIGSAC Conference on Com-
puter and Communications Security, pages 844–855.
Gao, J., Ling, H., Hu, W., and Xing, J. (2014). Transfer
learning based visual tracking with gaussian processes
regression. In European conference on computer vi-
sion, pages 188–203. Springer.
Ghodsi, Z., Gu, T., and Garg, S. (2017). Safetynets: Ver-
ifiable execution of deep neural networks on an un-
trusted cloud. In Advances in Neural Information Pro-
cessing Systems, pages 4672–4681.
Gilad-Bachrach, R., Dowlin, N., Laine, K., Lauter, K.,
Naehrig, M., and Wernsing, J. (2016). CryptoNets:
Applying neural networks to encrypted data with high
throughput and accuracy. In ICML, pages 201–210.
Hesamifard, E., Takabi, H., and Ghasemi, M. (2019). Deep
neural networks classification over encrypted data. In
ACM CODASPY, page 97–108.
Jie, L., Tommasi, T., and Caputo, B. (2011). Multiclass
transfer learning from unconstrained priors. In 2011
International Conference on Computer Vision, pages
1863–1870. IEEE.
Joachims, T. et al. (1999). Transductive inference for text
classification using support vector machines. In Icml,
volume 99, pages 200–209.
Kuncheva, L. I. and Rodriguez, J. J. (2007). Classi-
fier ensembles with a random linear oracle. IEEE
Transactions on Knowledge and Data Engineering,
19(4):500–508.
Kuzborskij, I., Orabona, F., and Caputo, B. (2013). From
n to n+ 1: Multiclass transfer incremental learning.
In Proceedings of the IEEE Conference on Computer
Vision and Pattern Recognition, pages 3358–3365.
Kuzborskij, I., Orabona, F., and Caputo, B. (2015). Transfer
learning through greedy subset selection. In Interna-
tional Conference on Image Analysis and Processing,
pages 3–14. Springer.
Kuzborskij, I., Orabona, F., and Caputo, B. (2017). Scalable
greedy algorithms for transfer learning. Computer Vi-
sion and Image Understanding, 156:174–185.
Long, M., Wang, J., Ding, G., Sun, J., and Yu, P. S. (2013).
Transfer feature learning with joint distribution adap-
tation. In Proceedings of the IEEE international con-
ference on computer vision, pages 2200–2207.
Lou, Q., Feng, B., Fox, G. C., and Jiang, L. (2019). Glyph:
Fast and accurately training deep neural networks on
encrypted data. arXiv preprint arXiv:1911.07101.
Madi, A., Sirdey, R., and Stan, O. (2020). Computing neural
networks with homomorphic encryption and verifiable
computing. In International Conference on Applied
Cryptography and Network Security, pages 295–317.
Springer.
Mormont, R., Geurts, P., and Mar
´
ee, R. (2018). Com-
parison of deep transfer learning strategies for digital
pathology. In Proceedings of the IEEE Conference on
Computer Vision and Pattern Recognition Workshops,
pages 2262–2271.
Nigam, K., McCallum, A. K., Thrun, S., and Mitchell, T.
(2000). Text classification from labeled and unlabeled
documents using em. Machine learning, 39(2):103–
134.
Patricia, N. and Caputo, B. (2014). Learning to learn, from
transfer learning to domain adaptation: A unifying
perspective. In Proceedings of the IEEE Conference
ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy
228

on Computer Vision and Pattern Recognition, pages
1442–1449.
Rohrbach, M., Ebert, S., and Schiele, B. (2013). Transfer
learning in a transductive setting. Advances in neural
information processing systems, 26:46–54.
Romera-Paredes, B., Aung, M. S., Pontil, M., Bianchi-
Berthouze, N., Williams, A. C. d. C., and Watson, P.
(2013). Transfer learning to account for idiosyncrasy
in face and body expressions. In 2013 10th IEEE In-
ternational Conference and Workshops on Automatic
Face and Gesture Recognition (FG), pages 1–6. IEEE.
Sanyal, A., Kusner, M., Gasc
´
on, A., and Kanade, V. (2018).
TAPAS: Tricks to accelerate (encrypted) prediction as
a service. In ICML.
SEAL (2018). Microsoft SEAL (release 3.0). http://
sealcrypto.org. Microsoft Research, Redmond, WA.
Simonyan, K. and Zisserman, A. (2014). Very deep con-
volutional networks for large-scale image recognition.
arXiv preprint arXiv:1409.1556.
Sirichotedumrong, W., Maekawa, T., Kinoshita, Y., and
Kiya, H. (2019). Privacy-preserving deep neural net-
works with pixel-based image encryption considering
data augmentation in the encrypted domain. In 2019
IEEE International Conference on Image Processing
(ICIP), pages 674–678. IEEE.
Srivastava, N. and Salakhutdinov, R. (2013). Discrimina-
tive transfer learning with tree-based priors. In NIPS,
volume 3, page 8. Citeseer.
Tanaka, M. (2018). Learnable image encryption. In
2018 IEEE International Conference on Consumer
Electronics-Taiwan (ICCE-TW), pages 1–2. IEEE.
Tommasi, T. and Caputo, B. (2009). The more you know,
the less you learn: from knowledge transfer to one-
shot learning of object categories. In BMVC, number
CONF.
Tommasi, T., Orabona, F., and Caputo, B. (2010). Safety
in numbers: Learning categories from few examples
with multi model knowledge transfer. In 2010 IEEE
Computer Society Conference on Computer Vision
and Pattern Recognition, pages 3081–3088. IEEE.
Tramer, F. and Boneh, D. (2018). Slalom: Fast, verifiable
and private execution of neural networks in trusted
hardware. arXiv preprint arXiv:1806.03287.
Wang, H., Nie, F., Huang, H., and Ding, C. (2011). Dyadic
transfer learning for cross-domain image classifica-
tion. In 2011 International conference on computer
vision, pages 551–556. IEEE.
Wang, W., Wang, H., Zhang, C., and Xu, F. (2015). Trans-
fer feature representation via multiple kernel learning.
In Twenty-Ninth AAAI Conference on Artificial Intel-
ligence.
Yang, Q., Ling, C., Chai, X., and Pan, R. (2006). Test-
cost sensitive classification on data with missing val-
ues. IEEE Transactions on Knowledge and Data En-
gineering, 18(5):626–638.
Yin, X., Han, J., Yang, J., and Yu, P. S. (2006). Effi-
cient classification across multiple database relations:
A crossmine approach. IEEE Transactions on Knowl-
edge and Data Engineering, 18(6):770–783.
Zhu, X. and Wu, X. (2006). Class noise handling for ef-
fective cost-sensitive learning by cost-guided iterative
classification filtering. IEEE Transactions on Knowl-
edge and Data Engineering, 18(10):1435–1440.
Zhu, X. J. (2005). Semi-supervised learning literature sur-
vey.
Zhu, Y., Chen, Y., Lu, Z., Pan, S. J., Xue, G.-R., Yu, Y.,
and Yang, Q. (2011). Heterogeneous transfer learning
for image classification. In Twenty-Fifth AAAI Con-
ference on Artificial Intelligence.
Zuber, M. and Fiore, D. (2016-2017). Hal: A library for
homomorphic authentication. http://www.myurl.com.
SecTL: Secure and Verifiable Transfer Learning-based inference
229
