Detection of Potential Manipulations in Electricity Market using

Machine Learning Approaches

Shweta Tiwari

1 a

, Gavin Bell

, Helge Langseth

1 b

and Heri Ramampiaro

1 c

Department of Computer Science, Norwegian University of Science and Technology (NTNU),

Sem Sælands vei 9, Trondheim, 7491, Norway

Optimeering AS, Oslo, Norway

Keywords:

Anomaly Detection, Bid Curves, Physical Electricity Market, Machine Learning.

Abstract:

Detecting potential manipulations by monitoring trading activities in the electricity market is a time-

consuming and challenging task despite the involvement of experienced market surveillance experts. This

is due to the increasing complexity of the market structure, contributing to the increase of deceptive anoma-

lous behaviours that can be considered as market abuses. In this paper, we present a novel methodology for

detecting potential manipulations in the Nordic day-ahead electricity market by using bid curves data. We

ﬁrst develop a method for processing and reducing the dimensionality of the historical bid curves data using

statistical techniques. Then, we train unsupervised machine learning-based models to detect outliers in the

pre-processed data. Our methodology captures the sensitivity of the electricity prices resulting from the com-

petitive bidding process and predicts anomalous market behaviours. The results of our experiments show that

the proposed approach can complement human experts in market monitoring, by pointing towards relevant

cases of manipulation, demonstrating the applicability of the approach.

1 INTRODUCTION

Following the deregulation of electricity sectors two

decades ago, electricity has become a standardized

cross-border trading commodity. Bids and offers are

made to balance the demand and supply of electric-

ity for a given area and each hour of a given day. A

competitive auction in electricity exchanges decides

the price of electricity. The market price of electricity

varies considerably from area to area and over time,

on a daily and hourly basis. This variation reﬂects

and is driven by changes in power generation capac-

ity, demand and transmission conditions. Changes in

external environmental variables such as weather con-

ditions can also result in substantial volatility in mar-

ket prices, and high levels of risk can be associated

with electricity trading. Renewables have become in-

creasingly crucial for the electricity market and are

increasing volatility (Wagner, 2014).

Nord Pool is a leading power trading market in

Europe, serving as an electricity exchange to several

https://orcid.org/0000-0003-3363-087x

https://orcid.org/0000-0001-6324-6284

https://orcid.org/0000-0003-0534-5924

markets in the Nordic region, the Baltics, Germany,

France, Netherlands, Belgium, Austria and the UK.

Due to the economic importance of the electricity

market, its real-time surveillance is essential to en-

sure and maintain well-functioning, transparent, ac-

cessible and fair trading. The existing surveillance

mechanism is typically undertaken by trained mar-

ket surveillance analysts, who monitor market activ-

ity and investigate possible rule breaches and mar-

ket manipulation attempts. However, the electricity

markets’ scale, size and complexity make the tra-

ditional rule-based surveillance inefﬁcient and time-

consuming because even domain experts can not an-

ticipate all forms of normal/abnormal behaviours to

be hard-coded in the monitoring system. There is a

need for automatic market monitoring methodologies

to assist and support human analysts in their surveil-

lance activities to ensure robust and comprehensive

market surveillance at manageable cost and complex-

ity.

Electricity price manipulation – see Background

section for more detail – is one of the primary abuses

in the electricity market, where the manipulation tar-

get is the MCP that causes price ﬂuctuation over a

period of time. In this paper, we develop a method-

Tiwari, S., Bell, G., Langseth, H. and Ramampiaro, H.

Detection of Potential Manipulations in Electricity Market using Machine Learning Approaches.

DOI: 10.5220/0010991800003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 3, pages 975-983

ISBN: 978-989-758-547-0; ISSN: 2184-433X

975

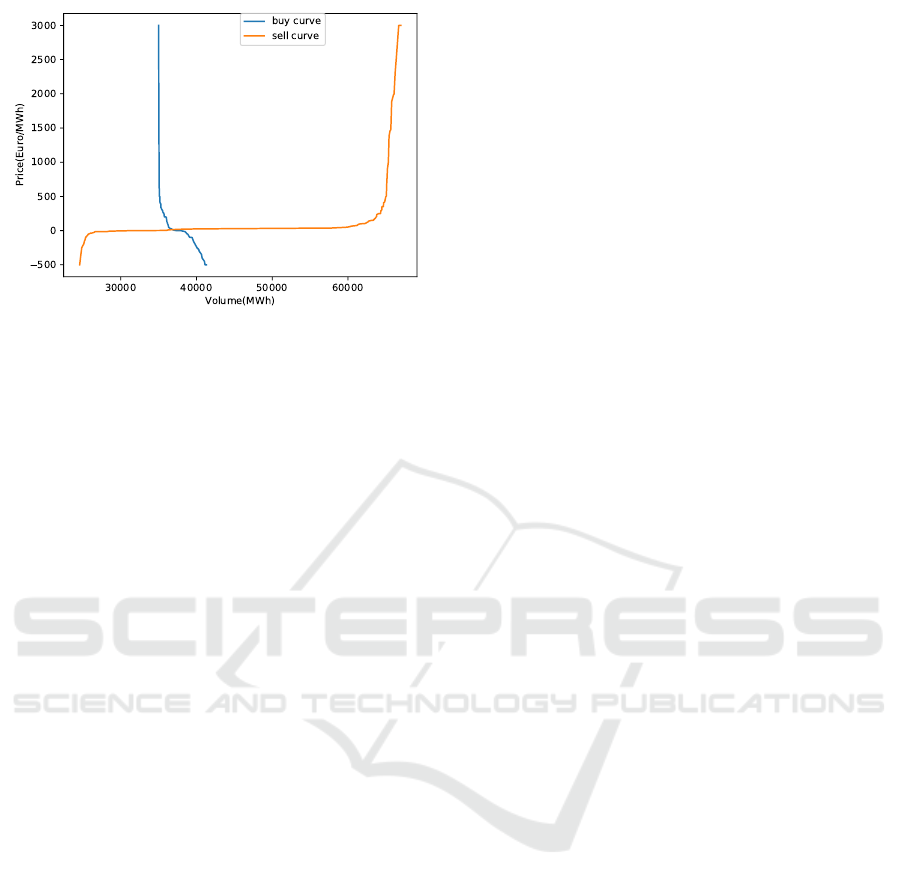
Figure 1: Aggregated buy and sell curves.

ology to detect potentially suspicious market events

using bid curves data, which to the best of our knowl-

edge, is a novel idea. Bid curves (sometimes called

‘order books’ or ‘demand-supply curves’ in different

markets) are the aggregation of all bids to buy and sell

electricity in the market for a given period. In a typ-

ical day-ahead market, once the deadline for traders

to submit their bids into the market is passed, these

bids are aggregated into two curves per trading period

– one for supply bids and one for demand bids – for

the following day. The resulting supply and demand

curves contain all the sell and buy prices and vol-

umes submitted by each trader, and then the reference

price, commonly known as the market clearing price

(MCP), is determined for the given trading period. A

typical aggregated supply and demand curve is illus-

trated in Figure 1. A typical trading period length is

one hour, and thus for every hour of a given day, there

will be one set of 2 bid curves and 24 such curve sets

for the entire day.

In our methodology, we ﬁrst use bid curves data

to extract useful features using statistical methods and

then use these features to train machine learning mod-

els to detect potential manipulations in the electricity

market based on detecting unusual changes in the sup-

ply curves. Our paper makes the following contribu-

tions:

• We propose a feature extraction method for the

bid curve data.

• We implement machine learning techniques to de-

tect anomalous changes in bid curves.

• We propose alerting methodologies based on de-

tecting anomalous bid curves, designed to reduce

the number of false positives by using the curves

and automatize the surveillance process.

2 RELATED WORK

After deregularization of electricity markets and

increasing disclosure of data from these mar-

kets, research interests in understanding the struc-

ture and behaviour of prices have substantially in-

creased. To gain insight into manipulative market be-

haviours/patterns, Rahimi and Sheffrin (2003), G

uler

and Gross (2005) have proposed frameworks for elec-

tricity market monitoring. In the early work, Fleten

and Pettersen (2005) pointed out that the bid curves

are one of the crucial aspects of electricity trading.

The bid curves contain information regarding various

sources of electricity, different markets and regions

that inﬂuence MCP. Thus, it is essential to explore

these curves to understand the bidding/pricing pat-

terns and behaviour of actors in the market. Availabil-

ity of hourly auction data (hourly bid curves) provides

an opportunity to analyse the market in more detail,

but this usually results in a large amount of data and

increases complexity. Work from Eichler et al. (2012)

proposed a methodology to simplify the bid curves

into a new curve using an autoregressive time series

model.

A methodology to reconstruct the bid curves us-

ing dimensionality reduction techniques and high di-

mensional statistical methods was proposed in (Ziel

and Steinert, 2016) and (Coulon et al., 2014). The

resulting curve exhibits many typical behavioural at-

tributes such as weekday/weekend effect, seasonal

changes. Ziel and Steinert (2016) suggested grouping

the possible bid prices to price classes by considering

a linear model for the bid volume for each price class.

They forecast the bid volumes in the price classes, re-

construct the buy and sell curve and receive the corre-

sponding MCP. We derived our motivation from this

work, particularly the idea of processing the original

bid curves for capturing the sensitivity of the MCP

forms the basis of our modelling approach. However,

we ﬁt regression splines to the sell curve to simplify

its representation instead of grouping the bid volumes

into classes that require high-dimensional statistical

methods.

3 BACKGROUND

Over the decades, the electricity market rapidly ex-

panded into an advanced trading system where many

actors are involved, see Figure 2 (Spot, 2009). The

analysis presented in our paper has been undertaken

on the Nord Pool’s Elspot (day-ahead) market for the

Nordic region. The actor can submit three types of

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

976

bids

in this market; hourly bids, block bids and ﬂex-

ible hour bids. In hourly bids, the actor has the in-

tention to buy or sell a volume of electricity from an

agent in a particular area at various bid prices for a

speciﬁc hour of the day. In a block bid, the actor has

the intention to buy or sell a volume of electricity at

a speciﬁc amount for at least three consecutive hours.

Whereas, in ﬂexible hour bids an actor can make ex-

tra bids to sell the volume of electricity at any hour

of the day depending on the bid price and situation of

the market at each hour (Fernandes et al., 2014)

TRADERS

Trade power

on physical

and ﬁnancial

market

PRODUCERS

Energy companies

and generators

CONSUMERS

Power intensive industry

Distributers

BROKERS

Electricity

Exchange

Figure 2: The commercial actors (players) and the ex-

change.

3.1 Price Formulation

A simple supply and demand model can describe the

Nordic electricity market. Actors (sellers and buy-

ers) participate in the auction process, where they give

bids for both price and volume for each hour of the

following day. After the deadline to submit the bids

ends, all the bids are aggregated into supply and de-

mand curves.

Power ﬂow occurs between two connected price

areas if there is sufﬁcient transmission capacity and

cheaper generation available in the exporting area for

use in the importing area. If transmission capacities

between two price areas are sufﬁcient for the ﬂow of

power, the market price in the two areas will be iden-

tical. If the transmission capacity between price areas

is not sufﬁcient to reach full price convergence across

the areas, congestion will lead to bidding areas having

different prices.

In addition, for each hour Nord Pool calculates

a “system price”, which is the MCP that would oc-

cur if there were no congestion between bidding areas

and all bids and offers were placed in a single supply

and demand curve for the entire market (equivalently,

https://www.nordpoolgroup.com

if the transmission capacity between each connected

price area were inﬁnitely large). The system price is

largely used and an index price in power contracts and

ﬁnancial derivative products.

The sales orders less than or equal to MCP will

be accepted, whereas buy orders which are higher or

equal to MCP are accepted (M

att

a and Johansson,

2011). Block bids are accepted if doing so improves

the socio-economic welfare. In practice, block bids

are entirely rejected or accepted based on their prices

being higher or lower than the average day-ahead area

price. In case of an exact match between the two

prices, the block bids may get fully accepted if doing

so results in maximizing social welfare.

The supply curve consists of bids from hy-

dropower, wind power, nuclear and condensing plants

(i.e. those that burn oil, coal and gas). Unregu-

lated production such as wind have variable costs of

near-zero, whereas condensing plants that produce

electricity with gas turbines have very high variable

costs. Hydro power also has very low direct genera-

tion costs; however regulated (controllable) hydro is

typically priced based on opportunity cost considera-

tions (via so-called water values, e.g. (Dueholm and

Ravn, 2004) ), reﬂecting the fact that a marginal MWh

of hydro production will substitute directly for an al-

ternative generation source.

The electricity markets have a price-setting mech-

anism characterized by supply and demand; the fac-

tors that affect supply and demand are in turn the fac-

tors affecting the price. Factors such as temperature

and other weather variables can drive both demand

(e.g. by increasing electrical heating demand) and

supply (by impacting levels of unregulated production

such as wind, solar and unregulated hydro). Other

drivers include fossil fuel prices, emissions (CO2)

prices, water reservoir levels, status of nuclear reac-

tors and plant outages, economic and business cy-

cles (Inspectorate, 2006).

3.2 Deﬁnition of Market Manipulation

Market manipulation prohibition under REMIT

pro-

vides a robust deﬁnition of market manipulation that

is used in all EU-regulated power markets:

1. The transactions which give or have intention of

giving misleading signals as to supply, demand or

price of a product.

2. The transactions which secure or have the inten-

tion of securing prices at artiﬁcial levels.

3. Fictitious device or deception.

https://www.emissions-euets.com/market-

manipulation-remit

Detection of Potential Manipulations in Electricity Market using Machine Learning Approaches

977

4. Disseminating false or misleading information.

There are several signiﬁcant challenges in identi-

fying such events, transactions, and actions. Firstly,

few examples of manipulation are cited in the lit-

erature, or identiﬁed and published in practice by

surveillance authorities. There is thus no comprehen-

sive labelled set of manipulation examples that can

be used to develop detection methods. Secondly, it

may be challenging to determine if a given market-

moving event or transaction results from a manipu-

lation attempt or a result of legitimate factors. For

example, a generation volume may be removed from

the market to manipulate price, or alternatively due

to environmental factors and regulations that restrict

generation from the plant for certain hours at short

notice. Thirdly, it may be hard to identify such

events/transactions because they may be combined

with other transactions.

Due to such challenges, it is hard for any one

method to identify explicitly “exact” actions or be-

haviour as manipulation. Instead, the approach un-

dertaken by surveillance authorities is often to collect

enough circumstantial and/or indicative evidence to

suggest manipulation has occurred. Such evidence

can include detecting unusual structures, patterns or

changes in individual bids and the bid and offer curves

in summation. Typically, a surveillance authority will

utilize a combination of automatic rule-based detec-

tion methods and manual examination of bids and

market results to identify potential incidences of ma-

nipulation. Those incidents with sufﬁcient evidence

to warrant; further, manual investigation are priori-

tized, and those with the highest priority are selected

for further analysis (private communication).

The assumption motivating the approach of this

paper is that if supply–side manipulation is success-

ful, it will result in an unusual change in the sup-

ply curve. Such manipulations are volume-based at-

tempts (such as removing or limiting available vol-

umes bid into the market) or price-based (such as in-

creasing bid prices in areas of the curve where a sup-

plier may have market power), or combinations of

these. More complex examples include utilizing com-

plicated block and hourly bid structures to force block

bid acceptance or ensure the selection of high-priced

bids to raise MCP. Such methods may be particularly

relevant in periods of high demand (so-called “tight”

markets), where small changes in supply can have a

substantial impact on the price (Directive, 2011).

4 METHODOLOGY

4.1 Data Preparation

One of our datasets consists of Nord Pool’s system-

level (whole market) bid curves, ranging from

01/06/2019 to 31/12/2019. The curve data is pub-

licly available on Nord Pool’s website. The dataset of

system-level price curves also contains the volume of

hourly accepted block bids – both demand and sup-

ply. Adding these accepted block volumes to the ad-

justed hourly bid and sell curves enables us to recreate

each hour’s system-level supply and demand curves

over the data horizon. We have 24 hourly bid buy

curves and 24 sell curves for the system price for each

day. Our study considers only sell curves; however,

the methodology is also directly applicable to demand

curves.

The other dataset we used is conﬁdential data pro-

vided by the Norwegian Water Resources and Energy

Directorate (NVE), the national regulatory authority

for the electricity market in Norway. The dataset con-

sists of price area curves of the area ‘NO2’ in Norway

for the same period as above. Norway has ﬁve price

areas (NO1, NO2, NO3, NO4, NO5) to handle trans-

mission constraints. Prices differ in the bidding areas

when the constraints are binding, with higher prices in

deﬁcit areas and lower in surplus areas (Hjalmarsson,

2000). Therefore, the area-price curves are different

from system-level price curves, but the curve funda-

mentals are the same.

4.2 Curve Processing

In the electricity markets, bids of unregulated renew-

able generation (sometimes called intermittent gen-

eration) are generally of very low prices in order to

ensure bid acceptance. The volumes of renewable

bids – wind, solar and unregulated hydro – are de-

termined mainly by extraneous environmental factors

such as cloud cover, temperature, precipitation, and

wind speeds. These factors add additional noise to the

curve structure that does not reﬂect potential manip-

ulation attempts and should be removed before mod-

elling.

While a surveillance authority ideally would have

information of the exact level of such generation ca-

pacities and bids available to precisely remove them,

this is not generally the case in many markets where

bids are not linked to speciﬁc assets but portfolios or

market actors. However, it is standard practice to bid

such volumes at the lowest price to ensure bid ac-

ceptance, particularly in markets such as Nord Pool,

where the chance of such bids being price setter is ex-

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

978

tremely low. Thus, to remove the inﬂuence of unreg-

ulated bids, each curve was adjusted to its minimum

volume.

4.2.1 Regression Splines

Since 2008 the electricity spot price is set to be be-

tween −500 and 3000 C/MWh, actors can make their

bids in this range only for selling or buying a certain

amount of electricity. The minimum order size in-

crement is 0.1 MW for one hour, and the minimum

price increment is 0.1 C/MWh. Hence, there are in to-

tal 35001 different possible prices on the entire price

grid, i.e. P={-500, -499.9, ..., 2999.9, 3000}. These

curves often contain different numbers of anonymized

bids that result in curves of different lengths from

hour-to-hour and day-to-day. Additionally, curves

contain a small amount of noise. For example, the

bid order changes due to small changes in bid prices

among actors, but the overall bid curve (and resulting

price levels) do not change.

We pre-process the curves to allow for a compar-

ison agnostic to granularity and noise. Regression

splines is a non-linear regression technique in which

the data is divided into multiple bins, and separate

functions ﬁt these bins. The points where the divi-

sion happens are called knots or breakpoints whereas

the function used for modelling is called as piece-

wise function. The piecewise function could be a

linear function or low degree polynomials. In this

study, we use continuous piecewise linear functions

(cpwlf) (Jekel and Venter, 2019) to simplify the bid

curves representation. The piecewise linear function

approximation of the curve structure was chosen due

to the curves’ regular and repeatable overall structure.

Bid curves in power markets typically have a steeply

sloping but very low priced ”must run” portion, a

ﬂat mid-priced portion, and a steep, high-priced peak

portion. The pwlf approach helps to correctly cap-

ture slopes and turn points into curves without being

overly disturbed by small ”noise” components. An

example of spline ﬁtting with ﬁve piecewise linear

functions to a sample sell curve is shown in Figure 3.

4.3 Features Extraction

As we can see in Figure 3, the left portion of the curve

has a big turn and again a big turn in the right portion,

whereas the middle portion is approximately linear

(less variation). By taking these turns in the account,

we ﬁt n piecewise functions to the curve. We can now

represent the curve in terms of knots and slopes of the

lines and consider them as our features to outlier de-

tection methods and train a clustering-based machine

learning model to identify the unusual changes in the

5000 10000 15000 20000 25000 30000 35000

500

1000

1500

2000

2500

3000

original data points

splines

volume

price

Figure 3: Continuous piecewise linear ﬁtting of sell curve

by splines.

curves. First, we scale the volumes by taking the dif-

ference between the ﬁrst volume value and the rest

of the volumes of a curve(we have to do it for ev-

ery hour since we have one curve each hour). We

then have volume values between 0 & 35000, and we

also discard the data which has prices greater than

2850

C/MWh. We tried to ﬁt 3, 5, 8 and 10 cpwlf

to the curves, and we found ﬁve cpwlf are the opti-

mum number for these curves because by ﬁtting less

cpwlf there is a possibility to miss some important

information (speciﬁcally in the high variant region)

whereas, if we consider too many cpwlf then there is

a chance of overﬁtting. We use Python library pwlf

to perform spline ﬁtting to our curves, which provides

the ﬂexibility to customize the parameters according

to the requirement.

4.4 Modelling

The task of detecting abnormal changes in bid curves

data relates to the outlier/novelty detection methods in

machine learning. The outlier detection is the identi-

ﬁcation of data points and/or patterns representing be-

haviours that deviate signiﬁcantly from those consid-

ered normal data (Hodge and Austin, 2004). Cluster-

ing, an unsupervised machine learning technique, is

one of the simplest anomaly detection methods used

for drawing references from a dataset consisting of

input data without any labelled response. Cluster-

ing separates similar data points in the same group or

cluster and dissimilar data points to other groups (Xu

and Wunsch, 2008). In our analysis we use different

clustering and outlier detection methods to identify

the unusual curve differences. First, we deﬁne curve

difference as following:

= d

n,h

− d

n−1,h

(1)

https://github.com/cjekel/piecewise linear ﬁt py.git

Detection of Potential Manipulations in Electricity Market using Machine Learning Approaches

979

where d

n,h

refers to the sell curve of the h

(h ∈

{0,1,2,...,23}) hour of the n

(n ∈ {1,2,3...,7}) day.

It is a standard practice in machine learning to nor-

malize the data before training any model when the

features have different ranges. Therefore, we nor-

malized all the features and then performed cluster-

ing by applying kmeans and k-nearest neighbor (Ra-

maswamy et al., 2000) algorithm and outlier detection

methods such as local outlier factor (Breunig et al.,

2000), one-class support vector machine (Sch

olkopf

et al., 2001) and isolation forest (Liu et al., 2008).

The goal here is, when δ

fall outside the pre-deﬁned

threshold then it will mark as outlier.

In kmeans the distance from each data point to its

cluster centroid is calculated using Euclidean distance

(D). The threshold is then deﬁne as:

threshold = min(m × max(D)) (2)

m = f × j, where f is outlier fraction and j is to-

tal number of data points. For the other methods,

we used a Python library PyOD

designed to perform

scalable outlier detection on multivariate data.

4.5 Alerts

Curve differences exceeding threshold values are

outliers that are used for alert generation. We

generate alerts by producing a ranked list in two

ways. First, an ordered list of outlier fractions f ∈

{0.01,0.02,0.03,0.04,0.05} is considered in which

outlying points with respect to lower fraction val-

ues are ranked higher than the newly appeared out-

lying points in higher fraction values. Second, we use

voting method to generate alerts in which a point is

ranked higher if it is marked as an outlier by a major-

ity of algorithms.

5 EXPERIMENTAL RESULTS

We have tested our methodology on two datasets de-

scribed in the previous section. In this section, we re-

port in detail the results of our methodology for both

datasets. There are three main steps involved in these

experiments. Step 1: generate outlier results using

unsupervised ML methods. Step 2: check other data

sources, such as weather forecasts, market messages

and non-ﬂexible production plans to ﬁnd explanations

for the identiﬁed outliers in the ﬁrst step. Step 3:

unexplained outliers are passed on to the domain ex-

perts.

https://github.com/yzhao062/pyod.git

4 2 0 2 4

Feature 1

Feature 2

normal

outlier

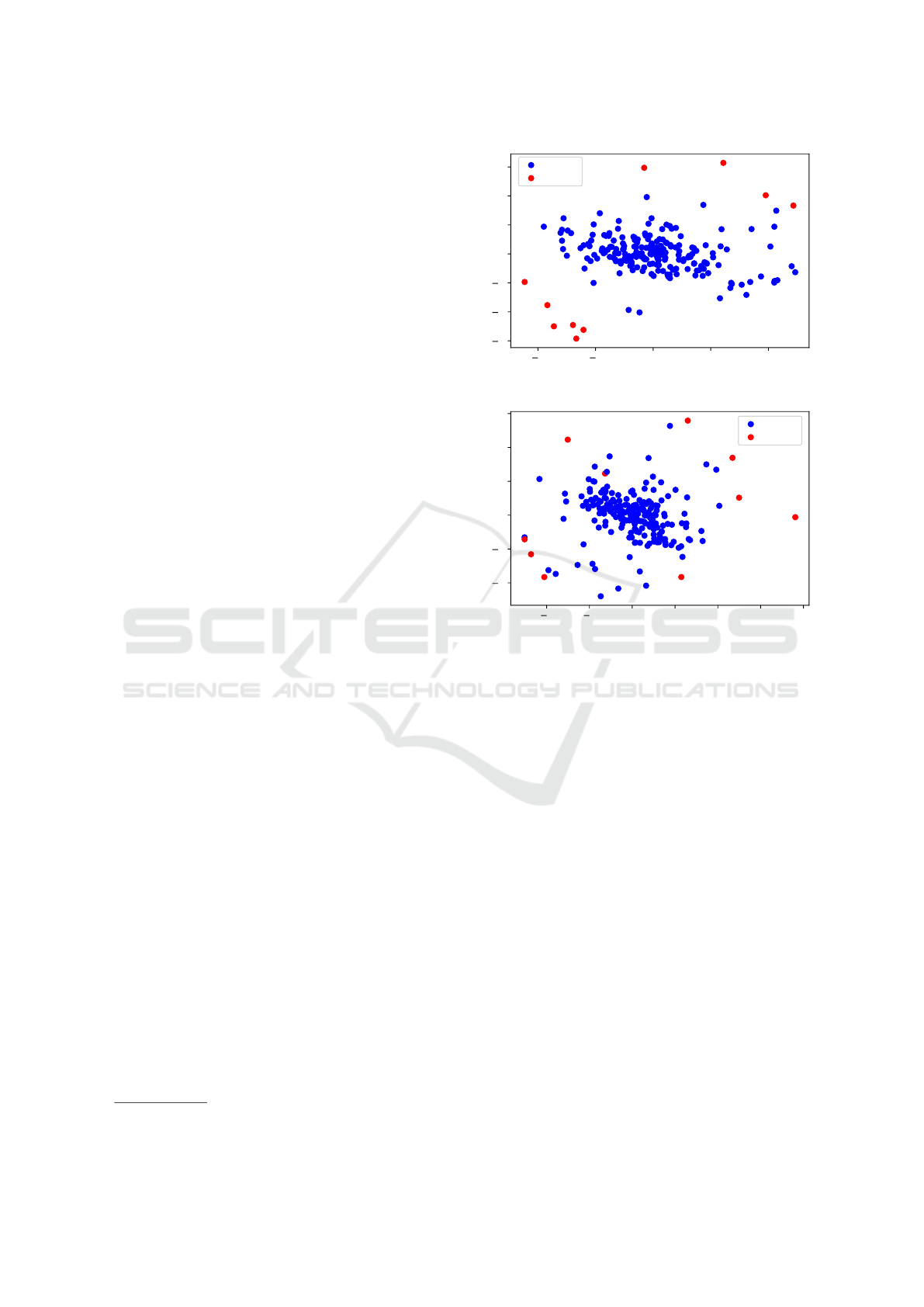
Figure 4: Outliers in h10 on system-level curves.

4 2 0 2 4 6 8

Feature 1

Feature 2

normal

outlier

Figure 5: Outliers in h19 on system-level curves.

5.1 Experiment 1

The ﬁrst set of experiments are performed on system-

level curves. We have considered data from two

hours – h10 and h19 – for our analysis, and for each

hour, we ran separate models to identify outliers. We

choose h10 and h19 because these are high demand

hours in the market. In a high demand period even

a small change in supply can substantially impact

the prices. Using the Principal Component Analysis

(PCA), we reduced the data dimensionality into two

features for visualisation purposes by using the Prin-

cipal Component Analysis (PCA). The points identi-

ﬁed as outliers by kmeans in h10 and h19 are shown

in Figure 4 and 5, respectively. For these plots, we

used the optimum value k = 2 and the outlier frac-

tion f = 0.05. We also tested the robustness of the

algorithm by choosing different random seeds for the

clusters. The sell curve representations of outliers in

h10 and h19 are shown in Figure 6 and 7, respec-

tively. In these ﬁgures, normal curves are represented

in blue colour, whereas other colours represent outly-

ing curves. As shown, in most of the cases, a signif-

icant amount of capacities (volumes) are removed or

added at d

n+1

as compared to d

. To perform Step

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

980

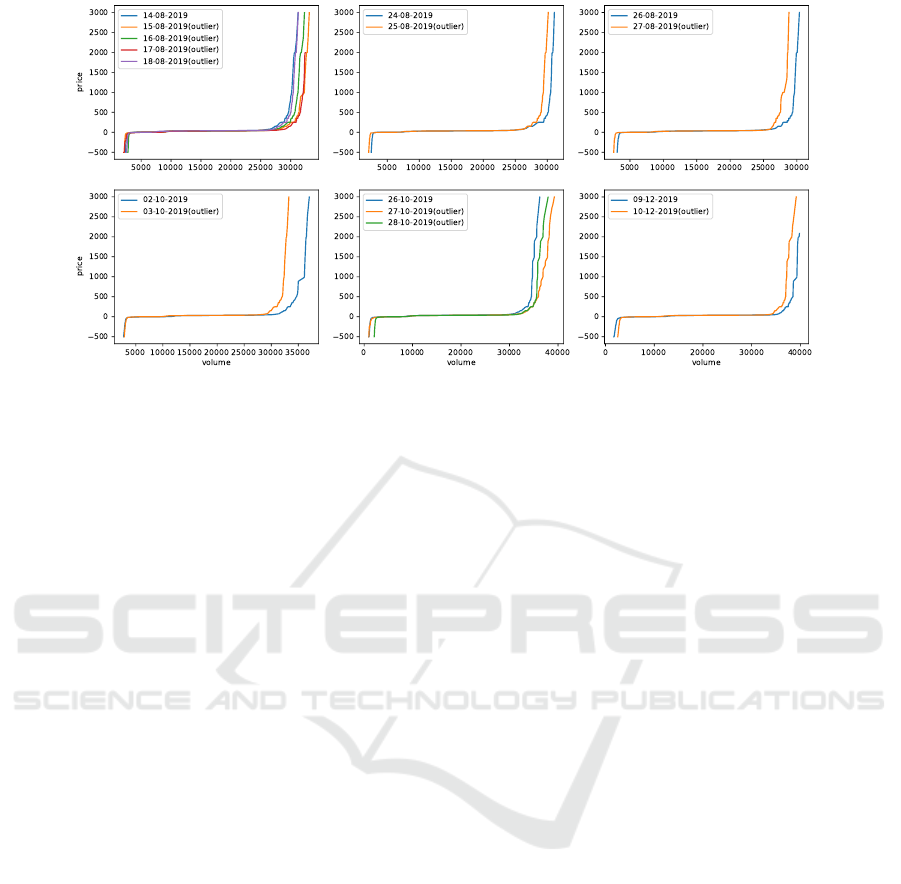
Figure 6: Outliers in h10. Curves in blue are the normal curves, and the outlying curves are shown in other colors.

2, data from other sources such as block volumes,

unavailability volumes, non-ﬂexible production plans

etc., can be used. A difference between values for

each outlier day from its previous day can be calcu-

lated for these sources. By taking these differences

into account, a shift in the curve can be explained by

an increase or decrease in the values of the data men-

tioned in the above sources. After ﬁltering, the unex-

plained outliers will pass on to an expert to perform

Step 3. However, currently, we do not have access

to any such data for the entire Nordics; therefore, we

cannot perform Step 2.

5.2 Experiment 2

We applied Isolation Forest in the price-area curves

to detect outliers. Similarly to the system-level curve

analysis, our approach robustly identiﬁed a small

number of outlier periods. For visualisation purposes,

we reduced the data into two dimensions using PCA.

Figures 8 and 9 illustrate the results for h10 and

h19, respectively. Due to privacy constraints, both

steps 2 and 3, in this case, were performed by the

market surveillance analysts from NVE. The expert

considered three factors: block volume, unavailabil-

ity volume, and non-ﬂexible production plans. For

these factors, a difference between values for each

outlier day from its previous day was calculated. A

shift in the curves is explained by an increase or de-

crease in values of the factors mentioned above. Mar-

ket surveillance analysts require further exploration

if shifts in the curves cannot be explained based on

these calculated differences. Due to industrial sensi-

tivity, we are not allowed to disclose the particular-

ity of Step 2, and we cannot visually illustrate the re-

sults obtained from the expert. Approximately 50% of

the times for which our system-generated alerts were

worthy of further investigation was conﬁrmed.

6 DISCUSSION

The presented approach has its limitations. One of

the main limitations is the unavailability of labelled

data that can serve as the ground truth. This, in turn,

might result in limitations in the experimental evalu-

ation, and thus correctly identifying normal and ma-

nipulative market events. As a consequence, any as-

sessment of the efﬁciency of alert algorithms is sub-

jective. Nevertheless, as our experiments have shown,

it is still possible to identify events that can serve as

a useful basis for correctly detecting anomalies. In

the proposed methodology, the alerts are generated

based on detecting outliers in the bid curves that cur-

rently contain only one source of information, which

are provided to human experts for further assessment.

Our model does not include other forms of infor-

mation, e.g. unavailable generation capacity, wind

ﬂow predictions, weather forecast and limited pro-

duction. As, we hypothesise that these might have

substantially improved the alert generation, exploring

including such information would is an interesting av-

enue for further research.

Finally, our method focuses only on the day-ahead

market. However, manipulators often carry out trad-

ing activities in more than one market, making manip-

ulation attempts highly deceptive. To cope with this,

the proposed methodology might beneﬁt from includ-

ing different feature sets and detection models to de-

tect manipulations effectively in inter-market settings.

Detection of Potential Manipulations in Electricity Market using Machine Learning Approaches

981

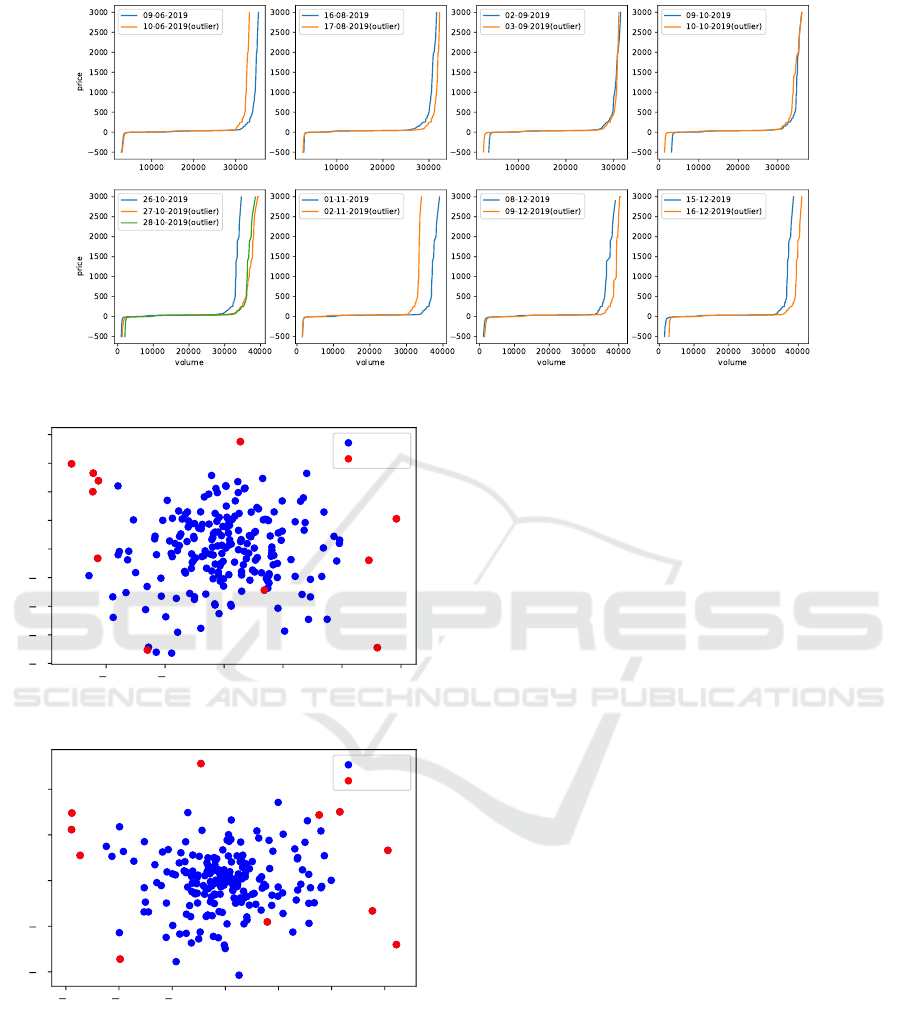
Figure 7: Outliers in h19, curves in blue are the normal curves and other colors represent outlying curves.

4 2 0 2 4 6

Feature 1

Feature 2

normal

outlier

Figure 8: Outliers in h10 on price-area curves.

6 4 2 0 2 4 6

Feature 1

Feature 2

normal

outlier

Figure 9: Outliers in h19 on price-areal curves.

7 CONCLUSION AND FUTURE

WORK

In this paper, we proposed a method that applies unsu-

pervised machine learning to detect potential manipu-

lations in the electricity market using bid curves data.

In contrast to the traditional approach of using time-

series data consisting of market-clearing price, which

is determined by the intersection of demand and sup-

ply curves, the proposed method uses bid curves data

that is the original source of the price and include the

sensitivity of the competitive bidding process, making

our method novel and effective for market manipula-

tion detection.

The methodology further uses the detected un-

usual changes in the day-ahead market to generate

alerts that can be used by regulatory surveillance au-

thorities to prioritize potential cases of manipulation

for further investigation. Further, they may identify

potential periods of manipulation at a market level,

which may result from complex interactions of mul-

tiple bids, and that may not be detected via bid-level

indicators. By systematically and consistently ana-

lyzing bid curve changes, our approach avoids the er-

ror and subjectivity that may result from human-based

manual assessment of bid curve developments over

time.

Our experimental ﬁndings suggest that surveil-

lance analysts could not explain around half of the

generated alerts using extraneous factors. This pro-

vides a strong indication that the methodology would

be highly useful as a complementary tool to assist hu-

man experts in market monitoring.

Altogether, we see this work as an initial step to-

wards a fully automated market monitoring tool. For

future work, we plan to extend this methodology to

incorporate other essential features such as weather

forecast and non-ﬂexible production plans to reduce

manual ﬁltering, and only the most relevant alerts

with no explanation will be presented to analysts.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

982

ACKNOWLEDGEMENTS

This work was funded by the Research Council of

Norway, NVE, and Optimeering and was carried out

at the Norwegian Open AI Lab, NTNU, and Opti-

meering.

REFERENCES

Breunig, M. M., Kriegel, H.-P., Ng, R. T., and Sander, J.

(2000). Lof: identifying density-based local outliers.

In Proceedings of the 2000 ACM SIGMOD interna-

tional conference on Management of data, pages 93–

104.

Coulon, M., Jacobsson, C., and Str

ojby, J. (2014). Hourly

resolution forward curves for power: Statistical mod-

eling meets market fundamentals. Energy Pric-

ing Models: Recent Advances, Methods and Tools;

Prokopczuk, M., Ed.

Directive, C. (2011). Regulation (eu) no 1007/2011 of the

european parliament and of the council of 27 septem-

ber 2011 on textile ﬁber names and related labelling

and marking of the ﬁbre composition of textile prod-

ucts. Ofﬁcial Journal of the European Union.

Dueholm, L. and Ravn, H. (2004). Modelling of short term

electricity prices, hydro inﬂow and water values in the

norwegian hydro system. In Proceedings, 6th IAEE

European Conference, Z

urich, 2004. IEEE.

Eichler, M., Sollie, J., and Tuerk, D. (2012). A new ap-

proach for modelling electricity spot prices based on

supply and demand spreads. In Conference on Energy

Finance, pages 1–4.

Fernandes, R., Santos, G., Prac¸a, I., Pinto, T., Morais, H.,

Pereira, I. F., and Vale, Z. (2014). Elspot: Nord pool

spot integration in mascem electricity market simula-

tor. In International Conference on Practical Applica-

tions of Agents and Multi-Agent Systems, pages 262–

272. Springer.

Fleten, S.-E. and Pettersen, E. (2005). Constructing bid-

ding curves for a price-taking retailer in the norwe-

gian electricity market. IEEE Transactions on Power

Systems, 20(2):701–708.

uler, T. and Gross, G. (2005). A framework for electric-

ity market monitoring. The University of Illinois at

Urbana-Champaign. NSF ECS-0224829.

Hjalmarsson, E. (2000). Nord pool: A power market with-

out market power. rapport nr.: Working Papers in

Economics, (28).

Hodge, V. and Austin, J. (2004). A survey of outlier de-

tection methodologies. Artiﬁcial intelligence review,

22(2):85–126.

Inspectorate, E. M. (2006). Price formation and competition

in the swedish electricity market. The Energy Markets

Inspectorate at the Swedish Energy Agency.

Jekel, C. F. and Venter, G. (2019). Pwlf: a python library for

ﬁtting 1d continuous piecewise linear functions. URL:

https://github. com/cjekel/piecewise linear ﬁt py.

Liu, F. T., Ting, K. M., and Zhou, Z.-H. (2008). Isolation

forest. In 2008 eighth ieee international conference

on data mining, pages 413–422. IEEE.

att

a, T. and Johansson, T.-F. (2011). The system price

of electricity on nord pool: A matter of fundamental

factors?

Rahimi, A. and Sheffrin, A. Y. (2003). Effective market

monitoring in deregulated electricity markets. IEEE

Transactions on Power systems, 18(2):486–493.

Ramaswamy, S., Rastogi, R., and Shim, K. (2000). Efﬁcient

algorithms for mining outliers from large data sets. In

Proceedings of the 2000 ACM SIGMOD international

conference on Management of data, pages 427–438.

Sch

olkopf, B., Platt, J. C., Shawe-Taylor, J., Smola, A. J.,

and Williamson, R. C. (2001). Estimating the support

of a high-dimensional distribution. Neural computa-

tion, 13(7):1443–1471.

Spot, N. P. (2009). The nordic electricity exchange and the

nordic model for a liberalized electricity market. Nord

Pool Spot, Norway.

Wagner, A. (2014). Residual demand modeling and applica-

tion to electricity pricing. The Energy Journal, 35(2).

Xu, R. and Wunsch, D. (2008). Clustering, volume 10. John

Wiley & Sons.

Ziel, F. and Steinert, R. (2016). Electricity price forecasting

using sale and purchase curves: The x-model. Energy

Economics, 59:435–454.

Detection of Potential Manipulations in Electricity Market using Machine Learning Approaches

983