A Formally Correct and Algorithmically Efﬁcient

LULC Change Model-building Environment

Franc¸ois-R

emi Mazy

1 a

and Pierre-Yves Longaretti

1,2 b

Universit

e Grenoble Alpes, CNRS, Inria, Grenoble INP, LJK, 38000 Grenoble, France

Universit

e Grenoble Alpes, CNRS-INSU, IPAG, CS 40700, 38052 Grenoble, France

Keywords:

Land Use Change, Land Cover Change, LULC, Model Development, Model Evaluation, Model Accuracy,

Density Estimation, Calibration, Allocation, Map Simulation.

Abstract:

The use of spatially explicit land use and land cover (LULC) change models is widespread in environmental

sciences and of interest in public decision-help. However, it appears that these models suffer from signiﬁcant

biases and shortcomings, the sources of which can be mathematical, conceptual or algorithmic. We formalize

a modeling environment that distinguishes a calibration-estimation module and an allocation module. We

propose an accurate calibration-estimation method based on kernel density estimation and detail an unbiased

allocation algorithm. Moreover, a method of evaluation of LULC change models is presented and allows us

to compare them on various fronts (accuracy, biases, computational efﬁciency). A case study based on a real

land use map but with known (enforced) transition probabilities is used. It appears that the estimation error of

the methods we propose is substantially improved over the best existing software. Moreover, these methods

require the speciﬁcation of very few parameters by the user, and are numerically efﬁcient. This article presents

an overview of our LULC change modeling framework; its various formal and algorithmic constituents will

be detailed in forthcoming papers.

1 INTRODUCTION

Land use and land cover (LULC) change is a ma-

jor driver of global change alongside the more vis-

ible issues of climate change and biodiversity loss.

The study of LULC change is of major interest

in analyzing and understanding a variety of socio-

environmental phenomena but also for decision-help

on mitigation and adaptation policies, and the litera-

ture on LULC change studies is by now quite substan-

tial. Different LULC change modeling strategies have

been developed over the last few decades to address

these research issues (static, dynamic, agent-based,

local or global scale, etc. . . ).

In the present work, we focus on spatially explicit,

statistical LULC change model building. Such mod-

els generally consists of estimating transition proba-

bilities from one land-use state to another based on

(usally) two land-use maps at different dates that re-

ﬂect changes in the past. These models are designed

to simulate new land use maps, in scenario-driven

projections of future land use and cover. Such allo-

https://orcid.org/0000-0001-8405-0141

https://orcid.org/0000-0002-4940-0756

cated maps can be used for a variety of purposes. For

example, they may be coupled to models of ecosys-

tem services to produce evaluations of their future

evolution. In fact, producing accurate spatially ex-

plicit projections of the effects of public decisions

bearing on social-ecological problems is a current is-

sue for such models (Verburg et al., 2019).

Statistical and spatially explicit LULC change

models constitute a popular approach to LULC

change modeling, and various model-building soft-

ware have already been devised in this framework.

Among the most well-known, one may quote Di-

namica EGO (Soares-Filho et al., 2002), Idrisi LCM

(Eastman et al., 1995), or the CLUE family of mod-

els (Verburg et al., 1999), the last member being

CLUMondo (van Vliet et al., 2015). However, these

software (and others) exhibit substantial differences

in results for the same case studies (Mas et al.,

2014; Prestele et al., 2016; Alexander et al., 2017),

which raises an important concern on the reliability

of the LULC change modeling process itself.

No study to date has clearly identiﬁed the origin of

the differences of behavior and outcome displayed by

the existing model-building software on a same prob-

Mazy, F. and Longaretti, P.

A Formally Correct and Algorithmically Efﬁcient LULC Change Model-building Environment.

DOI: 10.5220/0011000000003185

In Proceedings of the 8th International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2022), pages 25-36

ISBN: 978-989-758-571-5; ISSN: 2184-500X

Calibration

Land use at t

Explanatory variables at t

Estimation

Scenario for a time step dt

Explanatory variables at t

Land use at t

Allo cation

Allocated land use

at t

+ dt

iteration

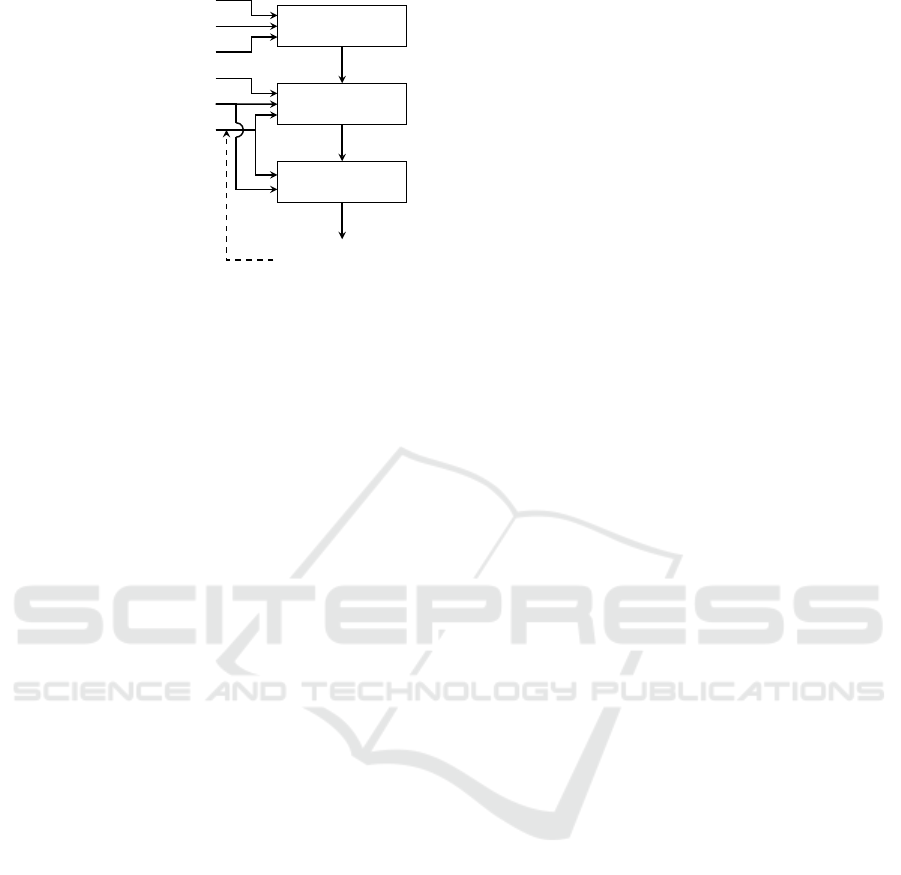
Figure 1: General architecture of a spatially explicit statis-

tical LULC change model.

lem, let alone proposed a formally correct theoretical

framework for this type of LULC change modeling.

Moreover, comparing different LULC change models

on their spatial outcomes is a poorly mastered opera-

tion in the literature (van Vliet et al., 2016) and more

precise evaluation methods are needed. Nevertheless,

as will be illustrated in the course of this work for

the three modeling environment just mentioned, these

discrepancies can be traced to differences in the for-

mal and algorithmic choices made in their elabora-

tion. In fact, quite a few of these choices were made

without paying sufﬁcient attention to the constraints

imposed by a correct ab initio formal investigation of

the probabilistic foundation of the problem, leading

to a number of errors and biases.

More precisely, we address these issue by focus-

ing successively on the calibration-estimation and al-

location processes in order to propose a fully formal-

ized and conceptually correct foundation for statisti-

cal spatially explicit LULC change analyses. We also

provide efﬁcient and bias-free algorithmic implemen-

tations of these processes, which constitute the core of

this approach to LULC change model-building. The

present work illustrates some of our main results on

these two fronts. A detailed exposition of the un-

derlying formal analyses and algorithmic implemen-

tations will be given in forthcoming dedicated papers.

The ﬁrst one will formalize in a rigorous ways statis-

tical LULC changes by groups of contiguous pixels

(patches), starting from the more common pixel by

pixel probability distributions, and introduce an allo-

cation algorithm to this effect, that will be explicitly

shown to be bias-free. The second one will be ded-

icated to the calibration and estimation of probabil-

ity transitions. Finally, the last article will provide a

systematic method of identiﬁcation and a systematic

analysis of the biases present in the software men-

tioned above.

This paper is organized as follows. The typical

structure of statistical spatially explicit LULC change

models is recalled in section 2. Next, a new and

accurate calibration-estimation method and an unbi-

ased allocation methods are brieﬂy overviewed in sec-

tion 3. We then propose an evaluation method for

LULC change models that allows us to compare their

results and performances; the most salient features are

described in section 4. The next section introduces

a case study to illustrate the methods of the previ-

ous sections, and presents some of our results (sec-

tion 5). Finally, the last section summarizes these

ﬁndings along with other important results on these

issues that will be established in our forthcoming pa-

pers on the topic.

We assume that a number of preliminary model-

ing choices are made prior to the comparison of per-

formances mentioned right above: elaboration of the

LUC typology, choice of explanatory variables, and

choice of the discretization (pixel) scale. Thus, we

exclude from the perimeter of our analysis the obvi-

ous inﬂuence of these choices on the results (Garc

ıa-

Alvarez et al., 2019).

2 LULC CHANGE MODEL

ARCHITECTURE

Spatially explicit statistical LULC change models

are generally (but not always) organized around two

main modules: calibration-estimation, and allocation

(Fig. 1). This allows us to investigate in turn their

underlying logic, formal foundation and algorithmic

implementation.

2.1 Calibration-estimation Module

We start from two raster (i.e., pixelized) LULC maps

at two different dates t

and t

as well as maps of

the d explanatory variables of interest, characterizing

LULC changes (e.g., altitude, distance to the roads,

etc. . . ). Pixel sizes can vary from a few meters to a

few tens of kilometers depending on case studies; the

largest maps may involve tens of millions of pixels.

The dates t

and t

differ typically by a few years.

Although changes occur in patches of contiguous

pixels, the calibration-estimation process focuses on

individual pixel probability distributions; patches are

then produced on this basis in the allocation module.

Pixels undergo a change from land use u to land use v.

Each pixel i is characterized by a collection (vector or

tuple) z

of values of the d explanatory variables. The

transition probability distribution must be evaluated

for all possible explanatory variables combinations y

present in the calibration maps, including those which

GISTAM 2022 - 8th International Conference on Geographical Information Systems Theory, Applications and Management

were not observed to undergo a transition but may be

expected to in the future. To this effect, one needs

to evaluate the conditional pixel transition probabil-

ity P(v|u, y). This involves a form of interpolation in

explanatory variable space, called estimation (Fig. 1).

2.2 Allocation Module

A new land use map is simulated from an initial one

(possibly different from the calibration maps), from

the explanatory variables (when needed) and from the

probability of land use change maps for each possible

LULC state change (Fig. 1). Allocations are made in

groups of contiguous pixels (patches). The process in-

volves a sampling algorithm and attributes a possible

new LULC state on the basis of the associated tran-

sition probability distribution and some patches con-

straints. The map obtained in this way is a particu-

lar instantiation of this probability distribution; many

others could have been produced for the same time

step, and all such maps are statistically equivalent, ex-

cept for statistical noise. This point is usually ignored

in existing model-building environments, although it

is crucial to identify errors and biases, as will be dis-

cussed later on. The details of our patch construction

method are involved but not critical for software per-

formance comparison (both in terms of accuracy and

execution time) and will therefore not be presented

here.

In the process the user provides a transition ma-

trix that characterizes the rates of change per time step

between each land use state, and characterized by an

overall probability P(v|u) for all possible LULC ini-

tial and ﬁnal states u,v. This matrix is usually speci-

ﬁed through scenarios.

2.3 Existing LULC Change

Model-building Environments

In the present work we focus on three of the most

widely used software (van Vliet et al., 2016): Dinam-

ica EGO, Idrisi LCM and CLUMondo. Our objective

is to contrast their performances (accuracy and com-

putational efﬁciency) to the modeling strategy and al-

gorithmic implementation we propose in the next sec-

tion.

Dinamica EGO ﬁts reasonably well in the archety-

pal structure of Fig. 1. Transition probabilities are

usually estimated from the use of weights of evi-

dence, applied after binning the user-deﬁned explana-

tory variables (Soares-Filho et al., 2002). This bin-

ning step requires to specify a number of parame-

ters, which turn out to have a very strong impact

on the obtained results. Moreover, this method of

estimat- ing transition probabilities is based on the

strong assumption of statistical independence of the

explanatory variables; it turns out that even modest

amounts of cross-correlation between these variables

may lead to non negligible errors in the estimated

transition probabilities. This software implements

an allocation method relying on a pixel pre-selection

process (pruning), implemented to reduce computa-

tional time); such pruning also produces signiﬁcant

biases in the results.

Idrisi LCM (Eastman et al., 1995) also im-

plements a calibration/allocation architecture, while

leaving the user with less control on modeling choices

than Dinamica EGO. This strategy is adopted on pur-

pose, in order for users with little expertise to never-

theless be able to implement a LULC change model.

The particular LCM version we have used is the one

bundled in Idrisi Selva. This software proposes differ-

ent models for estimating transition probabilities: lo-

gistic regression (LCM LR), SimWeight (LCM SW)

and Multi-Layer Perceptron (LCM MLP). The LCM

allocation module is very simple and deterministic, as

the allocation algorithm implemented in this software

essentially ignores the statistical nature of the process.

This results in simple but strongly biased allocation

rules.

Finally, the CLUE family of software (Verburg

et al., 1999), the latest of which is CLUMondo (van

Vliet et al., 2015), chooses to estimate the probabili-

ties of change from a single land use map, from which

it deﬁnes transition probabilities through a logistic re-

gression on all explanatory variables. Also, CLU-

Mondo does not allow the modeler to access its al-

location module independently.

3 CLUMPY: A NEW LULC

CHANGE MODEL-BUILDING

ENVIRONMENT

We present here in a succinct manner the meth-

ods used in our calibration-estimation and alloca-

tion modules. The closest analog in the existing

model-building environments is Dinamica EGO. The

main differences come from our more sophisticated

but more accurate and efﬁcient calibration-estimation

method, our demonstrably error- and bias-free allo-

cation method, and signiﬁcantly more efﬁcient al-

gorithms leading to substantial gains in computation

time in large problems.

These modules constitute the core of our model-

building environment, called CLUMPY (Comprehen-

sive Land Use Model in Python).

A Formally Correct and Algorithmically Efﬁcient LULC Change Model-building Environment

3.1 Calibration-estimation

3.1.1 Bayes Rule

The probability of transition from land use u to land

use v of a pixel characterized by the d-tuple of ex-

planatory variables y is noted P(v|u,y). This nota-

tion emphasizes the fact that this probability is con-

ditioned by the knowledge of the values of u and y.

Bayes rule allows us to express this probability in a

more convenient way for calibration purposes:

P(v|u,y) = P(v|u)

p(y|u,v)

p(y|u)

. (1)

The various factors on the right-hand side member

are deﬁned as follows. P(v|u) is the global transi-

tion probability, speciﬁed by a scenario provided by

the user. This quantity can also be computed directly

from the observed transitions between the calibration

maps at times t

and t

. Next, p(y|u) is a condi-

tional probability density. We use probability densi-

ties because explanatory variables are usually contin-

uous quantities, and we do not bin them in the end,

in order to produce a more accurate calibration pro-

cedure. By deﬁnition p(y|u)dy is the probability of

observing y within the small volume dy of explana-

tory variable space, for pixels of initial state u. Simi-

larly, p(y|u,v) is the probability density of y for pix-

els making the transition from states u to v. Note that

the calibration process, which is based on observed

transitions, uses these probabilities in the frequency

of occurrence meaning, while the allocation module

applies Bayes rule in a Bayesian sense.

The interest of using Bayes rule lies in the fact that

p(y|u) and p(y|u,v) are much simpler to estimate than

P(v|u,y). Indeed, it is then a question of estimating

density functions on y for a set of pixels of initial state

u for p(y|u) or potentially undergoing a LULC state

transition from u to v for p(y|u,v). This problem is

widely addressed in machine learning and is called

density estimation.

Consider a set of n calibration pixels, made of

all the pixels that actually underwent a LULC state

change from u to v and are directly extracted from two

calibration maps at time t

and t

. Each of these pixels

is characterized by its explanatory variables noted z.

We wish to estimate the transition probability of all m

pixels in our maps; these are by deﬁnition evaluation

pixels. Each of these pixels is characterized by its ex-

planatory variables noted this time y. The problem is

therefore to estimate P(v|u,y).

The idea is to calibrate a density estimator with the

calibration pixels for both probability densities and

then to estimate these probability densities for all pix-

els with the obtained density estimator. Finally, as the

global transition probability P(v|u) is given, we can

apply Bayes rule to obtain P(v|u,y).

3.1.2 Density Estimation by Kernel Density

Estimator (KDE)

Estimating a probability density is a widely addressed

problem in the machine learning literature (Scott,

2015). A simple and not very precise method is to

make histograms in explanatory variable space. This

requires to bin explanatory variables; unfortunately,

the choice of the bin size has a strong impact on

the results. Some related methods such as averaged

shifted histograms have been proposed to circumvent

the problem (Chamayou, 1980).

More sophisticated methods perform density es-

timates by positioning a kernel function K charac-

terized by a user-speciﬁed width parameter h (called

bandwidth) on each calibration data point and sum-

ming over all these kernels at the desired locations

of estimation (in explanatory variable space). This

is called kernel density estimation (Wand, 1992), or

KDE in short. This very efﬁcient method is how-

ever highly computationally intensive as soon as the

number of explanatory variables and elements (here,

pixels) increases. Many kernel functions may be

studied (e.g., gaussian kernels), and various methods

have been proposed to approximate the resulting fam-

ily of estimators (O’Brien et al., 2016; Charikar and

Siminelakis, 2017). However, these relatively com-

plex methods often require large amounts of mem-

ory since they allocate full matrices representing the

entire space of explanatory variables. Thus, when

confronted with more than a few explanatory vari-

ables, these methods can be inapplicable due to lack

of memory space on standard machines; the compu-

tation time also increases quite fast with the number

of dimensions.

Instead, we implemented a hybrid binning/KDE

method, that keeps part of the simplicity of simple

histograms with only a small degradation of the per-

formance of pure Kernel density estimator methods.

The binning is performed on a scale h/q smaller than

the bandwidth h (Wells and Ting, 2019), where q > 1

is an odd integer. A kernel density estimator is then

applied to the small bins themselves instead of the

original individual elements (pixels) in explanatory

variable space. One can then show that the larger

q, the smaller the approximation error. This hybrid

method maintains the spirit of continuous density es-

timation, while being much more computationally ef-

ﬁcient than direct KDE estimators (both in terms of

computational time and memory use). This is what

we used in our estimations of P(y|u) and P(y|u, v).

The choice of the kernel width h for the KDE

GISTAM 2022 - 8th International Conference on Geographical Information Systems Theory, Applications and Management

method is a very important issue due to its inﬂuence

on the quality of the estimation. Indeed, choosing a

too narrow bandwidth results in an over-interpretation

of the observational data and in noisy estimates. On

the other hand, a too broad bandwidth leads to under-

ﬁtting (or over-smoothing) and to a degradation of the

estimate of the probability density. The determina-

tion of the optimal width of the kernel is a non-trivial

problem and is widely discussed in the machine-

learning literature (Wand and Jones, 1994; Rudemo,

1982; Sain et al., 1994). However, these methods are

computationally very expensive as soon as the num-

ber of pixels is large and the number of dimensions

exceeds 3, which is very frequently the case in LULC

change studies.

This being said, in the LULC change context,

a slight over-smoothing is not a problem and can

even be interesting, because transition probabilities

are usually undersampled, and therefore noisy. Con-

sequently, we chose to determine the KDE bandwidth

h from the principle of maximum smoothing of Terrel

(Terrell, 1990), leading to

Terrel

(d + 8)

d+6

16 n (d + 2) Γ



d+8



, (2)

where K is the kernel density estimator. The slight

oversmoothing involved turns out to be essentially un-

noticeable in our tests, while this prescription con-

siderably reduces the computational burden of KDE

methods.

We have checked on various test problems, and will

soon show, that even simple kernel functions (such

as a square box, a triangle or a gaussian kernel) give

much more accurate results than existing calibration

methods.

Note ﬁnally that, because explanatory variables

are of widely different nature and not statistically in-

dependent, it is necessary to normalize them in or-

der to work with data of zero mean and covariance

matrix equal to the identity in explanatory variable

space. This operation is called “whitening transfor-

mation” in the machine learning literature. It makes

it legitimate to use a unique bandwidth in all dimen-

sions in the transformed explanatory variable space

and greatly simpliﬁes the numerical implementation

of our calibration-estimation method.

3.2 Allocation

In general, the allocation module takes as input a land

use map as well as the transition probability maps ob-

tained in the calibration-estimation module. The allo-

cation method presented here also requires the knowl-

edge of the explanatory variables of the input map.

The simulation of an allocated map produces a

speciﬁc statistical sampling of the transition proba-

bilities. So far, we have focused on pixel transition

properties. However, as already mentioned, we al-

locate pixel patches. Following the logic initiated in

Dinamica EGO, a ﬁrst pixel is selected according to

the transition probability distribution obtained by our

calibration-estimation procedure. This pixel is called

a “core pixel” or “pivot-cell”. Then, a speciﬁc pro-

cedure is applied to create a patch around this core

pixel. This procedure is characterized by different pa-

rameters such as the surface of the patch, and its elon-

gation. Patches created in this way reproduce some

of the statistical properties of actually observed tran-

sition patches, but are deﬁned algorithmically to pro-

vide some randomness in their shape.

The allocation modules implemented in the ex-

isting software turn out to be all biased to various

extents. Such biases have not yet been identiﬁed in

the literature, ﬁrst because a biasing criterion has not

been formulated, and second because the details of

these software allocation procedure is not fully docu-

mented. We have circumvented this last problem by a

combination of literature analysis, educated guesses,

retro-engineering, questions to model developers, and

re-implementation (when feasible) of these allocation

algorithms to check that our understanding of their

structure and content exactly reproduces the outcome

of the original software on a number of test problems.

We have also formulated a simple but powerful “no-

bias” criterion, which, in essence, requires that the

post-allocation probability distributions are identical

to the pre-allocation ones. This is in fact more of an

unavoidable self-consistency requirement, but it turns

out that none of the existing LULC change model-

building software does satisfy it.

This allowed us to implement a strategy of sys-

tematic identiﬁcation and characterization of the var-

ious biases present in existing model-building soft-

ware. We illustrate this process on a particularly im-

portant bias related to pruning, relying on an efﬁcient

bias-free algorithm which avoids the need for prun-

ing.

3.2.1 Pruning

LULC change models may involve a very large num-

ber of pixels (e.g., tens of millions). Therefore, it can

be interesting to pre-select a limited number of pixels

in order to speed up the allocation procedure. This

pre-selection is called pruning and is implemented by

Dinamica EGO and LCM in two different ways, both

of which turn out to be signiﬁcant sources of bias.

Dinamica EGO’s pruning method consists in rank-

ing pixels by decreasing order of transition probabil-

A Formally Correct and Algorithmically Efﬁcient LULC Change Model-building Environment

ity P(v|u,y). Pixels are then pre-selected in this or-

der in this list; the number of pre-selected pixels is

equal to the number of pixels necessary to reach the

targeted LULC change surface deﬁned by the user se-

lected scenario, multiplied by a pruning parameter F.

The default value is F = 10 (ten times as many pixels

as needed for the various transitions are pre-selected).

LCM ranks the pixels by decreasing order of

the probability density (or probability distribution if

binned) of the explanatory variables for this transi-

tion, p(y|u, v). Then LCM keeps the exact number

of pixels that are necessary to reach the targeted tran-

sition surface deﬁned by the selected scenario, and

has a speciﬁc procedure to resolve conﬂicts of al-

location for the same pixel. Thus, LCM’s pruning

method is also its allocation method since all pixels

selected in this way are directly allocated without any

further consideration. This procedure has the advan-

tage of simplicity and ensures that transitions occur

in patches (due to the spatial continuity of the ex-

planatory variables probability densities). However,

the maps allocated by LCM often suffer from a se-

vere lack of realism, and they always violate our self-

consistency no-bias requirement.

Although establishing which probability ordering

should in principle be used for pruning is not an

obvious task, we have proved that LCM’s choice

[p(y|u,v)] is the theoretically correct one; this ap-

plies although the correct allocation probability dis-

tribution is by deﬁnition P(v|u, y). This being said,

both Dinamica EGO and LCM pruning strategies are

strongly biased because they modify to various ex-

tents the probability distributions which should be en-

forced exactly. LCM is the more biased of the two, al-

though Dinamica EGO has chosen an incorrect prob-

ability ordering for pruning.

An unbiased pruning method necessarily con-

sists in a random sampling performed according to

p(y|u,v), and selects the number of kernel pixels

needed to reach the targeted number of transited

pixels. Thus, the probability distribution of this

pixel subsample will be statistically representative of

p(y|u,v) and there will be no unwarranted truncation

of this probability density distribution.

The motivation for applying a pruning procedure

lies in the numerical acceleration of the allocation

method for a very large number of pixels. How-

ever, the implementation in Python of the our allo-

cation procedure as presented in section 3.2.2 proves

to be numerically very efﬁcient without pruning, even

though the number of pixels in some of our case stud-

ies is very large (> 10

); this efﬁciency relies on

the use of dedicated Python functions, which perform

nearly as fast as equivalent C codes. Still, we have de-

signed a bias-free pruning algorithm, for possible use

in particular problems.

3.2.2 Unbiased Allocation

In addition to pruning, other biases can occur in the

allocation procedure. In particular, the creation of

patches around a core pixel automatically excludes

these patch pixels from the rest of the allocation pro-

cedure. However, they could just as well be selected

afterwards.

In order to resolve such potential conﬂicts, we de-

signed the following iterative allocation procedure for

a given initial land use state :

1. We know the transition probability P(v|u,y) of

each pixel for all (u,v). We can therefore apply

a generalized Von Neumann rejection sampling,

which allows us to test all possible states v at the

same time for any given u. We obtain an unbiased

sample of kernel pixels for each of the transitions

studied. If no kernel pixel is selected, the alloca-

tion procedure is terminated at this point.

2. A single kernel pixel is randomly and uniformly

drawn; its associated transition has been deter-

mined in the previous step.

3. The procedure of patch creation around this core

pixel is applied next. The selected pixels are actu-

ally allocated on the simulated map.

4. P(v|u) is updated, taking into account that a cer-

tain number of pixels have already been allocated.

This probability is therefore reduced for the rest

of the allocation procedure in the considered time

step.

5. p(y|u) is updated next because some elements

have already been allocated, which has modiﬁed

the probability density distribution of the explana-

tory variables.

6. p(v|u,y) is then recalculated from Bayes rule

Eq. (1); the probabilities involved in steps 4 and

5 are also updated. We then start again at step 1.

We have shown that a carefully designed algorithm

of this type is bias-free. This procedure is however

demanding since it requires to re-estimate very fre-

quently p(y|u). We therefore update this probabil-

ity distribution only when the percentage of allocated

pixels is signiﬁcant enough that the estimated prob-

ability is too far from the real distribution (in prac-

tice, after a ﬁxed small percentage of state changes

has been achieved). This may introduce a slight bias.

GISTAM 2022 - 8th International Conference on Geographical Information Systems Theory, Applications and Management

4 EVALUATION

A review of the literature shows that validating the re-

sults obtained by LULC change models is an uncom-

mon practice. This deﬁciency underlies some of the

doubts that may be raised on the robustness of LULC

change modeling (van Vliet et al., 2016). In any case,

before speciﬁc results may be validated, the modeling

framework itself should be validated. A ﬁrst attempt

along these lines has already been carried out on artiﬁ-

cal data (Mas et al., 2014) but the lack of exact knowl-

edge of the transition probabilities involved precluded

any detailed evaluation of the LULC change models

that were tested in this earlier work. Indeed, one of

the main problems of statistical LULC change mod-

eling is the estimation of the probability distribution

P(v|u,y) (section 3.1), and, furthermore, it is impos-

sible to know this probability distribution exactly in a

real case study. Validating this estimation of P(v|u,y)

therefore remains an essential objective.

We propose here a simultaneous validation

method for the calibration-estimation and global

calibration-estimation/allocation procedures, that al-

lows us to objectively compare different model-

building strategies. This is achieved by quantifying

the difference between the transition probabilities ob-

tained from our hybrid KDE estimation in the cali-

bration phase or in the post-allocation one, and ex-

actly speciﬁed pre-calibration transition probabilities.

We may proceed to this effect from semi-real or com-

pletely artiﬁcial data. We start from a (real or artiﬁ-

cial) LULC map at t = t

. We adopt an exactly known

transition probability distribution, P

∗

(v|u,y). This ex-

act transition probability may be deﬁned analytically

or numerically. Then, a new LULC map at time t = t

is produced with our allocation procedure (based on

this exact probability distribution and our patch cre-

ation algorithm).

This allows us to implement two validation pro-

cesses:

Calibration-estimation Comparison. We select a

calibration-estimation method from an existing

LULC change model-building environment, and

produce from the two maps just speciﬁed at t

and t

an estimate

P(v|u,y) of P

∗

(v|u,y). We re-

peat this process for all the calibration methods

we want to compare, including ours.

Calibration-estimation/Allocation Comparison.

We now wish to evaluate the relative efﬁciencies

of these modeling environments over the whole

calibration-estimation/allocation process. We

thus use as inputs the LULC map at t = t

and the

probability distribution

P(v|u,y) determined by

the previously described calibration-estimation

comparison process, for any of the model-

ing environments tested. We produce next a

new LULC map at t = t

from the associated

allocation procedure. We recover a new post-

allocation estimate

P(v|u,y) of P

∗

(v|u,y) from

the calibration-estimation method of the same

modeling environment. We repeat this process

for all the modeling environments we want to

compare, including ours.

The comparison of the exact (enforced) probability

distribution with the estimated ones can be done in

various and more or less sophisticated ways. In this

article, we limit ourselves to two very simple ap-

proaches. The ﬁrst one consists in producing graphs

of the estimated distributions

P(v|u,y) and the ex-

act one P

∗

(v|u,y) considered as a function of y, for

various one-dimensional cuts in explanatory variable

space, e.g., by ﬁxing all explanatory variables but one.

This gives a direct check of the accuracy of the var-

ious methods, but only on a limited (although ran-

domly chosen) set of locations in explanatory variable

space.

The second validation method is more global and

consists in calculating the average of the absolute er-

ror throughout explanatory variable space:

calib

∑

i=1



∗

(v|u,y

) −

P(v|u,y

)



tot

∑

i=1



∗

(v|u,y

) −

P(v|u,y

)



(3)

where m is the number of pixels where the dif-

ference is evaluated (generally, all pixels concerned

by the u → v transition in a map), and where

the subscript “calib” or “tot” refers either to the

calibration-estimation comparison process or to the

global calibration-estimation/allocation one.

By construction Eq. (3) tends to underesti-

mate large but localized differences. Using one-

dimensional cuts minimizes this possibility to some

extent. We could also, e.g., identify the largest abso-

lute difference, and count the number of pixels where

this difference is achieved within a given tolerance.

We avoid relative differences because they might be

very large where the transition probability is low, but

this would not necessarily reﬂect a notable inaccuracy

in the estimation itself.

In any case, we can measure the difference be-

tween the exact and estimated probability distribu-

tions, a validation test that has been never been per-

formed so far, and thus have a ﬁrst global evalua-

tion of the relative robustness of various calibration-

estimation and allocation modules (ours as well as

the ones implemented in existing model-building soft-

ware).

A Formally Correct and Algorithmically Efﬁcient LULC Change Model-building Environment

Our own calibration-estimation and allocation

procedures are tested simultaneously and not inde-

pendently in both comparison processes (as the sec-

ond map needed in these tests is produced by our al-

location procedure). One may therefore ask whether

they are both validated in this way. Several lines of

arguments show that this is the case, relying on a pri-

ori and a posteriori analyses. First, we have formally

proved that our allocation procedure is bias-free (the

proof will be given elsewhere), i.e., that it enforces the

correct transition probability distribution. Also, the

KDE density estimation procedures have been shown

to converge exactly to the correct density distribu-

tion in the machine-learning literature in the limit of a

large number of available points (this form of conver-

gence is weaker than for allocation, but still relevant).

This applies also to our own hybrid KDE calibration-

estimation method, except possibly close to bound-

aries in explanatory variable space due to the kernel

truncation correction applied there (not described in

our overview of the method). Second, the numeri-

cal efﬁciency of our algorithms allow us to produce a

large number (thousands) of calibration-allocation se-

quences for the same time step in a reasonable compu-

tation time. We checked on a number of test problems

that post-allocation transition probabilities (recovered

by our calibration-estimation procedure) converge in

expectation value to the enforced one by averaging

over these multiple allocations. These arguments pro-

vide an a posteriori validation of both procedures. In-

deed, having errors or biases introduced by one pro-

cedure nearly exactly compensated by the other is be-

yond unlikely, considering the very different strate-

gies used in their elaboration.

A similar concern may be raised about the fact

that using our own allocation procedure to produce

the t = t

LUC map for testing calibration-estimation

procedures may favor our method over the others.

This concern is misplaced for the same type of rea-

son: the way this second map was produced is irrel-

evant precisely because there is no relation between

our allocation procedure and any of the calibration-

estimation procedures we have tested. Also, we have

just shown (or at least convincingly argued, until

the above-mentioned proofs are available in print),

that our allocation procedure produces unbiased post-

allocation probability distributions, so that the amount

of bias (due in fact to statistical noise) produced on a

single t = t

map is limited. In any case, it applies

equally to all tested calibration methods, which are

therefore treated on the same footing in this respect.

5 RESULTS AND DISCUSSION

In this section we apply the evaluation methods pre-

sented in section 4. We thus deﬁne a case study that

is intended to be representative of commonly encoun-

tered LULC change problems. We put to the test our

own modules (section 3) as well as the ones imple-

mented in the existing model-building software intro-

duced in section 2.3. The parameters used for each

model are speciﬁed in the Appendix.

5.1 Case Study Short Description

We are interested in a study area of 94 square kilo-

meters located in the Is

ere d

epartement in France.

We focus on a smaller sector in the Southwest of the

town of Grenoble; we have raster maps describing

this smaller area at 15 meters of resolution (6.3 mil-

lion pixels), and use 7 different land use classes at the

coarsest typology level (water bodies, mineral areas,

forests, agricultural areas, urban areas, economic ac-

tivity areas and other), and up to several tens at the

ﬁnest level. These data have been used in a recent

project, whose objective was to explore the future of

ecosystem services at the 2040 horizon under various

land planning scenarios (Vannier et al., 2016; Vannier

et al., 2019a; Vannier et al., 2019b).

For our present purposes, we only focus on a sin-

gle transition, namely from agricultural areas (u) to

urban areas (v). This is one of the main transitions re-

sponsible for urban sprawl. We chose this transition

for the sake of clarity and simplicity. The number of

agricultural area pixels is ∼ 3.3 million.

We have selected three explanatory variables to

characterize this transition: elevation above sea level

in meters (y

), slope in degrees (y

) and shortest dis-

tance from urban areas in meters (y

). These are three

of the main explanatory variables typically used in ur-

ban sprawl studies relying on statistical LULC mod-

elling frameworks.

In line with the evaluation strategy described in

section 4, we enforce a speciﬁc transition probability

distribution, namely we adopt a multivariate Gaussian

distribution:

∗

(v|u,y) =



µ,Σ

) if {y

} ∈ D

0 else

(4)

where N

µ,Σ

refers to a normal distribution of mean

µ (vector of the means of the explanatory variables),

and covariance matrix Σ (covariance matrix of the ex-

planatory variables), (y

) is the vector of ex-

planatory variables, and D is a subset of the ex-

planatory variable space where the probability density

GISTAM 2022 - 8th International Conference on Geographical Information Systems Theory, Applications and Management

P(y|u) is larger than a (small) threshold (this avoids

potential problems in the application of Bayes rule

without introducing any signiﬁcant bias in the tran-

sition probability distribution). The exact deﬁnition

of µ, Σ and D are given in the Appendix.

5.2 Mean Absolute Error Comparison

The pixel-averaged absolute errors are calculated with

Eq. (3) of section 4 and reported in Table 1.

CLUMPY’s ε

calib

is about four times lower than

for the next best existing software with respect to

this evaluation criterion, Dinamica EGO. This con-

ﬁrms the quality of the KDE estimator relative to

other methods. As expected, ε

tot

> ε

calib

whatever the

model since the allocated map is a particular instanti-

ation of the estimated probability distribution, which

is itself an approximation of the exact one. We notice

also the inﬂuence of the pruning factor F of Dinam-

ica EGO: reducing this parameter results in a larger

error (note that F = 10 is the default value of this pa-

rameter). This ﬁnding is consistent with the fact that

Dinamica EGO’s pruning procedure performs a sharp

truncation of the probability density (section 3.2.1).

We can also repeat the allocation step in the com-

bined calibration-estimation/allocation process. We

have chosen to run it 100 times (last column of Ta-

ble 1), and average over these various runs in order

to improve the precision of the estimation of the tran-

sition probability distribution. This is ineffective for

LCM (ε

tot, 100

= ε

tot

), consistently with the fact that

LCM allocation procedure is deterministic (see sec-

tion 3.2.1). For Dinamica EGO, the improvement is

marginal, which reﬂects the error due to pruning. On

the other hand, CLUMPY displays a signiﬁcant im-

provement and comes very close to the value obtained

for the calibration-estimation comparison: ε

calib

≈

tot,100

. The allocation error itself has become negligi-

ble compared to the calibration-estimation one, con-

sistently with the fact that our allocation algorithm is

bias-free.

5.3 One-dimensional Cut Comparison

The graphs of the estimated distributions

P(v|u,y)

and

P(v|u,y) returned by the different models are vis-

ible in Fig. 2. This shows a one-dimensional cut at

ﬁxed altitude and slope, while using the shortest dis-

tance to existing urban areas as abscissa. The ex-

act transition probability, computed from P

∗

(v|u,y),

Eq (4), is also represented. There are two sub-

plots, one for calibration-estimation comparisons

[

P(v|u,y)], one for global calibration/allocation com-

parisons [

P(v|u,y)]. Although this is a limited and lo-

Table 1: Comparison of models through Eq. (3) for the

calibration-estimation and calibration/allocation compari-

son processes. DE = Dinamica EGO, for two different prun-

ing factors (F = 10 and 100). The last column results from

an average over 100 allocations of the same time step.

model ε

calib

tot

tot, 100

CLUMondo 3.56e

−3

LCM LR 3.35e

−3

6.59e

−3

6.59e

−3

LCM SW 1.75e

−3

5.85e

−3

5.85e

−3

LCM MLP 1.38e

−3

6.58e

−3

6.58e

−3

DE F=10 1.29e

−3

5.31e

−3

5.27e

−3

DE F=100 1.29e

−3

1.65e

−3

1.17e

−3

CLUMPY 3.37e

−4

9.84e

−4

3.39e

−4

cal comparison, this exempliﬁes the behavior of each

of the model-building algorithms.

Fig. 2a represents the transition probabilities esti-

mated by the calibration-estimation comparison pro-

cess. We observe a large disparity in the obtained es-

timations. It seems fair to say that the existing model-

ing environments fail to represent in an accurate way

the exact probability distribution, although it was cho-

sen to be relatively smooth. The dispersion in these

results must clearly contribute to the problem dis-

cussed in introduction, a point that will be quantiﬁed

more precisely in the future. Our own modeling en-

vironment (CLUMPY) performs very well, compara-

tively and in absolute.

Dinamica EGO displays a signiﬁcant deviation

from the exact curve which can be traced back to the

assumption of independence of explanatory variables

and to the pruning process (a point we will discuss

in more detail elsewhere). LCM SW and LCM MLP

deviate even more signiﬁcantly, especially in regions

where there have been very few, if any, observed tran-

sitions. Finally, CLUMondo and LCM LR follow the

trend of the ’exact’ curve. This is somewhat coinci-

dental as these models are parametric, i.e., they per-

form a logistic regression for a speciﬁc type of curve,

which is by chance similar to the one adopted here.

Had we used a more complex probability distribu-

tion dependence on y instead, e.g., a bimodal distri-

butions with two peaks, the result of LCM LR and

CLUMondo would have been much less convincing

(we checked this point).

Fig. 2b represents the transition probabil-

ities estimated from the whole calibration-

estimation/allocation comparison process. Let

us point out that this is a single run (no average

over a series of allocation for the same time step is

performed), which by deﬁnition presents a signiﬁcant

statistical noise (section 5.2) as this noise adds up

at every stage of the whole process. This being

said, once again, CLUMPY performs signiﬁcantly

A Formally Correct and Algorithmically Efﬁcient LULC Change Model-building Environment

Table 2: Computation time of the different modeling envi-

ronments for the case study of 5.1, and for the calibration-

estimation and global calibration/allocation comparison

processes (total column) of section 4. DE = Dinamica EGO

with two different pruning factors (F = 10 and 100).

model

Calibration

Total

Estimation

CLUMondo 45 sec 45 sec

LCM MLP 2 min 40 sec 3 min 18 sec

LCM SW 19 min 15 sec 19 min 53 sec

LCM LR 2 min 40 sec 3 min 18 sec

DE F=10

32 sec

35 sec

DE F=100 38 sec

CLUMPY 6 sec 11 sec

better than the other modeling environments. We

can observe very clearly the differences produced

by the pruning parameter and the assumption of

statistically independent explanatory variables for

Dinamica EGO (we will quantify elsewhere the

respective importance of these two sources of bias,

which are usually the most signiﬁcant). The F = 10

(orange line) corresponds to the default value of this

pruning parameter and produced a substantial bias

in this example. We also notice that LCM LR and

LCM MLP do not perform any allocation on this cut.

Indeed, the LCM pruning method only selects the

exact number of pixels to be transited (section 3.2.1).

The pixels with the highest probability

P(y|u,v)

being obviously not on this slice, no transition is

observed, which is a very clear illustration of the bias

involved in this allocation method.

5.4 Execution Time Comparison

Finally, we focus on the calculation times of the dif-

ferent models. Fast computations are important to be

able to perform a sufﬁcient number of simulations

of the same problem (this is never done in LULC

change modeling, but would in fact be required to ex-

tract meaningful statistical information, in agreement

with the probabilistic and Markovian nature of pro-

jections). This would also allow the user to perform

sensitivity analyses (something which again is never

attempted).

The results are summarized in Table 2. First we

point out that these results do not do justice to the

major computational advantage of CLUMPY on very

large problems (tens or hundreds of millions of pixels

and several LULC transitions), where it outperforms

all other modeling environments by a factor of at least

100 in computational time. However, for large prob-

lems, some of the methods evaluated do not even con-

verge in 24h, while CLUMPY converges in a matter

of minutes, which is why we chose a small enough

problem, in order for the comparison to be possible.

We still obtain a reasonable numerical efﬁciency

for CLUMPY compared to the other models. Note

that the KDE parameter q, which is set to 51 here lin-

early inﬂuences the calibration-estimation time. Hav-

ing a lower value of q speeds up the process but in-

creases the error in the estimated probability distri-

bution. Also, the allocation algorithm presented in

section 3.2 implies to recompute p(y|u) frequently

enough to obtain a bias-free allocation, and this also

introduces a computation time penalty.

CLUMPY is always more efﬁcient in comput-

ing dynamic distance maps than its closest competi-

tor, Dinamica EGO. The largest the problem, the

largest the gap in efﬁciency (CLUMPY is approx-

imately quadratically more efﬁcient than Dinamica

EGO with increasing problem size). Conversely, the

need to recompute probability distributions frequently

enough during the allocation step (in order to ensure

an unbiased allocation) is always a computation time

penalty for CLUMPY. In fact, Dinamica EGO would

greatly beneﬁt from a change in its algorithm of dy-

namic distance updating (such as the python function

SCIPY.NDIMAGE used by CLUMPY).

6 CONCLUSIONS

This paper introduces a new spatially explicit statisti-

cal LULC change modeling environment, CLUMPY.

This environment is based on sound theoretical con-

siderations, and is numerically efﬁcient. In partic-

ular, we will show explicitly in a series of papers

under preparation that our patch-oriented probabilis-

tic formulation of LULC state transitions is formally

correct, and that our algorithmic implementations of

these theoretical bases is bias-free. We will also

present an investigation strategy that allowed us to

identify the sources of biases and errors in existing

software in a systematic way, and correct them in

our new modeling environment. This endeavor is de-

signed to help reduce the differences of behavior be-

tween existing LULC change modeling environments

on a given problem and set of data pointed out in the

introduction, and to provide at least one such environ-

ment where remaining errors (mostly due to statistical

noise) are under strict control and can be precisely

quantiﬁed.

In the process, we have introduced a new calibra-

tion strategy inspired from the large body of work per-

formed on density evaluation in the machine-learning

community. Our implementation of this strategy

produces signiﬁcant improvements in the precision

GISTAM 2022 - 8th International Conference on Geographical Information Systems Theory, Applications and Management

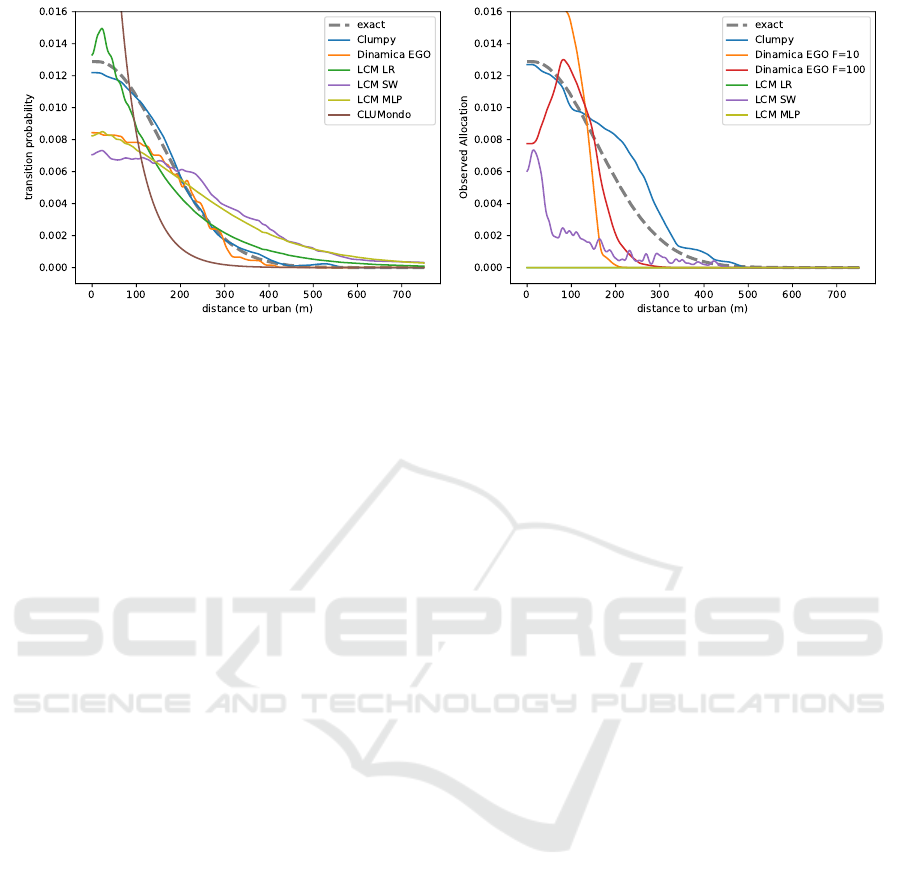
(a) Calibration-estimation comparison process. (b) Global calibration/allocation comparison process (for a

single allocation run).

Figure 2: Transition probability one-dimensional cut from agricultural to urban areas with respect to distance to existing urban

areas, with elevation set to 300 m and slope set to 2

of the calibration process, in comparison to exist-

ing calibration methods. We have also used a new,

bias-free, patch-allocation algorithm. This couple of

calibration-allocation procedures is always unbiased

and substantially more precise than existing ones. It

is more efﬁcient in terms of computational time on

small (millions of pixels) problems, and signiﬁcantly

faster (up to ∼ 100 times) than existing software on

large or very large problems (tens to hundreds of mil-

lions of pixels).

We have ﬁnally proposed an evaluation method

in section 4 allowing us to perform effective compar-

isons of the performances of various modeling envi-

ronments, including ours. This constitutes a ﬁrst step

towards a systematic validation procedure for LULC

change models. This method takes advantage of the

fact that it is both more relevant and more efﬁcient to

compare models in explanatory variable space rather

than in physical space. Indeed, LULC change cal-

ibration data are often undersampled, by necessity,

and the type of LULC change models analyzed here

is statistical in nature. Both features imply that try-

ing to reproduce transition locations exactly in phys-

ical space is often essentially impossible and mis-

leading. Instead, one should focus on reproducing

the correct probability structure in explanatory vari-

able space, and, to a lesser extent, in patch parame-

ter space (patch characteristics have not yet been seri-

ously characterized in existing LULC change model-

ing environments).

All these points will be elaborated upon in detail

in our forthcoming papers.

REFERENCES

Alexander, P., Prestele, R., Verburg, P. H., Arneth, A.,

Baranzelli, C., Batista e Silva, F., Brown, C., Butler,

A., Calvin, K., Dendoncker, N., Doelman, J. C., Dun-

ford, R., Engstr

om, K., Eitelberg, D., Fujimori, S.,

Harrison, P. A., Hasegawa, T., Havlik, P., Holzhauer,

S., Humpen

oder, F., Jacobs-Crisioni, C., Jain, A. K.,

Krisztin, T., Kyle, P., Lavalle, C., Lenton, T., Liu, J.,

Meiyappan, P., Popp, A., Powell, T., Sands, R. D.,

Schaldach, R., Stehfest, E., Steinbuks, J., Tabeau, A.,

van Meijl, H., Wise, M. A., and Rounsevell, M. D. A.

(2017). Assessing uncertainties in land cover projec-

tions. Global Change Biology, 23(2):767–781.

Chamayou, J. M. F. (1980). Averaging shifted histograms.

Computer Physics Communications, 21(2):145–161.

Charikar, M. and Siminelakis, P. (2017). Hashing-Based-

Estimators for Kernel Density in High Dimensions. In

2017 IEEE 58th Annual Symposium on Foundations of

Computer Science (FOCS), pages 1032–1043. ISSN:

0272-5428.

Eastman, J., Jin, W., Kyem, P., and Toledano, J. (1995).

Raster Procedure for Multi-Criteria/Multi-Objective

Decisions. Photogrammetric Engineering & Remote

Sensing, 61:539–547.

Garc

ıa-

Alvarez, D., Lloyd, C. D., Van Delden, H., and Ca-

macho Olmedo, M. T. (2019). Thematic resolution in-

ﬂuence in spatial analysis. An application to Land Use

Cover Change (LUCC) modelling calibration. Com-

puters, Environment and Urban Systems, 78:101375.

Mas, J.-F., Kolb, M., Paegelow, M., Camacho Olmedo,

M. T., and Houet, T. (2014). Inductive pattern-based

land use/cover change models: A comparison of four

software packages. Environmental Modelling & Soft-

ware, 51:94–111.

O’Brien, T. A., Kashinath, K., Cavanaugh, N. R., Collins,

W. D., and O’Brien, J. P. (2016). A fast and objective

multidimensional kernel density estimation method:

A Formally Correct and Algorithmically Efﬁcient LULC Change Model-building Environment

fastKDE. Computational Statistics & Data Analysis,

101:148–160.

Prestele, R., Alexander, P., Rounsevell, M. D. A., Arneth,

A., Calvin, K., Doelman, J., Eitelberg, D. A., En-

gstr

om, K., Fujimori, S., Hasegawa, T., Havlik, P.,

Humpen

oder, F., Jain, A. K., Krisztin, T., Kyle, P.,

Meiyappan, P., Popp, A., Sands, R. D., Schaldach, R.,

Sch

ungel, J., Stehfest, E., Tabeau, A., Meijl, H. V.,

Vliet, J. V., and Verburg, P. H. (2016). Hotspots of

uncertainty in land-use and land-cover change pro-

jections: a global-scale model comparison. Global

Change Biology, 22(12):3967–3983.

Rudemo, M. (1982). Empirical Choice of Histograms and

Kernel Density Estimators. Scandinavian Journal of

Statistics, 9(2):65–78.

Sain, S. R., Baggerly, K. A., and Scott, D. W. (1994). Cross-

validation of multivariate densities. Journal of the

American Statistical Association, 89(427):807–817.

Scott, D. (2015). Multivariate density estimation: Theory,

practice, and visualization: Second edition. Wiley.

Soares-Filho, B. S., Coutinho Cerqueira, G., and

Lopes Pennachin, C. (2002). Dinamica — A stochas-

tic cellular automata model designed to simulate the

landscape dynamics in an Amazonian colonization

frontier. Ecological Modelling, 154(3):217–235.

Terrell, G. (1990). The Maximal Smoothing Principle in

Density Estimation. Journal of the American Statisti-

cal Association, 85(410):470–477.

van Vliet, J., Bregt, A. K., Brown, D. G., van Delden, H.,

Heckbert, S., and Verburg, P. H. (2016). A review

of current calibration and validation practices in land-

change modeling. Environmental Modelling & Soft-

ware, 82:174–182.

van Vliet, J., Malek, Z., and Verbug, P. (2015). The CLU-

Mondo land use change model, manual and exercises.

Vannier, C., Bierry, A., Longaretti, P.-Y., Nettier, B., Cor-

donnier, T., Chauvin, C., Bertrand, N., Qu

etier, F.,

Lasseur, R., and Lavorel, S. (2019a). Co-constructing

future land-use scenarios for the Grenoble region,

France. Landscape and Urban Planning, 190:103614.

Vannier, C., Lasseur, R., Crouzat, E., Byczek, C., Lafond,

V., Cordonnier, T., Longaretti, P.-Y., and Lavorel, S.

(2019b). Mapping ecosystem services bundles in a

heterogeneous mountain region. Ecosystems and Peo-

ple, 15:74–88.

Vannier, C., Lefebvre, J., Longaretti, P.-Y., and Lavorel, S.

(2016). Patterns of Landscape Change in a Rapidly

Urbanizing Mountain Region. Cybergeo.

Verburg, P. H., Alexander, P., Evans, T., Magliocca, N. R.,

Malek, Z., Rounsevell, M. D., and van Vliet, J. (2019).

Beyond land cover change: towards a new generation

of land use models. Current Opinion in Environmental

Sustainability, 38:77–85.

Verburg, P. H., de Koning, G. H. J., Kok, K., Veldkamp,

A., and Bouma, J. (1999). A spatial explicit allocation

procedure for modelling the pattern of land use change

based upon actual land use. Ecological Modelling,

116(1):45–61.

Wand, M. and Jones, C. (1994). Multivariate plug-in band-

width selection. Computational Statistics, 9(2):97–

116.

Wand, M. P. (1992). Error analysis for general multtvariate

kernel estimators. Journal of Nonparametric Statis-

tics, 2(1):1–15.

Wells, J. R. and Ting, K. M. (2019). A new simple and

efﬁcient density estimator that enables fast systematic

search. Pattern Recognition Letters, 122:92–98.

APPENDIX

Case Study Transition Probability

Function

The parameters used to deﬁne the function P

∗

(v|u,y)

in Eq. (4) are the following:

µ = (150, 0,0) (5)

Σ =





843 325

843 10

−16.3

325 −16.3 10





(6)

D = {y | 0 ≤ y

≤ 616, 0 ≤ y

≤ 15, 0 ≤ y

≤ 60}

(7)

Models Parameters

In section 5, we use various land use change models

with the following parameters.

Dinamica EGO

We have used version 5.2.1 and all the calculations

were performed on a single CPU. The binning param-

eters are the following. The parameter increment is

ﬁxed at 15 meters for the elevation, 5

for the slope

and 10 meters for the distance to urban areas. The

minimum delta, the maximum delta and the tolerance

angle are respectively ﬁxed at 50, 500,000 and 5.0 for

all explanatory variables.

Idrisi LCM

We have an Idrisi Selva license, which is relatively old

(17.00). The estimation by logistic regression is done

without sampling. The parameters of SimWeight are

the default ones with notably the sample size ﬁxed at

1000. All the default parameters of MLP are kept.

CLUMondo

We have used version 1.4.0. The sampling parameter

is ﬁxed to 30% of all observations. The number of

cells distance between samples is ﬁxed to 2 with no

data values excluding and balanced sample enabled.

Clumpy

The KDE parameter q (section 3.1.2) is ﬁxed to 51.

This is the only user-deﬁned parameter in CLUMPY.

This default value should be appropriate for most ap-

plications.

GISTAM 2022 - 8th International Conference on Geographical Information Systems Theory, Applications and Management