A Privacy-Preserving Auction Platform with

Public Veriﬁability for Smart Manufacturing

Thomas Lor

unser

, Florian Wohner and Stephan Krenn

AIT Austrian Institute of Technology, Vienna, Austria

Keywords:

Multiparty Computation, Veriﬁable Computing, End-to-End Security, Authenticity.

Abstract:

The digitization trend in the manufacturing industry is gaining pace and novel cloud based market places will

play an important role in the transformation. However, existing market platforms are centrally organized and

can not provide the required level of data privacy and trustworthiness needed for the manufacturing industry.

In this work we study the security and privacy aspects for the case of a market platform for outsourcing in

manufacturing. We show that the requirements identiﬁed together with relevant stakeholder are challenging

and sometimes also contradicting on the ﬁrst sight. To address this challenge we combined different crypto-

graphic building blocks into a novel framework for more secure but transparent decentralized data markets. In

particular the framework combines secure multiparty computation with zero-knowledge proof of knowledge

methods and blockchain to enable ﬂexible sealed-bid auctions which are also publicly veriﬁable. For eval-

uation a proof-of-concept was developed and benchmarking results show that the framework can efﬁciently

address all requirements established.

1 INTRODUCTION

Emerging needs for novel secure data spaces are driv-

ing current developments in cloud computing and the

Internet of Things. One such domain is manufactur-

ing, where the sharing economy is expected to have

a signiﬁcant impact in multiple dimensions, rang-

ing from reduced costs, over increased innovative-

ness and competitiveness, to considerable environ-

mental beneﬁts. However, mutual distrust and data

sovereignty is of special concern in the manufactur-

ing industry, e.g., related to corporate secrets and cus-

tomer data.

Control over data is still hampered in large infras-

tructures and the trend to centralization is alarming

for a prosper economy. By connecting production fa-

cilities to the cloud, many security and compliance

approaches relying on a pure contractual basis (ser-

vice level agreements, SLA) must be reconsidered,

especially with respect to the existing oligopoly in

the cloud market. A clear understanding of emerg-

ing security and privacy issues is needed, and security

paradigms based on cryptography rather than SLAs

have to be considered in order to guarantee conﬁden-

https://orcid.org/0000-0002-1829-4882

https://orcid.org/0000-0003-2835-9093

tiality and data sovereignty in the cloud.

Contributions. In this work, we propose a net-

worked, decentralized architecture for end-to-end ver-

iﬁable yet privacy-preserving auctions, in order to

support future manufacturing clouds and market-

places. Our platform combines different technologies

in a new way to provide adequate protection of busi-

ness secrets as well as transparency and end-to-end

veriﬁability.

On the technical side, this is achieved by a com-

bination of secure multi-party computation and zero-

knowledge proofs of knowledge that also incorporates

the edge of the network to achieve the main proper-

ties envisaged by the different stakeholders. The plat-

form not only allows for determining the lowest bid,

but also advanced price-ﬁnding mechanisms based on

price-ratio methods. Our solution minimizes the nec-

essary mutual trust, not only between different bid-

ders but also towards the auctioneer. We implemented

a proof of concept of our approach, integrating and

extending a number of existing tools and frameworks,

e.g., for MPC and zkSNARKs. The performed bench-

marking demonstrates the practicality for realistic sets

of parameters for use cases encountered in our use

case.

Outline. The remainder of the paper is structured in

the following way. We provide a detailed overview of

Lorünser, T., Wohner, F. and Krenn, S.

A Privacy-Preserving Auction Platform with Public Veriﬁability for Smart Manufacturing.

DOI: 10.5220/0011006700003120

In Proceedings of the 8th International Conference on Information Systems Security and Privacy (ICISSP 2022), pages 637-647

ISBN: 978-989-758-553-1; ISSN: 2184-4356

637

related work and the state of the art in Section 2. In

Section 3 we present the new architecture and explain

how it addresses the requirements of our use case.

Our framework is then described in Section 4. The

evaluation results of our proof-of-concept implemen-

tation are reported in Section 5. Finally, we brieﬂy

conclude and discuss possible future extensions in

Section 6.

2 RELATED WORK

MPC can be considered the most practical approach

for generic computation on encrypted data. This

means that virtually any function can be computed in

an MPC system in principle, however, due to the over-

head introduced by MPC protocols they are slower

than a classical computer by orders of magnitudes.

Nevertheless, the ﬁrst realization of a real application

was demonstrated in an auction held for the Danish

sugar beets market in 2009 (Bogetoft and et al., 2009).

This was the ﬁrst large-scale and practical applica-

tion of multiparty computation and enabled farmers

to get a fair market clearing price. They used a local

setup with three computers in the same room and ran

a semi-honest MPC protocol to calculate the clear-

ing price. About 4000 values for prices were sup-

ported at most and 1229 bidders participated in the

auction. The inputs from the individual bidders were

encoded by veriﬁable secret sharing and the compu-

tation lasted for half an hour.

The basic problem of this setting is the lack of

scalability of the MPC protocols itself. The chosen

setup with 3 nodes prevents the bidders from directly

participating in the computation but requires them to

ﬁrst encode their inputs for the MPC nodes. The im-

proved security in this setting is evident, but to further

increase the trustworthiness of the system, and to de-

crease the trust assumptions in the MPC nodes, some

form of public veriﬁability would be desirable.

To cope with this issue new research combined the

mechanisms with blockchain and (non-interactive)

zero-knowledge proof (NIZK) techniques. The

blockchain is an ideal candidate to be used for stor-

age of relevant audit data in an accessible manner,

however, because all data written to the blockchain is

visible to every party additional machinery is required

to maintain conﬁdentiality and privacy. NIZKs enable

parties to publish proofs about statements without re-

vealing secrets per se (witnesses) and are therefore an

ideal tool to integrate blockchain with the conﬁden-

tiality preserving MPC functionality.

anchez (S

anchez, 2017) proposed Raziel, a sys-

tem that combines MPC and NIZK to guarantee the

privacy, correctness and veriﬁability of smart con-

tracts. The idea underlying Raziel is a smart con-

tract which in addition to the standard properties also

guarantees correctness of auctions. The validity of the

generated NIZKs can also be veriﬁed by third parties,

thereby achieving publicly veriﬁability.

Another approach to veriﬁable auctions has been

presented in (Galal and Youssef, 2018) and a soft-

ware prototype can be found on GitHub

. The solu-

tion combined homomorphic commitments and NIZK

together with a veriﬁable comparison protocol to

achieve a secure FPSBA. The system is veriﬁable

and privacy preserving against outsiders, however, a

trusted auctioneer is still required because he learns

all bids.

Furthermore, Blass and Kerschbaum (Blass and

Kerschbaum, 2018) presented Strain, a protocol to

implement sealed-bid auctions on top of blockchains

that protects the bid privacy against fully malicious

parties. In a nutshell, the protocol works as fol-

lows: bids are encrypted bitwise and are stored on

the blockchain. Bidders then to run interactive zero-

knowledge protocols generating proofs of relations

between bids, thereby realizing auctions in a peer-

to-peer fashion. Albeit being scalable by the peer-

to-peer nature, the protocol still needs a semi-trusted

auctioneer as arbiter and requires all parties to be on-

line during all auction phases. It also leaks the full

order of all bids compared to the winning bid as re-

quired by auctions.

Kosba et al. (Kosba and et al., 2016) presented

Hawk, a framework to establish privacy preserving

smart contracts on the Ethereum blockchain. Hawk is

intended to protect transaction data on chain by lever-

aging zero-knowledge proof techniques. The goal

was an easy-to-use framework providing a compiler

managing the cryptographic tasks. Up to our knowl-

edge, the Hawk framework has still not been released

yet. However, it is considered that the approach can-

not be efﬁciently integrated with MPC.

In another work (Galal and Youssef, 2019), Galal

and Youssef utilized Zero-Knowledge Succinct Non-

interactive Argument of Knowledge (zk-SNARK) to

realize privacy friendly auctions on a blockchain.

However, their solution makes use of a trusted auc-

tioneer who learns the bids. This is contrary to our

goals; however, the approach contains interesting as-

pects and by realizing the auctioneer in a distributed

fashion using MPC, the concept resembles the core

ideas of our approach. Additionally, cryptocurrencies

have been used to incentivize fairness and correctness,

and avoid deviations from the MPC or NIZK protocol.

In these systems money has to be escrowed in deposits

https://github.com/HSG88/AuctionContract

ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy

638

which are only returned if the behave honestly. This

in effect encourages parties to strictly follow the pro-

tocols to avoid the ﬁnancial penalty. Protocols in this

direction have been proposed in (Andrychowicz and

et al., 2014; Bentov and Kumaresan, 2014; Kumare-

san et al., 2016; Kumaresan and Bentov, 2016).

Baum (Baum et al., 2014) proposed publicly au-

ditable MPC; however, this work is mainly of theo-

retical interest and never really implemented. It also

integrates with SPDZ but is likely to be too expensive

for practical applications, as the idea is basically to

make each computational step veriﬁable by adding a

zero-knowledge proof.

3 MARKET PLATFORM

A key requirement in a cloud manufacturing is to op-

timally match supply and demand, i.e., available man-

ufacturing resources and customers’ needs. In the

following we thus present a veriﬁable and privacy-

preserving marketplace for manufacturing resources.

In our scenario, we consider a marketplace provider,

at which owners of manufacturing sites can sign up

as producers and register their machines as well as

meta information such as conﬁgurations, quality lev-

els, etc, cf. also Figure 1. Customers (or buyers) can

now put orders, and producers can provide bids to

win the order. Leveraging multi-party computation

to ensure conﬁdentiality, blockchain to immutably

store encrypted bids and results, and zero-knowledge

proofs to ensure integrity and veriﬁability, the market-

place will then match the bids against the order, and

announce the winning bid. The precise data ﬂow will

be described in Section 4.

3.1 Security Requirements

In the following, we introduce the security and pri-

vacy requirements to a marketplace for cloud manu-

facturing applications, which were derived in collab-

oration with industry partners. On a high level, we

found an environment which is aware of their assets

but is currently not sure how they could leverage the

data they own because of concerns regarding the in-

sufﬁcient protection of business critical information,

and the risk of a potentially colluding harmful envi-

ronment during auctions. More precisely, the require-

ments are as follows.

Conﬁdentiality. Conﬁdentiality of the producers’

bids is of utmost importance through all phases of the

auction. In particular, the bids do not only need to

be protected from unauthorized access through com-

petitors, but also from the platform provider. This is

because of the risk of this central entity colluding with

certain producers, thereby fully undermining the price

ﬁnding mechanisms.

Furthermore, our interviews with industry also

showed, that production and shop ﬂoor data can be

business critical. That is, competitors should not gain

any information about a producer’s current capacity

utilization, machinery status, or process information

on production lines.

Integrity. Besides the requirement of correctness in

the case of exclusively honest entities, it is necessary

that the integrity of an auction’s result can also be

guaranteed in the case of a malicious operator of the

marketplace. This even needs to hold in the case that

the provider is colluding with other entities in the sys-

tem, including producers and buyers, in order to en-

sure that no party can manipulate the outcome of the

auction in their own interest.

Availability. While this is often not considered in the

design of cryptographic protocols, it turned out to be

of high importance to our partners. On the one hand,

producers demand assurance that they will not miss

opportunities. On the other hand, related to integrity,

producers also need to be guaranteed that they cannot

be excluded from an auction; that is, whenever a pro-

ducer places an offer, it shall also be guaranteed that

this offer was indeed considered.

Anonymity and Pseudonymity. In addition to con-

ﬁdentiality of bids, producers may wish to even hide

the information whether or not they placed an offer

for a given auction, as this might already reveal sensi-

tive information about the current utilization or con-

dition of a production line. Depending on the spe-

ciﬁc business model of the marketplace, this require-

ment, however, needs to be balanced against the mar-

ketplace provider’s needs.

Fairness. Another important aspect for the clients

was fairness in terms of fair conditions. This can also

be interpreted as an open and transparent way of com-

putation and selection of the winning offer. However,

the evaluation criteria for matching and ranking need

to be clear and traceable. The goal is to establish a fair

comparison of offers on an comprehensible algorithm

to establish fair market prices.

Transparency. Finally, transparency requires that all

participants in the system are able to trace progress

and activities on a high level. Our partners were also

interested in historical data in case they were ofﬂine

for certain times and could not participate in auctions.

However, all this functionality needs to be achieved

without compromising any of the previous goals, es-

pecially those related to conﬁdentiality and privacy.

A Privacy-Preserving Auction Platform with Public Veriﬁability for Smart Manufacturing

639

Figure 1: Use case of cloud manufacturing and marketplace.

3.2 Auction Mechanism

Auctions are considered a good mechanism to achieve

fair market prices for goods. The underlying idea

is that every bidder in an auction bids the real value

which leads to a real market price. This market mech-

anism can be undermined in various ways by ma-

licious parties, especially in centralized online plat-

forms. As summarized in (Galal and Youssef, 2018)

there are four main types of auctions which are of

practical interest and two of which work on hidden

bids.

First-price sealed-bid auctions (FPSBA), where

bidders submit their bids in sealed envelopes to the

auctioneer, which opens them to determine the bidder

with the highest bid. Second-price sealed-bid auc-

tions (Vickrey auctions) are similar to FPSBA with

the exception that the winner pays the second highest

bid instead.

Additionally to the traditional approaches various

other price ﬁnding mechanisms are relevant in the in-

dustry. In the requirements assessment for a manu-

facturing marketplace, it became clear that it is not

only the price which is relevant for selection of the

best offer, but also other parameters. Currently deliv-

ery options, logistic costs, quality requirements and

other parameters are also part of the decision process

to select the best offer.

In that sense, it is essential to have a very ﬂexi-

ble mechanism for ranking offers. At the heart of our

matching mechanism is thus the idea of a matching

score, which allows to address additional targets and

be more versatile in conﬁguration. In this mechanism,

the buyer can deﬁne different criteria and priorities

among them, which should be taken into considera-

tion. This starts from basic capabilities of the pro-

duction facilities and can be arbitrarily extended for

additional topics as mentioned above. These param-

eters are deﬁned as part of the tender and distributed

along with it. The matching is then based on capa-

bilities of a producer, which are immutably registered

on a blockchain when signing up as producers or reg-

istering equipment. In essence, this leads to a case

where the price has to be combined with a matching

score to rank results.

Speciﬁcally interesting are price ﬁnding methods

based on linear interpolation. The so called price ra-

tio methods are often used to compare offers which

are not comparable otherwise. In this approach, a

score R for a given bid is computed as:

R = ω

max

+ ω

min

, (1)

where for simplicity we only consider a single crite-

rion here. In this equation, L means the level of fulﬁll-

ment of this criterion by an offer, which corresponds

to the matching score, and L

max

is the best level pos-

sible. The actual price for a certain offer is then given

in P, with P

min

being the lowest in the auction. The

and ω

are weights for the respective ratios on ful-

ﬁllment grade and pricing, which are deﬁned by the

buyer and can be either public and known to the pro-

ducers as part of the tender or also kept secret, de-

pending on the preferences of the buyer. By inspect-

ing the method it gets clear that not all values can be

computed at the edge, i.e., on the client side, as in

particular the ratio

min

of the prices requires the min-

imum over all offers.

From this analysis it becomes evident that sim-

ple price ranking is not enough for winner estimation

and the many possible options require a ﬂexible com-

puting system which goes beyond oblivious sorting

of bids. In fact, each buyer would like to deﬁne his

speciﬁc matching criteria and also decide on a rank-

ing mechanism to fulﬁll his needs. This turned out

to make the overall system architecture more chal-

lenging and rendered many smart contract based ap-

proaches from the literature inadequate. On the other

hand, the MPC solutions available can cope with the

ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy

640

degree of ﬂexibility required but do not provide means

for public veriﬁability as needed for our architecture.

4 FRAMEWORK

The proposed framework is designed to address the

security objectives deﬁned in Section 3.1, especially

bringing together typically contradicting goals of pri-

vacy and veriﬁability in a single solution. It has a

decentralized architecture and follows data minimiza-

tion principles.

By the use of secure multiparty computation the

platform itself is operated in a way that the provider

does not learn sensitive data and by making every step

of the of the tendering process veriﬁable the trustwor-

thiness is achieved. For end-to-end veriﬁability, pub-

licly veriﬁable zero-knowledge proofs of knowledge

are generated for all computations, even for the MPC

steps. Finally, to trace all interactions and proofs we

use a distributed ledgers which serves as a trust an-

chor and immutable append-only data base.

4.1 Data Flow

In the following we detail the data ﬂow in our plat-

form. To ease understanding, Figure 2 provides a

high-level overview, where we omit setup steps for

the sake of clarity.

Setup Phase. The following setup steps are necessary

to operate the system.

1. On the one hand, ZKSetup is used to generate the

common reference string (CRS) needed for the

NIZKs. On input the security parameter and a

circuit, this algorithm outputs the CRS which is

assumed to be implicit input to all further algo-

rithms and parties. It is important to note that the

system is speciﬁcally designed in a way that this

step is only needed once and does not need to be

invoked again if different ranking mechanisms are

used, as they are all supported by the speciﬁcally

designed circuit with built-in ﬂexibility. In prac-

tice this setup algorithm can be run in dedicated

setup ceremony, including, e.g., secure hardware

elements or dedicated MPC-based ceremonies.

2. On the other hand, RegUser is a protocol which

is run by the user and the platform to register with

the platform. It is used to generate necessary iden-

tities and credentials to authenticate the user and

set up the necessary permissions on the ledger.

Auction Phase. After the setup is complete the fol-

lowing steps are conducted in the protocol for a par-

ticular auction.

1. RegEqm. A client registers equipment (machine)

for usage in the system. On input machine param-

eters, this algorithm outputs a commitment to the

machine parameters which is then stored on the

ledger. The registration of new equipment has to

be done before a producer can participate in an

auction.

2. ITT. A buyer sends a request for quotation with

relevant parameters to all parties by storing them

to the blockchain.

3. Match. Based on the tender information received,

the producers compute a matching score for their

machines. Based on the score a local matching

decision is done to decide whether or not to par-

ticipate in the auction. If the producer does not

participate, the local process is aborted.

4. ComInput. If the producer is participating in

the bidding, it computes a NIZK for the match-

ing score and a commitment to the bid. The

bid commitment and the proof are stored in the

blockchain.

5. Input. In this step the producers (i.e., bidders)

send their bids together and matching scores to

the MPC system in a secret-shared fashion.

6. CkInput. The MPC system retrieves the cor-

responding commitments and proofs from the

blockchain and veriﬁes them in the encrypted do-

main. This is done by recomputing the com-

mitments on the shares (for bids and matching

scores) at each node and comparing the recon-

structed commitments with the plaintext ones.

Additionally, each node veriﬁes the proof for the

local matching score individually. If either of the

checks fails, the system complains about the pro-

ducer.

7. Compute. The MPC system calculates a ranking

based on scores and bids according to the ranking

function deﬁned by the buyer.

8. ZKProof. The MPC system generates a NIZK for

the winning bid, proving that it is the best ranked

result according the predeﬁned ranking function.

It does so by each node computing the proof on

its share of the result.

9. Reveal. To reveal the result in a veriﬁable form,

the winning bid is reconstructed from the encod-

ings as well as the ﬁnal proof enabling the ver-

iﬁcation of the winner calculation. The data is

recorded in the blockchain and ﬁnalizes a particu-

lar auction.

There are many variations possible in practice but

this will only result in subtle changes, e.g., if the win-

ning producer and/or bid has to be kept secret.

A Privacy-Preserving Auction Platform with Public Veriﬁability for Smart Manufacturing

641

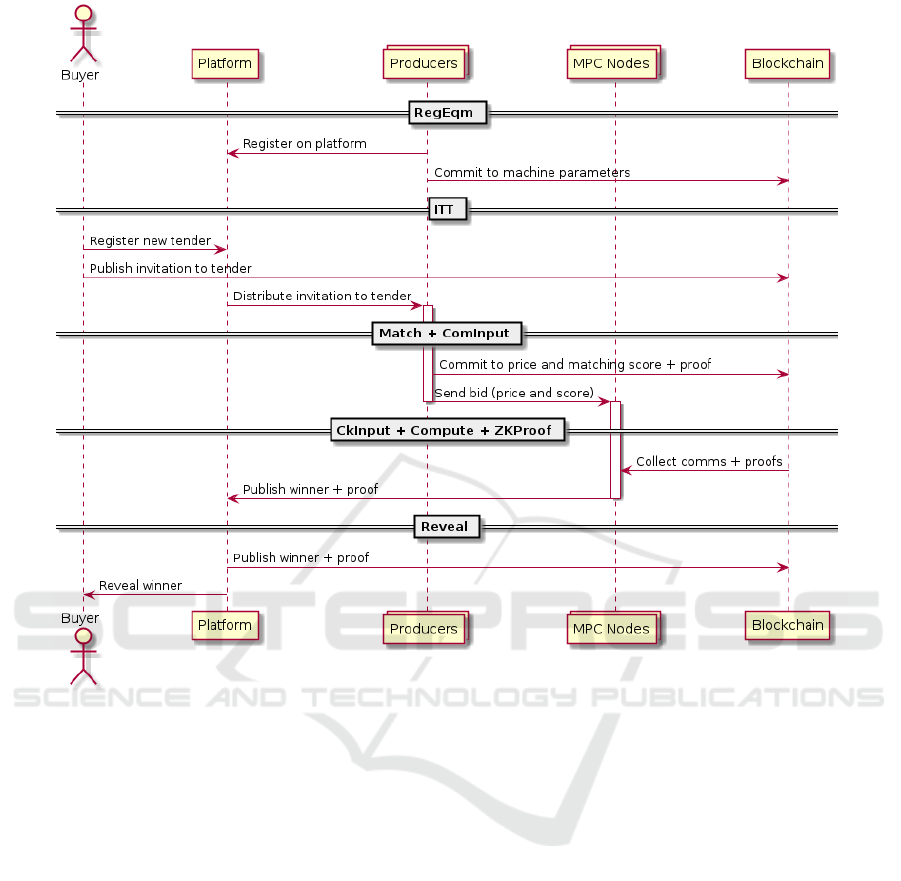
Figure 2: Sequence diagram for an auction.

4.2 Protocols

Different protocols have been used, extended and

integrated to achieve all desired properties for our

framework. At the core we combine multiparty com-

putation with non-interactive zero-knowledge proofs

of knowledge (NIZK) to achieve conﬁdentiality and

public veriﬁability that the same time. Regarding

MPC we do not rely on any speciﬁc protocol but only

require a method which is based on secret sharing.

However, because we aim at public veriﬁability the

correctness of the computation is going to hold even if

all nodes are corrupt. Therefore, depending on the in-

dividual assumptions made for the MPC deployment,

it can be sufﬁcient to rely on passively secure proto-

cols.

To achieve veriﬁability, the system is based on

adaptive zk-SNARKs as introduced in (Veeningen,

2017). Working with commitments to track different

steps in the process is essential to guarantee privacy

of sensitive data. However, the protocol is not guaran-

teeing any authenticity which is essential to track the

ﬂow from end to end. Therefore, we leverage ideas

from ADSNARK (Backes and et al., 2014) and use

signatures on the commitments to assure the authen-

ticity of the data right from the source. In our use

case both can be used, standard signatures but also

group signatures or delegated signatures (Krenn and

Lor

unser, 2021), if a certain degree of anonymity is

still required, e.g., if it should not be visible which

subsidiary of a larger organization the resources be-

long to.

An important requirement was to reduce the num-

ber of times the setup procedures of the zk-SNARKs

have to be executed. Ideally, it has only to be done

once when initializing the platform, and can then be

reused for all subsequent auctions. Therefore, we use

case a hybrid approach that turned out to be very ef-

ﬁcient. On the one hand we use the idea of subrou-

tines (sub-qaps), which are basically predeﬁned sub-

routines at setup time but can be connected during

proof generation by means of intermediate commit-

ments, to establish the required circuit. This con-

cept is very ﬂexible with only little overhead, i.e., the

ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy

642

additional commitments increase the proof size and

veriﬁcation time for each subroutine deﬁned. To en-

able even more freedom in the conﬁguration of rank-

ing algorithms we integrate the ideas of universal cir-

cuits as presented with MIRAGE (Kosba and et al.,

2020). Altogether, at setup time we generate a proof

circuitry which comprises both, static elements and

freely re-conﬁgurable components to get the best of

both worlds. Starting from a common pattern of auc-

tion markets, we can now instantiate the right build-

ing blocks to support a wide range of auction systems

with extensive conﬁguration options. To that end,

this approach is somehow similar to partially recon-

ﬁgurable hardware.

4.3 Security

In the following we will informally discuss the

achieved security goals, a more formal treatment is

planned as future work. Moreover, we also give some

design rational and explain several architectural deci-

sions.

Conﬁdentiality. The privacy of sensitive information

is protected in our framework by two main primitives.

On the one hand, MPC is used to compute the winner

of the auction in a privacy preserving way and sensi-

tive data is protected by the input privacy provided by

MPC.

On the other hand, to enable transparency we are

recording inputs at different stages in the blockchain.

To achieve conﬁdentiality there we use commitments

which are also hiding input. Given that sensitive in-

puts are never handled in cleartext in the system we

achieve strong cryptographic protection, which also

results in the discussed properties of bid privacy and

posterior privacy.

In our marketplace, we even apply a decentral-

ized matching which allows for local computation of a

matching score and therefore follows data minimiza-

tion principles. Alternatives would be a producer-

based matching or a platform-side matching, which

both would lead to problems: For the former, it would

be required to share sensitive information about avail-

able capacities and process information with potential

competitors, which directly violates the requirements.

For the latter, either the platform would learn sensitive

information or the matching would have to be done in

the encrypted domain.

Integrity and Correctness. In essence, the basic

idea of the framework is to preserve the integrity and

authenticity of data in the system and to prove the

correctness of each computation in between. How-

ever, instead of directly signing the input to the sys-

tem, only commitments are signed and also put in

a blockchain, which guarantees that producers are

bound to their bids and bids.

In our case we use the extractable commitments

presented in (Veeningen, 2017). In the original work

these particular commitments were used with a ded-

icated key to distinguish between input from differ-

ent parties, but this key is produced in the initial setup

phase and has to be distributed to parties, which opens

up many attack vectors in practical implementations.

We rely on locally generated private keys used to sign

the commitments, which never leave the local area

and are registered with the platform or the blockchain.

This would also allow for the use of group signatures

for even more ﬂexibility in the management of edge

components without sacriﬁcing the security.

After the tender is initiated and all bidders

recorded the required data to participate in the auc-

tion, the MPC computation is started. The input

is comprised of the private bid, the private match-

ing score as well as the data also recorded on the

blockchain, i.e., the commitments on initial machine

parameters and the matching score, thereby guaran-

teeing conﬁdentiality while still binding bidders to all

input values. Finally, the MPC network not only out-

puts the winning bid, but also a NIZK proving its op-

timality, thereby guaranteeing the correctness of the

ﬁnal result.

It is worth noting that the performed local match-

ing introduces another problem with the integrity of

data: As the matching score is relevant to calculate

the ranking on the platform, it has to be assured that

the score was computed correctly. Therefore, the bid-

der is required to generate a proof on the score before

sending it to the MPC system. We do so by forcing

the bidder to commit not only to the bid but also to the

matching score and additionally to generate a NIZK

which is then stored in the blockchain, letting every-

body to also verify the local pre-processing.

Finally, it is important to note that with this ap-

proach we are basically tweaking the security model

of MPC for the overall system. Because the cor-

rectness of the computation is publicly veriﬁable by

means of NIZKs, the integrity of the computation can

even be assured if all MPC nodes maliciously devi-

ate from the protocol speciﬁcation. Even more, in

our setting malicious behaviour can be attributed to

the right stakeholder, i.e., it is not possible to blame

the platform for malicious input from bidders or vice

versa. This is achieved by letting the MPC system

check all inputs for consistency with the information

in the blockchain before it computes a result. Only

if all inputs are consistent with the stored commit-

ments and the matching score is computed correctly,

the MPC system will incorporate the bid in the auc-

A Privacy-Preserving Auction Platform with Public Veriﬁability for Smart Manufacturing

643

tion, and only then it will be able to compute a proof

for the winning bid.

As a result, the full auction ﬂow is accompanied

with NIZKs and every participant can verify the cor-

rectness of the auction from end-to-end. Even if pri-

vacy is compromised by an adversary which compro-

mises enough MPC nodes to recover the bids, he will

not be able to inﬂuence the winning bid or market

mechanism.

Availability. The availability of the system is pro-

vided by a blockchain component which provides the

properties to serve as robust and immutable public ap-

pend only log. Depending on the deployment of the

MPC system, also robustness properties such as fair-

ness or guaranteed output delivery can be achieved.

Additionally, as the system is non-interactive, client-

side computations cannot be interrupted or blocked

by individual participants, resulting in a highly avail-

able decentralized architecture. Although the plat-

form server is currently needed to run auctions it

would also be possible to remove this single point of

failure.

Anonymity and Pseudonymity. For the given use

case it is not desired to build a completely open and

permissionless infrastructure. The clients in this sys-

tem are part of an ecosystem which requires some

level of assurance for producers and buyers. There-

fore, we only provide pseudonymity for certain steps

in the auction. The pseudonyms are maintained at the

platform which mainly prevents the buyers from by-

passing the business model of the brokerage role of

the platform. The only relevant issue for producers

might be that one can determine whether or not a spe-

ciﬁc producer has submitted a bit for a given auction.

This leakage can be easily abolished by always par-

ticipating in the auction protocol but with a ∞ bid.

Fairness. In our prototype, the tender information

was identiﬁed as public and could thus be put into the

blockchain, which also serves as a broadcast chan-

nel in this step, so that all participants are reliably in-

formed about new opportunities as well as the detailed

evaluation and ranking criteria of an auction.

Although for certain buyers it would be preferred

to not reveal the details of the ranking mechanism

(e.g., the weights in Eq. (1)), in all auctions will the

matching mechanism be transparent and consistent

for all producers.

Transparency. By logging every step into the

blockchain in a privacy-preserving way and also prov-

ing that all computations are correct, we achieve pub-

lic veriﬁability. Every user of the system will thus be

able to verify all auctions based on the public data

stored in the blockchain without compromising the

privacy of individual inputs, thereby achieving the re-

quirement of transparency.

5 EVALUATION

In order to evaluate the efﬁciency and practicability

of our framework, a proof-of-concept prototype has

been implemented in Python, which has been used

to study and benchmark different use cases. The ba-

sis for the implementation was existing work on PyS-

NARK

, qaptools

and MPyC

, which have been inte-

grated and extended with novel functionality, notably

Universal Circuits. The new framework seamlessly

integrates the steps along the data ﬂow.

All measurement results presented in this work

have been measured in a local setup on a single Intel

NUC computer equipped with an Intel(R) Core(TM)

i5-8259U CPU running at 2.30GHz maximum fre-

quency.

Winning Bid Computation. The basic operation in

winner determination is ﬁnding the maximum of the

ranked bids. The computation depends on inputs of

all bidders as well as the buyer and is therefore done

by the MPC system. We present measured comput-

ing times for computing the basic result for different

numbers of parties without any additional proofs in

Table 1. Note that the system we used to take the

measurements only had four CPU cores, so not all

of the increase in time between the settings with four

and ﬁve parties is attributable to the inherent compu-

tational overhead.

Table 1: Computation time (s) with increasing number of

nodes under 3 minutes.

#bids 3 parties 4 parties 5 parties

10 0.9 1.3 3.4

100 10.9 16 35

1000 115.3 176.8 -

The given measurements hold under the unreal-

istic assumption of no network latency. We there-

fore also performed measurements assuming differ-

ent network delays, as shown in Table 2, which sug-

gests that for our use cases the latency of the net-

work has a higher effect on the overall efﬁciency than

the selected MPC framework, see also (Lor

unser and

Wohner, 2020).

Winning Bid Proof Generation. For our use cases,

the generic approach of proving the correctness of ev-

https://github.com/meilof/pysnark

https://github.com/Charterhouse/qaptools

https://github.com/lschoe/mpyc

ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy

644

Table 2: Computation time (s) with increasing network la-

tency between 3 parties.

#bids 0 ms 2 ms 20 ms

10 0.9 1.1 4

100 10.9 11.4 36.6

1000 115.3 124.1 386.1

ery computational step turned out to be unnecessarily

inefﬁcient. Alternatively, the size of the equation sys-

tem used in the zkSNARK, i.e., the quadratic arith-

metic program (QAP), can be signiﬁcantly reduced

by generating a single proof at the end of the compu-

tation, showing the optimality of the announced win-

ning bid with respect to the deﬁned ranking function.

The proof can be deﬁned as simple as shown in the

following listing, where matching holds the match-

ing score of all bidders and prices_rec are a list of

all reciprocals of the prices submitted. The weights

deﬁned by the buyer are w_l and w_p, cf. also Eq. (1).

res is the output truth value which is 1 if and only if

no bid is ranked better than the winner.

1 res = 1

2 for l , p _ r e c in zi p ( matchings ,

3 pr i c es _rec ) :

4 score = w_l * l + w _p * p_ m in * p_rec

5 re s *= ( score >= s_min )

6 res = a u ct i on . g et _pu b li c _ o u t p u t ( res )

This type of proof turned out to be very efﬁcient and

the measurements in Table 3 show that all steps in

proof generation are extremely practical and are even

far below the times needed by the MPC system to

compute the winner.

Table 3: Performance comparison. Times are in seconds.

#bids t

Setup

QAP size t

Prove

veri f

10 0.4 226 0.3 0.02

100 3.6 2206 2.1 0.6

1000 22.3 22006 18.7 6.6

10000 186 220006 160 65

The same performance can be achieved if the win-

ning bid is not the very best but among a predeﬁned

threshold or at a particular place, i.e., like in the Vick-

rey auction. This variation can be achieved by count-

ing the number of bids above a threshold and option-

ally also below, which results in the same running

time as above.

Fixpoint Operations. To work with the quotient

method as shown above, division and ﬁxpoint oper-

ations are needed. Implementing this within the MPC

component would have had a signiﬁcant impact on

the performance and drastically limited the number

of bids which can be handled in reasonable time. We

therefore compute the reciprocal in the pre-processing

step at the producer and send it (together with the bid)

as input to the MPC system. To ensure end-to-end

veriﬁcation, we then also have to generate a proof that

the reciprocal was computed correctly, but this intro-

duces only minimal overhead. In our implementation

clients submit the price in integer and ﬁxpoint repre-

sentation together with the reciprocal and the result-

ing error term. This results in a very simple and ef-

ﬁcient proof computed on the producer side and even

less work for the MPC phase, because computation

of reciprocals would consume substantial resources.

The additional check necessary to prove consistency

of ﬁxpoint representation with price value is shown in

the listing below, where the res is 1 if and only if the

multiplication of the price p_fxp with the reciprocal

p_rec corrected by the error term p_err equals 1 and

the error term given by the representation is within the

allowed bound.

1 res = (( p _ f x p * p_rec + p_err ) == 1)

2 res *= ( s _ e r r * fxp m u l _ <= s_fxp )

zkSNARKs. As discussed in Section 3 a marketplace

for outsourcing manufacturing tasks requires a very

ﬂexible way to compare offers and match producers.

zkSNARKs lack in this respect, because they require

the circuits to be proved to be ﬁxed during the setup

phase. We circumvent this downside by integrating

two mechanisms: subroutines and reconﬁgurable cir-

cuits.

Subroutines. On the one hand, we use the properties

of adaptive zkSNARKs to also enable subroutines, as

already introduced in (Veeningen, 2017). Subroutines

are built by committing to their input and output and

therefore interconnect these modules to a larger cir-

cuit. This approach also provides the ﬁrst level of

reconﬁguration and reuse. Existing circuits can be

reused without any additional setup call and rewired

at runtime by using the according commitments as

wiring mechanism to enforce correctness of signals

along the computation chain. Figure 3 shows the main

structure used in our framework which the blocks be-

ing subroutines.

Figure 3: Internal structure of the proof generation.

Reconﬁgurable Circuits. Additionally to the de-

scribed subroutines we also incorporated universal

A Privacy-Preserving Auction Platform with Public Veriﬁability for Smart Manufacturing

645

circuits. They are general purpose computing blocks

which can be reconﬁgured at runtime without calling

setup routines. The concept has been inspired by MI-

RAGE (Kosba and et al., 2020) but integrated with the

subroutine mechanism, which is well suited for this.

In particular, to assure consistent use of signals within

the universal circuit the necessary additional permu-

tation and consistency check was realized as subrou-

tine. A dedicated subroutine was designed which does

all checks and was compared to the integrated ap-

proach of MIRAGE. For our implementation we re-

quired only a simpliﬁed version of the ﬁrst opcode

presented in the paper, because we did not need any

binary operations. The most interesting part four our

work was to understand the impact of the size of the

universal circuit on the proof generation time and to

compare the performance of the original approach in

mirage to our new way of integrating the permutation

and consistency checks.

Permutation and consistency check are performed

on public input li and private input zi which is part

of interface commitment for the universal circuit. Af-

ter calculation of sorted indices si the permutation

check scores p1 and p2 are calculated. Additionally,

the consistency checking score s is also calculated

and both necessary conditions for a successful check

are combined into the proof, i.e., assert p1 = p2 and

s = 0, which assures intermediary signals connect-

ing gates are consisten, which assures intermediary

signals connecting gates are consistent.

1 p1 = 1

2 p2 = 1

3 for i in r a n g e ( len ( zi ) ) :

4 p1 *= r2 - ( zi [ i ]+ r1 * l1 [ i ] )

5 p2 *= r2 - ( zi [ si [ i ] ] + r1 * l1 [ si [ 0 ] ] )

6 res = ( p1 == p2 )

7 s = 0

8 for i in r a n g e (1 , l en ( z1 ) ) :

9 s +=

10 (1 - ( l1 [ si [ i ] ] - l1 [ si [i -1 ] ] ) ) *

11 ( z1 [ si [ i ]] - z1 [ si [ i -1]])

12 res *= ( s == 0)

Generally, the use of commitments to intermedi-

ary results in circuits increases the size of the proof

as well as prooﬁng time. The overhead in size is not

an issue for our use case and veriﬁcation runtime is

typically not a problem at all for marketplaces. The

advantage of not requiring to call setup phase and

generation of additional CRS components is by far

more important in real world applications than the in-

creased size or running time experienced. In Table 4

we show the measured times universal circuit com-

posed of different amount of gates, ranging from 10

gates up to 10000 gates. The implemented opcode for

our conﬁguration consumes 35 equations in the QAP

(20 equations for the logic and 15 equations for the

consistency check) if directly combined in one sub-

routine. The overhead of 21 equations is required for

a minimal benchmarking setup.

Table 4: Performance for universal circuit with integrated

consistency checks. Times are in seconds.

#gates t

setup

Qap size t

prove

veri f

10 0.5 371 0.7 0.02

100 2.5 3521 2.2 0.02

1000 32 35021 38 0.1

10000 307 350021 378 0.9

To further reduce the time for proof generation,

we introduced a second approach for the integration

of the consistency checking mechanism. In particular

we realized the permutation and consistency check as

separate subroutines. This means that during conﬁg-

uration of the universal circuit a commitment to the

secret values is generated. This commitment is then

used together with the public conﬁguration values l

to perform the permutation and consistency check in

a standalone sub-QAP. The measurement results for

this variant is shown in Table 5. There can be seen

that the size for the logical part can be signiﬁcantly re-

duced by about 40% which directly results in reduced

proving times. Interestingly, the size of the QAP

needed to do permutation and consistency checking

is in the same order as the pure uc for our opcode and

leads to similar proving times. This is very convenient

because it naturally supports parallelization and leads

to a reduced overall time although in total about 10%

more equations have to be processed.

Table 5: Performance for uc usage with external consis-

tency check. Times are in seconds.

#gates uc-Qap t

prove

check-Qap t

prove

100 2004 0.8 1804 1.2

1000 20004 18 18004 19

10000 200004 160 180004 180

Overall Complexity. When considering static scor-

ing functions, the overall complexity of an auction is

not dominated by the runtimes given in Table 2 and

Table 3. When aiming for a general marketplace sup-

porting ﬂexible scoring functions, also the runtimes

presented in Table 5 are to be considered, where the

number of gates per bid strongly depends on the com-

plexity of the scoring function and auctioning logic.

For the case of a FPSBA with the scoring function

deﬁned in Eq. (1), two gates per bid are required.

ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy

646

6 CONCLUSION

In this work we showed that simple cryptographi-

cally secured sealed bid auctions are not suitable for

complex application scenarios like markets places in

the manufacturing domain. From the requirements

established together with relevant stakeholders, we

identiﬁed many challenging and partially contradict-

ing objectives which motivated the design of a new

architecture and framework. We combined differ-

ent cryptographic protocols into a framework which

can be used to build advanced data markets with

a new level of ﬂexibility, security and trustworthi-

ness. The framework enables secure and privacy-

preserving price ﬁnding for outsourcing tasks in the

production industry, but also beyond (Schuetz and

et al., 2021). For increased trustworthiness it enables

every participant to publicly verify all steps in the auc-

tion also in a privacy-friendly way. As core crypto-

graphic tools we combined secure multiparty compu-

tation with zero-knowledge proofs of knowledge and

enable a seamless experience for the designer of the

system. To assess the practical performance we im-

plemented a proof of concept and tested various sce-

narios. As our main result we were able to show

that many requirements given could be achieved with

our approach in a single framework and with prac-

tical performance. Furthermore, we also showed that

the proposed framework is suitable to realize complex

use cases in a proof of concept implementation.

In the future, it would be interesting to enable a

feedback mechanism for buyers in the form of a rat-

ing system, which, however, must not countervail the

privacy requirements of producers. Additionally, it

would be interesting to see how to extend our con-

cepts to more generic data processing tasks, e.g.,

statistics or optimization, and how to transfer it to

other domains.

ACKNOWLEDGEMENTS

This work has received funding from the European

Union’s Horizon 2020 research and innovation pro-

gramme under grant agreement No 890456 (SlotMa-

chine) and No 830929 (CyberSec4Europe), and the

Austrian Research Promotion Agency under the Pro-

duction of the Future project FlexProd (871395).

REFERENCES

Andrychowicz, M. and et al. (2014). Secure Multiparty

Computations on Bitcoin. In 2014 IEEE Symposium

on Security and Privacy, pages 443–458. IEEE.

Backes, M. and et al. (2014). ADSNARK: Nearly Practical

and Privacy-Preserving Proofs on Authenticated Data.

Cryptology ePrint Archive, Report 2014/617.

Baum, C., Damg

ard, I., and Orlandi, C. (2014). Publicly

Auditable Secure Multi-Party Computation. pages

175–196. Springer, Cham.

Bentov, I. and Kumaresan, R. (2014). How to Use Bitcoin

to Design Fair Protocols. In Advances in Cryptology

– CRYPTO 2014, pages 421–439.

Blass, E.-O. and Kerschbaum, F. (2018). Strain: A Secure

Auction for Blockchains. In Computer Security, pages

87–110. Springer, Cham.

Bogetoft, P. and et al. (2009). Secure Multiparty Computa-

tion Goes Live. In LNCS, pages 325–343.

Galal, H. S. and Youssef, A. M. (2018). Veriﬁable Sealed-

Bid Auction on the Ethereum Blockchain. Cryptology

ePrint Archive, Report 2018/704.

Galal, H. S. and Youssef, A. M. (2019). Trustee: Full Pri-

vacy Preserving Vickrey Auction on top of Ethereum.

CoRR, abs/1905.0.

Kosba, A. and et al. (2020). MIRAGE: Succinct Arguments

for Randomized Algorithms with Applications to Uni-

versal zk-SNARKs. Cryptology ePrint Archive, Re-

port 2020/278.

Kosba, A. E. and et al. (2016). Hawk: The blockchain

model of cryptography and privacy-preserving smart

contracts. In Security and Privacy, SP 2016, pages

839–858. IEEE Computer Society.

Krenn, S. and Lor

unser, T. (2021). Single-Use Delegatable

Signatures Based on Smart Contracts. In Reinhardt,

D. and M

uller, T., editors, ARES 2021, pages 40:1—-

40:7. ACM.

Kumaresan, R. and Bentov, I. (2016). Amortizing Secure

Computation with Penalties. In ACM SIGSAC, CCS

’16, pages 418–429, New York, NY, USA. Associa-

tion for Computing Machinery.

Kumaresan, R., Vaikuntanathan, V., and Vasudevan, P. N.

(2016). Improvements to Secure Computation with

Penalties. In ACM SIGSAC, Vienna, Austria, October

24-28, 2016, pages 406–417.

Lor

unser, T. and Wohner, F. (2020). Performance Compar-

ison of Two Generic MPC-frameworks with Symmet-

ric Ciphers. In SECRYPT 2020, pages 587–594.

anchez, D. C. (2017). Raziel: Private and veriﬁable smart

contracts on blockchains. IACR Cryptol. ePrint Arch.,

page 878.

Schuetz, C. G. and et al. (2021). A Privacy-Preserving Mar-

ketplace for Air Trafﬁc Flow Management Slot Con-

ﬁguration. In 2021 DASC, pages 1–9.

Veeningen, M. (2017). Pinocchio-Based Adaptive zk-

SNARKs and Secure/Correct Adaptive Function Eval-

uation. pages 21–39. Springer, Cham.

A Privacy-Preserving Auction Platform with Public Veriﬁability for Smart Manufacturing

647