Digital Surface Model Generation with Aerial Surveying System

“LEICA ADS80”

Vojkan Stanojević

, Zlatan Milonjić

, Dejan Đorđević

, Saša Bakrač

1,2 a

, Marko Stojanović

1,2 b

and Zoran Stevanović

Military Geographical Institute, Mije Kovačevića 5, Belgrade, Serbia

Military Academy, University of Defence, Veljka Lukica Kurjaka 33, Belgrade, Serbia

Ministry of Defence Republic of Serbia, Birčaninova 5, Belgrade, Serbia

stojanovicm80@yahoo.com, zoran.stevanovic.steki@gmail.com

Keywords: LiDAR, Digital Surface Models, Algorithms, Pushbroom Scanner, Semi-Global Matching, Orthorectification.

Abstract: The aerial imaging system LiDAR is data collection technology for Digital Surface Models (DSM) and Digital

Elevation Models (DEM). Digital line Pushbroom scanner Leica ADS80 can be used to obtain DSM / DEM

thanks to the recorded material. The data obtained using the ADS80 provide several advantages over LiDAR

results, especially since the generation of orthophotos can be based on the same data set. As a fundamental

approach, the principle of Semi-Global Matching (SGM) it is used, which is suitable for the process of

calculating digital models of high-performance and high-resolution surfaces. This paper presents the SGM

approach during processing images obtained by the ADS80 system, as well as comparing the results obtained

using the LiDAR system - in terms of data processing. A comparative analysis and comparison of SGP and

LiDAR ALS80 HP properties was performed, which is illustrated on a specific example. It has been shown

that SGM can be used as an alternative to the LiDAR system. For certain applications for which it is necessary

to generate a digital model of a high-resolution surface or to make orthophotos - thus saving additional flight

costs - SGM is the priority choice.

1 INTRODUCTION

In the last decade an aerial scanning system known as

LiDAR (Light Detection and Ranging) has been

affirmed as a key technology for obtaining high-

resolution digital surface models (DSM) as well as/or

for obtaining digital elevation models (DEM). At the

same time, there is a growing need to improve the

accuracy and higher resolution of digital surface

models and digital elevation models. The LiDAR

system is usually used to meet the above requirements

for various needs, including obtaining orthophotos.

However, considering the significant cost of

procurement, its use only for orthorectification

purposes is avoided. Taking into account the fact that

the application of the aerial photogrammetric

recording camera ADS80 from Leica Geosystems

provides multiple stereo coverage, the recorded

material can and should be used for photogrammetric

https://orcid.org/0000-0003-0211-3765

https://orcid.org/0000-0002-2193-1483

acquisition of digital surface models. Therefore, in

addition to the LiDAR system intended for data

acquisition, there is a need to develop procedures-

algorithms for generating digital surface models

based on data recorded by the ADS80 line scanner - a

digital camera for aerial photogrammetric recording.

Depending on the size of the pixels in the field

(Ground Sampling Distance - GSD), a high-

resolution DSM is generated, striving to match the

current image resolution. In other words, each point

of generated DSM corresponds to one pixel.

Algorithms that minimize both values and various

constraints at the global level are called global image

matching and are ranked among the best algorithms

in terms of achieving high quality and resolution. The

advantages of these algorithms are the performance

related to the Semi-Global Matching (SGM) principle

developed by Hirschmüller (Hirschmüller, 2008;

Hirschmüller and Bucher, 2010).

Stanojevi

c, V., Milonji

c, Z., Dordevic, D., Bakra

c, S., Stojanovi

c, M. and Stevanovi

c, Z.

Digital Surface Model Generation with Aerial Surveying System “LEICA ADS80”.

DOI: 10.5220/0011026700003185

In Proceedings of the 8th International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2022), pages 107-114

ISBN: 978-989-758-571-5; ISSN: 2184-500X

107

Semi-global matching approximates two-

dimensional, global aggregation of value matching by

a number of one-dimensional value trajectories.

Similar accuracy is still achieved as the application of

full global matching, but much faster - such as by

systematically comparing SGM with local and global

matching algorithms using different value functions

according to Hirschmüller and Scharstein

(Hirschmüller and Scharstein 2007; Szeliski, 2010).

As a result, SGM is further researched and improved

by different researchers for different types of

applications and data sets including aerial

photographs, terrestrial and satellite data or video

sequences.

It has been noticed that SGM meets customers

need for a high-resolution, high-performance digital

surface model. Taking into account the fact that the

SGM principle is well accepted with regard to the

quality of the results, the algorithm is adapted to the

unique properties of the ADS80 line Pushbroom

scanner using the existing software environment, with

a special highly optimized module.

The rest of this paper describes the process of

obtaining a digital surface model based on ADS80

data based on the SGM principle.

2 SEMI-GLOBAL MATCHING

SGM represents an approach to image (Hu at al.,

2015). The essence of the algorithm is in the method

of solving the coincidence or pairing of individual

identical parts of stereo pairs, so that the principle of

SGM is based on computer vision. Images

(snapshots) usually represent a two-dimensional

projection of a three-dimensional world.

2.1 Algorithm

To generate a digital surface model of the expected

accuracy, it is necessary to ensure the redundancy of

the input data, which is achieved thanks to multiple

images with a continuous pushbroom scanning with

100% overlapping. Since it is generated using

stereoscopic images, the DSM is usually represented

by a landscape dome which contains elevation

information about all the details above the surface,

including the tops of buildings in trees (Milonjic et

al., 2016).

Digital system for aerial photogrammetric

recording ADS80 represents the integration of three

technologies into one system for data collection in

digital form:

 Sensor Head (SH82),

 Global Positioning System (GPS) and

 Inertial Navigation System (INS) also known

as Inertial Measurement Unit (IMU).

Figure 1: Display of actual shapes (black), digital surface

model (blue) and digital terrain model (green).

Their combination can determine the coordinates

of points on the earth's surface with high accuracy.

As mentioned, the complete solution for

generating DSM is presented with Leica XPro

software, ie. DSM Extraction module based on Semi-

Global Matching principle.

Computer spatial stereo vision refers to the

registration of data, ie, the capture of images from two

or more cameras that are horizontally spaced from

each other (from different databases). In the case of

the ADS80 digital aerial photogrammetric recording

system, this was achieved by using a Pushbroom line

scanner with three shooting angles: backward - nadir

- forward:

Figure 2: Three different shooting angles.

In this way, it is possible to capture objects from

different angles (each object is captured three times),

so that based on the analysis of similarities and

differences in views, parameters used in computer

vision applications such as the reconstruction of the

original three-dimensional scene can be calculated.

So, each object and scene are recorded three times,

where, at first glance, they are slightly different. By

comparing derived stereo pairs, additional

information about the depth of the scene can be

obtained. The process of obtaining the depth of a

scene from a stereo pair is called space calculation

(Zhang et al., 2017).

GISTAM 2022 - 8th International Conference on Geographical Information Systems Theory, Applications and Management

108

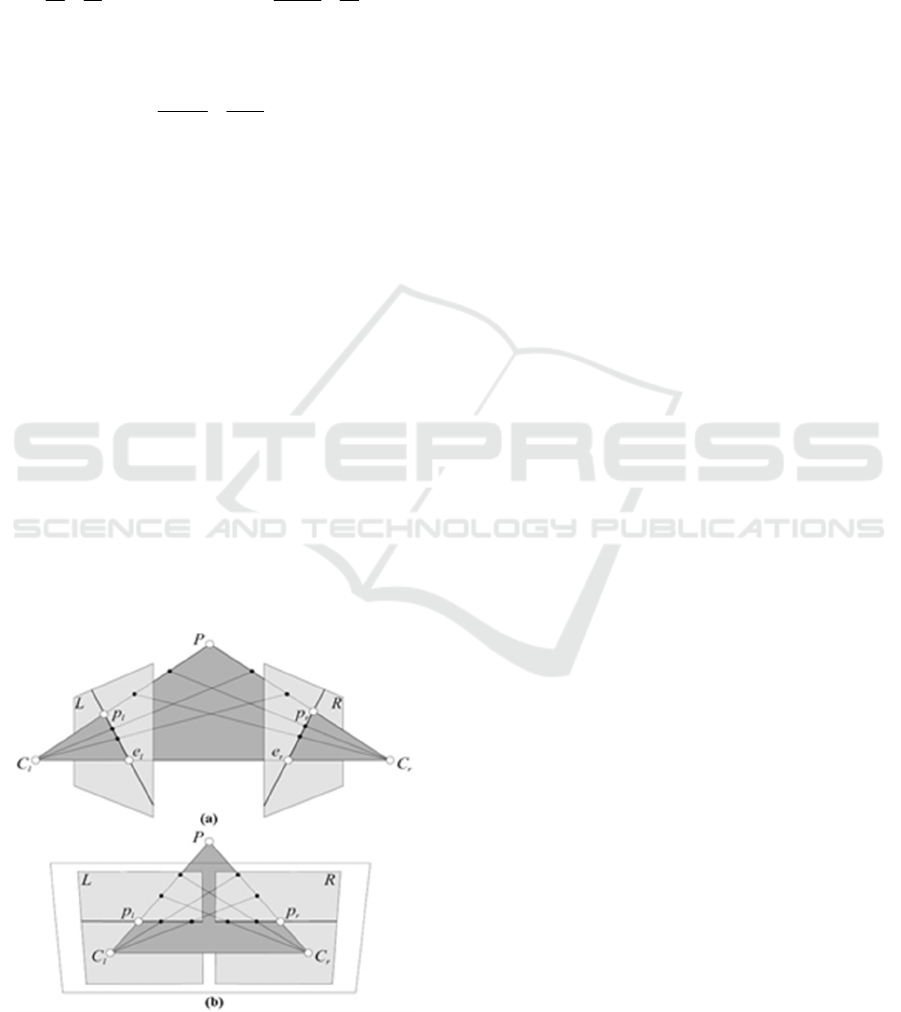
Since the geometry of the camera is known, it can

be concluded that the base distance B = C

- C

constant. Comparing similar triangles, it is possible to

determine the distance to the point (X, Y, Z) of the

object in space or the depth of the object Z by

applying triangulation:



and





)

so that the following equation can be derived:











(2)

The problem of pairing identical points or areas

based on stereo pairs is called the matching problem,

where the procedure is performed by algorithms that

include searching and comparing details. This process

can be greatly simplified by introducing certain

assumptions and limitations into the algorithms. The

assumptions applied in the algorithms of SGM

principles are:

 epipolar correction,

 Uniqueness pairing,

 smooth surface,

 pairing order.

2.1.1 Epipolar Correction

If the camera geometry is known, two-dimensional

search of matching points on images can be

simplified by one-dimensional search by applying

image correction based on epipolar geometry (Wang

et al., 2018).

Figure 3: Epipolar correction.

The epipolar correction of the images is shown in

Figure 3. The optical centres of the two cameras are

represented by points C

and C

, while a point on the

earth's surface is represented by point P. The

projection of that point P in the plane of the left

camera L is at point p

, and in the plane of the right

camera R is at point p

. Any other point located in the

P-C

direction will be projected on the p

-e

direction

called the epipolar projection line p

, where e

represents the epipole where geometrically represents

the image of the optical center of the left camera C

the right camera. The points can be projected in the

same way in the left chamber as in Figure 3a.

Correction of the images is achieved by straightening

the planes L and R so that p

-e

and p

-e

form a line in

the same plane as in the figure 3b:

If the projections of all points are corrected in the

same way, the result is that the matching elements of

the stereo pair are on the same horizontal line, which

allows the matching problem to be simplified and

solved by searching only in the direction of one axis:

= x

+ d while

)

In equation (3), the value d represents the

horizontal shift between two matching elements of

the image called the disparity. By calculating the

disparity for all elements of the image, a disparity

map is obtained.

2.1.2 Uniqueness of Pairing

The details in the stereo pair must be uniquely paired

to allow further processing in computer stereo vision

applications (Ye et al., 2018). This means that an

element of one image is paired with only one element

of another image. If the image contains large regions

of constant intensity (monochrome parts), then within

such a region a point from one image based on the

same intensity can be paired with any point or more

of them within the same region on another image and

vice versa. The biggest problem with stereo pair

pairing occurs due to the fact that certain elements do

not exist on both images. This phenomenon occurs

because not all details are visible for all cameras,

example, some scene parts are sheltered by objects

even though they are visible to another camera

(Figure 4).:

If there is no possibility of matching an element

of the image, the depth for that element cannot be

calculated and it is said that this element is sheltered

for another camera.

Digital Surface Model Generation with Aerial Surveying System “LEICA ADS80”

109

Figure 4: Example of shelter: P

- visible point for both

cameras; P

- sheltered point for the right camera.

Uniqueness pairing is applicable for opaque

surfaces. For transparent surfaces, one element of the

image can have two depths - the depth of the

transparent surface as well as the depth of the surface

in the background that is visible through the

transparent surface. The problem with uniqueness

pairing also occurs with oblique surfaces when during

the left and right projection of the same line there is a

difference in the projection length.

2.1.3 Smooth Surface

In terms of disparity, the smoothness of the objects

surface means that the values of disparities of

adjacent points differ very little. Larger differences in

the value of disparity occur at the boundaries of

objects where depth jumps occur between adjacent

elements of the image. Applying the surface

smoothness assumption increases the efficiency of

the stereopair pairing algorithm.

2.1.4 Pairing Order

If could be noticed two points of the scene P1 and P2,

whereby on one image the projection p1L of the point

P1 is located to the left of the projection p2L of the

point P2, then, in the case of the correct pairing

sequence, on the second image the projection p1R of

the point P1 is located to the left of the projection p2R

of the point P2. The assumption of such a pairing

sequence can be applied to most real scenes, and the

pairing order may change in certain situations.

The easiest way to pair the images is to pair each

element of one image individually with an element of

another image that completely matches or is most

similar to that element in terms of colour and contrast.

This approach, which is based on the pairing of

individual pixels, does not assume the smoothness of

the surfaces, i.e., the continuity of the disparity values

within the surfaces, whereby results with incorrectly

paired elements can be obtained. The cause of errors

when pairing individual pixels is found in a large

number of “candidates” that can match in colour. In

order to overcome this problem, the simplest

implementation of the surface smoothness

assumption is that adjacent pixels have a constant

disparity value. If a “window” is formed (for instance

of the size of 8x8 of image elements), for such a

window can be calculated the sum of the absolute

values of the differences in the intensity of individual

pixels within the window (Sum of Absolute

Differences), the sum of the absolute values of the

squares of the intensity of individual pixels within the

window (Sum of Squared Differences), a normalized

circular-correlation function or some other function

that measures the intensity of a window. By dragging

windows through the left and right images and

comparing the window intensity measure, windows

of the most similar intensity can be paired. Since the

window intensities are compared, it is possible to

calculate the disparity for the whole window, so that

for each element of the image inside the window (x,

y) a three-dimensional structure (x, y, d) is obtained

which is called the Disparity Space Image.

The biggest challenge when pairing certain parts

of the image using windows is choosing the window

size. If the windows are too small, errors may occur

as when pairing individual pixels due to the large

number of pairing candidates. In contrast, if larger

windows are used, the possibility of pairing the wrong

parts is reduced but an error occurs due to local

treatment of smoothness (constant disparity values

within the window) on the oversized part of the

image. The best results of pairing the appropriate

parts of the image using windows are achieved by

applying a variable window size in such a way that

smaller windows are used near depth jumps, while

larger windows are used in places that are further

away.

This value function is most used in semi-global

matching and is called the Mutual Information (MI)

function. MI function depends on entropy H both

from individual images and from the common

entropy of stereo pairs H

1,2

as well:

1,2

(D) –

1,2

)

By using quality images, the value of the common

entropy is small because one image can be predicted

by another, which increases their common

information (MI). All stereo image pairing algorithms

define a pairing consumption function when

performing a process of pairing pixels with common

information. The pairing consumption function is the

GISTAM 2022 - 8th International Conference on Geographical Information Systems Theory, Applications and Management

110

smallest for exact pairing and vice versa, in case of

incorrect pairing the pairing consumption function

increases.

The SGM approach is suitable for generating a

high-resolution DSM which matches the pixel value

in the field (Ground Sample Distance - GSD).

2.2 DSM Generation

The complete solution for generating DSM (Yang et

al., 2020) is presented with the Leica Xpro software

with DSM extraction module:

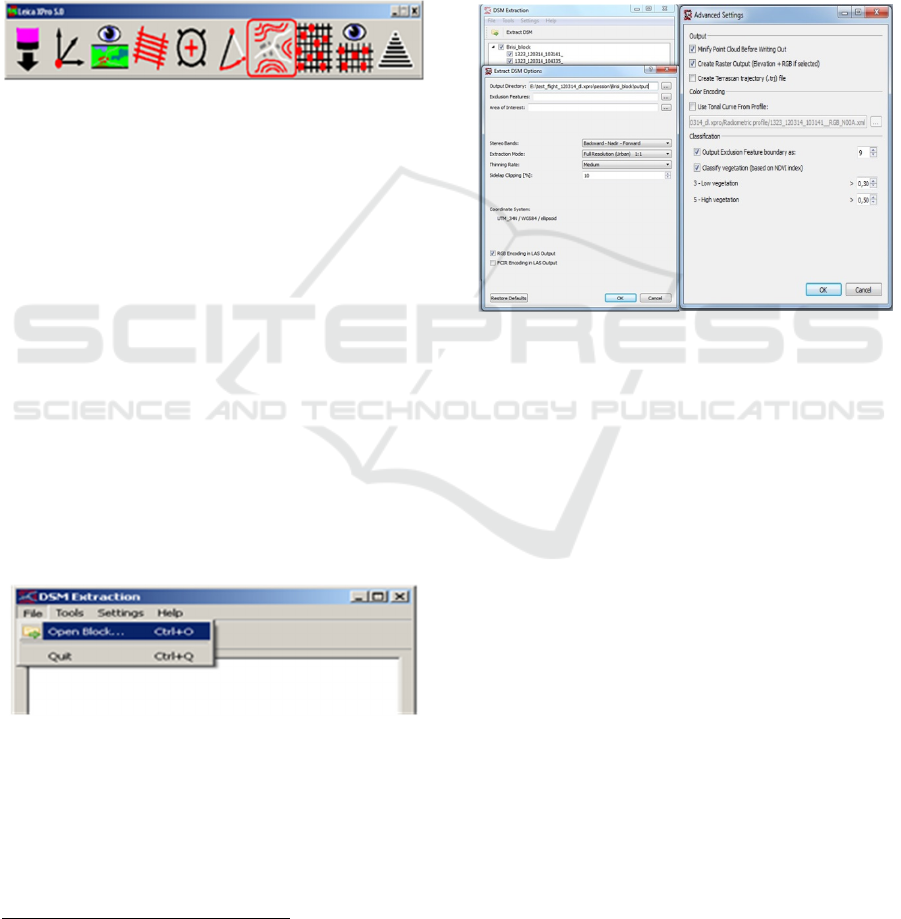
Figure 5: Leica XPro software main window (starting the

DSM Extraction module).

Software Leica Xpro consists of several modules

(applications). Unlike other modules, a module DSM

Extraction takes up the most system memory, so it is

necessary to provide a minimum of 8 gigabytes of

RAM for its operation. Since the significant time is

spent during the process of generating digital surface

models, it is recommended to use a local network of

high-performance computers (High Performance

Computing – HPC).

2.2.1 Input Data - Selection of Blocks and

Recordings Rows

As input data are used ADS L0

images (recording

rows) which are previously inserted in the Block

(module Block Preparation). The images can be of the

panchromatic or infrared spectrum and must have a

pyramidal structure formed.

Figure 6: Opening the block.

2.2.2 Defining Options for DSM Generation

After loading the block and selecting images to

generate DSM, additional adjustment of the digital

surface model extraction was performed:

Georeferenced images without radiometric and geometric

correction (

“raw” images).

 Exclusion features (exclusion from the

generation process) and Area of Interest – for

this step is necessary to provide shape file with

defined coordinate system (*.prj file); if

coordinate system (*.prj) file was not provided,

the module would use automatically WGS84

coordinate system,

 Stereo Bands – selection of stereo coverage,

where the following variants are possible:

- panchromatic: Backward – Nadir – Forward

- panchromatic: Backward – Nadir

- infrared: Backward – Nadir

Figure 7: Defining options for DSM generation.

To generate DSM using two stereo angles is a

significant waste of time but also better coverage of

point cloud. Otherwise, in specific cases (snow, etc.),

the use of the infrared spectrum is recommended

(Yang et al., 2020).

Possible variants of digital surface model

generation:

 Quick – a fast generation method used to gain

insight into the appearance of the model. The time

to generate the model is very short, but the point

density is also low,

 Full Resolution – full resolution - used for

orthorectification purposes. After processing of

the obtained point cloud, it is possible to derive a

digital terrain model (DTM),

 Full Resolution (Urban) – the full resolution for

urban areas is applied for the purposes of

modelling and visualization of urban areas. After

processing of the obtained point cloud, a digital

surface model can be derived (DSM).

There are three different degrees of point filtering:

 Mild – slightly, where the eye is filtered 95 %

points,

Digital Surface Model Generation with Aerial Surveying System “LEICA ADS80”

111

 Medium – mediocre, where the eye is filtered 97

% points and

 Aggressive – aggressively, where the eye is

filtered 99 % points.

After the generation process is completed, the

following results are obtained:

 A file with a dense point cloud in the format LAS

1.2,

 A file with a refined point cloud in the format las

1.2 and

 Processing results (*.log files).

All points contain GPS time of registration

(recording) in Nadir. Depending on need, the outputs

may contain both RGB and FCIR information.

3 RESULTS OF DIGITAL

SURFACE MODEL

GENERATION

The generation of a digital surface model was

performed using aerial survey data of urban area

Slankamen. The set of equipment consists of the Piper

Seneca V aircraft from the American manufacturer

Piper Aircraft and digital aerial photogrammetric

camera ADS80 from the Swiss manufacturer Leica

Geosystems AG, as well as the associated software.

Figure 8: Slankamen - test area.

The digital surface model was generated using the

module DSM Extraction, while data preparation was

done using the appropriate software modules Leica

XPro.

Figure 9: Details of the digital surface model - terrain

profile.

Similar to the Leica ADS80 digital aerial

photogrammetric camera, LiDAR is the result of

integrating three technologies into one system:

 Laser Scanning and Ranging System,

 Global Positioning System – GPS,

 Inertial Navigation System – INS (also known as

Inertial Measurement Unit – IMU) for registering

position changes between two GPS readings, as

well as to determine orientation and

 RGB/NIR (Red-Green-Blue/Near Infrared) high

resolution camera (optional).

Laser scanning represents a method of collecting

digital spatial data. The principle of the LiDAR

system is based on the emission of a high-frequency

laser beam that is partially reflected and partly

absorbed by the ground or other objects in space. The

time difference between the emitted and reflected part

of the laser beam gives the length between the

instrument and the points on the field, while the

coordinates of the points are obtained based on

measured distances, laser beam angles (mirror angles)

and elements of external orientation.

As an example of new technology for generating

digital surface models, the ADS80 system is

increasingly being used as an alternative. Digital

GISTAM 2022 - 8th International Conference on Geographical Information Systems Theory, Applications and Management

112

surface models are generated based on images taken

in ideal conditions (angle of sunlight, avoidance of

clouds and turbulence, ...). The accuracy of DSM

generation depends on the accuracy of aero

triangulation - about 0.5 GSD in position and about

1.5 GSD in height, whereby turbulence during flight

can affect the reduction of image quality; thus, and to

reduce the quality of DSM. Typical high resolution is

up to 5 cm and only top of the surface is measured

with processing time of 10.000-20.000 pts/s.

Considering LiDAR, vertical accuracy is up to 5 cm,

both top and ground of the surface are measured with

processing time of 1.000.000 pts/s.

In both cases, DSMs with many points are

obtained, so additional processing is necessary prior

to usage for certain purposes. The data can be

classified automatically with the aim of determining

a digital terrain model (DTM), urban areas or

vegetation with minimal manual interventions.

Significantly higher points density obtained by

applying the SGM algorithm facilitates the

identification of the data structure and reduces errors

during manual editing. In addition, the advantage in

addition to the possibility of using image matching

procedures is in the geometry of the image and the

continuous processing of the recorded aerial data

(Yang et al., 2020).

4 APPLICATION

 Basic survey (very suitable for orthorectification),

 Storing altitude data for the purposes of making

digital topographic maps,

 Production of digital and analogue orthophoto

plans and maps,

 Solving the problem of construction profiles in the

design of roads and military engineering projects,

 Three-dimensional representations of landforms

and flight simulations,

 Landscape architecture and spatial planning (3D

modelling of urban areas for the needs of spatial

analysis and visualization),

 Surveillance analyses,

 Management of natural resources and

aboveground infrastructure (data can be used for

classification of vegetation, forests, calculation of

forest wood volumes as well as for development

of information system of natural resources),

 Communication planning,

 Determining locations for dams and bridges,

 Hydrological and ecological modelling,

 Hydraulic modelling simulation,

 Analysis of geomorphological parameters

(exposure, slopes, curvature of the terrain),

 Basis for other types of spatial information

(satellite images, thematic maps, etc.)

5 CONCLUSION AND

PERSPECTIVES

This paper presents the acquisition of digital surface

models using the principle based on Semi-Global

Matching (SGM) using data obtained by ADS80

pushbroom scanner, as well as a comparison of

ADS80 and LiDAR systems. It can be concluded that

by applying the SGM principle can be derived very

consistent surface models comparing with the models

derived by the LiDAR sensor and which in the future

do not have to be only an alternative for generating a

digital surface model. Thanks to the high-resolution

images obtained using the ADS80 digital aerial

photogrammetric camera it is possible to derive high

density point clouds. Increasing the points density

reveals details which are difficult for a LiDAR sensor

to detect.

To conclude, it is shown that the obtained digital

surface models using the ADS80 system are an

effective alternative to data obtained using LiDAR

technology, especially in conditions where high

resolution is required. Although both data sets can

generally be used for orthorectification purposes, it is

better to choose the ADS80 system as it is based on

the same data set of identical geometry and resolution

- avoiding the additional cost of a LiDAR system

procurement.

Based on this practical experience and

forthcoming needs, the SGM principle will continue

to be refined and applied in practice. The goal is

definitive integration into the working environment

of the ADS system in the process of generating digital

surface models.

REFERENCES

Hirschmüller, H., Scharstein, D. (2007). Evaluation of Cost

Functions for Stereo Matching. Proc. IEEE Conference

on CVPR, Minneapolis, Minnesota.

Hirschmüller, H. (2008). Stereo Processing by Semiglobal

Matching and Mutual Information. IEEE Transactions

on Pattern Analysis and Machine Intelligence, Vol. 30,

No. 2.

Hirschmüller, H. and Bucher, T. (2010). Evaluation of

Digital Surface Models by Semi-Global Matching,

DGPF, Vienna, Austria.

Digital Surface Model Generation with Aerial Surveying System “LEICA ADS80”

113

Szeliski, R. (2010). The book , Computer Vision:

Algorithms and Applications, Springer.

Hu, H., Rzhanov, Y.;, Hatcher, P.J., Bergeron, R.D.

(2015). Binary adaptive semi-global matching based on

image edges. In Proceedings of the 7th International

Conference on Digital Image Processing, Los Angeles,

CA, USA, 9–10 April.

Milonjić, Z., Đorđević, D., Drobnjak, S. (2016).

Automatska ekstrakcija Digitalnog modela površi

savremenim metodama, SYM-OP-IS 2016

Zhang, Y., Zhang, Y., Mo, D., Zhang, Y., Li, X. (2017).

Direct digital surface model generation by semi-global

vertical, Remote Sens, 9, 214.

Wang, D., Liu, H., Cheng, X. (2018). A Miniature

Binocular Endoscope with Local Feature Matching and

Stereo Matching for 3D Measurement and 3D

Reconstruction, Sensors, 18, 2243.

Ye, L., Wu, B. (2018). Integrated image matching and

segmentation for 3D surface reconstruction in urban

areas, Photogramm. Eng Remote Sens, 84, 135–148.

Yang, W., Li, X., Yang , B., Fu., Y. (2020).

A Novel Stereo Matching Algorithm for Digital

Surface Model (DSM) Generation in Water Areas,

Remote Sensing, 12, 870; doi:10.3390/rs12050870

GISTAM 2022 - 8th International Conference on Geographical Information Systems Theory, Applications and Management

114