Scientific Data Analysis using Neo4j

Victor Chang

, Yeshwanth Kumar Songala

, Qianwen Ariel Xu

and Ben Shaw-Ching Liu

Department of Operations and Information Management, Aston Business School, Aston University, Birmingham, U.K.

Cybersecurity, Information Systems and AI Research Group, School of Computing, Engineering and Digital Technologies,

Teesside University, Middlesbrough, U.K.

Department of Marketing, Lender School of Business Center, Quinnipiac University, Hamden, CT 06518 U.S.A.

bsliu@QU.edu

Keywords: Smart Home, Ethics, Internet of Things, Data Analytics.

Abstract: There is new material regarding Neo4j algorithm questions posed in this report as well as where we did our

due diligence research to resolve them. These results often provide details, including inquiries recorded after

each monitoring period. Initially, a literature review supported the development of an initial data modeling,

which was further provided as experimental analysis. By using Neo4j Graph Database, graph analytics can

provide useful analysis.

1 INTRODUCTION

Due to recent innovations in social networks, e-

commerce and website tracking technology, data

collection and management have become a challenge

for data storage and retrieval. Today, we work with

data that cannot be stored in a traditional database

because it has a huge volume. There is no longer a

consensus that Relational Databases (RDBs) are the

best solution to data complexity problems and volume

growth in terms of scale.

Although RDB designs have shown to be flexible

and scalable in complex systems, Graph Databases

(GDBS) can be better in these two aspects (Pokorny,

2016). A GDB makes use of nodes, margins,

attributes, and graphs for data representation and

makes direct use of database objects seem like data

elements. Data may be connected to the other without

using intermediate folders or data views, and it is

possible to retrieve a highly complex query using a

single connection process in certain situations. Neo4j

is open-source and matches a broad adoption of the

ACID (Atomicity, Consistency, Isolation, and

Durability) properties is a highly scalable open-

source graph database with good interest (Neo4j

Graph Database Platform, 2021a). Under the

https://orcid.org/0000-0002-8012-5852

https://orcid.org/0000-0003-0360-7193

https://orcid.org/0000-0002-2950-9607

"network-driven" approach (there are said to be nodes

with associations and resources in the above), a

network with data items is made up of a web of

connections, like those in the latter. Relationships 1)

have an index annotation, which tells you about all

the interactions among the nodes they belong to; and

2) are expressed as items that have indices to their

respective contexts. When working with semi-

structured data, Neo4j performs as well as it is said to

do. Moreover, applications that tend to be hierarchical

fit well the project models.

2 BACKGROUND WORK

Disruptive technology represents an innovative

method that greatly changes how a customer, an

industry, or a company manages. Disruptive

technologies would sweep across the industries or

conventions it takes the place of due to their

demonstrable superiority (Smith, 2020).

Automobiles, electrical services, and consumer

products could represent different types of disruptive

technology in their respective eras. More recently,

disruptive industries consist of the Internet of Things,

cloud computing, fintech, robotics, and artificial

Chang, V., Songala, Y., Xu, Q. and Liu, B.

Scientiﬁc Data Analysis using Neo4j.

DOI: 10.5220/0011036700003206

In Proceedings of the 4th International Conference on Finance, Economics, Management and IT Business (FEMIB 2022), pages 75-84

ISBN: 978-989-758-567-8; ISSN: 2184-5891

intelligence (AI). Neo4j used in this paper is also one

of the disruptive technologies and has become a

leader in its industry.

Neo4j is disruptive in several ways. First of all, it

provides developers and data scientists with state-of-

the-art techniques to establish intelligent applications

and machine learning workflows in modern society,

which turns out available as a completely managed

cloud service or self-hosted (Neo4j, 2021). Second,

Neo4j is a persistent Java engine and an entirely

transactional database, in which structures can be

reserved based on graphs rather than tables. Third,

Neo4j employs native graph reservation, removing

restrictions of administrating and reserving data in a

highly regulated way. It is regarded as one of the most

prevalent and most used graph databases globally,

applied in various fields such as health, government,

automotive production, and military. Lastly, most

databases currently operate based on a server

accessible through a client library. Neo4j can run in

server and embedded modes depending on data

analysis requirements (Fernandes and Bernardino,

2018).

This paper analyses the dataset with numerous

algorithms in neo4j. We can learn how the

implementation and mutation work on large-scale

data set by these algorithms. The objectives of this

paper are as follows:

1) Finding the interconnectivity between nodes

and relationships using the Louvain

Community Detection Algorithm.

2) Finding the similar sets using the Jaccard

Similarity Algorithm.

3) Measuring the nodes and relationships using

Betweenness Algorithm.

4) Ranking the nodes and entities using Page

Ranking Algorithm.

5) Prioritizing the nodes using the Modularity

Detection Algorithm.

6) Node calculations using the Clustering

Coefficient Algorithm.

7) Finding the shortest path using the All-Pair

Shortest Algorithm.

8) Finding the node embeddings using the

Node2Vec Algorithm.

9) Finding the Strongly Connected components

between the nodes and relationships.

3 DATA MODELLING AND

EXTRACTION

The model involves depicting a disconnected network

of entities and their various attributes and

relationships on a general level, allowing users to

define general and complex structures. According to

its rules, a Graph database query is shaped to address

questions about Neo4j is written to meet the needs

and solve commercial and technological challenges in

the context of both technical and organizational issues

(Haojun et al., 2020).

To better understand the process of designing a

graph data model, let us take a small set of data from

the healthcare domain and walk through each step of

creating a graph data model. The data this paper used

is Safeguarding Adults.

Let us extract our graph database schema

visualization. As shown in Figure 1, this schema

contains nodes and relationships directed to each

node, where the region node and council node act as

constraints. The region node is directed to the council

node, which has a relationship of HAS_COUNCIL.

Suppose we want to find out which council in the

database can query between the region and council

nodes to find out the council sub-nodes. Each sub-

node is then followed by the relationship,

respectively.

The file loaded with headers and created nodes

with labels and properties can also create a graph

entity from a map. All the key/value pairs in the map

will be set as properties on the created relationship of

a node.

4 EXPERIMENTAL ANALYSIS

4.1 Louvain Community Detection

The Louvain community detection algorithm was

proposed in 2008 as a tool for communities that sped

up the analysis of complex networks. It has two

distinct stages: Local Moving Nodes and Aggregation

of the network.

The algorithm begins with a network of N nodes

connected by equal-weighted links (Hu et al., 2016).

During the first loop, the algorithm's operations, the

connections to all the networks are each given a group

to reside in their own nodes. Each node looks at the

neighboring nodes and judges if the one to be

"expanded" has a positive or negative effect on the

node-size community by looking for ways to reduce

the size of the existing node connections (Ryu and

FEMIB 2022 - 4th International Conference on Finance, Economics, Management and IT Business

Kim, 2016). If the increase in group benefit

outweighs the costs and individual gains, the node

would be added to the community. Otherwise, it will

stay in the same place. Any single instance of this

method is carried out on its own on all nodes before

no more change is observed (Ghosh et al., 2018). The

first iteration of the Louvain algorithm has reached a

local maximum as it finds the global maximum

expansion set of elements. If the initial network has

been created, in the first step, the algorithm expands

it by treating communities in the initial network as

nodes. When the second step is over, the algorithm

can then expand the result of the first phase to the new

network. These procedures are performed several

times before the network has no further connections

and optimum modularity has been achieved.

At the same time, the Louvain algorithm locator

tries to identify groups when expanding. It is most

often used because it is easy to use and fast.

As we stated, the Louvain approach is a

community discovery algorithm that detects

populations in networks. It maximizes each

community's modularity score. In contrast,

modularity quantifies the consistency of a node's

assignment to a group.

The output is visualized in Figure 1 below.

4.2 Jaccard Similarity Algorithm

The Jaccard Similarity, a concept introduced by Paul

Jaccard, refers to the measure of relationships

between sets. The formula for Jaccard similarity is

notated below.

The input for this algorithm is a bipartite,

disconnected graph comprising two disconnected sets

of nodes. Each partnership begins with first node

instances and finishes with instances of second-node

or subtypes.

The Node Similarity algorithm compares each

node that has outgoing relationships with another

node of the same kind (Neo4j Graph Database

Platform, 2021c). We collect the outgoing

neighborhood N(n) of each node n, that is, all nodes

m that have a connection from n to m. The algorithm

computes a similarity for each pair n, m, which is the

Jaccard similarity of N(n) and N(m) (m). The

algorithm strips away ambiguity by ignoring nodes

that are no longer in contact and a function of

numerical difficulty (Bie et al., 2020).

The algorithm generates new relationships

between pairs of the first node-set. Relationship

properties are used to express similarity ratings.

Figure 1: Community Detection graph.

Scientiﬁc Data Analysis using Neo4j

The table below shows the results from two nodes

with properties where each node has a similarity of 0.6.

Table 1: The score of each node respective to their labels

and properties.

From

Labels

From

Properties

To Labels

Properties

Similarity

REGION County REGION

Outer

Londo

0.6

REGION County REGION

Unitary

Authority

0.6

REGION County REGION

Metropolitan

District

0.6

REGION

Inner

Londo

REGION

Outer

Londo

0.6

REGION

Metropolitan

District

REGION

Unitary

Authority

0.6

REGION

Outer

Londo

REGION

Inner

Londo

0.6

REGION

Unitary

Authority

REGION

Metropolitan

District

0.6

4.3 Betweenness Centrality

Betweenness centrality measures how much power a

node has on the flow of knowledge in a graph. It is

often used to locate nodes that link two parts of a

graph (Chen et al., 2017).

Brandes' estimated algorithm for unweighted

graphs serves as the foundation for the GDS

implementation. The algorithm finds the unweighted

shortest path between two nodes in a graph (Vu and

Potika, 2020; Petersen et al., 2016). A score is

assigned to each node depending on the amount of

shortest paths that pass through it. Higher

betweenness centrality scores would be assigned to

nodes that often lie on the shortest paths between

other nodes (Roditty and Shapira, 2011; Jha and

Sunitha, 2017). The implementation takes up O(n +

m) space and runs in O(n * m) time, where n is the

number of nodes in the graph and m is the number of

relationships.

Vertices with a strong betweenness greatly impact

a graph due to their power over transferring

knowledge between multiple vertices (Chehreghani,

2014; Xu et al., 2019). This also suggests that

eliminating them from the network would create the

most disturbance of the network's knowledge flow.

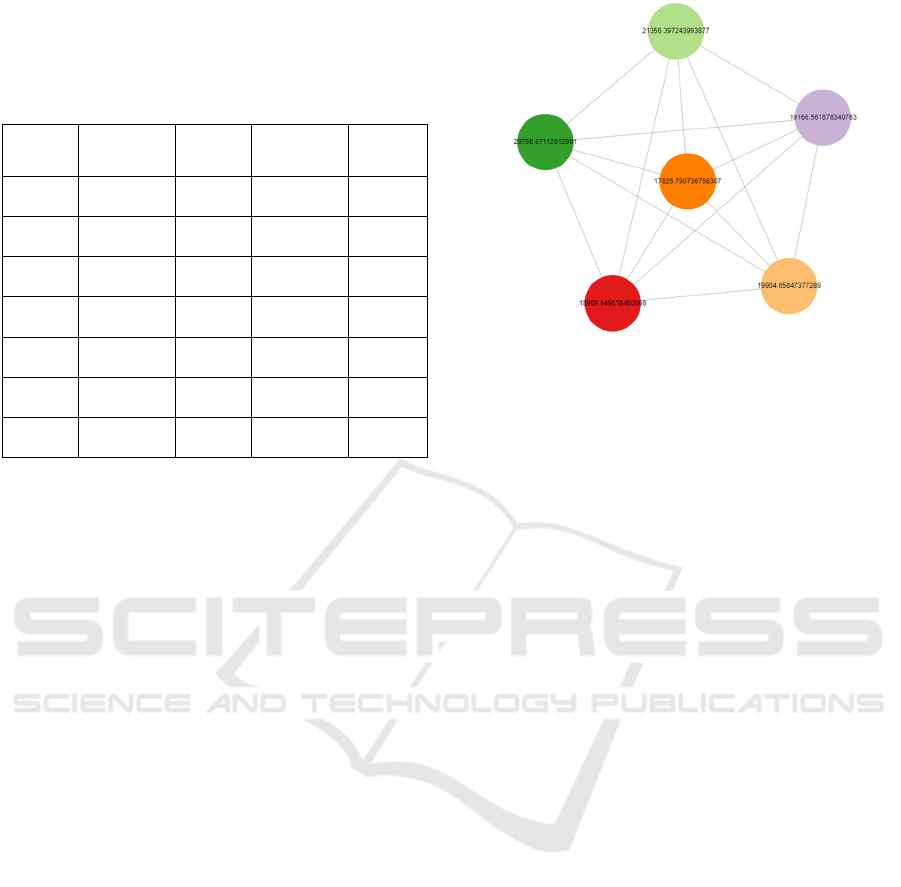
The output is visualized in Figure 2. We can see

the betweenness for each node with a higher rate of

29758.671120 and a lower rate of 17825.790736,

which has multiple connections between every node.

So, the shorted path of the node has a betweenness of

17825.790736.

Figure 2: Betweenness Centrality Graph.

4.4 Page Ranking Algorithm

This post proposes using a random walk algorithm

based on Personalized PageRank (PPR) to

disambiguate NEs. Firstly, a network graph with all

vertices connected was built (Tian, 2010). We run the

PPR algorithm on this graph, with the restriction that

only the highest-scoring candidate should become the

start point of a hop and efficiently filter out potential

noise. Since all candidates but the correct ones are

incorrect and most definitely wrong, limiting the

random walk (Altman and Tennenholtz, 2005).

The following characteristics are shared by our

system: 1) Our solution does not have training model

parameters since it is focused on a random walk

algorithm; 2) our process can better utilize the local

similarities between a region node and a council node,

and we customize the PPR algorithm to only

concentrate on one region node. Each graph node -

(m,c) is a pair of an entity mention m and a candidate

c; each node is given an initial normalized score for

all nodes for the same entity. If the data entry

referring to one of the two nodes includes a path to

the other node, we insert an edge between them.

Assuming that this relationship is bidirectional, we

conclude that this edge is undirected.

PageRank is a more sophisticated method of

calculating the value or significance of nodes than

merely counting the number of relationships that refer

to it (Scarselli et al., 2005). If a backlink comes from

a relevant node, it is assigned a higher weighting than

backlinks from unimportant nodes. A simple relation

from one node to another can be interpreted as a

ballot. However, not only is the number of votes

received by a page deemed significant but so is the

significance or validity of those who cast these votes.

FEMIB 2022 - 4th International Conference on Finance, Economics, Management and IT Business

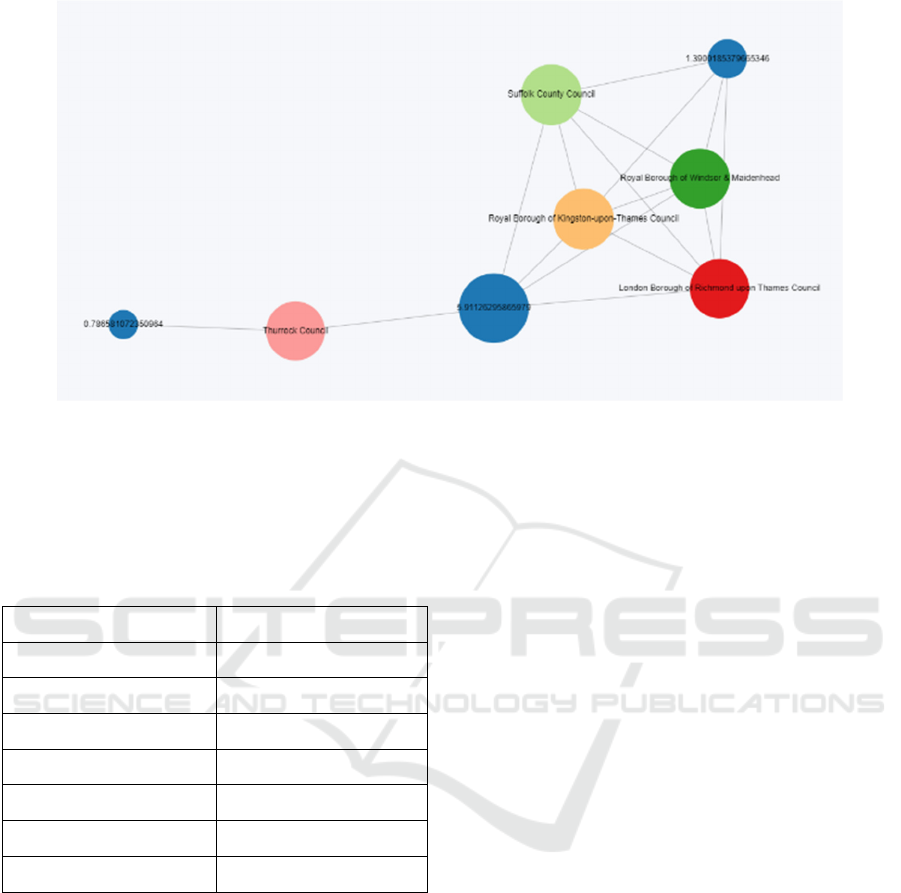
Figure 3: Graph showing the nodes connected with the page ranking.

Table 2 explains the page ranking and score with

the nodes where node(-) with the page rank of 19.633

has the highest score of 0.76244 and the lowest score

of 0.20486 from node 153, page rank of 0.803131.

Table 2: Results showing page ranking on each node.

Node Score

-, 19.633746216818693 0.7624459417182045

5, 1.0142337696277537 0.22313292682520117

76, 0.9820994517707731 0.22233425780285856

15, 1.0167618133593352 0.2222280314700857

85, 1.0115520314662718 0.22214709760622778

10, 0.9114799050759756 0.21350007391301917

153,0.8031313558603869 0.20486719490208813

As shown in Figure 3, the node with a page rank

of 1.390185 is connected to the multiple council

nodes with a higher page rank compared with other

nodes. The edge of the node is the node with a page

rank of 0.7858102, following with the council

Thurrock.

4.5 Modularity Detection Algorithm

When we consider vertices in a neighborhood to be

densely connected, the combination of these vertices

is often referred to as modules or groups. Moreover,

all the members of the same subgroup are like each

other. The challenge of community exploration is to

separate the network into clusters of vertices with

several edges inside clusters and little connections

within them. When evaluating the community

structure of a network, broad usage of modularity is

developed (Sun et al., 2020). This is particularly true

for the connectivity of groups and the extensibility of

modules. Node similarity and community similarity

are used for group identification. Most of the studies

so far are on locating some two connected nodes

based on local knowledge. It means that, while the

similarity of the community’s calculation ignores the

non-to-ness of local structure, it also analyses the

shared components pertinent to global

communication. However, the nature of two nodes'

interconnectedness is a key feature in network

expansion, and the extent of their interconnectedness

should be gauged to make it reliable. Currently, there

is nothing to be found in the literature about such an

approach.

There are also two different approaches to be

considered for finding new similarities between

nodes to expand this capacity to include global and

local communication (Meng et al., 2016). By utilizing

this general networking modularity, the conventional

modularity is established at a hierarchical scale, and

it unrolls each node's network to quantify the degree

of their relationship. Such actions quantify the level

of interconnectedness between the nodes and

subsequently create a group. The proposed similarity-

based generalized modularity measure is simplified to

the traditional one when the similarity matrix is

replaced by an adjacency matrix. It provides a

numerical weight to any partition of a network's

nodes following their communal characteristics. See

Figure 4.

Scientiﬁc Data Analysis using Neo4j

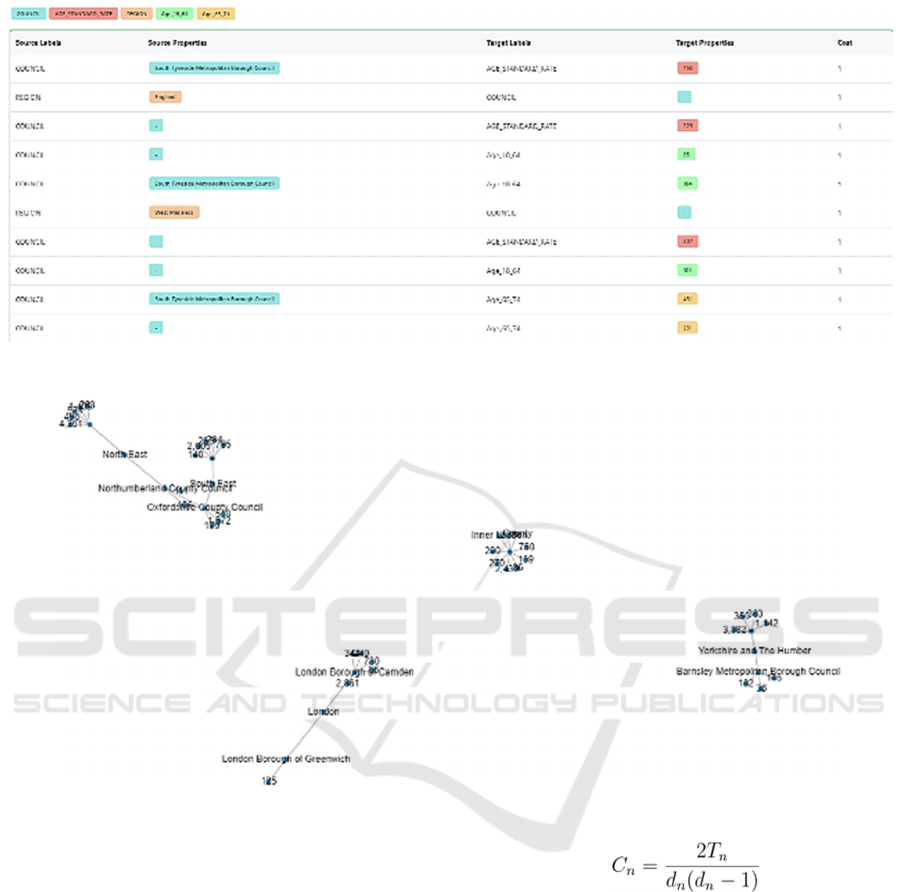
Figure 4: Result showing the modularity optimization on various nodes.

Figure 5: Graph showing the node optimized to respective modularity score.

The above table shows the modularity

optimization of nodes with source labels and

properties targeting other node labels. We can see that

the cost of all nodes was equal to 1. See Figure 5.

4.6 Clustering Coefficient Algorithm

The LCC (or Local Clustering algorithm) computes

the local clustering coefficients for each node in the

graph. The measure of the relatedness between nodes

denoted by the "Cn" of a given node defines the

probability that the nodes' "n" neighbors are also

associated. If we were calculating Cn, we could count

the number of triangles a node is involved in and the

degree of the node, and we have to do n node

calculations. To obtain the local clustering

coefficient, simply calculate the formula for cluster

ID as follows (Liao and Yang, 2017).

Furthermore, the algorithm will obtain the graph's

whole clustering coefficient of magnitude, not just the

isolated values. This is the root mean a square number

of the square of the local coefficients (Zhang et al.,

2014; Wang and Xu, 2019).

This can be done by declaring the gds local

clustering coefficient stream function and

configuring the parameters with node projection and

relationship projection (Qiu et al., 2006; Zhou, 2011).

In the next step, we yield the nodeId as coefficient

with utils of nodeId as node and coefficient ordering

them in the descending order to the integer limit.

FEMIB 2022 - 4th International Conference on Finance, Economics, Management and IT Business

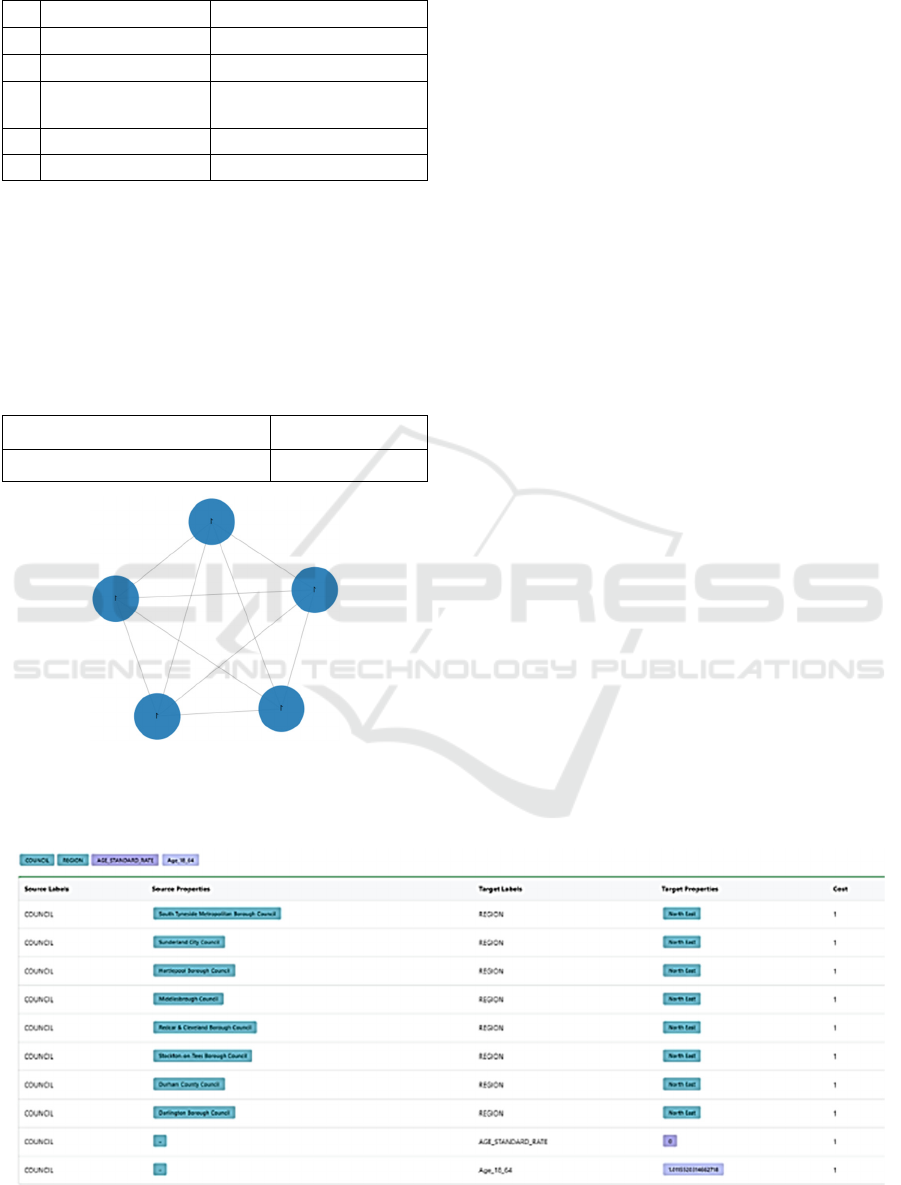
Table 3: Results showing the clustering coefficient.

name localClusteringCoefficient

1 "County" 1.0

2 "Inner London" 1.0

3 "Metropolitan

District"

1.0

4 "Outer London" 1.0

5 "Unitary Authority" 1.0

Now we are finding the average clustering

coefficient and node count by running the stats on

configuration, with the gds local clustering

coefficient function shown in Figure 6.

In the above, we declare the gds local clustering

coefficient function to determine the average

clustering and node count based on the configuration.

Table 4: Showing the average clustering on node count.

averageClusteringCoefficient nodeCount

0.02160838019616753 1408

Figure 6: Results showing the mapping between the

clustering coefficients.

4.7 All Pair Shortest Path

The All-Pairs Shortest Path (APSP) considers all of

the pair weights about the total weight. The runtime

complexity of this algorithm is less than that of using

the Single Source Shortest Path algorithm for a pair

of nodes in the graph (1).

In the scenario, certain nodes are unreachable, and

this means that no shortest path exists between certain

pairs of nodes. Since these nodes represent distinct

natural numbers, the algorithm would return the value

of Infinity, therefore, between them. The expandable

in plain text property does not allow text filtering, so

a value with a word whose text is Infinity (for

example, gds.util.Finite) was implemented to

improve.

Use-cases of All Pair Shortest Path:

1) Usage of the All-Pairs Shortest Path includes

providing services (which also involves

placement of facilities) and certain urban

issues, which would like to identify the

shortest path connecting different locations,

separate sets of locations.

2) Per pair of endpoints in the REWIRE’s

shortest route has an active role in REWIR's

network architecture, resulting in the full

bandwidth and minimum delay network

design.

Using the Neo4j database, we are loading our all-

shortest pair algorithm to configure the data with

node projection and relationship projection. The

parameters are limited to 10 nodes and relation type

with default and orientation directed as Natural. All

the nodes were checked while processing with empty

properties—declaring the start node and end node

null because we must find the shortest distance

between all nodes in the graph in Figure 7.

Figure 7: Results showing the score of the shortest pair with nodes and properties.

Scientiﬁc Data Analysis using Neo4j

4.8 Node Embeddings / Node2Vec

The graph is modeled using random walks in the

algorithm Node2V, a node embedding method that

computes a vector representation of each node in turn

(Moon et al., 2019). Walking through the community

in an unplanned sequence is conducted to provide

information on the general attributes of the place.

Randomly picking out a large number of

neighborhoods and iterating over their activation

patterns (neighborhood vectors) is used to train a

single hidden layer neural network. To help build a

neural network better understand the probability that

a certain node is walking, they are programmed to

look for the possibility of doing so.

The data set we have taken to produce some

dimensional analysis from node to vector. Scaling a

large amount of data can be done in seconds to

visualize the graph. It is useful to embed the nodes

with weight properties and iterations. For each

iteration, the time complexity may be different from

the result of the graph.

4.9 Strongly Connected Components

The Strongly Linked Components (SCC) algorithm

seeks the maximum number of connected nodes in a

guided network. If there is a guided path between

each pair of nodes in a set, it is called a strongly linked

part. It is often used early in the graph analysis phase

to help us understand how our graph is organized

(Neo4j Graph Database Platform, 2021b).

Tarjan described the first linear-time algorithm in

1972, and SCC is one of the earliest graph algorithms.

The depth-first search algorithm is commonly used to

decompose a guided graph into its closely linked

components (Hong et al., 2013).

In our implementation, we only used dynamic

graph data structures with associated lists for the

adjacency array. The graph generator class ensures

that each vertex is stored in a sequential position in

the adjacency list.

The guided graph interface specifies several

approaches to enforce that each node represents a

special data member of a generic form and two nodes

cannot be connected to the graph if they reflect the

same node (Xie and Beerel, 2000; Li et al., 2017). The

second attempt would simply be overlooked, and

several edges between two nodes are not permitted.

An abstract class node, which often acts as an

interface for the vertex of a guided graph, keeps a

record of its descendants and predecessors.

We need to call the gds scc stream function to

configure the node projections and relationship

projections, and we have to yield the node and

community where we collect all nodes and

community returning with the size and community

node limit. See Figure 8.

Figure 8: Strongly connected components Graph.

FEMIB 2022 - 4th International Conference on Finance, Economics, Management and IT Business

5 CONCLUSIONS

Everyone would be able to consider, model, and

forecast complex phenomena such as the distribution

of capital or knowledge, the mechanisms through

which contagions or network failures propagate, and

the impacts on and resiliency of groups using Neo4j

graph algorithms. Since Neo4j combines analytics

and transaction operations in a native graph platform,

you will be able to explore the inner nature of real-

world processes for new discoveries and design and

execute graph-based applications quicker and with

simplified workflows. That is the strength of a well-

planned strategy.

The universe revolves around relationships.

Neo4j graph analytics shows the significance of such

relations using realistic, streamlined graph algorithms

like those described above.

ACKNOWLEDGEMENTS

This work is partly supported by VC Research (VCR

0000153).

REFERENCES

Altman, Alon and Moshe Tennenholtz. (2005). Ranking

systems: the PageRank axioms. In Proceedings of the

6th ACM conference on Electronic commerce (EC '05).

Association for Computing Machinery, New York, NY,

USA, 1–8. DOI:https://doi.org/10.1145/1064009.1064

010

Bie, Zhi, Lufeng Qian, and Jie Ren. (2020). Community

Detection Algorithm based on Node Similarity in

Signed Networks. In 2020 3rd International Conference

on Algorithms, Computing and Artificial Intelligence

(ACAI 2020). Association for Computing Machinery,

New York, NY, USA, Article 52, 1–6. DOI:

https://doi.org/10.1145/3446132.3446184

Chehreghani, M.H. (2014). "An Efficient Algorithm for

Approximate Betweenness Centrality Computation,"

The Computer Journal, vol. 57, no. 9, pp. 1371-1382,

Sept. doi: 10.1093/comjnl/bxu003.

Chen, Dongming, Wei Zhao, Xinyu Huang, Dongqi Wang,

and Yanbin Yan. (2017). Centrality-based bipartite

local community detection algorithm. In Proceedings of

the Second International Conference on Internet of

things, Data and Cloud Computing (ICC '17).

Association for Computing Machinery, New York, NY,

USA, Article 62, 1–8. DOI: https://doi.org/10.1145/

3018896.3018958

Fernandes, D. and J. Bernardino, (2018). “Graph Databases

Comparison: AllegroGraph, ArangoDB, InfiniteGraph,

Neo4J, and OrientDB.” In Proceedings of the 7th

International Conference on Data Science, Technology

and Applications (DATA 2018), pages 373-380, DOI:

10.5220/0006910203730380.

Ghosh, S. et al. (2018)."Distributed Louvain Algorithm for

Graph Community Detection," 2018 IEEE International

Parallel and Distributed Processing Symposium

(IPDPS), pp. 885-895, doi: 10.1109/IPDPS.2018.00

098.

Haojun, F., L. Duan, B. Zhang and L. Jiangzhou, (2020).

"A Collective Entity Linking Method Based on Graph

Embedding Algorithm," 5th International Conference

on Mechanical, Control and Computer Engineering

(ICMCCE), 2020, pp. 1479-1482, doi:

10.1109/ICMCCE51767.2020.00324.

Hong, S., N. C. Rodia and K. Olukotun, (2013). "On fast

parallel detection of strongly connected components

(SCC) in small-world graphs," SC '13: Proceedings of

the International Conference on High Performance

Computing, Networking, Storage and Analysis, pp. 1-

11, doi: 10.1145/2503210.2503246.

Hu, B., Li, W., Huo, X., Ye, L., Minghui, G., & Pei, P.

(2016). Improving Louvain Algorithm for Community

Detection.

Jha, A. K. and N. R. Sunitha,(2017). "Evaluation and

optimization of smart cities using betweenness

centrality," 2017 International Conference on

Algorithms, Methodology, Models and Applications in

Emerging Technologies (ICAMMAET), pp. 1-3, doi:

10.1109/ICAMMAET.2017.8186729.

Li, W. et al., "An expanded distributed algorithm for

dynamic resource allocation over strongly connected

topologies," 2017 3rd IEEE International Conference

on Control Science and Systems Engineering

(ICCSSE), 2017, pp. 500-505, doi:

10.1109/CCSSE.2017.8087983.

Liao, Q and Y. Yang, (2017). "Incremental algorithm based

on wedge sampling for estimating clustering coefficient

with MapReduce," 7 8th IEEE International

Conference on Software Engineering and Service

Science (ICSESS), 2017, pp. 700-703, doi:

10.1109/ICSESS.2017.8343010.

Meng, Xiangfeng, Yunhai Tong, Xinhai Liu, Shuai Zhao,

Xianglin Yang and Shaohua Tan, (2016). "A novel

dynamic community detection algorithm based on

modularity optimization," 7th IEEE International

Conference on Software Engineering and Service

Science (ICSESS), 2016, pp. 72-75, doi:

10.1109/ICSESS.2016.7883018.

Moon, G. E., D. Newman-Griffis, J. Kim, A. Sukumaran-

Rajam, E. Fosler-Lussier and P. Sadayappan, (2019).

"Parallel Data-Local Training for Optimizing

Word2Vec Embeddings for Word and Graph

Embeddings," 2019 IEEE/ACM Workshop on Machine

Learning in High Performance Computing

Environments (MLHPC), pp. 44-55, doi:

10.1109/MLHPC49564.2019.00010.

Neo4j Graph Database Platform. (2021a). Graph Modeling

Guidelines - Developer Guides. [online] Available at:

<https://neo4j.com/developer/guide-data-modeling/>

[Accessed 9 April 2021].

Scientiﬁc Data Analysis using Neo4j

Neo4j Graph Database Platform. (2021b). Strongly

Connected Components - Neo4j Graph Data Science.

[online] Available at: <https://neo4j.com/docs/graph-

data-science/current/algorithms/strongly-connected-

components/> [Accessed 8 May 2021].

Neo4j Graph Database Platform. (2021c). Node Similarity

- Neo4j Graph Data Science. Retrieved 2 May 2021,

from https://neo4j.com/docs/graph-data-science/

current/algorithms/node-similarity/.

Petersen, P. F., H. Jóhannsson and A. H. Nielsen, (2016).

"Unweighted betweenness centrality for critical fault

detection for cascading outage assessment," IEEE

International Energy Conference (ENERGYCON),

2016, pp. 1-6, doi: 10.1109/ENERGYCON.20

16.7513973.

Pokorny, Jaroslav. (2016). Conceptual and Database

Modelling of Graph Databases. In Proceedings of the

20th International Database Engineering &

Applications Symposium (IDEAS '16). Association for

Computing Machinery, New York, NY, USA, 370–

377. DOI: https://doi.org/10.1145/2938503.2938547.

Qui, Baozhi, Chenke Jia and Junyi Shen, (2006). "Local

Outlier Coefficient-Based Clustering Algorithm," 2006

6th World Congress on Intelligent Control and

Automation, pp. 5859-5862, doi: 10.1109/WCICA.20

06.1714201.

Roditty, Liam and Asaf Shapira. (2011). All-pairs shortest

paths with a sublinear additive error. ACM Trans.

Algorithms 7, 4, Article 45 (September), 12 pages.

DOI: https://doi.org/10.1145/2000807.2000813

Ryu, S. and D. Kim, "Quick Community Detection of Big

Graph Data Using Modified Louvain Algorithm," 2016

IEEE 18th International Conference on High

Performance Computing and Communications; IEEE

14th International Conference on Smart City; IEEE 2nd

International Conference on Data Science and Systems

(HPCC/SmartCity/DSS), 2016, pp. 1442-1445, doi:

10.1109/HPCC-SmartCity-DSS.2016.0205

Scarselli, Franco, Sweah Liang Yong, Marco Gori, Markus

Hagenbuchner, Ah Chung Tsoi, and Marco Maggini.

(2005). Graph Neural Networks for Ranking Web

Pages. In <i>Proceedings of the 2005 IEEE/WIC/ACM

International Conference on Web Intelligence</i>

(<i>WI '05</i>). IEEE Computer Society, USA, 666–

672. DOI:https://doi.org/10.1109/WI.2005.67

Smith, T., (2020). "Disruptive Technology", Online.

Available at: https://www.investopedia.com/terms/d/

disruptive-technology.asp (Accessed 18 September

2021)

Sun, H., W. Jie, Z. Wang, H. Wang and S. Ma, (2020).

"Network Representation Learning Guided by Partial

Community Structure," in IEEE Access, vol. 8, pp.

46665-46681, doi: 10.1109/ACCESS.2020.2978517.

Tian, C. (2010). "A kind of algorithm for page ranking

based on classified tree in search engine," 2010

International Conference on Computer Application and

System Modeling (ICCASM 2010), pp. V13-538-V13-

541, doi: 10.1109/ICCASM.2010.5622891.

Vu, J. and K. Potika, (2020). "Edge Betweenness Centrality

on Trees," 2020 Second International Conference on

Transdisciplinary AI (TransAI), pp. 104-107, doi:

10.1109/TransAI49837.2020.00023.

Wang, M. and Y. Xu, (2019). "Research on Label

Propagation Algorithms Based on Clustering

Coefficient," 2019 IEEE 4th International Conference

on Cloud Computing and Big Data Analysis

(ICCCBDA), pp. 348-352, doi:

10.1109/ICCCBDA.2019.8725739.

Xie, Aiguo and P. A. Beerel, (2000). "Implicit enumeration

of strongly connected components and an application to

formal verification," in IEEE Transactions on

Computer-Aided Design of Integrated Circuits and

Systems, vol. 19, no. 10, pp. 1225-1230, Oct. doi:

10.1109/43.875347.

Xu, Z., J. Wu, S. Zhang and S. Du, (2019). "A

Comprehensive Service Function Chainings Mapping

Algorithm Based on Betweenness Centralities," 18th

International Conference on Optical Communications

and Networks (ICOCN), 2019, pp. 1-3, doi:

10.1109/ICOCN.2019.8934384.

Zhang, Rui, Lei Li, Chongming Bao, Lihua Zhou and Bing

Kong, (2014). "The community detection algorithm

based on the node clustering coefficient and the edge

clustering coefficient," Proceeding of the 11th World

Congress on Intelligent Control and Automation, pp.

3240-3245, doi: 10.1109/WCICA.2014.7053250.

Zhou, Qian, (2011). "A recent-biased clustering algorithm

of data stream," 2011 Second International Conference

on Mechanic Automation and Control Engineering, pp.

3803-3808, doi: 10.1109/MACE.2011.5987826.

FEMIB 2022 - 4th International Conference on Finance, Economics, Management and IT Business