Comparison of Free and Open PPP Services for Master-base

Positioning in Geodetic Disadvantaged Areas: Case Study along

the Sirba River in Sub-Saharan Africa

Elena Belcore

, Marco Piras

, Paolo Dabove

, Giovanni Massazza

and Maurizio Rosso

Politecnico di Torino, DIATI, Department of Environment, Land and Infrastructure Engineering, 10129 Turin, Italy

Agenzia Interregionale per Il Fiume Po (AIPo), 10024 Moncalieri, Italy

giovanni.massazza@agenziapo.it

Keywords: Point Positioning, High-precision GNSS, NRTK, Free and Open Services, Sub-Saharan Africa, Niger, Sirba

River, Sahel, Topographic Survey, Geodetic Disadvantaged Areas.

Abstract: The Precise Point Positioning (PPP) is a Global Navigation Satellite System (GNSS technique) for post- and

real-time processing. PPP has recently spread thanks to the high precision and accuracy positioning results

that it provides. Until some years ago, this technique was limited by long sessions of measurements and

professional software to obtain results with centimetre-level precision, using only one GNSS dual frequency

receiver. Nowadays, the PPP technique is well established among GNSS experts, and many software exists

to perform it. The PPP technique uses data from continuously operating reference stations (CORS) to process

the pseudo-range and carrier phase measurements. CORS can also be located very far from the surveyed area.

This makes PPP particularly suitable for GNSS surveys in areas considered disadvantaged for the lack of

geodetic infrastructures, such as CORS and known-coordinates points. Recently, PPP online free and open

tools have been made available by national agencies worldwide. This contribution analyses the PPP online

services as potential solutions for realising GNSS surveys in geodetic disadvantaged areas. Specifically, it

compares two PPP online services: the Canadian Spatial Reference System Precise Point Positioning tool

(CSRS-PPP) and Automatic Precise Positioning Service (APPS). In the analysis, the AUSPOS Online GPS

processing service that applies relative positioning technique based on the closest CORS was considered a

non-PPP post-processing online tool to compare results. Data were collected in South-West Niger, along Sirba

River, 900 km away from the closest CORS and 250 km far from the closest known-coordinates point. The

estimated coordinates' precision was tested for different session lengths (three scenarios of 3 hours, 1 hour,

and 30 minutes) over 17 sessions. Then, the precision was validated by analysing the one-year daily

acquisitions dataset (from CORS). The results revealed precisions and relative accuracies lower than 5 cm for

three hours' sessions. From the analysis of the short stationing sessions (i.e., one hour and half hour) emerged

that APPS provides the most confident solutions. As expected, the less performant service in CORS-

depressed areas is the relative positioning service AUSPOS.

1 INTRODUCTION

In the past years, the Global Navigation Satellite

System (GNSS) has overcome traditional survey

methods, becoming a standard tool in many surveying

sectors. Nowadays, GNSS systems play a lead role in

https://orcid.org/0000-0002-3592-9384

https://orcid.org/0000-0001-8000-2388

https://orcid.org/0000-0001-9646-523X

https://orcid.org/0000-0001-8831-4925

https://orcid.org/0000-0001-9504-0512

data acquisition thanks to the increasing number of

satellites, the low costing, the efficiency, and the

variety of available products. From 2002 forward

(Eren Kamil et al., 2009) Real-Time Kinematic

networks (NRTK) have spread. These networks are

composed of GNSS stations of known coordinates,

Belcore, E., Piras, M., Dabove, P., Massazza, G. and Rosso, M.

Comparison of Free and Open PPP Services for Master-base Positioning in Geodetic Disadvantaged Areas: Case Study along the Sirba River in Sub-Saharan Africa.

DOI: 10.5220/0011039600003185

In Proceedings of the 8th International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2022), pages 37-47

ISBN: 978-989-758-571-5; ISSN: 2184-500X

called Continuously Operating Reference Station

(CORS), and managed by a network software

installed in a control centre. The introduction of the

CORSs has allowed users to collect data using one

GNSS multi-frequency receiver (instead of two). This

is possible thanks to the direct connection between

the CORS and the dual-frequency receiver through

the control centre. Today, a dense world network of

permanent stations to process GNSS data exists (Kim,

Seo and Lee, 2014), and it has revolutionised the data

acquisition modalities (Grejner-Brzezinska et al.,

2007; Rizos, 2007).

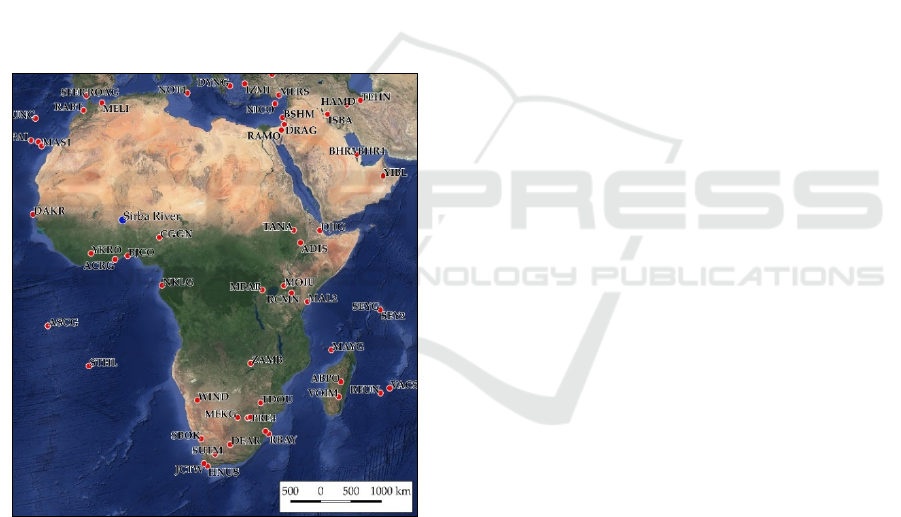
Despite today CORSs cover most of the world's

countries, some areas are still not included in the

network, such as some sub-Saharan countries (Figure

1). Considering the real-time positioning and the

NRTK method, the rover receiver needs to be within

a short distance (less than 60 km) from the reference

stations (Dabove and Manzino, 2014; Dabove, Cina

and Manzino, 2018).

Figure 1: CORS in Africa. The red dots indicate the stations

that provide observations to the International GNSS Service

(IGS), while the blue one is the study area. Data Source:

International GNSS Service (IGS), (https://www.igs.org/).

A short baseline is fundamental to minimise the

distance-dependent errors induced by the

troposphere, the ionosphere, and the orbital errors

(El-Mowafy, 2012, p. ). This specific requirement can

be an obstacle for realising NRTK surveys where

there are no CORS within hundreds of kilometres

(Elmezayen and El-Rabbany, 2019). A possibility to

overcome the lack of CORS is resorting to two GNSS

dual-frequency receivers in the rover-base modality.

This data collection method requires two GNSS

receivers communicating with each other (usually via

radio): one works as "base" or "master" (substituting

the permanent station) and the other as "rover" that

collects the coordinates of the points of interest for

the survey. The coordinates of the base station must

be known.

When a known-coordinates point is not available,

post-processing operations are compulsory to obtain

the base's correct position. One of the most common

post-processing methods is the PPP (Precise Point

Positioning). To perform it, data regarding satellites'

orbits and the ionosphere are needed to process the

pseudo-range and carrier phase measures of GNSS

multi-frequency receivers (Zumberge et al., 1997;

Kouba and Héroux, 2001; Bisnath and Gao, 2009).

These data are collected by permanent stations that

can also be located very far from the surveyed area

(Kouba and Héroux, 2001). In terms of East, North,

and Up components, the PPP can provide centimetre-

level precisions in static mode (Bisnath, Wells and

Dodd, 2003; Pan et al., 2015), if the phase

ambiguities are correctly fixed as integer values (Ge

et al., 2008; Collins and Bisnath, 2011). The PPP

corrections precision is also strictly dependent on the

measurement session's duration (Yigit et al., 2014;

Mohammed et al., 2018). Its effectiveness for the

estimation of the positions has been demonstrated by

several authors, e.g. (Zumberge et al., 1997; Kouba

and Héroux, 2001; Gao and Shen, 2002; Gao, Harima

and Shen, 2003) using precise orbits and satellite

clocks from IGS (Gao and Chen, 2004; IGS, 2019)

and many other providers (Jamieson Marian and

Gillins Daniel T., 2018; Mohammed et al., 2018;

Wang et al., 2018). RTK is a relative positioning

technique based on carrier-phase. A minimum of four

common satellites between the two receivers is

required. Tracking more than four satellites improves

the GPS position solution's precision and allows it to

obtain a sub-centimetre accuracy level. The excellent

accuracy results are also because errors and bias

deriving from the same satellite should be equals.

Thus, shorter is the baseline, and more similar are the

errors. Several error sources affecting positioning

accuracy in GNSS surveys exist (Karaim, Elsheikh

and Noureldin, 2018). Today relative technique

provides better solutions than the PPP technique in

terms of accuracy (Ocalan et al., 2016). The primary

reason is attributable to the lower effects of satellite

orbit errors over relative techniques than the PPP

technique.

Moreover, clock errors can be eliminated in

relative techniques using double differencing phase

GISTAM 2022 - 8th International Conference on Geographical Information Systems Theory, Applications and Management

measurements (Nistor and Buda, 2015). The primary

error sources of PPP (such as ionospheric and

tropospheric delay, clock bias) are usually mitigated

by: i) employing the combinations of dual-frequency

GNSS measurements to eliminate the first-order

ionospheric delay (Kouba and Héroux, 2001; Ocalan

et al., 2016); ii) applying external error correction

data (including satellite orbit and clock corrections);

and iii) modelling the tropospheric delay to correct it.

Since a part of tropospheric delay cannot be

efficiently modelled because of its high variability, it

is estimated (wet component of tropospheric delay).

Precise satellite orbit and clock information are used

to estimate the tropospheric residuals, and associated

gradients with proper stochastic models, which means

that the estimates are constrained by the prior

variance and its propagation value. Thus, PPP

depends on the accuracy level of this information

(Ocalan et al., 2016).

Even if RTK and PPP techniques provide similar

precision and accuracy, they require different setups.

On the one hand, RTK needs a complex configuration

and (generally) expensive equipment, but it rapidly

provides higher accuracy. It is worth remembering

that the base station must be placed very precisely on

a known-coordinate point to achieve high accuracy.

On the other hand, the PPP technique needs a more

straightforward setup, but it has lower accuracy and

longer initial convergence time (Nistor and Buda,

2015; Ocalan et al., 2016). Also, since PPP does not

use a base station, it is not affected by baseline length

bias and can provide full accuracy anywhere in the

world.

Until some years ago, the satellites' data, the

ionosphere information, and the specific software

necessary to perform PPP were not easily obtainable,

and the PPP was limited to few expert users, such as

academia and research institutes. Today, some

commercial and scientific solutions to perform PPP

exist (e.g., Bernese, GIPSY, and GAMIT). Such

software can efficiently perform PPP as long as

infrastructures with adequate computational power,

and skilled users are available. The PPP technique has

raised the attention of academia, industry, and

governments (Bisnath and Gao, 2009). In particular,

the last ones have dedicated specific attention to PPP,

and some of them shared the socio-economic benefits

of PPP with the public, providing ad hoc coordinates

online estimation services (Bisnath and Gao, 2009).

ANADIA 2.0 (Adaptation to climate change, disaster

prevention and agricultural development for food

security) is a project funded by the Italian Agency for

Development Cooperation (AICS) and executed by

Institute of BioEconomy of the National Research

Some governmental research centres provide PPP

online free services. It is sufficient to upload the

GNSS raw data to obtain correct position data from

the services. These free web-solutions for PPP do not

require high computational power or particularly

skilled users, but each service uses its estimation

algorithms. Thus, the results provided can be very

different. The scientific literature provides some

interesting analysis of PPP online services, where

known coordinates points are processed with

different PPP online services (Ozgur Uygur et al.,

2016; Arabi and Nankali, 2017; Oluyori, Ono and

Okiemute, 2019), and the estimated coordinates are

compared with known ones. Nevertheless, few of

these studies analyse data collected in geodetic

disadvantaged areas as far as the authors know.

Indeed, the lack of CORS and known coordinates

points is quite a frequent condition in sub-Saharan

rural areas, strongly affecting topographic surveys.

This work proposes a comparison between two

PPP online free services to correct RTK data

collected through rover-base modality (i.e., static

mode) in low-density CORS areas. The PPP services

considered are the Canadian Spatial Reference

System Precise Point Positioning tool (CSRS-PPP)

and the Automatic Precise Positioning Service

(APPS). A CORS-based post-processing free service

is considered in the analysis as a non-PPP post-

processing online tool: the AUSPOS Online GPS

processing service (AUSPOS). The precision, the

convergence time (meant as the length of time

required to reach centimetre-level positional

solutions), and the structure and condition of the

services' use are analysed in this paper. The data used

for the comparison were collected in February 2018

along Sirba River (southwest Niger) in the framework

of the ANADIA 2.0 project

2 INVESTIGATED SITE AND

SURVEY

ANADIA 2.0 project was born in 2017 to develop an

early warning system against floods and strengthen

the local technicians' competencies on monitoring

and forecasting river floods (Massazza et al., 2019).

Indeed, in the last decades, Sahelian floods have

become a relevant issue due to the ongoing climatic

Council of Italy (IBE-CNR) in partnership with the

Department of Regional and Urban Studies and Planning

of the Politecnico di Torino (DIST) and the National

Directorate for Meteorology of Niger (DMN).

Comparison of Free and Open PPP Services for Master-base Positioning in Geodetic Disadvantaged Areas: Case Study along the Sirba

River in Sub-Saharan Africa

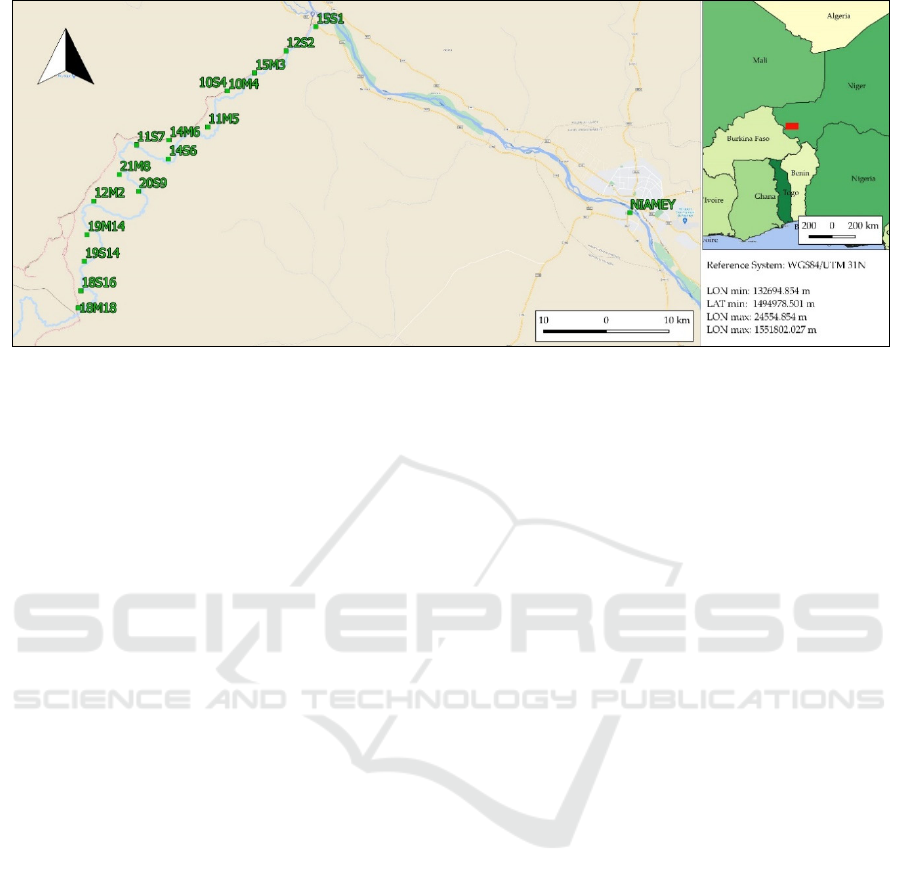
Figure 2: Section of Sirba River interested by the survey. The green squares identify the locations of the stations along the

river. The arrows indicate the flow direction of the rivers. OSM background.

and land use changes (Bigi, Pezzoli and Rosso, 2018;

Tamagnone et al., 2019). In this framework, high-

precision surface and hydraulic numerical models are

necessary as inputs for the development of forecasts

flood models (Massazza et al., 2020; Passerotti et al.,

2020; Tarchiani et al., 2020). Hence, to meet the

project's data requirements, a topographic survey was

carried out on the Middle Niger River Basin's main

tributary, the Sirba River (Figure 2). More than 100

cross-sections were measured along a reach of 108

km (one section per km), and flood-risked-exposed

infrastructures were measured during the dry period

(February) to take advantage of the intermittent flow

(Belcore et al., 2019; Tiepolo et al., 2019). 10 cm

accuracy for the Up component was required

(Massazza et al., 2019).

Despite the closest CORS to the study area are in

Nigeria and Ivory Coast, they are more than 900 km

away from the study region.

As discussed in the previous section, 900 km is a

too large baseline to guarantee centimetre-accuracy.

Besides, the closest known-coordinates points are

around 200 km away from the surveyed area.

Considering these particular conditions, the only

feasible way to collect data was an RTK survey in

master-rover modality with a radio-modem

connection. The PPP technique was used to post-

process the data and to estimate the coordinates of the

base stations. The data were collected with two

STONEX S10 dual-frequency receivers. The master

receiver was placed in 17 different stations along the

Sirba River (Figure 2), and 3,150 points were

measured with the rover receiver. Each master station

acquired data for at least two hours, considering a

session length of 3 hours and 22 minutes as

maximum. GPS, GLONASS, BEIDOU and SBAS

constellations were tracked.

Some instruments malfunctioning, attributed to

the high temperature, slowed down the data

collection. In the hottest hours of the day, the

temperature reached 40°C, and the master receiver

often overheated and stopped the communication

with the rover receiver. The communication

happened via radio using RTCM communication

protocol at 410-470 MHz frequency. The overheating

prevented acquisition longer than 3 hours for most of

the acquisition station. The receivers' communication

was even more limited by the local topography and

the abundant vegetation along the river. Regularly, if

the receivers were more than 3 km away from each

other, the communication stopped. In 9 days, were

measured 103 cross-sections along a river reach of

108 km. The raw measurements were saved in the

Receiver Independent Exchange Format (RINEX)

3.01 version with a sampling rate of 1s.

3 METHODOLOGIES

As previously discussed, two main possible

techniques are available for post-processing

purposes: the phase-based relative solution (base-

rover) or the PPP one (Dabove and Manzino, 2014).

In this paper, we will focus on the PPP approach (Cai

and Gao, 2007). Today many possibilities for

obtaining PPP solutions from online services exist

(Dawidowicz and Krzan, 2014; Dabove, Piras and

Jonah, no date): some of them consider only GPS

constellation (e.g., APPS), other ones also the

GLONASS satellites (CSRS-PPP). To exploit the use

GISTAM 2022 - 8th International Conference on Geographical Information Systems Theory, Applications and Management

of more than two GNSS constellations, the data

collected by the master receiver were stored in

RINEX 3.01 version and then post-processed using

two online PPP free services: 1) The Canadian Spatial

Reference System (CSRS-PPP), and 2) the Automatic

Precise Positioning Service of the Global Differential

GPS System (APPS). Additionally, data were

processed using a relative positioning online service,

3) Online GPS Processing Service (AUSPOS), as a

comparison against PPP technique geodetic

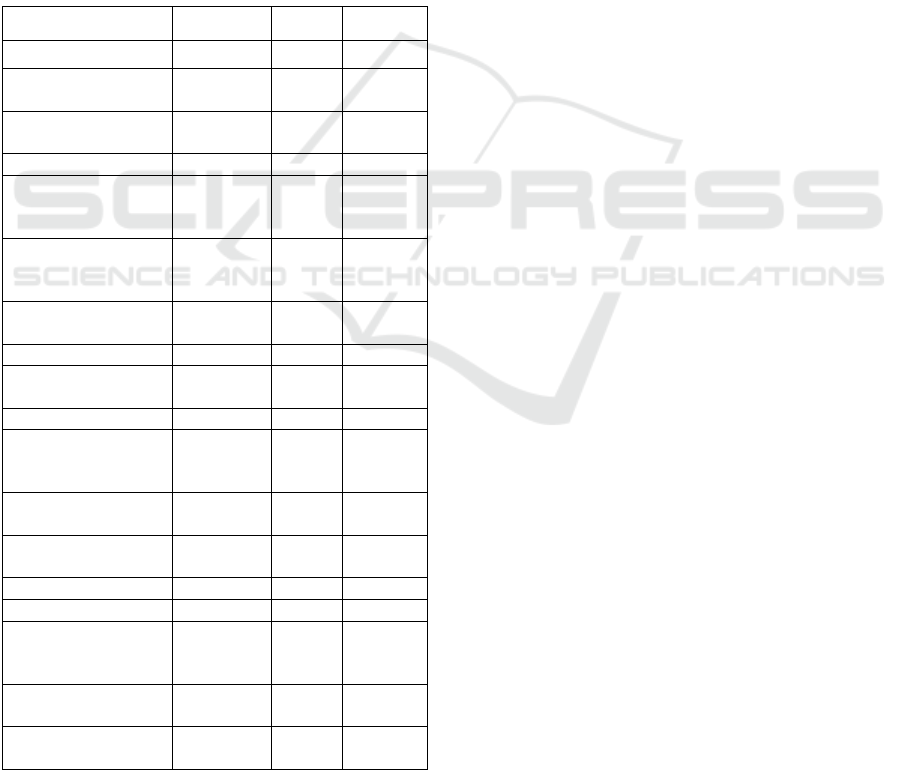
disadvantaged areas. A summed table was created

(Table 1) to recap the functioning of the three

services.

Table 1: Summary of the main characteristics of the three

services at the processing time, calculated on 10Mb file. *If

users submit RINEX V3 file, C2S (code measurement) and

L2S (phase measurement) from L2 frequency will NOT be

accepted.

CSRS-PPP APPS AUSPOS

RINEX version 3.x 2.x 2.11*

Maximum file size 300 Mb 10 Mb

Not

ecifie

Multi-file upload Yes Yes

Only via

FTP

FTP No Yes Yes

Height of the

antenna

Automatica

lly detected

Automa

tically

detecte

Manually

set

User-defined

elevation-dependent

data weighte

No Yes No

User-defined cut-off

No (default

7.5

)

Yes No

L1 code Yes Yes No

Upload of pressure

model

No Yes No

Direct results No Yes No

Compulsory

registration to the

website

Yes No No

Processing time

(

minutes

)

20 3 20

Reference system(s)

of the results

ITRF 2014,

NAD83

ITRF

2014

ITRF

2014

Orthometric hei

hts Yes No Yes

Elaboration re

ort Yes No Yes

Graphic restitution

of the elaboration

statistics

Yes No Yes

Ambiguity

resolution

No Yes Yes

GNSS constellations

rocesse

GPS+GL

ONASS

GPS GPS

4 RESULTS AND DISCUSSION

Before the PPP processing, the RINEX data were pre-

processed. The RINEX files version 3 were converted

into RINEX version 2.11 with the RTKCONV tool

that is part of the open source software RTKLIB

(http://www.rtklib.com/) (Takasu and Yasuda, 2009).

Furthermore, the frequency rate of acquisition was

reduced to one observation every 5 seconds to have

files of less than 10 Mb of size, which is the file size

limit of APPS service. The analysis considers the

precisions of the estimation of each service and the

relative accuracy (measured as the difference

between coordinates) of 17 stations (one station of

ANADIA 2.0 was excluded from this analysis

because it is located outside the Sirba River basin).

The final coordinates have been converted into

WGS84/UTM31N coordinates system. The APPS

service provides the σ values with 68% confidence,

while CSRS-PPP and AUSPOS calculates 95%

uncertainties. Therefore, the uncertainty values of

APPS were related to 2σ confidence. Table 2 shows

the session length and the date of acquisition for each

station. For the analysis, the stations were distributed

in three groups of uniform acquisition length: group

1 less than 2,5 hours acquisition length; group 2

between 2,5 and 3 hours; and group 3 more than 3

hours. The CSRS-PPP values had been taken as a

reference for comparing the services, as shown in

Equations 1 and 2.

ΔCSRS-APPS = EC_ CSRS - EC_APPS

(1)

ΔCSRS-AUSPOS = EC_CSRS – EC_AUSPOS

(2)

Where EC_ CSRS are the North, East and Ellipsoidal

height coordinates of each sample points estimated by

CSRS; EC_ APPS are the North, East and Ellipsoidal

height coordinates of each sample points estimated by

APPS; EC_ AUSPOS are the North, East and

Ellipsoidal height coordinates of each sample point

estimated by AUSPOS.

According to (Choy, Bisnath and Rizos, 2017), a

minimum of one hour is required for the horizontal

solution from a standard PPP static processing to

converge to 5 cm, and approximately 20 minutes are

required for 95% of solutions to reach a horizontal

accuracy of 20 cm (Seepersad and Bisnath, 2014).

Thus, three different scenarios of time acquisition

were created using RTKLIBCONV (Takasu and

Yasuda, 2009) to investigate the effectiveness of the

services on short acquisition time: full acquisition

length, session of one hour, session of half-hour.

Comparison of Free and Open PPP Services for Master-base Positioning in Geodetic Disadvantaged Areas: Case Study along the Sirba

River in Sub-Saharan Africa

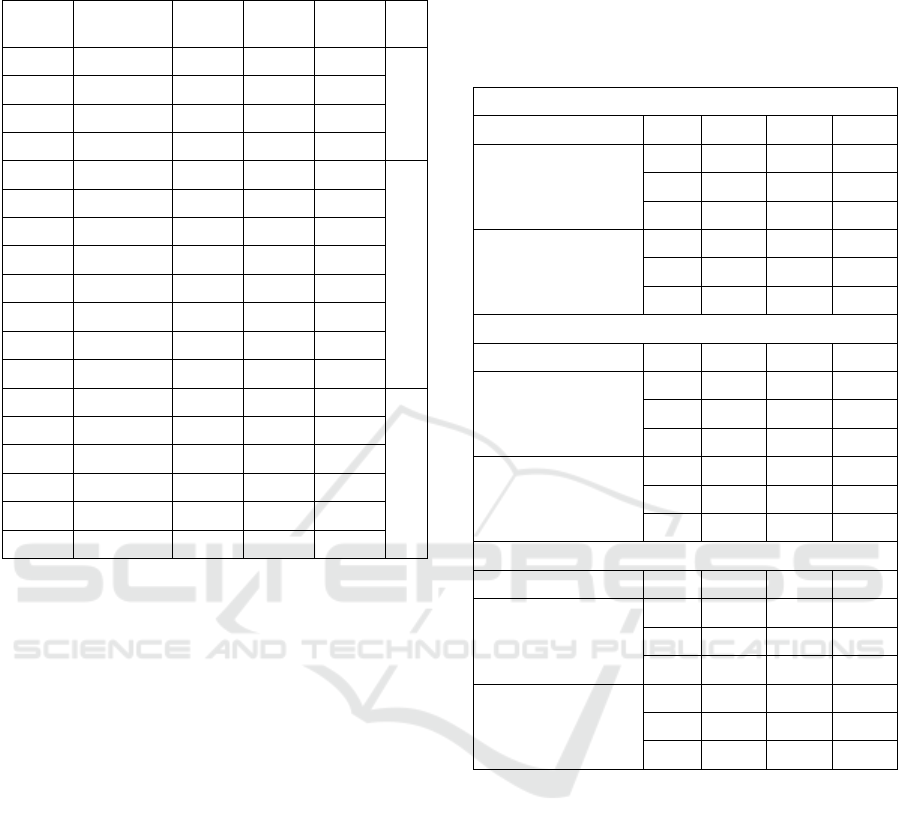
Table 2: Characteristics of the positions of the master

receivers (Stations) analysed. Gr =group, *dd/mm/yyyy.

Station

Date of

acquisition*

Starting

time

Ending

time

Session

length

12S2 12/02/2018 12:58 14:49 01:51

10S4 10/02/2018 15:08 17:07 01:59

14M6 14/02/2018 09:28 11:43 02:15

10M4 10/02/2018 10:28 12:54 02:26

15S1 15/02/2018 13:46 16:30 02:44

19S14 19/01/2018 14:02 16:49 02:47

20S9 20/01/2018 14:24 17:12 02:48

15M3 15/01/2018 08:17 11:08 02:51

18S16 18/01/2018 14:09 17:02 02:53

21M8 21/01/2018 08:53 11:46 02:53

14S6 14/01/2018 13:38 16:35 02:57

11M5 11/01/2018 09:05 12:05 03:00

11S7 11/01/2018 13:43 16:52 03:09

12M2 12/01/2018 08:50 12:05 03:15

18M18 18/01/2018 08:05 11:28 03:23

20M12 20/01/2018 08:45 12:09 03:24

19M14 19/01/2018 08:25 11:52 03:27

12S2 12/02/2018 12:58 14:49 01:51

Table 3 presents the minimum, maximum and

average values of Δ CSRS-APPS and ΔCSRS-

AUSPOS, calculated as illustrated in equations 1 and

2. The difference between CSRS and AUSPOS of the

East component ranges between 0 cm and 6.7 cm,

which is a clue of high data dispersion. This is

particularly evident from distances between the

average values of Groups 1 and 2, and it is a clear

indicator of the importance of stationing time longer

than 1 hour for improved precision. On the contrary,

the North component of the Δ CSRS-AUSPOS (and

the Δ CSRS-APPS too) is more stable.

Regarding the coordinates' precision, the

calculated uncertainties values range from 0.2 cm

(East and North of APPS) to 65 cm (Up component

of AUSPOS). The latter is not representative of the

analysis, and it was interpreted as an exceptional

event; thus, it was excluded in the computation of the

average. For AUSPOS, the distance from the

reference CORS plays a crucial role in estimating the

coordinate. In these analyses, the baseline ranges

from 500 km to 1500 km on 14 reference stations.

From the reference literature, we aspect Root Mean

Square (RMS) values of position errors for baseline

around 500 km less than 4 cm, and less than 6 cm on

each component (E, N, U) for baseline more than

1000 km. Such values are calculated over 24 hours of

acquisitions (Choi, Roh and Lee, 2014). For shorter

stationing time, the precisions fall down.

Table 3: Minimum, Maximum, and Average of the

differences between the coordinates estimated by CSRS,

APPS, and AUSPOS for each station in meters.

Grou

Min Max Av

CSRS-APPS

East 0.007 0.019 0.014

North 0.008 0.014 0.011

Up 0.005 0.046 0.024

CSRS-AUSPOS

East 0.005 0.067 0.023

North 0.001 0.014 0.007

Up 0.018 0.046 0.032

Group 2

Min Max Av

CSRS-APPS

East 0.001 0.026 0.01

North 0.002 0.011 0.006

0.006 0.037 0.016

CSRS-AUSPOS

East 0.001 0.013 0.008

North 0.002 0.005 0.003

0.006 0.069 0.029

Group 3

Min Max Av

CSRS-APPS

East 0.003 0.029 0.016

North 0.001 0.008 0.003

Up 0.001 0.024 0.011

CSRS-AUSPOS

East 0.000 0.04 0.021

North 0.002 0.004 0.003

Up 0.006 0.031 0.017

According to the report produced by Novatel

(NovAtel, 2019), we can expect around 10 cm RMS

values of the position errors for baseline length

between 700 km and 1000 km in 3-hours stationing.

These values reflect our measures: AUSPOS is closed

8 cm on the Up component. For groups 1 and 2, the

uncertainties on the East component estimated by

APPS are slightly lower than those of other services

(Figure 3). Figure 3 shows the graphical analysis of

East, North, and Up components' uncertainties values

and considers the full acquisition time and on 1-hour

acquisition time both. Similarly to Table 3, what

stands out in Figure 3 is the decrease of uncertainties

from Full-time acquisition (Group 3) and one hour

sessions (Group 1). CSRS-PPP and APPS provide the

lowest uncertainties values. With shorter acquisition

time, the confidence levels of CSRS-PPP and APPS

GISTAM 2022 - 8th International Conference on Geographical Information Systems Theory, Applications and Management

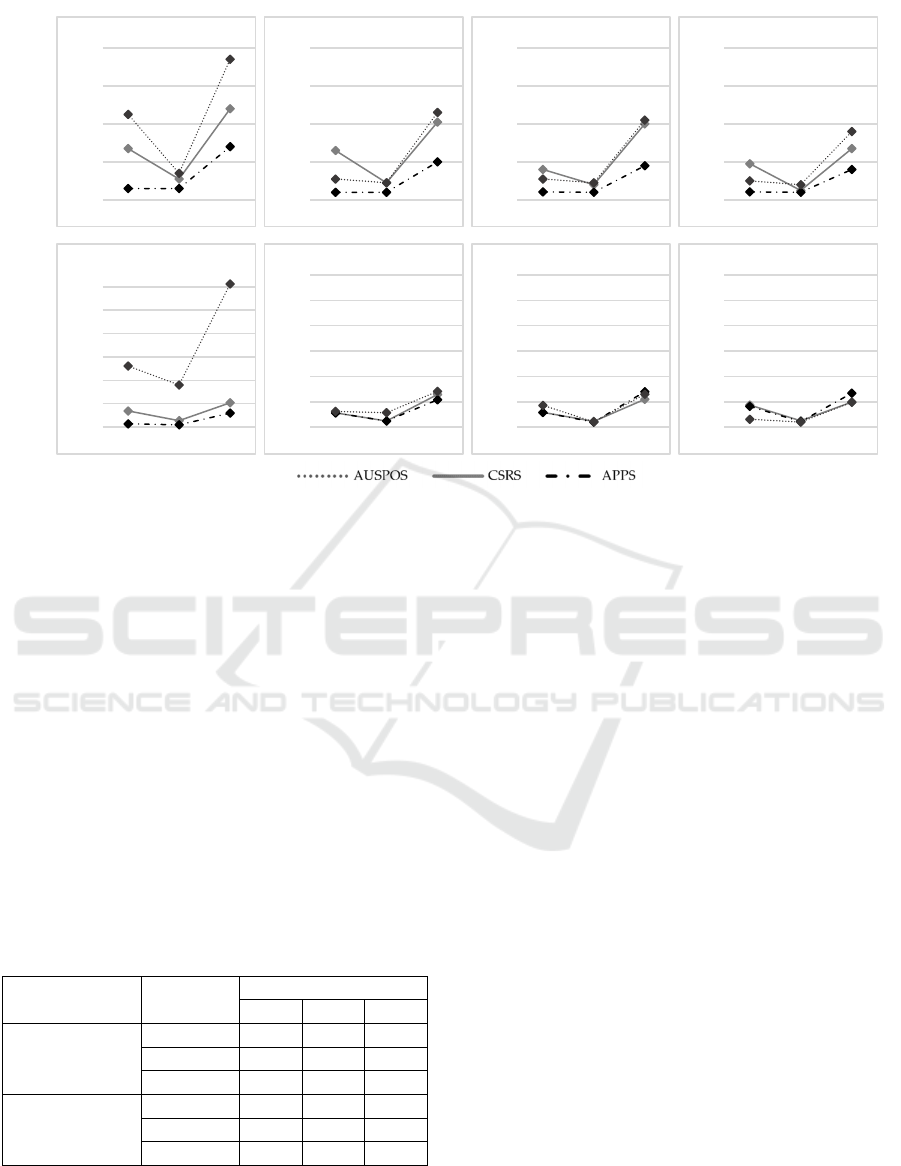
Figure 3: Graphical analysis of the uncertainties values of East, North, and Up coordinates of the three services, obtained

considering the full acquisition time and 1-hour acquisition time.

get closer (Figure 3), while AUSPOS shows similar

trends for some stations (i.e., 19M14 and 18M18) and

very different for other (station 12S2). Table 4 lists

the values of the difference between the coordinates

elaborated with the services on the 1-hour session.

Even if these trends are similar to full-acquisitions, a

significant distance between the Up components can

be observed: the ΔCSRS-APPS peaks 40 cm. For 30

minutes-acquisition time, AUSPOS did not provide

any results because one hour is the minimum

acquisition time required to perform the coordinates

estimations.

Table 4: Minimum, Maximum, and Average of the

difference between the coordinates estimated by CSRS,

APPS, and AUSPOS for each sample station (1hour

session).

Service ITRF

1 h session Δ (m)

Min Max Av

CSRS-APPS

East 0.001 0.140 0.030

North 0.000 0.374 0.032

Up 0.005 0.108 0.044

CSRS-AUSPOS

East 0.006 0.432 0.099

North 0.002 0.403 0.037

Up 0.033 0.286 0.165

CSRS-PPP and APPS's performances peak in the East

component of 20 cm and reach 50 cm on the Up

component.

5 DATA VALIDATION

The lack of CORS in Niger makes it challenging to

test the accuracy of PPP services. Since there are no

known-coordinates points to be used as a reference

for accuracy analysis, only the precision values can

be evaluated. To overcome this major constraint, we

analysed accuracies of post-processing services

solutions in sub-Saharan areas considering the data of

CORS settled in countries close to Niger. CORS at

the same latitude of the study area sought to guarantee

both the mean atmospheric conditions (in terms of

ionospheric and tropospheric delays) and satellite

geometry distribution. Another possible approach

could be to collect 24-hours of data to obtain results

independent of the satellite geometry distribution and

guarantee the solution's convergence, as described in

the literature (Li and Zhang, 2014; Ren et al., 2015).

However, it was impossible to realise long-session

sessions due to weather conditions. Hence, to check

the estimations' accuracy, raw-observations of a

CORS close to the surveyed area were analysed with

online services. The selected CORS was the YKRO

station (Yamoussoukro Tracking Station) in Cote

d'Ivoire (1000 km away from the study area) and part

of the IGS network (Table 5).

Full time session

1 hour session

0,02

0,04

0,06

0,08

EAST NORTH UP

2 SIGMA (m)

Station 12S2

0,02

0,04

0,06

0,08

EAST NORTH UP

2 SIGMA (m)

Station 20S9

0,02

0,04

0,06

0,08

EAST NORTH UP

2 SIGMA (m)

Station 19M14

0,02

0,04

0,06

0,08

EAST NORTH UP

2 SIGMA (m)

Station 18M18

0,00

0,10

0,20

0,30

0,40

0,50

0,60

EAST NORTH UP

2 SIGMA (m)

Station 12S2

0,00

0,10

0,20

0,30

0,40

0,50

0,60

EAST NORTH UP

2 SIGMA (m)

Station 20S9

0,00

0,10

0,20

0,30

0,40

0,50

0,60

EAST NORTH UP

2 SIGMA (m)

Station 19M14

0,00

0,10

0,20

0,30

0,40

0,50

0,60

EAST NORTH UP

2 SIGMA (m)

Station 18M18

Comparison of Free and Open PPP Services for Master-base Positioning in Geodetic Disadvantaged Areas: Case Study along the Sirba

River in Sub-Saharan Africa

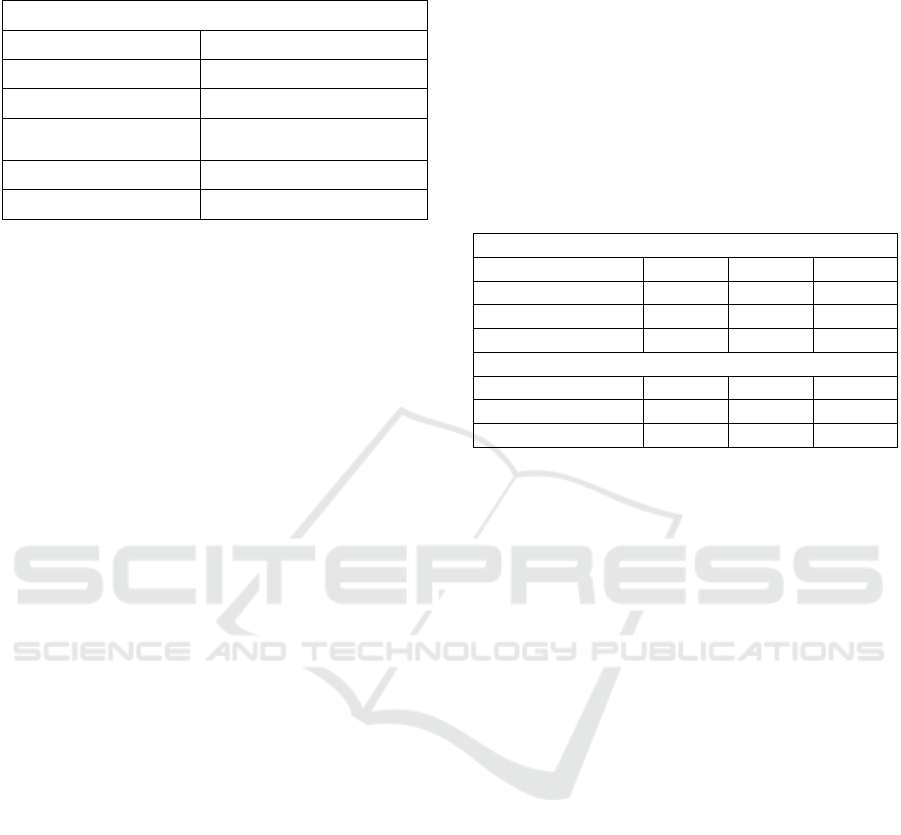
Table 5: Main characteristics of YKRO. Source: IGS

website.

YKRO Site Information

City Yamoussoukro

Country Cote d'Ivoire

Tectonic Plate African Plate

Approximate Position,

DMS

(

ITRF

)

LAT: +06°52' 14.0170"

LON: -05°14' 24.3347"

Elevation ellipsoid (m) 270.263

Date Installed 18-07-1999

This station was chosen because it is the closest

station (considering latitude) to the investigated area,

and it was operative at the time of the survey,

February 2018. Besides, it is away from the sea. This

may ensure atmosphere conditions as similar as

possible to the ones of the study area. YKRO data of

the survey days and the daily observations (12

each month of 2018) were downloaded from the IGS

website. The YKRO dataset was reduced to 3 hours-

lasting RINEX from 14.00 to 17.00, as the average

lasting and representative time for Sirba River

acquisitions. Data were processed with the online free

services and estimated coordinated compared to the

reference ones of the YKRO CORS (Table 5). The

results show relatively constant performances for the

North component and more disperse results for the

East and Up components. Figure 4 compares

summary statistics (average, minimum and maximum

values) for the differences calculated between real

and estimated coordinates. The highest dispersion of

the East component stands out in the graphs. CSRS

and APPS have similar trends on the components,

while AUSPOS, even if it has average values close to

one of the PPP, provided very unstable results for the

Up and East components. The results are never below

the 10 cm on East and North components while

reaching 1 cm on the Up component. According to the

literature, we should obtain precision under 20 cm on

horizontal components in 20 minutes. In our case,

CSRS-PPP did not provide results under 20 cm in a

half-hour on the East component. For example, in 30

minutes of session length, we reach the average

precision of 0.247 cm on the East component. The

results expected for one-hour sessions are

approximately 5 cm on horizontal components. APPS

fits well these general rules on East and North

components, while CSRS only focuses on the North

component.

The coefficients of determination (R

, listed in

Table 6) confirm these observations. They verify that

the estimated East component is the closest to the

three services' reference values, reaching 0.737 for

the CSRS-PPP service. AUSPOS records the most

disperse results in the Up component. In parallel, the

Root Mean Square Error (RMSE) calculated over

each service's estimations' position errors provides a

view of the accuracy. The East component presents

the highest values, followed by the North

components. The lowest-RMSE service is the APPS

for Up component.

Table 6: R

and RMSE values for the 2018 monthly dataset

of solutions provided by the analysed services.

Online Service East North Up

CSRS 0.235 0.737 0.273

AUSPOS 0.070 0.292 0.017

APPS 0.253 0.391 0.104

RMSE (m)

CSRS 0.220 0.193 0.016

AUSPOS 0.221 0.192 0.040

APPS 0.223 0.193 0.015

Regarding YKRO analysis, even if remarkable

differences between the coefficients of determination

are present, the RMSE values differ for no more than

0.2 centimetres in North and East components. The

estimated height above the ellipsoid by APPS is the

closest to the YKRO reference, only 1 mm on average

values from CSRS-PPP. It is worth mentioning that

AUSPOS does not use YKRO for the ambiguity

resolution, but it relies on stations that are placed

approximately 500-2000 km far from YKRO.

CSRS-PPP and APPS use different ephemerids.

This may affect the estimated coordinates because

they strongly affect PPP results, thus in the case of

very different products, we might have different

results. Besides this, the ephemerids seem not to

interfere in the estimations. Additional considerations

in terms of efficiency on the PPP online free services

can be addressed. APPS is the most rapid service in

terms of data processing, and it permits the analysis

of the large quantity of data (industrial application)

uploading the RINEX files on an FTP provided by

JPL (not tested in this contribute). APPS results are

provided directly from the website after a few

seconds (depending on the data size), while AUSPOS

and CSRS send the results via email. Nevertheless,

APPS has an interface that may look complicated for

non-GIPSY-expert users, and it does not provide the

results in a report. CSRS-PPP is very functional

because the upload process is intuitive, and the results

report is easily interpretable.

GISTAM 2022 - 8th International Conference on Geographical Information Systems Theory, Applications and Management

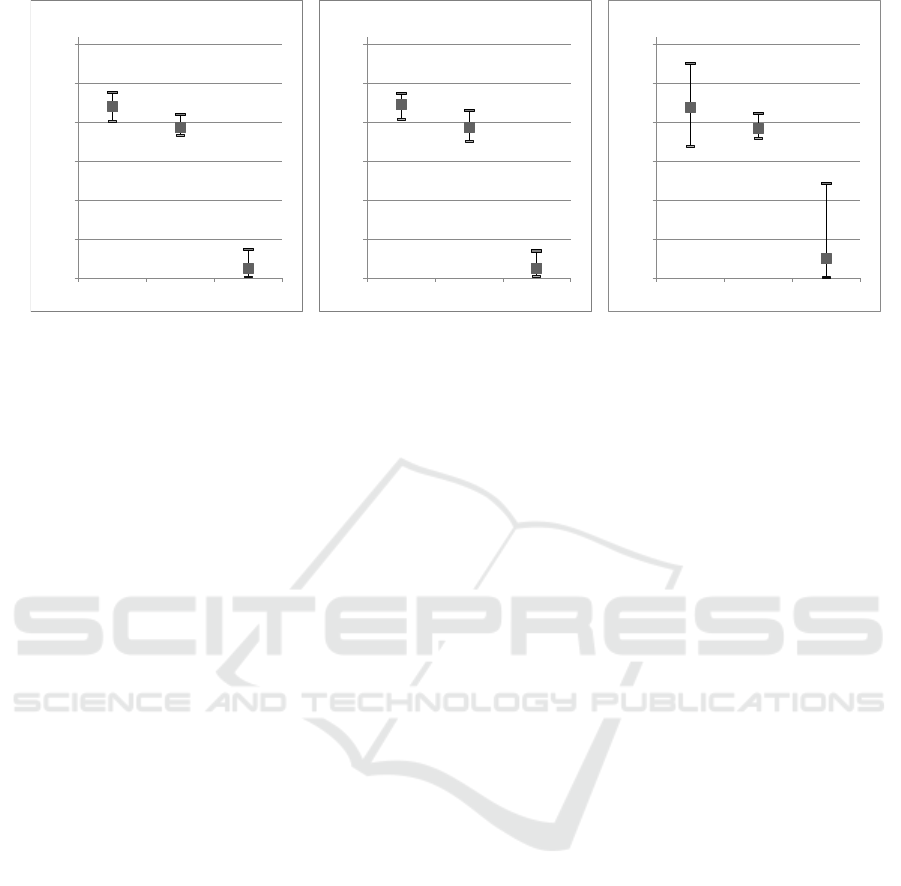
Figure 4: Average (square), Minimum and Maximum values of the difference between the coordinates estimated by online

post-processing services and the real coordinates. Average, minimum, and maximum are calculated for AUSPOS (a), CSRS

(b), and APPS (c).

6 CONCLUSIONS

The present work aimed to assess PPP online services'

quality as free solutions for topography surveys in

critical areas, based on a real case study's

performances. According to the analysis we

performed in the Niger area, the online PPP services

are adequate and useful for the post-processing

corrections of the master-rover RTK survey. The

relative accuracy analysis of the services results in

closer estimations of coordinates between CSRS-PPP

and APPS. CSRS-PPP guarantees satisfying

performances and provides steady results also for

short sessions. As expected, the relative positioning

technique (performed by AUSPOS) provides the least

precise results due to the study area's geodetic

remoteness. Besides this, AUSPOS performance is

quite good, considering the analysis's baseline length

is never below 500 km. These considerations,

confirmed by the one-year YKRO analysis, underline

the PPP technique's excellent reliability in areas

outside the CORS network. It is worth underlining

that it was impossible to perform a complete and

exhaustive statistical analysis since the available

dataset is relatively poor. Moreover, the lack of

known-coordinates points and session's impossibility

for more than 3 hours prevented a proper accuracy

analysis of PPP services by real framework

comparison. The difficulty of data gathering is part of

the criticality of the study area.

Even if the estimated coordinates of YKRO

CORS showed poor accurate results, they were

acceptable for the ANADIA 2.0 project, which

needed at least 10 cm precision on the Up component.

In the framework of the project, the Canadian CSRS-

PPP was used, which, although it is less precise than

APPS, provides detailed statistics regarding the

coordinates' corrections and is user-friendly. The

cross-sections measured were elaborated and

interpolated in a Digital Terrain Model used for the

high-precision hydraulic numerical model. Nigerien

technicians of the ministerial office in charge of

meteorology and water resources have actively

participated in the field surveys, appreciating the

RTK master-rover survey's potential and the PPP

online services. Furthermore, the 18 known and

correct coordinate stations used for surveying could

be the basis for a future local framework. In

conclusion, the PPP has proved to be an effective,

efficient, and economical solution to realise precision

surveys in critical areas such as sub-Saharan ones.

ACKNOWLEDGEMENTS

A special thanks to the National Directorate for

Meteorology of Niger (DMN) and the Directorate for

Hydrology of Niger (DH) for the precious work

realised for the survey. The authors would like to

thank Vieri Tarchiani (IBE-CNR) and Maurizio

Tiepolo (POLITO-DIST) for supporting field

activities during the project.

REFERENCES

Arabi, M. and Nankali, H.R. (2017) ‘Accuracy Assessment

of Online PPP Services in Static Positioning and Zenith

Tropospheric Delay (ZTD) Estimation’, Geospatial

Engineering Journal, 8(3), pp. 59–69. Available at:

0,00

0,05

0,10

0,15

0,20

0,25

0,30

East North Up

a) CSRS-PPP

0,00

0,05

0,10

0,15

0,20

0,25

0,30

East North Up

b) APPS

0,00

0,05

0,10

0,15

0,20

0,25

0,30

East North Up

c) AUSPOS

Comparison of Free and Open PPP Services for Master-base Positioning in Geodetic Disadvantaged Areas: Case Study along the Sirba

River in Sub-Saharan Africa

http://gej.issge.ir/article-1-198-en.html (Accessed: 27

February 2020).

Belcore, E. et al. (2019) ‘Raspberry Pi 3 multispectral low-

cost sensor for UAV-based remote sensing. Case study

in south-west Niger’, ISPRS - International Archives of

the Photogrammetry, Remote Sensing and Spatial

Information Sciences, XLII-2/W13, pp. 207–214.

doi:10.5194/isprs-archives-XLII-2-W13-207-2019.

Bigi, V., Pezzoli, A. and Rosso, M. (2018) ‘Past and Future

Precipitation Trend Analysis for the City of Niamey

(Niger): An Overview’, Climate, 6(3), p. 73.

doi:10.3390/cli6030073.

Bisnath, S. and Gao, Y. (2009) ‘Current State of Precise

Point Positioning and Future Prospects and

Limitations’, in Sideris, M.G. (ed.) Observing our

Changing Earth. Berlin, Heidelberg: Springer

(International Association of Geodesy Symposia), pp.

615–623. doi:10.1007/978-3-540-85426-5_71.

Bisnath, S., Wells, D. and Dodd, D. (2003) ‘Evaluation of

Commercial Carrier-Phase-Based WADGPS Services

for Marine Applications’, in. Proceedings of the 16th

International Technical Meeting of the Satellite

Division of The Institute of Navigation (ION GPS/GNSS

2003), pp. 17–27. Available at: http://www.ion.org/pu

blications/abstract.cfm?jp=p&articleID=5178 (Access

ed: 2 February 2021).

Cai, C. and Gao, Y. (2007) ‘Precise Point Positioning Using

Combined GPS and GLONASS Observations’, Journal

of Global Positioning Systems, 6(1), pp. 13–22.

doi:10.5081/jgps.6.1.13.

Choi, B.-K., Roh, K.-M. and Lee, S.J. (2014) ‘Long

Baseline GPS RTK with Estimating Tropospheric

Delays’, Journal of Positioning, Navigation, and

Timing, 3(3), pp. 123–129. doi:10.11003/JPNT.

2014.3.3.123.

Choy, S., Bisnath, S. and Rizos, C. (2017) ‘Uncovering

common misconceptions in GNSS Precise Point

Positioning and its future prospect’, GPS Solutions,

21(1), pp. 13–22. doi:10.1007/s10291-016-0545-x.

Collins, P. and Bisnath, S. (2011) ‘Issues in Ambiguity

Resolution for Precise Point Positioning’, in.

Proceedings of the 24th International Technical

Meeting of the Satellite Division of The Institute of

Navigation (ION GNSS 2011), pp. 679–687. Available

at: http://www.ion.org/publications/abstract.cfm?jp=p

&articleID=9628 (Accessed: 2 February 2021).

Dabove, P., Cina, A. and Manzino, A.M. (2018) ‘Single-

Frequency Receivers as Permanent Stations in GNSS

Networks: Precision and Accuracy of Positioning in

Mixed Networks’, in Cefalo, R., Zieliński, J.B., and

Barbarella, M. (eds) New Advanced GNSS and 3D

Spatial Techniques. Cham: Springer International

Publishing (Lecture Notes in Geoinformation and

Cartography), pp. 101–109. doi:10.1007/978-3-319-

56218-6_8.

Dabove, P. and Manzino, A.M. (2014) ‘GPS & GLONASS

Mass-Market Receivers: Positioning Performances and

Peculiarities’, Sensors, 14(12), pp. 22159–22179.

doi:10.3390/s141222159.

Dabove, P., Piras, M. and Jonah, K.N. (no date) ‘Statistical

comparison of PPP solution obtained by online post-

processing services’, 2016 IEEE/ION Position,

Location and Navigation Symposium (PLANS)

[Preprint]. Available at: https://www.academia.edu/

25487168/Statistical_comparison_of_PPP_solution_o

btained_by_Online_Post-Processing_Services_30_PU

BLICATIONS_45_CITATIONS_SEE_PROFILE_Sta

tistical_comparison_of_PPP_solution_obtained_by_O

nline_Post-Processing_Services (Accessed: 4

September 2019).

Dawidowicz, K. and Krzan, G. (2014) ‘Coordinate

estimation accuracy of static precise point positioning

using on-line PPP service, a case study’, Acta

Geodaetica et Geophysica, 49(1), pp. 37–55.

doi:10.1007/s40328-013-0038-0.

Elmezayen, A. and El-Rabbany, A. (2019) ‘Precise Point

Positioning Using World’s First Dual-Frequency

GPS/GALILEO Smartphone’, Sensors, 19(11), p.

2593. doi:10.3390/s19112593.

El-Mowafy, A. (2012) ‘Precise Real-Time Positioning

Using Network RTK’, Global Navigation Satellite

Systems: Signal, Theory and Applications [Preprint].

doi:10.5772/29502.

Eren Kamil et al. (2009) ‘Results from a Comprehensive

Global Navigation Satellite System Test in the CORS-

TR Network: Case Study’, Journal of Surveying

Engineering, 135(1), pp. 10–18. doi:10.1061/(ASCE)

0733-9453(2009)135:1(10).

Gao, Y. and Chen, K. (2004) ‘Performance Analysis of

Precise Point Positioning Using Rea-Time Orbit and

Clock Products’, Positioning, 1(8), pp. 0–0. Available

at: http://www.scirp.org/Journal/Paperabs.aspx?paper

id=253 (Accessed: 4 September 2019).

Gao, Y., Harima, K. and Shen, X. (2003) ‘Real-Time

Kinematic Positioning Based on Un-differenced carrier

Phase Data Processing’, in Proceedings of the 2003

National Technical Meeting of The Institute of

Navigation. National Technical Meeting of The

Institute of Navigation, Anaheim, CA, pp. 362–368.

Available at: https://www.ion.org/publications/abstract

.cfm?articleID=3779 (Accessed: 4 September 2019).

Gao, Y. and Shen, X. (2002) ‘A New Method for Carrier-

Phase-Based Precise Point Positioning’, Navigation,

49(2), pp. 109–116. doi:10.1002/j.2161-4296.2002

.tb00260.x.

Ge, M. et al. (2008) ‘Resolution of GPS carrier-phase

ambiguities in Precise Point Positioning (PPP) with

daily observations’, Journal of Geodesy, 82(7), pp.

389–399. doi:10.1007/s00190-007-0187-4.

Grejner-Brzezinska, D.A. et al. (2007) ‘Efficiency and

Reliability of Ambiguity Resolution in Network-Based

Real-Time Kinematic GPS’, Journal of Surveying

Engineering, 133(2), pp. 56–65. doi:10.1061/

(ASCE)0733-9453(2007)133:2(56).

IGS (2019) IGS Network. Available at: http://www

.igs.org/network (Accessed: 4 September 2019).

Jamieson Marian and Gillins Daniel T. (2018)

‘Comparative Analysis of Online Static GNSS

Postprocessing Services’, Journal of Surveying

GISTAM 2022 - 8th International Conference on Geographical Information Systems Theory, Applications and Management

Engineering, 144(4), p. 05018002. doi:10.1061/

(ASCE)SU.1943-5428.0000256.

Karaim, M., Elsheikh, M. and Noureldin, A. (2018) ‘GNSS

Error Sources’, Multifunctional Operation and

Application of GPS [Preprint]. doi:10.5772

/intechopen.75493.

Kim, M., Seo, J. and Lee, J. (2014) ‘A Comprehensive

Method for GNSS Data Quality Determination to

Improve Ionospheric Data Analysis’, Sensors, 14(8),

pp. 14971–14993. doi:10.3390/s140814971.

Kouba, J. and Héroux, P. (2001) ‘Precise Point Positioning

Using IGS Orbit and Clock Products’, GPS Solutions,

5(2), pp. 12–28. doi:10.1007/PL00012883.

Li, P. and Zhang, X. (2014) ‘Integrating GPS and

GLONASS to accelerate convergence and initialization

times of precise point positioning’, GPS Solutions,

18(3), pp. 461–471. doi:10.1007/s10291-013-0345-5.

Massazza, G. et al. (2019) ‘Flood Hazard Scenarios of the

Sirba River (Niger): Evaluation of the Hazard

Thresholds and Flooding Areas’, Water, 11(5), p. 1018.

doi:10.3390/w11051018.

Massazza, G. et al. (2020) ‘Downscaling Regional

Hydrological Forecast for Operational Use in Local

Early Warning: HYPE Models in the Sirba River’,

Water, 12(12), p. 3504. doi:10.3390/w12123504.

Mohammed, J. et al. (2018) ‘An Assessment of the Precise

Products on Static Precise Point Positioning using

Multi-Constellation GNSS’, in. 2018 IEEE/ION

Position, Location and Navigation Symposium

(PLANS), pp. 634–641. Available at: http://www.ion.

org/publications/abstract.cfm?jp=p&articleID=15820 (

Accessed: 2 February 2021).

Nistor, S. and Buda, A.S. (2015) ‘Ambiguity Resolution In

Precise Point Positioning Technique: A Case Study’,

Journal of Applied Engineering Sciences, 5(1), pp. 53–

60. doi:10.1515/jaes-2015-0007.

NovAtel (2019) Resolving Errors, NovAtel. Available at:

https://www.novatel.com/an-introduction-to-gnss/chap

ter-5-resolving-errors/ (Accessed: 12 November 2019).

Ocalan, T. et al. (2016) ‘Accuracy Investigation of PPP

Method Versus Relative Positioning Using Different

Satellite Ephemerides Products Near/Under Forest

Environment’, Earth Sciences Research Journal, 20(4),

pp. D1–D9. doi:10.15446/esrj.v20n4.59496.

Oluyori, P.D., Ono, M.N. and Okiemute, E.S. (2019)

Comparisonof OPUS, CSRS-PPP and MagicGNSS

Online Post-processing Software of DGPS

Observations for Geometric Geoid Modelling in FCT,

Abuja. SSRN Scholarly Paper ID 3373295. Rochester,

NY: Social Science Research Network. Available at:

https://papers.ssrn.com/abstract=3373295 (Accessed:

27 February 2020).

Ozgur Uygur, S. et al. (2016) ‘Accuracy Assessment for

PPP by Comparing Various Online PPP Service

Solutions with Bernese 5.2 Network Solution’, 18, pp.

EPSC2016-7102. Available at: http://adsabs.harvard.

edu/abs/2016EGUGA..18.7102O (Accessed: 27

February 2020).

Pan, S. et al. (2015) ‘Real-Time PPP Based on the Coupling

Estimation of Clock Bias and Orbit Error with

Broadcast Ephemeris’, Sensors, 15(7), pp. 17808–

17826. doi:10.3390/s150717808.

Passerotti, G. et al. (2020) ‘Hydrological Model

Application in the Sirba River: Early Warning System

and GloFAS Improvements’, Water, 12(3), p. 620.

doi:10.3390/w12030620.

Ren, X. et al. (2015) ‘Multi-constellation GNSS precise

point positioning using GPS, GLONASS and BeiDou

in Australia’, in. International Global Navigation

Satellite Systems (IGNSS) Symposium, International

Global Navigation Satellite Systems Society, pp. 1–13.

Available at: https://researchbank.rmit.edu.au/view/r

mit:35729 (Accessed: 4 September 2019).

Rizos, C. (2007) ‘Alternatives to current GPS-RTK

services and some implications for CORS infrastructure

and operations’, GPS Solutions, 3(11), pp. 151–158.

doi:10.1007/s10291-007-0056-x.

Seepersad, G. and Bisnath, S. (2014) ‘Challenges in

Assessing PPP Performance’, Journal of Applied

Geodesy, 8(3), pp. 205–222. doi:10.1515/jag-2014-

0008.

Takasu, T. and Yasuda, A. (2009) ‘Development of the

low-cost RTK-GPS receiver with an open source

program package RTKLIB’, International symposium

on GPS/GNSS, 1, p. 6.

Tamagnone, P. et al. (2019) ‘Hydrology of the Sirba River:

Updating and Analysis of Discharge Time Series’,

Water, 11(1), p. 156. doi:10.3390/w11010156.

Tarchiani, V. et al. (2020) ‘Community and Impact Based

Early Warning System for Flood Risk Preparedness:

The Experience of the Sirba River in Niger’,

Sustainability, 12(5), p. 1802. doi:10.3390/su120

51802.

Tiepolo, M. et al. (2019) ‘Flood Assessment for Risk-

Informed Planning along the Sirba River, Niger’,

Sustainability, 11(15), p. 4003. doi:10.3390/su1115

4003.

Wang, L. et al. (2018) ‘Validation and Assessment of

Multi-GNSS Real-Time Precise Point Positioning in

Simulated Kinematic Mode Using IGS Real-Time

Service’, Remote Sensing, 10(2), p. 337. doi:10.

3390/rs10020337.

Yigit, C.O. et al. (2014) ‘Performance evaluation of short

to long term GPS, GLONASS and GPS/GLONASS

post-processed PPP’, Survey Review, 46(336), pp. 155–

166. doi:10.1179/1752270613Y.0000000068.

Zumberge, J.F. et al. (1997) ‘Precise point positioning for

the efficient and robust analysis of GPS data from large

networks’, Journal of Geophysical Research: Solid

Earth, 102(B3), pp. 5005–5017. doi:10.1029

/96JB03860.

Comparison of Free and Open PPP Services for Master-base Positioning in Geodetic Disadvantaged Areas: Case Study along the Sirba

River in Sub-Saharan Africa