Kolmogorov’s Gate Non-linearity as a Step toward Much Smaller

Artiﬁcial Neural Networks

Stanislav Selitskiy

School of Computer Science and Technology, University of Bedfordshire, Park Square, Luton, LU1 3JU, U.K.

Keywords:

Nonlinearity, Activation Function, Normalization, Dynamic Pruning, Kolmogorov-Arnold, Representation

Theorem.

Abstract:

The deep architecture of today’s behemoth “foundation” Artiﬁcial Neural Network (ANN) models came to be

not only because we can do that utilizing computational capabilities of the underlying hardware. The direction

of the ANN architecture development was also set at the early stages of ANN research by using algorithms and

models that proved to be effective, however limiting. The use of the small set of simple nonlinearity functions

moved ANN architectures in the direction of accumulating many layers to achieve reasonable approximation

in the emulation of the complex processes. Narrow efﬁcient input domain of the activation functions also

led to computational complexities of adding normalization, regularization and back, de-regularization, de-

normalization layers. Such layers do not add any value to the process emulation and break the topology and

memory integrity of the data. We propose to look back at forgotten shallow and wide ANN architecture to

learn what we can use from then at the current state of technology. In particular, we would like to point at the

Kolmogorov-Arnold theorem that has such implications for ANN architectures that, given a wide choice of

volatile activation functions, even 2-layer ANN of O(n) parameters complexity and Ω(n

) relations complexity

(where n is an input dimensionality), may approximate arbitrary non-linear transformation. We investigate the

behaviour of the emulation of such volatile activation function using gated architecture inspired by the LSTM

and GRU type cells, applied to the feed-forward fully connected ANN, on the ﬁnancial time series prediction.

1 INTRODUCTION

Current explosive development in Deep Learning

(DL) resulted in the emergence of the huge “founda-

tion” models with tens (Rosset, 2020), or hundreds

of (Brown et al., 2020), and now trillions of billions

of learnable parameters in view (Fedus et al., 2021),

which could be trained in a reasonable time only with

the use of enormous computational resources of the

leading AI-involved companies. Training of the mod-

els came with the millions of dollars price-tag of the

used energy and generated carbon footprint (Strubell

et al., 2019; Lottick et al., 2019), and stochastic

parroting all kinds of the worst human biases com-

ing from the trash Internet content without creating

any world model. The waste of resources is multi-

plied by the race to produce better, often marginally

better results. The closed private control over such

models raise questions of researchers’ inequality and

stifﬁng and starving alternative directions of the re-

search (Bender et al., 2021; Bommasani et al., 2021).

Despite all the resource waste, these models have

questionable performance in general settings (Schick

and Sch

utze, 2020), and can be not only not beneﬁ-

cial enough, but also harmful (Blodgett and Madaio,

2021).

These very large DL models, a positive re-

branding of which to the “foundation” models boils

to (Field, 2021), are still based on the few handful

basic Artiﬁcial Neural Network (ANN) algorithms

and architectures proposed in the 60s-80s. The sim-

plest and easiest to integrate with algorithms, married

with the accessibility of the computational resources

and data availability, have gotten the most traction.

However, when these brute-force models meet the

next inevitable technical, scale-ability, or cost ceiling,

that event may incentivize both Machine Learning

(ML) researchers and practitioners to revisit the more

complex or complicated to implement algorithms to

overcome limitations and inefﬁciencies of the current

mainstream models.

Widely used in DL, the foundation algorithms in-

clude perceptron implementation as a linear transfor-

mation of the input data via matrix multiplication and

externally added nonlinearity via simple “activation

function” (Rosenblatt, 1958), back-propagation of the

492

Selitskiy, S.

Kolmogorov’s Gate Non-linearity as a Step toward Much Smaller Artiﬁcial Neural Networks.

DOI: 10.5220/0011060700003179

In Proceedings of the 24th International Conference on Enterprise Information Systems (ICEIS 2022) - Volume 1, pages 492-499

ISBN: 978-989-758-569-2; ISSN: 2184-4992

objective function derivative to the learnable parame-

ters of the model (Rumelhart et al., 1986), and gradi-

ent descent-based objective function optimization al-

gorithms. Element-wise matrix manipulation layers

sprung to existence the powerful non-sequential ANN

architectures such as Convolutional Neural Networks

(CNN) (LeCun et al., 1998), and Recurrent Neural

Networks (RNN) (Rumelhart et al., 1986). These ar-

chitectures reduced the high computational demands

of the generic ANN in exchange for specialization

limitations. The algorithms mentioned above also put

limitations and speciﬁc demands on the ANN archi-

tectures and preparation of the input data. In more

detail, we discuss these limitations and demands in

Section 2.

To overcome limitations and problems associated

with the current ANN architectures, alternative ob-

jective or activation functions (Ramachandran et al.,

2017b; Misra, 2020; Naveen, 2021; Ramachandran

et al., 2017a) were introduced, as well as popular reg-

ularization and generalization layers as Batch Nor-

malization (Ioffe and Szegedy, 2015) and Dropout

(Hinton et al., 2012). However, the stochastic nature

of the latter and their inherent conﬂict calls for a ques-

tion of whether we are able to come to more intelli-

gible ways to address these problems. Of course, the

scope of the paper is limited, and in the Section 3 we

discuss only a few aspects of the proposed nonlinear-

ity injection on required ANN architecture depth and

data normalization requirements.

In Section 4 we describe the ﬁnancial time series

data set that was used in computational experiments

of the market index prediction, its partition, normal-

ization schemes, and accuracy metrics. The reason

for choosing a ﬁnancial time series data set for in-

put to illustrate the proposed nonlinearity algorithm

is that dimensionality of the input and output data in

such problems as market index predictions is low, and

it is easy to visualize how the algorithm works.

In the following Section 5, the set up of the com-

putational experiments are described, and in Section 6

results of the experiments performed on existing and

proposed architectures are compared. Section 7 dis-

cusses results, makes conclusions and proposes future

direction of the research.

2 BASIC MACHINE LEARNING

ALGORITHMS AND RELATED

PROBLEMS

In a general deﬁnition, ML task could be viewed as

a ﬁnding of the transformation from an inconvenient

to deal with input space, usually of the higher ba-

sis set cardinality, to a more convenient target space,

such that for each element i represented in the input

space the resulting transformation prediction would

be in the neighbourhood of the element’s represen-

tation in the target space: f : X 7→ Y , where for

∀x

∈ X , ∀y

∈ Y : f (x

) ∈ N

A widely used mathematical space abstraction is

a linear vector space. In such a case, an ML trans-

formation of the input vector x ∈ X ⊂ R

from a m-

dimensional linear space into n-dimensional space Y

can be represented as: f : X ⊂ R

7→ Y ⊂ R

, m > n.

While the target space neighbourhoods and objective

functions are deﬁned via open balls of a radius in

some metric deﬁned over distance function, for ex-

ample Euclidean sum of square errors l = ( f (x) −

( f (x) − y).

In ANN implementation, such a transformation

can be represented as a composite linear transforma-

tion, which can be expressed via multiplication of the

input vector x

by a matrix W

, and non-linear trans-

formation by an activation function a

z = f (x) = a

◦ f

. .. a

◦ f

(x), ∀x ∈ X ⊂ R

(1)

where

= f

) = W

, and a

, for example

ReLU: z

i j

= a

( ˆy

i j

) = ˆy

i j

Out of multiple proposed over the years optimiza-

tion algorithms for ﬁnding parameters of the activa-

tion function a

and linear transformation matrices W

variations gradient descent together with back prop-

agation of the objection function derivative base on

the chain rule

∂l

∂x

∑

∂l

∂y

∂x

became predominately

popular.

The above algorithms greatly simpliﬁed compu-

tation and efﬁciently used available hardware. How-

ever, imposed limitations of the structure of the data

and ANN with which they work efﬁciently. As we can

see above, activation and objective functions must be

differentiable, desirably easy-differentiable, smooth,

monotone, and agree to each other to create low ex-

treme and stable optimization search space (for exam-

ple, that is why cross-entropy is used with softmax or

logistic activation). As a result, the nomenclature of

the practical, general-purpose activation and objective

functions is quite scarce. Separation of the linear and

simple non-linear transformations into distinct layers

also impoverish the simulation ability of the ANN and

naturally pushes architectures into the DL direction to

achieve model complexity via high numbers of layers.

The domain of the input data to the sigmoid ac-

tivation functions, which ensures efﬁcient, or at all

functioning of the learning algorithms, is quite nar-

row. Otherwise, we face either their saturation and

Kolmogorov’s Gate Non-linearity as a Step toward Much Smaller Artiﬁcial Neural Networks

493

problem of “vanishing gradients”, or, especially for

RNN - problem of “gradient explosion” (Kanai et al.,

2017). The former problem must be addressed by

the data normalization, and the latter - by regulariza-

tion. Those computational problems and their compu-

tational solutions may lead to higher-level structural

problems of breaking the topology of the data and in-

troducing unneeded data relations. And then, to battle

artiﬁcially introduced artefacts by normalization and

regularization layers or parameters, we have to add

more layers like Dropout that de-regularizes data di-

mensions and ﬁnd “principal” dimensions that better

“explain” data which allows us to get the desired low-

dimensional problem representation.

3 PROPOSED SOLUTION

Instead of battling the self-inﬂicted wounds described

above, can we try to not introducing them in the ﬁrst

place? To do that, we may want to step back an

look at the general ML problem formulation, which

is quite close to Hilbert’s 13

mathematical problem

of the coming centuries (Hilbert, 1902), which could

be formulated in a loose general way as: for each al-

gebraic (or continuous in a later formulation) func-

tion f : X ⊂ R

7→ R there exists superposition of

the ﬁnite number k of functions φ

: Y

⊂ R

7→ R

such that f (x) =

∑

i=1

), where Y

is a subspace

of X : ∀Y

⊂ X , m ≥ n

≥ 3 (Akashi, 2001).

A. Kolmogorov solved the problem for n ≥ 3, and

then his student V. Arnold extended the solution to

n ≥ 2 in the following form:

f (x) = f (x

, . . . , x

) =

∑

q=0

(

∑

p=1

)) (2)

where Φ

and φ

are continuous R 7→ R functions

(Kolmogorov, 1961).

In application to ANN, Kolmogorov-Arnold su-

perposition theorem could be viewed as a represen-

tation of 2-layer ANN (where inputs to inner func-

tions φ

could be viewed as local perception ﬁelds

of various scale) with dimension speciﬁc nonlineari-

ties built-in into perceptrons (or put before them on

the input channels). The practicality of such ANN,

as a Universal Approximator, was disputed in (Girosi

and Poggio, 1989), in particular, because of the non-

smoothness, hence non-practicality, of the inner φ

functions. However, these objections were rebutted

in (K

urkov

a, 1991). In (Pinkus, 1999) φ

activation

functions are even called ”pathological”.

Adopting and utilizing in practice the

Kolmogorov-Arnold view model of ANN may

require bringing back many of the old ML algorithms

that lost their popularity to the mainstream ones.

However, this discussion would be far above the

scope of this paper. Here, we only touch on the topic

of simulating volatile non-smooth, “pathological”

activation functions, which are not prone to non-

normalization saturation, using gated architecture

inspired by the LSTM (Hochreiter and Schmidhuber,

1997) or GRU (Cho et al., 2014) cells. The use

of gated mechanisms in other ANN architectures

was investigated in (van den Oord et al., 2016)

for image processing CNNs, and in (Kalchbrenner

et al., 2016) for one-dimensional CNN applied to

machine translation. As an autonomous activation

function, such gated cells were proposed to be used

in (Dauphin and Grangier, 2016) for introducing

stochastic nonlinearity into Belief Networks by other

specialized “expert” ANNs and dubbed as Gated

Linear Units (GLU) in (Dauphin et al., 2016).

The proposed solution can be seen as a part of

the Gated Linear Unit (GLU) family of activations.

Using Directed Acyclic Graph (DAG) ANN, one can

implement a cell (let us call it Kolmogorov’s Gate or

KGate for short) of perceptrons with logistic sigmoid

activations that would work as allow or do not allow

gates at saturation domain, or multiplicative scaling of

the main trunk of ANN, in the non-saturation domain

of input values. Perceptrons with hyperbolic tangent

activation would work as update/forget, or the mean

shift gates on the main ANN trunk, working together

with the linear input transformation through the mul-

tiplication gate, Formula 3.

= (W

+ (τ ◦ W

)  (W

))  σ ◦ W

∀x

∈ X

⊂ R

, ∀x

∈ X

⊂ R

(3)

where x

is an ANN input, x

is an input of the

layer, W

is the linear transformation of the main

trunk, W

, W

are linear transformations

inside the KGate cell, and τ, σ are hyperbolic tan-

gent and logistic sigmoid activation functions, respec-

tively.

In a way, KGate functioning can be seen similar

to a multi-layer ANN with ReLU activations. A sin-

gle layer perceptron without nonlinearity activation

functions (or, as a matter of fact, multi-layer ANN

with no activations, which collapses into a single-

layer perceptron just with other coefﬁcients in the lin-

ear transformation matrix) has a static transformation

matrix. Addition of the ReLU activation can be seen

not only as an addition of another composite function:

z = a ◦ Wx. It also can be seen as family of the linear

transformation matrices, some of them having zero

rows: z = {W

}x. The choice of which matrix of the

ICEIS 2022 - 24th International Conference on Enterprise Information Systems

494

family to use for the transformation is made in a table

function manner depending on the input. It could be

easily shown that multi-layer ANN with ReLU acti-

vations can also be represented as a single perceptron

with the family of transformation matrices, each of

which differs from others in at least one coefﬁcient.

A particular transformation matrix from the family is

chosen at the moment of the test “computation”.

In a way, one can envision ReLU ANN nonlin-

earity as a “pseudo-quantum” data point cloud func-

tion, non-rigorously speaking, of course. Such a func-

tion would be still computationally deterministic, lo-

cally piece-wise continuous, smooth and monotone

(because of its local linearity), but globally not con-

tinuous and not-predictable on the intuition level until

a particular input data point is chosen to compute.

Similarly, while DAG ANN with KGate on the

side of the main ANN trunk is continuous and dif-

ferentiable on each layer, and thus, back-propagation

and gradient descent algorithms still work, the non-

linearities introduced by the gates into the main ANN

trunk may manifest themselves as highly volatile

cloud functions, Figure 3.

Another aspect of the building Kolmogorov style

ANN is selecting (or evolving) those “principal” neu-

rons that would best beneﬁt the process approxima-

tion by pruning secondary noise neurons. The follow-

ing explicit approach is not part of the KGate solution,

which prunes connection implicitly, but is a perspec-

tive direction of the method hybridization.

Following Ivakhnenko (Ivakhnenko, 1971), the

multi-layer neural-network models could be grown by

the Group Method of Data Handling (GMDH) using

a neuron activation function deﬁned by a short-term

polynomial. The GMDH is capable of generating

new layers capable of predicting new data most ac-

curately. The GMDH generates new neurons to be

ﬁtted to the training data in each layer. A given num-

ber of the best-ﬁtted neurons are selected to the next

layer. The number of layers increases whilst the spe-

cial, so-called exterior criteria have a tendency to de-

crease. The use of such selection criteria enables the

GMDH to efﬁciently avoid the network over-ﬁtting,

as described in (Farlow, 1981; Sashegyi and Madala,

1994). In particular, ML methods have been efﬁ-

ciently used to solve problems such as detection of

abnormal patterns (Nyah et al., 2016b; Nyah et al.,

2016a) and evaluation of brain development (Jakaite

et al., 2011; Schetinin et al., 2011). The reliable re-

sults have been achieved in prediction of trauma sur-

vival (Jakaite et al., 2010; Schetinin et al., 2018b;

Schetinin et al., 2018a), air-trafﬁc collision avoid-

ance (Schetinin et al., 2018c), as well as in detec-

tion of bone pathology (Jakaite et al., 2021; Akter and

Jakaite, 2019).

Yet another Universal Approximation ANN ar-

chitecture was proposed at the end of the 80s - Ra-

dial Basis Functions (RBF) ANN (Broomhead and

Lowe, 1988). It could be viewed as a “soft gate”

which activates the transformation matrix coefﬁcients

in Gaussian proportion to the proximity of the test

signal to the training signals this transformation ma-

trix coefﬁcients were trained at (Park and Sandberg,

1991). An apparent drawback of the architecture

is its “ﬂufﬁness” due to the non-reuse of the neu-

rons for the “missed” test-time data input, making the

RBF ANNs less dense or compact compared to Deep

ReLU ANNs. Still, RBF is a viable architecture and

is used in niche applications (Kurkin et al., 2018; Be-

heim et al., 2004).

4 DATA SET

For a ﬁrst pass of testing a new ANN cell, a sim-

ple transformation was used - ﬁnancial series 1-day

forecast based on a short period (2-weeks) prior data.

Such a low dimensional transformation from the 10-

dimensional input space into 1-dimensional output

space and relatively small and easy to peer in ANN

would allow us to see what kind of nonlinearity the

KGate cell creates.

In particular, data from the Warsaw Stock Ex-

change during the crisis during 2007 − 2009 were

chosen due to their volatility, hence, topological in-

tegrity violation upon normalization. The data rep-

resent the daily rate of return on the main index

WIG. Data between January 18

2007 and August

2009 were used, which counts for 655 obser-

vations of the daily returns downloaded from https:

//tradingeconomics.com/poland/stock-market. De-

tailed statistical analysis of the data set is out of the

scope of the paper; however, general intuition about

this strongly non-stationary time series can be ob-

tained from Figure 2. The data set has clear upward

trends at the beginning (circa 140 observations), at the

end (approximately 120 observations), and a precipi-

tous downward trend in the middle, with a minimum

value 21274, maximum of 67569, mean at 44441, and

standard deviation 13632.

The data were divided into 13 subsets, each con-

sisting of 50 observations used for the training of the

models. Each ”observation” was comprised of 10

days values, and the output ”label” value was the 11

day. Each following observation starts with a 1 day

shift. The number of the training sessions is ﬁrst 11,

and the number of observations in the session (40). It

was deﬁned in such a way that none of the training

Kolmogorov’s Gate Non-linearity as a Step toward Much Smaller Artiﬁcial Neural Networks

495

data (including the label day) would touch the follow-

ing test session data. The number of the test sessions

is last 12. Each session’s 50 observations were used

as test data. Models’ parameters were reset for each

session, and training was done anew.

As an accuracy metrics, we use the Mean Ab-

solute Percentage Error (MAPE) deﬁned as follows:

MAPE =

∑

t=1

−F

|, and Root Mean Square Er-

ror (RMSE): RMSE = (

∑

t=1

− F

)

, where A

and F

are the actual and predicted indexes at a given

day t, respectively, and n is the number of test obser-

vations.

5 EXPERIMENTS

The experiments were run on the Linux (Ubuntu

20.04.3 LTS) operating system with two dual Tesla

K80 GPUs (with 2 × 12GB GDDR5 memory each)

and one QuadroPro K6000 (with 12GB GDDR5

memory, as well), X299 chipset motherboard, 256 GB

DDR4 RAM, and i9-10900X CPU. Experiments were

run using MATLAB 2021b.

Experiments were done on MATLAB with Deep

Learning Toolbox. ANN models were trained using

the “adam” learning algorithm with 0.1 initial learn-

ing coefﬁcient, mini-batch size 32, and 1000 epochs.

In comparison to the KGate ANN model, Fig-

ure 1, eight other ANN architectures were tested, and

results presented here: auto-regression (AR) ANNs

with no activation function, with ReLU activations,

and with hyperbolic tangent (Tanh) activations, Long-

Short Term Memory (LSTM) trained on the single,

whole 40 data points sequence, and Sequence-to-

sequence LSTM and Gated Recurrent Unit (GRU),

trained in a manner similar to other fully-connected

ANNs - on 40 sequences consisted of 10 data points.

The author’s GMDH (Ciemny Marcin, 2022), and

BRF ANN implementations were also compared.

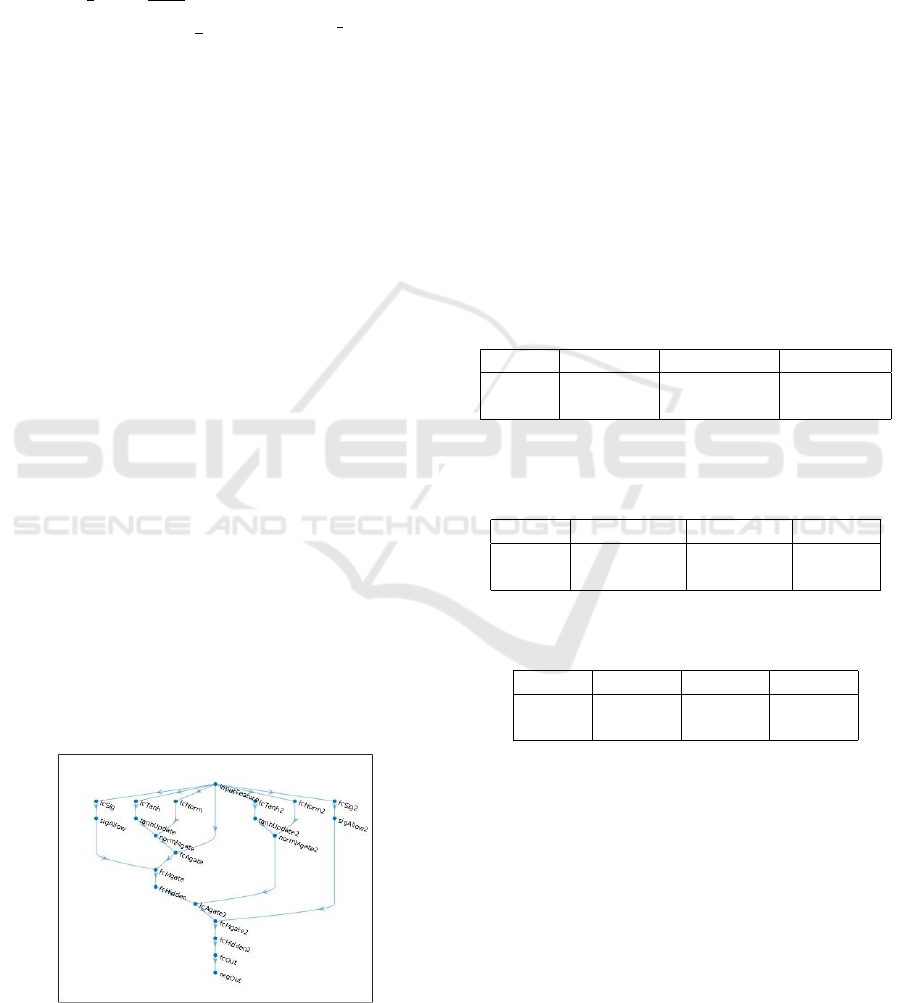
Figure 1: KGate ANN schema.

All feed-forward fully-connected ANNs have 2

Kolmogorov ANN style hidden layers with n+1 neu-

rons in the ﬁrst and 2n + 1 neurons in the second

layer. LSTM networks also have 2 LSTM layers

with the same number of hidden state neurons. All

ANNs have 1-dimensional regression output with the

sum of quadratic errors cost function. KGate cells,

in their linear transformation layers, have also n + 1,

and 2n + 1 neurons in the ﬁrst and second cell, re-

spectively. The code for all models and training

and test data are available for download at GitHub:

https://github.com/Selitskiy/ICEIS2022.

6 RESULTS

Two sets of computational experiments were con-

ducted on all 9 models: with min-max normalization

and without any normalization.

Table 1: Error of the WSE prediction for 2-layers AR ANN,

ReLU and Tanh ANN models on normalized data.

Error AR ANN ANN ReLU ANN Tanh

MAPE 0.01790 0.02505 0.02380

RMSE 1056.57 1436.16 1383.89

Table 2: Error of the WSE prediction for Sequential LSTM,

Sequential GRU and LSTM ANN models on normalized

data.

Error LSTM Seq. GRU Seq, LSTM

MAPE 0.02339 0.02502 0.08641

RMSE 1241.91 1387.42 4633.01

Table 3: Error of the WSE prediction for RBF, GMDH and

KGate ANN models on normalized data.

Error RBF GMDH KGate

MAPE 0.02538 0.01729 0.02649

RMSE 1559.84 953.44 1518.50

The accuracy results for all 9 models for the min-

max normalized input data are presented in Table 1,

Table 2 and Table 3. The accuracy for not normalized

input data are shown in Table 4, Table 5 and Table 6.

For experiments with normalized data, the majority

of the models demonstrated similar accuracy-wise re-

sults, with AR ANN and GMDH leading, especially

the latter one, and sequence-to-value LSTM notice-

ably lagging behind the sequence-to-sequence LSTM

or GRU. As expected, for non-normalized data ex-

periments, ANNs with saturable activations such as

Tanh, Sigmoid and containing them LSTM and GRU

failed to train. RBF ANN failed to produce numeric

results, and GMDH had convergence issues with huge

ICEIS 2022 - 24th International Conference on Enterprise Information Systems

496

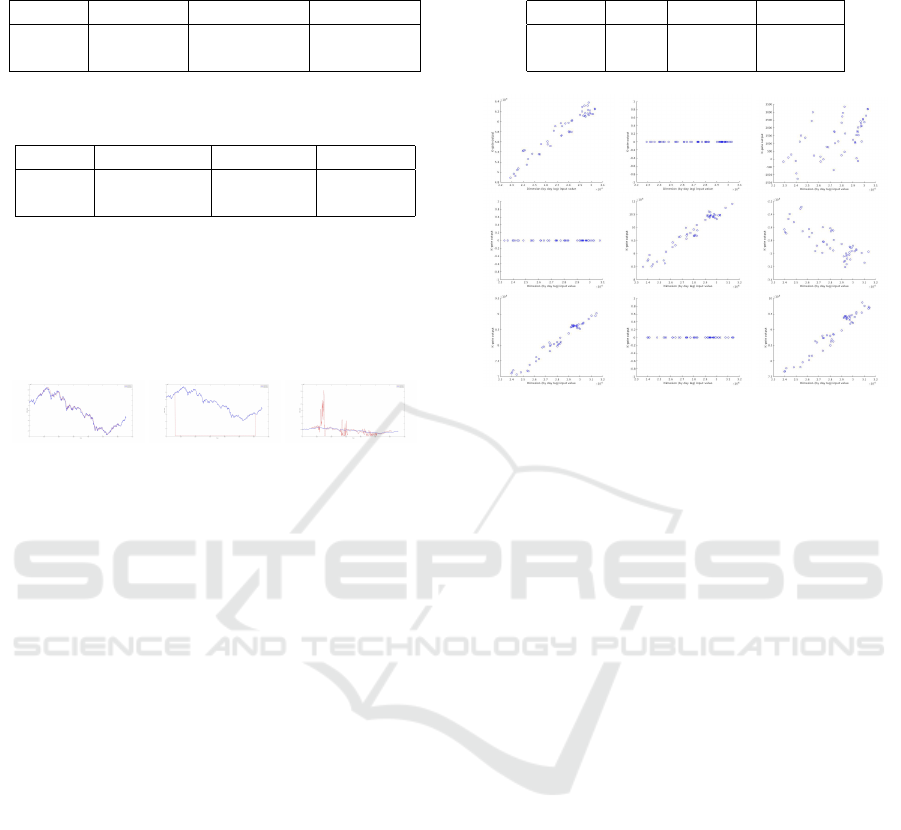
Table 4: Error of the WSE prediction for 2-layers AR ANN,

ReLU and Tanh ANN models on non-normalized data.

Error AR ANN ANN ReLU ANN Tanh

MAPE 0.01950 0.02360 0.99425

RMSE 1047.23 1411.43 46239.9

Table 5: Error of the WSE prediction for 2-layers AR ANN,

ReLU and Tanh ANN models on non-normalized data.

Error LSTM Seq. GRU Seq, LSTM

MAPE 0.99495 0.99414 0.99420

RMSE 46232.6 46235.43 46653.96

error spikes, apparently because of its polynomial na-

ture, see Figure 2. AR ANN still performed the best

but noticeably dropped its accuracy compared to nor-

malized data. Only ReLU ANN and KGate improved

their performance on non-normalized data, the latter

beating the ﬁrmer.

Figure 2: Error classes of the WSE prediction of the models

on non-normalized data. Left: AR, ReLU, KGate; Center:

Tanh, Sigmoid, LSTM, GRU; Right: GMDH.

For KGate ANN experiments, sessions 8 and 11

demonstrated the highest and smallest accumulated

errors, respectively. For session 11, activations on the

main trunk of ANN generated by the 1

KGate, per

channels 1 − 9 are shown in Figure 3.

Channels 2, 4, 8, 10, forming a Null-space (being

mapped to 0), are effectively pruned out of the ANN.

Figure 4 demonstrates which input channels were im-

plicitly pruned out from the test data processing at the

ﬁrst and second KGate, depending on the training data

of the session.

7 DISCUSSION, CONCLUSIONS,

AND FURTHER RESEARCH

The novelty of the KGate activation function cell is

in the original schema of the combination of the sig-

moid, hyperbolic tangent and linear transformations,

targeting the use in the non-data-normalizing ANNs,

as well as the use in the Kolmogorov style ANN de-

manding volatile “pathological” activation functions,

and in the self-pruning evolving ANNs.

We can see that KGate ANN performed well in

terms of the MAPE and RMSE accuracy metrics for

WSE prediction in the chosen time interval, espe-

cially for non-normalized input data. The aim of cor-

rectly handling non-normalized data is achieved, es-

Table 6: Error of the WSE prediction for Sequential LSTM,

LSTM and KGate ANN models on normalized data.

Error RBF GMDH KGate

MAPE - 0.37000 0.02272

RMSE - 38296.9 1304.12

Figure 3: Activations generated by the 1

KGate by chan-

nels 1 − 9 for non-normalized input WSE data for session

11, all observations.

pecially on the backdrop of the failure of the RNN and

ANN with saturable activation functions. However,

even in ﬁnancial crisis conditions, the task of 1-day

ﬁnancial series prediction is not complex enough to

make far-reaching conclusions. The basic AR ANN

performed quite similarly still better; therefore, the

more complex tasks in the time-series domain will

be the perspective research. Also, not only regres-

sion prediction but other tasks as classiﬁcation and in

other ML application domains should widen the cur-

rent limitations of this study. Those tasks on which

shallow regression ANNs and deep ReLU ANN fail

will be good perspective benchmarks for the KGate

architecture evaluation.

On a more fundamental level, it could be seen that

KGate is capable of providing highly volatile cloud

activation functionality and quasi-linear or binary al-

low/not allow functionality, depending on the data.

The former quality has valuable potential for use in

the Kolmogorov style ANNs that could be an alterna-

tive to the current huge “foundation” DL models and

is a direction for further research. The latter, implicit

pruning capability of the ANN connection is useful

for the advice of the explicit pruning in the evolu-

tionary ANN architectures, which also help to reduce

the size of the ANN models, and experimenting with

KGate us in such architectures as a prospective theme

for the further research as well.

Kolmogorov’s Gate Non-linearity as a Step toward Much Smaller Artiﬁcial Neural Networks

497

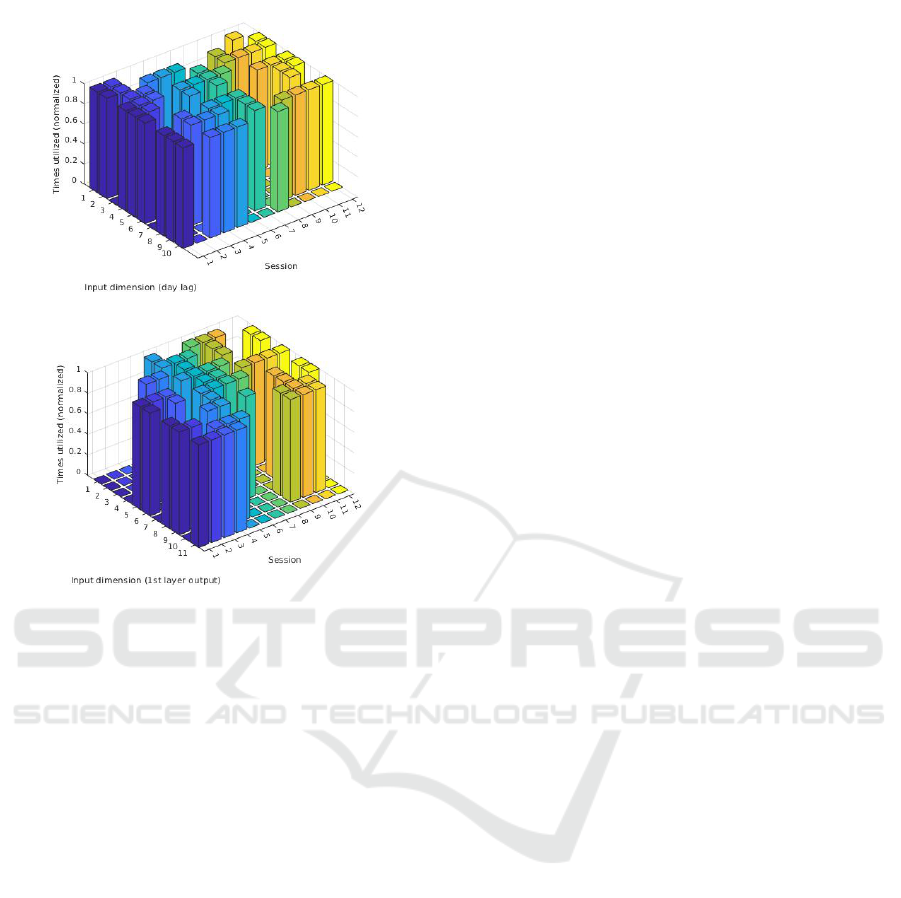
Figure 4: Non-zero channels generated by the KGates per

session. Top - by the 1

, bottom - by the 2

KGate.

REFERENCES

Akashi, S. (2001). Application of ε-entropy theory to

kolmogorov—arnold representation theorem. Reports

on Mathematical Physics, 48(1):19–26. Proceedings

of the XXXII SYMPOSIUM ON MATHEMATICAL

PHYSICS.

Akter, M. and Jakaite, L. (2019). Extraction of texture fea-

tures from x-ray images: Case of osteoarthritis detec-

tion. In Yang, X.-S., Sherratt, S., Dey, N., and Joshi,

A., editors, Third International Congress on Informa-

tion and Communication Technology, pages 143–150,

Singapore. Springer Singapore.

Beheim, L., Zitouni, A., Belloir, F., and de la Housse, C.

d. M. (2004). New rbf neural network classiﬁer with

optimized hidden neurons number. WSEAS Transac-

tions on Systems, (2):467–472.

Bender, E. M., Gebru, T., McMillan-Major, A., and

Shmitchell, S. (2021). On the dangers of stochastic

parrots: Can language models be too big? In Pro-

ceedings of the 2021 ACM Conference on Fairness,

Accountability, and Transparency, FAccT ’21, page

610–623, New York, NY, USA. Association for Com-

puting Machinery.

Blodgett, S. L. and Madaio, M. (2021). Risks of AI foun-

dation models in education. CoRR, abs/2110.10024.

Bommasani, R., Hudson, D. A., Adeli, E., Altman, R.,

Arora, S., von Arx, S., Bernstein, M. S., Bohg, J.,

Bosselut, A., Brunskill, E., Brynjolfsson, E., Buch,

S., Card, D., Castellon, R., Chatterji, N. S., Chen,

A. S., Creel, K., Davis, J. Q., Demszky, D., Don-

ahue, C., Doumbouya, M., Durmus, E., Ermon, S.,

Etchemendy, J., Ethayarajh, K., Fei-Fei, L., Finn, C.,

Gale, T., Gillespie, L., Goel, K., Goodman, N. D.,

Grossman, S., Guha, N., Hashimoto, T., Henderson,

P., Hewitt, J., Ho, D. E., Hong, J., Hsu, K., Huang,

J., Icard, T., Jain, S., Jurafsky, D., Kalluri, P., Karam-

cheti, S., Keeling, G., Khani, F., Khattab, O., Koh,

P. W., Krass, M. S., Krishna, R., Kuditipudi, R., and

et al. (2021). On the opportunities and risks of foun-

dation models. CoRR, abs/2108.07258.

Broomhead, D. S. and Lowe, D. (1988). Radial basis

functions, multi-variable functional interpolation and

adaptive networks. Technical report, Royal Signals

and Radar Establishment Malvern (United Kingdom).

Brown, T. B., Mann, B., Ryder, N., Subbiah, M., Kaplan, J.,

Dhariwal, P., Neelakantan, A., Shyam, P., Sastry, G.,

Askell, A., Agarwal, S., Herbert-Voss, A., Krueger,

G., Henighan, T., Child, R., Ramesh, A., Ziegler,

D. M., Wu, J., Winter, C., Hesse, C., Chen, M., Sigler,

E., Litwin, M., Gray, S., Chess, B., Clark, J., Berner,

C., McCandlish, S., Radford, A., Sutskever, I., and

Amodei, D. (2020). Language models are few-shot

learners.

Cho, K., van Merrienboer, B., G

ulc¸ehre, C¸ ., Bougares, F.,

Schwenk, H., and Bengio, Y. (2014). Learning phrase

representations using RNN encoder-decoder for sta-

tistical machine translation. CoRR, abs/1406.1078.

Ciemny Marcin, S. S. (2022). Gmdh-type neural networks

for predicting ﬁnancial time series: A study of infor-

mational efﬁciency of stock markets. In Advances

in Systems Engineering. Proceedings of the 28th In-

ternational Conference on Systems Engineering, IC-

SEng 2021, December 14-16, Wrocław, Poland. Lec-

ture Notes in Networks and Systems, volume 364,

pages 141–150. Springer International Publishing.

Dauphin, Y. and Grangier, D. (2016). Predicting dis-

tributions with linearizing belief networks. CoRR,

abs/1511.05622.

Dauphin, Y. N., Fan, A., Auli, M., and Grangier, D.

(2016). Language modeling with gated convolutional

networks. CoRR, abs/1612.08083.

Farlow, S. J. (1981). The gmdh algorithm of ivakhnenko.

The American Statistician, 35(4):210–215.

Fedus, W., Zoph, B., and Shazeer, N. (2021). Switch trans-

formers: Scaling to trillion parameter models with

simple and efﬁcient sparsity. CoRR, abs/2101.03961.

Field, H. (2021). At Stanford’s “foundation models” work-

shop, large language model debate resurfaces. Morn-

ing Brew.

Girosi, F. and Poggio, T. (1989). Representation proper-

ties of networks: Kolmogorov’s theorem is irrelevant.

Neural Computation, 1(4):465–469.

Hilbert, D. (1902). Mathematical problems. Bulletin of the

American Mathematical Society, 8(10):437–479.

Hinton, G. E., Srivastava, N., Krizhevsky, A., Sutskever,

I., and Salakhutdinov, R. (2012). Improving neural

networks by preventing co-adaptation of feature de-

tectors. CoRR, abs/1207.0580.

ICEIS 2022 - 24th International Conference on Enterprise Information Systems

498

Hochreiter, S. and Schmidhuber, J. (1997). Long Short-

Term Memory. Neural Computation, 9(8):1735–1780.

Ioffe, S. and Szegedy, C. (2015). Batch normalization: Ac-

celerating deep network training by reducing internal

covariate shift. CoRR, abs/1502.03167.

Ivakhnenko, A. G. (1971). Polynomial theory of complex

systems. IEEE transactions on Systems, Man, and Cy-

bernetics, (4):364–378.

Jakaite, L., Schetinin, V., Hladuvka, J., Minaev, S., Ambia,

A., and Krzanowski, W. (2021). Deep learning for

early detection of pathological changes in x-ray bone

microstructures: case of osteoarthritis. Scientiﬁc Re-

ports, 11.

Jakaite, L., Schetinin, V., Maple, C., and Schult, J. (2010).

Bayesian decision trees for EEG assessment of new-

born brain maturity. In The 10th Annual Workshop on

Computational Intelligence UKCI 2010.

Jakaite, L., Schetinin, V., and Schult, J. (2011). Feature

extraction from electroencephalograms for Bayesian

assessment of newborn brain maturity. In 24th In-

ternational Symposium on Computer-Based Medical

Systems (CBMS), pages 1–6.

Kalchbrenner, N., Espeholt, L., Simonyan, K., van den

Oord, A., Graves, A., and Kavukcuoglu, K. (2016).

Neural machine translation in linear time. CoRR,

abs/1610.10099.

Kanai, S., Fujiwara, Y., and Iwamura, S. (2017). Pre-

venting gradient explosions in gated recurrent units.

In Proceedings of the 31st International Conference

on Neural Information Processing Systems, NIPS’17,

page 435–444, Red Hook, NY, USA. Curran Asso-

ciates Inc.

Kolmogorov, A. N. (1961). On the representation of contin-

uous functions of several variables by superpositions

of continuous functions of a smaller number of vari-

ables. American Mathematical Society.

Kurkin, S. A., Pitsik, E. N., Musatov, V. Y., Runnova, A. E.,

and Hramov, A. E. (2018). Artiﬁcial neural networks

as a tool for recognition of movements by electroen-

cephalograms. In ICINCO (1), pages 176–181.

urkov

a, V. (1991). Kolmogorov’s Theorem Is Relevant.

Neural Computation, 3(4):617–622.

LeCun, Y., Bottou, L., Bengio, Y., Haffner, P., et al. (1998).

Gradient-based learning applied to document recogni-

tion. Proceedings of the IEEE, 86(11):2278–2324.

Lottick, K., Susai, S., Friedler, S. A., and Wilson, J. P.

(2019). Energy usage reports: Environmental aware-

ness as part of algorithmic accountability. CoRR,

abs/1911.08354.

Misra, D. (2020). Mish: A self regularized non-monotonic

activation function. In BMVC.

Naveen, P. (2021). Phish: A novel hyper-optimizable acti-

vation function.

Nyah, N., Jakaite, L., Schetinin, V., Sant, P., and Aggoun,

A. (2016a). Evolving polynomial neural networks for

detecting abnormal patterns. In 2016 IEEE 8th Inter-

national Conference on Intelligent Systems (IS), pages

74–80.

Nyah, N., Jakaite, L., Schetinin, V., Sant, P., and Aggoun,

A. (2016b). Learning polynomial neural networks of a

near-optimal connectivity for detecting abnormal pat-

terns in biometric data. In 2016 SAI Computing Con-

ference (SAI), pages 409–413.

Park, J. and Sandberg, I. W. (1991). Universal approxi-

mation using radial-basis-function networks. Neural

Computation, 3(2):246–257.

Pinkus, A. (1999). Approximation theory of the mlp model

in neural networks. Acta numerica, 8:143–195.

Ramachandran, P., Zoph, B., and Le, Q. V. (2017a). Search-

ing for activation functions. CoRR, abs/1710.05941.

Ramachandran, P., Zoph, B., and Le, Q. V. (2017b). Swish:

a self-gated activation function. arXiv: Neural and

Evolutionary Computing.

Rosenblatt, F. (1958). The perceptron: a probabilistic model

for information storage and organization in the brain.

Psychological review, 65(6):386.

Rosset, C. (2020). Turing-NLG: A 17-billion-parameter

language model by Microsoft - Microsoft Research.

[Online; accessed 16. Jan. 2022].

Rumelhart, D. E., Hinton, G. E., and Williams, R. J. (1986).

Learning representations by back-propagating errors.

Nature, 323(6088):533–536.

Sashegyi, K. D. and Madala, R. V. (1994). Initial conditions

and boundary conditions. In Mesoscale Modeling of

the Atmosphere, pages 1–12. Springer.

Schetinin, V., Jakaite, L., and Krzanowski, W. (2018a).

Bayesian averaging over decision tree models: An ap-

plication for estimating uncertainty in trauma severity

scoring. International Journal of Medical Informatics,

112:6 – 14.

Schetinin, V., Jakaite, L., and Krzanowski, W. (2018b).

Bayesian averaging over decision tree models for

trauma severity scoring. Artiﬁcial Intelligence in

Medicine, 84:139–145.

Schetinin, V., Jakaite, L., and Krzanowski, W. (2018c).

Bayesian learning of models for estimating uncer-

tainty in alert systems: Application to air trafﬁc con-

ﬂict avoidance. Integrated Computer-Aided Engineer-

ing, 26:1–17.

Schetinin, V., Jakaite, L., and Schult, J. (2011). Informa-

tiveness of sleep cycle features in bayesian assess-

ment of newborn electroencephalographic maturation.

In 2011 24th International Symposium on Computer-

Based Medical Systems (CBMS), pages 1–6.

Schick, T. and Sch

utze, H. (2020). It’s not just size that mat-

ters: Small language models are also few-shot learn-

ers. CoRR, abs/2009.07118.

Strubell, E., Ganesh, A., and McCallum, A. (2019). Energy

and policy considerations for deep learning in NLP.

CoRR, abs/1906.02243.

van den Oord, A., Kalchbrenner, N., and Kavukcuoglu,

K. (2016). Pixel recurrent neural networks. CoRR,

abs/1601.06759.

Kolmogorov’s Gate Non-linearity as a Step toward Much Smaller Artiﬁcial Neural Networks

499