
Extracting Mass Transportation Networks from General Transit Feed
Specification Datasets
Gergely Kocsis
a
and Imre Varga
b
Department of IT Systems and Networks,
University of Debrecen, Kassai str. 26, Debrecen, Hungary
Keywords:
GTFS, Public Transport, Networks.
Abstract:
In several smart-city applications the networks of the mass-transportation systems can be bases of investi-
gations. In this paper we show how one can extract a network of connected stops from the General Transit
Feed Specification (GTFS) feed of a given service provider. We have also implemented this process as a tool
(gtfs2net) that is available for use at the GitHub page of the project. On of our most important finding is
that since providers do not follow the specification in a coherent way regarding the use of parent stations the
problem of close stops has to be manually handled. In order to show how our tool works in practice we have
provided some extracted networks with their properties.
1 INTRODUCTION
Investigation of abstract networks of mass transporta-
tion providers is used frequently in smart city appli-
cations (Besenczi et al., 2021). Finding these net-
works however is not always trivial. There are sev-
eral maps online (even some that are free and open to
be used) that contain location of stops as well. From
these sources it is possible to get a network of stops
where the connection between them may be described
by some sort of physical relation (e.g. a connect-
ing road). In many cases however it is much reason-
able to name two stops connected if there is a direct
bus/tram/train trip between them.
One possible solution may be the use of the Gen-
eral Public Transit Feed Specification (GTFS) de-
scribed timetables of transportation service providers.
The General Transit Feed Specification is a current
format for public transportation schedules and the re-
lated geographic information (Harrelson, 2021). Be-
sides the opportunity of public transit agencies to pub-
lish their own transit data it lets software developers
to write applications that use this data to help users
in their daily lives. Numerous agencies provide their
public GTFS datasets, but they create them in differ-
ent manner (Wessel and Farber, 2019; Hansson et al.,
2019; Kujala et al., 2018a; Sienkiewicz and Hołyst,
a
https://orcid.org/0000-0003-0018-4201
b
https://orcid.org/0000-0003-3921-2521
2005; Braga et al., 2014). The native analysis of
these sources is already a widely studied topic by the
networks scientist comunity (Vuurstaek et al., 2020;
Fortin et al., 2016; Wong, 2013; von Ferber et al.,
2007; Gallotti and Barthelemy, 2015; Jiang, 2007;
L
¨
ammer et al., 2006; Porta et al., 2006). However the
extraction of abstract networks from these sources is a
much less known field. Moreover in most cases even
if the extracted networks are available the process is
not or only partially published (Kujala et al., 2018b).
In a simple GTFS based application a public trans-
port stop is just a geographical location with a few
meters in dimension. The feeds describe the connec-
tions of the stops as well. For a passenger however,
who travels probably some kilometers, a short walk
can be also included into the journey. This results in
connections between close stops, which are not con-
nected by the official datasets. As we found, it is
much harder to find sources to build such networks
on this basis.
Below we will show how one can extract abstract
transportation networks from these feeds. In Section
2. we briefly introduce the important parts of the spec-
ification. In Sections 3 and 4 we show the process
and the implementation aspects how to extract such
an abstract network from a provided feed. In Section
5 we show some basic properties of some extracted
networks to give an example how these networks can
later be used. Finally in Section 6 we conclude our
work and present our future plans.
Kocsis, G. and Varga, I.
Extracting Mass Transportation Networks from General Transit Feed Specification Datasets.
DOI: 10.5220/0011080700003197
In Proceedings of the 7th International Conference on Complexity, Future Information Systems and Risk (COMPLEXIS 2022), pages 85-91
ISBN: 978-989-758-565-4; ISSN: 2184-5034
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
85

2 GENERAL TRANSIT FEED
SPECIFICATION
In the last 15 years the General Transit Feed Spec-
ification (GTFS) become the de-facto standard for
describing timetables of public transportation ser-
vices. The static component of the GTFS consists
of comma-separated values in simple text files con-
tained within a ZIP file. Each line of a file contains
a record of the given data table, covering various re-
quired and optional fields. There are mandatory and
optional files in the dataset. This section focuses on
just some of the files.
• stops.txt: It describes locations (e.g. stops, sta-
tions) related to the public transportation network
(PTN). Besides the official name of the place and
its precise latitude and longitude other informa-
tion can be stored in a record. One of these is the
parent station which can be used to define rela-
tionship among stops, platforms or boarding areas
of the premise.
• trips.txt: The trips are directional sequences
of stops connected by a transit vehicle during a
specific time period.
• routes.txt: A transit route is a directionless set
of trips concerning the same stops, so these trips
are displayed to riders as a single service.
• stop_times.txt: Times when a vehicle arrives
at and departs from stops for all the trips. These
records connect the trips, the stops and timing in-
formation.
The records of the files are interconnected by identi-
fiers. Stop time records contains stop id and trip id
fields in order to connect to the respective records.
The route id field joins the routes and trips.
3 EXTRACTING ABSTRACT
TRANSPORTATION
NETWORKS FROM GTFS
FEEDS
Even though the original aim of GTFS is to provide a
standard for describing several aspects of public trans-
portation for network scientists one of the most prac-
tical use of it is that an abstract transportation network
can be extracted from the feed. However getting such
a network is not as trivial as one would think at the
first sight mostly because of two problems: i.) Lo-
cal Transportation Providers sadly do not follow the
specification fully in all cases or they follow it in dif-
ferent ways. ii.) It is not always exact what network
scientists would like to mean under a node or an edge
of the network.
To see the full picture let us see what is needed to
build a network in an ideal case. Our desired network
will have stops as its nodes and edges describing that
any time in the timetable there is a direct connection
between two stops. Thus to get the nodes we need
to process the stops.txt file of the GTFS feed. Be-
side several other fields, a record containing a stop has
the id of the stop (stop id) serving as the unique iden-
tifier of it. In cases when we have only standalone
stops and no groups of stops are presented this field is
enough to have a node. However in many cases some
of the stops are grouped because e.g. they are parts of
a bigger station. This relation is described by the lo-
cation type and the parent station fields of the record.
For an ordinary stop, the location type is 0. If it is
a part of a bigger station its parent station field con-
tains a stop id referring to the parent stop. A parent
stop (parent station) has a location type of 1. Note
that the location type of a stop can also take values of
2, 3 and 4 but as practice shows these values are much
less commonly used.
Giving an answer to the first above raised question
the nodes of our abstract network can usually be the
stops except in cases when a stop is contained by a
parent station. In this latter case the station itself can
be the node instead.
As mentioned above the edges of an abstract net-
work should be the connections between the stops.
unfortunately this information is not stored directly
in the datasets. The easiest way to get it is to pro-
cess the stop_times.txt file. In this file a stop of a
trip of a vehicle is described in each record. After the
fields describing the trip’s properties the stop id field
here describes in which stop the vehicle stops. The
stop sequence tells what is the number of the stop in
the trip. It is easy to understand therefore if we have
read two records of the same trip with consecutive se-
quence numbers the stops mentioned in these records
can be treated as being neighbors in a way that there
is a directed edge from the stop with the smaller se-
quence number to the other.
The problem with the above described method of
finding edges is that it does not count with the pres-
ence of parent stations. This means that for example if
we have two stations with let us say three stops in both
that are connected by some trips directly, we will not
get a network with two nodes and two directed edges,
but we will get eight nodes some edges directly be-
tween the stops of the stations and no edges between
the stations themselves. Referring to the stops and
stations this way is however misleading in most of the
cases, so we suggest to use the parent stations of those
COMPLEXIS 2022 - 7th International Conference on Complexity, Future Information Systems and Risk
86
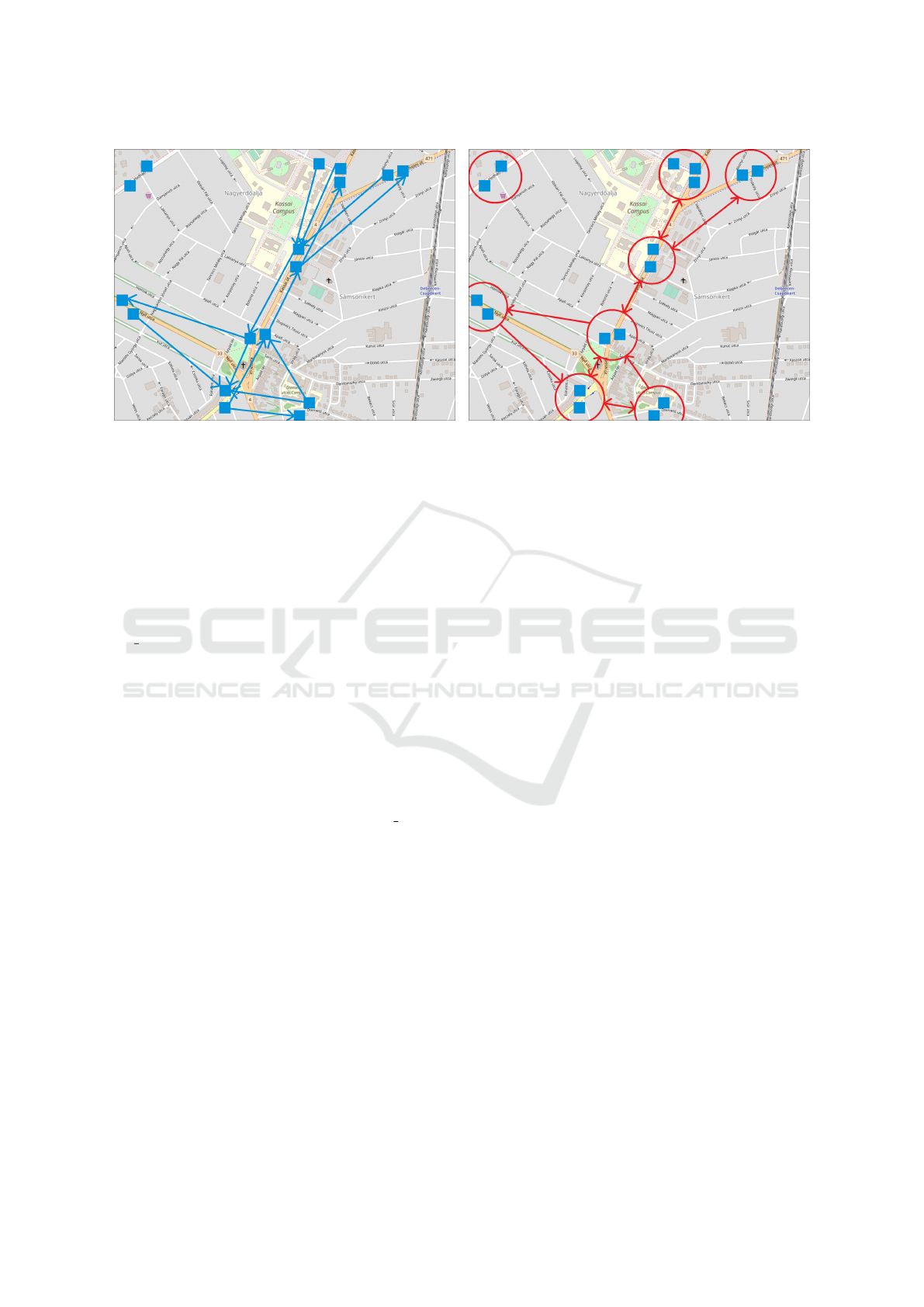
Figure 1: The effect of using virtual stations on the abstract topology of bus stations. left: Bus stations (blue squares) around
Debrecen University IT Campus and their connections (blue arrows). right: Stops merged by virtual stations (red circles) and
their connections (red arrows). (Picture source: OpenStreetMap.org).
stops that have one as the ends of these edges without
allowing the presence of multi-edges.
Extracting a network from a GTFS feed following
the above rules means that as a result we will get a
network with a number of nodes
N = N
station
+ N
stop
(1)
where N
stop
means only those stops whose par-
ent station field is empty. Note that this number N
may be lower than the original number of stops, since
multiple stops may have been replaced by similar sta-
tions.
The set of edges also has a lower number of el-
ements than the number of connections read from
stop_times.txt file. A connection described by two
consecutive records of the file will describe a new
edge only if there is no such edge added already to
the network. Also note that if one or both ends of the
edge is described by a stop having a parent station,
the edge will be added to the network so that it con-
nects the parent station(s) of the stop(s) and not the
original stop(s) as it was described above.
One can say that the above method is a reason-
able way of getting the network from the feed and
theoretically it is. The problem is that in many cases
GTFS feed providers do not follow the proper struc-
ture in their feed (semantically), meaning that in sev-
eral cases parent stations are not contained in the same
way.
• In some cases there are absolutely no parent sta-
tions. Naturally this may be a real case for small
enough companies.
• Other feeds contain parent stations but only for
the real stations containing several stops (or plat-
forms) in them and ignoring stops e.g. on two
sides of the same road.
• Again some others say that close stops shall also
be handled together by one parent station (e.g.
two stops at two opposite site of the same road
usually with similar names). Note however that
these parent stations are not real buildings or lo-
cations in most of the cases.
It may be a topic of arguments which aspect is the
proper use of the format. In some already existing
solutions this aspect is not taken into account (Kujala
et al., 2018b), from the point of view of getting the
network from the feed however we found that maybe
the best solution is to give the control to the scientists
getting the network.
Namely, while processing GTFS data of a given
transportation provider (stops, stop times, parent sta-
tions) we say that not only explicitly described parent
stations take the place of stops of a station but also,
if the distance between stations is smaller than a so
called merging limit r we replace these stations by a
virtual station acting as the parent station of the af-
fected stops.
The effect of the merging of stops by virtual sta-
tions is illustrated on Figure 1 using the map of bus
stations around the IT Campus of University of De-
brecen. Note that by the introduction of virtual sta-
tions the number of nodes in the network strongly de-
creases (from 17 to 8), while the number of edges
shows a much consolidate decrese (from 14 to 13 –
counting bidirectional edges as 2). This transaction
also has an effect on the connectedness of the graph,
since separate clusters of stations may be merged in
the resulted network.
Defining the above method more precisely, a new
virtual station will be used for all those stops s
a
∈ S
Extracting Mass Transportation Networks from General Transit Feed Specification Datasets
87

for which
∃s
b
∈ S → d(s
a
,s
b
) < r (2)
where d(s
a
,s
b
) is the geographical distance calculated
using the Haversine formula (Rosetta Code Commu-
nity, 2021) that is based on the longitudinal and latitu-
dinal positions of the stops that can be read from the
stops.txt file of the GTFS feed. One may note that
as a result of the transitive property of this relation,
two stops that are more far than r can be contained
by the same virtual station if they both have the same
station in between a distance of r.
4 IMPLEMENTATION ASPECTS
OF THE EXTRACTION
Providing an out of the box tool to do the extraction
we have implemented a tool in Java that can process
unzipped GTFS feeds and results a network as a .txt
file described by the edges of the network. Namely in
each line of the file an edge is listed by containing the
starting and arriving stops separated by a comma.
Figure 2: The UML class diagram of the network converter
tool. The Stop class is an inner class of GTFSTools.
One can note on Figure 2 that the GTFSTools
class has 4 public methods. readStops(...) builds
the nodes of the network, readStopTimes(...)
connects them (or the parent stations of them) by
edges, while printStopsAsNetworkToFile(...)
prepares the exported network file. The
registerCloseStopsAsOne(...) method is
needed to be called only if one would like to merge
stops close to each other to one. If this is needed it
has to be called just before the readStopTimes(...)
method. The r: int parameter of this latter method
specifies the merging distance below which we accept
two stops to be merged.
It has to be mentioned that finding the close stops
in a set of stops is not a trivial problem especially if
we try to take care on the efficiency aspects. Finally
in our solution we have used the recursive algorithm
described in Alg. 1. Note that what we have imple-
mented is at the background a one dimensional Sur-
rounding Cell Registration algorithm (Ogami, 2021)
where we first find the close stops according to the
longitudinal distances and then keep only those from
the potential close stops whose Haversine distance is
small enough (smaller or equal to r).
Algorithm 1: Algorithm to merge close stops by virtual sta-
tions.
Input: Set of stops and parent stations, r
Output: Set of stops and virtual parent
stations
1 Copy the stops (their references) to a sorted
list stops. (Sorted by the longitudinal
position of them)
2 actIdx=0, bottomIdx=0, topIdx=0
3 for actIdx ∈ 0..stops.size do
4 bottomIdx=the first stop’s index in the list
for which stops[botomIdx].lonPos >
stops[actIdx].lonpos-r
5 topIdx=the last stop’s index in the list for
which stops[topIdx].lonPos <
stops[actIdx].lonpos+r
6 for idx ∈ bottomIdx..topIdx do
7 if
distance(stops[idx],stops[actIdx])<r
then
8 Add stops[idx] to the set of close
stops
9 for each stop in the list of close stops do
10 repeat steps 4, 5, 6
A natural outcome of this algorithm is that by in-
creasing the value of the checked distance r, we get
less nodes in our resulted network. An interesting
question is that what may be a reasonable value for
r in order not to loose too many stops but still elimi-
nate the cases when e.g. stops at two sides of the same
road are handled as being independent (since maybe
no common parent station has been added to them).
In order to be able to give a hint how to select
the value of r we have checked the dependence of
the number of nodes N on the distance r for several
GTFS feeds (A detailed description of each feed and
the sources of them are available at the GitHub of the
project’s data (Kocsis and Varga, 2021b)).
Our findings are summed up on Figure 3. As one
may observe increasing the merging distance r at the
first some meters does not affect much the number of
stops since it is really rare that there are two inde-
pendent stops this close (without being two stops of
COMPLEXIS 2022 - 7th International Conference on Complexity, Future Information Systems and Risk
88

Figure 3: Normalized number of nodes N
r
/N
r
0
=0
in the net-
work as a function of the merging distance r. Note that
for most feeds a strong decrease starts around r = 100m or
r = 200m. Inset: non-local transport network cases on a
longer scale. See detailed description of the data at (Kocsis
and Varga, 2021b).
a station). As the trends show in most cases however
somewhere around 100 − 200 meters the number of
stops N starts to fall down rapidly showing that this
distance may be the desired one describing close sta-
tions that may be merged in order to see a more valid
picture of the network of mass transportation systems.
This finding is consistent to the intuitive guess
based on studying mass transportation maps, that the
distance of such stations should be somewhere around
150 meters. The exact value however is to be decided
based on the actual data since special local properties
may affect it.
One may also note on Figure 3 that while most of
the curves move together following an inverse logistic
shape, there are some of them that seem to have dif-
ferent behavior. Examining these cases however soon
reveals that these exceptional cases are for transporta-
tion feeds describing non-local or non-exclusively-
local transportation networks, like train, ferry and
inter-city bus networks. Nevertheless drawing these
data on a longer scale shows that their qualitative be-
havior do not differ (see Figure 3 inset). We see simi-
lar falling of the curves as before for these cases as
well, just the place of it is around 2-4 kilometers.
It has to be noted however that merging stops more
than 2 kilometers far from each other may not have
any practical use especially knowing that luckily in
the case of train stations it is really rare that compa-
nies register the two directions as individual stops (not
even grouped by a parent station).
5 INVESTIGATION OF SOME
RESULTED NETWORKS
In order to see how our tool works on extracting net-
works from GTFS feeds in practice we have used it
for several transportation feeds available online. We
have collected these sources under the GitHub page
of our project (Kocsis and Varga, 2021a), (Kocsis and
Varga, 2021b) and also we have uploaded there the re-
sulted abstract networks in .txt format. A conclud-
ing table of these extracted networks together with
some basic properties of them are shown on Figure
4. Note that there are huge differences in the number
of nodes of the networks for different sources. Some
service providers have only a bit more than 100 nodes,
while some of them have ten-thousands.
In most of the cases the union of close nodes
(merging stops within r = 150m distance by virtual
parent stations) decreases the number of nodes al-
most to the half of the original node number in case
of r = 0m. This confirms the assumption that stops
at the opposite side of roads, or being close to each
other in different ways are quite frequent in the source
data sets (note again the position of bus stops on the
real map shown on Figure 1). These related stops
are handled independently by most of the GTFS feeds
however from the passengers’ point of view they usu-
ally mean the same location during their journey on
the urban public transport system. Contrarily, there
are some systems (like New York City subway or the
Hungarian train system e.g.) that are almost unaf-
fected by our algorithm, namely the merging process
does not change too much the number of nodes (in
case of r = 150). These are however mainly railway
systems, where the opposite direction traffic use the
same platform or if there are multiple platforms, they
are contained by parent stations already in the original
transportation feed.
Some extracted networks in case of r = 0m con-
tain only one cluster of nodes, meaning that all the
nodes are available from any nodes via a link se-
quence. This practically means that passengers can
travel from a stop to any other by the given public
transport system. Nevertheless a significant portion of
the analyzed systems fall apart several isolated clus-
ters, where there is no connection at all between the
nodes of these separate clusters. It seems strange if
a public transport systems does not provide any ser-
vice to connect different regions, but we will see that
usually this is just a side effect of the missing parent
stations of close stops. Usually but not exclusively
one of these clusters is much larger then others, so
beside the giant cluster there are several minor clus-
ters of stops and stations.
Extracting Mass Transportation Networks from General Transit Feed Specification Datasets
89
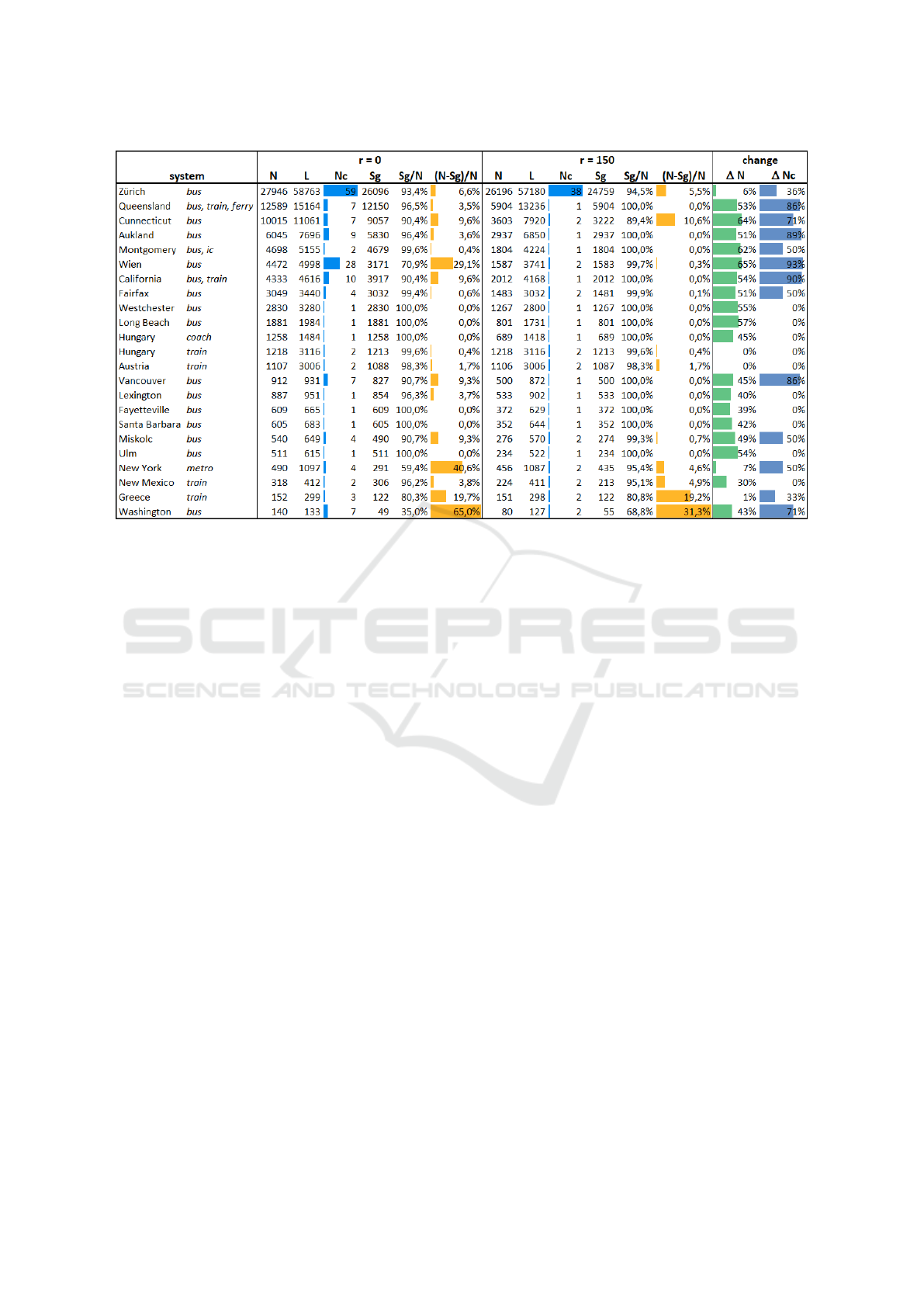
Figure 4: Basic properties of networks extracted from some example GTFS feeds for merging distance r = 0m and r = 150m.
Note the huge level of change implied as a result of merging close stops (see the last two columns). N: number of nodes in
the network, L: number of edges in the network, N
c
: number of clusters, S
g
: size of the giant cluster.
Our algorithm can transform this network by the
merging of near stops to create a new virtual station.
Our results show that using r = 150m distance im-
plies that almost all networks compose only one or
two clusters. For a passenger this means that a few
steps long walk can dramatically improve the connec-
tivity of the network. It should be mentioned, that the
only exception is the GTFS feed of Z
¨
urich, where the
service provider operates services not exclusively in
Z
¨
urich, but in further places as well resulting in small
independent clusters. The numerical results can be
seen on Figure 4.
6 CONCLUSIONS
In this paper we have given a basic introduction to
the structure of General Transit Feed Specification
highlighting the most important properties of it from
the aspect of extracting a network of connected stops
from the source feeds. Besides describing the process
we have even implemented the extraction in a free to
use tool.
We have put a special focus on the use (or not
use) of parent stations in GTFS feeds. As a possi-
ble solution to handle the problem of close stops in
the extracted networks we used the merging distance
r to describe how close stops are to be handled as be-
ing stops of the same so called ‘’virtual station”. In
some example networks extracted from various GTFS
feeds we have investigated the effect of increasing r.
We have found that the intuitive value of r = 150m
is a reasonable choice also from the aspect of our nu-
merical investigations. We have presented some basic
properties of these networks at the end.
Our ongoing research now has a focus on the use
of the tool providing more mass-transportation net-
works to be used by other scientists (with the descrip-
tion of these networks). Integrating the API of Open-
MobilityData would be e.g. a very useful extension.
We also plan to further upgrade the tool to make the
extracted network depend on more parameters. And
also we would like to provide a simple Graphical User
Interface to make the tool even more easy to be used.
We have found that building a web service for this aim
would not be worthy.
ACKNOWLEDGEMENTS
This work was supported by the EFOP-3.6.1-16-
2016-00022 project.
The project is co-financed by the European Union and
the European Social Fund.
COMPLEXIS 2022 - 7th International Conference on Complexity, Future Information Systems and Risk
90

REFERENCES
Besenczi, R., B
´
atfai, N., Jeszenszky, P., Major, R., Monori,
F., and Isp
´
any, M. (2021). Large-scale simulation
of traffic flow using markov model. PLOS ONE,
16(2):e0246062.
Braga, M., Santos, M. Y., and Moreira, A. (2014). New
Perspectives in Information Systems and Technolo-
gies, chapter Integrating Public Transportation Data:
Creation and Editing of GTFS Data, pages 53–62.
Springer.
Fortin, P., Morency, C., and Tr
´
epanier, M. (2016). Inno-
vative gtfs data application for transit network analy-
sis using a graph-oriented method. Journal of Public
Transportation, 19(4).
Gallotti, R. and Barthelemy, M. (2015). The multilayer tem-
poral network of public transport in great britain. Sci-
entific Data, 2:140056.
Hansson, J., Pettersson, F., Svensson, H., and Wretstrand,
A. (2019). Preferences in regional public transport: a
literature review. European Transport Research Re-
view, 11:38.
Harrelson, C. (2021). GTFS Reference. Google.
https://developers.google.com/transit/gtfs.
Jiang, B. (2007). A topological pattern of urban street net-
works: Universality and peculiarity. Physica A: Sta-
tistical Mechanics and its Applications, 384:647–655.
Real city map topology, traffic information (80scale-
free.
Kocsis, G. and Varga, I. (2021a). Github page of the project.
https://github.com/kocsisger/gtfs2net.
Kocsis, G. and Varga, I. (2021b). Github page of the used
gtfs feeds. https://github.com/kocsisger/gtfs.
Kujala, R., Weckstr
¨
om, C., Darst, R. K., Mladenovi
´
c,
M. N., and Saram
¨
aki, J. (2018a). A collection of pub-
lic transport network data sets for 25 cities. Scientific
Data, 5:180089. GTFS network collections of cities,.
Kujala, R., Weckstr
¨
om, C., Darst, R. K., Mladenovi
´
c,
M. N., and Saram
¨
aki, J. (2018b). A collection of pub-
lic transport network data sets for 25 cities. Scientific
Data, 5(180089).
L
¨
ammer, S., Gehlsen, B., and Helbing, D. (2006). Scaling
laws in the spatial structure of urban road networks.
Physica A: Statistical Mechanics and its Applications,
363:89–95. 20 german cities road network, distribu-
tion of cars on roads.
Ogami, Y. (2021). Fast algorithms for particle searching
and positioning by cell registration and area compar-
ison. Trends in Computer Science and Information
Technology, 007-016(6(1)).
Porta, S., Crucitti, P., and Latora, V. (2006). The network
analysis of urban streets: A dual approach. Physica A,
369:853–866. Complex network of roads of 6 cities,
node-edge swapping representation, maps, P(k), acc,
avk, apl.
Rosetta Code Community (2021). Haversine formula.
https://rosettacode.org/wiki/Haversine formula.
Sienkiewicz, J. and Hołyst, J. A. (2005). Statistical analysis
of 22 public transport networks in poland. Physical
Review E, 72:046127.
von Ferber, C., Holovatch, T., Holovatch, Y., and
Palchykov, V. (2007). Network harness: Metropolis
public transport. Physica A: Statistical Mechanics and
its Applications, 380:585–591.
Vuurstaek, J., Cich, G., Knapen, L., Ectors, W., Yasar, A.-
U.-H., Bellemans, T., and Janssens, D. (2020). Gtfs
bus stop mapping to the osm network. Future Gener-
ation Computer Systems, 110:393–406.
Wessel, N. and Farber, S. (2019). On the accuracy of
schedule-based gtfs for measuring accessibility. Jour-
nal of Transport and Land Use, 12(1):475–500.
Wong, J. C. (2013). Use of the general transit feed speci-
fication (GTFS) in transit performance measurement.
PhD thesis, Georgia Institute of Technology.
Extracting Mass Transportation Networks from General Transit Feed Specification Datasets
91
