Optimizing Multi-Quay Berth Allocation using the Cuckoo Search

Algorithm

Sheraz Aslam

, Michalis P. Michaelides

and Herodotos Herodotou

Department of Electrical Engineering, Computer Engineering and Informatics, Cyprus University of Technology, Cyprus

Keywords:

Multi-Quay Container Terminals, Multi-Quay Berth Allocation Problem, Cuckoo Search Algorithm, Port

Efﬁciency, Intelligent Maritime Transportation.

Abstract:

Proper utilization of port resources and efﬁcient berth planning play a crucial role in minimizing port conges-

tion and overall handling costs. Therefore, this study focuses on efﬁcient berth planning in maritime container

terminals composed of multiple quays. In particular, this study addresses the Multi-Quay Berth Allocation

Problem (MQ-BAP), where a continuous berthing layout is considered along with dynamic ship arrivals and

practical constraints such as safety time windows and safety distances between ships. Since MQ-BAP is an

NP-hard problem, this study proposes a metaheuristic-based approach, the Cuckoo Search Algorithm (CSA)

for solving the problem. A comparative study is also performed using real data instances collected from the

Port of Limassol, Cyprus, against a genetic algorithm solution proposed in the recent literature, as well as

the optimal exact solution implemented using MILP. The results of the experiments show the effectiveness of

our proposed CSA approach in handling real-world berth allocation in ports with multiple quays while also

considering practical constraints.

1 INTRODUCTION

Maritime transport accounts for 90% of the world’s

seaborne trade and 74% of all goods imported in, or

exported from Europe are carried by ships (Aslam

et al., 2020). According to a recent report on maritime

transport conducted by the United Nations Confer-

ence on Trade and Development (UNCTAD) in 2021

(UNCTAD, 2021), total global containerized trade

has increased by 45.45%, with Twenty-Foot Equiv-

alent Units (TEUs) totaling 110 million in 2010 and

rising to 160 million TEUs in 2021. The container

trafﬁc has also increased in 2021, even though it was

reduced in 2020 compared to 2019 due to the pan-

demic situation.

Maritime Container Terminals (MCTs) play a crit-

ical role in meeting the growing demand for seaborne

trade. To deal with the growing demand for MCTs,

there is a need to optimize their operations, beneﬁt-

ing from current technologies and optimization-based

approaches. Following this practical need, the devel-

opment of novel and efﬁcient methods for optimiz-

https://orcid.org/0000-0003-4305-0908

https://orcid.org/0000-0002-0549-704X

https://orcid.org/0000-0002-8717-1691

ing terminal operations has attracted immense atten-

tion from academia and industry (Lind et al., 2020,

2021; STEAM, 2022; STM, 2022). Michaelides et al.

(2019) have investigated the factors inﬂuencing the

various waiting times at the Port of Limassol, Cyprus,

both from a quantitative and a qualitative perspective.

For shipping, and particularly for short sea shipping,

there are obvious and immediate beneﬁts from im-

proving efﬁciency by supporting all actors involved

in the port call process to engage more easily, to give

shipping companies, port service providers, and ship

agents better information and decision support sys-

tems to boost their efﬁciency and that of their port

(Lind et al., 2019). Hence, MCTs’ operators need to

employ suitable strategies and approaches for proper

utilization of the port resources and to avoid the afore-

mentioned issues.

As MCTs handle huge volumes of containers, they

are constantly challenged to increase their produc-

tivity by introducing numerous software and hard-

ware innovations, e.g., in terminal design, cargo han-

dling equipment, automated/efﬁcient berthing oper-

ations, and operations research. MCTs can be di-

vided into three main areas, namely seaside, mar-

shaling yard, and landside areas, with each area hav-

ing its own set of terminal operations (Hsu and Chi-

124

Aslam, S., Michaelides, M. and Herodotou, H.

Optimizing Multi-Quay Berth Allocation using the Cuckoo Search Algorithm.

DOI: 10.5220/0011081200003191

In Proceedings of the 8th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2022), pages 124-133

ISBN: 978-989-758-573-9; ISSN: 2184-495X

ang, 2019). The main problems in the seaside oper-

ations include the Berth Allocation Problem (BAP),

the Quay Crane Assignment Problem (QCAP), and

the Quay Crane Scheduling Problem (QCSP) (Aslam

et al., 2021). In this study, we address the ﬁrst deci-

sion problem, namely the allocation of berths to ar-

riving ships, known as BAP. On the ﬂeet side, the

berth allocation plan determines both the berthing po-

sition and the berthing time for arriving vessels to re-

duce costs, waiting times, handling times, and depar-

ture delays. On the port side, on the other hand, an

efﬁcient berth allocation plan determines how many

ships can be handled in a planning period, with the

goal of maximizing proﬁt and making appropriate use

of port resources.

The BAP has attracted a lot of attention

from the research community and several ap-

proaches/techniques have been developed to opti-

mize seaside operations. For example, in Dulebenets

(2020), an evolutionary algorithm is proposed to deal

with BAP, where the main objective is to reduce the

weighted total service cost. Another study also deals

with BAP, while additionally considering uncertain-

ties in the operational time of ships (Xiang and Liu,

2021). In particular, an exact approach is developed

and K-means clustering is used to model the uncer-

tainty. The proposed method performs well; how-

ever, it is only suitable for small data instances. A

hybrid heuristic-based Genetic Algorithm (GA) is de-

veloped in Bacalhau et al. (2021) to solve the BAP

to avoid the issue of high computation time in ex-

act approaches. The authors combine Dynamic Pro-

gramming (DP) with the standard GA to solve large-

scale problems that minimize service cost. Guo et al.

(2021) deal with BAP, taking into account the uncer-

tainty in handling times of vessels. They develop

an optimization method to solve the BAP, combin-

ing particle swarm optimization and machine learn-

ing. Here, machine learning is used to check the re-

lationship between handling time and weather condi-

tions to model the uncertainty in handling time. They

conduct several experiments and the results conﬁrm

the effectiveness of the proposed method compared

to its counterparts. A study presented in Cheimanoff

et al. (2021) also addresses continuous and dynamic

BAP, in which a metaheuristic-based reduced vari-

able neighborhood search method is developed to op-

timally allocate berths to arriving vessels. The study

also considers tidal constraints for optimal berth as-

signment, and the main objective of this study is to

reduce the total service time of vessels. In addition, a

machine learning algorithm is used to tune the param-

eters of the metaheuristic. The proposed method has

been tested on several datasets (small and large scale)

Time (hour)

s10

Quay length (m)

Quay 1 Quay 2

Quay length (m)

Figure 1: An illustration of two continuous berthing quays

with 10 arriving ships.

and the results were compared with the exact method.

The comparative study shows the effectiveness of the

metaheuristic approach over other methods proposed

in the literature.

Most of the aforementioned studies deal only with

the allocation of berths at a single quay, assuming

that it forms one straight line in which vessels can

be berthed according to their length and the positions

of other vessels. However, this assumption is not re-

alistic for several ports around the globe, which con-

sist of multiple separate line segments or quays for

berthing (Frojan et al., 2015). For example, the Port

of Limassol in Cyprus has seven continuous berthing

quays. Considering multiple quays adds a new dimen-

sion to the BAP; the problem of assigning vessels to

quays in addition to assigning berthing positions and

times for each separate quay. This requires a multi-

ple space-time representation, as can be seen in Fig-

ure 1. Very few studies have dealt with the Multi-

Quay BAP (MQ-BAP). One study presented in Fro-

jan et al. (2015) proposes a set of priority rules and

uses GA to address the MQ-BAP. However, in their

problem formulation, the total length of the quay is

evenly distributed among the number of quays, while

the evaluation is only performed over random data.

Another study proposes a set of heuristics based on

general variable neighborhood search (Krimi et al.,

2020). Even though this approach is shown to be very

efﬁcient in solving this problem, in certain cases it

proposes solutions that are far (up to 40%) from the

optimal.

The motivation of this study is to develop a Multi-

Quay BAP model and solution that can be applied

in a real port, such as the Port of Limassol, Cyprus.

As such, we consider additional practical constraints

of the port, including the preferred berthing quay of

each arriving ship, a safety time interval between con-

secutive vessels entering the port, as well as a safety

time and distance between vessels berthed at a par-

ticular quay. First, the MQ-BAP is modeled as a

mixed-integer linear model and then solved by the

Optimizing Multi-Quay Berth Allocation using the Cuckoo Search Algorithm

125

metaheuristic-based cuckoo search algorithm (CSA).

Furthermore, we also implement the exact method us-

ing MILP and a popular heuristic method using GA

for comparison. We conduct experiments using real

data from one week of operations at the Port of Li-

massol and the results conﬁrm the effectiveness of our

proposed method.

The remaining paper is organized as follows.

Problem deﬁnition and formulation are presented in

Section 2. Next, Section 3 presents the details of the

proposed CSA method and Section 4 discloses simu-

lation setting, data instances, and simulation results.

Finally, Section 5 concludes this study.

2 PROBLEM DESCRIPTION

In this section, we ﬁrst introduce the MQ-BAP along

with assumptions, and then we formulate the problem

as a mixed-integer linear problem.

2.1 Problem Deﬁnition

In contrast to existing studies, and to make the prob-

lem more practical, this work considers MCT with

multiple quays (having continuous berthing layouts)

to berth arriving vessels, i.e., Q = {1, ...|Q|}. A con-

tinuous quay q ∈ Q consists of a section of the berth

line at the MCT and arriving ships can be moored at

any point along the berth line, representing the avail-

able berthing positions at q, i.e., B

= {1, ...|B

|}.

The set T indicates the set of time intervals consid-

ered for planning, i.e., T = {1, 2, 3, ...|T |}. There is

a set of arriving ships S = {1, 2, 3, ...|S|} and each

ship s ∈ S has multiple known characteristics, includ-

ing Length of Ship (LoS), Expected Time of Arrival

(ETA), Expected Time of Departure (ETD), Handling

Time (HT), and Preferred Berthing Quay (PBQ). Ta-

ble 1 presents the mathematical notations that are

used in this section.

The objective of this study is to determine the

berthing quay, berthing position, and berthing time

for all arriving ships in S in order to minimize the

total cost associated with the berthing process. The

cost against ship s includes handling cost C

, waiting

cost C

, penalty cost due to late departures C

, and

penalty cost due to allocation of ships to non-optimal

berthing quay C

noq

. The handling cost includes the

cost of loading and unloading of containers and de-

pends on the handling time T

of ship s. The wait-

ing cost is calculated based on the waiting time T

which is the difference between the estimated arrival

time T

and the berthing time T

. The late departure

penalty cost C

depends on the late departure time

, which is deﬁned as the difference between the

operations ﬁnishing time T

and the requested depar-

ture time T

of each ship. The last penalty cost C

noq

is added if the ship s is not moored to its preferred

berthing quay (PBQ) but rather it is moored to an al-

ternative berthing quay (ABQ), since more resources

are needed to move containers over a longer distance.

ABQs are introduced in this study to constraint the

algorithm to select only appropriate quays (i.e., either

the preferred or alternative quays) for berthing a ves-

sel since in practical scenarios, not all quays can han-

dle all vessels (e.g., due to lack of proper equipment).

2.2 Assumptions

The problem under consideration and the solution are

based on the following assumptions:

• The number of incoming ships in the planning pe-

riod is known;

• When a vessel commences operations at a partic-

ular quay, it cannot be interrupted until the opera-

tions are completed;

• Berths from any quay become available immedi-

ately after a ship completes its operations;

• The number and length of the quays are known;

• The ETA along with ETD for all arriving ships are

known;

• The handling time for each vessel is known;

• Each vessel has a PBQ and an optional list of

ABQs that are known in advance;

• All berths are assumed to be free at the beginning

of the time horizon (time = 0);

• All penalty costs for all vessels are known;

2.3 Mathematical Formulation

The total handling cost of a ship s that is planned

for berthing at position B

of a particular quay Q

time T

includes a waiting cost, a handling cost, and

a penalty for late departure, presented as:

Cost(s, Q

, B

, T

) = T

·C

+ T

·C

· f (Q

, B

, PBQ

, ABQ

, C

noq

)

+ T

·C

(1)

The ﬁrst term in Equation (1), T

·C

, shows the wait-

ing cost when a ship s has to wait for mooring. The

waiting time T

of ship s is calculated as the differ-

ence between the ETA T

and berthing time T

VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems

126

Table 1: Mathematical Notations.

Name Explanation

ABQ

Alternative berthing quays for ship s

Berthing position of ship s at quay Q

Handling cost per time unit (hour) for ship s

Waiting cost per time unit (hour) for ship s

noq

Penalty cost against non-optimal berthing

quay (ﬁxed cost) for ship s

Penalty cost against late departure per time

unit (hour) for ship s

Length of ship s

Length of quay q

PBQ

Preferred berthing quay of ship s

Berthing quay of ship s

SD Safety distance (in meters) between two

ships during berthing

SE Safety entrance time between two ships

ST Safety time between two ships during

berthing on the same quay

Berthing time of ship s

Expected/estimated arrival time of ship s

Finish time of operations (loading and/or

unloading) of ship s

Handling time of ship s

Late departure time of ship s

Requested departure time of ship s

Waiting time of ship s

s ∈ S = {1, 2, ..., |S|} Individual ship

q ∈ Q = {1, 2, ..., |Q|} Berthing quay

b ∈ B

= {1, 2, ..., |B

|} Berthing position in quay q

t ∈ T = {1, 2, ..., |T |} Single time period

= T

− T

, ∀ s ∈ S (2)

The second term in Equation (1), T

· C

f (Q

, B

, PBQ

, ABQ

, C

noq

) represents the total pro-

cessing cost of ship s that was incurred by unloading

and loading containers from/to ship s, where T

and

denote handling time for ship s and handling cost

per unit time, respectively.

Without loss of generality, this work

also introduces the penalty function

f (Q

, B

, PBQ

, ABQ

, C

noq

), which penalizes the

handling cost due to non-optimal quay assignment,

as presented in Equation (3). The penalty cost equals

0 if ship s is moored at its preferred berthing quay

PBQ

and C

noq

if s is moored at one of the alternative

berthing quays ABQ

. Otherwise, the penalty is set

to inﬁnite to ensure the algorithm will never perform

such an assignment.

f (Q

, B

,PBQ

, ABQ

, C

noq

) =











0 , if Q

= PBQ

noq

, else if Q

∈ ABQ

∞ , otherwise

(3)

The ﬁnal term T

·C

in Equation (1) calculates the

late departure penalty cost against ship s when it de-

parts after a requested departure time. The delay in

departure time T

of ship s is computed as the differ-

ence between the time of operations completion T

and the requested time of departure T

= max{T

− T

, 0}, ∀ s ∈ S (4)

where, T

can be calculated as,

= T

+ T

, ∀ s ∈ S (5)

The primary objective of the MQ-BAP is to allo-

cate optimal quays and berthing positions along with

berthing times to arriving ships such that the total pro-

cessing cost (that includes waiting cost, handling cost,

and various penalties) can be minimized, as presented

by the following objective function:

minimize

∑

s ∈ S

∑

q ∈ Q

∑

b ∈ B

∑

t ∈ T

Cost(s, q, b, t) · x

sqbt

(6)

subject to the following constraints.

sqbt

∈ {0, 1}, ∀ s ∈ S, q ∈ Q, b ∈ B

, t ∈ T (7)

The variable x

sqbt

is 1 if ship s is assigned to berthing

position b of quay q at berthing time slot t, and 0 oth-

erwise.

∑

q ∈ Q

∑

b ∈ B

∑

t ∈ T

sqbt

= 1, ∀ s ∈ S, (8)

Constraint (8) states that each ship is assigned to a

particular quay q and berthing position b only once

(at time t) during the planning period T .

≥ T

, ∀ s ∈ S. (9)

Constraint (9) deﬁnes that the proposed berthing time

for particular ship s must be equal or greater than

its expected arrival time T

+ L

≤ L

, ∀ s ∈ S, (10)

Constraint (10) ensures that the summation of the pro-

posed berthing position B

and the ship length L

must

always be equal to or less than the quay length L

Optimizing Multi-Quay Berth Allocation using the Cuckoo Search Algorithm

127

∑

j̸=s ∈ S

+SD

∑

b=B

−L

−SD+1

+ST

∑

t=T

−T

−ST +1

jqbt

= 0,

∀ s, j ∈ S, q ∈ Q

(11)

Constraint (11) avoids scheduling overlapping of two

or more ships. For example, suppose ship s is sched-

uled to berth at time 6h, has a processing time of 5h,

uses berth position 600m, and its length is 300m. As

per constraint (11), no other vessel can use position

from 600m to 900m (as length of ship s is 300m) in

the time interval 6h to 11h. Furthermore, another ves-

sel j with a length of 200m and a processing time of

4h cannot be berthed at positions from 401m to 900m

(ignoring the safety distance) in the time interval 3h to

11h (ignoring the safety time) because it would over-

lap with previous vessel s. Furthermore, constraint

(11) is also responsible for keeping the safety distance

SD and safety time ST between two ships in order to

avoid any dangers during berthing. Visually, this con-

straint ensures that any two rectangles (denoting the

time intervals and berthing positions allocated to ves-

sels) shown in Figure 1 can never overlap.

− T

≥ SE ∀ s ̸= j ∈ S, (12)

Finally, constraint (12) ensures a minimum safety en-

trance time period SE between sequential berthings,

regardless of berthing quay, since at the Port of Li-

massol, like many other ports around the world, there

is a single port entrance that all ships must sequen-

tially enter to berth (see the red triangle in Figure 2).

3 PROPOSED METHOD

In this study, we employ the Cuckoo Search Algo-

rithm (CSA) to address MQ-BAP. CSA is a meta-

heuristic optimization algorithm developed by (Yang

and Deb, 2009). The CSA is inspired by the breed-

ing mechanism of some cuckoo species, which are

fascinating because of their beautiful sounds and ag-

gressive reproduction mechanism. Some cuckoos lay

their eggs in communal nests of other species, where

they try to remove the eggs of other birds in or-

der to improve the hatching probability of their own

eggs. Then, other birds, probably from other species,

known as host birds take care of cuckoo eggs. How-

ever, if the host birds realize that some eggs do not

belong to them, then the cuckoo eggs are disposed

of or current nests are destroyed and built elsewhere.

In particular, some cuckoo species (e.g., new world

brood-parasitic Tapera) specialize in the mimicry of

the pattern or color of eggs and they lay their eggs in

nests of relevant species in order to reduce the prob-

ability of their eggs being thrown or destroyed (Gan-

domi et al., 2013). Overall, the CSA works based on

the behavior of cuckoos for laying eggs and adopts

three idealized rules (Yang and Deb, 2009):

1. each cuckoo bird dumps only one egg at a time in

a random nest;

2. the best nests having high quality eggs are kept

and used for the next generation;

3. the number of host nests is ﬁxed and the egg laid

by a cuckoo is detected by a host bird with proba-

bility p

∈ (0, 1).

The mapping of CSA to MQ-BAP is as follows. A

single nest shows a set of solutions containing the

mooring positions and mooring times of all arriving

ships. An egg in a nest denotes a berthing time or

berthing position in a berthing quay for an arriving

ship, whereas, a cuckoo egg shows a novel (or better)

solution (i.e., a berthing time or position in a quay).

The total search space of the problem at each iteration

is reﬂected by the total number of host nests, which is

ﬁxed (100 host nests are assumed in this study). In

addition, each nest includes 2N eggs, where N shows

the number of ships that have arrived at a given time.

Therefore, the total number of eggs in a nest is twice

the total number of ships arriving. This is because

we need two solutions for each ship (i.e., one is the

berthing time and the other is the berthing position).

The overall goal of the algorithm is to use cuckoo

eggs (better solutions) to replace the not-so-good eggs

in the various nests.

4 SIMULATION RESULTS

In this section, we present the simulation setup along

with the simulation results. We propose and imple-

ment metaheuristic-based CSA for the berth alloca-

tion problem when considering multiple quays (MQ-

BAP). We also implement the GA, a popular meta-

heuristic approach proposed in Salhi et al. (2019), and

the exact solution using MILP for comparison pur-

poses. Simulations are performed on a PC with Core

i7 using MATLAB 2018b. Regarding the dataset,

we employ real-world data collected from the Port of

Limassol, Cyprus, which contains information about

each arriving ship, i.e., ETA, ETD, LoS, processing

time of ship, and preferred berthing quay (as the Port

of Limassol has multiple quays). The data are col-

lected directly from a port calls database and are con-

verted into a more suitable format for processing. For

example, time is discretized into ﬁxed-time intervals

for easier processing by the scheduling algorithms. In

VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems

128

Table 2: Example data for 10 ships (out of the 28 ships) in our dataset that arrived at the Port of Limassol, Cyprus).

Ship # ETA (day\time) HT (min.) ETD (day\time) PBQ LoS (meters)

1 1\04:00 919 1\22:30 Container/ Ro-Ro Quay 194

2 1\05:30 1490 2\06:50 East Quay 139

3 1\14:00 1285 2\12:50 West Quay 84

4 1\15:00 5700 5\14:03 East Quay 89

5 1\17:00 5970 5\21:00 West Quay 190

6 2\04:30 470 2\13:50 Container/ Ro-Ro Quay 159

7 2\05:00 168 2\09:30 Container Quay 196

8 2\08:00 440 2\15:55 North Quay 155

9 3\04:00 905 3\20:50 Container/ Ro-Ro Quay 175

10 3\03:30 1331 4\06:15 Container Quay 277

Figure 2: A satellite view of the Port of Limassol, Cyprus illustrating its seven berthing quays (taken from ais.cut.ac.cy

(2022)).

the future, we plan to implement a graphical user in-

terface for visualizing the output of the algorithm to

the berth planner in a user-friendly manner. Table 2

shows a sample of the collected data for 10 arriving

ships. The full dataset contains a total of 28 ships that

arrived at the port during a period of one week. We

implement the proposed and compared methods on

the same dataset and the results are presented later in

this section. As for cost calculations, we assume the

handling cost is 10 euro/hour, the waiting cost is 20

euro/hour, and the late departure cost is 20 euro/hour.

A satellite view of the Port of Limassol is shown in

Figure 2. There are a total of seven quays in the Port

of Limassol but only ﬁve appear in the dataset (i.e.,

only the ones that handle commercial trafﬁc), namely

Container/ Ro-Ro Quay, Container Quay, East Quay,

West Quay, and North Quay, and are all of different

lengths, as shown in Table 3. Note that all arriving

ships have a preferred berthing quay for performing

loading and unloading operations, but currently, the

dataset does not include a preferred berthing position

or alternative berthing quays.

Figure 3 shows the berth allocation plan obtained

by the 3 implemented solutions: (a) CSA, (b) GA,

and (c) MILP. The berthing plan is developed accord-

ing to the objective function of this study (given in

Equation (6)) and considering all constraints. In this

ﬁgure, the horizontal axis shows the berthing time di-

vided into 30-minute intervals, and the vertical axis

shows the berthing positions of the arriving vessels.

Optimizing Multi-Quay Berth Allocation using the Cuckoo Search Algorithm

129

(a) Solution by CSA

(b) Solution by GA

Figure 3: Berth allocation solutions over one week for ﬁve quays at the Port of Limassol, Cyprus.

VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems

130

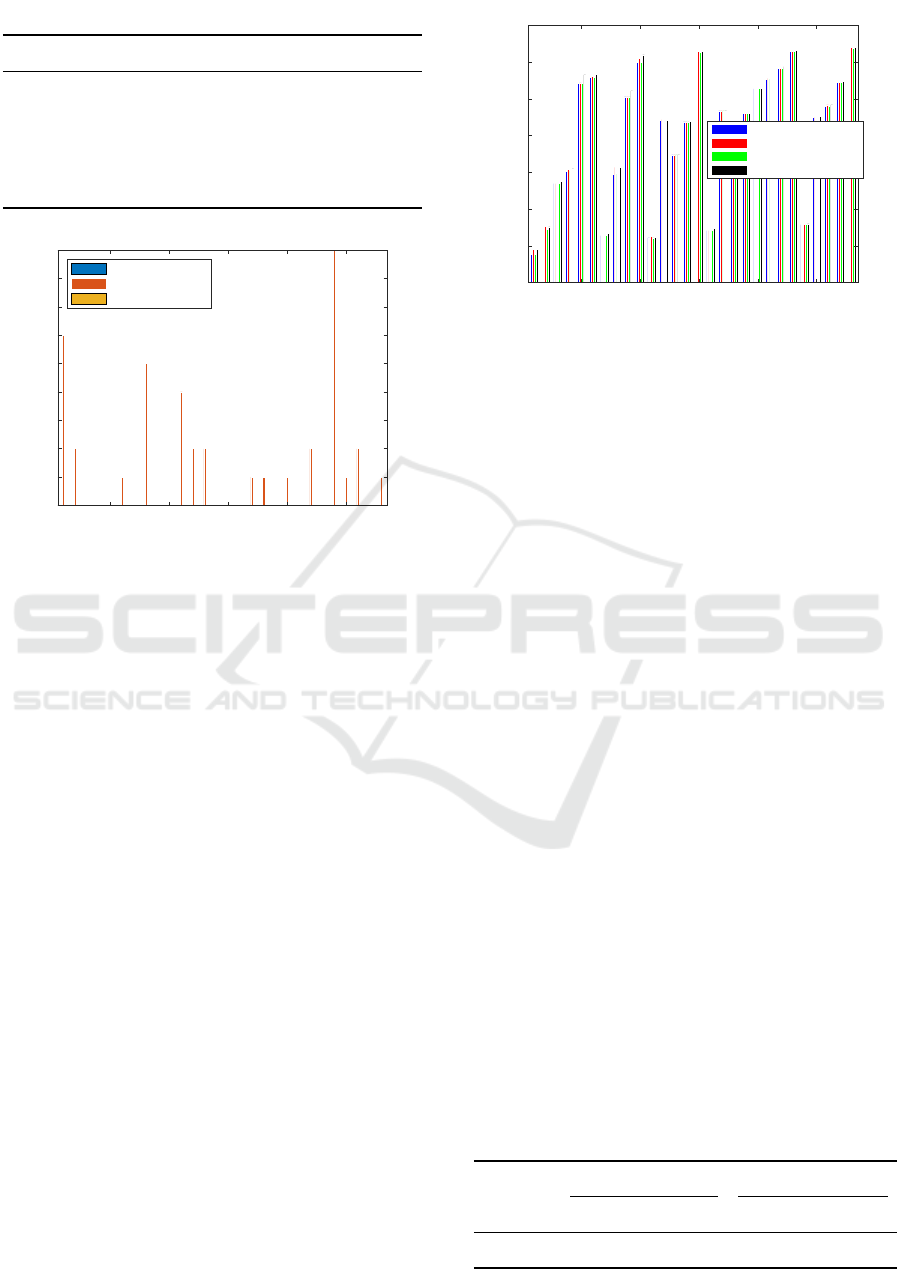
Table 3: Quays at the Port of Limassol, Cyprus.

Quay # Quay name Length (m)

1 Container/ Ro-Ro Quay 450

2 Container Quay 800

3 East Quay 480

4 West Quay 770

5 North Quay 430

5 10 15 20 25

Ships

Time (30-min interval)

Waiting time by CSA

Waiting time by GA

Waiting time by MILP

Figure 4: Waiting time for all arriving ships when using

all three algorithms, i.e., CSA, GA, and MILP. The only

induced waiting times are reported when using GA.

Each rectangle demonstrates the berthing positions

and berthing time intervals assigned to each ship.

Furthermore, the label next to the rectangle corre-

sponds to the vessel index. For example, ship 8 ar-

rives at 8:00 on the second day and the PBQ is ‘North

Quay’. It can be observed that the CSA (see Figure

3a) efﬁciently assigns a berth (without any waiting

time) to ship 8 at its PBQ. However, if we look at

the berth allocation for ship 8 for GA (see Figure 3b),

we can observe that ship 8 has to wait for an opti-

mal berthing and the waiting time is 5 time slots (2.5

hours). However, despite the delay of 5 time slots

in berthing, ship 8 can reach the desired departure

time. Figure 3c shows the optimal berth allocation

plan computed using the exact method, i.e., MILP.

Figure 4 clearly shows that MILP and CSA always

provide an optimal solution with regards to minimiz-

ing waiting times because there is no waiting time

before berthing. However, using GA, 14 out of the

28 ships have to wait, with a maximum waiting time

of 9 slots (4.5 hours) before they can berth. As for

the departure time, we can see from Figure 5 that no

ship departs late when using any of the three algo-

rithms, i.e., CSA, GA, and MILP. Even with GA, sev-

eral ships are late in docking, but they can still achieve

the desired departure time. In this case, penalty cost

for waiting time is calculated, and therefore the to-

5 10 15 20 25

Ships

100

150

200

250

300

350

Time (30-min interval)

Solution by CSA

Solution by GA

Solution by MILP

Requested departure time

Figure 5: Requested and proposed departure times when

using all three algorithms, i.e., CSA, GA, and MILP.

tal handling cost (shown in Equation 1) using GA is

higher than our proposed CSA and MILP methods.

Note that the total handling cost is the sum of the total

waiting cost, the handling cost (including the penalty

for non-optimal quay assignment), and the penalty for

late departure.

Table 4 shows the total handling cost for the 28

vessels and the computational time for all three algo-

rithms. From this table, it can be seen that the total

costs of the CSA and MILP methods are the same,

which shows that CSA achieves an optimal solution

for all arriving ships for this particular dataset. How-

ever, for GA, the total cost is 11.2% higher because

some of the ships have to wait for a long time before

berthing. As for the computation time, MILP takes

910.76 seconds and, as expected, its computation time

is orders of magnitude higher than the other two algo-

rithms. However, our proposed CSA method and GA

solve the same problem in near real time, with only

4.49 and 1.79 seconds, respectively. Even though GA

achieves the minimum computation time (1.79 sec-

onds) to handle a week’s worth of data, it fails to pro-

vide an optimal solution.

It is worth noting that for larger problems, the

exact method (MILP) cannot be used because it re-

portedly requires over 100 hours CPU time for large

datasets (Aslam et al., 2021). Such times are cer-

tainly not acceptable in the context of MCT oper-

ations. From the above discussion, it appears that

CSA can provide an optimal or near-optimal solution

within an acceptable computation time.

Table 4: Comparison of proposed and benchmark methods.

Total Cost (Euro) Comp. Time (Sec)

Method: CSA GA MILP CSA GA MILP

1-week 5385 6025 5385 4.49 1.79 910.76

Optimizing Multi-Quay Berth Allocation using the Cuckoo Search Algorithm

131

5 CONCLUSION

Over the past decade, international maritime trade has

increased dramatically. In order to serve the growing

number of vessels arriving at the terminal for loading

and unloading, MCTs need to increase their efﬁciency

by using various technologies and methods. This

study focuses on the Multi-Quay BAP and proposes

a metaheuristic-based CSA method to solve the prob-

lem. A continuous berthing layout is considered and

the ships arrive dynamically. The problem is ﬁrst for-

mulated as a mixed-integer linear problem and then

solved by CSA. In addition, two benchmark meth-

ods (i.e., GA and MILP) are also implemented in this

study for comparison. To conﬁrm the performance of

our proposed method, simulations are conducted us-

ing real data from the Port of Limassol, Cyprus. The

data contains 28 ships arriving in a period of one week

and intending to dock at ﬁve different quays. The re-

sults of the experiments conﬁrm the beneﬁts of the

proposed method with 11.2% lower cost than GA and

200x lower computation time than MILP.

In the future, we plan to examine the perfor-

mance of the proposed CSA method on larger real-

world datasets, containing several vessels and span-

ning longer planning time periods (days to weeks).

We also plan to extend the modeling to incorporate

a hybrid berthing layout that includes both discrete

and continuous berthing layouts. Finally, we plan to

investigate the application of the CSA in solving the

berth allocation problem combined with the related

quay crane assignment and scheduling problems.

ACKNOWLEDGEMENTS

This work was supported by the European Re-

gional Development Fund and the Republic of Cyprus

through the Cyprus Research and Innovation Founda-

tion (STEAM Project: INTEGRATED/0916/0063).

REFERENCES

ais.cut.ac.cy (2022). Map of the Port of Limassol, Cyprus

by Ship Tracking Intelligence Platform. https://ais.cut.

ac.cy.

Aslam, S., Michaelides, M. P., and Herodotou, H. (2020).

Internet of ships: A survey on architectures, emerging

applications, and challenges. IEEE Internet of Things

Journal, 7:9714–9727.

Aslam, S., Michaelides, M. P., and Herodotou, H.

(2021). Dynamic and continuous berth allocation us-

ing cuckoo search optimization. In VEHITS, pages

72–81.

Bacalhau, E. T., Casacio, L., and de Azevedo, A. T. (2021).

New hybrid genetic algorithms to solve dynamic berth

allocation problem. Expert Systems with Applications,

167:114198.

Cheimanoff, N., Fontane, F., Kitri, M. N., and Tchernev,

N. (2021). A reduced vns based approach for the dy-

namic continuous berth allocation problem in bulk ter-

minals with tidal constraints. Expert Systems with Ap-

plications, 168:114215.

Dulebenets, M. A. (2020). An adaptive island evolutionary

algorithm for the berth scheduling problem. Memetic

Computing, 12(1):51–72.

Frojan, P., Correcher, J. F., Alvarez-Valdes, R., Koulouris,

G., and Tamarit, J. M. (2015). The continuous

berth allocation problem in a container terminal with

multiple quays. Expert Systems with Applications,

42(21):7356–7366.

Gandomi, A. H., Yang, X.-S., and Alavi, A. H. (2013).

Cuckoo search algorithm: a metaheuristic approach

to solve structural optimization problems. Engineer-

ing with computers, 29(1):17–35.

Guo, L., Wang, J., and Zheng, J. (2021). Berth allocation

problem with uncertain vessel handling times consid-

ering weather conditions. Computers & Industrial En-

gineering, 158:107417.

Hsu, H.-P. and Chiang, T.-L. (2019). An improved shuf-

ﬂed frog-leaping algorithm for solving the dynamic

and continuous berth allocation problem (dcbap). Ap-

plied Sciences, 9(21):4682.

Krimi, I., Todosijevi

c, R., Benmansour, R., Ratli, M.,

El Cadi, A. A., and Aloullal, A. (2020). Modelling and

solving the multi-quays berth allocation and crane as-

signment problem with availability constraints. Jour-

nal of Global Optimization, 78(2):349–373.

Lind, M., Michaelides, M., Ward, R., Herodotou, H., and

Watson, R. (2019). Boosting data-sharing to improve

short sea shipping performance: Evidence from limas-

sol port calls analysis. Technical Report 35, UNCTAD

Transport and Trade Facilitation Newsletter No. 82 -

Second Quarter.

Lind, M., Michaelides, M. P., Robert, W., and Richard,

W. T. (2020). Maritime informatics. Springer.

Lind, M., Michaelides, M. P., Robert, W., and Richard,

W. T. (2021). Maritime informatics: Additional Per-

spectives and Applications. Springer.

Michaelides, M. P., Herodotou, H., Lind, M., and Watson,

R. T. (2019). Port-2-port communication enhancing

short sea shipping performance: The case study of

Cyprus and the Eastern Mediterranean. Sustainabil-

ity, 11(7):1912.

Salhi, A., Alsouﬁ, G., and Yang, X. (2019). An evolutionary

approach to a combined mixed integer programming

model of seaside operations as arise in container ports.

Annals of operations research, 272(1-2):69–98.

STEAM (2022). STEAM: Sea Trafﬁc Management in the

Eastern Mediterranean. https://steam.cut.ac.cy.

STM (2022). STM: Sea Trafﬁc Management Validation.

http://stmvalidation.eu/.

UNCTAD (2021). Review of maritime transport 2021.

United Nations Conference on Trade and Devel-

VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems

132

opment, New York. https://unctad.org/system/ﬁles/

ofﬁcial-document/rmt2021 en 0.pdf.

Xiang, X. and Liu, C. (2021). An expanded robust optimisa-

tion approach for the berth allocation problem consid-

ering uncertain operation time. Omega, 103:102444.

Yang, X.-S. and Deb, S. (2009). Cuckoo Search via L

evy

Flights. In World Congress on Nature & Biologically

Inspired Computing (NaBIC), pages 210–214. IEEE.

Optimizing Multi-Quay Berth Allocation using the Cuckoo Search Algorithm

133