Classiﬁcation Techniques Use to Empirically Validate Redundancy

Metrics as Reliability Indicators based on Fault-proneness Attribute

Dalila Amara

and Latifa Ben Arfa Rabai

Universit

e de Tunis, Institut Sup

erieur de Gestion de Tunis, SMART Lab, Tunis, Tunisia

Keywords:

Software Reliability, Software Redundancy Metrics, Software Metrics Validation, Fault-proneness.

Abstract:

Software metrics are proposed as quantitative measures of internal quality factors like cohesion and complex-

ity. For the external ones such as reliability and maintainability, they are usually predicted by means of various

metrics of internal attributes. In this context, we have focused on a suite of four entropy-based software redun-

dancy metrics considered as software reliability indicators. Despite their important purpose, they are manually

computed and only theoretically validated. Hence, we have implemented an empirical approach for assessing

these metrics, using a set of programs retrieved from real software projects. Given that software reliability

as external attribute, cannot be directly evaluated, we employ other measurable quality factors representing

direct reﬂections of this attribute. Among them, defect density and fault-proneness are widely used as means

to measure and predict software reliability based on software metrics. The basic idea is to generate an empiri-

cal dataset embodying for each program, the values of the redundancy metrics and the values of one of these

measurable attributes. In our previous work, we have studied their relationship with the defect density attribute

in order to validate them as useful reliability indicators. Promising results indicating the usefulness of these

metrics as defect density indicators are obtained. Classifying modules (functions or classes) as defective or not

defective is also an important reliability indicator. Literature review shows that software reliability counts on

its fault-prone modules and more trusted software consists of less fault-prone units. Therefore, we aim in this

paper to propose an empirical approach to validate the redundancy metrics as signiﬁcant reliability indicators.

The validation is carried out using the accuracy measure and results show that the fault proneness attribute can

be predicted using the redundancy metrics with a good accuracy rate of 0.82.

1 INTRODUCTION

One common way to verify and validate software

quality is software testing which consists on identi-

fying software faults (Lyu et al., 1996). This process

takes too much time and requires a large amount of

resources (Gondra, 2008). Therefore, methodologies

of predicting software quality prior the testing phase

are required to increase the efﬁciency of time, effort

and cost usage. Software quality prediction requires

the development of a measurement plan providing

the needed data on software factors (Arvanitou et al.,

2017). Software quality measurement consists on

assigning numbers or symbols to software factors to

evaluate their performance using software metrics

(Nakai et al., 2016; Fenton and Bieman, 2014).

These metrics provide quantitative values of different

software factors related to the process and product

https://orcid.org/0000-0001-9938-2384

https://orcid.org/0000-0002-5657-4682

entities. In addition, they are used to develop quality

prediction models (Reddivari and Raman, 2019).

Most of software metrics were deﬁned to evaluate

internal quality attributes including coupling and

complexity (Chidamber and Kemerer, 1994). For

external attributes like reliability and maintainabil-

ity, their measurement was usually determined by

combining different metrics measuring internal char-

acteristics (Briand and W

ust, 2002; Jabangwe et al.,

2015). According to (Fenton and Bieman, 2014),

external attributes are more difﬁcult to understand

than internal ones since they depend on the program

behaviour and they are available at later phases

of the development process. Thus, further studies

focusing on the prediction of these attributes still

required. Authors in (Mili et al., 2014) proposed a

suite of metrics to monitor software reliability by

evaluating the code redundancy based on Shannon

entropy measure. The main limitation of this suite is

the lack of an empirical validation showing its utility

Amara, D. and Rabai, L.

Classiﬁcation Techniques Use to Empirically Validate Redundancy Metrics as Reliability Indicators based on Fault-proneness Attribute.

DOI: 10.5220/0011081900003176

In Proceedings of the 17th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE 2022), pages 209-220

ISBN: 978-989-758-568-5; ISSN: 2184-4895

209

as reliability indicator. As software reliability is an

external attribute that cannot be directly evaluated,

we have focused on measurable attributes that reﬂect

it to address this issue. In our previous work (Amara

et al., 2021), we have studied the relationship be-

tween the redundancy metrics and the defect density

attribute in order to validate them as useful reliability

indicators. Promising results indicating the useful-

ness of these metrics as defect density indicators

are obtained. Fault-proneness was also identiﬁed

as an important reliability indicator (Gondra, 2008;

Singh et al., 2018). Authors in (Verma and Kumar,

2017) noted that software reliability counts on its

fault-prone modules; more trusted software consists

of less faultprone units. Thus, it will be possible

to monitor software reliability by predicting the

number of faultprone modules based on software

metrics (Gyimothy et al., 2005; Olague et al., 2007;

Jabangwe et al., 2015).

Therefore, we aim in this paper to use the fault-

proneness attribute to answer this question: Are

redundancy metrics useful for software reliability

prediction? To perform the empirical assessment

and validation of the redundancy metrics, the data

collection phase is required. For that step, Apache

Common Mathematics Library was deployed in this

research. Given its availability, two main elements of

data are obtained:

• Different classes satisfying the redundancy met-

rics’ assumption (Metrics are computed at

method-level. These methods manipulate input

and output variables. This means programs with

input states represented by the declared variables

and output states represented by the modiﬁed

states of these variables (Mili et al., 2014)) are se-

lected to compute them in order to construct an

empirical data set containing the values of these

metrics.

• The bug information of the selected classes

needed to compute the values of the fault-

proneness attribute was unavailable. Therefore, a

fault injection procedure was used to obtain them

and to perform the empirical validation of the re-

dundancy metrics. Thus, in this study, the dataset

we used to perform our validation and to train and

evaluate the classiﬁcation models contains the val-

ues of the redundancy metrics for each function

and the related fault-proneness (0 or 1) attribute.

Different experiments based on classiﬁcation tech-

niques are conducted to address these issues. The val-

idation is carried out using the accuracy measure and

results conﬁrm the predictive capability of the redun-

dancy metrics for software fault prediction.

The paper is organized as follows: Section 2 sum-

marizes the purpose of the redundancy metrics and

provides an overview of software fault-proneness pre-

diction. Section 3 presents the empirical validation

approach, the data set collection and analysis proce-

dures. Section 4 describes the performed experiments

and results. Section 5 presents the discussion and

threats to validity. Finally, Section 6 includes the con-

clusion.

2 RELATED WORKS

In this section, we present the purpose of the redun-

dancy metrics. We also provide an overview of soft-

ware fault prediction using software metrics.

2.1 Software Reliability

Software reliability is an important software qual-

ity attribute deﬁned as the probability of failure-free

operation for a speciﬁed period of time in a speci-

ﬁed environment. It can be described by other sub-

characteristics like maturity, availability, fault toler-

ance and recoverability (Febrero et al., 2016; Amara

and Rabai, 2017). For (Bansiya and Davis, 2002), it

is one of high-level quality attributes that cannot be

directly observed and measured.

Different models based on direct metrics were

proposed to predict it (Catal and Diri, 2009; Radjen-

ovi

c et al., 2013). These models used software met-

rics (called independent variables) to evaluate mea-

surable reliability attributes (called dependent vari-

able) like defect density, fault-proneness and defect

count (Briand and W

ust, 2002). Authors in (Mili

et al., 2014) also proposed a suite of four metrics

to monitor programs reliability based on their redun-

dancy. Different forms of software redundancy were

deﬁned including information redundancy (code re-

dundancy) (Shannon, 2001), functional redundancy

(Asghari et al., 2018) and time redundancy (Dubrova,

2013). The redundancy metrics proposed by (Mili

et al., 2014) assess the information redundancy pro-

vided by the different states of the program (Shannon,

2001). These states reﬂect the uncertainty about the

outcome of the program’ variables. The terminology

related to program states includes (Mili et al., 2014):

• Software program state: is the set of values given

by its variables which may change by one or more

actions (functions) of the program.

• State space: is the set of values taken by the de-

clared program variables.

ENASE 2022 - 17th International Conference on Evaluation of Novel Approaches to Software Engineering

210

• Initial state space: is the state of the program rep-

resented by its input variables.

• Current state (actual state): represents the differ-

ent states that the program may be in at any given

point in the program.

• Final state space: represents the state of the pro-

gram that is produced by its outputs for the rele-

vant initial states.

• State redundancy: the extra range of values al-

lowed by a program than it is needed to represent

the program states. The state redundancy is rep-

resented by the initial and ﬁnal state redundancy

metrics deﬁned above.

Example 1 illustrates these deﬁnitions.

Example 1: Let a program (method) g deﬁned by:

int s; /∗ state space of g∗/

s=2; /∗ initial state of g ∗/

s=s+1; /∗ internal state 1 of g∗/

s=2∗s; /∗ internal state 2 of g∗/

s=ss=s+12; /∗ ﬁnal state of g ∗/

2.2 Software Redundancy Metrics Suite

Redundancy metrics were deﬁned based on Shannon

entropy measure of programs code (Shannon, 2001).

Four metrics were deﬁned which are initial state re-

dundancy, ﬁnal state redundancy, functional redun-

dancy and non-injectivity (Mili et al., 2014).

2.2.1 Initial and Final State Redundancy

Metrics

The state redundancy represents the gap between the

declared state and the actual state (really used) of a

program (Mili et al., 2014; Ayad et al., 2018). For in-

stance, the age of an employee is generally declared

as an integer variable type. However, only a restrict

range i.e between 0 and 120 is really required. This

means that 7 bits are sufﬁcient to store the age vari-

able but the typical 32 bits size of an integer variable

is used. The unused bits measure the code redun-

dancy. The program moves from its initial states (σ

)

to its ﬁnal states (σ

), then two state redundancy mea-

sures namely initial state redundancy (ISR) and ﬁnal

state redundancy (FSR) were deﬁned by:

ISR(g) =

H(S) − H(σ

)

H(S)

(1)

FSR(g) =

H(S) − H(σ

)

H(S)

(2)

Notation:

ISR is the gap between the declared state and the

initial state of the program.

FSR is the gap between the declared state and the

ﬁnal state of the program

S is the program’ declared state represented by

its all declared variables.

H(S) is the state space of the program as the max-

imum entropy (bits) taken by its declared

variables.

is the initial state of the program g, repre-

sented by its input variables.

H(σ

) is the state space (entropy) of the initial pro-

gram’ state.

is the ﬁnal state of the program given by its

output variables.

H(σ

) is the entropy of the ﬁnal program’ state.

To compute the state redundancy (SR) metric (ISR

and FSR), each data type is mapped to its width in

bits. For instance, for Java language, the entropy of

variable declarations of basic data types is illustrated

in Table 1.

Table 1: Entropy for basic data type.

Data type Entropy

Boolean 1

Byte 8

Char, short 16

Int, ﬂoat 32

Double, long 64

Example 2: Let a program (method) g deﬁned by:

int x, y, z; // the program state is represented by x, y

and z variables

x= 21; // initial state of x

y= 90; // initial state of y

z=(x+y)/2; // ﬁnal state

The declared space of this program is deﬁned by

three integer variables; x, y and z, hence, using the

metrics deﬁnitions, H(S) = 96 bits since 3 integer vari-

ables are used. Its initial state is deﬁned by three

variables; x, y and z. The input variables x and y

require respectively 5 and 7 bits to be stored. The

output variable z has a free range (32 bits). Hence

H(σ

) = 5+7+32= 44 bits. For the ﬁnal state, is de-

termined by the state of the variable z (its entropy),

H(σ

) =H((21+90)/2)=6 bits, then: ISR= (96-44)/96

=0.54 FSR= (96-6)/96 =0.93

Classiﬁcation Techniques Use to Empirically Validate Redundancy Metrics as Reliability Indicators based on Fault-proneness Attribute

211

2.2.2 Functional Redundancy Metric (FR)

According to (Mili et al., 2014; Ayad et al., 2018), the

functional redundancy metric is a function from initial

states to ﬁnal states. It reﬂects how initial states are

mapped to ﬁnal states. For a program (function) g, FR

is the ratio of the output data delivered by g prorated

to the input data received by g and given by:

FR =

H(Y )

H(X)

(3)

Notation

X is a random variable representing the pro-

gram’ input data.

Y is a random variable that represents the pro-

gram’ output data.

H(Y) is the entropy of the output data delivered by

H(X) is the entropy of input data passed through

parameters, global variables, read state-

ments, etc.

In Example 2, H(S) = 96 bits. The Random variable

Y is deﬁned by the integer variable z represented

by 32 bits. Then, H(Y ) = log

) = 32bits.

H(X) is the input data received by g and repre-

sented by the two integer variables x and y. Then,

H(X) = 2 ∗log

) = 64bits. FR is given by :

FR =

= 0.5

2.2.3 Non-injectivity (NI)

According to (Catal and Diri, 2009), a major source of

program (function) redundancy is its non-injectivity.

An injective function is a function whose value

changes whenever its argument does. A function is

non-injective when it maps several distinct arguments

(initial states σ

) into the same image (ﬁnal states σ

NI was deﬁned by:

NI =

H(σ

|σ

)

H(σ

)

H(σ

) − H(σ

)

H(σ

)

(4)

In Example 2, NI is equal to (44-6)/44=0.86.

2.3 Overview of Software

Fault-proneness Prediction

Fault-proneness consists on classifying modules

(functions or classes) as defective or not defective

(Singh et al., 2018). For (Rathore and Kumar, 2017;

Kumar et al., 2017), software fault prediction (SFP)

consists on identifying faulty modules as software

parts containing faults. This attribute was usually esti-

mated and predicted using predictive models compro-

mised of software metrics (Gondra, 2008). The early

application of these models helps reducing the test-

ing effort (Singh et al., 2018) as the identiﬁed defect-

prone parts are tested with more rigor compared to

other ones. In addition, effective resource allocation

and reduction in cost and development time will be

obtained (Kalaivani and Beena, 2018).

Different software fault prediction models have

been studied since 1990. The development of these

models was performed using classiﬁcation techniques

as fault-proneness attribute consists on classifying

modules (functions or classes) as defective or not

defective. These models play a crucial role in un-

derstanding, evaluating and improving the quality of

software systems. According to (Singh et al., 2018),

the early application of these models helps to reduce

the testing effort as testing activities will be planned.

Also, the parts of software system identiﬁed as defect-

prone will be tested with more rigor in comparison

to other system parts (Gondra, 2008). In the same

context, (Kalaivani and Beena, 2018) noted that the

early identiﬁcation of faulty software parts provides

an effective resource allocation and reduces the cost

and time of software development. Numerous studies

were deﬁned to predict this attribute based on soft-

ware metrics.

(Menzies et al., 2004) conducted an experiment

where different fault prediction models were con-

structed using CART, NB and J48 algorithms over dif-

ferent projects taken from PROMISE repository. Re-

sults showed that the performance provided by NB is

better than that is provided by J48.

(Olague et al., 2007) investigated six different ver-

sions of Mozilla Rhino project. The goal of the study

was to study the ability of C&K, QMOOD, MOOD

suites of metrics in predicting faulty modules. They

applied the Univariate and multivariate binary logistic

regression to the cited suites. The authors concluded

that C&K and QMOOD suites are very useful for fault

prediction by contrast to the MOOD.

(Zhou et al., 2010) examined C&K metrics suite

for a defect prediction models based on LR, NB, RF

algorithms. The data set under study consists on KC1

project taken from NASA data set. The objective was

to predict the severity of faults. Authors concluded

that the best fault prediction is achieved by most of

C&K metrics expected NOC.

(Catal and Diri, 2009) conducted a comparative

analysis to study the efﬁciency of RF and NB algo-

rithms in predicting fault-proneness modules. Au-

thors examined C&K metrics suite taken from NASA

data sets. Results showed that for large data sets, RF,

ENASE 2022 - 17th International Conference on Evaluation of Novel Approaches to Software Engineering

212

provides the best prediction, whereas, for small data

sets, NB provides best results.

(He et al., 2015) compared the performance of LR,

J48, NB, SVM, DT and BN algorithms in predicting

faulty classes. They examined 34 releases obtained

from 10 open source’ PROMISE projects. Authors

concluded that SVM and DT perform well in predict-

ing faulty classes.

(Kaur and Kaur, 2018) compared the performance

of Bagging, J48, DT, RF and NB classiﬁers. They

constructed different defect prediction models based

on C&K and QMOOD metrics. Authors concluded

that only Bagging and J48 are the best defect predic-

tors.

(Lomio et al., 2021) have also compared the per-

formance of Machine and Deep Learning models

models in predicting faults. They have conducted a

case study among 33 Java projects and results showed

that deep learning provide a more accurate fault detec-

tion accuracy.

2.4 Formulation of the Research

Hypothesis

The presented fault prediction studies highlighted the

usefulness and the effectiveness of classiﬁcation tech-

niques in fault-proneness prediction. Thus, to validate

the redundancy metrics as reliability indicators using

fault-proneness attribute, we have designed the fol-

lowing hypotheses:

• H1 (Alternative Hypothesis): redundancy met-

rics are signiﬁcant indicators of software fault-

proneness attribute.

• H2 (Null Hypothesis): there is no signiﬁcant re-

lationship between the redundancy metrics and

fault-proneness attribute.

Through these hypothesis, we aim to verify if a re-

lationship between the different metrics and fault-

proneness attribute exists in order to conﬁrm their

utility in monitoring software reliability.

3 EMPIRICAL VALIDATION OF

REDUNDANCY METRICS AS

FAULT-PRONENESS

INDICATORS

3.1 Empirical Validation Approach

According to (Rathore and Kumar, 2017; Kumar

et al., 2017), the fault prediction was conducted based

on three main steps:

1. Data set collection and exploration. This step con-

sists on collecting data related to software metrics

and faults.

2. Data set analysis and models building. This step

consists on performing the data set analysis, data

splitting into learn and test sets and models build-

ing.

3. Models performance evaluation. Numerous eval-

uation measures were deﬁned to evaluate the over-

all performance of the prediction models.

3.2 Data Set Collection

The development of fault prediction models starts by

data set collection phase that requires two main el-

ements; software metrics and software faults. Data

related to these elements can include data from sim-

ilar software projects or existed software metrics and

historical fault data-sets of previous projects (Tura-

bieh et al., 2019). In this paper, the fault-proneness

attribute indicating whether a module is fault-free

(0) or fault-prone (1) will be considered to perform

our validation work. As explained in our previ-

ous work (Amara et al., 2021), as redundancy met-

rics are computed from the programs states manip-

ulated by its variables, software classes containing

functions of input/output types were selected. This

means programs (functions) with input states repre-

sented by the declared variables and output states

represented by modiﬁed states of these variables.

We have focused on Apache Commons Math library

(https://commons.apache.org/) (Kumar and Rathore,

2018) to selected different classes from which the

metrics were computed.

To select the needed repository, we have consid-

ered Apache Commons products library which re-

spects all our requirements and hypothesis. Then,

from the selected repository, we have considered

a set 43 classes (see (Amara et al., 2021)) con-

taining functions manipulating variables in the in-

put and the output state. A description of

each class and its related function is available

at http://commons.apache.org/proper/commonsmath/

javadocs/api-3.6/. As this library contains only the

source code and the associated unit tests, we have

used fault injection procedure to obtain the fault-

proneness values.

One of the well-known fault injection techniques

is mutation testing which consists on automatically

seeding into each class’ code a number of faults (or

mutations). The fault injection procedure is used to

obtain fault data set. This prevents us to compute

fault-proneness values at the class-level as all of the

classes contain faults. Therefore, we ought to com-

Classiﬁcation Techniques Use to Empirically Validate Redundancy Metrics as Reliability Indicators based on Fault-proneness Attribute

213

pute this attribute at the function-level. The redun-

dancy metrics will be also computed at this level lead-

ing to increase the size of our data set. Details of

the redundancy metrics and fault-proneness comput-

ing are described in the subsequent sub-sections.

3.2.1 Redundancy Metrics Collection

We have computed the redundancy metrics at the

function-level of each class as all classes will contain

faults. The process we used to compute these metrics

consists of the following steps:

• For each class, we have considered each function

separately to generate the different metrics.

• For each function, we have focused on its input

and output variables. Then, we have computed the

metrics for random inputs using their equations

(1) to (4).

• The output of this process is an Excel ﬁle in which

the four redundancy metrics values of the different

functions of each class were saved.

These steps were performed using the Eclipse de-

velopment environment (version: Neon.3 Release

(4.6.3)). Details of metrics computing are available

in (Amara et al., 2021).

3.2.2 Fault Data Set Collection

Software fault-proneness attribute is a direct reﬂec-

tion of software reliability since as noted by (Karim-

ian and Babamir, 2017; Reddivari and Raman, 2019),

more trusted software consists of less fault-prone

units. Software fault prediction (SFP) consists on

classifying modules (functions or classes) as defec-

tive or not defective by identifying the faulty modules

as software parts containing faults (Singh et al., 2018;

Rathore and Kumar, 2017; Turabieh et al., 2019). Ac-

cording to (Gondra, 2008), this attribute can be es-

timated and predicted using prediction models based

on software metrics.

Fault injection procedure is performed based on auto-

mated mutation tools like MuJava, MuEclipse, PiTest

and much more (Delahaye and Du Bousquet, 2013).

In our research work, PiTest is used within Maven en-

vironment. To inject faults, we have adopted the fol-

lowing steps:

• All possible faults which are active by default in

PiTest are injected into the source code of the se-

lected classes These faults include the replace-

ment of binary arithmetic operations by another

ones (+ by -, - by +, * by /, / by *), etc.

• PiTest runs, and related reports are generated.

They indicate for each function, the type and the

location of the injected fault.

• PiTest reports are analyzed to identify for each

function whether it is fault-free or not. Thus, we

have determined the value of fault-proneness at-

tribute (1 or 0) as follows:

– If all injected faults are detected (killed),

then the function is not defective (killed) and

the value 0 (fault-free) is assigned to fault-

proneness attribute of this function. An exam-

ple of non-defective function is depicted in Fig-

ure 1.

Figure 1: Non-Defective method (all injected faults are de-

tected).

– If at least one of the injected faults is masked

(survived), then this function is considered as

defective and the value 1 is assigned to the at-

tribute fault-proneness for this function. An ex-

ample of defective function is depicted in Fig-

ure 2.

Figure 2: Defective method (There is at least one masked

fault from those injected).

The ﬁnal obtained data set contains for each method

the values of the redundancy metrics and the associ-

ated fault proneness attribute indicating whether this

function contains faults (1) or not (0).

3.3 Data Set Analysis

In this section, we have performed the data explo-

ration and correlation analysis. Data exploration is an

important step required before the application of clas-

siﬁcation techniques to analyze the data set. Thus, we

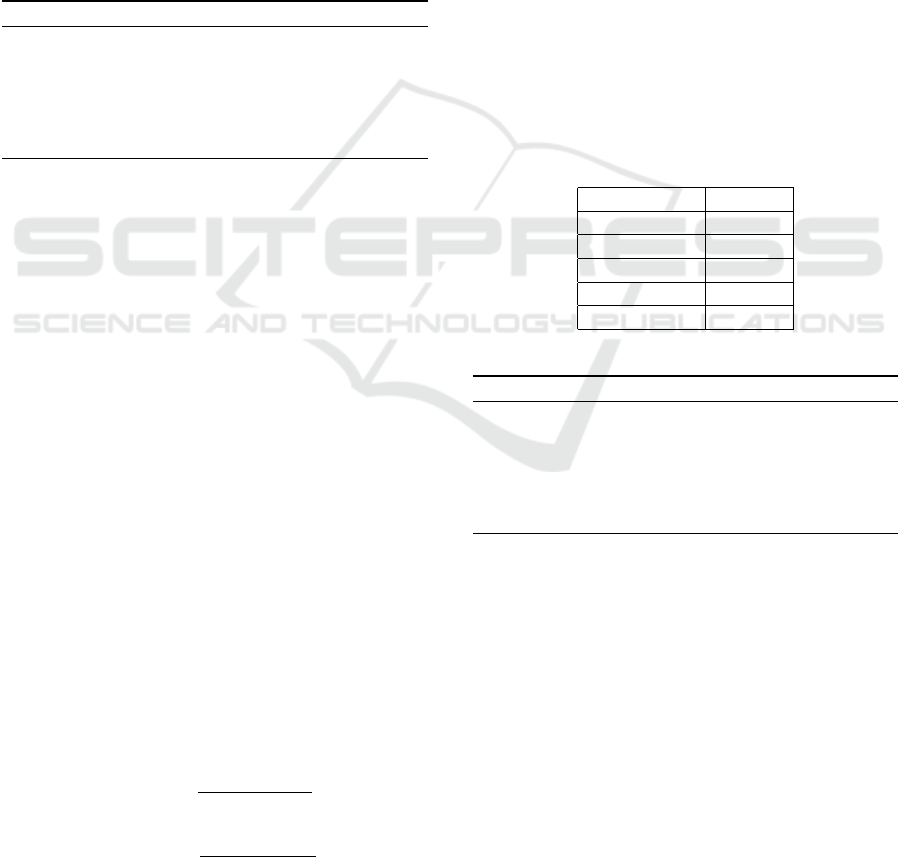
visualize in Figure 3, the percentage of fault-prone (1)

and no-fault prone (0) functions. Figure 3 shows that

ENASE 2022 - 17th International Conference on Evaluation of Novel Approaches to Software Engineering

214

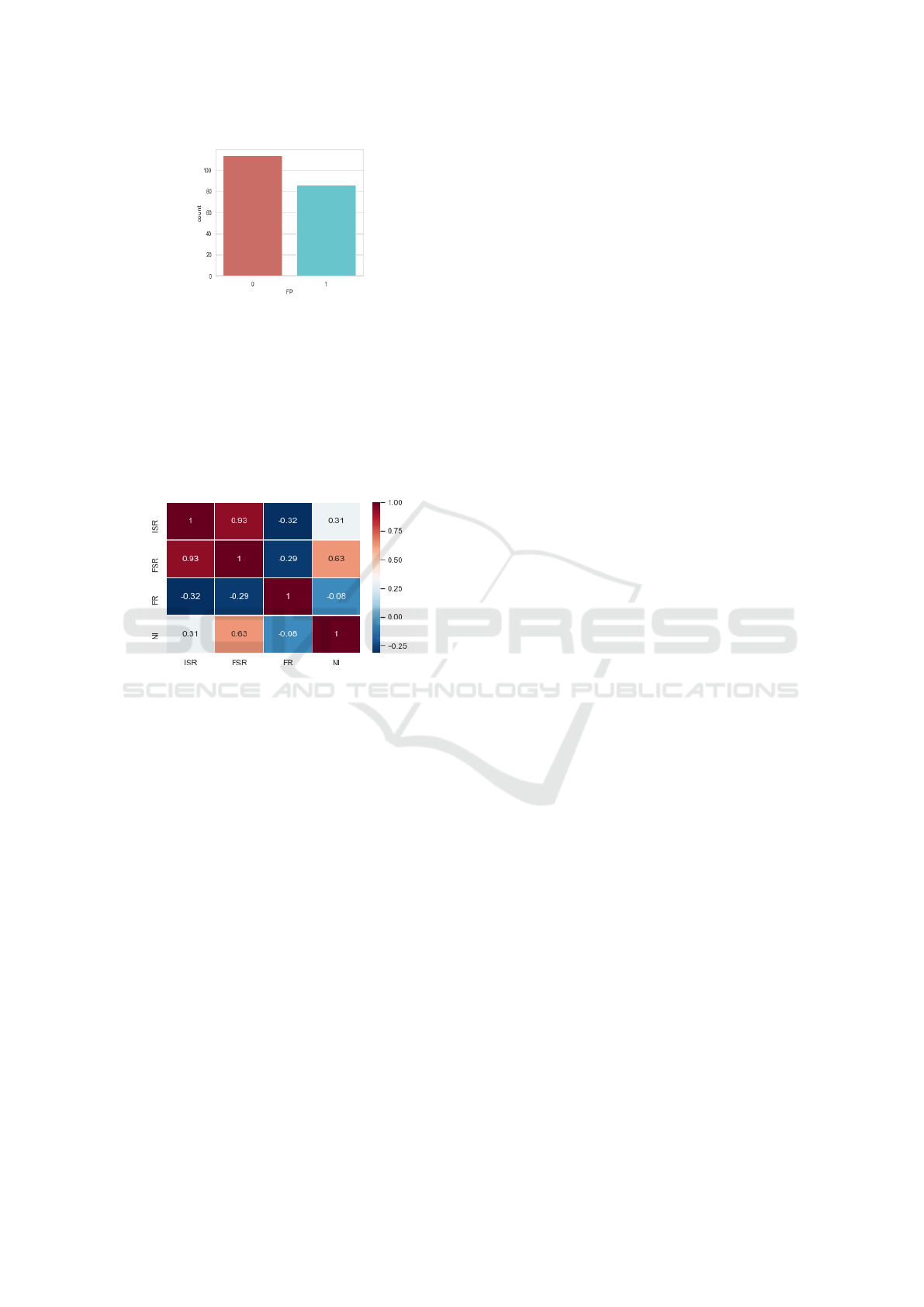
Figure 3: Data exploration.

43% of functions in the selected classes are defective

and 57% are fault-free.

We have used the correlation matrix to identify the

correlation between the independent variables; ISR,

FSR, FR and NI. The objective is to consider metrics

which are not inter-correlated in order to achieve bet-

ter model accuracy. Results are illustrated in Figure 4.

Figure 4 shows a strong correlation between ISR and

Figure 4: Pearson correlation coefﬁcients between the inde-

pendent variables.

FSR as their correlation coefﬁcient is strong and equal

to 0.93. FSR and NI have also signiﬁcant correlation

as their correlation coefﬁcient is 0.63. Therefore, FSR

will be omitted in our prediction. ISR and FSR met-

rics are strongly correlated as the FSR metric is com-

puted using the value of H(σ

) which in turn depends

on the value of H(σ

) used to compute ISR metric

(See equations (1) and (2)). Therefore any changes in

ISR values will lead to changes in FSR and NI ones

which explain their correlation.

4 EXPERIMENTS AND RESULTS

This section summarizes the well-used software fault

prediction techniques and presents the performed ex-

periments.

4.1 Software Faults Prediction

Techniques

The development of fault prediction models requires

the use of software prediction techniques. To select

which technique to use, we have to focus ﬁrst on the

response variable we aim to predict. In this paper,

the output to predict is fault-proneness classifying

modules (functions or classes) as fault-prone or

fault-free. Therefore, classiﬁcation techniques are

useful to predict this attribute using the redundancy

metrics. Different classiﬁcation techniques were

deﬁned including Decision Trees (DT), Support

Vector Machine (SVM), Naive Bayes (NB), Logistic

Regression (LR), Random Forest (RF) and much

others (Prasad et al., 2015; Turabieh et al., 2019;

Malhotra, 2015; Singh et al., 2018).

As discussed in section 2, several studies are

proposed to predict the fault-proneness attribute

based on these techniques. The objective is to

validate different software metrics or to compare the

performance of these techniques. Most of these stud-

ies showed up the effectiveness of the classiﬁcation

techniques in predicting fault-proneness attribute.

However, we have stated that different criteria like

the size of the used data set (Catal and Diri, 2009),

the level of metrics’ computing (Koru and Liu,

2005) provide a variation in the performance of these

techniques. As our main objective is to study the

usefulness of the redundancy metrics in reﬂecting

fault-proneness attribute and not to compare the

classiﬁcation techniques, we have started by applying

some of them to reach this issue.

4.2 Experiments

To build the classiﬁcation models, we have proceeded

as follows:

1. To start with, data exploration phase is performed

as explained above. In addition, required Python

packages are imported.

2. Next, data set analysis and models building are

performed. In this step, we have studied the corre-

lation between the independent variables (redun-

dancy metrics) to consider only metrics that are

not inter-correlated as explained above. Also, data

is divided into two parts; train data (80%) and test

data (20%). In addition, the different cited clas-

siﬁcation techniques are used to build prediction

models based on the train data.

3. Finally, the prediction is performed on the test

data and evaluated based on different performance

Classiﬁcation Techniques Use to Empirically Validate Redundancy Metrics as Reliability Indicators based on Fault-proneness Attribute

215

evaluation measures.

The presented steps are performed based on appropri-

ate modules and scripts available in the Python lan-

guage and used to build the different considered clas-

siﬁcation techniques in order to test the stated hypoth-

esis.

4.3 Results

In this section, we present the results of predicting

faulty and non faulty modules using the classiﬁcation

techniques in order to answer the speciﬁed question;

”Is there a signiﬁcant correlation between the redun-

dancy metrics and the fault-proneness attribute?”.

Then, we compare their performance based on differ-

ent performance evaluation measures.

4.3.1 Common Performance Evaluation

Measures

Various measures were deﬁned to evaluate the perfor-

mance of the classiﬁcation techniques(Elish and El-

ish, 2008; Abaei and Selamat, 2014; Reddivari and

Raman, 2019). A binary classiﬁer uses data instances

in the test data to predict either they are positive or

negative. Then, four possible outcomes are obtained:

True positive (TP), False positive (FP), True negative

(TN), and False negative (FN). These four outcomes

are presented in a confusion matrix from which dif-

ferent measures were derived:

• Precision: indicates how many classes are actu-

ally defect-prone from those returned by a model.

The best value of this measure is 1. The high value

of precision indicates fewer FP (correct elements

which are classiﬁed incorrectly as defect-prone el-

ements). This measure is deﬁned by : Precision =

TP / TP+FP

• Recall: indicates how many of the defect-prone

classes are returned actually by a model. The best

value of this measure is 1. High value of recall

measure indicates lower number of FN (defective

classes non indicated by the model). It is deﬁned

by: Recall = TP / TP+FN

• Accuracy: indicates the rate of correct classiﬁ-

cation. It is presented as ratio of the number of

correctly predicted modules to the total number

of modules and deﬁned by: Accuracy = TP+TN /

TP+TN +FP+FN

• Area under the curve (AUC) : is a curve with two

dimensions; x-axis is represented by FP and y-

axis is represented by TP.

4.3.2 Results

The presented evaluation measures are used to

evaluate the performance of the different used classi-

ﬁcation techniques. Results are illustrated in Tables 2

to 6.

Table 2: Results of DT prediction model.

(a) Performance measure

Precision Recall F1-score

0 0.83 0.87 0.70

1 0.81 0.76 0.79

Accuracy 0.82

(b) Confusion matrix

1 0

1 20 3

0 4 13

Table 3: Results of LR prediction model.

(a) Performance measure

Precision Recall F1-score

0 0.61 0.83 0.70

1 0.56 0.29 0.38

Accuracy 0.60

(b) Confusion matrix

1 0

1 19 4

0 12 5

Table 4: Results of NB prediction model.

(a) Performance measure

Precision Recall F1-score

0 0.63 0.83 0.72

1 0.60 0.35 0.44

Accuracy 0.82

(b) Confusion matrix

1 0

1 19 4

0 11 6

Tables 2 to 6 illustrate the different evaluation

measures obtained for the selected classiﬁcation

ENASE 2022 - 17th International Conference on Evaluation of Novel Approaches to Software Engineering

216

Table 5: Results of SVM prediction model.

(a) Performance measure

Precision Recall F1-score

0 0.70 0.83 0.76

1 0.69 0.53 0.60

Accuracy 0.70

(b) Confusion matrix

1 0

1 19 4

0 8 9

Table 6: Results of RF prediction model.

(a) Performance measure

Precision Recall F1-score

0 0.80 0.87 0.83

1 0.80 0.71 0.77

Accuracy 0.80

(b) Confusion matrix

1 0

1 20 3

0 4 13

techniques. Thus, for each technique, we have

summarized the classiﬁcation report providing us

with the values of the presented performance evalu-

ation measures and we have presented the confusion

matrix from which these measures are computed. As

shown in these tables, the support measure for the

different techniques indicates that the data tested for

1 (fault-prone functions) is 17 and for 0 (fault-free

functions) is 23. For these values, we have stated

that:

• The precision measure shows that DT and RF per-

form well in predicting fault-prone modules with

values of respectively 0.81 and 0.80. NB and

SVM perform moderately with a precision val-

ues of respectively 0.60 and 0.69. Precision shows

also that LR is the least effective model for fault-

proneness prediction with precision value of 0.56.

• In terms of recall and F-measure, LR and NB clas-

siﬁers had low comparable performance and these

measures range from 0.29 to 0.44. SVM has a

moderate F-measure and recall rate that ranges

from 0.53 to 0.60. DT and RF have the highest

recall and F-measure rate that ranges from 0.71 to

0.79.

• Accuracy shows that LR and NB are the least ef-

fective models for fault-proneness prediction as

their accuracy rates are respectively of 0.60 and

0.62. For SVM classiﬁer, it has a moderate accu-

racy rate that is 0.7. DT and RF have the high-

est accuracy rates that are respectively of 0.82 and

0.81.

• Confusion matrix shows that for LR, there were

23 points in the ﬁrst class (label 0) and 17 in the

second one (1). From these 17 points, we have

stated that:

– LR and NB present comparative results and

succeed in identifying respectively 5 and 6 of

those correctly in label 1, but 12 and 11 were

respectively marked as label 0.

– For SVM, from the 17 points, it succeed in

identifying 9 of those correctly in label 1,

whilst, 8 points were marked as label 0.

– Concerning DT, we have stated that from the 17

points, the model succeed in identifying 13 of

those correctly in label 1 and only 4 points were

marked as label 0. The same results were given

by the RF classiﬁer.

We summarize in Table 7, the accuracy rate of the

different techniques.

Table 7: Accuracy rate for the selected classiﬁers.

Classiﬁer Accuracy rate

Logistic Regression 60%

Naive Bayes 62%

Support Vector Machine 70%

Decision Tree 82%

Random Forest 80%

Taking accuracy as the most used models’ eval-

uation measure, results in Table 7 show that DT is

the most appropriate technique followed by RF suc-

ceeded in measuring fault-proneness attribute based

on redundancy metrics.

5 DISCUSSION, THREATS TO

VALIDITY AND COMPARISON

WIDTH RELATED WORKS

This section summarizes the results and presents the

identiﬁed threats to validity. Also, a comparison with

the related works is presented.

Classiﬁcation Techniques Use to Empirically Validate Redundancy Metrics as Reliability Indicators based on Fault-proneness Attribute

217

5.1 Overall Discussion of Results and

Threats to Validity

We have experimented with different popular clas-

siﬁers the usefulness of the redundancy metrics as

reliability indicators using fault-proneness attribute.

A set of 200 functions selected from Commons-math

Apache project is used. Considering accuracy as

the evaluating parameter, results show that the

fault proneness attribute can be predicted using the

redundancy metrics with a good accuracy rate of

0.82. This leads us to accept the stated H1 hypothesis

indicating that the redundancy metrics are useful

indicators of fault proneness attribute and reject the

null hypothesis of no relationship between these two

variables. Therefore, these results can be used as

ﬁrst guidance to predict faulty modules based on the

redundancy metrics.

We have obtained promising results proposing vali-

dated ISR and NI redundancy metrics as signiﬁcant

reliability indicators for the both considered defect

density and fault-proneness attributes. However, we

have noted several threads to validity:

• First, the proposed redundancy metrics are seman-

tic as they depend on the program functionality;

each program (function or class) has its state rep-

resented by the manipulated variables. Hence,

each time the used variables in the program in-

put state change, the output state will change, and

the values of the redundancy metrics will change

too. Therefore, the proposed computing process

described in the previous work is not fully auto-

mated and it is implemented separately for each

program.

• Second, as more we use larger training data sets

and optimizing model parameters, better we im-

prove the model prediction performance (Singh

et al., 2018), our data set can be extended to en-

hance the performance of the proposed prediction

model.

• Comparing the redundancy metrics with other ex-

isted metrics validated as fault-proneness indica-

tors can enhance their performance as signiﬁcant

quality indicators.

• Performing other experiments using the same

dataset and the same classiﬁcation techniques by

taking into account different metrics that include

internal attributes such as complexity and cohe-

sion measured by C&K metrics (Chidamber and

Kemerer, 1994) and compare results with entropy

metrics.

5.2 Comparison between Our Proposed

Approach and Related Works

In (Ayad et al., 2018), authors have proposed an em-

pirical validation of the redundancy metrics using the

rate of mutants as quality attribute. We compare our

work with their work in Table 8.

Table 8: Some differences and similarities between the re-

lated works and our work.

Criteria (Ayad et al.,

2018)

Our work

Suite of

metrics

(Independent

variables)

ISR, FSR, FR

and NI

ISR, FSR, FR

and NI

Quality

attribute

(Dependent

variable)

Survival rate of

mutants

Fault-proneness.

Data

repository

Apache Com-

mon Mathemat-

ics Library

Apache Com-

mon Mathemat-

ics Library.

Size of the

used data

set

- 19 functions - 200 func-

tions for fault-

proneness

attribute.

Quality

attribute

collection

procedure

Fault injection

procedure based

on PiTest tool

is used then

PiTest reports

are analyzed to

obtain the values

of the considered

attribute.

Fault injection

procedure based

on PiTest tool

is used then

PiTest reports

are analyzed to

obtain the values

of the considered

attribute.

Statistical

techniques

- Correlation

analysis between

the independent

variables is not

performed.

- Linear multi-

variate regres-

sion technique is

used.

- Correlation

analysis between

the independent

variables is

performed.

- Different

classiﬁcation

techniques are

used.

Results All redundancy

metrics are iden-

tiﬁed as signiﬁ-

cant indicators of

the survival rate

of mutants.

Only ISR and

NI are identiﬁed

as signiﬁcant

indicators of de-

fect density and

fault-proneness

attributes.

ENASE 2022 - 17th International Conference on Evaluation of Novel Approaches to Software Engineering

218

Only ISR and FR are considered in our ex-

perimentation because we have identiﬁed a strong

correlation between ISR and FSR as shown in Figure

4 which leads us to omit the FSR metric. Concerning

the FR metric, we have included it in our experimen-

tation, but we have stated that it hasn’t any change on

the results contrary to ISR and NI.

As shown in Table 8, little works are proposed

to empirically validate the redundancy metrics as

reliability predictors. The presented comparison

shows that:

• The same validation approach was used. In both

cases, data set is ﬁrst collected, then, data analy-

sis, models building and performance evaluation

steps are performed. In addition, the work de-

scribed in (Ayad et al., 2018) is comparable to our

work as the same data repository is used to com-

pute the metrics.

• Authors in (Ayad et al., 2018) showed that all of

the redundancy metrics are signiﬁcant predictors

of the survival rate of mutants and software re-

liability. However, in our validation work, only

ISR and NI metrics appeared to be adequate in

predicting software reliability using defect density

and fault-proneness attributes. The lack of corre-

lation tests between the independent variables in

their study and the difference in selecting relia-

bility quality attributes can explain these different

results. On another hand, the nature of the con-

sidered fault-proneness quality attribute as depen-

dent variable lead us to use various classiﬁcation

techniques.

6 CONCLUSION AND

PERSPECTIVES

Initial state redundancy, ﬁnal state redundancy, non-

injectivity, and functional redundancy metrics were

proposed to assess the code’ redundancy in order to

monitor software reliability. However, all of these

metrics are manually computed and theoretically

presented. In this research, we aim at empirically

validating these metrics as signiﬁcant reliability

indicators. We have used the fault proneness attribute

as a direct reﬂection of software reliability to reach

our objective.

We have used an empirical database including a

set of Java functions taken from the Commons Math

Library, all related redundancy metrics’ values, and

the fault-proneness attribute as a direct reliability

indicator. Five classiﬁcation techniques (LR, SVM,

DT, RF, and NB) are then used to assess the rela-

tionship between these two variables. The obtained

results can be used as ﬁrst guidance to predict faulty

modules based on the redundancy metrics. The

primary contribution is to assess the capability of the

redundancy metrics in predicting faulty modules.

As the initial state redundancy metric only mea-

sures the program redundancy in its initial and ﬁnal

states without considering the redundancy of its

internal states, we propose in the future work, to

improve this metric by considering its internal states

in order to reﬂect the overall program redundancy. In

addition, replicated studies with large sized software

should be carried out so that generalized results can

be obtained.

REFERENCES

Abaei, G. and Selamat, A. (2014). A survey on soft-

ware fault detection based on different prediction ap-

proaches. Vietnam Journal of Computer Science,

1(2):79–95.

Amara, D., Fatnassi, E., and Ben Arfa Rabai, L. (2021).

An empirical assessment and validation of redundancy

metrics using defect density as reliability indicator.

Scientiﬁc Programming, 2021.

Amara, D. and Rabai, L. B. A. (2017). Towards a new

framework of software reliability measurement based

on software metrics. Procedia Computer Science,

109:725–730.

Arvanitou, E. M., Ampatzoglou, A., Chatzigeorgiou, A.,

Galster, M., and Avgeriou, P. (2017). A mapping study

on design-time quality attributes and metrics. Journal

of Systems and Software, 127:52–77.

Asghari, S. A., Marvasti, M. B., and Rahmani, A. M.

(2018). Enhancing transient fault tolerance in embed-

ded systems through an os task level redundancy ap-

proach. Future Generation Computer Systems, 87:58–

65.

Ayad, A., Marsit, I., Omri, N. M., Loh, J., and Mili, A.

(2018). Using semantic metrics to predict mutation

equivalence. In International Conference on Software

Technologies, pages 3–27. Springer.

Bansiya, J. and Davis, C. G. (2002). A hierarchical model

for object-oriented design quality assessment. IEEE

Transactions on software engineering, 28(1):4–17.

Briand, L. C. and W

ust, J. (2002). Empirical studies of qual-

ity models in object-oriented systems. In Advances in

computers, volume 56, pages 97–166. Elsevier.

Catal, C. and Diri, B. (2009). A systematic review of soft-

ware fault prediction studies. Expert systems with ap-

plications, 36(4):7346–7354.

Chidamber, S. R. and Kemerer, C. F. (1994). A metrics

suite for object oriented design. IEEE Transactions

on software engineering, 20(6):476–493.

Classiﬁcation Techniques Use to Empirically Validate Redundancy Metrics as Reliability Indicators based on Fault-proneness Attribute

219

Delahaye, M. and Du Bousquet, L. (2013). A comparison

of mutation analysis tools for java. In 2013 13th Inter-

national Conference on Quality Software, pages 187–

195. IEEE.

Dubrova, E. (2013). Fault-tolerant design. Springer.

Elish, K. O. and Elish, M. O. (2008). Predicting defect-

prone software modules using support vector ma-

chines. Journal of Systems and Software, 81(5):649–

660.

Febrero, F., Calero, C., and Moraga, M.

A. (2016). Software

reliability modeling based on iso/iec square. Informa-

tion and Software Technology, 70:18–29.

Fenton, N. and Bieman, J. (2014). Software metrics: a rig-

orous and practical approach. CRC press.

Gondra, I. (2008). Applying machine learning to software

fault-proneness prediction. Journal of Systems and

Software, 81(2):186–195.

Gyimothy, T., Ferenc, R., and Siket, I. (2005). Empirical

validation of object-oriented metrics on open source

software for fault prediction. IEEE Transactions on

Software engineering, 31(10):897–910.

He, P., Li, B., Liu, X., Chen, J., and Ma, Y. (2015). An

empirical study on software defect prediction with a

simpliﬁed metric set. Information and Software Tech-

nology, 59:170–190.

Jabangwe, R., B

orstler, J.,

Smite, D., and Wohlin, C.

(2015). Empirical evidence on the link between

object-oriented measures and external quality at-

tributes: a systematic literature review. Empirical

Software Engineering, 20(3):640–693.

Kalaivani, N. and Beena, R. (2018). Overview of software

defect prediction using machine learning algorithms.

International Journal of Pure and Applied Mathemat-

ics, 118(20):3863–3873.

Karimian, F. and Babamir, S. (2017). Evaluation of classi-

ﬁers in software fault-proneness prediction. Journal

of AI and Data Mining, 5(2):149–167.

Kaur, A. and Kaur, I. (2018). An empirical evaluation of

classiﬁcation algorithms for fault prediction in open

source projects. Journal of King Saud University-

Computer and Information Sciences, 30(1):2–17.

Koru, A. G. and Liu, H. (2005). Building effective

defect-prediction models in practice. IEEE software,

22(6):23–29.

Kumar, L., Misra, S., and Rath, S. K. (2017). An empirical

analysis of the effectiveness of software metrics and

fault prediction model for identifying faulty classes.

Computer Standards & Interfaces, 53:1–32.

Kumar, S. and Rathore, S. S. (2018). Software Fault Pre-

diction: A Road Map. Springer.

Lomio, F., Moreschini, S., and Lenarduzzi, V. (2021). Fault

prediction based on software metrics and sonarqube

rules. machine or deep learning? arXiv preprint

arXiv:2103.11321.

Lyu, M. R. et al. (1996). Handbook of software reliabil-

ity engineering, volume 222. IEEE computer society

press CA.

Malhotra, R. (2015). A systematic review of machine learn-

ing techniques for software fault prediction. Applied

Soft Computing, 27:504–518.

Menzies, T., DiStefano, J., Orrego, A., and Chapman, R.

(2004). Assessing predictors of software defects. In

Proc. Workshop Predictive Software Models.

Mili, A., Jaoua, A., Frias, M., and Helali, R. G. M. (2014).

Semantic metrics for software products. Innovations

in Systems and Software Engineering, 10(3):203–217.

Nakai, H., Tsuda, N., Honda, K., Washizaki, H., and

Fukazawa, Y. (2016). Initial framework for software

quality evaluation based on iso/iec 25022 and iso/iec

25023. In 2016 IEEE International Conference on

Software Quality, Reliability and Security Companion

(QRS-C), pages 410–411. IEEE.

Olague, H. M., Etzkorn, L. H., Gholston, S., and Quat-

tlebaum, S. (2007). Empirical validation of three

software metrics suites to predict fault-proneness of

object-oriented classes developed using highly itera-

tive or agile software development processes. IEEE

Transactions on software Engineering, 33(6):402–

419.

Prasad, M., Florence, L., and Arya, A. (2015). A study

on software metrics based software defect prediction

using data mining and machine learning techniques.

International Journal of Database Theory and Appli-

cation, 8(3):179–190.

Radjenovi

c, D., Heri

cko, M., Torkar, R., and

Zivkovi

c, A.

(2013). Software fault prediction metrics: A system-

atic literature review. Information and software tech-

nology, 55(8):1397–1418.

Rathore, S. S. and Kumar, S. (2017). An empirical

study of some software fault prediction techniques

for the number of faults prediction. Soft Computing,

21(24):7417–7434.

Reddivari, S. and Raman, J. (2019). Software quality pre-

diction: An investigation based on machine learning.

In 2019 IEEE 20th International Conference on Infor-

mation Reuse and Integration for Data Science (IRI),

pages 115–122. IEEE.

Shannon, C. (2001). A mathematical theory of communica-

tion. ACM SIGMOBILE mobile computing and com-

munications review, 5:3–55.

Singh, A., Bhatia, R., and Singhrova, A. (2018). Taxonomy

of machine learning algorithms in software fault pre-

diction using object oriented metrics. Procedia com-

puter science, 132:993–1001.

Turabieh, H., Mafarja, M., and Li, X. (2019). Iterated fea-

ture selection algorithms with layered recurrent neural

network for software fault prediction. Expert Systems

with Applications, 122:27–42.

Verma, D. K. and Kumar, S. (2017). Prediction of defect

density for open source software using repository met-

rics. J. Web Eng., 16(3&4):294–311.

Zhou, Y., Xu, B., and Leung, H. (2010). On the ability

of complexity metrics to predict fault-prone classes in

object-oriented systems. Journal of Systems and Soft-

ware, 83(4):660–674.

ENASE 2022 - 17th International Conference on Evaluation of Novel Approaches to Software Engineering

220