
Multivariate Interpolation at the Edge to Infer Faulty IoT Sensor Metrics
Marcos Paulo Konzen
1,4 a
, Patric Lincoln Ramires Izolan
1 b
, F
´
abio J
´
unior Griesang
1 c
,
Paulo Silas Severo De Souza
2 d
, Tiago Coelho Ferreto
2 e
, Arthur Francisco Lorenzon
3 f
,
Marcelo Caggiani Luizelli
3 g
, Julio Carlos Balzano De Mattos
4 h
, Cinara Ewerling Da Rosa
1 i
and F
´
abio Diniz Rossi
1 j
1
Federal Institute Farroupilha, Alegrete, Brazil
2
Pontifical Catholic University of Rio Grande do Sul, Porto Alegre, Brazil
3
Federal University of Pampa, Alegrete, Brazil
4
Federal University of Pelotas, Pelotas, Brazil
Keywords:
IoT, Modeling, Sensors, Simulation.
Abstract:
Virtual sensors are software entities that allow the estimation, through models, of critical variables in a given
environment. Metrics can be modeled computationally to estimate the values measured by a sensor without
installing it physically in the specified location. The monitoring and control of its variables by the edge are of
great importance, as they are directly related to increased productivity. This article presents the idea behind
virtual sensors, discusses some challenges and trends, presents such sensors’ modeling for estimating values,
and gives results based on a Smart Farming case study. The results show that the virtual sensors’ estimated
values are very close to reality, which shows that our method can be used with very high confidence.
1 INTRODUCTION
Edge Computing (Mahmoudi et al., 2018) is a
paradigm that complements the Cloud Computing
model, aiming to process data on servers close to
users, that is, close to where data is generated and
consumed. In this way, data travels shorter distances,
which dramatically reduces latency to a few millisec-
onds. For this reason, Edge Computing is a cru-
cial factor in the consumption of data coming from
the Internet of Things (IoT). More and more sensors,
cameras, and systems will monitor the entire indus-
trial production process, evaluating and supervising
the equipment’s performance. All of this has as main
objectives: saving resources, decreasing the average
a
https://orcid.org/0000-0002-8765-970X
b
https://orcid.org/0000-0002-2391-7159
c
https://orcid.org/0000-0002-0136-3482
d
https://orcid.org/0000-0003-4945-3329
e
https://orcid.org/0000-0001-8485-529X
f
https://orcid.org/0000-0002-2412-3027
g
https://orcid.org/0000-0003-0537-3052
h
https://orcid.org/0000-0002-0619-9271
i
https://orcid.org/0000-0002-9077-5031
j
https://orcid.org/0000-0002-2450-1024
time spent on production, and raising the quality of
products. Sensors may measure position, tempera-
ture, pressure, and other physical or chemical param-
eters. A sensor is a technical component that converts
physical or chemical quantities in an electrical signal.
However, there are cases where the desired physical
amount cannot be measured directly through a physi-
cal sensor due to cost, energy, convenience, failure, or
other practical reasons, such as geography or space.
Based on these specific contexts, virtual sensors ap-
pear as a viable option.
This article introduces a new approach to estimate
values of a virtual position (so-called virtual sensor)
based on values collected from real sensors within
the same region. Our contributions can be summa-
rized as follows: (i) a multivariate interpolation model
for estimating values at positions addressed by vir-
tual sensors; (ii) a simulation for estimating the val-
ues assigned to virtual sensors, considering the phys-
ical sensors distributed in the environment; (iii) an al-
gorithmic implementation that allows using the pro-
posed mathematical model in real environments; and
(iv) evaluations of the proposed model against well-
known techniques in the literature, demonstrating the
advantages of the model presented in this article. Op-
280
Konzen, M., Izolan, P., Griesang, F., De Souza, P., Ferreto, T., Lorenzon, A., Luizelli, M., Balzano De Mattos, J., Ewerling Da Rosa, C. and Rossi, F.
Multivariate Interpolation at the Edge to Infer Faulty IoT Sensor Metrics.
DOI: 10.5220/0011084100003200
In Proceedings of the 12th International Conference on Cloud Computing and Services Science (CLOSER 2022), pages 280-287
ISBN: 978-989-758-570-8; ISSN: 2184-5042
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

timizing the farms’ production process is the main
reason for applying IoT to the production line. It al-
lows today’s equipment that makes up the farms’ in-
dustrial yard to be connected in a network. It means
that it makes all industrial machinery work automat-
ically using highly programmable intelligent sensors.
The main difference to the current scenario, which is
already packed with modern equipment, is that people
control these machines. With Smart Farms, the mar-
ket can expect in a few years that these machines will
be independent and interact with each other and with
the general farm system. It means that the equipment
will make decisions without human intervention.
2 VIRTUAL SENSORS
The virtual sensor is not a physical sensor but behaves
as such. Virtual sensors are software-driven models
that use available information from other measure-
ments and parameters to calculate an estimate of the
metric of interest, approximating the behavior of a
physical sensor. A virtual sensor can be created as
a function of other real physical sensors, and there
must be a correlation between the inputs and the vir-
tual sensor. A virtual sensor can simulate and replace
a real physical sensor through modeling that estimates
output values with the same reliability as a real sensor.
These sensors can act as a backup, where the use of a
physical sensor is made impossible by several factors
such as remote geographic location or sensor failure
(Liu et al., 2009).
Virtual sensor modeling can be based on empiri-
cal data, where historical data is used to derive a cor-
relation between outputs and inputs. It can be found
in analytics, which uses physical formulas for mod-
eling. The models proposed in the literature indicate
two ways virtual sensors provide values: analytical
and empirical models. In analytical models, the vir-
tual sensor calculates metrics based on physical laws.
In contrast, in empirical models experience is incor-
porated into the calculus (Liu et al., 2009). The defi-
nition of the modeling technique depends on the sen-
sor design, application, and mathematical calculation
approach. Another goal of using virtual sensors is to
replace a physical sensor and its functions. In this
type of application, the main objective is to replace a
real sensor in case of failures or the impossibility of
installing a physical sensor on site. The related work
reveals that the application areas of virtual sensors are
quite different. We chose to classify applications into
large areas to facilitate visualization in this work.
• Industry: Virtual sensors are modeled to produce
new measurement data in order to improve pro-
duction processes (Shao et al., 2018). In (Tong
and Zewen, 2017) virtual sensors are created to
estimate measurements in places where it is not
possible to use a real sensor, for example, mea-
suring the performance of machines or measuring
chemical processes in oil extraction.
• Environment: Wang, Zhao, and Cui (Wang et al.,
2015) describe the use of virtual sensors to mon-
itor algal blooms. In (Asy’ari et al., 2019) virtual
sensors are used to measure solar radiation.
• Health: Erturk and Vollero (Erturk and Vollero,
2020) developed virtual sensors to improve surgi-
cal accuracy. In (Gupta and Mukherjee, 2016) vir-
tual sensors are used to monitor and predict hem-
orrhages in remote patients.
• Agriculture S
´
anchez-Molina (et al.) (S
´
anchez-
Molina et al., 2015) developed a virtual sensor
applied to monitoring the amount of water in the
biomass of the tomato crop. Moura (et al.) (Zhang
et al., 2020) uses virtualized sensors to provide
different measures of soil irrigation based on sta-
tistical data.
• Sensors-as-a-Service: This category appears as
a new trend in IoT. It creates virtual sensors to
make data from physical sensors available in the
cloud. In this way, different applications can use
data from these virtual sensors for their solutions
without the developer having access to the phys-
ical sensor (Fanti et al., 2018) (Ilyas et al., 2020)
(Flores et al., 2018).
Different virtual sensor modeling techniques are
presented in the literature. In this work, the modeling
techniques were divided into large areas to facilitate
work classification as shown in Table 1.
Table 1: Virtual sensor modeling techniques.
Technique Article
Machine Learning Models
(Wang et al., 2015)
(Asy’ari et al., 2019)
(Yuan et al., 2020)
(Ilyas et al., 2020)
(Zhang et al., 2020)
Mathematical Models
(Cristaldi et al., 2020)
(Tong and Zewen, 2017)
(Fanti et al., 2018)
(Shao et al., 2018)
(Sutarya and Mahendra, 2015)
Generic Models
(S
´
anchez-Molina et al., 2015)
(Gupta and Mukherjee, 2016)
(Flores et al., 2018)
(Erturk and Vollero, 2020)
Virtual sensor modeling applied in the industry
uses machine learning techniques or mathematical
models. Virtual sensors applied in Health and Agri-
culture mostly use modeling techniques based on
generic models. Finally, Sensor-as-a-Service is mod-
Multivariate Interpolation at the Edge to Infer Faulty IoT Sensor Metrics
281
eled using different types of modeling techniques.
Therefore, more and more virtual sensors are be-
ing implemented in various applications, and multiple
methods are used to model these sensors. However, it
is still a challenge to determine which modeling tech-
nique is the most suitable according to the type of ap-
plication, considering the types and amount of input
data of the models, the response time, and the compu-
tational resources needed for the modeling.
3 PROPOSED METHOD
The initial resource for a refined development of the
numerical method is strongly associated with the de-
pendence on the location of the plotted mesh nodes
with a minimum number of elements. In this sense,
our proposal focus on discretizing the domain of a
simple geometric mesh in 2D through triangulation.
Therefore, we use concepts from the geometry of tri-
angles. For this, consider A = (x
A
, y
A
), B = (x
B
, y
B
)
and C = (x
C
, y
C
) the Cartesian coordinates of three
points of a plane where the area with the sign of a
triangle (S
ABC
) is given by:
S
ABC
=
1
2
det
x
A
y
A
1
x
B
y
B
1
x
C
y
C
1
. (1)
If the area of the triangle is null (S
ABC
= 0),
then the points A, B, and C are collinear (may be
coincident). This collinearity of the points is de-
fined as a degenerated triangle and otherwise a non-
degenerated triangle. Additionally, if A, B and C are
arranged counterclockwise, we have S
ABC
= +∇ABC
and clockwise, S
ABC
= −∇ABC, where ∇ABC is the
conventional area of a triangle ∆ABC. This definition
introduces the decomposition property for the signed
area; that is, given a point P in the plane, there are
three other sub-triangles (∆PBC, ∆PCA, and ∆PAB).
Note that the sum of the areas of these sub-triangles
is equal to the area of ∆ABC. From there, it is possi-
ble to define whether the point P is located inside the
triangle ∆ABC. For this to occur, it is enough that all
areas of the sub-triangles are positive. Based on these
concepts, it is initially possible to identify the posi-
tion of the virtual sensor (P) concerning three physi-
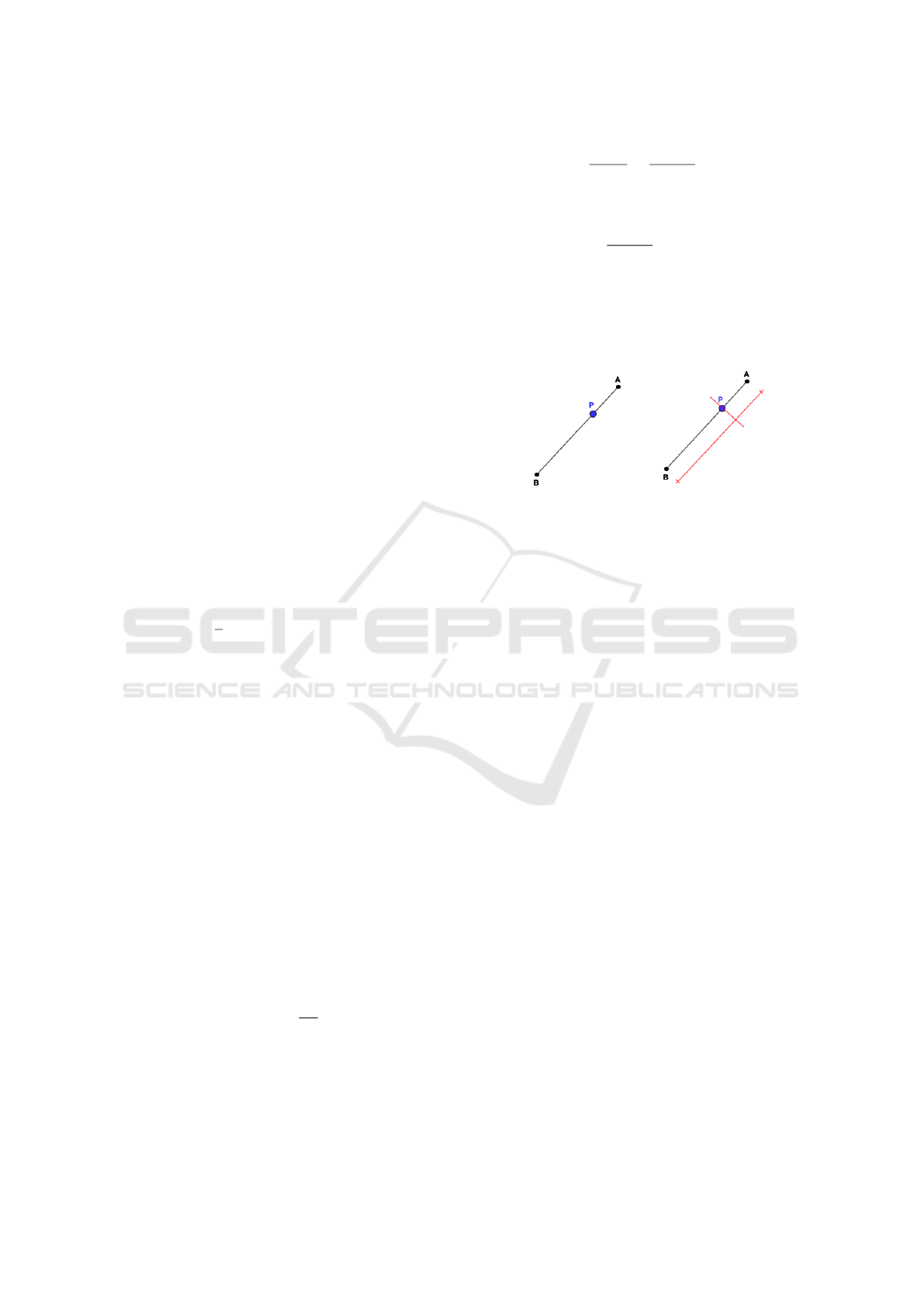
cal sensors (A, B, and C). In the first case, the point P
belongs to one of the segments of the ∆ABC; for ex-
ample, in Figure 1 where P ∈ AB, we have that ∆ABP
is defined as a degenerated triangle. In this situation,
to estimate the position of the point P, the linear poly-
nomial interpolation method between the points A and
B (a first-degree polynomial) will be used through the
following relation:
y − y
A
x − x
A
=
y
B
− y
A
x
B
− x
A
. (2)
Then
y = y
A
+ (y
B
− y
A
)
x − x
A
x
B
− x
A
at a point P = (x, y) (3)
which can be derived geometrically from Figure 1.
This function represents, by approximation, a sup-
posed function that would initially represent the im-
ages of a discontinuous interval contained in the do-
main.
(a) (b)
Figure 1: First case.
On the other hand, in the second case, the hypoth-
esis of a non-degenerated triangle ∆ABP is addressed;
it is assumed that P is not aligned to the points A and
B. Therefore, a new condition is assigned, requiring
this virtual sensor to triangulate among three physi-
cal sensors (A, B, and C). For this, the areas of the
sub-triangles must be all positive (Figure 2). If it is
identified that the point P is external to the triangle,
new vertices are assigned until the desired hypothe-
sis is found. In order to generate a mesh with good
formal patterns, the Delaunay method (Chew, 1989)
and the barycentric method (Pait, 2018) are initially
considered, which use the concept of dividing a no-
table point known as the barycenter. The barycen-
ter of the triangle is the noteworthy point of intersec-
tion of the three medians known as the center point
of weights. This method has an advantage in mesh
mapping as well as a good convergence acceleration
of the method. However, for the application of this
method, a refinement of the mesh would be neces-
sary, with the use of successive points to obtain new
internal nodes in the mesh, defined as a barycentric
subdivision. Note that the greater the number of ele-
ments in a mesh, the more costly and slower the com-
putational simulation. This situation is not interest-
ing for the feasibility of this study, which seeks to
interact in remote locations with low computational
resources. Given this fact, the option of this method
will be re-adapted to a technique that will reduce the
computational requirement and keep the data to a de-
sirable standard. However, the position of the vir-
tual sensor being restricted only to the barycenter of
CLOSER 2022 - 12th International Conference on Cloud Computing and Services Science
282

the physical sensors limits the problematization ap-
proach. In this sense, an alternative is to define the
point P from barycentric coordinates (u, v and w) in
relation to the triangle ∆ABC. It means that point P is
defined through the weighted average of the vertices
of the triangle with weights u, v and w, that is,
P =
uA + vB + wC
u + v + w
= (u : v : w). (4)
Therefore, the proposed technique moves the
barycenter to the P point of interest, defined by the
barycentric coordinate. Thus, it is possible to apply
multivariate interpolation (three linear interpolations)
based on the straight line from the angle that intersects
the opposite line.
Figure 2 demonstrates this process. In Figure 2
the point is defined inside the triangle. In Figure 2 the
first linear interpolation is performed. Figures 2 and 2
present the linear interpolation of the other two lines.
In the end, the three interpolated values are averaged
in order to estimate the value of the virtual sensor P.
4 EVALUATION AND
DISCUSSION
In this section, we evaluate the effectiveness of our
method in estimating the values of virtual sensors in
IoT environments. We start by describing our setup
(§4.2). We present the following experiments: (i)
we conduct a sensitivity analysis to find the best set
of parameters to the compared algorithms (§4.3), and
(ii) we assess the performance of our proposal against
other algorithms (§4.4).
4.1 Case Study: Smart Farms
Population growth and technological advances have
led the agribusiness sector to invest in new meth-
ods, processes, and innovative equipment to produce
more and better. In practice, the Smart Farm con-
cept demonstrates these advances in the sector, where
information and communication technology has be-
come strong allies of rural producers. The purpose
of adopting this new farm concept is to improve effi-
ciency and expand the sector’s productivity. The de-
mand for food has increased considerably, along with
the delivery speed (Memon et al., 2016). The Smart
Farm is based on the insertion of the countryside pro-
ducers and their activities in totally digital and in-
stantaneous information, enabling faster and more as-
sertive decision-making. For example, smart cameras
are already part of the farm’s reality. They have an
internal computer that can identify an image through
its format and colors and alert the farmer of possi-
ble risks to the plantation. When a threat appears, the
camera sends warning signals and messages via SMS,
email, and audible tones. With this, the producer can
avoid damage and take action quickly. Such threats
can be people wanting to steal supplies, equipments,
or even animals.
Another application is the use of drones in produc-
tion control and evaluation. The device, which can
be interconnected with a real-time image observation
system, has been used to detect pests, diseases, plant-
ing failures, and so on. From the top, the view of the
entire production is much broader and can be zoomed
in if necessary to observe some detail closely. By po-
sitioning the drone at the top, it is also possible to vi-
sualize the plant’s color, detect the presence of fungi,
and take photos to assist the agronomist in the analy-
sis. In addition, the drone also helps to monitor crop
development in real-time, making the analysis much
more effective than monitoring via car or motorcycle.
With the images captured, it is possible to carry out a
chronological analysis of the planting, helping devise
strategies for greater productivity, such as choosing
better soil collection points for analysis. Smart Farms
also may present built-in sensors at all stages of culti-
vation and in their equipment. In this way, when trav-
eling through the field, they can collect different types
of data, such as light levels, soil conditions, irriga-
tion, air quality, and climate. The farmer can analyze
them and make preventive decisions based on these
data. Streamlining repetitive tasks also became possi-
ble through robots programmed through their sensors.
They entered data to walk across the entire field and
work autonomously, weeding, watering, pruning, and
harvesting.
Sensors are often the smallest and most fragile
components of this intelligent environment. In most
cases, sensors are geographically distributed and ex-
posed to weather effects. It can lead to failures, and
consequently, impact productivity. Another factor
that this article addresses is those places that are dif-
ficult to access and where it is not possible (or chal-
lenging) to place a sensor to carry out the measure-
ment, for example, very high treetops or at the bot-
tom of dams. It can delay or even derail important
alerts for the production environment. This article
aims to overcome the issues addressed above and pro-
poses modeling and estimating values through virtual
sensors that will be consumed by edge devices. The
proposed modeling is performed empirically, based
on values obtained from physical sensors around the
point of interest (virtual sensor). Virtual sensors are
not new within the ICT area (e.g., intelligent agents
Multivariate Interpolation at the Edge to Infer Faulty IoT Sensor Metrics
283
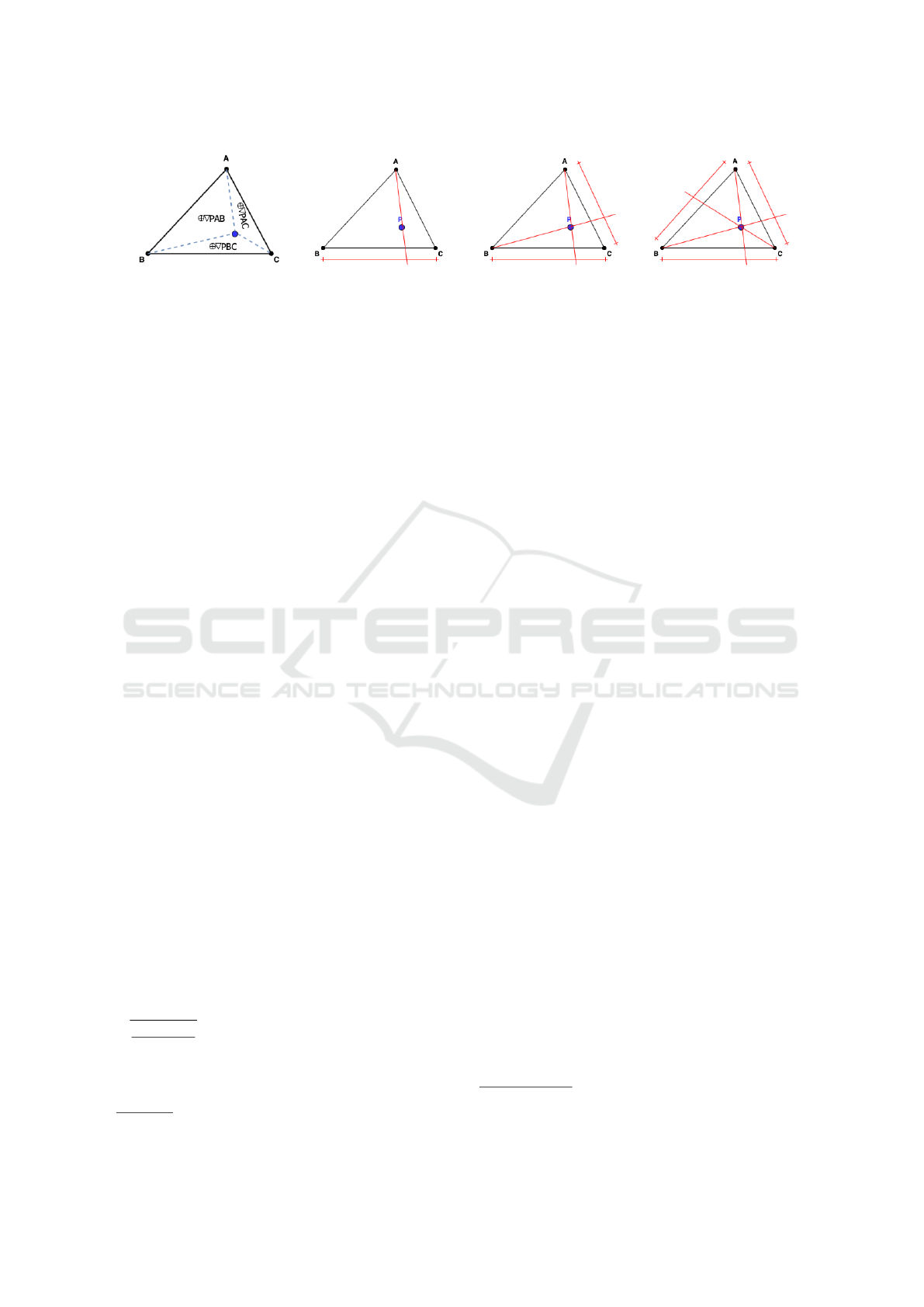
(a) (b) (c) (d)
Figure 2: Second case.
and monitoring software). Still, it has been emerging
as an option that fits very well in IoT environments.
4.2 Experimental Setup
We compare our method with two well-known
distance-based data imputation techniques, k-Nearest
Neighbors (kNN) (Fix and Hodges, 1989), and In-
verse Distance Weighting (IDW) (Franke, 1982), and
a naive triangulation-based algorithm. Both kNN and
IDW estimate values based on the values of nearby
elements (in our context, physical sensors) with avail-
able data. While kNN estimates the values of virtual
sensors based on the arithmetic mean of the values
of their k nearest neighbors, IDW weights the known
observations of the k nearest neighbors based on their
distance to the virtual sensor so that closer neighbors
get more influence on the inference. The naive trian-
gulation algorithm iteratively creates a mesh of trian-
gles using the Delaunay algorithm and uses the first
triangle it finds that surrounds the virtual sensor to es-
timate its value.
Our evaluation uses a real dataset with observa-
tions of 80 weather stations from the south region of
Brazil maintained by the National Institute of Mete-
orology (Inmet). Each weather station contains 8784
data points collected hourly during 2020 describing
temperature, atmospheric pressure, and relative air
humidity. According to INMET, this dataset is used
to drive strategic decisions in the country’s agriculture
sector. Table 2 presents statistical information about
the dataset. We intentionally omitted data from some
arbitrary weather stations in the dataset during the ex-
periments. After the tests, we compare estimated val-
ues from the evaluated techniques to the actual mea-
surements to assess the accuracy of inferences.
We evaluate the accuracy of compared techniques
based on two well-known error metrics: (i) Root
Mean Square Error (RMSE), which is given by
q
∑
n
i=1
( ˆy
i
−y
i
)
2
n
and measures the differences between
n predicted values ˆy and the expected values y based
on the square root of the average of squared er-
rors, and (ii) Mean Absolute Error (MAE), given by
∑
n
i=1
| ˆy
i
−y
i
|
n
, that measures the average of the abso-
lute errors. While both metrics help measure infer-
ences’ accuracy, a few large errors in a set of obser-
vations will increase the RMSE to a greater degree
than MAE, as it squares the differences before cal-
culating the average error. In our experiments, we
use MAE to account for the overall accuracy of the
techniques. At the same time, RMSE helps us iden-
tify the techniques’ ability to achieve steady results
while estimating the values of virtual sensors in dif-
ferent locations. We build a discrete-event simulator
that leverages object-oriented features of Python lan-
guage to mimic the behavior of weather stations from
the INMET dataset. We conducted the experiments
in a host machine with a quad-core Intel processor i7-
8650U@1.9GHz and 16GB of RAM running a Linux
Ubuntu 20.04.2 LTS (kernel 5.11.0-25-generic) and
Python 3.8.10. We assume that all of these algorithms
are present in the edge servers that collect the data
and can, in real-time, fill the missing sensor data gap
with data from virtual sensors. Our simulator and the
dataset used during the tests are publicly available in
our GitHub repository
1
.
4.3 Sensitivity Analysis
Before comparing the algorithms, we evaluate how
the number of neighbors k affects the performance
of distance-based algorithms (kNN and IDW). To this
aim, we execute these algorithms with different val-
ues of k, assessing their RMSE and MAE in the three
evaluated scenarios. As shown in Figures 3 and 4, k =
8 leads to the best results for both algorithms when
estimating the values of virtual sensors regarding at-
mospheric pressure and temperature, which have less
dispersed data (see the standard deviation in Table 2).
In these scenarios, narrowing the number of neighbor
sensors used to perform inferences affects the accu-
racy of algorithms as sensor values are more or less
uniformly distributed based on their geographical po-
sition. On the other hand, k = 32 was the best pa-
rameter for estimating global solar radiation. Such a
scenario comprises more sparsed data, which favors
1
https://github.com/paulosevero/virtual-sensors-
triangulation
CLOSER 2022 - 12th International Conference on Cloud Computing and Services Science
284
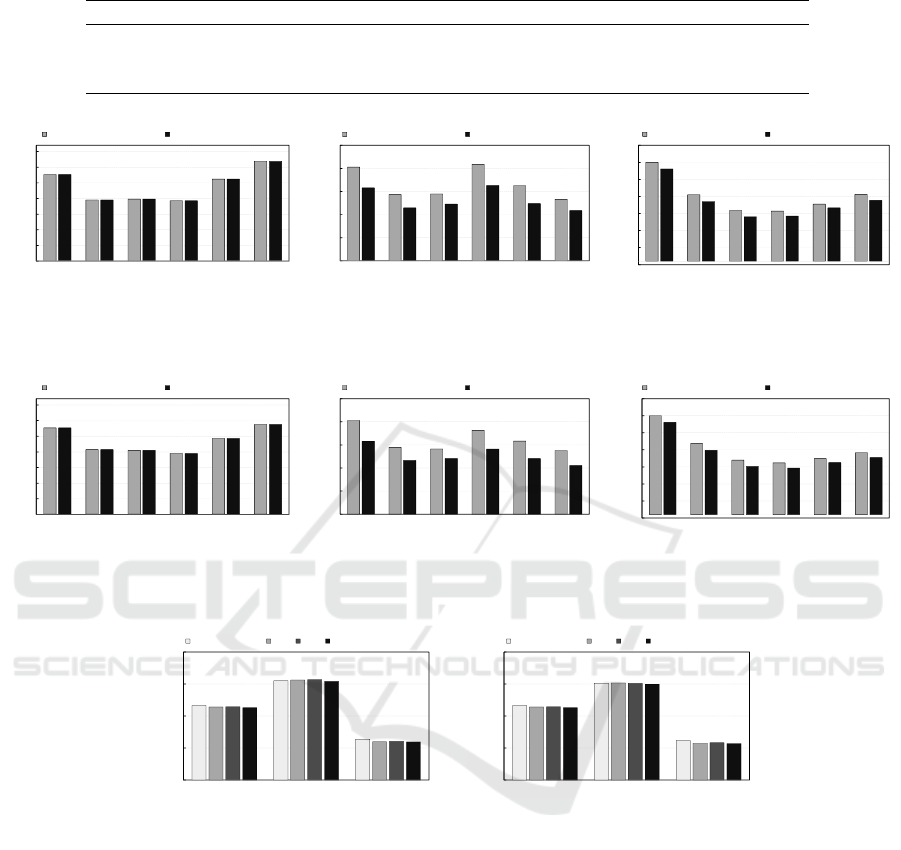
Table 2: Statistical information about the dataset.
Scenario Mean Standard Deviation Minimum Maximum
Temperature 13.9526 4.2081 -20.9 32.1
Atmospheric Pressure 960.8239 43.3078 811 1027.7
Global Solar Radiation 1467.0968 1111.4419 0 4806.6
27.69
19.54
19.82
19.30
26.21
31.91
27.69
19.54
19.82
19.30
26.21
31.91
0
5
10
15
20
25
30
35
1 2 4 8 16 32
Error
Number of Neighbors (k)
Root Mean Square Error (RMSE) Mean Absolute Error (MAE)
(a) Atmospheric Pressure
203
143
145
209
163
133
158
115
123
163
124
109
0
50
100
150
200
250
1 2 4 8 16 32
Error
Number of Neighbors (k)
Root Mean Square Error (RMSE) Mean Absolute Error (MAE)
(b) Global Solar Radiation
3.00
2.05
1.59
1.57
1.77
2.06
2.81
1.85
1.40
1.42
1.67
1.88
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
1 2 4 8 16 32
Error
Number of Neighbors (k)
Root Mean Square Error (RMSE) Mean Absolute Error (MAE)
(c) Temperature
Figure 3: Sensitivity analysis of k-Nearest Neighbors (kNN).
27.69
20.72
20.51
19.50
24.29
28.77
27.69
20.72
20.51
19.50
24.29
28.77
0
5
10
15
20
25
30
35
1 2 4 8 16 32
Error
Number of Neighbors (k)
Root Mean Square Error (RMSE) Mean Absolute Error (MAE)
(a) Atmospheric Pressure
203
145
141
181
158
138
158
117
121
141
120
106
0
50
100
150
200
250
1 2 4 8 16 32
Error
Number of Neighbors (k)
Root Mean Square Error (RMSE) Mean Absolute Error (MAE)
(b) Global Solar Radiation
3.00
2.18
1.70
1.62
1.74
1.92
2.81
1.98
1.52
1.47
1.63
1.77
0.00
0.50
1.00
1.50
2.00
2.50
3.00
3.50
1 2 4 8 16 32
Error
Number of Neighbors (k)
Root Mean Square Error (RMSE) Mean Absolute Error (MAE)
(c) Temperature
Figure 4: Sensitivity analysis of Inverse Distance Weighting (IDW).
21.26
128
1.89
19.30
133
1.57
19.50
138
1.62
18.24
122
1.56
0
1
10
100
1000
Atmospheric Pressure Global Solar Radiation Temperature
Root Mean Square Error
(RMSE)
Simple Triangulation kNN IDW Proposed Algorithm
(a) Root Mean Square Error (RMSE)
21.25
107
1.72
19.30
109
1.42
19.50
106
1.47
18.24
99
1.38
0
1
10
100
1000
Atmospheric Pressure Global Solar Radiation Temperature
Mean Absolute
Error
(MAE)
Simple Triangulation kNN IDW Proposed Algorithm
(b) Mean Absolute Error (MAE)
Figure 5: Accuracy results of the compared algorithms.
more neighbors during the inference of virtual sen-
sors.
4.4 Simulation Results
Looking at the results in Figure 5, we notice that the
error rates of all techniques grow more or less linearly
based on the degree of dispersion of data points of
the evaluated scenarios (atmospheric pressure, global
solar radiation, and temperature). Accordingly, all
strategies achieve higher accuracy when estimating
temperature and atmospheric pressure, as these sce-
narios have lower standard deviation than the global
solar radiation scenario. Among the compared meth-
ods, kNN and IDW were the most impacted by data
dispersion. They estimate the values of virtual sen-
sors based on the average values of k nearest sensors
with known data, which allows spread observations to
disturb their calculation. As such, kNN and IDW had
the worst results in terms of RMSE in global solar ra-
diation, as it presents the highest standard deviation
amongst the evaluated scenarios.
While kNN and IDW fall short on providing accu-
rate inferences about the global solar radiation of vir-
tual sensors, the triangulation-based methods manage
to get lower error rates by estimating the value of vir-
tual sensors based on reference points created with an
interpolation that is located closer to the virtual sen-
Multivariate Interpolation at the Edge to Infer Faulty IoT Sensor Metrics
285

sor than the physical sensors in the environment. The
main reason behind the superior results of the pro-
posed method against the Simple Triangulation relies
on which triangle is used to estimate the value of vir-
tual sensors. While Simple Triangulation picks the
first triangle it finds surrounding the virtual sensor, the
proposed method goes further and looks for the trian-
gle comprised of physical sensors closer to the virtual
sensor. In that way, the proposed method manages
to get more accurate linear interpolations, resulting in
superior results (RMSE 4.87% lower than Simple Tri-
angulation).
When estimating the temperature of virtual sen-
sors, Simple Triangulation exhibited the worst re-
sults, ignoring the distance between the virtual sen-
sor and the points used in the triangulation. On the
other hand, the lower data dispersion in the dataset fa-
vored IDW and kNN that managed to get the third and
second-best results. Once again, the proposed method
achieved gains of 0.7% and 2.9% in terms of RMSE
and MAE compared to the second-best solution (in
this case, kNN) by inferring the value of virtual sen-
sors based on interpolated values of nearby reference
points within the triangles it generated.
4.5 Potential Impact on Smart Farms
The applicability of virtual sensors on smart farms al-
lows the analysis of data referring to a target without
direct contact with it through mathematical resources
based on real optical-electronic sensors. In addition,
virtual sensors will enable the creation and filling of
reliable data in maps of areas with no real sensors.
It is vitally essential for monitoring sparse areas and
over metrics measured by geographically remote de-
vices. Tools that use virtual sensors facilitate data
collection in the regions that are difficult to access
and collaborate with the monitoring of dynamic pro-
cesses in nature. Several advantages make IoT-Edge
an important issue, especially in the current context
of society, as it can show geographic and historical
data relating to natural and social spaces. In addi-
tion, we currently discuss environmental preservation
as a global agenda in various educational and political
events around the globe and used in the monitoring
and analysis of natural resources. Among the most
relevant areas in which virtual sensors can positively
affect production.
One of the leading practices of virtual sensors is
associated within its use in Agriculture, as this tech-
nology has great potential, as it is possible to obtain
various information such as estimated planted area,
plant and crop health, pest detection in the planta-
tion, and observation of the production process, plant
counting, soil cover analysis, etc. The virtual sen-
sor can become one of the main tools of precision
agriculture because monitoring agricultural produc-
tion can provide productivity results never achieved
and reduce several operating costs. In addition, vir-
tual sensors can be used to analyze and monitor risk
areas, enabling the control of hurricanes, erosion,
and floods through satellite images and geoprocessing
techniques and the meteorological monitoring of the
earth and follow natural events. Through aerial im-
ages, it is also possible to assess the impacts of natural
disasters and allow strategies for prevention, combat,
and rescue. For example, drones with multispectral
cameras can identify hot spots in cave-in zones and
indicate survivors.
For forest areas, virtual sensors can be used to an-
alyze data regarding the distribution of forest areas,
advance deforestation activities, calculate volumes,
identify species, etc. Considering how relevant the
theme of environmental preservation has become in
recent years, especially in the world’s political en-
vironment, virtual sensors can become a fundamen-
tal tool for decision-making in the management and
management of natural resources, such as analyzing
and monitoring water resources, calculating and es-
timate physical and chemical parameters of soil and
water, determine the climatic characteristics of a re-
gion, identify critical points in anthropized areas, de-
termine the region’s relief, observe the behavior of
fauna in a region of interest, etc.
5 CONCLUSION AND FUTURE
WORK
Virtual sensors have internally implemented a model
with secondary input variables that can be measured
and output the variable of interest inferred. A virtual
sensor can infer values from positions where there
are no real sensors or where real sensors are inactive.
In this work, we proposed new modeling and imple-
mentation of virtual sensors based on the real sensor
values consumed by edge servers. The results of our
model were superior in terms of accuracy compared to
proposals in the literature based on IoT-Edge ecosys-
tems. To test our proposal, we used a well-know IoT
environment, a Smart Farm scenario.
Based on simulations using real-world traces, we
observe that our method can estimate the value of vir-
tual sensors with a high degree of accuracy, reducing
the RMSE and MAE by up to 5.5% and 5.8%, re-
spectively, compared to existing approaches. In fu-
ture work, we intend to incorporate a multivariate
technique that uses multiple correlated variables from
CLOSER 2022 - 12th International Conference on Cloud Computing and Services Science
286

nearby locations to estimate the value of virtual sen-
sors.
ACKNOWLEDGEMENT
This work was financed in part by the Coordenac¸
˜
ao
de Aperfeic¸oamento de Pessoal de N
´
ıvel Superior -
Brasil (CAPES) – Finance Code 001. Also, this work
was partially supported by Conselho Nacional de
Desenvolvimento Cient
´
ıfico e Tecnol
´
ogico – CNPq
– 313111/2019-7. This work also received fund-
ing from S
˜
ao Paulo Research Foundation (FAPESP)
– 2018/23092-1, 2020/05183-0, 2020/05115-4; and
Rio Grande do Sul Research Foundation (FAPERGS)
– 19/2551-0001266-7, 19/2551-0001224-1, 19/2551-
0001689-1, 21/2551-0000688-9.
REFERENCES
Asy’ari, M. K., Musyafa’, A., Noriyati, R. D., and Indri-
awati, K. (2019). Soft sensor design of solar irra-
diance using multiple linear regression. In 2019 In-
ternational Seminar on Intelligent Technology and Its
Applications (ISITIA), pages 56–60.
Chew, L. P. (1989). Constrained delaunay triangulations.
Algorithmica, 4(1-4):97–108.
Cristaldi, L., Ferrero, A., Macchi, M., Mehrafshan, A., and
Arpaia, P. (2020). Virtual sensors: a tool to improve
reliability. In 2020 IEEE International Workshop on
Metrology for Industry 4.0 IoT, pages 142–145.
Erturk, M. A. and Vollero, L. (2020). Gsp for virtual sen-
sors in ehealth applications. In 2020 IEEE 44th An-
nual Computers, Software, and Applications Confer-
ence (COMPSAC), pages 1683–1688.
Fanti, M. P., Mangini, A. M., Roccotelli, M., Nolich, M.,
and Ukovich, W. (2018). Modeling virtual sensors for
electric vehicles charge services. In 2018 IEEE Inter-
national Conference on Systems, Man, and Cybernet-
ics (SMC), pages 3853–3858.
Fix, E. and Hodges, J. L. (1989). Discriminatory analy-
sis. nonparametric discrimination: Consistency prop-
erties. International Statistical Review/Revue Interna-
tionale de Statistique, 57(3):238–247.
Flores, H., Hui, P., Tarkoma, S., Li, Y., Anagnostopoulos,
T., Kostakos, V., Luo, C., and Su, X. (2018). Sen-
sorclone: A framework for harnessing smart devices
with virtual sensors. In Proceedings of the 9th ACM
Multimedia Systems Conference, MMSys ’18, page
328–338, New York, NY, USA. Association for Com-
puting Machinery.
Franke, R. (1982). Scattered data interpolation: tests
of some methods. Mathematics of computation,
38(157):181–200.
Gupta, A. and Mukherjee, N. (2016). Rationale behind the
virtual sensors and their applications. In 2016 Interna-
tional Conference on Advances in Computing, Com-
munications and Informatics (ICACCI), pages 1608–
1614.
Ilyas, E. B., Fischer, M., Iggena, T., and T
¨
onjes, R. (2020).
Virtual sensor creation to replace faulty sensors us-
ing automated machine learning techniques. In 2020
Global Internet of Things Summit (GIoTS), pages 1–6.
Liu, L., Kuo, S. M., and Zhou, M. (2009). Virtual sensing
techniques and their applications. In 2009 Interna-
tional Conference on Networking, Sensing and Con-
trol, pages 31–36.
Mahmoudi, C., Mourlin, F., and Battou, A. (2018). Formal
definition of edge computing: An emphasis on mo-
bile cloud and iot composition. In 2018 Third Inter-
national Conference on Fog and Mobile Edge Com-
puting (FMEC), pages 34–42.
Memon, M. H., Kumar, W., Memon, A., Chowdhry, B. S.,
Aamir, M., and Kumar, P. (2016). Internet of things
(iot) enabled smart animal farm. In 2016 3rd Inter-
national Conference on Computing for Sustainable
Global Development (INDIACom), pages 2067–2072.
Pait, F. M. (2018). The barycenter method for direct opti-
mization. arXiv preprint arXiv:1801.10533.
Shao, W., Chen, S., and Harris, C. J. (2018). Adaptive soft
sensor development for multi-output industrial pro-
cesses based on selective ensemble learning. IEEE
Access, 6:55628–55642.
S
´
anchez-Molina, J., Rodr
´
ıguez, F., Guzm
´
an, J., and
Ram
´
ırez-Arias, J. (2015). Water content virtual sen-
sor for tomatoes in coconut coir substrate for irriga-
tion control design. Agricultural Water Management,
151:114–125. New proposals in the automation and
remote control of water management in agriculture:
agromotic systems.
Sutarya, D. and Mahendra, A. (2015). Virtual sensor for
time series prediction of hydrogen safety parameter
in degussa sintering furnace. In 2015 2nd Interna-
tional Conference on Information Technology, Com-
puter, and Electrical Engineering (ICITACEE), pages
81–86.
Tong, W. and Zewen, D. (2017). Soft sensor modeling
method of dynamic liquid level based on improved ks
algorithm. In 2017 29th Chinese Control And Deci-
sion Conference (CCDC), pages 6510–6515.
Wang, Z., Zhao, Z., Li, D., and Cui, L. (2015). Data-
driven soft sensor modeling for algal blooms moni-
toring. IEEE Sensors Journal, 15(1):579–590.
Yuan, X., Zhou, J., Huang, B., Wang, Y., Yang, C., and
Gui, W. (2020). Hierarchical quality-relevant feature
representation for soft sensor modeling: A novel deep
learning strategy. IEEE Transactions on Industrial In-
formatics, 16(6):3721–3730.
Zhang, M.-Z., Wang, L.-M., and Xiong, S.-M. (2020). Us-
ing machine learning methods to provision virtual sen-
sors in sensor-cloud. Sensors, 20(7).
Multivariate Interpolation at the Edge to Infer Faulty IoT Sensor Metrics
287
